Bayesian projection of life expectancy accounting for the HIV/AIDS epidemic

Abstract

Background

While probabilistic projection methods for projecting life expectancy exist, few account for covariates related to life expectancy. Generalized HIV/AIDS epidemics have a large, immediate negative impact on the life expectancy in a country, but this impact can be mitigated by widespread use of antiretroviral therapy (ART). Thus, projection methods for countries with generalized HIV/AIDS epidemics could be improved by accounting for HIV prevalence, the future course of the epidemic, and ART coverage.

Methods

We extend the current Bayesian probabilistic life expectancy projection methods of Raftery et al. (2013) to account for HIV prevalence and adult ART coverage in countries with generalized HIV/AIDS epidemics.

Results

We evaluate our method using out-of-sample validation. We find that the proposed method performs better than the method that does not account for HIV prevalence or ART coverage for projections of life expectancy in countries with a generalized epidemic, while projections for countries without an epidemic remain essentially unchanged.

Conclusions

In general, our projections show rapid recovery to pre-epidemic life expectancy levels in the presence of widespread ART coverage. After the initial life expectancy recovery, we project a steady rise in life expectancy until the end of the century.

Contribution

We develop a simple Bayesian hierarchical model for long-term projections of life expectancy while accounting for HIV/AIDS prevalence and coverage of ART. The method produces well-calibrated projections for countries with generalized HIV/AIDS epidemics up to 2100 while having limited data demands.

1. Introduction

Probabilistic projections of mortality measures are important for many applications, including population projection and pension and healthcare planning. Until recently, most projections of mortality measures were deterministic, although the United Nations (UN) has recently started to base its official projections of mortality on probabilistic methods. Most projections, deterministic or probabilistic, do not incorporate cause-of-death information or other covariates.

Lee and Carter (1992) developed a method for projecting a mortality measure probabilistically. The Lee–Carter method projects age-specific mortality rates and is widely used today. It requires at least three time periods of age-specific death rates, an amount of data that is not available in many countries. The method assumes that the logarithm of the age-specific death rates will increase linearly in the future, which may not be optimal for long-term projections (Lee and Miller 2001). Alho and Spencer (1985) developed a method for incorporating uncertainty in population forecasting, addressing fertility, mortality and migration separately. However, the authors state this method is designed to be used for shortterm projections. Girosi and King (2008) proposed a Bayesian method for smoothing age-specific death rates over both age and time. Even though this method allows for the incorporation of covariates, it has been shown to perform well only for countries with good vital registration data. Like the Lee–Carter method, the Girosi and King (2008) method assumes a constant rate of increase. Lutz, Sanderson, and Scherbov (1998) developed an expert-based method for probabilistic projections of population that incorporates subjective probabilistic projections for several demographic measures, including life expectancy.

Raftery et al. (2013) and Raftery, Lalic, and Gerland (2014) presented a Bayesian hierarchical model (BHM) for projecting male and female life expectancy probabilistically and jointly for all countries of the world to 2100, and the UN now uses this method for its official mortality projections and as an input for its official population projections (United Nations 2015). We extend the model in Raftery et al. (2013) to include covariate information about generalized HIV epidemic prevalence and coverage of antiretroviral therapy (ART) in each country. A country is said to have a generalized HIV/AIDS epidemic when HIV prevalence is greater than 1% in the general population and is not concentrated in at-risk subgroups. While there are many diseases that have a high impact on mortality in a given country, the generalized HIV epidemic is unusual in that it dramatically increases age-specific mortality rates at prime adult ages. Its demographic impact is therefore different from that of other diseases, which tend primarily to affect mortality rates for very young and/or older ages.

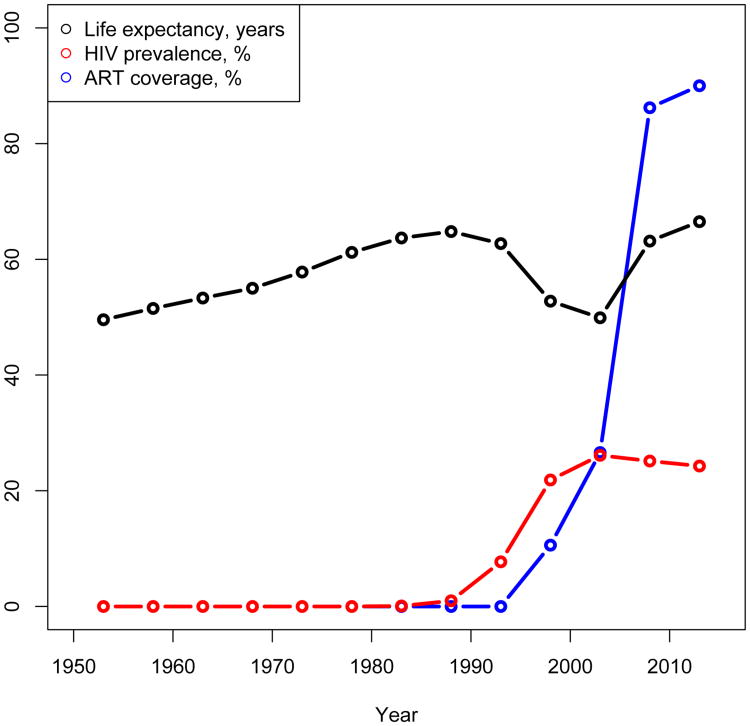
Figure 1 shows the rise of the HIV epidemic and the corresponding evolution of life expectancy at birth in Botswana. There was a sharp lowering of life expectancy with the rise of the epidemic and then a rapid recovery to pre-epidemic levels following the widespread introduction of ART.

Figure 1. Life expectancy at birth (black), HIV prevalence (red) and ART coverage (blue) for Botswana from 1950-1955 to 2005-2015.

To incorporate covariate information into a probabilistic projection model, we must also have a method for projecting the covariate of interest into the future. UNAIDS developed the Spectrum/EPP methodology for projecting HIV prevalence and demographic measures, including life expectancy at birth, while accounting for HIV prevalence and ART coverage, among other things (Stover, Brown, and Marston 2012; Stanecki, Garnett, and Ghys 2012; Futures Institute 2014). The method is quite complicated and requires fine-grained data on a number of demographic and health measures for each country. It is recommended for reconstructing the HIV epidemic, including the time of onset, in a particular country and for projecting the epidemic up to five years into the future. It is not designed for long-term HIV prevalence projections, which in turn are important for long-term population projections (UNAIDS 2014: 9).

We use a version of the EPP package for projections of HIV prevalence to 2100 written in R (Brown et al. 2010). We develop a model for projecting life expectancy at birth while accounting for HIV prevalence and ART coverage that is simpler and more practical for long-term projections than Bayesian probabilistic methods.

2. Methodology

2.1 Data

We use estimates of past and present female life expectancy at birth from the United Nations World Population Prospects (WPP) 2015 Revision (United Nations 2015) for 201 countries. The UN produces estimates of past and present period life expectancy at birth and age-specific mortality rates by five-year periods and five-year age groups; these are updated every two years. There are estimates for each country of the world for each five-year period from 1950 to 2015. We do not use life expectancy inputs for Cambodia and Rwanda from the time periods of the genocides in these countries.

To fit the model, we use UNAIDS estimates of past HIV prevalence and ART coverage for 40 countries with generalized epidemics. We use 1,000 trajectories of HIV prevalence, using the same assumptions as Brown et al. (2010). Additionally, we use a single deterministic trajectory of ART coverage from UNAIDS in the projection stage. ART is relatively new in many generalized epidemic countries, with the first coverage estimates available for the time period 2000–2005. Data relating to coverage tends to be noisy. We code HIV prevalence as zero for all countries not experiencing a generalized HIV epidemic.

2.2 Review of joint probabilistic projections of male and female life expectancy

Our methodology builds on the Bayesian hierarchical model for joint probabilistic projection of female and male life expectancy used by the UN (Raftery et al. 2013; Raftery, Lalic, and Gerland 2014), which proceeds as follows: First, we estimate the Bayesian hierarchical model for female life expectancy using Markov chain Monte Carlo (MCMC), then we make probabilistic projections of female life expectancy from the present day to 2100. We then make projections of male expectancy based on the projected values of female life expectancy (Raftery, Lalic, and Gerland 2014). The model provides a way for projection for one country to be improved using information from other countries.

At the lowest observation level, the Bayesian hierarchical model for female life expectancy at birth is

$$\mathrm{\Delta }{\ell }_{c,t}\equiv {\ell }_{c,t+1}-{\ell }_{c,t}=g({\ell }_{c,t}|{\theta }^{(c)})+{\epsilon }_{c,t+1},{\epsilon }_{c,t}~N(0,{(\omega f({\ell }_{c,t}))}^2),$$ (1)

where ℓ_c,t is the female life expectancy at birth for country c in time period t, g(·|θ^(c)) is the expected five-year gain in life expectancy, modeled as a double logistic function of current life expectancy and governed by country-specific parameters, θ^(c), ε_c,t+1 is a random perturbation around the expected gain, and f(ℓ_c,t) is a smooth function of life expectancy. The double logistic function for country c is

$$g({\ell }_{c,t}|{\theta }^{(c)})=\frac{k^c}{1+exp(-\frac{A_1}{{\mathrm{\Delta }}_2^c}({\ell }_{c,t}-{\mathrm{\Delta }}_1^c-A_2{\mathrm{\Delta }}_2^c))}+\frac{z^c-k^c}{1+exp(-\frac{A_1}{{\mathrm{\Delta }}_4^c}({\ell }_{c,t}-{\sum }_{i=1}^3{\mathrm{\Delta }}_i^c-A_2{\mathrm{\Delta }}_4^c))},$$

where ${\theta }^{(c)}=({\mathrm{\Delta }}_1^c,{\mathrm{\Delta }}_1^c,{\mathrm{\Delta }}_1^c,{\mathrm{\Delta }}_1^c,k^c,z^c)$, A₁, A₂ are constants. The parameter z^c is the expected country-specific asymptotic five-year gain in life expectancy. The other parameters govern the maximum value and the pace of rise and fall of expected five-year gains in life expectancy.

At the second level of the model, the country-specific parameters θ^(c) are assumed to be drawn from the following truncated normal-world distributions:

$$\begin{array}{c}{\mathrm{\Delta }}_i^c|{\sigma }_{{\mathrm{\Delta }}_i}\stackrel{\text{iid}}{~}{\text{Normal}}_{[0,100]}({\mathrm{\Delta }}_i,{\sigma }_{{\mathrm{\Delta }}_i}^2),i=1,\cdots ,4,\\ k^c|{\sigma }_k\stackrel{\text{iid}}{~}{\text{Normal}}_{[0,10]}(k,{\sigma }_k^2)\\ z^c|{\sigma }_z\stackrel{\text{iid}}{~}{\text{Normal}}_{[0,0.653]}(z,{\sigma }_z^2).\end{array}$$

The truncation of the normal distribution for z^c is informed by observed gains in maximum age at death among countries with the highest life expectancies (Wilmoth et al. 2000). At the third, top level of the model, hyperprior distributions are specified for the world parameters θ = (Δ₁, Δ₂, Δ₃, Δ₄, k, z, ω). The hyperpriors are proper and diffuse. See Raftery et al. (2013) for more details.

The Bayesian hierarchical model is estimated using MCMC via Metropolis–Hastings, Gibbs sampling, and slice sampling steps, yielding a joint posterior distribution of all the model parameters (Raftery et al. 2013). The smooth function f(ℓ_c,t), specifying how the variance of the perturbations depends on life expectancy, is estimated separately and is treated as known in the MCMC algorithm. Note that the overall variance parameter ω is not treated as known and is estimated by the MCMC algorithm.

Once the model has been estimated, projections of life expectancy are made based on each posterior sample of θ^(c) and a random perturbation, ε_c,t+1, drawn from a N(0, (ωf(ℓ_c,t))²) distribution, where ω is drawn from the posterior distribution. After female projections of life expectancy are made, projections of male life expectancy, ${\ell }_{c,t}^m$, are made by modeling the gap between the two (Raftery, Lalic, and Gerland 2014).

2.3 Probabilistic projections of life expectancy accounting for HIV prevalence

We expand the BHM to account for generalized HIV/AIDS epidemics by adding a co-variate to the observation level of the model. To define the covariate, let HIV_c,t and ART_c,t be the HIV prevalence and ART coverage in percent of country c at time period t, respectively. Then the quantity HnA_c,t = HIV_c,t × (100 – ART_c,t) can be viewed as approximating the percentage of the population who are infected but do not receive ART therapy. The covariate we found to best predict change in life expectancy was the change in this quantity, namely ΔHnA_c,t–1 = HnA_c,t – HnA_c,t–1. Our expanded observation equation is then

$$\mathrm{\Delta }{\ell }_{c,t}=g({\ell }_{c,t}|{\theta }^{(c)})+{\beta }_{HnA}\mathrm{\Delta }Hn{A}_{c,t-1}+{\epsilon }_{c,t+1}.$$ (2)

The parameter β_HnA is constant across countries and is estimated by MCMC along with the other parameters of the Bayesian hierarchical model. It has a diffuse prior distribution, chosen to be proper (i.e., a valid probability distribution) but spread out enough that reasonable changes in it would have little impact on the final inference. Specifically, the prior distribution of β_HnA that we use is $N(\mathrm{0,0.25}\times \frac{\mathit{\text{Var}}(\mathrm{\Delta }{\ell }_{c,t})}{\mathit{\text{Var}}(\mathrm{\Delta }Hn{A}_{c,t})})=N({\mathrm{0,0.83}}^2)$ (i.e., with standard deviation 0.83, or variance 0.83² = 0.69), where the prior variance is determined by the sample variances of observed changes in life expectancy and observed changes in HnA_c,t. The posterior distribution of β_HnA is N(−0.64, 0.17²) and is estimated with the other parameters in the MCMC via Gibbs sampling updates.

After estimation, we project female life expectancy in the same manner as outlined in Section 2.2. However, we make a projection based on each posterior sample of (θ^(c), β_Hna) and a random perturbation. We account for uncertainty in the HIV trajectories by using 1,000 yearly trajectories of HIV projections from EPP (Brown et al. 2010). For each country c and year t, we find the median, z_t,c, of projected adult HIV prevalence output from EPP. We use a single UNAIDS deterministic projection to 2100 as a baseline reference, and we construct 1,000 trajectories from the single UNAIDS trajectory by using 1,000 multipliers of the form $\frac{z_{t,c}^k}{z_{t,c}}$, at each time point t for k = 1, …, 1000, where $z_{t,c}^k$ is prevalence at time t in country c in the k-simulated trajectory. Thus the UNAIDS deterministic trajectory serves as the median trajectory of HIV prevalence to 2100, and the EPP trajectories determine the uncertainty. We construct five-year averages from the yearly trajectories to be used in the projection stage. From these, we use a single deterministic trajectory of ART coverage to compute 1,000 trajectories of ΔHnA_c,t for all countries. We sample from the 1,000 trajectories of ΔHnA_c,t with equal probability to be used in the projection stage.

For the country of Liberia, the prevalence is projected to be so low in the future (close to 0) that the multipliers are unrealistically large. We therefore treated it slightly differently. For this country we calculated $z_{t,c}^k-z_{t,c}$ for each time point t. We then added this distance to the UNAIDS trajectory to yield 1,000 trajectories with the UNAIDS trajectory as the median and borrowed the uncertainty from the EPP trajectories.

The methods of Raftery et al. (2013) and Raftery, Lalic, and Gerland (2014) did not use the generalized HIV epidemic countries in model estimations. By contrast, our estimation of the BHM does include these countries. The covariate values are set to zero for nonepidemic countries. Thus, the estimation of country-specific parameters and the projection of life expectancy for nonepidemic countries change negligibly; we are effectively fitting the model in (1) for these countries. For epidemic countries, the model in (2) allows us to adjust for the effects of HIV on life expectancy in the linear term and to interpret g(·|θ^(c)) as the expected five-year gain in life expectancy in the absence of the epidemic. Even though high HIV prevalence takes a big toll on a country's life expectancy at birth in the absence of ART, ART extends an infected person's life substantially. Several epidemiological case studies show that HIV-positive individuals have nearly normal life expectancy when treated with ART (Mills et al. 2011; Johnson et al. 2013). In a country where ART coverage is high, a generalized HIV epidemic affects life expectancy like a chronic disease would (Deeks, Lewin, and Havlir 2013).

Similarly to Raftery et al. (2013), the distribution of the random perturbations in the projection stage is ε_c,t+1 ∼ N(0, (ω × f(ℓ_c,t,i)²), where ω is a model parameter, f(ℓ_c,t,i) is a smooth function, and i is an indicator of generalized HIV epidemic. To estimate f(ℓ_c,t,i), we fit the model in (2) using the same function f(ℓ_c,t) as used by Raftery et al. (2013). Then, using mean posterior estimates of g(ℓ_c,t|θ^(c)), we projected life expectancy forward from 1950–1955 to the 2010–2015 period using only the mean model in (2) with no random perturbations. We then calculated absolute residuals for these projections. We fit LOWESS curves to the absolute residuals for nonepidemic countries and for epidemic countries separately. A LOWESS curve fits a smooth curve to points using weighted least squares in estimation.

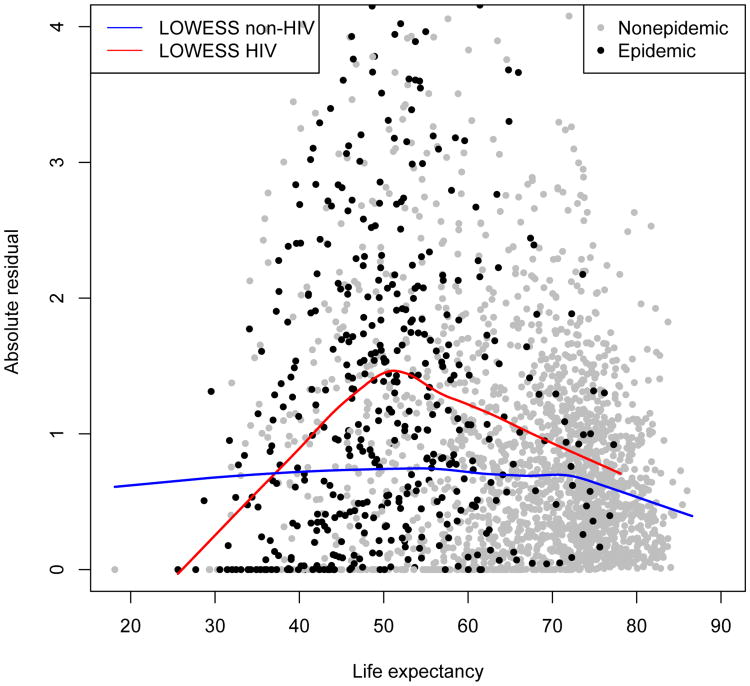
These curves can be seen in Figure 2. The black dots represent the absolute residuals from HIV countries, and the red LOWESS curve is fit to these points. The gray dots represent the absolute residuals from nonepidemic countries, and the blue curve is fit to these points. Here one can see that the countries experiencing a generalized epidemic have more variability than the nonepidemic countries. This variability is propagated into the future for epidemic countries. For nonepidemic countries, f(ℓ_c,t,i=nonHIV) is the blue curve in Figure 2. For epidemic countries f(ℓ_c,t,i=HIV) is the maximum of the blue and red curves up to the highest observed life expectancy for an HIV country to date, namely 78.1. For projected female life expectancies above 78.1 years, we use the blue curve plus a constant that is equal to the vertical difference between the red and blue curves at 78.1 years.

Figure 2. Estimating the variance in the model.

Note: The black dots represent absolute residuals for epidemic countries; the grey dots represent absolute residuals for nonepidemic countries. The blue line is the LOWESS fit to the nonepidemic residuals. The red line is the LOWESS fit to the epidemic residuals.

2.4 Model validation

We performed predictive out-of-sample validation to assess our model. First, we fit the model in (2) using data from 1950–1955 up to 2000–2005 and projected female life expectancy for the time periods 2005–2010 and 2010–2015. We also fit the model in (2) using data from 1950–1955 up to 2005–2010 and projected female life expectancy for the time period 2010–2015.

Table 1 presents our results. The first column designates the set of countries for which the metrics have been calculated. Note that although the calibration of predictive intervals is designed to be nominal for all countries, we include the subset of HIV countries for more detail. The second and third columns reflect the period of data used to train and validate the model, respectively. The fourth column contains the number of countries for which the subsequent calibration metrics are calculated.

Table 1. Predictive validation results for female life expectancy.

Countries	Training period	Test period	n	Model	MAE	Coverage
						80%	95%
HIV	1950–2005	2005–2015	69	No covariates	3.47	0.49	0.58
				ΔHnA	2.29	0.71	0.87
	1950–2005	2005–2010	40	No covariates	2.40	0.53	0.63
				ΔHnA	2.22	0.68	0.83
	1950–2005	2010–2015	29	No covariates	4.95	0.45	0.52
				ΔHnA	2.39	0.76	0.93
	1950–2010	2010–2015	29	No covariates	2.24	0.59	0.62
				ΔHnA	1.74	0.83	0.97
All	1950–2005	2005–2015	390	No covariates	1.15	0.83	0.91
				ΔHnA	0.94	0.88	0.96
	1950–2005	2005–2010	201	No covariates	0.84	0.85	0.92
				ΔHnA	0.81	0.90	0.96
	1950–2005	2010–2015	189	No covariates	1.49	0.80	0.91
				ΔHnA	1.09	0.86	0.97
	1950–2010	2010–2015	189	No covariates	0.74	0.84	0.91
				ΔHnA	0.66	0.89	0.97

There were 12 countries for which no new data became available between the publication of the 2012 UN estimates in WPP 2012 (United Nations 2013) and the 2015 UN estimates in WPP 2015 (United Nations 2015). Hence, the WPP 2015 life expectancy estimate for the time period 2010–2015 is actually the projection of life expectancy for this period from the WPP 2012. As such, there is no observed life expectancy for these countries for the time period 2010–2015, and so we excluded these countries in this time period from the validation exercise. In the fifth column, covariates refers to the model in (1), and ΔHnA refers to the model in (2).

The last three columns contain our metrics. The mean absolute error (MAE) is calculated as

$$\frac{1}{n}\sum _{c\in \mathcal{C}}\sum _{t\in \mathcal{T}}|{\widehat{\ell }}_{c,t}-{\ell }_{c,t}|,$$ (3)

where ℓ̂_c,t is the median projection of female life expectancy for country c in time period t. In (3), 𝒞 is the set of countries involved in calculating the MAE (either the HIV countries or all countries), 𝒯 is the set of five-year time periods involved as shown in the third column, and n is the number of country–time period combinations as shown in the fourth column. The last two columns show the proportion of countries whose 80% and 95% posterior predictive intervals contain the observed life expectancy in the validation period of interest.

In all the out-of-sample scenarios, we saw substantial improvements in coverage for HIV countries after accounting for HIV prevalence and ART coverage. We broke down the two-period out-of-sample exercise into the two projection periods to get more detailed information about the HIV countries. In 2005–2010, the model with no covariates missed 15 out of 40 HIV countries at the 95% level. When we accounted for HIV prevalence and ART coverage, the number of HIV countries missed went down by over half, to only 7 at the 95% level. For 2010–2015, the model with no covariates missed 14 out of 29 HIV countries at the 95% level, while accounting for HIV prevalence and ART coverage reduced this to only two HIV countries in the time period 2010–2015. In the leave-two-time-periods-out validation exercise, we saw a decrease in MAE for the HIV countries in every case, while the MAE remained unchanged for the non-HIV countries. For the non-HIV countries, the addition of the covariate in the model in (2) changed coverage negligibly.

When fitting the model using data from 1950–1955 up to 2005–2010 and projecting female life expectancy for 2010–2015, we also saw improvements. Our coverage was much closer to the target nominal proportion for HIV countries after accounting for HIV prevalence and ART coverage. We missed 11 HIV countries out of 29 in the model with no covariates but only one HIV country after accounting for the HIV epidemic. The MAE also decreased when accounting for HIV prevalence and ART coverage.

Predictive validation results for male life expectancy are shown in Table 2 in Appendix B, and the conclusions are broadly similar.

The current method used by the UN to project life expectancy in the presence of the HIV epidemic is the Spectrum/EPP package (Futures Institute 2014; Stanecki, Garnett, and Ghys 2012; Stover, Brown, and Marston 2012). However, Spectrum is a complicated method with heavy data demands and is intended only for short-term projections up to five years into the future. Therefore, an important question is whether our simpler method can produce short-term projections similar to those of the more complex Spectrum method.

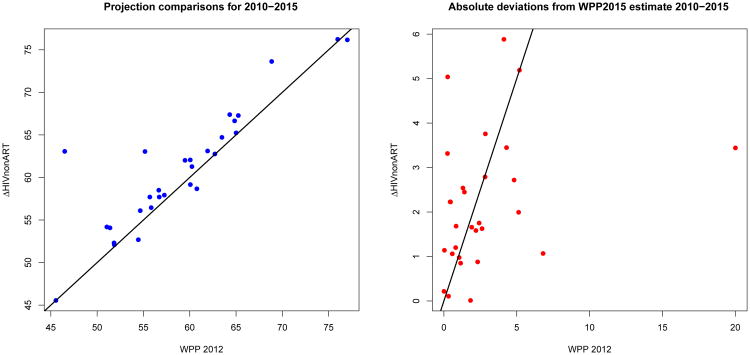
To answer this, we fit our model (2) using WPP 2012 estimates of female life expectancy from 1950–1955 up to 2005–2010 (United Nations 2013). Then we projected female life expectancy to 2010–2015. We compared the projections from our simpler model designed to make long-term projections to the WPP 2012 projection for 2010–2015 made using Spectrum. In the left panel of Figure 3, we see that the five-year projections from our simpler method are similar to the projections from the more complicated Spectrum. In fact, the correlation between the projections from our proposed model and those published in WPP 2012 is 0.89.

Figure 3. Comparison between short-term projections in WPP 2012 using Spectrum, and our simpler method.

Note: Left: On the x-axis are projections of female life expectancy in 2010–2015 produced using Spectrum and published in WPP 2012. On the y-axis are projections of female life expectancy in 2010–2015 produced by fitting the model in (2) with WPP2012 data up to 2005–2010. The projections are mostly similar and remain close to the y = x line. Right: This figure shows the absolute deviations of WPP 2012 female life expectancy projections for 2010–2015 from the WPP 2015 estimates on the x-axis, and the absolute deviations of projections using (2) from the WPP 2015 estimates on the y-axis. Overall they are similar, with one extreme improvement using (2) for the country of Botswana.

The right panel of Figure 3 shows the absolute deviation from the WPP 2015 estimate of female life expectancy in 2010–2015 for the projections published in WPP 2012 on the x axis and for our projections on the y axis. The WPP 2012 projections have a mean absolute error of 2.70 years using the WPP 2015 estimate for comparison. The projections produced with the model in (2) have a mean absolute error of 2.17 years.

The large outlier in the right panel of Figure 3 is the country of Botswana: it corresponds to the largest deviation seen in the left panel of Figure 3. Botswana has the highest HIV prevalence in the world, at 24.3% in 2010–2015 and has seen a recent scale-up of ART coverage. The boost in ART coverage yielded a rapid recovery in life expectancy of nearly 20 years from the WPP 2012 estimate for the 2005–2010 time period. Our model captures this large jump in life expectancy. In summary, our model produces similar projections to the current methodology designed for short-term projections, but using a much simpler model with smaller data requirements.

3. Case studies

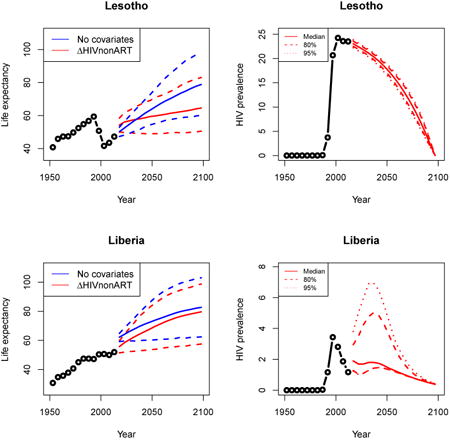
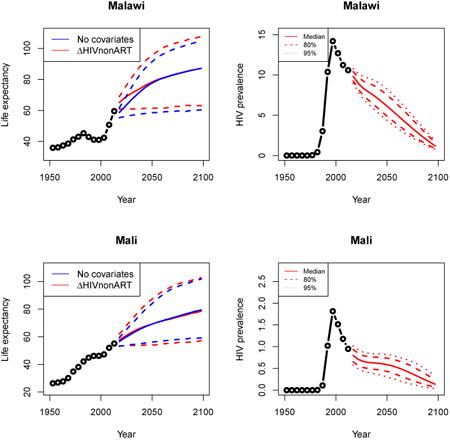
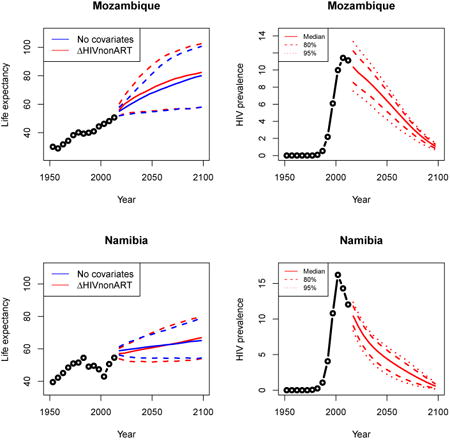
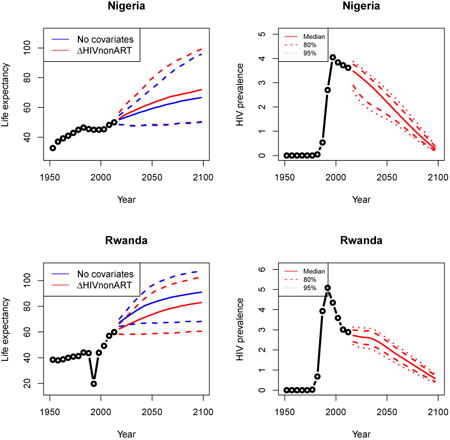
We now give specific results for five countries that illustrate specific aspects of the method. Results for all countries considered here as having generalized epidemics are given for female life expectancy in Appendix A and for male life expectancy in Appendix B.

3.1 Medium epidemic: Nigeria

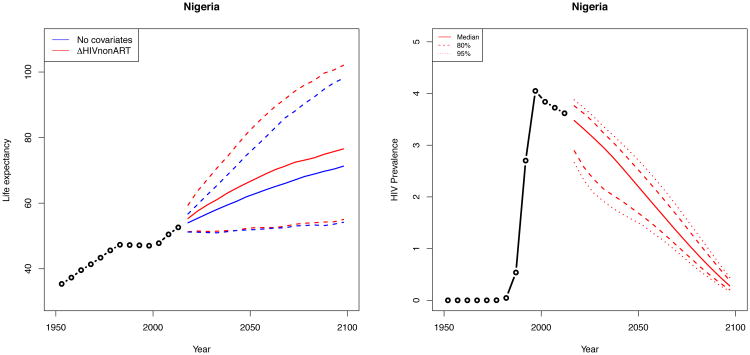
Nigeria, located in West Africa, is the most populous country on the continent. It had an HIV prevalence of 3.6% in 2010–2015. Figure 4 shows a comparison between projections of life expectancy under the model (1) with no covariates in blue and the model (2) with the HIV covariate in red.

Figure 4. Projections of female life expectancy in Nigeria (left) and the single trajectory of past estimates of HIV (right).

Note: The left panel shows projections of female life expectancy in Nigeria under the model in equation (1) in blue and equation (2) in red. The solid lines represent medians, and the dashed lines are the 95% intervals. After accounting for HIV prevalence and ART coverage, we see slightly more uncertainty about the future life expectancy in Nigeria and slightly higher median projections. The right panel shows the single trajectory of past estimates of HIV we use in model fitting in black and probabilistic trajectories of HIV prevalence from EPP we use in our projections.

The median projections of female life expectancy are higher than those projected when not accounting for the HIV/AIDS epidemic, and accounting for the epidemic leads to more uncertainty about the future trajectory of female life expectancy in Nigeria.

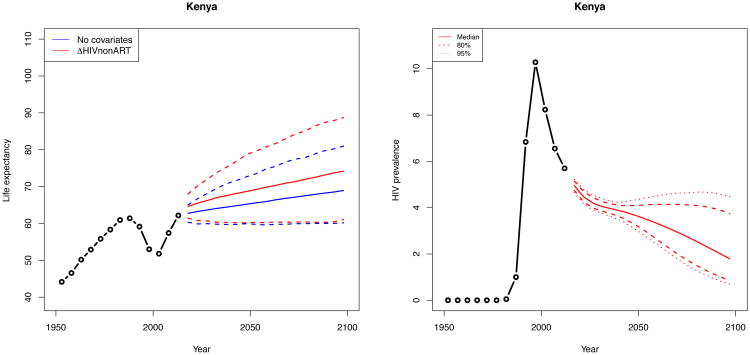
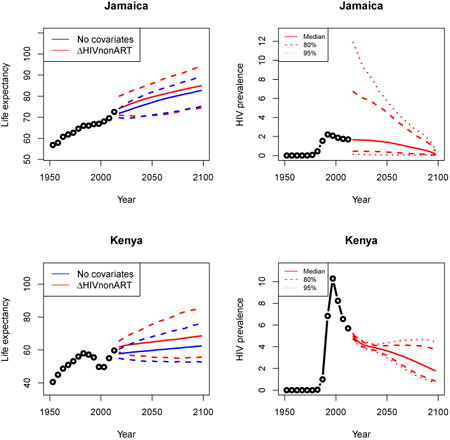
3.2 Medium epidemic: Kenya

Kenya in East Africa has a medium-sized epidemic with HIV prevalence at 5.7% in 2010–2015. Figure 5 shows that Kenya has already recovered to pre-epidemic life expectancy levels. After accounting for HIV prevalence and ART coverage, we project a slightly higher median female life expectancy to 2100 with more uncertainty at all time periods.

Figure 5. Projection of female life expectancy in Kenya (left) and the single trajectory of past estimates and future trajectories of HIV (right).

Note: The left panel shows projection of female life expectancy in Kenya under the model in equation (1) in blue and equation (2) in red. The solid lines represent medians, and the dashed lines are the 95% intervals. After accounting for HIV prevalence and ART coverage, we see a higher median projection of life expectancy with more uncertainty. The right panel shows the single trajectory of past estimates and future trajectories of HIV.

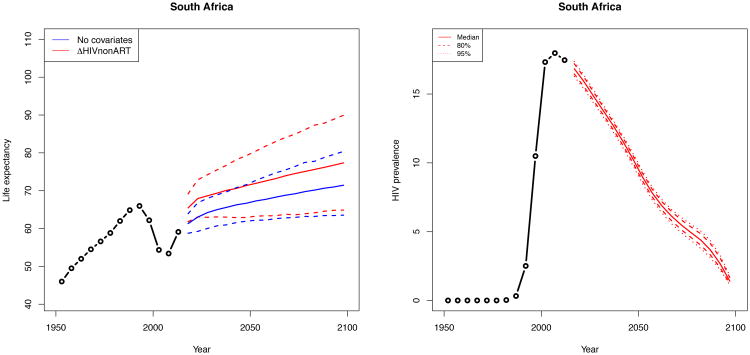
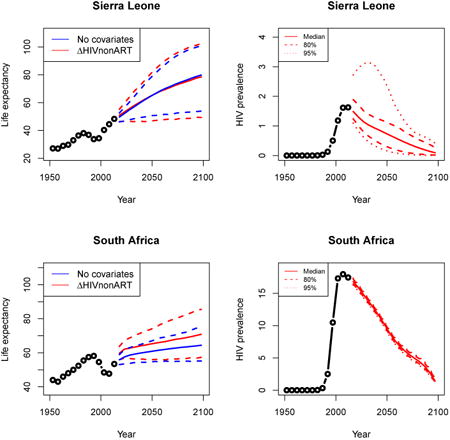
3.3 Widespread epidemic: South Africa

South Africa has the largest HIV/AIDS epidemic in the world in absolute numbers. The estimated average prevalence in the 2010–2015 time period was 17.5% (United Nations 2015). Figure 6 shows a comparison between projections of life expectancy under the model in (1) in blue and the model in (2) in red. Figure 6 reflects the clear impact of ART coverage on recovery in life expectancy under a large epidemic. After accounting for HIV prevalence and ART coverage, we project an initial recovery to pre-epidemic life expectancy levels with a steady rise through the end of the century. When not accounting for the HIV epidemic and, particularly, ART coverage, the model projects median end-of-century life expectancy only slightly higher than South Africa's life expectancy before the HIV/AIDS epidemic. Thus, not accounting for HIV and ART in the model leads to projections that are contrary to the epidemiological literature referenced in Section 2.3, showing that life expectancy recovers quickly after a scale-up of ART coverage.

Figure 6. Projection of female life expectancy in South Africa (left) and the single trajectory of past estimates of HIV (right).

Note: The left panel shows projection of female life expectancy in South Africa under the model in equation (1) in blue and equation (2) in red. The solid lines represent medians, and the dashed lines are the 95% intervals. After accounting for HIV prevalence and ART coverage, we see an initial recovery of life expectancy to pre-epidemic levels followed by a steady rise through the end of the century. The right panel shows the single trajectory of past estimates of HIV we use in model fitting in black. In red we have the median, 80% interval, and 90% interval of probabilistic trajectories of HIV prevalence from EPP we use in our projections.

As mentioned in Section 2.4, there are a number of countries for which the UN did not have up-to-date life expectancy data at the time of publication of the WPP 2015, including South Africa. The UN estimates the female life expectancy for the period 2010–2015 as 59.1 years (United Nations 2015). Statistics South Africa has published mid-year estimates of life expectancy for each calendar year (Statistics South Africa 2010, 2011, 2013, 2014, 2015), and averaging these gives an estimate for the five-year period 2010–2015 of 60.7 years. When we fit our model with data up to 2005–2010 and project forward five years to 2010–2015, our 95% interval for 2010–2015 is (56.6, 65.1). When we fit our model with data only up to 2000–2005 and project forward ten years to 2010–2015, our 95% interval for 2010–2015 is (51.6, 63.7). In both cases, our interval captures the outcome, whether measured by the UN or Statistics South Africa, and in particular the rapid increase in life expectancy due to the widespread rollout of ART.

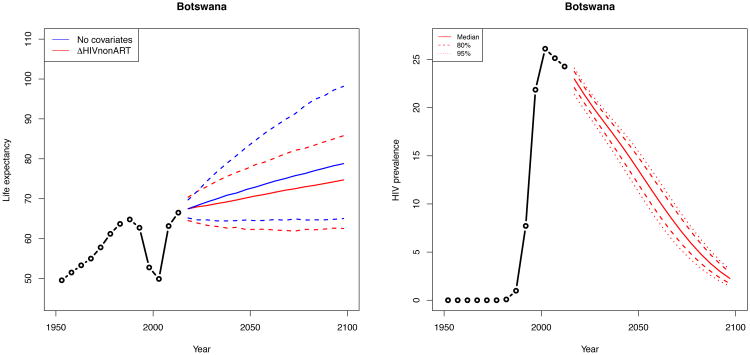
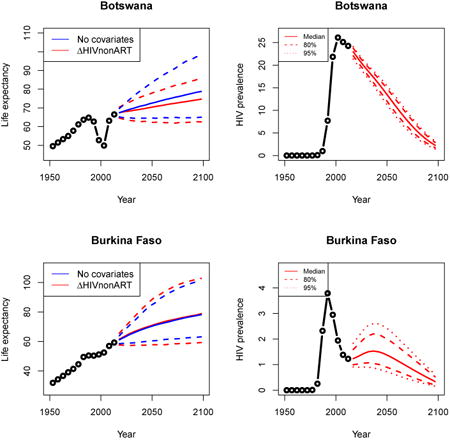
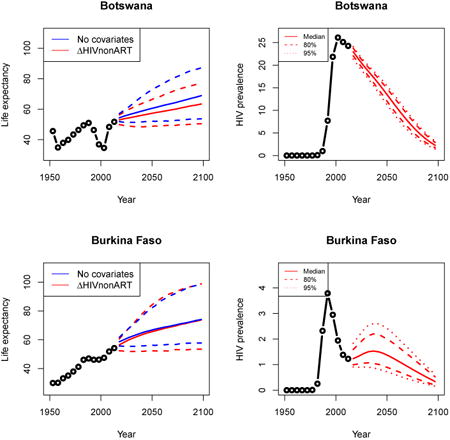
3.4 Widespread epidemic: Botswana

HIV prevalence rose early and quickly in Botswana, and the ART scale-up was also quick. This led to a rapid recovery in life expectancy in the 2005–2010 time period. After accounting for the epidemic and ART, we project a slightly slower rise in median life expectancy with more certainty than the model that does not account for the epidemic. This is in agreement with the epidemiological literature cited in Section 2.3 suggesting that HIV/AIDS will affect life expectancy as a chronic disease would after ART has become pervasive.

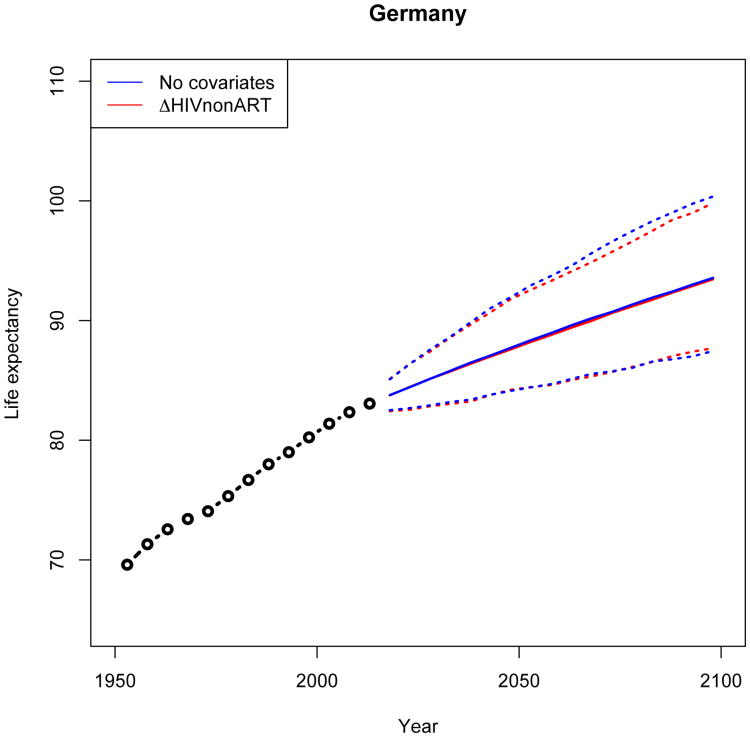
3.5 No epidemic: Germany

Germany is an example of a country that does not have a generalized epidemic. As can be seen in Figure 8, projections of life expectancy under the model in (1) and the model in (2) differ negligibly in both median and uncertainty.

Figure 8. Projection of female life expectancy in Germany.

Note: This figure shows projection of female life expectancy in Germany under the model in equation (1) in black and equation (2) in red. The medians are identical, and the predictive intervals differ negligibly.

4. Discussion

We have developed a probabilistic method for projecting life expectancy while accounting for generalized HIV/AIDS prevalence and ART coverage. Our method has relatively modest data requirements. Through predictive validation we have shown that our method improves upon life expectancy projections for countries with generalized HIV/AIDS epidemics using the method in Raftery et al. (2013), while leaving projections for nonepidemic countries essentially unchanged. Our projections improve in terms of both the mean absolute error of point predictions and the calibration of predictive intervals. Our method produces similar short-term projections to the UNAIDS Spectrum/EPP package, with a simpler model that requires much less data. Moreover, the method can produce long-term projections out to 2100.

Our model reflects the literature consensus mentioned in Section 2.3 that HIV prevalence will have large impacts on life expectancy only in the absence of ART. Once ART covers a large proportion of the infected population, there is a one-time gain in life expectancy towards pre-epidemic levels, and the effects will be modest afterwards.

Our method can be combined with population projection methods to make probabilistic population projections which account for the HIV/AIDS epidemic. Sharrow et al. (2016) convert our probabilistic projections of life expectancy to age- and sex-specific mortality rates using model life tables for countries with an HIV/AIDS epidemic (Sharrow, Clark, and Raftery 2014). Probabilistic projections of population size are then made using the cohort–component method (Raftery, Alkema, and Gerland 2014; Ševčíková and Raftery 2016).

One limitation of our method is the quality of the ART coverage data and projections. As ART coverage is relatively new and hard to measure, the data we have is noisy. Improvements in ART data quality would likely result in improvements in projections for the generalized HIV epidemic countries. Given high-quality data, our method could also be extended to account for other covariates that explain changes in life expectancy. The data would need to be available for every country used in model fitting back to 1950. Methodology for projecting the covariates would also be required.

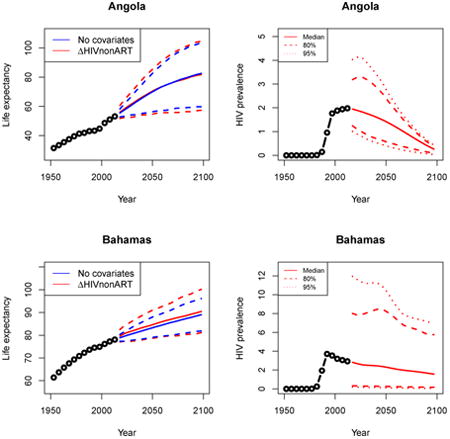
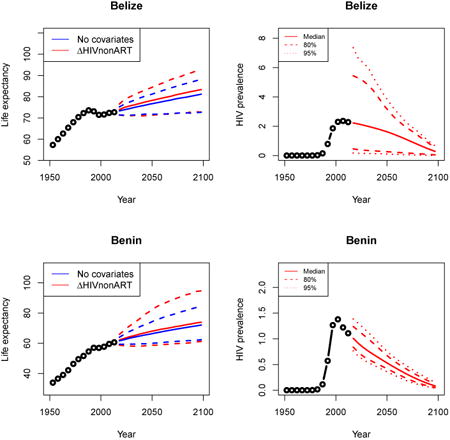
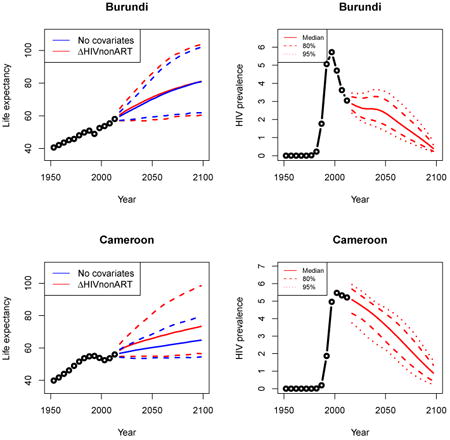
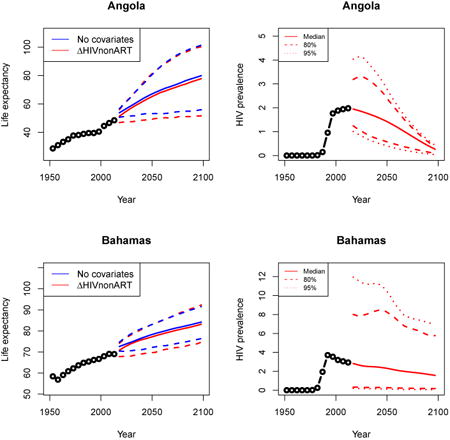
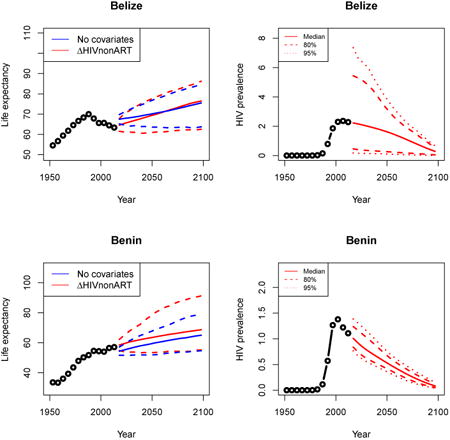
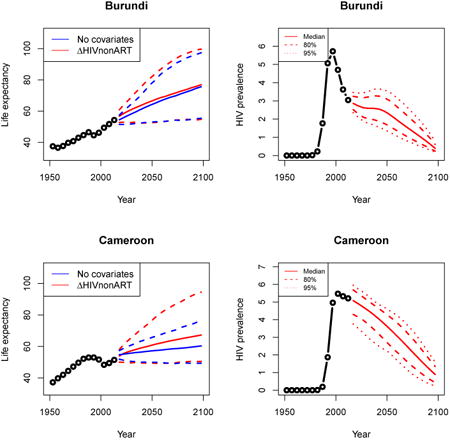
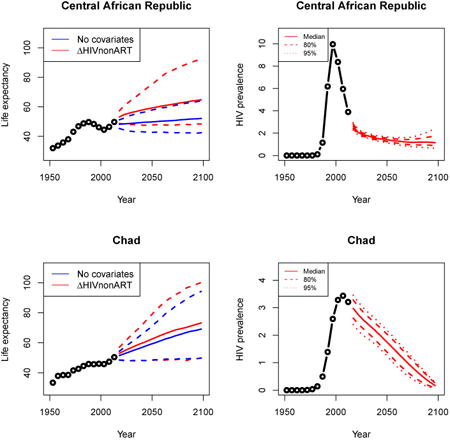
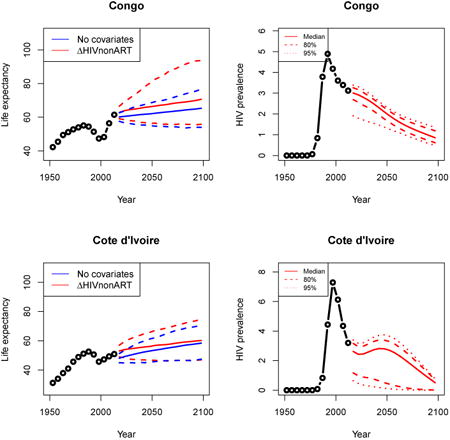
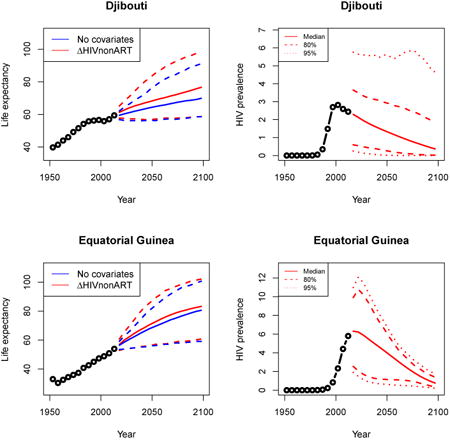
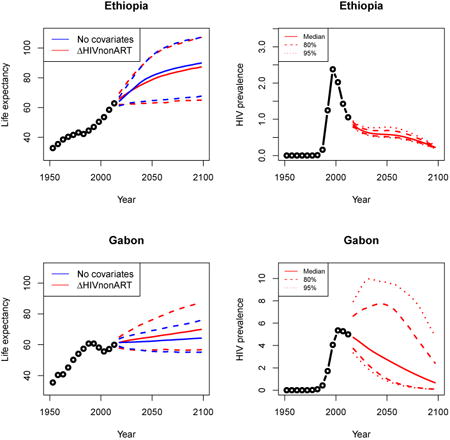
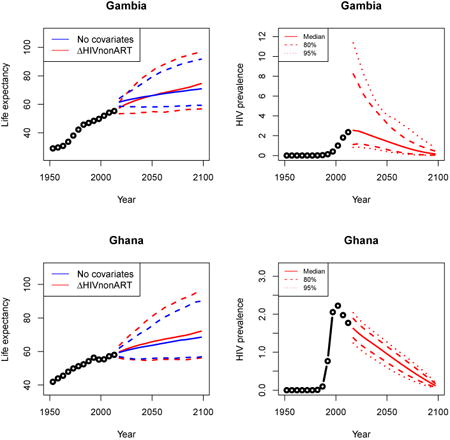
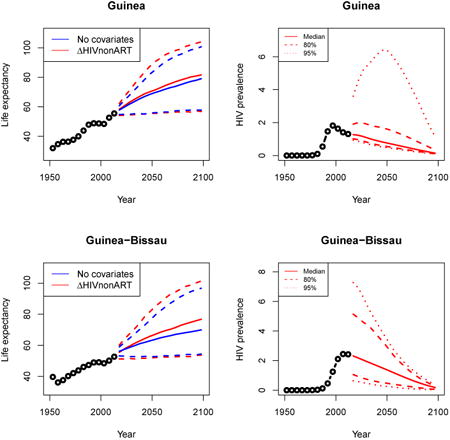
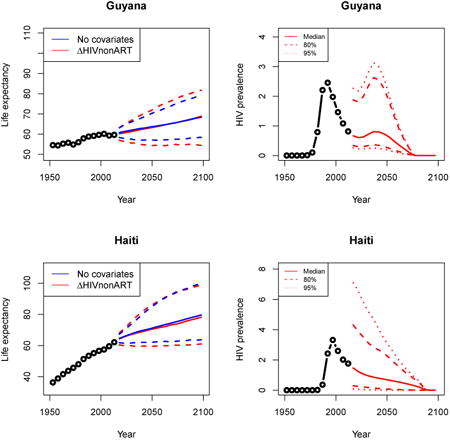
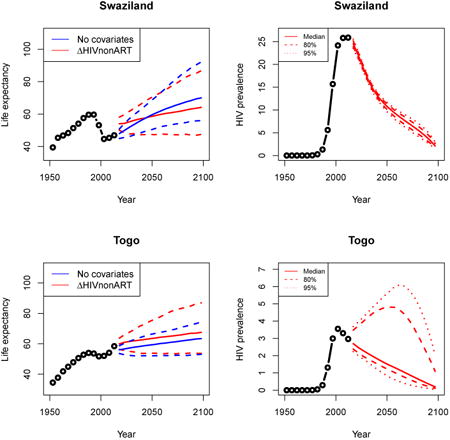
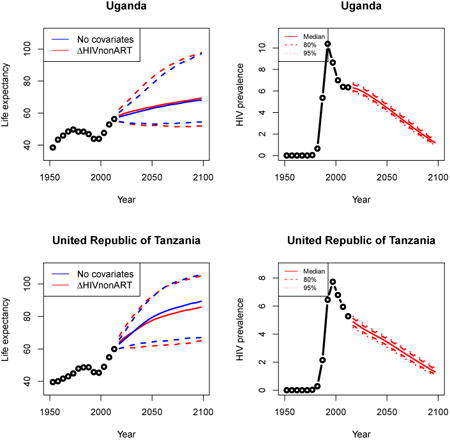
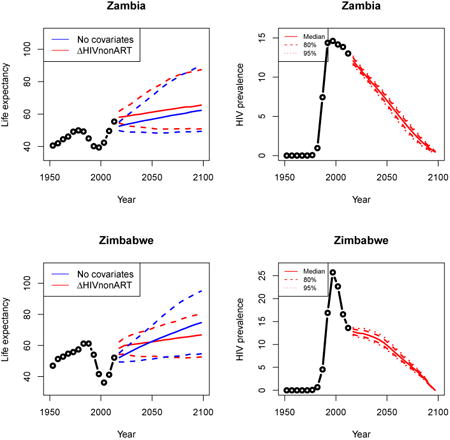
Appendix A: Female life expectancy and adult HIV prevalence projections

In the left panel of every row below are projections of life expectancy using our model (2) for all countries we treat as generalized epidemic countries. The right panel shows our observed trajectories of HIV prevalence and our projections of HIV prevalence made using a single trajectory of HIV prevalence for each country allowing the EPP projections to give uncertainty. The format of these figures is the same as that of Figures 4–7 in Section 3.

Figure 7. Projection of female life expectancy in Botswana (left) and a dampened, slow-rising median projection of life expectancy (right).

Note: The left panel shows projection of female life expectancy in Botswana under the model in equation (1) in blue and equation (2) in red. The solid lines represent medians, and the dashed lines are the 95% intervals. After accounting for HIV prevalence and ART coverage, we see a dampened, slow-rising median projection of life expectancy with less uncertainty.

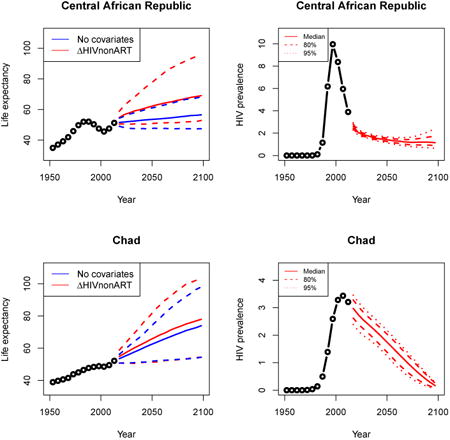
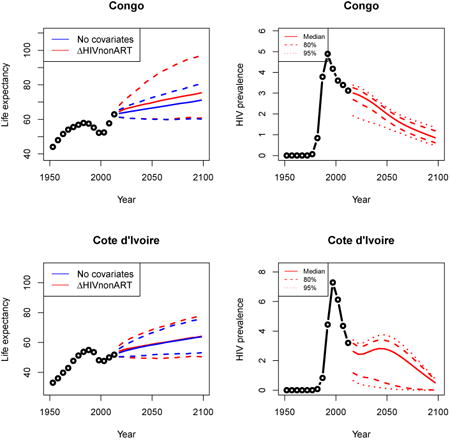
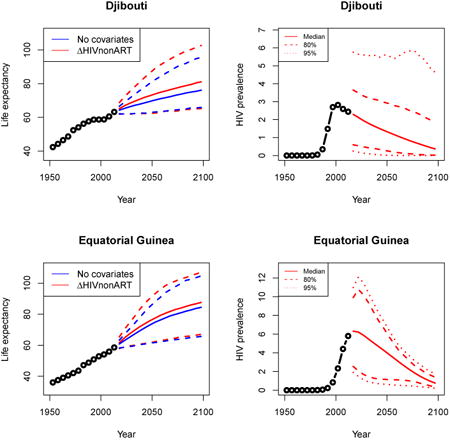
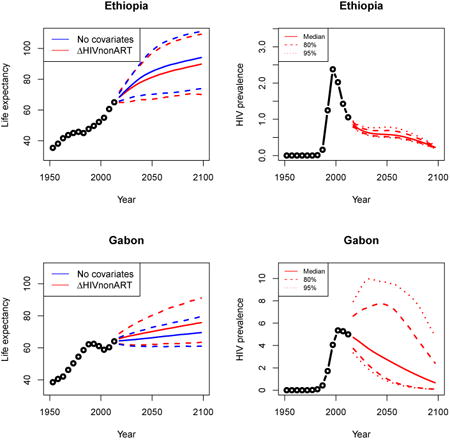
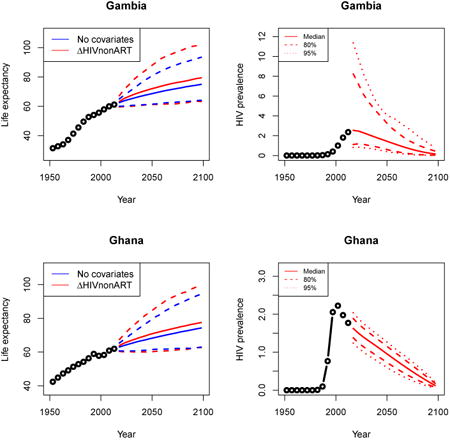
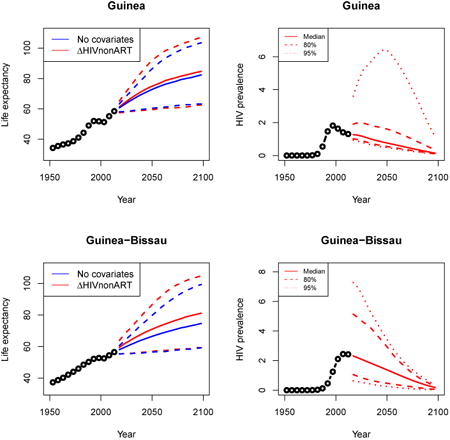
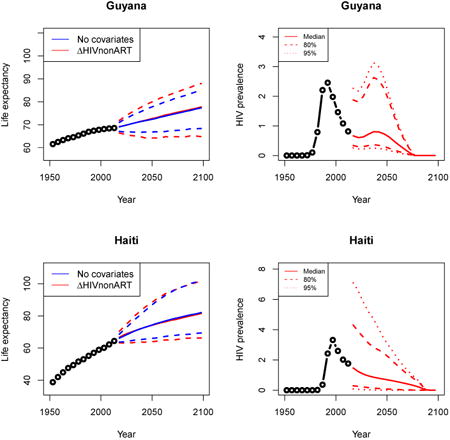
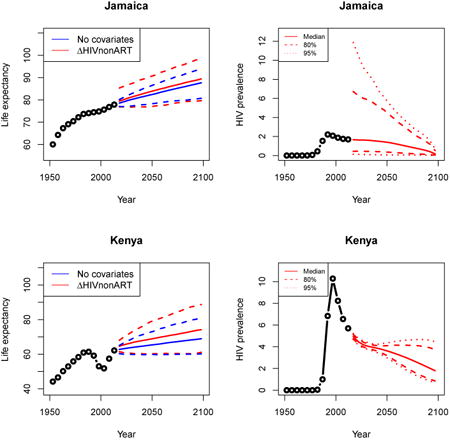
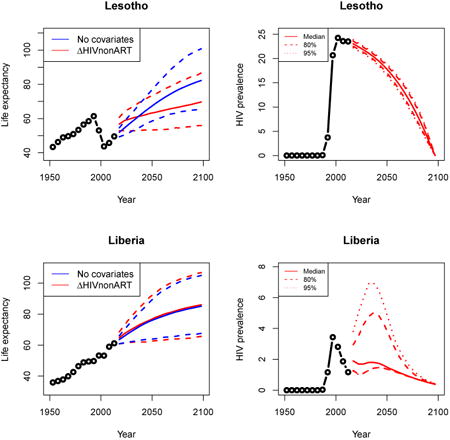
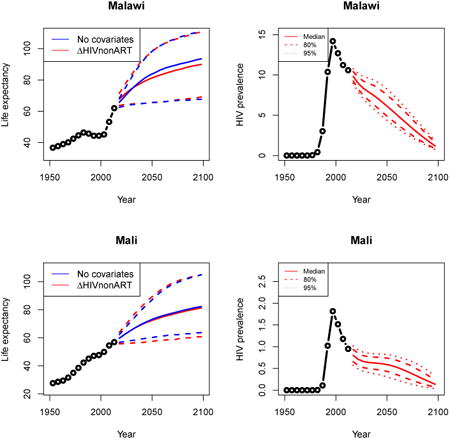
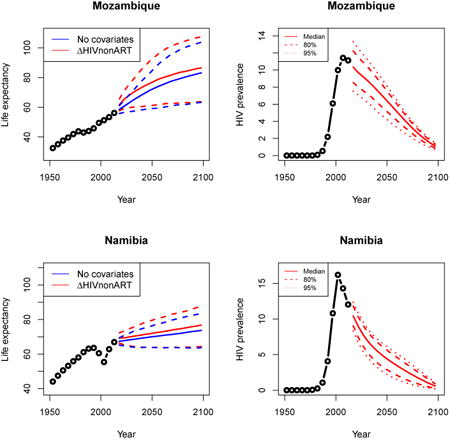
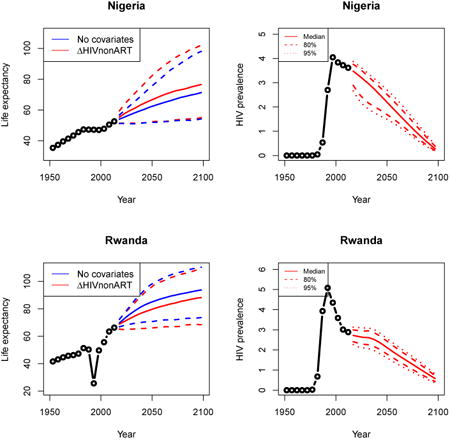
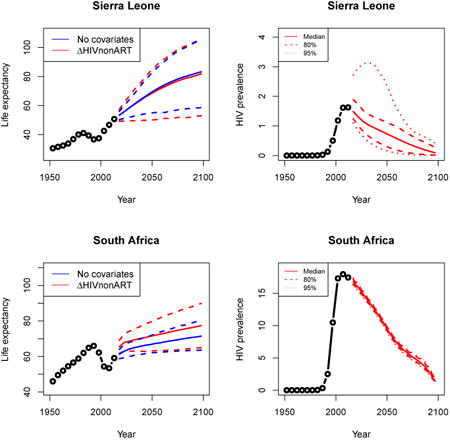
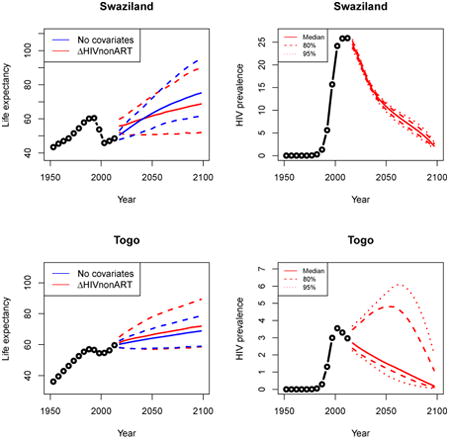
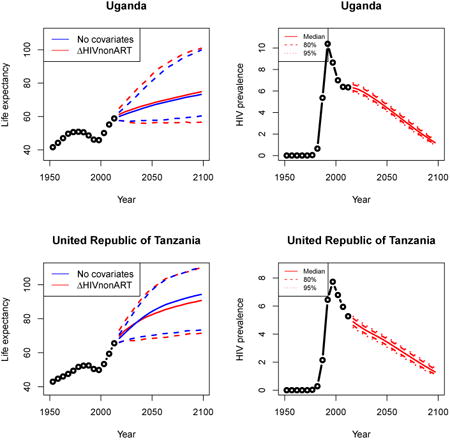
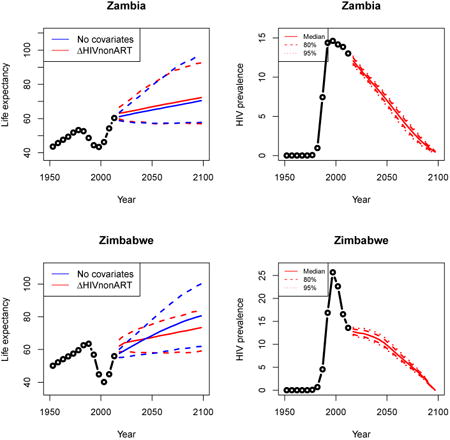
Appendix B: Male life expectancy and adult HIV prevalence projections

Table 2. Out-of-sample validation results for male life expectancy projected using the gap model in Raftery, Lalic, and Gerland 2014.

Countries	Training period	Test period	n	Model	MAE	Coverage
						80%	95%
HIV	1950–2005	2005–2015	69	No covariates	3.74	0.36	0.51
				ΔHnA	2.49	0.75	0.84
	1950–2005	2005–2010	40	No covariates	2.69	0.40	0.55
				ΔHnA	2.41	0.73	0.80
	1950–2005	2010–2015	29	No covariates	5.19	0.31	0.45
				ΔHnA	2.60	0.79	0.90
	1950–2010	2010–2015	29	No covariates	3.22	0.38	0.55
				ΔHnA	1.81	0.76	0.86
All	1950–2005	2005–2015	390	No covariates	1.46	0.79	0.88
				ΔHnA	1.23	0.86	0.94
	1950–2005	2005–2010	201	No covariates	1.11	0.80	0.89
				ΔHnA	1.05	0.87	0.94
	1950–2005	2010–2015	189	No covariates	1.83	0.77	0.88
				ΔHnA	1.43	0.86	0.95
	1950–2010	2010–2015	189	No covariates	1.20	0.76	0.86
				ΔHnA	0.99	0.82	0.90

Note: The first column represents the set of countries used in the subsequent calibration calculations. The second column represents the time period of data used to fit the model, and the third column represents the time periods used in validation. The fourth column represents the number of countries used in validation. In the fifth column, “No Covariates” represents the model in (1) and “ΔHnA” represents the model in (2). The sixth column contains the MAE as defined in Section 2.4. The seventh and eighth columns contain coverage metrics for the 80% and 95% predictive intervals respectively.