Bayesian Additive Regression Trees using Bayesian Model Averaging

Abstract

Bayesian Additive Regression Trees (BART) is a statistical sum of trees model. It can be considered a Bayesian version of machine learning tree ensemble methods where the individual trees are the base learners. However for datasets where the number of variables p is large the algorithm can become inefficient and computationally expensive. Another method which is popular for high dimensional data is random forests, a machine learning algorithm which grows trees using a greedy search for the best split points. However its default implementation does not produce probabilistic estimates or predictions. We propose an alternative fitting algorithm for BART called BART-BMA, which uses Bayesian Model Averaging and a greedy search algorithm to obtain a posterior distribution more efficiently than BART for datasets with large p. BART-BMA incorporates elements of both BART and random forests to offer a model-based algorithm which can deal with high-dimensional data. We have found that BART-BMA can be run in a reasonable time on a standard laptop for the “small n large p” scenario which is common in many areas of bioinformatics. We showcase this method using simulated data and data from two real proteomic experiments, one to distinguish between patients with cardiovascular disease and controls and another to classify aggressive from non-aggressive prostate cancer. We compare our results to their main competitors. Open source code written in R and Rcpp to run BART-BMA can be found at: https://github.com/BelindaHernandez/BART-BMA.git

1 Introduction

Advances in technology and data collection have meant that many fields are now collecting and analysing bigger datasets than ever before (Lynch, 2008). This has brought the analysis of high-dimensional data to the forefront of statistical analysis (Bühlmann and Van De Geer 2011 ; Fujikoshi et al. 2011; Zhao et al. 2012). In many areas of research, especially biomedical applications, it is common to have very detailed data on a relatively small set of observations, resulting in what is known as a “small n large p” problem, where the number of variables p is much larger than the number of observations n. This precludes the use of many standard statistical techniques (Hernández et al., 2014).

Random forests (RF), first proposed by Breiman (2001), is a popular method for dealing with high-dimensional data, mainly because of its computational speed and high accuracy. It is a non-parametric method and so does not make any major distributional assumptions about the data. RF automatically allows for nonlinear interaction effects, a desirable property in many high-dimensional datasets (Nicodemus et al. 2010; Archer and Kimes 2008). The standard output of the RF method not only reports the accuracy of the algorithm, but also gives a variable importance measure for each variable which tells the user which variables were the most predictive. However, as RF is a machine learning algorithm and does not use a statistical model, it does not provide probability-based uncertainty intervals.

Bayesian methods have proven popular in many areas of research, in part because they are robust to overfitting in the presence of small sample sizes and can handle missing or incomplete data (Beaumont and Rannala 2004; Wilkinson 2007; Hernández et al. 2015). They allow the inclusion of external information from previous experiments, scientific literature or other sources in a principled manner, which is an advantage over non-Bayesian statistical and machine learning techniques (Wilkinson, 2007). They also permit known experimental and biological variability to be incorporated into a prior probability distribution (Harris et al., 2009). A key benefit of using model-based approaches is that they give access to the full posterior distribution of all unknown parameters in the model, which can be useful in decision-making. Machine learning algorithms by default usually provide point estimates only and so decisions are made ignoring the uncertainty surrounding these estimates.

Bayesian Additive Regression Trees (BART) Chipman et al. (2010) is a Bayesian tree ensemble method similar in idea to gradient boosting (Friedman, 2001a), which combines the advantages of Bayesian models with those of ensemble methods such as RF. The advent of a parallelised R software package called bartMachine (Kapelner and Bleich, 2014a) and the R package dbarts (Chipman et al., 2014) has made BART a feasible option for the analysis of a wide range of datasets. As BART is a model-based approach, it yields credible intervals for predicted values, in contrast to the default output of machine learning algorithms such as RF. However as explained later in Section 2.3, the algorithm for BART can become computationally inefficient for data sets with large numbers of variables.

In this article we propose an alternative fitting algorithm for BART which we refer to as Bayesian Additive Regression Trees using Bayesian Model Averaging (BART-BMA). BART-BMA modifies the original BART method in a number of ways to make the algorithm more efficient for high-dimensional data. BART-BMA can be seen as a bridge between RF and BART in that it is model-based yet will run on high-dimensional data. One of the main reasons of BART can struggle in high dimensions is that it uses Markov Chain Monte Carlo (MCMC) to sample from the posterior distribution of the tree space. Rather than using MCMC and saving every iteration of the MCMC chain for each tree to memory, BART-BMA greedily grows sums of trees models and uses an efficient variant of Bayesian model averaging called Occam's window to average over the set of sums of trees which are most probable (Madigan and Raftery, 1994). The method discards models with low posterior probability and focuses final predictions on the subset of models with the highest posterior probabilities. In order to improve model selection speed, BART-BMA uses a greedy search algorithm to find predictive split points, so only high quality splits are proposed when growing tree models. Thus BART-BMA is computationally feasible for high-dimensional datasets, does not require specialised hardware or software and brings with it the advantages of a model-based approach.

In this paper we showcase BART-BMA using a simulated example as well as two real applications to proteomic experiments. The article is organised as follows. Section 2 reviews existing tree-based variable selection models such as RF (Breiman, 2001) and BART (Chipman et al., 2010). Section 3 describes our proposed model and explains the differences between it and BART. Section 4 compares BART-BMA to BART, RF and Extremely Randomised Trees (ERT) for a number of simulated datasets and applies these methods to two proteomics datasets. We conclude with discussion in Section 5.

2 Tree-Based Models

In this section we review the existing methods RF and BART. Tree-based models have long been used for prediction and classification, going back to 1963 for the analysis of survey data (Morgan and Sonquist 1963; Morgan 2005). Tree-based modelling came to the fore with the seminal work of Quinlan (1979, 1986), and particularly the Classification and Regression Tree (CART) method of Breiman et al. (1984).

Decision trees consist of internal nodes and splitting rules of the form x_p ≤ c, where x_p refers to the pth explanatory variable in design matrix X and c is a threshold value within the range of values of variable x_p. Observations which satisfy the splitting rule are sent to the left hand daughter node and those which do not are sent to the right hand daughter node. An illustration of this process is given for one of our examples in Figure 3. Observations are further iteratively split into left and right hand daughter nodes as they pass through each internal node in turn until a terminal node is reached.

Figure 3.

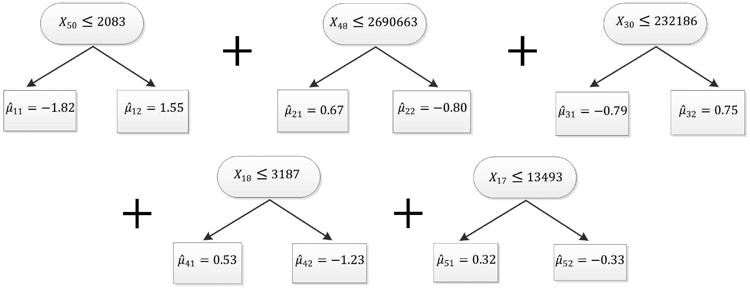
Prostate cancer Data: BART-BMA sum of trees model with the highest posterior probability.

One of the main reasons for the popularity of tree models over standard statistical models such as linear regression is that decision trees automatically search for and include nonlinear interaction effects. It was later noted however that individual decision trees tend to overfit and to be sensitive to the training data they were built on. To counteract this, ensemble methods were proposed where multiple models are aggregated or averaged over to give a more stable and generalisable solution (Breiman 1996a; Breiman 1996b; Friedman 2001b).

2.1 Random Forests (RF)

RF (Breiman, 2001) is one of the most popular tree-based ensemble algorithms and has been used in many fields (Ham et al. 2005; Svetnik et al. 2003; Daz-Uriarte and Alvarez de Andrés 2006). RFs use an average of multiple CART decision trees. Each decision tree in the RF algorithm is based on a bootstrap sample of observations and trees are grown by splitting on a random sample of variables in each internal node. In this way RFs avoid overfitting by reporting accuracy on the out of bag samples that were not used to build the tree model and so give a cross-validated estimate of model performance.

Rather than using a statistical model, RF performs an exhaustive search for split points on various subsets of data. Each tree in the RF is grown to maximal depth such that each terminal node in the tree contains a minimum of one observation for classification and a minimum of 5 observations for regression. Therefore individual trees tend to be quite large and complex. The main reasons for the popularity of RFs are that they are generally accurate, are computationally fast and work for large datasets. Also, the algorithm provides a variable importance score for each variable used. The two main variable importance scores used are the decrease in Gini impurity, which is generally used for classification problems, and the mean decrease in accuracy, which is generally used for regression problems. Thus the RF can be used for interpretation and explanation, unlike other black box algorithms such as support vector machines and neural networks which do not provide variable importance scores by default.

Extremely Randomised Trees (ERT) are a related tree ensemble method (Geurts et al., 2006). The main difference between the two is that individual trees are built on the full training data rather than a bootstrap sample as in RF. Also, trees are grown by choosing a split variable and split point at random from the set of split rules available at each internal node rather than performing an exhaustive search as in RF. In Section 4 we compare RF and ERT to their Bayesian counterparts BART and BART-BMA.

2.2 Bayesian Additive Regression Trees (BART)

2.2.1 BART likelihood

BART is a Bayesian tree ensemble model where the response variable Y is estimated by a sum of Bayesian CART trees (Chipman et al., 2010). Given an n × p matrix of explanatory variables X, let x_k = [x_k1, …, x_kp] be the kth row (i.e. the kth observation) of X. The basic BART model is

$$Y_k=\sum _{j=1}^{m}g(x_k;T_j,M_j)+{\varepsilon }_k,$$ (1)

where g(x_k; T_j, M_j) is a CART decision tree as described in Chipman et al. (1998), T_j refers to decision tree j = 1 … m (where m is the total number of trees in the model), M_j are the terminal node parameters of T_j, and ${\varepsilon }_k\stackrel{\text{iid}}{~}N(0,{\sigma }^2)$ where σ² is the residual variance. Each tree T_j also contains a set of splitting variables and split points; one for each internal node in the tree.

2.2.2 BART priors

To form the Bayesian model, prior distributions are required for the parameters. In Chipman et al. (2010), these are set by assuming prior independence of the trees T_j, and similarly the terminal node parameters M_j = (μ₁₁ … μ_ij) (where I = 1 … b_j indexes the terminal nodes of tree j). With judicious choices for these probability distributions which exploit conjugacies, many of the parameters can be marginalised out of the model; this greatly speeds up model fitting (see Section 2.2.4). In particular this marginalisation avoids the need for reversible jump type algorithms. The form of the prior used by Chipman et al. (2010) is:

$$p(M_1,\dots ,M_m,T_1,\dots ,T_m,\sigma )\propto [\prod _j\prod _{i}p({\mu }_{ij}|T_j)p(T_j)]p(\sigma ).$$ (2)

The prior distribution of the terminal node parameters μ_ij for a given tree T_j is

$${\mu }_{ij}|T_j\stackrel{\text{iid}}{~}N(0,{\sigma }_0^2),$$

where ${\sigma }_0=\frac{0.5}{e\sqrt{m}}$ and e is a user-specified hyper-parameter (usually fixed) with recommended values between 1 and 3. To set the prior distribution of the μ_ij, Chipman et al. (2010) noted that 𝔼(Y|X) is modelled as a sum of m μ_ij parameters. Chipman et al. (2010) then use an empirical Bayes prior for the μ_ij so that 𝔼(Y|X) lies within the range of values of Y with high probability. Here the response variable Y is centered at zero and scaled to have minimum and maximum values at −0.5 and 0.5 respectively before analysis, yielding a scaled variable Y_scaled. For this reason the prior mean of μ_ij is usually set to 0. The prior terminal node standard deviation parameter σ₀ is set such that e√mσ₀ = 0.5, and e is chosen such that the prior implies that 𝔼(Y|X) lies between −0.5 and 0.5 with high probability. For example e = 2 sets a 95% prior probability that the 𝔼(Y_scaled|X) lies between -0.5 and 0.5.

Chipman et al. (2010) place a regularisation prior on the tree size and shape p(T_j) to discourage any one tree from having undue influence over the sum of trees (Chipman et al., 2010). The probability that a given terminal node within a tree T_j is further split into two children nodes is α(1 + d_i)^−β, where d_i is the depth of internal node i and α and β are parameters (usually fixed) which determine the size and shape of tree T_j respectively (Chipman et al., 1998). Thus $p(T_j)={\prod }_{i=1}^{u_j}\alpha {(1+d_i)}^{-\beta }$, where u_i indexes the internal nodes of tree T_j. The default values recommended by Chipman et al. (2010) are α ∈ (0, 1) and β > 0. This puts high probability on bushy trees where all the terminal nodes end at a similar depth.

Chipman et al. (2010) assume that the model precision σ⁻² has a conjugate prior distribution ${\sigma }^{-2}~Ga(\frac{\nu }{2},\frac{\nu \lambda }{2})$, with degrees of freedom ν and scale λ respectively.

2.2.3 BART posterior

Combining equations (1) and (2) we obtain the posterior distribution:

$$p(\mathcal{T},M,\sigma |X,Y)\propto p(Y|X,\mathcal{T},M,\sigma )[\prod _j\prod _{i}p({\mu }_{ij}|T_j)p(T_j)]p(\sigma ),$$ (3)

where p(Y|X, 𝒯, M, σ) is the likelihood for a given sum of trees, and 𝒯 is the set of all trees, i.e. 𝒯 = {T₁, …, T_m}.

2.2.4 BART Model Fitting

Chipman et al. (2010) use a Markov chain Monte Carlo (MCMC) sampler to obtain a posterior distribution of the set of trees 𝒯, terminal node parameters M, and residual standard deviation σ. New trees in the BART algorithm are proposed using a Metropolis-Hastings sampler which selects from one of four proposal moves: GROW (node birth), PRUNE (node death), CHANGE (changing splitting rules) and SWAP (swapping internal nodes). An overview of the algorithm used by Chipman et al. (2010) is shown in Algorithm 1. Chipman et al. (2010) show that a backfitting algorithm, whereby individual trees are updated whilst all others are held constant, has some desirable computational properties.

The Chipman et al. (2010) algorithm involves calculating the full conditionals p(T_j, M_j|X, Y, σ, 𝒯_(j),M_(j)) and p(σ|X, Y, 𝒯, M), where 𝒯_(j) refers to the set of all trees except that of tree j (similarly M_(j)). Chipman et al. (2010) note that p(T_j, M_j|X, Y, σ, 𝒯_(j), M_(j)) depends on (𝒯_(j), M_(j), Y, X) only through R_j = Y – Σ_l≠j g(x; T_l, M_l), the vector of partial residuals of the model excluding tree j. Thus the draws from the full conditionals p(T_j, M_j|R_j, σ) can be obtained through two separate steps:

1. calculating p(T_j|R_j, σ) ∝ p(T_j)p(R_j|T_j, σ), i.e. proposing and accepting/rejecting a new tree from the current partial residuals; then

2. drawing from p(M_j|T_j, R_j, σ), i.e. sampling a new set of terminal node parameters for the new tree.

The conjugate prior on the terminal node parameters p(μ_ij|T_j) (as previously introduced in Section 2.2.2) allows the μ_ij parameters to be marginalised out of the full conditional for R_j|T_j, σ⁻²:

$$p(R_j|T_j,{\sigma }^{-2})=\prod _{i=1}^{b_j}{\int }_{-\infty }^{+\infty }p(R_{ij}|{\mu }_{ij},{\sigma }^{-2})p({\mu }_{ij})p({\sigma }^{-2})d{\mu }_{ij}.$$ (4)

Integrating out the μ_ij parameters greatly reduces the fitting complexity as the calculation of the conditional distribution of the partial residuals for each tree T_j does not have to take account of the changing dimensionality of the terminal node parameters as trees are grown and pruned. The analytic form of p(R_j|X, T_j, σ⁻²) can be seen in Appendix A. An explanation of BART for classification problems can also be seen in Appendix B

Chipman et al. (2010) provide a posterior variable importance score which can be used for variable selection or to rank variables according to their importance. Chipman et al. (2010) use the variable inclusion proportion, equal to the proportion of times a variable was selected over all posterior MCMC samples in the sum of trees model.

2.3 Issues with current tree-based methods

A major advantage of RF is that it is fast enough to be applied to high-dimensional datasets on a standard laptop. One disadvantage is that in its default version it does not provide an assessment of uncertainty about the prediction. Only point predictions of Ŷ are given with no estimate of the variability of these predicted values. Other extensions of the original RF algorithm have however been proposed which can provide estimates of the uncertainty using methods such as jackknife estimates (Wager et al., 2014), conformal prediction (Johansson et al., 2014) and quantiles (Meinshausen, 2006). Lakshminarayanan et al. (2016) and Hutter et al. (2014) also discuss forest algorithms which can estimate predictive uncertainty.

BART on the other hand is a fully specified Bayesian model and so can automatically provide estimates of model and predictive uncertainty. However two main bottlenecks are noted in the BART model where p is large. The first is that using a uniform prior to choose predictive splitting rules in each internal node of each tree may produce MCMC chains with high rejection rates for large p. Thus the MCMC algorithm becomes inefficient, especially if the number of truly predictive variables is small. The second is that for high-dimensional data the BART algorithm can become inefficient when the length of the MCMC chains and the size of each sum of trees is large, a by-product of p being large. This is because the set of trees 𝒯 for each iteration of each MCMC chain must be saved to memory to enable prediction of an external dataset if it is not provided at the time of training the model.

The Bayesian CART models used in BART as described in Chipman et al. (1998) have previously been found to suffer from mixing issues as the CHANGE and SWAP steps of the MCMC algorithm only allow for local updates of proposed trees. Some alternative methods have been proposed such as in Wu et al. (2007) who propose a “restructure” step in the MCMC algorithm, whereby alternative tree structures are searched for which would result in the same terminal nodes as the current proposed model. They also suggest an alternative tree prior which focuses on the number of nodes in a tree and whether the tree is balanced or skewed. A number of alternative tree proposal algorithms have also been proposed to improve mixing of MCMC chains in individual Bayesian CART models for high dimensional data (Pratola, 2016; Lakshminarayanan et al., 2015).

In the next section we propose BART-BMA as a means of avoiding the issue of high rejection rates and large memory requirements with high dimensional data by greedily growing trees which result in an improvement in predictive accuracy. We use a greedy implementation of Bayesian model averaging to ensure that we obtain suitably variable posterior trees.

3 BART-BMA

We define BART-BMA as an ensemble of BART models which uses a sum of Bayesian decision trees as its base learner. We use the same likelihood as the standard BART model (Chipman et al., 2010), and make one small change to the prior for computational convenience (see Section 3.2). The main difference between BART-BMA and standard BART is the model fitting algorithm. Rather than using MCMC we perform a greedy search for predictive splitting rules and only grow sum of trees models based on this set of most predictive splits. We then use an efficient implementation of Bayesian Model Averaging to average over multiple sum of trees models (multiple sets of trees) and keep those with high posterior probability.

Each set of trees in BART-BMA is treated as a single model. We create multiple sets of trees in a greedy fashion which are averaged over to produce our final predictions. In other words BART-BMA averages over the L sets of trees with the highest posterior probability. Each set of trees averaged over by BART-BMA contains m trees which are greedily grown using a greedy search method for finding predictive splitting rules as described in Section 3.4. The BART-BMA method is described in this section and the BART-BMA algorithm is shown in Appendix C.

3.1 BART-BMA Likelihood

We use the same likelihood as the Chipman et al. (2010) BART model. However, we re-write it in matrix form for ease of later calculation. We now write Y as the vector (Y₁, …, Y_n) and let Y|𝖯, M, ${\sigma }^{-2}~N({\sum }_{j=1}^m{J}_j{M}_j,{\sigma }^{2}I)$, where J_j is an n × b_j binary matrix whose (k, i) element denotes the inclusion of observation k = 1 … n in terminal node i = 1…b_j of tree j. We let W = [J₁ … J_m] be an n × ω matrix, where $\omega ={\sum }_{j=1}^m{b}_j$, and $O={[M_1^T\dots M_m^T]}^T$ be a vector of size ω of terminal node means assigned to trees T₁, …, T_m. We can then write Y|O, σ⁻² ∼ N(WO, σ²I). As in Chipman et al. (2010) we shift and scale the response variable to have mean 0 and standard deviation 1, so that Y^TY = n.

3.2 BART-BMA priors

Our only change to the standard BART set of priors is to revert to the original terminal node prior p(μ_ij) suggested in Chipman et al. (1998). This is:

$${\mu }_{ij}|T,\sigma ~N(0,\frac{{\sigma }^2}{a}),$$

which contrasts with the Chipman et al. (2010) terminal node prior:

$${\mu }_{ij}|T_j~N(0,{\sigma }_0^2).$$

The reason we change back to this older version is that the conditional distribution of p(R_j|T_j, σ) in the BART algorithm requires the residual standard deviation σ (or rather the precision σ⁻²) for every update in the MCMC algorithm, as shown in Appendix A. Since we are trying to marginalise analytically over as many parameters as possible, we revert to the earlier standard conjugate prior used in Chipman et al. (1998). The fundamental advantage of this prior for μ_ij is that computational simplicity. We now marginalise out both the terminal node means and the model precision of the sum of trees likelihood. We expand on the mathematics below in Equation (5).

3.3 BART-BMA fitting

The matrix setup of the likelihood together with the priors given above allows us to calculate a marginal likelihood as:

$$p(Y|X,\mathcal{T})=\int \int p(Y|O,{\sigma }^{-2})p(O)p({\sigma }^{-2})\mathit{\text{dO}}d{\sigma }^{-2},$$

which yields:

$$p(Y|X,\mathcal{T})\propto {[\nu \lambda -(Y^{T}W){(W^{T}W+aI)}^{-1}(W^{T}Y)+Y^{T}Y]}^{-\frac{n+\omega +\nu }{2}}.$$ (5)

This allows us to specify the marginal likelihood p(Y|X, 𝒯) for each set of trees summed over 𝒯 rather than for each individual tree as in BART. The marginal likelihood is similar to that of the original BART model (Chipman et al., 2010); the only slight difference is our terminal node prior. The consequence of this change of prior is that we can marginalise over both the terminal node parameters O and the model precision σ⁻², unlike BART which includes an update for σ⁻² as part of the MCMC algorithm.

3.4 Greedily Growing Trees

As discussed in Section 2.3, uniformly proposing splitting rules for tree internal nodes, as used by BART, can become inefficient as the number of variables increases. With high-dimensional data we argue for adopting a greedier search in order to focus the algorithm towards predictive splitting rules, and so we use a greedy search method for finding predictive split points. We then only grow trees T_j within each set of trees 𝒯 using this set of most predictive split rules. We suggest the use of two methods for finding predictive splitting rules which will be discussed here.

3.4.1 PELT

Univariate change point detection algorithms in general search for distributional changes in an ordered series of data. Searching for predictive split points for a single variable in a decision tree has an equivalent goal i.e. it is desirable to find split points which maximise the separation of the response variable between daughter nodes. Hawkins (2001) showed that searching for individual split points using a single variable in a decision tree is equivalent to searching for change points in a univariate stochastic process (See also Appendix E.1). Building on this, we use a change point detection algorithm called Pruned Exact Linear Time (PELT) to search greedily for predictive split points (Killick et al., 2012).

We use PELT to find good splitting rules for each tree T_j in 𝒯 rapidly. The PELT algorithm allows us to detect changes in the mean or variance of the tree response variable R_j with respect to each variable x_p in turn, where each change point is treated as a potential splitting rule to grow a tree. Here R_j is ordered with respect to x_p. PELT and its use in the BART-BMA model is summarised and described in detail in Appendix E.1.

3.4.2 Grid Search

An alternative search algorithm offered by BART-BMA is the grid search. Here each variable x_p in dataset X is split into grid_size + 1 equally spaced partitions within the range of x_p and each partition value is then used as a potential split point. Increasing grid_size finds better solutions but makes the algorithm slower. We found that grid_size = 15 struck a good balance and gave good performance in most cases.

Regardless of the method used to find predictive split rules, trees are greedily grown using the best numcp% of the total splitting rules based on their residual squared error. By default this set of numcp% predictive splits are identified before the tree is grown. Therefore only trees using this set of most predictive splitting rules are considered for inclusion in the BART-BMA model. However, splitting rules can also be searched for as trees are being grown (within each internal node of each tree) which may improve the accuracy of the BART-BMA model. See Appendix E.2 for more details.

Once a tree has been greedily grown using one of the methods discussed above, the predicted values for observations falling in each terminal node R_iJ are set to the mean of the full conditional of p(μ_ij|…), as shown in Appendix D.1.

3.5 Averaging over sums of trees

Rather than use MCMC to fit the above model (which would give simmilar results to standard BART) we propose to use a greedier algorithm which finds good sums of trees, and subsequently weights them according to their likelihood and tree complexity. The algorithm we propose is greedy in two senses. First, it builds trees by finding optimal splits, and second, it discards poorly performing sets of trees by keeping only those within a reasonable multiplicative window of the best performing set of trees.

3.5.1 Occam's Window

As it is not possible to perform an exhaustive search of the model space especially when p is large, we use a greedy and efficient version of BMA called Occam's window (Madigan and Raftery, 1994). Here only the models which fall within Occam's Window are averaged over using

$${\mathit{\text{BIC}}}_{\ell }-{argmin}_{\ell }({\mathit{\text{BIC}}}_{\ell })\le log(o).$$ (6)

where ℓ indexes the sets of trees accepted into Occam's Window (the set of sum of trees models with the highest posterior probabilities to date). As BART-BMA searches the model space, it approximates the posterior probability of each set of trees using the BIC (7). The lowest (best) BIC of any set of trees encountered so far is saved and any set of trees whose BIC falls within a given threshold log(o) of the best model is saved to memory, while those outside of Occam's window are discarded. Hence only those models for which there is high support from the data are maintained and those whose predictions are considerably worse than the best model are eliminated from consideration. Our experience has led us to use o =1,000 as a general default value, however this value could also be chosen by cross validation.

For each set of trees 𝒯 in Occam's window, the posterior probability of 𝒯 is approximated using the BIC, defined as

$${\mathit{\text{BIC}}}_{\ell }=-2(log(p(Y|X,{\mathcal{T}}_{\ell })))+Blog(n)$$ (7)

(Schwarz, 1978). In equation (7), p(Y|X, 𝒯_ℓ) is the marginal likelihood for the set of trees 𝒯_ℓ as described in Section 3.1, B is the number of parameters in 𝒯_ℓ.

Each set of trees 𝒯_ℓ initially accepted in Occam's window is iteratively fit until either a user-specified number of iterations is reached or no more sets of trees are accepted in Occam's window. It should be noted that as models with better (lower) BIC are added to Occam's Window, this may eliminate some models which were previously within Occam's Window. Thus Occam's window constantly updates the best list of sets of trees as the algorithm proceeds. We have found that setting the number of trees in the sum, namely m in Equation (1), to 5 generally works well. One possible consequence of this approach is that although each individual model outside of Occam's window has very low posterior probability, if there are multiple such models this may combined account for a large section of the model space. Ignoring models with low posterior probability is therefore the tradeoff when an exhaustive model search is not possible as is the case with the examples shown in Section 4.

Once the sets of trees within Occam's window have been selected with the BART-BMA model, the predicted response values are then calculated as a weighted average of the predicted values from the selected sets of trees 𝒯_ℓ. Each set of trees is weighted by its approximate posterior probability, w_ℓ/Σ_kw_k, where w_ℓ is the model weight for sum of trees ℓ in Occam's window, defined as

$$w_{\ell }=exp(-0.5{\mathit{\text{BIC}}}_{\ell }).$$ (8)

3.6 Variable Importance

We provide a variable importance score, which is simply the estimated posterior expectation of the number of splitting rules involving the variable. For each sum of trees model ℓ with posterior probability w_ℓ as calculated in (8), let κ_pℓ be the number of splitting rules containing variable x_p in model ℓ. Our variable importance score is then

$$\widehat{\text{Imp}}(x_p)=\frac{{\sum }_{\ell =1}^L{w}_{\ell }{\kappa }_{p\ell }}{{\sum }_{p=1}^P{\sum }_{\ell =1}^L{w}_{\ell }{\kappa }_{p\ell }}.$$ (9)

Whilst many different important scores exist this variable importance score is directly analagous to that proposed by Chipman et al. (2010).

We provide the full algorithm for BART-BMA in Appendix C. In order to provide credible and prediction intervals for Ŷ, we use a post-hoc Gibbs sampler, the details of which are given in Appendix D.

3.7 BART-BMA for Classification

BART-BMA can also be used for binary classification. We follow the same strategy as Chipman et al. (2010) (described in Appendix B) by introducing the latent variables $Z_k~N({\sum }_{j=1}^{m}g(x_k;T_j,M_j),1)$, where

$$Y_k=\{\begin{array}{cc}1& \text{if}{Z}_k>0\\ 0& \text{otherwise},\end{array}$$

Our method requires estimates of Z_k so that the previously introduced BART-BMA algorithm for continuous responses can be run without modification. We simply fix the Z_k for all k at the start of the algorithm. In practice we have found that this approach works well if we set all Z_k = Φ⁻¹(0.001) ≈ −3.1 if y_k = 0 and Z_k = Φ⁻¹(0.999) = 3.1 if y_k = 1

Once the Z_k values are set, BART-BMA uses these as the new response for the tree, updates the residuals R_j and iteratively fits trees as before. In order to set predicted Rȃ_j values in the terminal nodes, BART-BMA uses the mean of the full conditional for M_j, as shown in Appendix D.1.

4 Results

We compare BART-BMA to RF, ERT and BART for a number of simulated datasets and also for two real proteomic data sets for the diagnosis of cardiovascular disease and aggressive versus non-aggressive prostate cancer.

All analyses reported in this section were computed using a HP Z420 Workstation with 32GB RAM. To allow for comparison of the two most used software packages for BART, we use both the bartMachine R package (version 1.2.3; Kapelner and Bleich, 2014b) as well as the dbarts R package (version 0.8-7; Chipman et al., 2014). RF was run using the randomForest R package (version 4.6-12; Liaw and Matthew, 2015). ERT was also included as a benchmark tree ensemble method using R package extraTrees (version 1.0.5). All methods and results were obtained using R version 3.2.0 (https://cran.r-project.org/bin/windows/base/old/3.2.0/).

4.1 Friedman Data

As in Chipman et al. (2010) we use simulated data based on Friedman (1991) to compare the results of BART-BMA, RF and BART. The original simulated dataset of Friedman (1991) had 5 uniform predictor variables x₁ … x₅ where

$$y=10sin(\pi x_1{x}_2)+20{(x_3-0.5)}^2+10x_4+5x_5+\varepsilon .$$ (10)

In order to see how RF, ERT, BART and BART-BMA compared over various dataset sizes, seven datasets were constructed by appending random noise variables to the truly important variables shown in (10) above, such that the total number of variables in each data set was p = (100, 1000, 5000, 10000, 15000, 100000, 500000) where x₁ … x_p are uniform random variables and ε∼N(0, 1). Each method was compared across the seven datasets using five-fold cross-validation and the cross-validated root-mean squared error (RMSE) was recorded. At first, default values for all model parameters were used to allow for a fair comparison between the methods. For the original version of BART using the dbarts package, the parameters were also tuned to show the best result for each dataset. This was done as in many cases default versions of dbarts and bartMachine performed poorly because the MCMC algorithm did not converge. Hence for each of the seven datasets, the number of samples after burn-in ( ndpost) was varied using three different values (1000, 5000, 10000) and the number of trees in the BART model was varied for three different values ntree = (50, 200, 500) so nine different models were run for each of the seven datasets tested. All other parameters were left at their default values.

In each case, the best model with respect to the RMSE was chosen and convergence was checked by inspecting the trace plots for the post burn in samples of the residual variance parameter σ² as was also done in Chipman et al. (2010) and Kapelner and Bleich (2014a). BART using bartMachine was not tuned as there were memory issues when increasing the length of the MCMC chain past the default value of 1,000. Note ERT and bartMachine could not run for p =100,000 or p =500,000. Non-default dbarts also could not be run for the largest dataset with p = 500, 000. For the Friedman datasets BART-BMA results are shown using the GRID search, as in all cases the number of observations is n = 500 (see Appendix E.1 for default recommendations) all other parameters for BART-BMA and RF remained at their default settings.

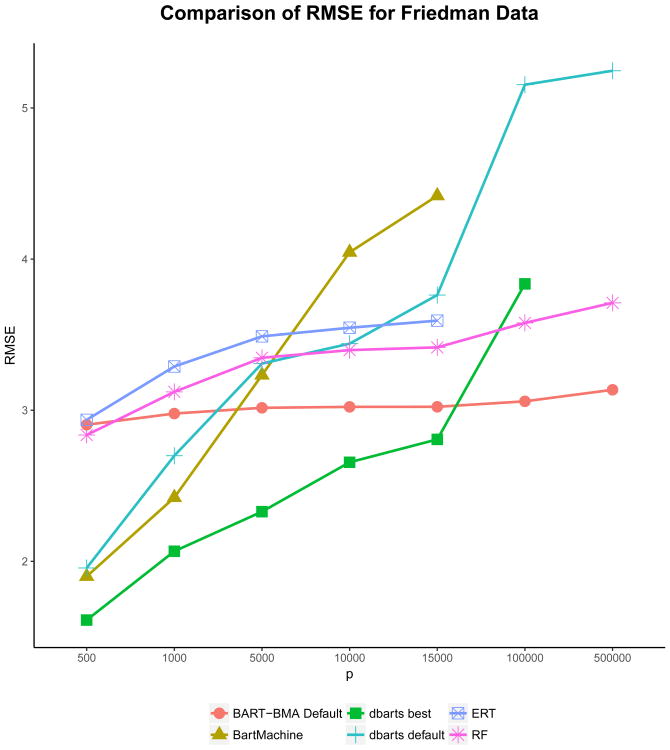
4.1.1 Friedman Data: Model Accuracy

Figure 1 shows the results for the model accuracy of the four methods for the simulated Friedman data. Note that BART was run using both the bartMachine and dbarts packages for comparison. Here we can see that the non-default BART model using the dbarts package performed the best with regards to RMSE for small datasets where p ≤ 15, 000. However, once the number of variables was increased past p = 15,000, BART-BMA outperformed RF, ERT and all BART models. In fact BART-BMA outperformed RF, ERT and BART models in all cases where p > 15,000, regardless of the method used for finding splits or whether the splitting rules were updated before or during the tree growing process. It should be noted that for p =100,000 the tuned dbarts model did not converge with its best setting where the length of the MCMC chain was 10,000 iterations (shown in Figure 1). Increasing the length of the chain to 50,000 iteration was attempted in this case but would not run.

Figure 1.

Friedman example: Comparison of RMSE for the 7 simulated Friedman datasets where p = 100, 1000, 5000, 10000, 15000, 100000, 500000. As n = 500 the GRID method was used to search for the subset of best splits.

For p ≥ 100,000 ERT, bartMachine and non-default versions of dbarts (for p =500,000) gave memory errors and became computationally infeasible. Because BART-BMA uses a greedy approach rather than MCMC, however, it performed well for p =500,000 and even outperformed RF in terms of model accuracy.

4.1.2 Friedman Data: Model Calibration

In order to assess the calibration performance of the prediction intervals from all four models, we show the average coverage of the out-of-sample 95% prediction intervals and the average interval width for each of the simulated datasets in Table 1. As the standard RF and ERT do not provide confidence intervals, we used conformal prediction intervals as described in Johansson et al. (2014) and Norinder et al. (2014) using the conformal package (Cortes, 2014) in R to allow for a comparison across all four methods. If the method is calibrated, on average we would expect 95% of the intervals to contain the true value of y. The results for ERT are not shown in Table 1 as the confidence intervals could not run for p > 5000 and intervals for datasets where p ≤ 5,000 were much wider and had less coverage than RF.

Table 1.

Friedman example: coverage for out-of-sample 95% prediction intervals and average interval width for BART-BMA, RF using conformal intervals, bartMachine and dbarts. The closer the coverage to 95% the better, and the smaller the interval width the better. Items in bold refer to the best calibrated model with respect to interval coverage and interval width for each simulated dataset.

	Coverage					Average Interval Width
p	BART BMA	RFCP Intervals	bart Machine	dbarts default	dbarts best	BART BMA	RFCP Intervals	bart Machine	dbarts default	dbarts best
100	94.8%	96.0%	96.2%	84.0%	75.4%	11.70	11.18	7.74	5.77	3.90
1000	94.4%	98.0%	97.4%	74.4%	79.6%	11.70	12.39	11.22	6.37	5.27
5000	93.8%	98.0%	98.8%	81.6%	84.2%	11.67	12.96	17.06	8.68	6.47
10000	94.0%	99.0%	96.6 %	85.4%	81.8%	11.67	12.87	17.09	10.26	7.59
15000	94.0%	96.0%	96.6 %	86.6%	83.2%	11.67	13.22	18.54	11.34	8.38
100000	94.6%	99%	-	76.4%	86%	11.79	14.35	-	13.12	5.20
500000	93.4%	-	-	75.0%	-	11.74	-	-	13.01	-

From Table 1 it can be seen that BART-BMA is the best calibrated across the 5 simulated datasets shown, as its coverage is as close or closer to 95% than the other models in all cases. Blank entries in Table 1 indicate that either the model could not be run for these datasets (as for bartMachine and dbarts) or that the algorithm was stopped after it failed to run within a time limit of 5 days as for conformal.

The right hand side of Table 1 shows the average interval width for BART-BMA, RF using conformal intervals, bartMachine and dbarts. For all six datasets for which it ran, the tuned BART model using the dbarts package had the shortest interval width. However this should be seen in the context of the fact that dbarts was the worst calibrated of all four methods and in none of the cases reaches close to 95%. For this reason the interval widths for dbarts are not highlighted in Table 1. For larger datasets where p > 1000, BART-BMA had a much shorter mean interval width than either bartMachine or RF using conformal intervals and had the most accurate coverage. Overall BART-BMA was more accurate (for larger datasets) and better calibrated than RF or either BART method.

The interval widths of the BART-BMA prediction intervals in Table 1 are robust with respect to the number of irrelevant variables p, which may seem surprising at first glance. This does make sense however, because, as we will see later, BART-BMA attaches relatively high posterior probability to the important variables, and almost zero total posterior probability to the unimportant variables, even when p is extremely large. It substantially outperforms the other methods in this regard. As a result, the BART-BMA prediction interval is determined almost exclusively by the five important variables and so it makes sense that it would be insensitive to the number of unimportant variables.

Appendix F shows the average coverage and interval width for the 50% and 75% out-of-sample prediction intervals. With respect to the 50% intervals, the BART-BMA model was well calibrated when p ≤ 1000, but it was slightly undercalibrated for larger datasets, as was RF using conformal intervals. dbarts was the worst calibrated across all datasets assessed. bartMachine on the other hand was overcalibrated for p ≤ 10,000 and undercalibrated for p = 15000. For 75% intervals, the BART-BMA model outperformed the other methods for all except p =100 and 15,000 where had only marginally worse coverage. For larger datasets (p ≥ 15000) the BART-BMA model not only had the best coverage but also had the shortest interval width.

4.1.3 Friedman Data: Variable Importance

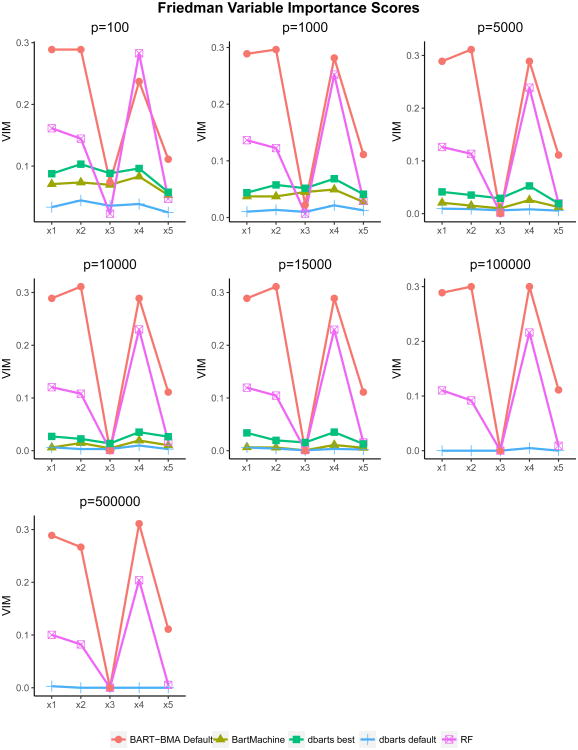
These data are simulated, so it is known that variables x₁ … x₅ are truly important and all other variables are random noise. The average importance for variables x₁ … x₅ over the five cross-validation folds is reported in Figure 2. Whilst the BART and BART-BMA models provide direct access to the variable inclusion probabilities, the mean decrease in accuracy provided by RF had to be converted to a scale of 0-1 in order to allow for a fair comparison between the size of the variable importance scores assigned to each variable. Importance scores for ERT were not included here as they are not provided as standard output from the extraTrees package in R.

Figure 2.

Friedman example: variable importance scores for the truly important variables x₁ … x₅ for each of the 7 Friedman datasets. As n = 500 the GRID method was used to search for the subset of best splitting rules in BART-BMA, where all splitting variables had equal prior probability of being selected. BART-BMA and BART ( bartMachine and dbarts) scores show the mean variable inclusion probability, RF scores show the mean decrease accuracy expressed as a probability.

The BART-BMA method had much larger average variable importance scores than RF, bartMachine and dbarts for variables x₁, x₂ and x₅ for all values of p. For x₄, BART-BMA had substantial variable importance scores, as did RF. For x₃, BART-BMA had larger variable importance scores than the all other methods except the dbarts best method for p ≤ 1,000, and all four methods had low variable importance scores for p ≥1,000. Across all methods variables 1, 2 and 4 were consistently ranked higher than variables 3 or 5. Both bartMachine and the dbarts default method had strikingly low variable importance scores for the truly important variables, regardless of the numbers of noise variables. The tuned dbarts best method performed slightly better than bartMachine for all datasets where it ran, however it still assigned low importance to these variables when compared to RF or BART-BMA.

Table 2 shows the sum of the variable importance scores assigned to the random variables x₆ … x_p. Across all seven datasets BART-BMA correctly selected only the truly important variables in its model and except where p =500,000 never included any of the random noise variables. RF outperformed both bartMachine and default and tuned versions of dbarts in terms of accurate variable importance scores.

Table 2.

Friedman example: Sum of the Variable Importance Scores assigned to the unimportant variables x₆ … x_p. As n = 500 the GRID method was used for BART-BMA where all variables had equal prior probability of being selected. The method which assigns the lowest importance to random variables is considered the best. Items in bold show the best method for each of the five simulated datasets.

p	BART BMA	RF	bart Machine	dbarts default	dbarts best
100	0	0.35	0.63	0.82	0.57
1000	0	0.45	0.81	0.93	0.74
5000	0	0.50	0.92	0.96	0.82
10000	0	0.52	0.95	0.97	0.88
15000	0	0.53	0.97	0.98	0.88
100000	0	0.57	-	1.00	0.99
500000	0.02	0.61	-	1.00	-

In order to further assess the overall quality of the variable importance scores assigned across all variables we used the $\text{Brier score}=\frac{1}{P}{\sum }_{p=1}^P{(I_p-{\mathit{\text{VIS}}}_p)}^2$ where I_p = 1 for the truly important variables x₁ … x₅, and I_p = 0 otherwise. Hence the model with the lowest Brier score is considered the best. Brier scores for all seven simulated datasets are shown in Table 3. The variable importance scores from BART-BMA gave the best overall performance across all seven datasets, and RF came second, outperforming both implementations of dbarts and bartMachine for each of the datasets with regards to the Brier score.

Table 3.

Friedman example: $\text{Brier score}=\frac{1}{P}{\sum }_{p=1}^P{(I_p-{\mathit{\text{VIS}}}_p)}^2$ where I_p = 1 for truly important variables x₁ … x₅ and I_p = 0 otherwise. Hence the lower the Brier score the better the model variable selection. Items in bold show the best model with respect to the Brier score.

p	BART BMA	RF	bart Machine	dbarts default	dbarts best
100	3.24 × 10−2	3.82 × 10−2	4.30 × 10−2	4.66 × 10−2	4.17 ×10−2
1000	3.26 × 10−3	4.00 × 10−3	4.62 × 10−3	4.87 × 10−3	4.49 × 10−3
5000	6.55 × 10−4	8.18 × 10−4	9.68 × 10−4	9.85 × 10−4	9.31 × 10−4
10000	3.28 × 10−4	4.13 × 10−4	4.89 × 10−4	4.95 × 10−4	4.75 × 10−4
15000	2.18 × 10−4	2.76 × 10−4	3.29 × 10−4	3.31 × 10−4	3.18 × 10−4
100000	3.28 × 10−5	4.21 × 10−5	-	4.99 × 10−5	4.98 × 10−5
500000	6.62 × 10−6	8.54 × 10−6	-	9.99 × 10−6	-

Overall, BART-BMA outperformed RF and BART in terms of the quality of its variable importance score, and did not include any random noise variables in its models regardless of the size of the dataset.

Bleich et al. (2014) discuss various ways of choosing appropriate thresholds for the variable inclusion proportions to use BART for variable selection such as the “local” and “global max threshold” options. Both of these involve permuting the response variable and running the BART model a number of times. The variable importance scores for each run using the permuted response are then used to generate a null distribution of variable inclusion proportions for each variable. The local threshold selects the (1 – α) quantile for each variable over P permutations and selects the predictor variable x_k if its (1 – α) quantile exceeds this threshold. The Global max threshold on the other hand chooses the maximum inclusion proportion generated for each variable over all permutations in the null distribution. The threshold for selecting a variable is then given by getting the (1 – α) quantile across the P permutations of the maximum values for each null variable inclusion proportion. These thresholds were not assessed for all datasets shown here, as especially for large data sets the BART models were computationally demanding and required a lot of memory and so running BART multiple times for these datasets was not practical. Indeed in Figure 1 it can be seen that bartMachine would not run for p >15,000 and non-default dbarts would not run for p =500,000 even on a workstation with 30Gb RAM.

4.2 Prostate Cancer Data

Prostate cancer is a heterogeneous disease. In some men it manifests itself as an acute, aggressive and rapidly advancing condition, and in other men as a slowly progressing disease that is responsive to existing treatment regimes for significant periods of time. It is widely recognised that existing methods to classify the grade of the disease (using serum PSA levels, digital rectal examination and Gleason score) are not well suited for monitoring its progression or establishing the optimal timing of treatment interventions (Logothetis et al., 2013). It is therefore important to be able to distinguish between aggressive and non-aggressive forms of the disease in a timely manner.

Here we show the results of an experiment where the expression levels of 51 peptides were measured using multiple reaction monitoring (MRM) on 63 patients with prostate cancer. Of these patients, 21 had extra capsular extension which is a surrogate for aggressive disease, while the remaining 42 had localised disease which had not spread beyond the boundaries of the prostate gland.

To access model performance we use the precision recall curve (Raghavan et al., 1989). The precision of a model is another term for the positive predictive value and measures the $\frac{\sum \text{True Positives}}{\sum \text{True Positives}+\sum \text{Flase Positives}}$. Here it measures the probability of a patient having extra capsular extension given that the model predicted they had extra capsular extension. The recall of a model is another name for the specificity and measures $\frac{\sum \text{True Negatives}}{\sum \text{True Negatives}+\sum \text{False Positives}}$. In this case the recall measures the probability of a patient being diagnosed as extra capsular extension by the model given they actually had extra capsular extension. The precision recall curve shows the precision of a model over varying thresholds of the recall and the area under this curve is known as the area under the precision recall curve (AUPRC), for which the higher the value the better.

Table 4 shows the comparison of BART-BMA, RF, ERT and BART using the bartMachine and dbarts packages for this dataset in terms of the classification rate and the AUPRC. All results are based on out of sample data using five-fold cross-validation. Here all methods have been set to their default values. Non-default options for bartMachine and dbarts were also run as described in Section 4.1 however the tuned models did not improve the classification of AUPRC over the default model. From Table 4 it can be seen that BART-BMA using the PELT search performed best in terms of classification accuracy, identifying 79% of the cases correctly. The BART-BMA model took a weighted average over 100 sum of tree models which were included in Occam's window. It also performed best in terms of AUPRC with an area of 0.68. Here the PELT rather than the GRID search was used as the sample size for this experiment was small (n ≤ 200).

Table 4.

Prostate cancer data: Classification rate, area under the precision recall curve (AUPRC) and CPU run time in seconds (standard deviation in brackets) for BART-BMA, RF and BART. Methods with higher classification rate, AUPRC and lower CPU running time are more desirable. Elements in bold show the best method with respect to each of the criteria.

	BART BMA	RF	ERT	bart Machine	dbarts
Classification
Rate	0.79	0.71	0.75	0.71	0.69
AUPRC	0.68	0.67	0.60	0.65	0.60

Table 5 shows the five most important variables chosen across the three models considered. Again as a VIM is not provided for ERT using the extraTrees package ERT is not included here. From Table 5 it can be seen that BART-BMA, RF and both versions of BART agreed that variables 50 and 18 were the two most important for this dataset. RF, bartMachine and dbarts all chose variables 50, 18, 2 and 3 in their top five. BART-BMA tended to assign higher inclusion probabilities to a smaller number of variables than RF or either version of BART which tended to assign lower inclusion probabilities across a larger number of variables. In this case BART-BMA assigned a high variable importance score to variable 50 showing that this variable was present in 22.5% of the total splits across sum of trees models. If variables were chosen at random we would expect each variable to have an inclusion probability of 0.019 for this dataset and so across all cases a higher than random importance was assigned to the most important variables.

Table 5.

Prostate cancer data: Top five most important variables for each method. BART-BMA and BART scores show the mean variable inclusion probability, RF scores show the mean decrease in Gini index expressed as a probability. As n < 200 the PELT method was used to search for the subset of best splitting rules.

Variable	BART BMA	RF	bart Machine	dbarts
50	0.225	0.082	0.025	0.022
18	0.168	0.052	0.024	0.021
2		0.035	0.021	0.021
3		0.042	0.022	0.021
4			0.021
30	0.103
31	0.071			0.021
25	0.050
44		0.037

Like RF, BART-BMA gives access to the sum of trees models in Occam's window at the end of the algorithm. This makes the results of BART-BMA easy to interpret. To illustrate, Figure 3 shows the sum of trees model for the prostate cancer data which had the highest posterior probability. BART-BMA chose a sum of five trees, where each tree split on only one variable. Here the set of proteins analysed in this experiment were chosen based on the outcome of a previous experiment and are not expected to interact, so it is interesting to note that the individual trees in the most probable sum of trees model did not include any variable interactions.

4.3 Cardiovascular Disease

This section describes an experiment to distinguish patients with cardiovascular disease from control patients. This experiment was undertaken on 498 patients, 150 of whom had a cardiovascular disease and 348 of whom were healthy. A total of 36 proteins were measured by a targeted approach (MRM) in each patient sample. Table 6 shows the cross-validated results for this experiment with respect to the classification rate and the AUPRC for each method. BART-BMA, ERT and dbarts were slightly more accurate than either RF or BART using bartMachine and correctly predicted 70% of the patients. With respect to the AUPRC however, BART-BMA did not perform as well as the other methods (see Table 6) with BART using the bartMachine package performing the best by this measure. The BART-BMA method averaged over 3 sets of trees in this case. For this data, tuning the bartMachine and dbarts methods beyond their default values did not lead to an increase in accuracy or AUPRC.

Table 6.

Cardiovascular disease data: Classification rate, area under the precision recall curve (AUPRC) and CPU run time in seconds (standard deviation in brackets) for BART-BMA, RF and BART. Methods with higher classification rate, AUPRC and lower CPU running time are more desirable. Elements in bold show the best method with respect to each of the criteria.

	BART BMA	RF	ERT	bart Machine	dbarts
Classification
Rate	0.70	0.69	0.70	0.69	0.70
AUPRC	0.43	0.46	0.46	0.49	0.48

Table 7 shows the five most important variables chosen by each of the methods. As can be seen, all four models chose quite similar proteins in this case with BART-BMA and RF agreeing on four of their top five, and bartMachine and dbarts agreeing on three of their top five. BART-BMA tended to assign a higher inclusion probability to a smaller set of proteins whereas RF and BART using the default number of trees tended to spread the probability across a larger number of variables. If the model were assigning probabilities uniformly across variables we would expect a probability ∼ 0.03 which is the probability assigned to 4 of the top 5 variables included by both versions of BART and two of those included by RF. BART-BMA in all cases assigned a much higher than random inclusion probability to its most important variables.

Table 7.

Cardiovascular disease data: Top five most important variables for each method. BART-BMA and BART scores show the mean variable inclusion probability, RF scores show the mean decrease in Gini index expressed as a probability. As n > 200 the GRID method was used to search for the subset of best splitting rules.

Variable	BART BMA	RF	bartmachine	dbarts
14	0.33	0.05	0.04	0.035
4	0.16	0.03		0.030
24	0.14	0.05	0.03
3	0.06	0.03	0.03
34	0.06
2			0.03
10			0.03
13		0.03		0.029
12				0.031
18				0.030

5 Discussion

We have proposed a Bayesian tree ensemble method called BART-BMA which modifies the BART method of Chipman et al. (2010) and can be used for datasets where the number of variables is large. Instead of estimating the tree node parameters using MCMC, BART-BMA uses a different fitting algorithm which involves greedily searching for predictive splitting rules to grow predictive trees and also using a greedy implementation of Bayesian model averaging. This greedy fitting algorithm has been found to be quite efficient, especially for high dimensional data, as only a subset of the best splitting rules are considered for growing trees and only the subset of most predictive sum of trees models are averaged over and saved to memory. Changing the terminal node priors to those used in Chipman et al. (1998) means that the model precision is needed only for calculation of the prediction credible intervals and not in the calculation of the likelihood. As such, a fast post hoc Gibbs sampler can be run, yielding estimates of predictive uncertainty in addition to point predictions.

BART-BMA proposes an efficient strategy for finding good splitting rules which works particularly well for high-dimensional data, where the uniform prior used by BART can become computationally intensive. BART-BMA borrows elements of both BART and RF in that it is a sum of trees ensemble model which averages over multiple sums of trees and as such offers a model-based alternative to machine learning methods for high-dimensional data.

BART-BMA can be seen as a bridge between RF and BART in that it is a model-based sum of trees method like BART and therefore can provide estimates of predictive uncertainty, but BART-BMA also averages over multiple sum of trees models in a similar way to RF. Like RF, BART-BMA not only provides a variable importance score but also provides access to the sums of trees chosen in the final model. In general BART-BMA tends to choose shallower and more interpretable trees than RF, as only splits which result in a high posterior probability are included.

We have showcased BART-BMA using both simulated and real life proteomic datasets and have shown its usefulness for high-dimensional data. We have found that BART-BMA is competitive with RF and BART in terms of speed and accuracy.

We envisage future applications and extensions for BART-BMA including dealing with missing data as well as for use on longitudinal data and extending this model to the family of generalised linear models. BART-BMA could also be parallelised to reap further gains in computational speed.

Table 8.

Coverage for out-of-sample 50% prediction intervals and average interval width for BART-BMA, RF using conformal intervals bartMachine and dbarts for the Friedman example. Perfect calibration is 50% hence the model with the lowest average interval width and a coverage as close to 50% as possible is most desirable. Items in bold refer to the best calibrated model with respect to interval coverage and the shortest average interval width for each simulated dataset

	Coverage					Average Interval Width
p	BART BMA	RF CP Intervals	bart Machine	dbarts default	dbarts best	BART BMA	RF CP Intervals	bart Machine	dbarts default	dbarts best
100	50.0%	49.0%	52.8%	48.0%	39.0%	4.02	4.29	2.60	2.40	1.57
1000	49.0%	51.0%	53.6%	33.8%	40.8%	4.04	4.89	3.55	2.58	2.12
5000	47.2%	48.0%	59.4%	38.0%	40.4%	4.01	5.03	5.63	3.46	2.49
10000	47.0%	46.0%	52.4%	45.4%	41.0%	4.01	4.89	5.76	4.07	2.99
15000	46.6%	49.0%	48.4%	43.8%	40.4%	4.01	5.05	6.27	4.60	3.32
100000	47.2%	50%	-	39%	46%	4.06	5.40	-	5.43	5.20
500000	44.0%	-	-	33.8%	%	4.03	-	-	5.36

Table 9.

Coverage for out-of-sample 75% prediction intervals and average interval width for BART-BMA, RF using conformal prediction bartMachine and dbarts for the Friedman example. Perfect calibration is 75% hence the model with the lowest average interval width and a coverage as close to 75% as possible is most desirable. Items in bold refer to the best calibrated model with respect to interval coverage and interval width for each simulated dataset.

	Coverage					Average Interval Width
p	BART BMA	RF CP Intervals	bart Machine	dbarts default	dbarts best	BART BMA	RF CP Intervals	bart Machine	dbarts default	dbarts best
100	75.8%	75%	77.2%	70.4%	61.2%	6.86	6.84	4.45	4.08	2.69
1000	74.0%	79%	79.0%	59.4%	62.6%	6.89	7.89	6.16	4.44	3.63
5000	72.6%	79%	87.0%	61.0%	64.8%	6.84	8.48	9.74	5.97	4.34
10000	73.4%	78%	76.8%	68.6%	64.2%	6.84	8.62	9.89	7.10	5.19
15000	73.4%	78%	75.2%	69.0%	67.0%	6.84	8.47	10.73	7.91	5.73
100000	71.8%	79%	-	59.0%	73.4%	6.91	9.30	-	9.21	8.88
500000	70.2%	-	-	56.6%	-	6.88	-	-	9.14	-

Appendix.

A BART full conditional distribution p(R_j|X, T_j, σ⁻²)

Using the forms of p(μ_ij) and p(σ^-2) described in Section 2.2.2 gives rise to the following full conditional distribution of the partial residuals for the BART model:

$$p(R_j|X,T_j,{\sigma }^{-2})\propto \prod _{i=1}^b{(n_i{\sigma }^{-2}+{\left(\frac{0.5}{e\sqrt{m}}\right)}^{-2})}^{-\frac{1}{2}}{\sigma }^{-2\frac{n+\nu }{2}-1}\times exp(-\frac{{\sigma }^{-2}}{2}(\sum _{\iota =1}^{n_i}{R}_{\iota ij}^2+\nu \lambda ))exp(\frac{n_i^2{\overline{R}}_{ij}^2{\sigma }^{-4}}{2(n_i{\sigma }^{-2}+{\left(\frac{0.5}{e\sqrt{m}}\right)}^{-2})})$$ (11)

where n_i is the number of observations in terminal node i of tree j and R̄_ij is the mean of the partial residuals R_j for terminal node i in tree j.

B BART for Classification

For binary classification Chipman et al. (2010) follows the latent variable probit approach of Albert and Chib (1993). Latent variables Z_k are introduced so that

$$Y_k=\{\begin{array}{cc}1& \text{if}{Z}_k>0\\ 0& \text{otherwise}.\end{array}$$

The sum of trees prior is then placed on the Z_k so that $Z_k~({\sum }_{j=1}^{m}g(x_k;T_j,M_j),1)$. It follows that Y_k is Bernoulli with

$$P(Y_k=1|x_k)=\mathrm{\Phi }(\sum _{j=1}^{m}g(x_k;T_j,M_j)),$$ (12)

where Φ is the standard normal cumulative distribution function (CDF), used here as the link function. Note that there is no residual variance parameter σ² in the classification version of the model.

Using the same prior distribution structure as in Section 2.2.2, the full posterior distribution of this version of the model is:

$$p(T,M,Z|X,Y)\propto p(Y|Z,T,M)[\prod _j\prod _{i}p({\mu }_{ij}|T_j)p(T_j)],$$ (13)

where the top level of the likelihood (i.e. the first term on the right hand side) is a deterministic function of the latent variables. The conditional prior distributions of the terminal node parameters μ_ij|T_j are set exactly as described in Section 2.2.2 except that ${\sigma }_0=\frac{3}{e\sqrt{m}}$ instead of ${\sigma }_0=\frac{0.5}{e\sqrt{m}}$. This is in order to assign high prior probability to the interval (Φ[−3], Φ[3]) which corresponds to the 0.1% and 99.9% quantiles of the normal CDF.

The fitting algorithm proposed by Chipman et al. (2010) for the classification model is nearly identical to that of their standard algorithm. The only difference is that the latent variables Z_k introduce an extra step in the Gibbs algorithm. The full conditional distributions of Z_k| … are:

$$Z_k|\dots ~\{\begin{array}{cc}min\left[N\right({\sum }_{j}g(x_k;T_j,M_j),1),0]& \text{if}{Y}_k=1,\\ max\left[N\right({\sum }_{j}g(x_k;T_j,M_j),1),0]& \text{if}{Y}_k=0.\end{array}$$ (14)

The partial residuals in the tree updates are of course now based on the latent variables Z_k for updating of individual trees.

C BART-BMA Algorithm overview

D BART-BMA Posthoc Gibbs Sampler

In order to provide credible intervals for the point predictions, Ŷ, provided by BART-BMA, we run a post-hoc Gibbs sampler. For each sum of trees model 𝒯_ℓ in Occam's window a separate chain in the MCMC algorithm is run. For each model 𝒯_ℓ, each terminal node parameter μ_ij in each tree T_j is then updated followed by an update of σ². The details of the updates for the full conditional of p(μ_ij|T_j, R_j, σ²) and of p(σ²) are explained in further detail in the following sections. The Gibbs sampler yields credible and prediction intervals for each set of sum of trees models accepted by BART-BMA along with the updates for σ⁻² for each set of trees accepted in the final BART-BMA model. The final simulated sample from the overall posterior distribution is obtained by selecting a number of iterations from the Gibbs sampler for each sum of trees model proportional to its posterior probability, and combining them. The post-hoc Gibbs sampler used by BART-BMA is far less computationally expensive than that of BART as it requires only an update for μ_ij and σ from the full conditional of each sum of trees model, which is merely a draw from a normal distribution and an inverse-Gamma distribution respectively (see Sections D.1 and D.2 respectively).

D.1 Update of p(M_j|T_j, R_ιji, σ²)

Let M_j = (μ_1j … μ_ij) index the b_j terminal node parameters of tree T_j, and R_kij be the partial residuals for observations k belonging to terminal node i used as the response variable to grow tree T_j. BART-BMA assumes that the prior on terminal node parameters is μ_ij|T_j, $\sigma ~N(0,\frac{{\sigma }^2}{a})$, as in Chipman et al. (1998). The prior distribution of the partial residual is R_j|…∼N(μ_ij, σ²).

The full conditional distribution of M_j is then

$$\begin{array}{c}p(M_j|T_j,R_{kij},\sigma )\propto p(R_{kij}|T_j,M_j,\sigma )p(M_j|T_j)\\ \propto \prod _{k=1}^{n_i}p(R_{kij}|T_j,M_j,\sigma )p(M_j|T_j),\end{array}$$ (15)

where k indexes the observations within terminal node i of tree T_j and n_i refers to the number of observations which fall in terminal node i.

The draw from the full conditional of p(M_j| …) is then a draw from the normal distribution

$$M_j|T_j,R_{kij},\sigma ~N(\frac{{\sum }_{k=1}^{n_i}{R}_{\iota ij}}{n_i+a},\frac{{\sigma }^2}{n_i+a}).$$ (16)

The full conditional of M_j| … depends only on σ in the variance parameter, making it slightly more efficient than the update of M_j using the BART prior which depends on σ in both the mean and variance parameter.

D.2 Update of p(σ²)

BART-BMA performs the update for p(σ) in the same way as (Chipman et al., 2010). The full conditional distribution of σ² is:

$$p({\sigma }^2|R_j,T_j,M_j)\propto \prod _{k=1}^{n}p(R_j|T_j,M_j,{\sigma }^2)p({\sigma }^2),$$ (17)

where $R_j~N({\sum }_{j=1}^{m}g(x_k.T_j,M_j),{\sigma }^2)$ and $\frac{1}{{\sigma }^2}~\text{Gamma}(\zeta ,\eta )$, where ζ and η are equal to $\frac{\nu }{2}$ and $\frac{\nu \lambda }{2}$, respectively.

BART-BMA makes the draw for σ² in terms of the precision ${\sigma }^{-2}=\frac{1}{{\sigma }^2}$ where p(σ⁻²|R_j, T_j, M_j) is calculated as:

$${\sigma }^{-2}|R_j,T_j,M_j~\text{Gamma}(\zeta ,\frac{1}{2},\frac{P}{2}+\frac{1}{\eta }),$$ (18)

where P = Σ_k [Y_k – Σ_j g(x_k, T_j, M_j)]². The next value of σ⁻² is then drawn from (18) and the value of σ is calculated by getting the reciprocal square root of that value.

E Greedy Tree Growing Extra Details

E.1 The PELT Algorithm

Univariate change point detection algorithms in general search for distributional changes in an ordered series of data. For example if normality is assumed then such an algorithm may look for changes in the mean or variance of the data. Searching for predictive split points for a single variable in a tree has an equivalent goal i.e. it is desirable to find split points which maximise the separation of the response variable between the left and right hand daughter nodes. For this reason we use a change point detection algorithm called PELT (Pruned Exact Linear Time) in BART-BMA to find predictive split points and greedily grow trees.

PELT was originally proposed to detect change points in an ordered series of data y_1:n =(y₁, …, y_n) by minimising the function

$$\underset{\delta }{min}[\sum _{\theta =1}^{\mathrm{\Theta }+1}[C(y_{({\delta }_{\theta -1}+1):{\delta }_{\theta }})+D]].$$ (19)

Here there are Θ change points in the series at positions δ_1:Θ = (δ₁, …, δ_Θ) which results in Θ + 1 segments. Each changepoint position δ_θ can can take the value 1… n – 1. For example if a change point occurs at position δ₁ = 5 and another occurs at position δ₂ = 12 the second segment where θ = 2 will contain the values for y_(6:12). The function C(·) is a cost function of each segment θ containing observations y_{(δθ–1+1):δθ}. In the results which follow, the cost function used is twice the negative log likelihood assuming that y has a univariate normal distribution. Finally, D is a penalty for adding additional change points, default values for which are discussed below.

PELT extends the optimal partitioning method of Yao (1984) by eliminating any change points which cannot be optimal. This is achieved by observing that if there exists a candidate change point s where δ < s < S which reduces the overall cost of the sequence, then the change point at δ can never be optimal and so is removed from consideration (Killick et al., 2012). An algorithm describing how we use PELT to greedly grow trees is described in Algorithm 3:

One disadvantage to using PELT for large datasets is that the number of change points detected by the PELT algorithm is linearly related to the number of observations, which can reduce the speed of the BART-BMA algorithm for large n. Our experience is that D = 10 log(n) performs well as a general default for the PELT penalty when n < 200. For larger values of n we recommend using a higher value for D or the grid search option instead (see Section 3.4.2) in order to limit the number of split points detected per variable. We implement a version of PELT which is equivalent to the PELT.meanvar.norm function from the changepoint package in R (Killick et al., 2014). This function searches for changes in the mean and variance of variables which are assumed to be normally distributed. Additional change points are accepted if there is support for their inclusion according to the log likelihood ratio statistic.

E.2 Updating Splitting Rules

By default we choose the best numcp% of the total splitting rules before the tree is grown and only trees using the most predictive splitting rules are considered for inclusion. However the best splitting rules can also be updated for each internal node i in each tree T_j, similarly to how RF creates trees. We have found that updating splitting rules at each internal node generally results in fewer trees T_j being included in each sum of trees model, however, each tree T_j within the sum of trees models averaged over in the final model tends to be deeper and to choose splits that are similar to the primary splits of trees in the RF. We have found that updating the splitting rules at each internal node can in some cases increase the predictive accuracy, but generally at the expense of computational speed.

F Out of sample prediction intervals

This appendix shows the results for the calibration of the Friedman example using 50% and 75% prediction intervals.

G Choice of Default Values for BART-BMA

This section will show some of the preliminary investigations which guided the choice of default settings for the BART-BMA algorithm such as the choice of the size of Occam's Window, the penalty on the PELT parameter and the size of sum of tree models to be averaged over. In the results that follow the following datasets are shown: Ozone, Compactiv, Ankara and Baseball datasets. These were also used as the benchmark datasets for the bartMachine package Kapelner and Bleich (2014b).

For each for the four datasets shown, varying amounts of random noise variables were appended to test the sensitivity of the parameters to the dimensionality of the dataset. In all, 17 different values for the number of random noise variables appended were tested ranging from 100 to 15, 000 so each parameter value of interest was run/tested a total of 68 times.

For the value of Occam's Window, 20 values were evaluated ranging from 100 to 100, 000. A contour plot showing the relative RMSE for the Baseball, Ankara, Compactiv and Ozone datasets can be seen in Figure 4. Here the RMSE value for each dataset has been divided by its minimum value which allows for fair comparison across datasets.

Figure 4.

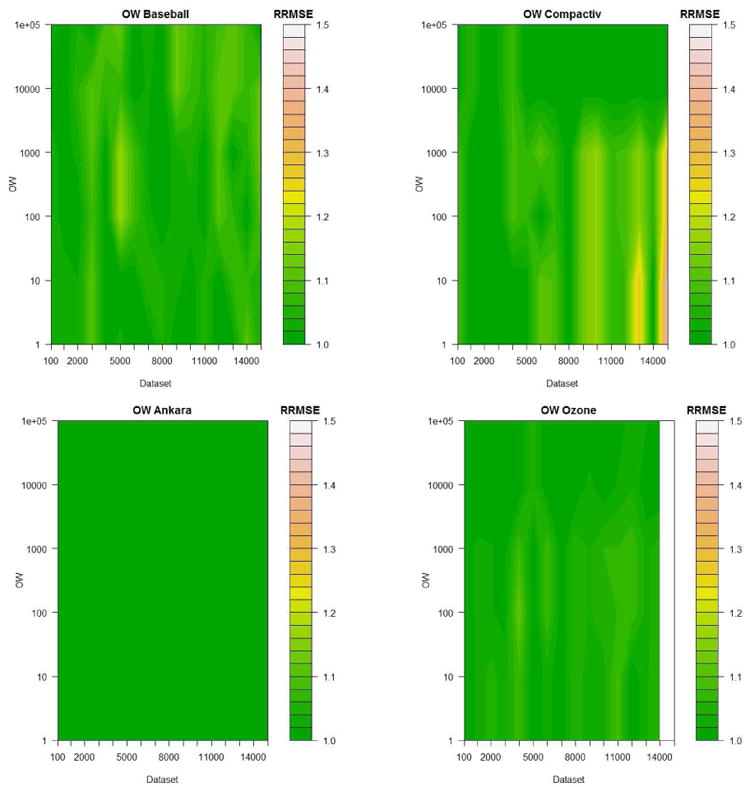
Example of experiments to guide default value chosen to determine the size of Occam's Window o = 1000

In general we recommend a default value of OW = 1000 as it seems to work well on the majority of datasets tested as can be seen here (and in other datasets not shown). It was decided that the additional computational complexity involved in setting OW = 10000 was not worth the marginal gain in accuracy for the datasets tested.

Figure 5 shows the same experiments conducted by ranging the multiple pen used in the PELT penalty D = pen log(n) from 1 to 20. Here we can see that a value of D = 10 log(n) works well in the majority of the datasets shown.

Figure 5.

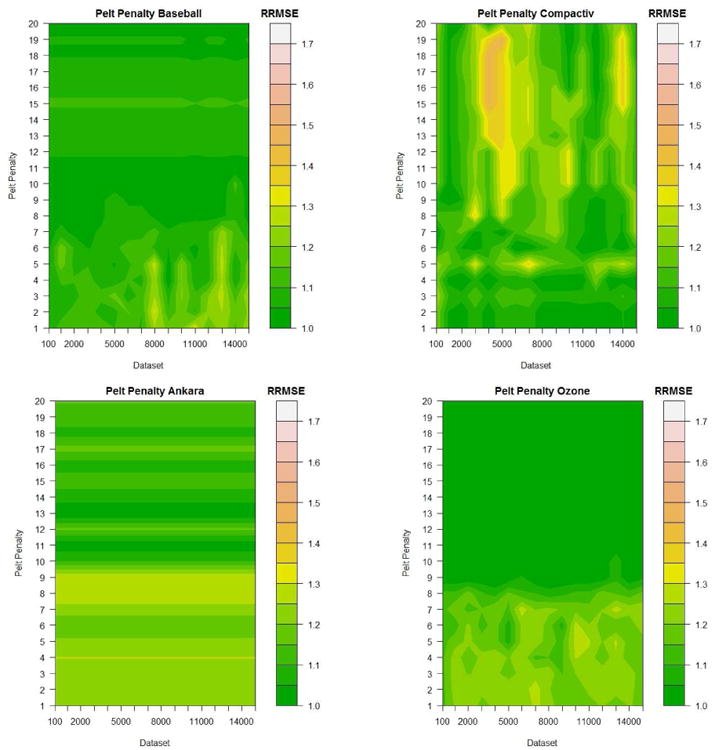
Example of experiments conducted to guide default value chosen to determine the size of the PELT parameter pen where D = pen log(n) given Occam's Window o = 1000

Figure 6 shows the same datasets where Occam's window is fixed at its default value of OW=1000 and the PELT penalty parameter is fixed at D=10Log(n). Here 7 increments for numcp were chosen ranging from 5% to 100%.

Figure 6.

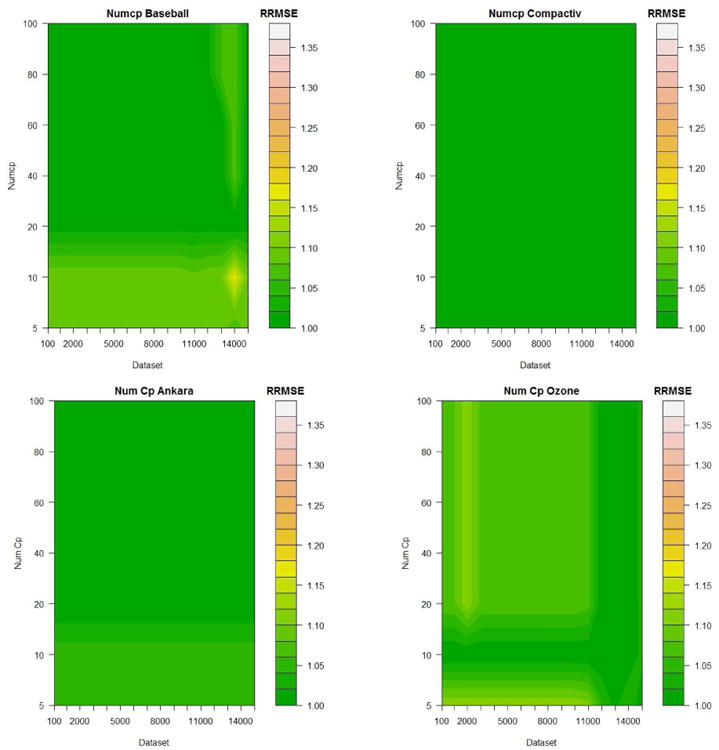
Example of experiments conducted to guide default value chosen to determine the numcp