Challenges and approaches to predicting RNA with multiple functional structures

Abstract

The revolution in sequencing technology demands new tools to interpret the genetic code. As in vivo transcriptome-wide chemical probing techniques advance, new challenges emerge in the RNA folding problem. The emphasis on one sequence folding into a single minimum free energy structure is fading as a new focus develops on generating RNA structural ensembles and identifying functional structural features in ensembles. This review describes an efficient combinatorially complete method and three free energy minimization approaches to predicting RNA structures with more than one functional fold, as well as two methods for analysis of a thermodynamics-based Boltzmann ensemble of structures. The review then highlights two examples of viral RNA 3′-UTR regions that fold into more than one conformation and have been characterized by single molecule fluorescence energy resonance transfer or NMR spectroscopy. These examples highlight the different approaches and challenges in predicting structure and function from sequence for RNA with multiple biological roles and folds. More well-defined examples and new metrics for measuring differences in RNA structures will guide future improvements in prediction of RNA structure and function from sequence.

INTRODUCTION

The blueprint for biological life is written in the sequence of RNA nucleotides. As we begin to decipher this exquisitely complex and evolving genetic code, we discover multiple layers of information and gene regulation. The primary structure, or sequence; the secondary structure or pattern of base-pairing and noncanonical motifs; the tertiary structure or three-dimensional shape of an RNA; and the quaternary structure or molecular folding partners, all play a role in information transfer and processes of the genetic code. The quest to predict RNA structure and function from sequence is increasingly inspired and spurred onward with an abundance of data from new sequencing technologies. Although only 1%–2% of the human genome encodes proteins, approximately 80% of the human genome encodes RNA (ENCODE Project Consortium 2007, 2011). New RNA folding challenges emerge as sequence databases grow.

The initial idea of one gene encoding one protein and one function was disproven as alternative splicing, frameshifting, and ambisense viral genomes that code for proteins in both the sense and antisense directions were discovered (Nguyen and Haenni 2003; Jangi and Sharp 2014; Caliskan et al. 2015). Similarly, the idea of one RNA sequence folding into a single lowest energy structure is fading as new RNA structures and functions are discovered. Riboswitches, a mechanism of gene regulation primarily known in prokaryotes that responds to metabolites with an RNA conformational switch, are the simplest case of an RNA sequence with two functional structures (Antunes et al. 2018). A recent genome-wide study of RNA base-pairing reveals that approximately 20% of eukaryotic RNA fold into multiple shapes in vivo, as evidenced by crosslinking pairs that are incompatible with a single structure (Lu et al. 2016). RNA viral genomes must adopt multiple functional RNA folds during the viral life cycle as the RNA genome transcribes, translates, recruits host molecular resources, evades host defenses, and packages into new virus particles (Schroeder 2009; Kutchko et al. 2018). Thus, the goal of predicting RNA structure and function is shifting from predicting a single lowest energy structure to the identification of functional structural features in an ensemble of RNA structures.

The traditional view of RNA folding funnels converging to a single low free energy structure may be better represented for riboswitches by a funnel with two wells (Fig. 1). A low broad folding basin with multiple low-energy folds and low-energy barriers for conformational changes may better describe RNA with multiple folds, such as viral RNA genomes that must refold at different life cycle stages. Different protein binding partners may selectively bind and stabilize structures from such a low-energy ensemble. Stabilization through protein binding may not require refolding the RNA but simply recognition of nucleotide sequences or loop motifs that favor specific and tight binding and thus shift the dynamic equilibrium of RNA conformations.

FIGURE 1.

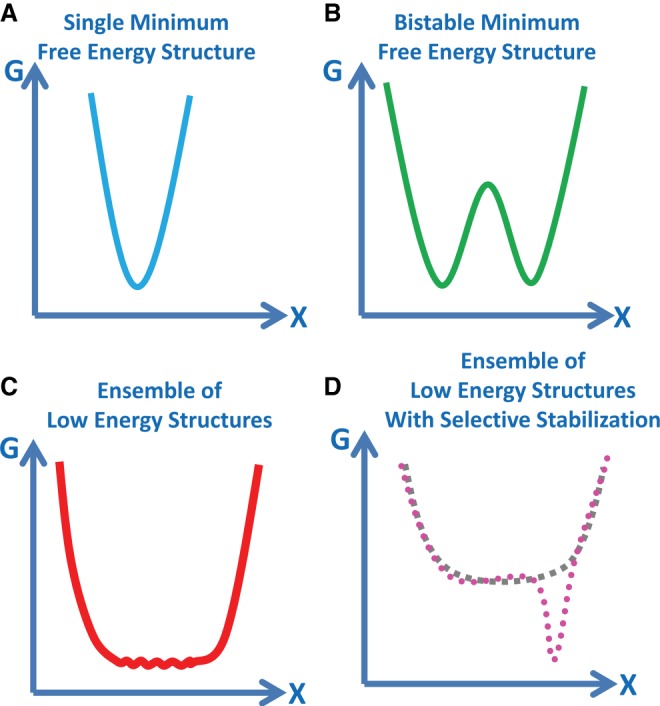
Models of the RNA folding problem. (A) A single minimum free energy structure is predicted for a single sequence in a traditional folding funnel. The conceptual graph plots free energy (G) versus conformational space (X). (B) A bi-stable free energy structure model has the two lowest energy structures with a high-energy barrier between the two folds. This model extends the single minimum free energy (MFE) model to riboswitches binding a ligand, for example. (C) An ensemble of low-energy structures resembles a low basin of possible structures rather than a folding funnel that converges to a single conformation. There are low or no energy barriers between different conformations. The bottom curve may be bumpy rather than smooth, although free energies may not distinguish very different structures. (D) An ensemble of low-energy structures (gray dashed line) may be selectively stabilized (magenta circles) by RNA binding a ligand or protein that recognizes motifs within the low-energy ensemble of structures.

This review focuses on current computational methods that address RNA folding challenges for predictions of RNA with multiple folds. Other recent reviews aptly provide an update on RNA folding tools (Fallmann et al. 2017; Lim and Brown 2018) and approaches specific for RNA riboswitch aptamers (Antunes et al. 2018). In this review, after a brief discussion of the RNA folding problem, we describe a combinatorially complete approach, two algorithms that analyze the Boltzmann ensemble to identify sequences with multiple folds, and three free energy minimization approaches to predicting RNA structures with more than one functional fold. All these approaches incorporate experimental constraints for RNA folding. Finally, we discuss two recent experimentally characterized viral RNA sequences that fold into more than one functional conformation and thus pose challenges for future RNA structure prediction development.

HIERARCHICAL RNA FOLDING

Because RNA typically follows a hierarchical folding pathway (Tinoco and Bustamante 1999; Zhang et al. 2017; Gracia et al. 2018; Šponer et al. 2018), prediction of RNA secondary structure followed by RNA tertiary structure is often a successful strategy. The pattern of Watson–Crick pairing provides significant constraints that reduce the complexity of tertiary structure prediction. The free energies of secondary structure motifs such as nearest neighbor Watson–Crick pairs range from −0.9 to −3.4 kcal/mol and are more stable than free energies of tertiary interactions that range from −0.3 to −1.5 kcal/mol (Xia et al. 1998; Turner 2000; Bisaria et al. 2017). Thus, the free energies of RNA secondary and tertiary structure motifs support a model of modular, hierarchical folding in RNA. In vivo-like folding conditions and molecular crowding favor cooperative folding and differentially affect the stabilities of secondary and tertiary structure motifs (Kilburn et al. 2016; Leamy et al. 2017, 2018) and suggest a hierarchical model based on structure. Although in vivo folding is dominated by nonequilibrium kinetic processes such as cotranscriptional folding and RNA processing events (Mahen et al. 2005, 2010; Kilburn et al. 2016; Hua et al. 2018), hierarchical folding based on thermodynamic stabilities remains an effective paradigm for RNA structure prediction. All the participants in the recent RNA Puzzles competition use this step-wise approach to folding RNA structures (Miao et al. 2017). The advances in RNA tertiary structure prediction can be applied to secondary structure predictions of RNA with two or more folds, as demonstrated by the RNA Puzzles participants’ approaches to riboswitch prediction (Miao et al. 2017) and modular energetic frameworks for RNA folding (Bisaria et al. 2017).

Figure 2 shows an example of the primary, secondary, tertiary, and quaternary structure folding for a small noncoding RNA in a bacteriophage packaging motor called prohead RNA (pRNA). This 120-nt sequence folds into a single secondary structure that is well predicted by phylogenetic analysis and verified by chemical probing experiments (Bailey et al. 1990; Hao and Kieft 2014, 2016). Computational predictions for pRNA sequences have improved over the past ten years as a result of improvements in the thermodynamics database and an expanded number of test cases for a wider variety of RNA sequences (Lorenz et al. 2011; Xu and Mathews 2016). The multibranch loops in the phi29 pRNA adopt more than one conformation in crystal structures (Ding et al. 2011; Zhang et al. 2013), and the bulge loop in the GA1 pRNA adopts multiple conformations unless a metal ion is bound (Gu et al. 2016). pRNA molecules self-assemble to form dimers, trimers, and multimers in vitro and a ring in the context of the prohead bacteriophage (Bailey et al. 1990; Chen et al. 1999; Morais et al. 2008; Gu and Schroeder 2011; Hao and Kieft 2014, 2016). Thus, RNA may adopt multiple conformations on many levels of RNA folding. This review focuses on predicting multiple conformations in RNA secondary structure formation. (See Table 1.)

FIGURE 2.

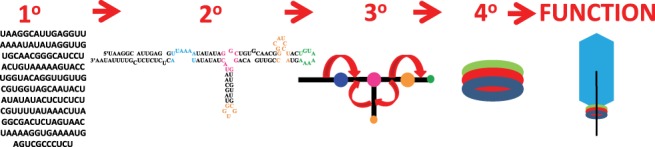
Hierarchical RNA folding. The primary structure is the sequence; in this example, the sequence of GA1 prohead RNA. The secondary structure is the pattern of Watson–Crick pairs and noncanonical motifs, such as bulge loops, multibranch loops, and hairpin loops. The primary and secondary structures for GA1 pRNA were first reported in Bailey et al. (1990). The tertiary structure is the three-dimensional shape of the molecule. In this ball-and-stick model of pRNA, the orientations of the helices (shown as black sticks) are flexible around the loops (shown as balls). The dynamic helical angles are represented by curly red arrows. The quaternary structure is interactions of the RNA with other RNA, protein or ligands. In the case of GA1 pRNA, the pRNA forms a ring (red circle) with a ring of ATPases (blue circle) and connector proteins (green circle). The function of GA1 pRNA is to package the bacteriophage DNA genome (black line) into a preformed capsid (blue hexagon).

TABLE 1.

Programs for predicting or analyzing RNA ensembles with multiple conformations

TRADITIONAL RNA FOLDING APPROACHES

Phylogenetic analysis and free energy minimization are two common approaches to generating an RNA secondary structure. Phylogenetic analysis and identification of covariation in Watson–Crick base pairs remains the gold standard for RNA secondary structure prediction. Patterns of covariation and sequence conservation are often used to identify structural motifs in RNA transcriptome sequences but require cautious interpretation and rigorous statistical validation (Rivas et al. 2017). Phylogenetic analysis requires multiple aligned sequences and sufficient sequence diversity to identify covariation. If an RNA has multiple folds, then nucleotide covariation may not be present. However, high mutual information scores for nucleotides can reveal evolutionary evidence for multiple folds for an RNA sequence (Ritz et al. 2013). Covariation may also not be observed in protein coding regions when the conservation of amino acid sequence and tRNA codon optimization influence the RNA primary structure more strongly than RNA folding. mRNA and viral RNA, for example, often show little nucleotide covariation. Evolutionary couplings and maximum entropy models may better describe complex RNA interaction networks in multiple folds, RNA tertiary interactions, and RNA–protein interactions (Weinreb et al. 2016).

Free energy minimization can provide a secondary structure model for a single or multiple RNA sequences. The thermodynamic database that forms the foundation for free energy minimization is still being updated with improved thermodynamic parameters for noncanonical RNA loop motifs (Phan et al. 2017; Zuber et al. 2017). One approximation of the Zuker–Steigler algorithm is that substructures with suboptimal energies will not be combined, which very efficiently reduces the search for the minimum energy structure (Zuker and Stiegler 1981; Mathews 2006). For example, in a region with two possible suboptimal hairpins, each hairpin will occur in a structure in the set of suboptimal structures, but no structure will include both hairpins (Mathews 2006). Free energy minimization approaches for secondary structure prediction do not yet fully consider RNA folding kinetics, cotranscriptional folding, changes with RNA tertiary interactions, protein binding, quaternary interactions, and the complex effects of in vivo conditions that include molecular crowding and both diffuse and specific interactions with metal ions and charged metabolites. Recent advances in techniques to monitor cotranscriptional folding in vitro also provide new challenges for RNA structure prediction of multiple conformations and folding kinetics (Mahen et al. 2005; Strobel et al. 2017, 2018; Hua et al. 2018). Incorporation of experimental constraints from chemical or enzymatic probing, NMR, or phylogeny can improve RNA secondary structure prediction (Mathews et al. 2004; Havgaard and Gorodkin 2014; Sloma and Mathews 2015; Backofen et al. 2018). The ability to chemically probe RNA structures in vivo and genome-wide using next generation sequencing technology has created an urgent need for methods to better predict RNA structures with more than one conformation, which is common in living cells.

A single lowest energy fold, however, may not represent well the RNA folding landscape. Free energies may not distinguish very different structures, especially for long RNA sequences with many possible folds. For example, the STMV RNA sequence has two possible structures that share only 498 of 1058 nt in common base pairs but differ by only 0.2 kcal/mol, which is well within experimental error of the thermodynamic parameters (Schroeder 2009; Stone et al. 2015). Base-pairing probabilities can be computed with free energy-based prediction tools and the McCaskill algorithm (McCaskill 1990). Base-pairing probabilities can identify regions with a high probability of folding and regions with multiple energetically equivalent structures. Using stochastic sampling methods, i.e., the random sampling of the Boltzmann-weighted ensemble of RNA structures, centroid structures may better represent groups of similarly folded structures (Ding et al. 2004, 2005; Quarrier et al. 2010; Rogers et al. 2017). When the minimum free energy structure and the centroid structure predictions differ significantly, this may be an indicator that free energy minimization approaches are limited and additional experimental information or tools are necessary.

COMBINATORIALLY COMPLETE APPROACH

The first combinatorially complete approach to tRNA structure prediction, i.e., the direct enumeration of every possible secondary structure for a given RNA sequence and Watson–Crick pairing rules, took so much computational time that the approach was deemed impractical for solving the RNA folding problem (Pipas and McMahon 1975). Advances in computer power and parallelization strategies, however, can overcome this limitation. Swellix, a new computational tool (Sloat et al. 2017), generates a complete set of secondary structures for a 76-nt tRNA Phe sequence in <2 h on an XE6 node of the Blue Waters supercomputer. Swellix is a combinatorially complete approach to computing all possible nonpseudoknotted combinations of helices for an RNA sequence without using thermodynamics. Thermodynamic parameters can be used to evaluate and score the RNA structures in Swellix output, but Swellix does not use thermodynamics to generate structures. Swellix counts helices rather than base pairs and groups similar helices in bundles in order to efficiently explore all possible structures. Experimental data from crystallography, cryoelectron microscopy, chemical probing, and phylogeny can be incorporated into Swellix in order to reduce the conformational space for a sequence.

Swellix can generate a profile of the frequency of motifs for protein or small molecule binding. For example, a Swellix computation of all possible structures for a 141-nt HERV RNA revealed that a loop that binds HIV tat and two loop sequences that bind HIV rev occur in 4.58%, 2.80%, and 4.58% of all possible nonpseudoknotted structures, respectively (Sloat et al. 2017). Loops that are known to bind small molecule therapeutics can also be profiled with Swellix. For example, two highly asymmetric loop sequences in hepatitis C viral RNA that bind drug molecules also occur in 4.41% and 2.71% of the structures in the complete set of possible structures for HERV RNA. The Swellix analysis generated 12,518,055,094 structures in 6.65 h on the Blue Waters supercomputer. Neither the minimum free energy structure (MFE), predicted suboptimal structures, nor the centroid structure contained the loop motifs that bind HIV proteins or hepatitis C drug candidates. The MFE and the centroid were not similar at all for this HERV RNA and no predicted base pairs were highly probable, which all indicated that the assumptions of free energy minimization approaches may not be applicable to this RNA sequence. The assumptions of hierarchical and thermodynamically driven folding are often reasonable approximations. However, sometimes kinetics, protein binding, RNA tertiary structure formation, or motifs that are not yet included in the thermodynamic database have a significant impact on RNA folding. In these cases, a complete enumeration approach that generates a profile of frequencies for motifs of interest can be useful.

Although Swellix efficiently searches conformational space of a sequence, the longest sequence studied thus far is 418 nt within 48 h on an XE6 node of the Blue Waters computer. The computational time generally grows exponentially with sequence length. The average size of the 5,391,569 RNA sequences in the RFAM database is 435 (Nawrocki et al. 2015). Thus, Swellix could be applied to many types of RNA in the RFAM database, although some RNA would be too long. For example, the untranslated regions (UTR) rather than the entire mRNA or other small domains of noncoding RNA would be more tractable for Swellix analysis. Pairing constraints from crosslinking or phylogenetic covariation and helix constraints from cryoelectron microscopy or crystallography are the most effective constraints for reducing conformational space (Bleckley and Schroeder 2012), and more experimental constraints enable longer sequences to be computed with Swellix. However, computational resources are the only fundamental limit to combinatorially complete approaches, and advances in computing power and efficiency continue apace.

ANALYSIS OF BOLTZMANN ENSEMBLES TO IDENTIFY SEQUENCES WITH MULTIPLE FOLDS

RNA sequences with a propensity for multiple folds can be identified through analysis of the Bolztmann ensemble of structures for a sequence to identify multimodal patterns (Ding et al. 2004; Rogers and Heitsch 2014; Lin et al. 2018). Ding and Lawrence developed the sfold algorithm to generate a statistical sampling of the Boltzmann-weighted ensemble of structures for a given sequence and thermodynamic parameter database (Ding et al. 2004). The RNA profiling tool in the GTfold program uses a helix abstraction to analyze the Boltzman ensemble of structures (Rogers and Heitsch 2014). The selected profiles reveal the most probable combination of helices and are useful for identifying sequences with more than one probable fold. The most informative base pair (MIBP) algorithm (Lin et al. 2018) includes several metrics to identify sequences that have high propensity for multiple folds, analyze the effects of SHAPE pseudoenergy terms on the Boltzmann distribution, and provide insight on why some sequences fold into mainly one structure and others fold into multiple structures. Mutual information is the amount of information one base pair contains about another base pair, and the sum of a pair's mutual information with every other base pair provides information about the overall RNA secondary structure. The base pair with the highest sum of mutual information with every other base pair is the MIBP. Interestingly, the most probable conflicting pair has the most pairwise mutual information with the MIBP and is a particularly useful metric for indicating that an RNA sequence may have more than one fold using the MIBP algorithm (Lin et al. 2018). High values in SHAPE reactivities, low sequence conservation, and high Shannon entropy in SHAPE-MaP experiments are good experimental indicators for RNA sequences or regions of long RNAs that may have more than one conformation (Siegfried et al. 2014). Shannon entropy is a measure of uncertainty in a message, and has different interpretations when the information in the message is an RNA, DNA, or protein sequence, sequence alignments, RNA secondary structures, mutations, or other data. While RNA sequences can be referred to as multimodal, high Shannon entropy, or high SHAPE, this review will use the nomenclature of “RNA with multiple conformations” or “multiconformational ensembles.”

FREE ENERGY MINIMIZATION APPROACHES

We next highlight three free energy minimization approaches to predicting multiple functional secondary structures for a single RNA sequence. The three approaches all use the same database of free energy parameters, incorporate experimental constraints from chemical probing, and share the same goal of predicting more than one structure from a sequence. The approaches differ in the selection of test cases, the methods for clustering analysis, and the metrics for distinguishing ensembles of RNA structures.

Rsample is a new tool in the RNAstructure software package that uses thermodynamic data, partition functions, stochastic sampling, and chemical probing data in computations of RNA with multiple conformations (Spasic et al. 2018). The approach explicitly considers that a sequence may fold into more than one conformation, samples RNA structure models, and optimizes the comparison between the experimental chemical probing data and estimated chemical probing data from a calculated ensemble. In the first steps, a partition function calculation and stochastic sampling generate an ensemble of RNA structures for a given sequence. Then estimated chemical probing reactivities are calculated for the ensemble, and a pseudo-free energy bonus term for reactivities is incorporated as a restraint in the folding predictions. Next, stochastic sampling computations and clustering analysis generate centroid structures. For five test cases, the HIV-1 rev responsive element (RRE) and four riboswitches, that have two experimentally identified conformations and SHAPE (selective hydroxyl acylation by page electrophoresis) chemical probing data, Rsample generated centroids for each conformation with accuracies for the best centroid ranging from 81.7% to 100%. The method was also applied to an FMN riboswitch with three possible conformations in both the bound and unbound states. The incorporation of chemical probing data improved predictions ∼10% relative to predictions without chemical probing data. With more data on RNA with multiple conformations and optimization of the heuristically determined parameters, Rsample will further improve prediction accuracy and interpretation of in vivo genome-wide chemical probing experiments.

REEFFIT, RNA Ensemble Extraction from Footprinting Insights Technique, is a free energy minimization approach to predicting multiple RNA conformations and uses additional data from mutate-and-map strategies (Cordero and Das 2015). The mutate-and-map strategy systematically incorporates mutations into a sequence and identifies mutations that cause a significant change in chemical probing reactivities. REEFFIT uses a chemical reactivity distribution based on analysis of the RNA Mapping Database (Cordero et al. 2012) and crystal structures in the Protein Databank (Rose et al. 2017), a set of RNA secondary structures from the ALLSub program in RNAstructure (Reuter and Mathews 2010), and likelihood function to generate predictions of RNA sequences with multiple conformations. The program was initially optimized on an in silico data set of 20 RNA sequences from the Rfam database (Nawrocki et al. 2015; Kalvari et al. 2018). The program was tested on three naturally occurring RNA with experimentally well-defined bi-stable states as well as one natural sequence and one designed sequence that each form three stable conformations. REEFFIT accurately predicts 95% of the helices present in structures with at least 25% population in the ensemble and has a low false discovery rate of ∼10%. Currently the main limitation is detecting low percentage populations of structures, which is especially challenging for long sequences with large ensembles. Improvements in the thermodynamic database (Turner and Mathews 2009), more data in the chemical mapping database, and more test cases of RNA with experimentally determined structures will further development of this approach.

The EnsembleRNA program includes aspects of Boltzmann sampling and mutational analysis and utilizes unique metrics for identifying diverse structures (Woods et al. 2017). The EnsembleRNA method begins with a sequence and computes the partition function for the wild type and all single point mutations. Then the maximally different structures according to Shannon entropy and hierarchical clustering are selected for calculation of Boltzmann suboptimal sampling computations. In order to generate a two-dimensional representation of conformational space, structures are grouped by hierarchical clustering and RNAShapes abstraction (Giegerich et al. 2004; Janssen and Giegerich 2015), a method of broadly identifying helices and loop regions, then arranged according to a multidimensional scaling (MDS) metric. The method was validated using adenine riboswitch and SHAPE probing data. The two adenine-bound conformations and three unbound conformations were accurately identified. The method was also tested on the human β-actin mRNA sequence with both in vitro and in vivo SHAPE-MaP experiments. Interestingly, in regions with similar SHAPE reactivities in vitro and in vivo, high median reactivity correlated with multiple alternative conformations. Surprisingly, the two mRNA binding sites for the ZBP1 protein showed higher reactivities in vivo versus in vitro, which lacks the proteins. Rather than indicating protein footprinting as expected, the high SHAPE reactivities may indicate occupancy of protein binding and flexible secondary structure rearrangements. Although only one mRNA was the focus of the study, this method can be expanded to gain new insights into the many in vivo conformations of mRNA that regulate gene expression.

VIRAL RNA WITH EXPERIMENTALLY DEFINED COMPLEX LANDSCAPES

All of the approaches to predicting RNA structures with multiple conformations and complex folding landscapes will benefit from more experimentally well-defined test cases. The review now discusses two recent examples of viral RNA that have been studied with chemical probing and either NMR or single molecule fluorescence resonance energy transfer (smFRET). In each case, existing RNA structure prediction tools were adapted to solve the specific RNA folding problems. In addition to all the structures of riboswitches (Antunes et al. 2018), these new NMR and smFRET approaches to characterization of RNA with more than one functional structure provide new test cases and insights into how an RNA sequence can encode and utilize many different shapes and functions. Further development of RNA structure prediction tools will be necessary to meet these challenges.

The 3′-UTR of the brome mosaic virus has three distinct possible folds, a folded conformation with a pseduoknot, an intermediate, and a tertiary unfolded conformation that forms a series of short hairpins, which depend on sodium, potassium, and magnesium ion concentrations. The three conformations of this 169-nt RNA can be isolated and studied by SHAPE chemical probing. Folding of this RNA has also been studied by smFRET to identify the three distinct conformations and their relative abundance in different combinations of salt concentrations (Vieweger and Nesbitt 2018). Using SHAPE reactivities of the pure isolated conformations and the population of each fraction as determined by smFRET, the SHAPE reactivities in heterogeneous conformational mixtures can be deconvoluted. The low-level SHAPE reactivities were most indicative of transition from single-stranded to double-stranded conformation, while the largest SHAPE reactivities were interpreted to report mainly on flexibility in single-stranded regions. This approach highlights the challenges in interpreting chemical probing reactivities for RNA that may form heterogeneous populations of structures. RNAstructure software was used to generate RNA secondary structures using SHAPE restraints. Interestingly, the 3′ end pseudoknot interaction unfolds first before the hairpin conformations unfold. In addition to providing insight into the folding pathway of this viral RNA, this approach will be generally useful for RNA with distinct stable folds and provide important data for optimizing predictions of RNA with multiple conformations.

The 3′-UTR of hepatitis C virus also folds into more than one conformation. The 385-nt 3′ end of the genomic RNA can adopt an open conformation of six hairpins or a kissing loop complex that forms in a magnesium-dependent manner. The final 98 nt of the 3′ end, also called 3X′, can form a structure with three hairpins or two hairpins, in which two hairpins have completely refolded to form one new longer hairpin. The presence of the kissing loop hairpin partner can induce this structural change (Kranawetter et al. 2017). The 3X′ sequence can also form a dimer that facilitates genome dimerization for packaging (Cantero-Camacho et al. 2017). NMR spectroscopy has been used to characterize these conformational changes. Selective deuterium labeling and lr-AID (Keane et al. 2016), a method that identifies the unusual chemical shift of the central adenine H2 proton in the motif 5′UAA3′/3′AUU5′, has been used to characterize both the transition from open to kissing loop conformation and the structural rearrangements from two to three hairpins in 3X′ (Kranawetter et al. 2017). In addition, the Monte Carlo Tightly Bound Ion (MCTBI) (Sun et al. 2017) and Vfold 3D RNA folding software (Zhao et al. 2017) have been used to model the different conformations of the 3′-UTR and the metal ion binding sites. This viral RNA example is particularly challenging because the conformational change depends on both magnesium and the presence of 5′ upstream hairpin structures.

FUTURE OUTLOOK FOR MULTICONFORMATION RNA STRUCTURE ENSEMBLE PREDICTION

In the future, more examples of experimentally well-defined multiconformational states will help optimize approaches for RNA structure prediction. NMR spectroscopy and smFRET are powerful tools to probe the many states that RNA may adopt. The PARIS method for in vivo crosslinking also has great potential to provide many examples of RNA with multiple folds (Lu et al. 2016). Advances in cryoelectron microscopy and tomography with direct electron detectors, better contrast techniques, and single particle tracking will make direct observation of single RNA molecules in many conformations possible (Miyazaki et al. 2010; Merk et al. 2016; Zhang et al. 2018). The cryoelectron microscopy community has also developed advanced software for grouping similar conformations of complex macromolecular assemblies (Frank 2017). The minimum number and lengths of RNA helices from cryoelectron microscopy or crystallography also provide a powerful constraint for RNA folding (Schroeder et al. 2011; Bleckley and Schroeder 2012; Bleckley et al. 2012).

There is also a need for good metrics to evaluate differences between RNA structures. The AnalyseDist tool in the Vienna RNA software package includes several options for calculating matrix distances by Ward's method, Saitou's neighbor joining method, or Shapiro's cost matrix for coarse structures (Bonhoeffer et al. 1993; Lorenz et al. 2011). For example, the RNA base pair distance metric calculates the number of base pairs in common between two RNA secondary structures, and the RNApdist function compares the dot plots from partition functions for two RNA ensembles (Bonhoeffer et al. 1993). Dot plots are one way to summarize and visualize base-pairing probabilities for an RNA sequence. The idea of Shannon entropy, a measure of uncertainty or disorder in information theory, also provides metrics to distinguish different structures. For example, the EnsembleRNA methods use Shannon entropy for base-pairing probabilities as a metric in clustering analysis (Woods et al. 2017; Spasic et al. 2018). The Shannon entropy can be calculated for base pairs, the full two-dimensional base-pairing probabilities, or thermodynamic structural entropy (Shapiro 1988; Rivas and Eddy 2001; Woods et al. 2017). The molecular interpretation of the Shannon entropy statistic depends on the type of data, such as RNA sequence alignments, sequence point mutations, SHAPE-MaP data, or thermodynamic calculations. The RNAEnsemble approach also introduces a novel metric for measuring nestedness of RNA structures. The nestedness is calculated from the number of inner and outer stacks and loops in structures that are represented using the RNAShapes abstraction for helices (Giegerich et al. 2004; Woods et al. 2017). This metric is then used in metric multidimensional scaling in order to generate a visual map of RNA ensembles.

Thus, with new metrics and more experimentally defined examples of multiconformation RNA ensembles, RNA structure prediction will continue to improve. The expectation of a single minimum free energy structure for an RNA sequence will change to a deeper appreciation for the many possible diverse structures encoded in an RNA sequence. Accurate predictions will guide the interpretation of the abundant ongoing transcript and transcriptome-wide structure probing experiments. A full understanding of the multiconformational RNA ensembles will improve rational design and reduce off-target effects of small RNA that target mRNA for siRNA or CRISPR guide RNA applications. Accurate RNA ensemble information will also facilitate target site selection of highly probable motifs for siRNA, guide RNA, or small organic molecule therapeutics. An ensemble approach to RNA structure prediction will also facilitate discovery of how proteins and ligands selectively stabilize certain conformations and shift the population distribution of conformations. Perhaps ligands or proteins can be rationally designed to enrich low population states. Among the many layers of information and gene regulation encoded in the human transcriptome, there are multiple opportunities to use this information to improve human health. The structure prediction tools described here are one step forward toward reading and understanding all the information in the genetic code.