Evaluation of consistency for multiple experiments of a single combination in the time-dependence mixture toxicity assay

Abstract

Test-to-test consistency was evaluated for a single binary combination of organic chemicals using an assay that examined toxicity over multiple exposure times. Six experiments were conducted. The toxicity of 3-chloro-2-butanone (3C2B), methyl crotonate (MC) and the mixture (MX) was evaluated in each experiment at 15, 30 and 45-min of exposure using the Microtox^® system. Concentration-response (x/y) curves were generated via the five-parameter logistic minus one-parameter (5PL-1P) curve-fitting function and used to develop predicted x/y curves for the dose-addition (DA) and independence (I) models of combined effect. A variety of toxicity (e.g., EC₅₀) and time-dependent toxicity (TDT) endpoints, 5PL-1P parameters, and various combined effects metrics (e.g., MX/DA) were calculated. Test-to-test consistency was evaluated via the coefficient of variation (CV) or, for TDT, the standard deviation of mean values. In the study, CVs obtained for single-chemical and mixture toxicity endpoints (EC₂₅, EC₅₀, and EC₇₅) at each exposure time were <20, as were those for the predicted DA and I curves. For the MX/DA metric, mixture toxicity was consistent with that predicted for DA at each exposure time in each experiment with CVs <6, despite some substantial variation in TDT for MC-alone at the EC₂₅ and for the 30 to 45-min time-interval. There was lower variation in TDT for 3C2B and for MX. Mean and CV values for 5PL-1P-derived slope and asymmetry parameters were also assessed to provide bases for comparisons in future reports.

Introduction

Research on chemical mixture toxicity is an area of considerable activity. Recent studies have included research in the areas of environmental (Altenburger et al. 2015) and human health (Toccalino et al. 2012, Muthusamy et al. 2016), ecotoxicology (Kim et al. 2013, Białk-Bielińska et al. 2017), and aquatic toxicology (Dietrich et al. 2010, Tipping and Lofts 2013). Commonly examined chemicals included pesticides (Belden et al. 2007, Phillips et al. 2010, Nowell et al. 2014), polycyclic aromatic hydrocarbons (Landrum et al. 2012), pharmaceuticals (Houtman et al. 2014, Watanabe et al. 2016), nanoparticles (Lopes et al. 2016) endocrine disruptors (Webster 2013), and metals (Balistrieri et al. 2015). Such studies have been conducted on simple and complex environmental mixtures. The variety of these studies and the types of organisms, assays, and predictive models used have been based on the goals of the studies and derived from the complexities of chemical fate and distribution, exposure and uptake processes, chemical reactivity, toxicokinetics and metabolism, and abiotic factors.

Recent work in this lab has utilized the Microtox^® system to evaluate time-dependence in mixture toxicity. These studies have examined toxicity of selected mixtures of industrial organic chemicals (e.g., Gagan et al. 2007, Dawson et al. 2008), developed and evaluated the 5PL-1P function for concentration-response curve-fitting (Dawson et al. 2012, 2016) and examined the viability of using time-dependent toxicity (TDT) of the individual chemicals for predicting TDT of the mixtures (Dawson et al. 2014a). The design of these studies has included multiple tests of individual chemicals (Dawson et al. 2010, 2011, 2014b, 2016) thereby allowing for assessment of test-to-test consistency of those data, but none of these studies had evaluated such consistency over several tests of the same mixture. For this system to be a reliable approach for evaluating mixture toxicity of commonly used industrial organics such an assessment was needed.

To conduct the study it was determined that both of the individual chemicals selected for mixture testing should have increasing toxicity over exposure time (i.e., TDT >0). Chemicals lacking TDT tend to be unreactive (Gagan et al. 2007), thereby exerting reversible toxicity primarily via effects on the cell membrane (e.g., non-polar narcosis). Additionally, it was determined that neither chemical should have fully time-dependent toxicity (i.e., TDT ≥100%) as those agents appear to exert only irreversible toxic effects. Previous testing had suggested that there would be higher test-to-test variability in TDT for chemicals with mid-range TDT (i.e., TDT between about 20 and 80%), as such chemicals appear to have two modes of toxic action –reversible toxicity, especially at lower concentrations during earlier exposure times, and some form of irreversible action, most notably at higher concentrations and later in exposure (Gagan et al. 2007). For these reasons 3C2B and MC were selected as the single-chemicals to be used in this study as they have mid-range TDT. Six experiments of the chemical combination 3C2B-MC were conducted to evaluate test-to-test consistency of the model system. Data from each experiment were recorded and analyzed to evaluate consistency of the results for this model system.

Materials and Methods

Chemicals and reagents

Chemicals used in toxicity testing were purchased (Sigma-Aldrich, Milwaukee, WI) at ≥97% purity and used as received. Stock solutions for 3C2B, MC and the 3C2B-MC mixture (MX) were freshly prepared just prior to testing. Microtox^® reagent, reconstitution solution, and diluent were obtained from Modern Water, Inc. (New Castle, DE).

Toxicity testing

Utilizing the quorum-sensing activity of the marine bacterium Aliivibrio fischeri (Urbanczyk et al. 2007), inhibition of bioluminescence was assessed using a calibrated Microtox^® 500 analyzer (Dawson et al. 2014a, b). Six experiments were conducted. Each consisted of three toxicity tests: 3C2B-alone, MC-alone and MX within a 4.5 – 5 hr period. For all experiments the tested concentrations (nominal) were prepared via serial dilution (dilution factor = 1.75) and corrected for density since both chemicals were liquids at room temperature.

In each test, seven concentrations were evaluated in duplicate along with a duplicated control treatment. The 3C2B concentrations tested were the same in experiments 1–3 and were changed slightly for experiments 4–6. Concentrations of MC were also the same for experiments 1–3, but varied in each of experiments 4–6. For a given experiment, the MX concentration series always used the second highest concentration of 3C2B-alone and of MC-alone to form its highest concentration, with the other MX concentrations resulting from the 1.75 dilution factor used (see Supplementary Tables S1–S6). Initial bioluminescent readings were taken before chemical exposure; following exposure light readings were made at 15, 30 and 45-min.

Curve-fitting

Concentration-response (x/y) data were input to SigmaPlot^® (v. 11.0; Systat Software, Chicago, IL) and fitted to sigmoid curves using the 5PL-1P function (Dawson et al. 2012). This method utilized four parameters: EC₅₀, slope, maximum effect and asymmetry.

Curve fitting was performed using:

$$y=max÷{[1+{(xb÷x)}^{slope}]}^s$$

with y = % effect, max = maximum effect, x = concentration, s = asymmetry. The variable xb was determined using:

$$xb={EC}_{50}\times {10}^{[(1÷slope)\times \mathrm{l}\mathrm{o}\mathrm{g}(2^{(1÷s)}-1)]}$$

Initial parameters for the regressions were automatically estimated while employing three constraints: a) EC₅₀ > 0; b) 0.1< s <10; and c) max = 100. Maximum effect values were constrained to 100% to provide consistency in calculating TDT values (Dawson et al. 2016). For each exposure time, single-chemical x/y data were used to calculate EC₂₅, EC₅₀, and EC₇₅ values. The EC₅₀ was defined as the half-maximal effective concentration, while the EC₂₅ and EC₇₅ were the one-quarter and three-quarters-maximal effective concentrations, respectively. Percent effect values for each replicate were determined using Microtox^® Omni software. Slope and asymmetry values were also calculated.

For analyzing MX data, concentrations of MC were converted to concentration-equivalents of 3C2B using a conversion factor obtained by dividing the concentration of 3C2B by the concentration of MC (Dawson et al. 2010). This conversion allowed the total chemical concentration of the mixture to be made relative to those for 3C2B-alone, so that toxicity plots of the mixture at any exposure duration could be visualized alongside the plots of 3C2B and MC. The same curve-fitting methods used for the single-chemical data were used for MX data.

Calculation of time-dependent toxicity (TDT) values

To quantify changes in toxicity over exposure time, TDT values were calculated at the 25, 50 and 75% effect-levels (Gagan et al. 2007) and for the 15 to 30-min, 30 to 45-min and 15 to 45-min time-intervals using the appropriate time-factors for each. Time-factors (0.5 for 15 to 30-min, 0.333 for 30 to 45-min and 0.667 for 15 to 45-min) were calculated via the following equation:

$$(t_2-t_1)/t_2$$

with t₂ being the later time of the exposure interval and t₁ the earlier time of that interval. Then the equations below were used to calculate TDT:

$${d=EC}_{x_{t_1}}-{EC}_{x_{t_2}}$$

$$e=d÷({EC}_{x_{t_1}}\times f_{t_1:t_2})$$

$$TDT=e\times 100$$

with EC_x being the effect-level (i.e. 25, 50, or 75%) and $f_{t_1:t_2}$ being the appropriate factor for the time-interval. As an example, for a hypothetical chemical with a 15-min EC₅₀ of 90 mg/L and a 45-min EC₅₀ of 30 mg/L, the TDT at 50% effect for the 15 to 45-min time-interval was 100%, as shown below:

$$\text{a})90mg/L-30mg/L=60mg/L$$

$$\text{b})60mg/L÷(90mg/L\times 0.667)=1$$

$$\text{c})1\times 100=100\mathrm{\%}$$

Values for the TDT₂₅ or TDT₇₅ were calculated in the same manner by incorporating the appropriate time-factor and EC₂₅ or EC₇₅ data, respectively.

In addition to effect-level and time-interval TDT values for each individual experiment, mean TDT values for effect-level (i.e., mTDT₂₅, mTDT₅₀, and mTDT₇₅) and time-interval (i.e., mTDT_15:30, mTDT_30:45, and mTDT_15:45) were also calculated for each experiment. Mean TDT values for a given effect-level were determined by:

$${mTDT}_x=\frac{\left({TDT}_{15:30}+{TDT}_{30:45}+{TDT}_{15:45}\right)}{3}$$

in which x represents the selected effect-level (i.e., 25, 50, or 75%). Mean TDT values for a given time-interval were calculated as follows:

$${mTDT}_{t1:t2}=\frac{\left({TDT}_{25}+{TDT}_{50}+{TDT}_{75}\right)}{3}$$

in which t₁:t₂ represents the selected time-interval (i.e., 15 to 30, 30 to 45 or 15 to 45-min). It was previously shown that mTDT_15:45 values for single-chemicals were of value in predicting mTDT_15:45 for binary mixtures (Dawson et al. 2014a).

Calculation of predicted dose-addition and independence curves

Predicted x/y curves for dose-addition (DA) were calculated as described previously (Dawson et al. 2011). When chemicals A and B (i.e., 3C2B and MC respectively, in this study) are dose-additive the EC₅₀ for the A+B mixture is graphically left-shifted by a dose-ratio (DR) factor of 2 when the chemicals are equieffective. This is calculated using the equation:

$$Add50=\frac{a50}{DR50}$$

with Add50 being the EC₅₀ for dose-addition, a50 the EC₅₀ for the more potent chemical and b50 (see below) the EC₅₀ for the less potent agent. The DR50 was determined by:

$$DR50=1+\left(\frac{a50}{b50}\right)$$

Calculations of EC₂₅ and EC₇₅ values for the predicted DA curve were also made. Taken together these predicted values (EC₂₅, EC₅₀, and EC₇₅) permitted calculation of the predicted dose-addition curve via the curve-fitting procedures described above.

Predicted curves for the independence (I) model (Bliss 1939) were calculated using a user-generated transform within SigmaPlot^® as:

$$yA+\left[yB\mathrm{*}\frac{(100-yA)}{100}\right]$$

with yA and yB being the percent effect values for chemicals A and B, respectively.

Combined effects determination

Dose-additivity quotient (AQ) and independence quotient (IQ) values were calculated as metrics of combined effect for the mixtures. These values were determined by dividing the respective EC₅₀ value for the mixture at a given exposure time by the predicted EC₅₀ value for DA or I, respectively (Dawson et al. 2014b) at that exposure time. For example, a hypothetical AQ₅₀ calculation for a MX with a 45-min EC₅₀ of 22.1 mg/L and a predicted 45-min EC₅₀ value of 23.4 mg/L for DA is 0.94. Previously this lab has considered AQ and IQ values from 0.90 to 1.10 as being consistent with DA and I, respectively (Dawson et al. 2016). The AQ and IQ values were also determined for the 25 and 75% effect-levels at each exposure time.

Since the slope of a MX curve can be different than that for chemical A, chemical B or both a second combined effects metric was developed for both DA (i.e., MX/DA) and I (i.e., MX/I) (Dawson et al. 2016). To calculate MX/DA and MX/I the concentrations of 3C2B and concentration equivalents of MC (calculated as noted above) at the EC₂₅, EC₅₀, and EC₇₅ of the mixture were summed (i.e., EC_25+50+75) and divided by the sum of those same effect-level concentrations for the predicted DA curve and for the predicted I curve, respectively. These metrics allowed for a more complete assessment of combined effect from the 25 – 75% effect-levels than did examining mixture toxicity at only the 50% effect-level (Dawson et al. 2016).

Slope quotients

A variety of slope quotient values were also calculated for the toxicity data. Slopes of the x/y curves were determined at each exposure time for 3C2B-alone, MC-alone, and MX and for the predicted DA and I curves. Slope quotient values for each single-chemical and mixture versus DA and I were determined simply by dividing the observed slope by the predicted DA or I slope at the exposure time of interest.

Calculation of observed minus predicted TDT

By calculating TDT for each single-chemical and mixture at each effect-level and time-interval it was possible to compare observed mixture TDT (MX TDT_obs) with predicted mixture TDT (MX TDT_pred) from the single-chemical data (Dawson et al. 2014a). The MX TDT_obs value for a given experiment was its mTDT_15:45 value. The MX TDT_pred value for that experiment was calculated using the single-chemical mTDT_15:45 values for that experiment; calculated as follows:

$$MX{TDT}_{pred}=\frac{\left(3C2B{mTDT}_{15:45}+MC{mTDT}_{15:45}\right)}{2}.$$

Then observed minus predicted TDT for the mixture (MX TDT_{obs – pred}) was calculated as:

$$MX{TDT}_{obs-pred}=MX{TDT}_{obs}-MX{TDT}_{pred}.$$

Because MX TDT_pred can be either greater-than or less-than the MX TDT_obs, to accurately calculate the mean for MX TDT_{obs – pred} values, the absolute values were used.

Data Quality Assessments and Statistical Procedures

The quality of x/y data was evaluated in two ways. Fitting of x/y data using the 5PL-1P function was assessed by calculating coefficient of determination (r²) values. Test-to-test consistency for EC_x, EC_25+50+75, slope, slope quotient, s, and the combined effects metrics (i.e., MX/DA, MX/I, AQ₅₀, and IQ₅₀) was evaluated by calculating the coefficient of variation (CV) using:

$$CV=\frac{100*s.d.}{mean}.$$

This approach has been noted to be preferable to using the standard deviation (s.d.) when data are collected by multiple operators (Steel and Torrie 1980). For TDT data, since some effect-level and time-interval TDT values for MC were negative, s.d. of mean values were directly used to evaluate test-to-test consistency.

For assessing statistical significance, data means were evaluated differently depending on whether the mean values of interest were paired or consisted of more than two groups. For pairwise comparisons the t-test was used unless the Shapiro-Wilk Normality Test failed; in the latter instances the Mann-Whitney Rank Sum Test was used to evaluate median values. For comparison of means across three groups, One-Way Analysis of Variance (ANOVA) was used. When there were significant differences among groups and the data were normally distributed, the Holm-Sidak multiple-comparison test was used. When the data were not normally distributed, the Kruskal-Wallis One-Way ANOVA on Ranks test was used to evaluate median values. All statistical procedures were conducted within SigmaPlot. Statistical significance was set at p < 0.05.

Results

Concentration-response (x/y) data

Six experiments were conducted in the study with each experiment including a test of 3C2B-alone, MC-alone and MX. The x/y data for each experiment are provided in the supplementary data tables (S1–S6).

Single-Chemical Toxicity Data

For each experiment, the EC₂₅, EC₅₀, and EC₇₅ values were calculated for 3C2B-alone and MC-alone after 15, 30 and 45-min of exposure (Table 1). At each effect-level, toxicity increased upon longer exposure for both chemicals, as noted by the lower EC_x values at longer exposure times. For each chemical, effect-level, and exposure time the coefficient of variation (CV) for mean values was <20.0 (Table 1), ranging from a low of 5.6 (3C2B 15-min EC₅₀) to a high of 17.7 (MC 45-min EC₂₅).

Table 1.

Consistency^a of EC_x toxicity data (mg/L) for 3C2B and MC tested alone

	15-min			30-min			45-min
Experiment #	EC25	EC50	EC75	EC25	EC50	EC75	EC25	EC50	EC75
3C2B – 1	7.9	21.5	56.2	5.3	14.1	35.4	4.2	10.9	26.6
3C2B – 2	6.9	19.7	52.0	4.8	13.5	34.3	3.7	10.4	25.9
3C2B – 3	6.4	18.1	47.8	4.6	13.0	32.8	3.6	10.2	25.4
3C2B – 4	7.1	19.9	54.1	5.4	15.1	39.1	4.7	12.6	31.1
3C2B – 5	6.7	19.7	54.3	5.5	15.4	39.0	4.6	12.8	31.2
3C2B – 6	7.0	20.2	55.4	5.8	15.6	40.5	5.2	13.0	32.1
mean	7.0	19.8	53.3	5.2	14.4	36.8	4.4	11.6	28.7
CV	7.1	5.6	5.7	8.2	7.6	8.5	14.1	10.9	10.6
MC – 1	83.2	245.1	610.4	77.5	204.4	456.6	74.2	193.8	407.2
MC – 2	70.0	211.6	541.9	68.7	184.5	421.0	70.3	183.5	385.9
MC – 3	70.8	221.1	554.5	67.9	193.7	436.7	67.4	187.2	395.8
MC – 4	54.7	175.1	461.5	49.5	146.6	342.9	50.2	140.5	302.8
MC – 5	59.8	182.4	469.7	59.0	155.1	348.4	51.2	138.3	297.0
MC – 6	63.3	202.7	502.6	53.1	156.9	360.5	52.6	141.9	304.2
mean	66.9	206.3	523.4	62.6	173.5	394.4	61.0	164.2	348.8
CV	15.0	12.5	10.8	16.9	13.7	12.6	17.7	16.1	15.1

^amean and coefficient of variation (CV) values obtained from data calculated to four decimal places

Mixture and predicted dose-addition and independence curve data

As with the single-chemical tests, effect-level toxicity values were calculated at each exposure time for MX data. Toxicity increased with increased exposure time at each effect-level (Table 2: columns 3, 6, and 9). As with the single-chemical data, CV values for MX data were always <12.0 (Table 2), ranging from a low of 10.2 (15-min EC₂₅) to a high of 11.8 (15-min EC₅₀).

Table 2.

Consistency^a of experimental (mg/L) mixture (MX) toxicity and predicted (mg/L) mixture toxicity for the dose-addition (DA) and independence (I) models

		EC25			EC50			EC75
Time	Experiment #	MX	DA	I	MX	DA	I	MX	DA	I
15-min	MX – 1	3.9	4.5	4.1	11.5	12.6	11.0	31.5	32.4	25.4
	MX – 2	3.6	3.9	3.4	11.0	11.3	9.6	29.8	29.4	22.7
	MX – 3	3.4	3.7	3.2	10.0	10.9	9.2	27.6	28.3	22.0
	MX – 4	3.5	3.8	3.3	10.4	11.4	9.5	28.9	30.6	22.9
	MX – 5	3.0	3.3	2.9	8.9	9.9	8.3	24.9	26.3	19.7
	MX – 6	3.0	3.1	2.6	8.5	9.4	7.8	24.1	24.4	18.8
	mean	3.4b	3.7b	3.2b	10.1c	10.9c	9.3c	27.8d	28.6d	21.9e
	CV	10.2	13.3	15.0	11.8	10.7	12.2	10.3	10.2	10.8
30-min	MX – 1	3.3	3.4	3.2	9.2	9.1	8.4	22.8	21.9	18.6
	MX – 2	2.7	3.1	2.8	8.5	8.5	7.7	21.8	20.8	17.4
	MX – 3	2.7	3.0	2.6	8.1	8.4	7.4	20.7	20.5	17.2
	MX – 4	2.9	3.1	2.7	8.4	9.0	7.8	21.5	22.4	18.2
	MX – 5	2.5	2.9	2.7	7.1	8.0	7.3	18.3	19.2	16.1
	MX – 6	2.6	2.6	2.3	7.0	7.3	6.4	17.6	17.6	14.5
	mean	2.8f	3.0f	2.7f	8.1g	8.4g	7.5g	20.5h	20.4h	17.0i
	CV	10.5	9.5	11.2	10.6	8.1	8.7	10.1	8.6	8.7
45-min	MX – 1	2.9	2.9	2.7	7.9	7.5	7.0	18.9	17.5	15.5
	MX – 2	2.3	2.6	2.4	7.3	7.2	6.6	18.3	16.8	14.9
	MX – 3	2.2	2.5	2.2	6.9	7.1	6.3	17.2	16.8	14.7
	MX – 4	2.6	2.9	2.6	7.5	7.9	7.1	18.4	18.6	16.1
	MX – 5	2.2	2.5	2.2	6.2	6.9	6.2	15.2	15.9	13.8
	MX – 6	2.2	2.4	2.4	5.9	6.3	6.0	14.0	14.5	12.6
	mean	2.4j	2.7j	2.4j	6.9k	7.2k	6.5k	17.0l	16.7l	14.6l
	CV	11.0	7.8	8.6	11.2	7.7	7.0	11.6	8.5	8.4

^amean and coefficient of variation (CV) values were obtained from data to four decimal places

^{b, c, f, g, j, k, l}grouped means with the same designation were not significantly different (one-way ANOVA, p > 0.05)

^{d,e; h,i}means at these exposure times were significantly different (Holm-Sidak test, p < 0.05)

To assess mixture toxicity against the DA and I models, predicted DA and I curves were calculated from the single-chemical data. Predicted toxicity values (presented as 3C2B-equivalent concentrations in mg/L) also showed increased toxicity with increased exposure time (Table 2: columns 4, 7, and 10 for DA; columns 5, 8 and 11 for I). For both DA and I, CV values at each effect-level and exposure time were ≤15.0.

Mean toxicity data were evaluated for statistical differences (Table 2). Mean values for MX and DA showed no significant differences at any exposure time. Mean I values were not significantly different from those for MX and DA at the EC₂₅ and EC₅₀ at any exposure time. However, mean I values at the EC₇₅ were significantly different than the respective EC₇₅ means for MX and DA at 15 and 30-min of exposure.

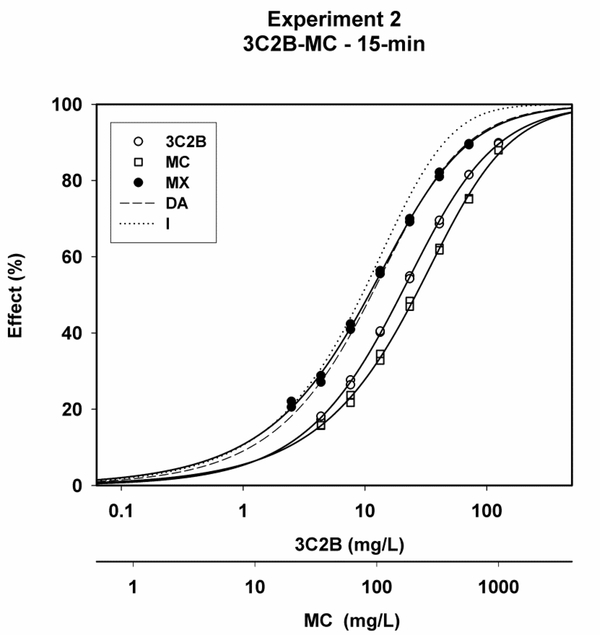
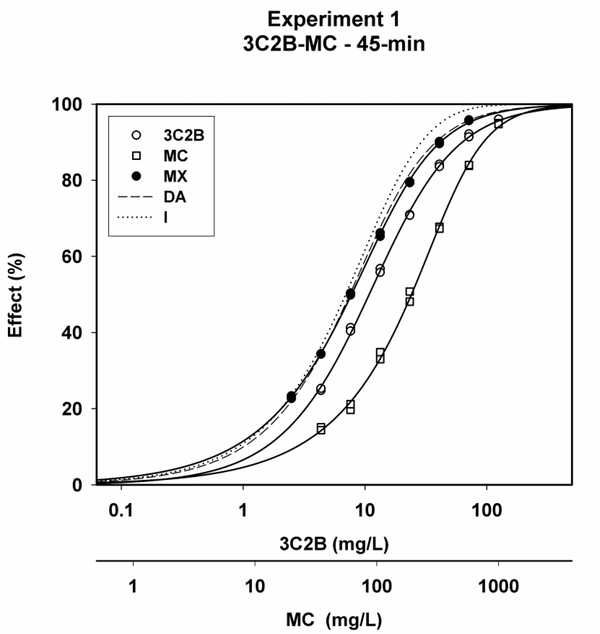
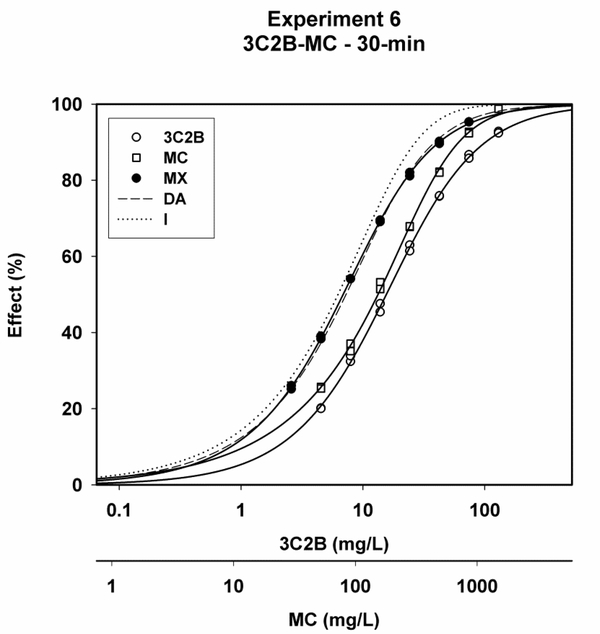
Representative plots of x/y data for 3C2B, MC, MX, and the predicted DA and I curves showed that MX curves plotted more closely to the predicted DA curves than to the predicted I curves (Figs. 1–3).

Figure 1.

Concentration-response curves for 3-chloro-2-butanone (3C2B), methyl crotonate (MC) and the 3C2B-MC mixture (MX) after 15-min of exposure in experiment #2, along with predicted curves for the dose-addition (DA) and independence (I) combined effects models. Experimental MX toxicity was better aligned visually with the predicted DA curve than the predicted I curve.

Figure 3.

Concentration-response curves for 3-chloro-2-butanone (3C2B), methyl crotonate (MC) and the 3C2B-MC mixture (MX) after 45-min of exposure for experiment #1, along with predicted curves for the dose-addition (DA) and independence (I) combined effects models.

Slope, asymmetry (s) and coefficient of determination (r²) values

As an important element of 5PL-1P curve-fitting, slope values were recorded for 3C2B, MC, and MX at each effect-level and exposure time (Supplementary Table S7: columns 2–4). Individual slope values tended to increase upon increased exposure time for the single-chemicals and mixtures; as did the mean values. Standard deviations for mean slope at 15, 30 and 45-min were ±0.05, ±0.05, and ±0.08, respectively for 3C2B, ±0.11, ±0.10, and ±0.09, respectively for MC and ±0.08, ±0.08, and ±0.07, respectively for MX. Resulting CV values for slope means were <10.0, ranging from 3.7–7.2. Slopes for MC were significantly different from those for 3C2B and MX at each exposure time, but slopes were only significantly different between 3C2B and MX at 45-min (Holm-Sidak test, p <0.05).

Asymmetry (s) values were not equal to 1.0, thereby indicating that plotted x/y data were not symmetrical (Supplementary Table S7: columns 5 – 7). Mean and CV values for s were calculated for each chemical and mixture at each effect-level and exposure time. All mean s values were <1.0 and CV values ranged from 7.7 to 24.1. Median or mean s values were significantly different between MC and both 3C2B and MX at 15-min (Tukey test, p <0.05) and 30-min (Holm-Sidak test, p <0.05), respectively. At 45-min, the mean s values were significantly different between 3C2B and MC (Holm-Sidak test, p <0.05) but not between MC and MX or 3C2B and MX (Holm-Sidak test, p ≥0.05).

To assess the quality of x/y data curve-fitting with the 5PL-1P function, r² values were determined for all tests at each exposure time (Supplementary Table S7: columns 8–10). Individual test r² values ranged from 0.9971 to 0.9998. Mean r² values were ≥0.9990 for the 3C2B and MX tests and ≥0.9982 for MC tests. In all cases CV values for the means were ≤0.07.

Time-dependent toxicity (TDT) data for individual tests

Individual TDT values were calculated for each test of 3C2B and MC at the 25, 50 and 75% effect-levels and each of the three exposure time-intervals: 15 to 30-min, 30 to 45-min and 15 to 45-min (Table 3). For 3C2B, individual TDT values were generally lower at 25% effect than at the 50 and 75% effect-levels for each time-interval. For MC, TDT also increased with increasing effect-level, but the increase was more marked than for 3C2B. By calculating the averages for TDT values across all six experiments, s.d. values at each effect level and time-interval were determined. These showed higher test-to-test variability for MC than for 3C2B. This was especially noted for the 30 to 45-min interval at TDT₂₅ (7.7%±17.1). For 3C2B, the highest s.d. value for TDT data was also for the 30 to 45-min interval at TDT₂₅ (50.7%±16.2).

Table 3.

Consistency^a of individual test time-dependent toxicity (TDT_x)^b values for 3C2B, MC and their binary mixtures (MX)

	TDT25			TDT50			TDT75
Experiment #	15–30 min	30–45 min	15–45 min	15–30 min	30–45 min	15–45 min	15–30 min	30–45 min	15–45 min
3C2B – 1	64.9	61.0	69.3	69.1	68.6	74.3	74.0	74.8	79.1
3C2B – 2	61.2	66.3	68.9	63.5	67.6	70.7	68.2	73.3	75.3
3C2B – 3	55.3	64.8	64.9	56.5	64.0	65.4	62.9	67.2	70.2
3C2B – 4	48.4	36.9	50.3	47.6	50.3	54.8	55.6	61.1	63.7
3C2B – 5	37.7	48.6	48.0	43.4	51.2	52.6	56.2	59.9	63.7
3C2B – 6	34.9	26.9	37.3	45.0	51.1	53.6	53.9	62.5	63.3
average	50.4	50.7	56.4	54.2	58.8	61.9	61.8	66.5	69.2
± s.d.	12.3	16.2	13.2	10.6	8.8	9.5	8.0	6.4	6.8
MC – 1	13.7	12.6	16.2	33.2	15.5	31.4	50.4	32.4	49.9
MC – 2	3.7	-7.1	-0.7	25.7	1.6	19.9	44.6	25.0	43.2
MC – 3	8.1	2.2	7.1	24.8	10.1	23.0	42.5	28.1	42.9
MC – 4	18.7	-3.7	12.3	32.5	12.5	29.6	51.4	35.1	51.6
MC – 5	2.7	39.8	21.7	30.0	32.6	36.3	51.6	44.3	55.2
MC – 6	32.3	2.4	25.2	45.2	28.7	45.0	56.5	46.9	59.2
average	13.2	7.7	13.6	31.9	16.8	30.9	49.5	35.3	50.3
± s.d.	11.1	17.1	9.5	7.4	11.7	9.1	5.1	8.7	6.5
MX – 1	30.7	40.9	40.4	40.8	42.8	47.7	54.8	51.5	59.8
MX – 2	48.5	49.3	55.1	45.7	44.9	51.6	54.0	48.4	58.1
MX – 3	41.3	51.6	51.5	39.6	45.0	47.7	50.4	50.8	56.8
MX – 4	31.7	41.0	41.0	38.4	34.8	42.9	50.9	44.6	54.8
MX – 5	30.8	39.9	40.0	39.7	39.6	45.6	53.0	51.0	58.5
MX – 6	31.7	40.4	40.8	35.9	48.1	46.7	53.7	62.0	62.9
average	35.8	43.9	44.8	40.0	42.5	47.0	52.8	51.4	58.5
± s.d.	7.4	5.2	6.7	3.3	4.7	2.9	1.7	5.8	2.7

^aaverage and standard deviation (s.d.) values were obtained from data calculated to four decimal places

^bpercentage-based TDT_x values were calculated at the 25 (TDT₂₅), 50 (TDT₅₀), and 75% (TDT₇₅) effect levels for each time-interval in each experiment

Mixture TDT was also determined at each effect-level and time-interval (Table 3). As with the single-chemicals, TDT increased with increased effect-level and was always highest for the 15 to 45-min interval. The highest s.d. value for MX was for the 15 to 30-min interval at TDT₂₅ (35.8%±7.4). Variability in TDT was lower for MX than for either 3C2B or MC.

Mean effect-level and time-interval TDT values for individual tests

Individual TDT values for each of the six experiments were used to generate mean TDT (mTDT) values for each experiment – at both effect-level and time-interval (Supplementary Table S8). The trend for mTDT values showed increased mTDT with increased effect-level for 3C2B, MC and MX. The time-interval with the highest mTDT was 15 to 45-min for each. In addition for MC, mTDT for the 30 to 45-min interval (i.e., mTDT_30:45) was lower than for mTDT_15:30 and mTDT_15:45.

Combined effects determination vs. the dose-addition and independence models

For each of the six MX tests, the sum of the 3C2B-equivalent concentrations at the EC₂₅, EC₅₀, and EC₇₅ (i.e., EC_25+50+75) were calculated at each exposure time (Table 4: column 3). These sums were also calculated for the predicted DA curve and the predicted I curve at each exposure time (Table 4: columns 4, 5). One-way analysis of variance and the Holm-Sidak multiple comparison test indicated that the mean EC_25+50+75 values for I at 15-min and 30-min were significantly different than those for MX and DA, whereas there was no statistical difference in mean EC_25+50+75 values between MX, DA and I at 45-min.

Table 4.

Consistency^a of actual mixture (MX) vs. predicted dose-addition (DA) and independence (I) concentrations (mg/L) and combined effects values for the mixtures

		EC25+50+70b
Time	Experiment #	MX	DA	I	MX/DAc	MX/Id	AQ50e	IQ50f
15-min	MX – 1	46.95	49.50	40.52	0.95	1.16	0.91	1.05
	MX – 2	44.37	44.57	35.66	1.00	1.24	0.97	1.15
	MX – 3	40.99	42.92	34.40	0.96	1.19	0.92	1.09
	MX – 4	42.82	45.87	35.70	0.93	1.20	0.91	1.09
	MX – 5	36.80	39.42	30.90	0.93	1.19	0.90	1.07
	MX – 6	35.62	36.85	29.27	0.97	1.22	0.90	1.08
	mean	41.26g	43.19g	34.41h	0.96i	1.20j	0.92k	1.09l
	CV	10.6	10.5	11.6	2.5	2.4	3.0	3.1
30-min	MX – 1	35.35	34.38	30.22	1.03	1.17	1.01	1.09
	MX – 2	33.03	32.32	27.82	1.02	1.19	1.00	1.11
	MX – 3	31.42	31.91	27.28	0.98	1.15	0.96	1.08
	MX – 4	32.90	34.57	28.70	0.95	1.15	0.93	1.08
	MX – 5	27.97	30.17	26.09	0.93	1.07	0.89	0.98
	MX – 6	27.17	27.47	23.27	0.99	1.17	0.96	1.09
	mean	31.31m	31.80m	27.23n	0.98i	1.15j	0.96k	1.07l
	CV	10.1	8.4	8.8	4.0	3.5	4.8	4.4
45-min	MX – 1	29.68	27.88	25.26	1.06	1.18	1.06	1.12
	MX – 2	27.85	26.63	23.85	1.05	1.17	1.05	1.11
	MX – 3	26.30	26.43	23.24	1.00	1.13	0.97	1.09
	MX – 4	28.37	29.47	25.81	0.96	1.10	0.94	1.05
	MX – 5	23.61	25.25	22.29	0.94	1.06	0.90	1.00
	MX – 6	22.07	23.22	20.99	0.95	1.05	0.93	0.98
	mean	26.32o	26.48o	23.57o	0.99i	1.11j	0.97k	1.06l
	CV	11.1	8.1	7.7	5.3	4.7	5.8	5.5

^amean and coefficient of variation (CV) values obtained from data to four decimal places

^bsum of the EC₂₅, EC₅₀, and EC₇₅ values expressed as 3C2B-equivalent concentrations

^cMX/DA = MX EC_25+50+75 / DA EC_25+50+75 at a given exposure time

^dMX/I = MX EC_25+50+75 /I EC_25+50+75 at a given exposure time

^edose-additivity quotient value at the EC₅₀ only

^findependence quotient value at the EC₅₀ only

^g,hgrouped means with different letters were statistically different (Holm-Sidak test, p < 0.05)

^i,jmean MX/DA and MX/I values at that exposure time were statistically different (t-test, p ≤ 0.003)

^k,lmean AQ₅₀ and IQ₅₀ values at that exposure time were statistically different (t-test, p ≤ 0.02 or lower)

^m,ngrouped EC_25+50+75 means with different letters were statistically different (Holm-Sidak test, p < 0.05)

^ogrouped EC_25+50+75 means were not significantly different in one-way ANOVA

Calculating EC_25+50+75 for MX, DA and I facilitated comparison of MX toxicity vs. the DA and I combined effects models using the MX/DA and MX/I metrics, respectively (Table 4: columns 6, 7). In each individual test, mixture toxicity was consistent with dose-addition at each exposure time, with MX/DA values being from 0.93–1.00 at 15-min, 0.93–1.03 at 30-min and 0.94–1.06 at 45-min. Mean MX/DA values were 0.96, 0.98 and 0.99 at those respective times with the CV for each being <6.0 (Table 4: column 6). However, individual MX/I values were consistent with independence (i.e., 0.90 ≤ MX/I ≤ 1.10) in only 4 of 18 cases over the three exposure times (Table 4: column 7). Mean MX/I values decreased across increased exposure time, from 1.20 at 15-min to 1.11 at 45-min, with CV values for MX/I means being <5.0 at each exposure time. Statistically at each exposure time, MX/DA mean values were significantly different from those for MX/I (t-test, p ≤0.003).

Determinations of mixture toxicity using AQ and IQ values at the 50% effect-level for the individual mixtures were made (Table 4: columns 8–9) for comparison with the MX/DA and MX/I metrics. At a given exposure time, both the individual and mean AQ₅₀ and IQ₅₀ values were most often lower than the respective MX/DA and MX/I values. Additionally, the AQ₅₀ values were consistent with DA, with one exception at 30-min (MX–#5), and the IQ values were more frequently consistent with I than were the MX/I values (i.e., 14/18 for the former, 4/18 for the latter). At each exposure time, mean AQ₅₀ and IQ₅₀ values were significantly different from each other (t-test, p ≤0.02).

Predicted dose-addition and independence slope and slope quotient values

Slopes of predicted x/y curves for DA and I were determined at each exposure time (Supplementary Table S9: columns 3, 4). The mean DA slope increased from 1.32 to 1.47 to 1.57 as exposure time increased from 15 to 30 to 45-min, respectively. The mean I slope also increased with increased exposure time from 1.73 to 1.88 to 1.95. At each exposure time the difference in mean slope values for DA and I curves was statistically significant (p <0.001).

Slope quotient (SQ) values for 3C2B, MC and MX versus DA and I were determined at each exposure time (Supplementary Table S9: columns 5–10). The respective mean SQ values at 15, 30 and 45-min for 3C2B with DA or I changed little over exposure time. In contrast, the respective mean SQ values for both MC and MX with DA or I increased with increased exposure time. In all instances the differences in mean SQ values between DA and I at a given exposure time were statistically significant at p ≤0.002.

Observed vs. predicted TDT for the mixtures

Mixture TDT was determined for each experiment. A previous study demonstrated that, for binary combinations, averaging the 25, 50 and 75% effect-level TDT values for the individual chemicals over the 15 to 45-min interval could be used to predict MX TDT over the same interval (Dawson et al. 2014a). This was done in this study to determine test-to-test consistency of the prediction (Supplementary Table S10). Observed MX TDT_15:45 varied from 46.2–54.9% (mean = 50.1±3.1), while predicted MX TDT_15:45 was from 43.7–53.4% (mean 47.1±3.3). Values for observed minus predicted TDT_15:45 (TDT_{obs – pred}) were from −4.1% to +8.7% (mean = 4.4%±2.7).

Mean and s.d. values for TDT_{obs – pred} values obtained for the six MX tests in this study were compared with those for chemicals with irreversible toxicity (i.e., TDT ≥ 100%; Supplementary Table S10). The data for six combinations of agents having irreversible toxicity were taken from a previous study (Dawson et al., 2014a). In the current study, as noted above, TDT_{obs – pred} ranged from −4.1 to +8.7% while a tighter range (−1.4% to +4.5%) and a smaller mean value (1.7%±2.0) for TDT_{obs – pred} were observed for the selected combinations in which both chemicals had irreversible toxicity.

Discussion

Consistency of single-chemical toxicity data

Test-to-test consistency of single-chemical toxicity data was assessed by CV values at each effect-level for each exposure time (Table 1). Calculating the CV allows one to relate the variation observed for one chemical to that of another. In this study, these values were always <20 for both 3C2B and MC, well within the acceptable range for aquatic toxicity tests as CV values were below the upper limit of 40 for intra-laboratory variability (Moore et al. 2000; Hagen et al. 2009, Piazza et al. 2012). Previous studies with this system have reported CVs for the EC₅₀ similar to those obtained herein (Dawson et al. 2014b, 2016). While CVs tended to be slightly higher for the EC₂₅ than for the EC₅₀ or EC₇₅, they were similar.

Consistency of mixture and predicted dose-addition and independence curve data

In addition to that assessed for single-chemical toxicity, test-to-test consistency was evaluated for MX and the predicted DA and I data. In all cases, CV values were ≤15.0 (Table 2) and those at the EC₂₅ tended, again, to be slightly higher than those for the higher effect-levels. As with the single-chemical data, the mixture data were considered to have acceptable test-to-test consistency, since all CVs were <40.

Consistency of slope, asymmetry (s) and coefficient of determination (r²) values

Slope CV values were <8 for 3C2B, MC, MX and the predicted DA and I curves at each effect-level and exposure time (Supplementary Tables S7, S9). It is not clear from the literature what CV values for slope are considered to be acceptable in examining test-to-test consistency of a toxicity assay, as these are not often reported. However, by examining the standard deviations for mean values, they were less-than ±10% of the slope value. Calculating CVs is a simple way to put standard deviation values on a percentage basis to facilitate comparisons from lab-to-lab and study-to-study.

For asymmetry data, CVs were as high as 24.1 (Supplementary Table S7) suggesting more variability than that observed for EC_x and slope. This is not surprising as s values below 1.0 indicate that x/y data at lower effect-levels are less symmetrical than at higher effect-levels. In this system, generally, for a given test there tended to be greater variability in replicate responses at lower concentrations than at higher concentrations.

Quality of fitting x/y data using the 5PL-1P function was assessed by r² values. The x/y data for 3C2B, MC and MX at each effect-level and exposure time were well-fitted using 5PL-1P with mean r² values being ≥0.9982. The s.d. values for mean r² data were from ±0.0002 to ±0.0007 and CVs were ≤0.07, both indicating minimal variation in quality of fitting the x/y data.

Consistency of time-dependent toxicity (TDT) data

As noted above (Methods), calculating CV values for TDT data would be misleading in instances where toxicity actually decreased (i.e., TDT <0%) in a given time-interval. Therefore, since MC had some instances of negative TDT, s.d. values were directly used to assess test-to-test consistency of TDT data – for both the individual tests (Table 3) and for mean effect-level and time-interval values within each individual test (Supplementary Table S8). These s.d. values tended to be higher at the EC₂₅ than at the higher effect-levels. Overall, they were lowest for MX and highest for MC. If it is the case that chemicals having mid-range TDT exert toxicity that is partly due to irreversible toxicity and partly due to reversible effects, it is likely that variability in the irreversible toxic effects associated with a chemical or mixture would be observed most prominently at lower effect-levels where those effects may just be beginning to be manifested. For MC, especially from 30 to 45-min, the variation was sizable but worst at the EC₂₅, for which actual TDT was <10% in four tests and negative (i.e., decreased toxicity) for two of those four. It is also likely that from one test to the next, there is variability in the time it takes for the bacteria to become fully metabolically active, thereby affecting TDT.

By examining s.d. values for mean TDT of each individual test across the six experiments, test-to-test consistency was deemed acceptable even though the variability in individual tests of MC was rather high in the instances noted above. It was noted that the MX generally had lower s.d. for TDT than did either 3C2B or MC alone. The reason for this result is unclear.

Consistency of combined effects vs. the dose-addition and independence models

By summing the 3C2B and the 3C2B-equivalent concentrations for MC, it was possible to compare the sum of the chemical concentrations at the 25, 50 and 75% effect-levels (i.e., EC_25+50+75) in MX testing with the predicted values for DA and I (Table 4). Across the six experiments CVs for mean EC_25+50+75 were <12, so test-to-test consistency was deemed likely to be acceptable; although this is the first time this calculation has been made.

The EC_25+50+75 values served as the basis for calculating two combined effects metrics for mixture toxicity versus the DA (i.e., MX/DA) and I (i.e., MX/I) models. For these metrics, at each exposure time CVs were <6.0 suggesting acceptable test-to-test variability for mixture toxicity. For DA, MX/DA values were consistent with DA (i.e., 0.90 ≤ MX/DA ≤ 1.10) in each test at each exposure time. Based on the MX/I metric, mixture toxicity was generally not consistent with I.

Statistical analyses supported the combined effects findings. First, the mean EC_25+50+75 values were not significantly different between MX and DA at any of the exposure times, but those values for MX and DA were significantly different from those for I at 15 and 30 minutes. Also, MX/DA values were significantly different from MX/I values at each respective exposure time, as were AQ₅₀ vs. IQ₅₀ values.

As noted in previous studies with this system (Dawson et al. 2014b, 2016), the results obtained herein support the use of the MX/DA and MX/I metrics in preference to AQ₅₀ and IQ₅₀ values. The former provide relevant information on closeness of mixture toxicity to the chosen model within the range from 25 to 75% effect, rather than just at 50% effect. This conclusion was drawn because the actual MX curve can be close to that for a given model at 50% effect but not necessarily at lower or higher effect-levels (e.g., Dawson et al. 2016, Figs. 3–4).

Consistency of slope quotient data

Although x/y curve slope and AQ and IQ slope quotient (SQ) values have been noted in previous studies (Dawson et al. 2010, 2011), they have not yet received scrutiny as to their value in mixture toxicity assessment. They are presented here to provide a baseline for forthcoming reports, as slope CVs for 3C2B, MC, MX, DA and I were always <8.0 and across the six experiments, CVs for SQ values were always ≤8.5 (Supplementary Tables S7, S9).

Consistency of observed vs. predicted TDT for the mixtures

Time-dependent toxicity (TDT) of the individual chemicals has been shown to be useful for predicting TDT of the mixtures (Dawson et al. 2014a). For the six 3C2B-MC mixture experiments in this study, values for MX TDT_obs were always within 10% of the predicted values (i.e., MX TDT_pred; see Supplementary Table S10) with the standard deviation being ±2.7%. The range was only slightly larger than that for a series of six selected combinations in which both chemicals had irreversible toxicity. Likewise the mean for MX TDT_{obs – pred} values for 3C2B-MC mixtures was only slightly higher than that for chemical combinations that induced only irreversible toxic effects. Since chemicals having both reversible and irreversible toxicity were expected to have greater variability than those having only irreversible toxicity, the results suggest that this time-dependence mixture toxicity assay is repeatable and can be useful as part of risk assessment.

Conclusions

Consistency of the toxicity results across the six experiments was within the acceptable range, based on CV values for EC_x, EC_25+50+75, slope, s, and the four combined effects metrics. For TDT, higher levels of variation in testing were observed for MC at the EC₂₅ and the 30 to 45-min time-interval. For 3C2B and MX, TDT values showed less variability across the effect-levels and time-intervals evaluated. Despite the higher TDT variability for MC, the combined effects metric MX/DA was consistent with predicted effects for the DA model for all 18 assessments (i.e., at each of the three exposure times for each of the six experiments). The results of this study suggest that this simple assay is a useful approach for examining mixture toxicity on a time-dependent basis. Additionally, the substantial amount of data generated in testing could prove useful in risk assessment.

Figure 2.

Concentration-response curves for 3-chloro-2-butanone (3C2B), methyl crotonate (MC) and the 3C2B-MC mixture (MX) after 30-min of exposure for experiment #6, along with predicted curves for the dose-addition (DA) and independence (I) combined effects models.