Abstract
We aimed to describe the development of an inference model for computer-aided diagnosis of lung nodules that could provide valid reasoning for any inferences, thereby improving the interpretability and performance of the system. An automatic construction method was used that considered explanation adequacy and inference accuracy. In addition, we evaluated the usefulness of prior experts’ (radiologists’) knowledge while constructing the models. In total, 179 patients with lung nodules were included and divided into 79 and 100 cases for training and test data, respectively. F-measure and accuracy were used to assess explanation adequacy and inference accuracy, respectively. For F-measure, reasons were defined as proper subsets of Evidence that had a strong influence on the inference result. The inference models were automatically constructed using the Bayesian network and Markov chain Monte Carlo methods, selecting only those models that met the predefined criteria. During model constructions, we examined the effect of including radiologist’s knowledge in the initial Bayesian network models. Performance of the best models in terms of F-measure, accuracy, and evaluation metric were as follows: 0.411, 72.0%, and 0.566, respectively, with prior knowledge, and 0.274, 65.0%, and 0.462, respectively, without prior knowledge. The best models with prior knowledge were then subjectively and independently evaluated by two radiologists using a 5-point scale, with 5, 3, and 1 representing beneficial, appropriate, and detrimental, respectively. The average scores by the two radiologists were 3.97 and 3.76 for the test data, indicating that the proposed computer-aided diagnosis system was acceptable to them. In conclusion, the proposed method incorporating radiologists’ knowledge could help in eliminating radiologists’ distrust of computer-aided diagnosis and improving its performance.
Introduction
Advances in imaging modalities have made it possible to acquire large amounts of medical image data for radiologists to assess, increasing their workload. Computer-aided diagnosis (CAD) has been developed to decrease the workload and categorized into two types [1]: computer-aided detection (CADe), which supports lesion detection [2–4], and computer-aided diagnosis (CADx), which supports differential diagnosis [5–7]. CAD systems, particularly CADx systems, employ an inference model to present suggestions to radiologists based on the data input (e.g., imaging findings).
Several studies have reported the usefulness of CAD for lung nodules [8–12]. Shiraishi et al. proposed a system that calculated the possibility of the presence of a malignant lung nodule from two clinical parameters and 75 imaging features, using linear distinct analysis in chest radiographs [8]; they showed that radiologists’ performance significantly improved with the use of CADx. In addition, Chen et al. proposed a CADx system that estimated nodule type based on 15 image features, using an ensemble model of artificial neural network with chest computed tomography (CT) [9]. Notably, their system showed performance comparable to that of senior radiologists while classifying the nodule type. Nevertheless, CADx systems are rarely used in clinical practices, possibly because radiologists distrust the suggestions of the CAD system because they do not provide explanations for the decisions. Supporting this, Kawamoto et al. suggested that CAD should at least provide adequate details about the reasoning for any inference results [13]. Accordingly, we believe that the barriers to its use could disappear, or at least diminish, if the CAD system could provide justifications for its suggestions.
Remarkably, few systems offer reasons behind their suggestions. Green et al. proposed such a system based on sensitivity analysis with electrocardiogram interpretation [14], whereas Kawagishi et al. proposed a system that disclosed the reasoning based on the influence on the inference result in chest CT [15]. Although their inference models showed high accuracy of the inferences and high adequacy of the reasons, the reports did not describe the model construction. However, it can be challenging to manually construct an inference model with high accuracy and high adequacy because the number of possible models is vast. Although various automatic construction methods have been proposed [16–19], they have only considered inference accuracy as a performance metric and not explanation adequacy or subjective interpretability.
In our study, we have proposed a method for automatically constructing inference models using a metric that considers explanation adequacy and inference accuracy. Moreover, we have evaluated the usefulness of radiologists’ knowledge while constructing these models.
Materials and methods
This retrospective study was approved by the Ethics Committee of Kyoto University Hospital (Kyoto, Japan), which waived the requirement of informed consent. The notations used in this paper are shown in Table 1.
Table 1. List of notations.
| Notation | Description | Example |
|---|---|---|
| D | “Diagnosis” as the inference target node (random variable) | NA |
| di | state of random variable D | d1, primary lung cancer |
| Xj | imaging findings and clinical data as the other nodes (random variable) | shape, tumor marker |
| xjk | state of random variable Xj | x31, irregular |
| E | Evidence, as a set of xjk | {x11, x21} |
| p(di|E) | posterior probability of di when E is given to the inference model | NA |
| df | inference diagnosis with the highest posterior probability among p(di|E) | d1, primary lung cancer |
| Rc | reason candidate (a proper subset of E) | If x11 and x21 are given as E, then Rc can be {x11, x21}, {x11}, {x21}. |
| |Rc| | the number of elements of Rc | If Rc is {x11, x21}, then |Rc| is 2. |
| Rct | Rc with only one element | {x11} |
| I(Rc) | influence of Rc on the inference diagnosis df | NA |
| p(df) | prior probability of the inference diagnosis df | NA |
| pd(Rc) | difference between p(df|Rc) and p(df) for the inference diagnosis df | NA |
| V(S) | the performance metric of inference model S | NA |
| Vr(S) | explanation (reasoning) adequacy of inference model S | NA |
| Vi(S) | inference accuracy of inference model S | NA |
| Rg | Reference reasons (1–7 imaging findings and/or clinical data chosen by radiologists) | “shape is polygon,” “diameter is small and cavitation exists,” and “satellite lesion exists” |
| Rd | Reasons derived by the inference system | “shape is polygon” and “diameter is small and cavitation exists” |
Abbreviation: NA, not available
Dataset
We used thin-slice chest CT images and clinical information of 179 patients treated at Kyoto University Hospital. Each case had 1–5 pulmonary nodules, ranging in size from 10 to 30 mm, with the clinical diagnosis confirmed pathologically, clinically, or radiologically as primary lung cancer, lung metastasis, or benign lung nodule. Of note, we used 79 cases as training data for constructing the inference model and the remaining 100 cases as test data for evaluating the performance of the model.
Without the knowledge of the clinical diagnosis, two radiologists (A and B) analyzed a representative nodule for each case and recorded 49 types of imaging findings as ordinal or nominal data. In addition, 37 clinical data types, including laboratory data and patient history of malignancies, were collected from patients’ electronic medical records; these data were used as the input information for the inference models (see Supporting information, S1 File). The clinical diagnosis data were used as reference for evaluating inference accuracy; based on these diagnoses, two other radiologists (C and D) selected a set of 1–7 imaging findings and/or clinical data as the reference explanations for diagnosis (e.g., “shape is polygon,” “diameter is small and cavitation exists,” and “satellite lesion exists”).
Inference model
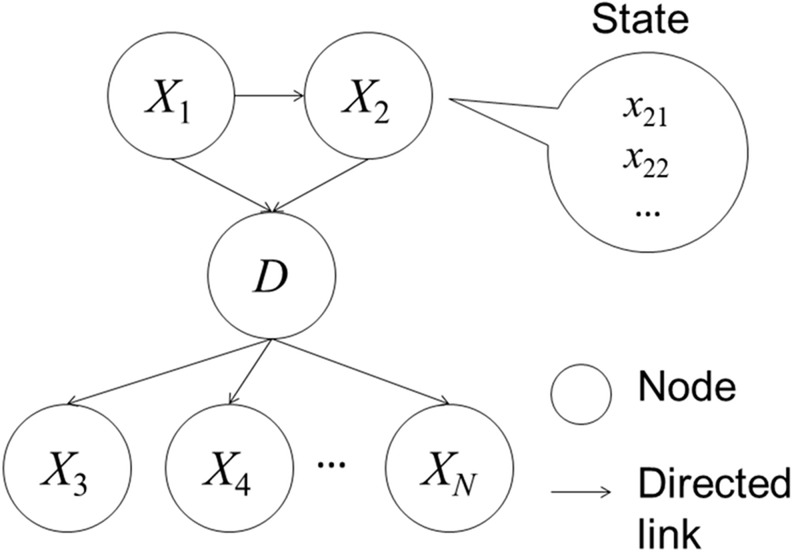
The inference computational model infers diagnosis (primary lung cancer, lung metastasis, or benign lung nodule in our study) from the input image findings and clinical data. As the inference model, we employed a Bayesian network, a directed acyclic graphical model that includes nodes and directed links. Fig 1 provides an example of a Bayesian network (directed acyclic graphical model). Each node represents a random variable, and each directed link represents relationship between variables.
Fig 1. An example of a Bayesian network (directed acyclic graphical model).
The Bayesian network has nodes (circles) and directed links (arrows). Each node and directed link represent a random variable and relationship, respectively. Each node can have a discriminate value (state).
In Fig 1, D denotes diagnosis as the inference target node, and Xj (j = 1, 2, …, N) denotes the imaging findings (e.g., shape) and clinical data (e.g., tumor marker) as the other nodes. Each node can have a discriminate value of di or xjk; for example, D takes di (i = 1, 2, 3; e.g., d1: primary lung cancer) and Xj takes xjk (e.g., for shape, k = 1, 2, …, 8 and j = 3, with x31 = irregular). Further, maximum value of k ranges from two to eight depending on Xj. Next, E denotes Evidence [20] as a set of xjk used for information input in the inference models. The posterior probability of di is denoted by p(di|E) when E is set in the inference model, and df indicates the inference diagnosis with the highest posterior probability among p(di|E).
The inference result can be calculated based on the Bayesian network structure using a probability propagation algorithm [20]. With a change in the Bayesian network structure (graphical model), the probability propagation path is also changed, indicating that the structure of the graphical model affects the inference result. We obtained the prior probability distributions for each node from the training data and calculated the conditional probabilities for each node based on links.
Reason derivation
Herein, we illustrate how the reasons are derived from Evidence (E) to justify the inference results. First, the notation for deriving reasons and the examples of notation usage are explained. E is given as a set of xjk, and Rc (reason candidate) is defined as a proper subset of E that can be selected as a reason, e.g., when the graphical model comprises D (diagnosis), X1 (nodule size), and X2 (cavitation) as nodes, if x11 (diameter is small) and x21 (cavitation exists) are specified as E, then Rc comprises only these two elements, and {{x11, x21}, {x11}, {x21}} represent all possible values of Rc. This notation allows the reasons to be derived from E. The influence, I(Rc), is defined as a quantitative measure to select Rc based on the graphical model. Its calculation is summarized in S2 File; to summarize, it represents the influence of Rc on the inference result (df): I(Rc) > 0 indicates a positive influence, whereas I(Rc) < 0 indicates a negative influence. I(Rc) is defined by the following equations:
| with pd(Rc) defined as | (1) |
| (2) |
In Eqs 1 and 2, p(df) denotes the prior probability of df, and |Rc| denotes the number of elements of Rc. As stated in the section detailing the inference model, p(df) is calculated from the training data. Based on these equations, when Rc comprises only one element (i.e., |Rc| = 1), I(Rc) equals pd(Rc) and is simply defined as the difference between p(df|Rc) and p(df). For |Rc| > 1, I(Rc) is calculated from pd(Rc) and an additional penalty term, f(Rc), introduced to consider possible synergy among the multiple elements.
To explain the synergetic effect on I(Rc), we use the notation Rct (t = 1, 2, …) for the subset of Rc, with only one element of Rc, e.g., when all possible values of Rc are {{x11, x21}, {x11}, {x21}}, then Rc1 = {x11} and Rc2 = {x21}. Note that Rct is also the reason candidate in this example (|Rct| = 1). If pd(Rc = {x11}) and pd(Rc = {x21}) are comparatively higher than pd(Rc = {x11, x21}), then f(Rc = {x11, x21}) is also high, and we regard that {x11} and {x21} are more adequate than {x11, x21} as the reasons (e.g., “diameter is small” is more adequate than the combination of “diameter is small” AND “cavitation exists”). By contrast, if pd(Rc = {x11}) and pd(Rc = {x21}) are comparatively lower than pd(Rc = {x11, x21}), then f(Rc = {x11, x21}) is also low, and the combination of elements {x11, x21} is regarded as more adequate than {x11} and {x21} (e.g., the combination of “diameter is small” AND “cavitation exists” is more adequate than “cavitation exists”).
f(Rc) is defined as follows by calculating an element-wise total positive effect (fp) and a total negative effect (fn):
| (3) |
| (4) |
| (5) |
In Eq 3, sgn(∙) denotes a sign function, and fp − fn can be considered a net effect of the non-synergetic influence of each element in Rc. f(Rc), as a synergetic influence, is set to zero when the sign of the element-wise influence fp—fn is different from pd(Rc). That is to say, f(Rc) can work as penalty term when the sign of fp—fn is equal to that of pd(Rc). When the value of the element-wise influence is larger than pd(Rc), the synergetic influence is considered negligible, and f(Rc) is set to pd(Rc), providing an I(Rc) of zero. L2 regularization is frequently used as penalty term in machine learning algorithm (i.e., support vector machine [21]). The difference between L2 regularization and Eqs (4)–(5) is the separation based on the sign. Therefore, it is expected that effect of our penalty term is similar to that of L2 regularization. Based on Eqs 1 and 3, I(Rc) can then be rewritten as follows for |Rc| ≥ 2:
| (6) |
The maximum number of elements in Rc (|Rc|) is set to two to reduce the computational complexity. Further, I(Rc) is calculated for all possible candidates of Rc with |Rc| = 1 or 2. At most, the best three reason candidates are selected as appropriate reasons for each model. If I(Rc) is <0.05 * p(df), the reason is rejected.
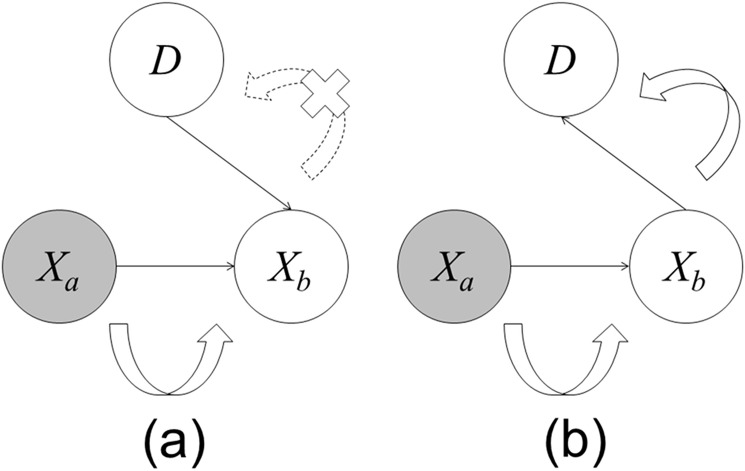
Effect of model structure on deriving reasons
The structure of the graphical model, comprising nodes and directed links, affects both the inference result and reason derivation for the Bayesian network. Fig 2 shows an example of the probability propagation for two different structures of the graphical models. These models have three nodes (diagnosis node, D, and two other nodes, Xa and Xb). Model A has two directed links, from Xa to Xb and from D to Xb. Similarly, model B has two directed links, from Xa to Xb and from Xb to D. The direction of the link between Xb and D is different between the two models. The results are different when Evidence is given to Xa in the networks; in model A, propagation occurs from Xa to Xb but not from Xb to D, whereas in model B, propagation occurs in both directions. Thus, because Xa does not influence D in model A, it is not selected as a reason. In this way, the model structure influences the probability propagation (inference result) and reasons.
Fig 2. An example of probability propagation.
Curved arrows represent the propagation direction, dotted curved arrow with an X indicates no propagation, and gray circle (Xa) represents a node where Evidence is given. (a) Model A: Propagation does not occur from Xa to D. (b) Model B: Propagation occurs from Xa to D.
Metric
To automatically construct the inference model, its performance has to be calculated. Moreover, because we regard the reasons as important for evaluating the inference results, we require the performance measure to reflect explanation adequacy and inference accuracy. Several studies have suggested a trade-off between explanation adequacy and inference accuracy [22, 23]. Based on the consensus of the radiologists in our study, we used the following metric to evaluate the inference models:
| (7) |
Herein, S denotes an inference model, V(S) denotes the performance metric of S, Vr(S) denotes the explanation adequacy of S, and Vi(S) denotes the inference accuracy of S. The values of Vr(S), Vi(S), and V(S) range from zero to one. Remarkably, this metric considers the explanation adequacy and inference accuracy of S. We also employ F-measure, which is commonly used in information retrieval, as Vr(S), providing a harmonic mean of precision and recall (completeness). The relationships among F-measure, precision, and recall are as follows:
| (8) |
| (9) |
| (10) |
Here, Rg denotes a reference set of standards for a case (i.e., 1–7 imaging findings and/or clinical data selected by the two radiologists), Rd denotes a set of reasons derived by the inference system, and |∙| denotes the number of elements of a set. Rg ∩ Rd denotes the intersection between Rg and Rd. For this, Rd is obtained from Rc with I(Rc) up to three Rc. If there are >3 possible Rc, then Rd is obtained as follows:
| (11) |
where represents Rc with the highest, second highest, and third highest values of I(Rc), respectively, and “∪” denotes an operator of union.
The accuracy of the inference model, Vi(S), is defined as m / n, where m denotes the number of cases correctly inferred by the models, and n denotes the total number of cases.
Automatic model construction
The number of possible Bayesian network structures dramatically increases as the number of nodes increases; from these, structures with high performance must be effectively searched. Therefore, we use the Markov chain Monte Carlo (MCMC) method [24] to construct the model, S, and iteratively find the most appropriate model, i.e., with the maximum value of V(S). We use the metric and MCMC method to automatically construct the Bayesian model as follows:
Set an initial model to the current model (Scurrent), and initialize the iteration count (M = 1).
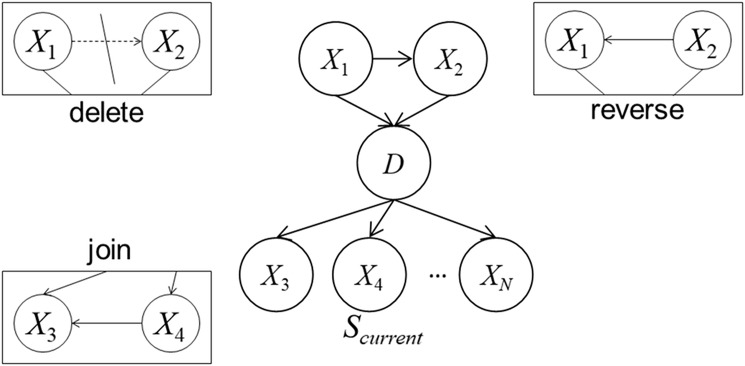
Create a temporary model (Stemp) by updating Scurrent. The update action is probabilistically selected as one of the following, with a probability based on the Scurrent structure: (1) deleting a link, (2) reversing a link, or (3) creating a new link (see Fig 3). If the action is not appropriate (e.g., Stemp has a cyclic loop in its structure), Step 2 is iterated.
Calculate V(Stemp) with 5-fold cross validation of the training data.
- Probabilistically replace Scurrent with Stemp with the following probability (Pm):
where β represents the damping ratio (0 < β < 1). Note that Pm is small (difficult to replace) when V(Scurrent) > V(Stemp) or when M is large.(12) If M reaches the iteration limit (Ml) or Scurrent has not been replaced Mc times, then Scurrent is output as the final model. If not, M = M + 1 is set, and the process returns to Step 2.
Fig 3. Three types of update to the graphical model.
Delete denotes unlinking an existing link, reverse denotes reversing an existing link, and join denotes creating a new link.
In Step 2, Stemp is created with a probability based on the current model Scurrent, enabling setting a different Stemp at another trial even while using the same Scurrent.
In this process, we set the core values as follows: β = 0.999, Ml = 10000, and Mc = 2500. If the inference accuracy Vi(S) of the final model is <0.70 for the training data, the model is discarded because the low inference accuracy is expected to negatively influence the model’s acceptability by the radiologists. For the same reason, if Vi(S) is <0.70, we set V(S) to Vi(S) and Vr(S) to 0 in Step 3, which eliminates the time-consuming calculation of Vr(S). The number of parent nodes is limited to no more than two because of limited computational resources.
Initial model with and without prior knowledge of radiologists
The final model depends on the initial model and metric V(S). To evaluate the effect of the initial model on the performance of the final model, we examined initial models with and without the radiologists’ expert knowledge. The radiologists’ knowledge is represented as links between the diagnostic node and other nodes in the initial model. When no prior knowledge is included, no link is present in the initial model. We conducted multiple trials of model construction with the same initial model because each trial could experience different paths, as already described.
Subjective evaluation of inference model
The two radiologists (A and B, who did not set the reference standards) were asked to subjectively evaluate the model with the best performance. Based on the clinical diagnosis, inference result, and derived reasons, a subjective rank was assigned to each case on a 5-point scale, wherein ranks 5, 3, and 1 represented beneficial, appropriate, and detrimental, respectively.
Results
Finally, 13 models with prior knowledge and five without prior knowledge were constructed after 37 trials. The remaining 19 models were discarded because they did not meet our predefined criteria. Table 2 shows the performance of the best three models with and without prior knowledge. S1 and S2 Tables show the performance of the other 10 and 2 models with and without prior knowledge, respectively. Among the 13 models with prior knowledge, the performance of the best model with the test data was as follows: F-measure (Vr) = 0.411, accuracy (Vi) = 72.0%, and metric (V) = 0.566. Among the five models without prior knowledge, the performance of the best model with the test data was as follows: F-measure (Vr) = 0.274, accuracy (Vi) = 65.0%, metric (V) = 0.462.
Table 2. Performance of the best three inference models with and without prior knowledge.
| Training data | Test data | ||||||
|---|---|---|---|---|---|---|---|
| Prior knowledge | Model | F-measure (Vr) | Accuracy (Vi) (%) | Metric (V) | F-measure (Vr) | Accuracy (Vi) (%) | Metric (V) |
| with | Best | 0.399 | 75.9 | 0.579 | 0.411 | 72.0 | 0.566 |
| 2nd | 0.324 | 70.9 | 0.516 | 0.325 | 76.0 | 0.542 | |
| 3rd | 0.363 | 70.9 | 0.536 | 0.328 | 74.0 | 0.534 | |
| without | Best | 0.342 | 72.2 | 0.532 | 0.274 | 65.0 | 0.462 |
| 2nd | 0.314 | 74.7 | 0.530 | 0.222 | 63.0 | 0.426 | |
| 3rd | 0.361 | 77.2 | 0.566 | 0.250 | 60.0 | 0.425 | |
According to Table 2, although the accuracy of three models without prior knowledge was comparable to that of three models with prior knowledge when applied to the training data, their performance (F-measure, accuracy, and metric) without prior knowledge was worse than that with prior knowledge when using the test data. Iteration numbers for the MCMC method in the three best models with prior knowledge were 2934, 2948, and 3126, while the corresponding numbers in those without knowledge were 2873, 5567, and 8642.
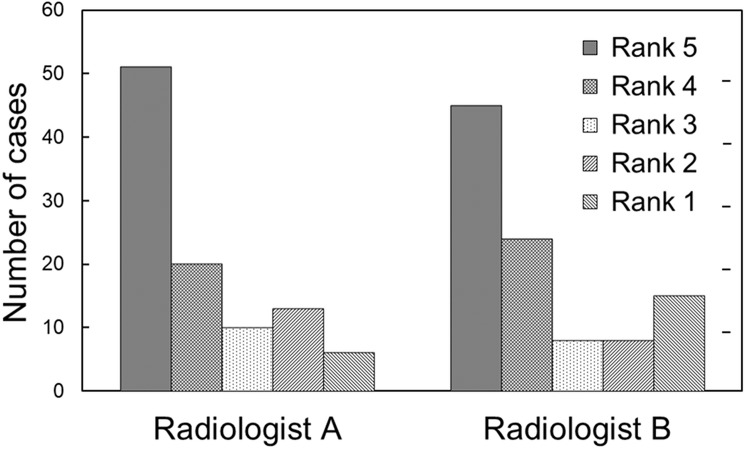
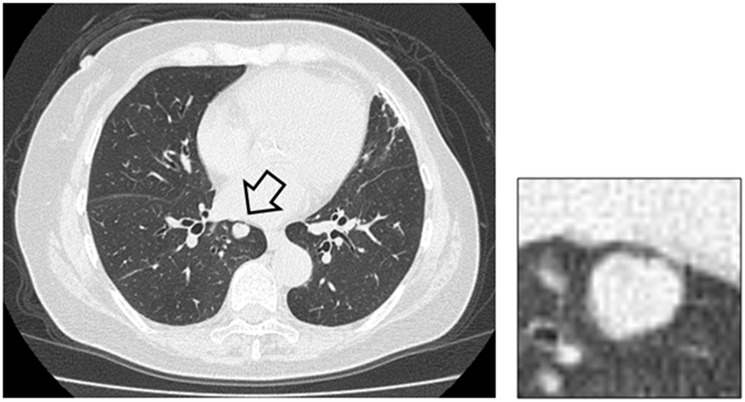
Based on Table 2, we selected the best model constructed with prior knowledge (metric = 0.566) for the subjective evaluation. The average subjective ranks obtained from the two radiologists were 3.97 and 3.76. Fig 4 shows the frequencies of ranks recorded by the two radiologists, indicating that the mode of the ranks for each radiologist was 5. Rank 1 had the lowest frequency for Radiologist A, whereas rank 3 was less frequent than rank 1 as per Radiologist B. Fig 5 illustrates an example of misclassification by the inference system, in a case where a benign lung nodule was classified as a metastasis, and the three reasons for this were “shape is round,” “contour is smooth,” and “patient was diagnosed with malignancy during the past five years.” Both radiologists gave this a rank of 1.
Fig 4. Frequencies of subjective ranks recoded by two radiologists.
Note: Ranks 5, 3, and 1 in the 5-point scale represent beneficial, appropriate, and detrimental, respectively.
Fig 5. An example of misclassification and inadequate reasoning by the inference system.
A benign lung nodule (arrow) was classified as metastasis.
To compare our Bayesian-network-based method, inference and reasoning of lung nodules were performed using gradient tree boosting (xgboost) [25,26]. Please refer to the Supporting information (S3 File) for the comparison.
Discussion
We proposed a method for the automatic construction of a CADx system that could provide justification for its inference results. By incorporating radiologists’ knowledge into the model construction, we found that explanation adequacy and inference accuracy improved. To the best of our knowledge, few studies in radiology have sought to develop a CADx system that can provide valid reasoning for its inference results. Indeed, Langlotz et al. suggested that physicians not only based their trust in an inference system on good prediction performance but also on whether they understood the reasoning behind the predictions [27]. However, although Green et al. proposed an inference system for electrocardiogram that presented its reasoning [14], the same has not been proposed for radiology. Accordingly, our CADx system for lung nodules was capable of providing valid reasons for its inferences, with high explanation adequacy and high inference accuracy.
As shown in Table 2, the models with prior knowledge from radiologists were more robust and superior to those without prior knowledge. Because the accuracies of the models without prior knowledge were comparable to those with prior knowledge in the training data, we speculate that the models without prior knowledge overfitted the training data. In effect, the radiologists’ knowledge prevented overfitting and improved the generalizability of the system. Consistent with this, a previous study showed that the Bayesian network performance in assessing mammograms was improved by incorporating experts’ knowledge [28].
The present study gained other benefits from expert involvement, e.g., the iteration numbers for the MCMC method were smaller in the models with prior knowledge than in those without prior knowledge. In addition to improving the model robustness, prior knowledge boosted the convergence speed of our inference models.
The two radiologists (A and B) subjectively evaluated the model we constructed, giving an average rank more than 3. A large controlled study in the non-medical domain [29] has shown that providing reasoning and trace explanations for context-aware applications could improve user understanding and trust in the system. In line with this finding and the acceptability of our method to the radiologists participating in the present study, we expect that our CADx system could, at least, diminish an important barrier to the uptake of CADx systems.
Several methods for automatic model construction were proposed in previous studies. These methods can be divided into two types [20,30]: (i) constraint-based methods [16,20,30,31] and (ii) search-and-score methods [19,20,30,32]. In constraint-based methods, relationship between nodes, such as conditional independency [31] or mutual information [16], are used to construct Bayesian network structure automatically. That is to say, if conditional independency is indicated or values of mutual information meet predefined criteria, existence of the links between the nodes are judged. For example, PC algorithm utilizes conditional independency for judging whether links are deleted or connected in Bayesian network structure [31]. Because constraint-based methods evaluate the relationship between nodes using training data, efficiency of entire Bayesian network structure is not assured when using the constraint-based methods. In search-and-score methods, Bayesian network structure is evaluated by score such as Bayesian score function, BIC, MDL, and MML (Vr, Vi, and V in our study). Based on the scores obtained from entire Bayesian network structures, better structure is searched or selected. MCMC is used for searching Bayesian network structure in our method and the previous study [19], and greedy algorithm is used in K2 algorithm [32]. In general, greedy algorithm, such as K2 algorithm, frequently sticks in local minimum/maximum, and cannot reach global minimum/maximum [19]. MCMC can break out of this local minimum/maximum and obtain better score [19]. As shown, our proposed method is classified as search-and-score methods. It is possible to use hybrid method of constraint-based methods and search-and-score methods. For example, in MCMC step of our method, the links between two nodes where conditional independency is indicated can be ignored when updating Bayesian network structure, which will make convergence speed of our proposed method faster.
In conventional methods of structure learning, inference accuracy is mainly optimized, and explanation adequacy is frequently ignored. We focused on both inference accuracy and explanation adequacy in our study. In addition, our proposed method can speculate reasoning for prediction of one particular lung nodule. These two points are the major differences between our proposed method and conventional methods of Bayesian network structure learning/conventional CAD.
There are several limitations in the current study. First, the number of parent nodes for the Bayesian network is limited to no more than two. In the case of a directed graph, such as Bayesian network, the number of possible structures can reach 3B (where B = NC2 and N is the number of nodes). By limiting the number of parent nodes, it is possible to decrease computational cost for model construction, but this might have been at the expense of missing the optimal model. Second, despite restricting the number of model structures, the number of model candidates is still huge. Consequently, the automatic model construction in the MCMC process can reach the local minimum. Although our inference models converged to a reasonable model for the radiologists, this might not have been the optimal model. Third, the computational cost of model construction is large, with one trial requiring 30–40 hours to complete, making it difficult to construct models with different random seeds. Finally, the two radiologists only evaluated the best model. In future research, it will be preferable to perform subjective evaluation of more inference models.
Conclusions
In conclusion, we have proposed a method of automatic model construction for CADx of lung nodules that had high explanation adequacy and high inference accuracy. Notably, not only were the models constructed with prior knowledge from radiologists superior to those constructed without prior knowledge but the radiologists also considered the reasons provided for the inference results to be acceptable. Overall, these results suggest that our proposed CADx system might be acceptable in clinical practice and could eliminate the usual distrust of such systems among radiologists. We will perform further observational studies using our CAD system.
Supporting information
Except one model, performance of these models with prior knowledge was better than that of the best three models without prior knowledge (please compare S1 Table with Table 2).
(DOCX)
(DOCX)
(DOCX)
(DOCX)
To compare our Bayesian-network-based method, inference and reasoning were performed using gradient tree boosting.
(DOCX)
Acknowledgments
This work was partly supported by the Innovative Techno-Hub for Integrated Medical Bio-imaging of the Project for Developing Innovation Systems, from the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan and by JSPS KAKENHI (Grant Number JP16K19883). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Data Availability
Japanese privacy protection laws and related regulations prohibits us from revealing any health-related private information such as medical images to the public without written consent, although the laws and related regulations allow researchers to use such health-related private information for research purpose under opt-out consent. We utilized the medical images under acceptance of the ethical committee of Kyoto University Hospital under opt-out consent. It is almost impossible to take written consent to open the data to the public from all patients. For data access of our de-identified health-related private information, please contact Kyoto University Hospital. The request for data access can be sent to the following e-mail addresses of three authors: nmizuho@kuhp.kyoto-u.ac.jp, yakami@kuhp.kyoto-u.ac.jp, and tkubo@kuhp.kyoto-u.ac.jp. The other data are available from the corresponding author. As shown,the authors cannot make their study’s data publicly available at the time of publication. However, except health-related private information, all authors commit to make the data underlying the findings described in this study fully available without restriction to those who request the data, in compliance with the PLOS Data Availability policy. For data sets involving personally identifiable information or other sensitive data, data sharing is contingent on the data being handled appropriately by the data requester and in accordance with all applicable local requirements. According to Japanese Medical Practitioners' Act and Medical Care Act, Japanese hospitals must preserve health-related private information in long-term data storage. Therefore, Japanese hospitals, including Kyoto University Hospital, equips facility for the long-term storage.
Funding Statement
This work was partly supported by the Innovative Techno-Hub for Integrated Medical Bio-imaging of the Project for Developing Innovation Systems, from the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan and by JSPS KAKENHI (Grant Number JP16K19883). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. Canon Inc. provided support in the form of salaries for several authors (MK, GA, YI, and HY), but did not have any additional role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript. The specific roles of these authors are articulated in the ‘author contributions’ section.
References
- 1.Giger ML, Chan HP, Boone J. Anniversary Paper: History and status of CAD and quantitative image analysis: The role of Medical Physics and AAPM. Med. Phys. 2008;35(12):5799–5820. 10.1118/1.3013555 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Warren Burhenne LJ, Wood SA, D'Orsi CJ, Feig SA, Kopans DB, O'Shaughnessy KF, et al. Potential contribution of computer-aided detection to the sensitivity of screening mammography. Radiology 2000;215(2):554–562. 10.1148/radiology.215.2.r00ma15554 [DOI] [PubMed] [Google Scholar]
- 3.Shiraishi J, Li F, Doi K. Computer-aided diagnosis for improved detection of lung nodules by use of posterior-anterior and lateral chest radiographs. Acad Radiol. 2007;14(1):28–37. 10.1016/j.acra.2006.09.057 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.O'Connor SD, Yao J, Summers RM. Lytic metastases in thoracolumbar spine: computer-aided detection at CT—preliminary study. Radiology 2007;242(3):811–816. 10.1148/radiol.2423060260 [DOI] [PubMed] [Google Scholar]
- 5.Fukushima A, Ashizawa K, Yamaguchi T, Matsuyama N, Hayashi H, Kida I, et al. Application of an artificial neural network to high-resolution CT: usefulness in differential diagnosis of diffuse lung disease. AJR Am J Roentgenol. 2004;183(2): 297–305. 10.2214/ajr.183.2.1830297 [DOI] [PubMed] [Google Scholar]
- 6.Burnside ES, Rubin DL, Fine JP, Shachter RD, Sisney GA, Leung WK. Bayesian network to predict breast cancer risk of mammographic microcalcifications and reduce number of benign biopsy results: initial experience. Radiology 2006;240(3):666–673. 10.1148/radiol.2403051096 [DOI] [PubMed] [Google Scholar]
- 7.Jesneck JL, Lo JY, Baker JA. Breast mass lesions: computer-aided diagnosis models with mammographic and sonographic descriptors. Radiology 2007;244(2):390–398. 10.1148/radiol.2442060712 [DOI] [PubMed] [Google Scholar]
- 8.Shiraishi J, Abe H, Engelmann R, Aoyama M, MacMahon H, Doi K. Computer-aided diagnosis to distinguish benign from malignant solitary pulmonary nodules on radiographs: ROC analysis of radiologists' performance—initial experience. Radiology 2003;227(2):469–474. 10.1148/radiol.2272020498 [DOI] [PubMed] [Google Scholar]
- 9.Chen H, Xu Y, Ma Y, Ma B. Neural network ensemble-based computer-aided diagnosis for differentiation of lung nodules on CT images. Acad Radiol. 2010;17(5):595–602. 10.1016/j.acra.2009.12.009 [DOI] [PubMed] [Google Scholar]
- 10.Awai K, Murao K, Ozawa A, Nakayama Y, Nakaura T, Liu D, et al. Pulmonary nodules: estimation of malignancy at thin-section helical CT—effect of computer-aided diagnosis on performance of radiologists. Radiology 2006;239(1):276–284. 10.1148/radiol.2383050167 [DOI] [PubMed] [Google Scholar]
- 11.Iwano S, Nakamura T, Kamioka Y, Ikeda M, Ishigaki T. Computeraided differentiation of malignant from benign solitary pulmonary nodules imaged by high-resolution CT. Comput Med Imaging Graph. 2008;32(5):416–422. 10.1016/j.compmedimag.2008.04.001 [DOI] [PubMed] [Google Scholar]
- 12.Way T, Chan HP, Hadjiiski L,Sahiner B, Chughtai A, Song TK, et al. Computer-aided diagnosis of lung nodules on CT scans. Acad Radiol. 2010;17(3):323–332. 10.1016/j.acra.2009.10.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kawamoto K, Houlihan CA, Balas EA, Lobach DF. Improving clinical practice using clinical decision support systems: a systematic review of trials to identify features critical to success. BMJ 2005;330:765 10.1136/bmj.38398.500764.8F [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Green M, Ekelund U, Edenbrandt L, Bjork J, Forberg JL, Ohlsson M. Exploring new possibilities for case-based explanation of artificial neural network ensembles. Neural Netw. 2009;22(1):75–81. 10.1016/j.neunet.2008.09.014 [DOI] [PubMed] [Google Scholar]
- 15.Kawagishi M, Iizuka Y, Satoh K, Yamamoto H, Yakami M, Fujimoto K, et al. Method for disclosing the reasoning behind computer-aided diagnosis of pulmonary nodules. Medical Imaging Technology 2011;29(4):163–170. [Google Scholar]
- 16.Suzuki J. A construction of Bayesian networks from databases based on an MDL principle. In: UAI'93 Proceedings of the Ninth international conference on Uncertainty in artificial intelligence, 1993, pp 266–273.
- 17.Geman S, Geman D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Machine Intell. 1984;6(6):721–741. [DOI] [PubMed] [Google Scholar]
- 18.Friedman N. The Bayesian structural EM algorithm. In: UAI'98 Proceedings of the Fourteenth conference on Uncertainty in artificial intelligence, 1998, pp 129–138
- 19.Friedman N, Koller D. Being Bayesian about network structure. A Bayesian approach to structure discovery in Bayesian networks. Mach. Learn. 2003;50(1–2):95–125. 10.1023/A:1020249912095 [Google Scholar]
- 20.Jensen FV, Nielsen TD. Bayesian networks and decision graphs (second edition). 2007; Springer, New York [Google Scholar]
- 21.Chang C-C, Lin C-J. LIBSVM: a library for support vector machines. ACM Trans Intell Syst Technol. 2011; 2(3):1–27. [Google Scholar]
- 22.Ishibuchi H, Nojima Y. Analysis of interpretability-accuracy tradeoff of fuzzy systems by multiobjective fuzzy genetics-based machine learning. Int. J. Approx. Reason. 2007;44(1):4–31. 10.1016/j.ijar.2006.01.004 [Google Scholar]
- 23.Gacto MJ, Alcala R, Herrera F. Adaptation and application of multi-objective evolutionary algorithms for rule reduction and parameter tuning of fuzzy rule-based systems. Soft Comput. 2009;13(5):419–436. 10.1007/s00500-008-0359-z [Google Scholar]
- 24.Andrieu C, Freitas N, Doucet A, Jordan MI. An introduction to MCMC for Machine Learning. Mach. Lear. 2003;50(1–2):5–43. 10.1023/A:1020281327116 [Google Scholar]
- 25.Chen T, Guestrin C. XGBoost: A Scalable Tree Boosting System. Proc 22nd ACM SIGKDD Int Conf Knowl Discov Data Min—KDD ‘16. 2016:785–794.
- 26.Nishio M, Nishizawa M, Sugiyama O, Kojima R, Yakami M, Kuroda T, et al. Computer-aided diagnosis of lung nodule using gradient tree boosting and Bayesian optimization. PLoS One. 2018. April 19;13(4):e0195875 10.1371/journal.pone.0195875 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Langlotz CP, Shortliffe EH. Adapting a consultation system to critique user plans. International Journal of Man-Machine Studies 1983; 9(5):479–496. 10.1016/S0020-7373(83)80067-4 [Google Scholar]
- 28.Velikova M, Lucas PJ, Samulski M, Karssemeijer N. On the interplay of machine learning and background knowledge in image interpretation by Bayesian networks. Artif Intell Med. 2013. January;57(1):73–86. 10.1016/j.artmed.2012.12.004 [DOI] [PubMed] [Google Scholar]
- 29.Lim BY, Dey AK, Avrahami D. Why and Why Not Explanations Improve the Intelligibility of Context-Aware Intelligent Systems. In Proceedings of the 27th international Conference on Human Factors in Computing Systems (Boston, MA, USA, April 04–09, 2009). CHI '09. ACM, New York, NY, 2119–2128.
- 30.Neapolita RE. Learning Bayesian Networks. Upper Saddle River: Prentice-Hall Inc.; 2004 [Google Scholar]
- 31.Spirtes P, Glymour C, Scheines R. Causation, Prediction, and Search. 2nd ed Cambridge: MIT Press; 2000 [Google Scholar]
- 32.Cooper GF, Herskovits E. A Bayesian method for the induction of probabilistic networks from data. Machine learning 1992;9:309–347 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Except one model, performance of these models with prior knowledge was better than that of the best three models without prior knowledge (please compare S1 Table with Table 2).
(DOCX)
(DOCX)
(DOCX)
(DOCX)
To compare our Bayesian-network-based method, inference and reasoning were performed using gradient tree boosting.
(DOCX)
Data Availability Statement
Japanese privacy protection laws and related regulations prohibits us from revealing any health-related private information such as medical images to the public without written consent, although the laws and related regulations allow researchers to use such health-related private information for research purpose under opt-out consent. We utilized the medical images under acceptance of the ethical committee of Kyoto University Hospital under opt-out consent. It is almost impossible to take written consent to open the data to the public from all patients. For data access of our de-identified health-related private information, please contact Kyoto University Hospital. The request for data access can be sent to the following e-mail addresses of three authors: nmizuho@kuhp.kyoto-u.ac.jp, yakami@kuhp.kyoto-u.ac.jp, and tkubo@kuhp.kyoto-u.ac.jp. The other data are available from the corresponding author. As shown,the authors cannot make their study’s data publicly available at the time of publication. However, except health-related private information, all authors commit to make the data underlying the findings described in this study fully available without restriction to those who request the data, in compliance with the PLOS Data Availability policy. For data sets involving personally identifiable information or other sensitive data, data sharing is contingent on the data being handled appropriately by the data requester and in accordance with all applicable local requirements. According to Japanese Medical Practitioners' Act and Medical Care Act, Japanese hospitals must preserve health-related private information in long-term data storage. Therefore, Japanese hospitals, including Kyoto University Hospital, equips facility for the long-term storage.