Blind Source Separation Based Motion Detector for Imaging Super-Paramagnetic Iron Oxide (SPIO) Particles in Magnetomotive Ultrasound Imaging

Abstract

In magnetomotive ultrasound (MMUS) imaging, an oscillating external magnetic field displaces tissue loaded with super-paramagnetic iron oxide (SPIO) particles. The induced motion is on the nanometer scale, which makes its detection and its isolation from background motion challenging. Previously, a frequency and phase locking (FPL) algorithm was used to suppress background motion by subtracting magnetic field off (B-off) from on (B-on) data. Shortcomings to this approach include long tracking ensembles and the requirement for B-off data. In this article, a novel blind source separation based FPL (BSS-FPL) algorithm is presented for detecting motion using a shorter ensemble length than FPL and without B-off data. MMUS imaging of 2 phantoms containing an SPIO-laden cubical inclusion and 1 control phantom was performed using an open-air MMUS system. When background subtraction was used, contrast, and contrast to noise ratio (CNR) were respectively 1.20 ± 0.20 and 1.56 ± 0.34 times higher in BSS-FPL as compared to FPL-derived images for ensemble lengths < 3.5s. However, contrast and CNR were similar for BSS-FPL and FPL for ensemble lengths ≥ 3.5s. When only B-on data was used, contrast and CNR were 1.94 ± 0.21 and 1.56 ± 0.28 times higher respectively in BSS-FPL as compared to FPL-derived images for all ensemble lengths. Percent error in the estimated width and height was 39.30 ± 19.98 % and 110.37 ± 6.5 % for FPL and was 7.30 ± 7.6 % and 16.21 ± 10.29 % for BSS-FPL algorithm. This study is an important step toward translating MMUS imaging to in vivo application, where long tracking ensembles would increase acquisition time and B-off data may be misaligned with B-on due to physiological motion.

I. Introduction

IN RECENT years, nanoparticles have emerged as exciting contrast agents to study biological events at the cellular and molecular levels. Magnetic nanoparticles are currently being extensively used as imaging contrast agents in various imaging modalities such optical imaging and magnetic resonance imaging (MRI) due to their small size and the magnetic response to an external magnetic field [1]. However, MRI imaging is expensive and not real-time, and optical imaging suffers from shallow penetration depth. Ultrasound imaging is a suitable candidate for molecular imaging due to its low-cost, realtime imaging capabilities, ease-of-use, and ability to penetrate deeper tissue. Although ultrasound imaging cannot visualize nanoparticles directly due to their small size and weak acoustic scattering, ultrasound is effective for characterizing motion. In 2006, Oh et al. [2] demonstrated magnetomotive ultrasound (MMUS) imaging, in which a high-strength, time varying magnetic field was used to induce motion within magnetically labeled tissue, and ultrasound imaging was used to detect the internal tissue motion. In this manner, MMUS is capable of detecting magnetic nanoparticles through their dynamic motion response to an externally applied magnetic field. MMUS imaging has been applied in tissue mimicking phantoms [3], [4] as well as in animals ex vivo [5]–[7] and in vivo [8], [9] since its introduction in 2006.

The amplitude of the tissue motion in MMUS imaging depends upon the particle distribution, particle magnetization, magnetic field strength and gradient, and the mechanical properties of the surrounding medium [10]. Displacements are on the order of nanometers, which prevents detection by conventional ultrasound motion estimation methods. Performance of such methods is impacted by electronic noise, signal decorrelation, finite tracking-lengths, bandwidth, and sampling rates. The degree to which these parameters impact motion estimation is given by the Cramer-Rao Lower Bound (CRLB), which places a limit on the minimum estimation error variance that can be achieved in a specific imaging situation by an unbiased estimator [11]. Notably, to the extent that the displacement estimation error (i.e., noise) spectrum overlaps with the true motion signal, conventional frequency domain filtering methods are not effective for separating motion from noise.

Efforts to develop more robust magnetomotive motion detection have been made previously [3], [6], [12]. Evertsson et al. developed a frequency- and phase-sensitive algorithm that rejects motion that is outside the frequency of and out of phase with the magnetic field oscillation [3]. Pope et al. proposed a new motion detection method similar to the algorithm by Evertsson et al. with additional suppression of low-frequency noise by filtering on differential phase. Further, Pope et al. collected data both with the modulated magnetic field turned on (B-on) and off (B-off), and generated MMUS images by background subtracting the frequency and phase-locked B-off image from the B-on image [6]. While effective for stationary targets, background suppression may be less useful when the acquisitions are poorly registered due to movement of the imaged subjects. A method that separates motion signal from noise without subtracting the B-off data would be a major step in translating MMUS in vivo.

Regression filters [13] offer an alternative to frequency domain approaches for signal separation. Adaptive regression filtering can be accomplished using blind source separation (BSS). BSS via principal component analysis (PCA) has been used in ultrasound imaging for clutter rejection, physiological motion filtering, and acoustic radiation force impulse (ARFI)-induced displacement filtering [14]–[18]. Mauldin et al. [17] developed a PCA based motion estimator to detect ARFi-induced motion with reduced error in motion estimation due to noise and speckle decorrelation.

The objective of this work is to develop a BSS-based motion detection algorithm for MMUS imaging of super-paramagnetic iron oxide (SPIO) particles. Our BSS based algorithm uses complex ultrasound data, which enables separation of signal components based on the direction of motion encoded as phase changes in the complex principal components. This novel BSS-based algorithm for detecting motion in the context of MMUS imaging is combined with the general FPL method to create the “BSS based FPL (BSS-FPL) algorithm.” Our hypothesis is that BSS-FPL performs better than a traditional FPL algorithm when the ensemble length of ultrasound data is short, and when B-off data is not available for background rejection. Our hypothesis is herein tested in three tissue mimicking phantoms, and the performances of the BSS-FPL and FPL methods are compared [19].

II. Materials and Methods

A. Phantom Mold

A custom rectangular, acrylic phantom mold was constructed with dimensions of 8 × 10 × 5 cm (axial × lateral × elevational). The mold was enclosed on five sides, and the sixth side was left open to pour gelatin into the mold. The side perpendicular to the pouring side was removable to allow for ultrasound imaging. This method of imaging from a perpendicular side allowed us to avoid imaging through the boundary between layers of gelatin, as this interface could contain air bubbles. A 1 cm³ removable cube (acted as a negative mask) was used to create a cubical void within phantom that could later be filled with SPIO-laden gelatin. The SPIO-laden gelatin served as the inclusion. To locate inclusion boundaries in B-mode, the mold contained four fiducial markers of 0.64 mm diameter Alloy-510 Phosphor Bronze wire with low magnetic susceptibility. Three of the fiducial markers were oriented parallel to the elevational direction, while the fourth was oriented parallel to the lateral direction. Since the locations of and separations between the markers were known, they could be used to determine the location of the inclusion within the phantom even when the inclusion was isoechoic with the background material.

B. Tissue-Mimicking Phantoms

Three tissue-mimicking phantoms were created at a physiologically-relevant acoustic attenuation and speed of sound using a modified version of the recipe described in [20], [21]. All three phantoms had background Young’s moduli of 10 kPa. In order to achieve the desired stiffness, the concentration (C) of gelatin was calculated using the relationship between C and Young’s modulus (Y), Y = 0.0034 C^2.09 [21]. Gelatin from porcine skin, gel strength 300, Type A (Sigma-Aldrich G2500) was used. Phantoms #1 and #2 had a 1 cm³ cubical inclusion containing SPIO nanoparticles with Young’s moduli of 5 kPa and 20 kPa, respectively. Recipe for creating inclusions containing SPIO nanoparticles was adapted from [6]. Synthetic graphite nanopowder (Sigma-Aldrich 282863) and 1-propanol (Sigma-Aldrich W292818) were used in both the inclusion and the background for an estimated acoustic attenuation of 0.3 dB/cm/MHz and a speed of sound of 1540 m/s, respectively. In order to achieve an iron concentration of 3.6 mg Fe/mL, an aqueous solution of 5 mg/mL Iron (II, III) Oxide Nanopowder (Sigma-Aldrich, 637106), an equal concentration of lauric acid (Sigma-Aldrich, W261408), and 25 μL/mL ammonium hydroxide 28-30 wt% in water (Fischer 205840010), were used. Inclusions were isoechoic with background in both phantoms. Phantom #3 was identical to Phantom #2, but in order to serve as a magnetomotive sham, it contained no iron oxide. The sham inclusion’s graphite concentration was increased to 12.5 wt% so that it would appear bright in B-mode images in order to serve as validation for the inclusion boundary estimation process using fiducial markers. Table 1 summarizes material concentrations by weight for all three custom gelatin phantoms.

TABLE I.

Material Concentrations by Weight (wt%) for Custom Gelatin Tissue-Mimicking Phantoms

	Material Component
Phantom	Gelatin (%)		Graphite (%)		n-propanol (%)		SPIO mg Fe/ml
	INC	BKD	INC	BKD	INC	BKD	INC
1	3.2	4.5	4.4	4.4	3.0	3.0	3.6
2	6.3	4.5	4.4	4.4	3.0	3.0	3.6
3	6.3	4.5	12.5	4.4	3.0	3.0	0.0

C. MMUS Data Acquisition

Imaging was performed using our open-air MMUS system described in [6]. Ultrasound images were acquired using an UltraSonix SonixTouch Research scanner (Analogic Corporation, Peabody, MA) with an L14-5/38 linear array transducer operating at a transmit frequency of 10 MHz. The transmit-receive focus was set to 10 mm with transmit and receive F/ 0.7 and 1.0, respectively. Two water-cooled solenoid electromagnets with grain-oriented electric steel cores were positioned laterally on either side of the transducer to create a magnetic field in the imaging area. The magnets were operated anti-parallel and were positioned 10.5 cm apart and tilted 10° from the vertical in order to produce a 0.02 T²/m magnetic gradient in the center of the imaging region. The average magnetic field in the inclusion region (with both magnets producing a modulated magnetic field) measured 0.03 T. The peak magnetic field 5 mm below the core of each individual magnet was 0.13 T. The magnets were driven with a square-root-sinusoidally-varying voltage by two KEPCO ATE 75-15M, 1000W power supplies (KEPCO, New York, USA), and an Agilent 33522A arbitrary waveform generator to create a 2 Hz sinusoidally varying magnetic gradient force in the imaging region. The ultrasound scanner triggered the waveform generator such that the first frame of the ultrasound RF data always corresponded with a known phase of the magnetic force. B-mode frames were acquired at 61.7 fps to generate 8 s ensemble length datasets at each tracking location. Two sets of data were collected by turning the magnetic field modulation off and on. For each phantom, data were acquired at five different elevational planes with respect to the elevational fiducial marker. Acquired RF data were transferred to a computational workstation for custom processing using MATLAB (Mathworks Inc., Natick, MA).

D. Blind Source Separation Based Frequency and Phase Locked (BSS-FPL) Algorithm

BSS is a method for recovering unobserved signals or “sources” from several realizations of their mixture in an adaptive manner [22]. Principal component analysis (PCA) adaptively recovers source signals by assuming that the signals are orthogonal and Gaussian distributed. PCA can be performed by the Karhunen–Loeve (KL) transform, which transforms the input data matrix into its orthogonal basis functions with a corresponding energetic signature. This standard approach to PCA was paired with the FPL method in the BSS-FPL algorithm for the detection of SPIO particle motion. Fig. 1 outlines the steps involved in the BSS-FPL algorithm. A detailed description of the FPL algorithm can be found in [6].

Fig. 1.

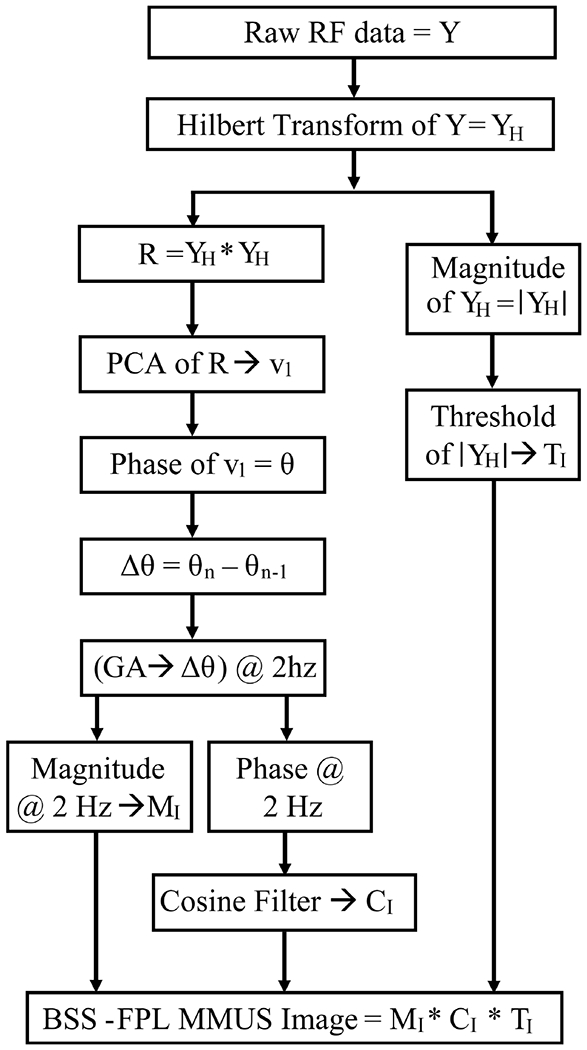
Steps for detecting motion in MMUS imaging using the BSS-FPL algorithm. PCA = principal component analysis; v₁ = the most energetic Eigen vectors; n = 2, 3, …, ensemble length, GA = Goertzel algorithm.

For the BSS-FPL algorithm, the Hilbert transform was applied to the raw radio frequency data that was sampled in depth and ensemble time to form complex data. An autocorrelation matrix, R, of complex data, Y_H, was computed though $R=Y_H^{\ast }{Y}_H$, where $Y_H^{\ast }$ is the conjugate transpose of Y_H. The dimensions of Y_H were L × N, where L is the number of samples through depth, and N is the number of ensemble time samples. Complex PCA [23] was performed to diagonalize R, which yielded complex eigenvectors,

$$V^{-1}\mathit{RV}=\Lambda =\mathit{Diag}\left\{{\lambda }_i\right\}$$ (1)

where V is the set of eigenvectors v_i arranged in a column (i.e., dimension = N × 1), with V = [v₁, v₂, v₃,…,v_N], and λ_i are the associated eigenvalues of the autocorrelation matrix, R. The most energetic complex eigenvector, v₁, was identified, and its phase (argument) was computed. Note that, PCA was applied to translating axial kernels, i.e for each pixel, L axial samples surrounding that pixel were selected, and PCA was applied to the data with dimension L × N. For this investigation, L was λ (0.15 mm) or 4* λ (0.60 mm), and N was 61, 93, 124, 155, 217, 279, 341, or 465 time samples. λ is the wavelength of the ultrasound assuming a speed of sound of 1540 m/s. Note that, computation of PCA was independent on each lateral line.

For BSS-FLP, each v₁ was used as input to the FPL algorithm [6] (instead of the RF data). Low-frequency noise was suppressed using the differential phase, which was computed by subtracting the phases of v₁ at successive ensemble time samples. Note that this calculation of the differential phase served as a high-pass filtering operation. Then, the Goertzel algorithm (GA) [24], a computationally efficient method for computing a single Fourier component from a discrete Fourier transform, was used to extract the 2 Hz Fourier component of the differential phase. Then, the magnitude and phase of the Fourier component at 2 Hz were calculated. Using the magnitude of the 2 Hz component, a 2D magnitude image M_I was formed. The phase of the 2 Hz component was used in a cosine filter [6] to identify motion that was in phase with the magnetic force. Application of cosine filtering generated a 2D image C_I with values ranging from 0 to 1. A binary 2D image T_I was formed by thresholding the B-mode image (i.e., magnitude of the Hilbert transformed complex data). Pixels with B-Mode magnitudes lower than 40% of the average B-mode image magnitude were rejected to ensure sufficient reflected intensity for motion detection. Finally, MMUS images were formed by taking the product of M_I, C_I, and T_I.

Two separate MMUS images were generated using magnetic field on (B-on) and off (B-off) data. A separate MMUS image was created by subtracting image generated using the B-off from the image generated using the B-on data. Median filter with a kernel size of 1 mm was used to smooth all MMUS images. Finally, for parametric MMUS image display, pixel intensity was converted to the dB scale with normalization relative to the maximum value. To show difference in FPL and BSS-FPL derived images, normalized images were subtracted and then converted to dB scale. The dynamic range was set to [−6 0] dB.

E. Performance Evaluation Metrics

Once parametric MMUS images were rendered, the performance of BSS-FPL and FPL algorithms was compared in terms of contrast, contrast to noise ratio (CNR), and estimated height and width of the detected inclusion.

For contrast and CNR calculations, the region of interest (ROI) inside the inclusion was defined as the concentric rectangle with 90% of the true height and width of the inclusion (red contour in Fig. 2(a)). The background ROI was defined as two rectangles positioned adjacent to the inclusion, each with a height equal to the height of inclusion’s ROI and width equal to the half of width of inclusion’s ROI (blue contour in Fig. 2(a)). The inclusion boundaries were determined using the location of fiducial markers (marked by arrows in Fig. 2(a)). Contrast was computed as the ratio of difference and sum of the median pixel intensity of the inclusion (μ_INC) and background μ_BKD) ROIs:

$$\text{Contrast}=\frac{\mid {\mu }_{\mathrm{INC}}-{\mu }_{\mathrm{BKD}}\mid }{{\mu }_{\mathrm{INC}}+{\mu }_{\mathrm{BKD}}}$$ (2)

Medians were selected over means to make the measurements robust to outliers. The CNR was computed as the difference in the median pixel intensity of the ROIs, divided by the image noise, taken as the standard deviation of the background (σ_BKD).

$$\mathrm{CNR}=\frac{\mid {\mu }_{\mathrm{INC}}-{\mu }_{\mathrm{BKD}}\mid }{{\sigma }_{\mathrm{BKD}}}$$ (3)

Fig. 2.

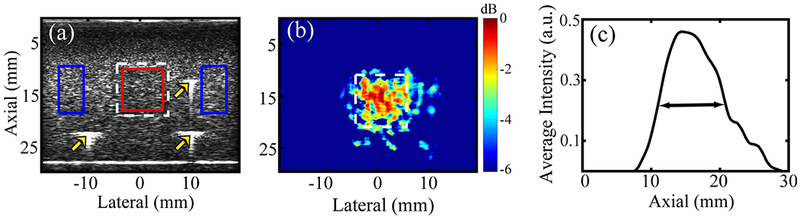
(a) B-mode ultrasound image of phantom #1 with the inclusion boundary marked with a white dashed line. The red and blue contours represent regions of interest (ROIs) in the inclusion and the background, respectively. Three bright points (marked by arrows) in the B-mode indicate locations of fiducial markers. (b) BSS-FPL derived parametric MMUS image of phantom #1 using axial kernel length = λ and ensemble length = 5.5 s. The color bar indicates the normalized MMUS image intensity in dB, with normalization relative to the maximum value. (c) Laterally-averaged pixel intensity as a function of axial distance. The Full-width-at-half-max (double arrow) of the curve was used to estimate the inclusion height. True height of the inclusion is 10 mm.

To estimate the width of the detected inclusion, the MMUS image was converted to a binary image by setting pixel intensities greater than −6 dB to 1. Then, average pixel intensity of the binary image over the axial dimension was calculated for each lateral location. The full-width-at-half-maximum (FWHM) of the axially-averaged intensity as a function of lateral position was used to estimate the width of inclusion. Similarly, the height of the inclusion was estimated by calculating the FWHM of the laterally-averaged pixel intensity as a function of axial position.

CNR, contrast, estimated height and width were stratified into two groups: “B-on” and “background subtracted” data for each ensemble, each phantom, and each algorithm. A 2-sample Wilcoxon rank sum test was carried out to compare B-on and background subtracted data. A separate 2-sample Wilcoxon rank sum test was carried out to compare FPL and BSS-FPL algorithms. Statistical significance level of p ≤ 0.05 was used. All statistical analyses were carried out using MATLAB.

III. Results

Fig. 2(b) shows a parametric MMUS image rendered using BSS-FPL with an ensemble length of 5.5 s and an axial kernel length of λ. The average magnitude of displacement in the inclusion, measured as described by Pope et al. [6], was 21.3 ± 10.6 nm (data not shown for brevity). The parametric MMUS image was converted to a binary image. Fig. 2(c) shows laterally-averaged pixel intensity of the binary image as a function of axial distance. The FWHM of the curve was used to estimate inclusion height. Estimated height was 9.4 mm as compared to the true height of 10 mm.

Fig. 3 qualitatively compares MMUS images of the phantoms with (Phantom #2) and without (Phantom #3) an SPIO laden inclusion (bottom and top rows respectively). Three observations are notable. First, neither FPL nor BSS-FPL algorithms detected an inclusion when the inclusion was free of SPIO nanoparticles (panels b-c). Second, inclusion boundaries derived using the locations of fiducial markers matched the inclusion boundaries apparent in the B-Mode image of the hyperechoic inclusion (panel a). This is meaningful because it suggests that the fiducial markers are effective indications of the inclusion boundaries when the inclusion is isoechoic with the background. Third, both FPL and BSS-FPL algorithms comparably detected the presence of the SPIO-laden inclusion (panels e-f).

Fig. 3.

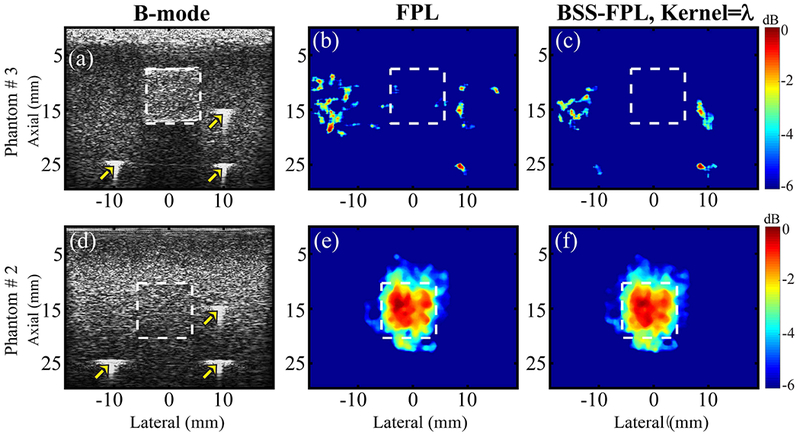
For phantoms #3 (with sham stiff inclusion, top row) and #2 (with SPIO-laden stiff inclusion, bottom row), B-mode ultrasound (a, d) and parametric MMUS images derived using FPL (b, e) and BSS-FPL with kernel length = λ (c, f). White dashed lines delineate the inclusion boundaries derived using the locations of fiducial markers (marked by arrows). RF data with ensemble length = 7.5 s were used. The color bar indicates MMUS image intensity on a dB scale with normalization relative to the maximum value.

Fig. 4 qualitatively compares the performance of FPL and BSS-FPL algorithms for detecting the soft, SPIO-laden inclusion in phantom #1 using B-on and background subtracted data. Ensemble lengths of 1.0 s and 7.5 s were used to derive the MMUS images. Four observations are notable. First, when B-on data was used, BSS-FPL derived MMUS images were better matched to the true inclusion shape than the FPL algorithm irrespective of ensemble lengths (panels b-c versus a and panels f-g versus e). Second, when background subtracted data was used, the performance of both algorithms was comparable for both ensemble lengths (panels j-k versus i and n-o versus m). Third, the outcome of the BSS-FPL algorithm was not significantly impacted by the axial kernel length or by whether or not the B-off data were subtracted. Fourth, the apparent location of the inclusion was better matched with the inclusion’s true location for the longer ensemble length (i.e., panel f versus b, n versus j, etc.).

Fig. 4.

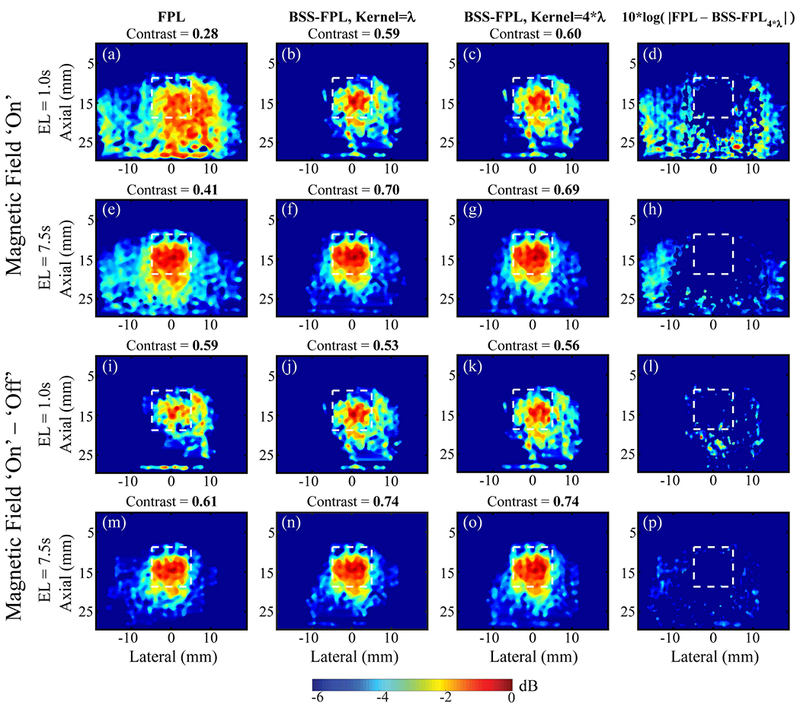
FPL and BSS-FPL-derived MMUS images of phantom #1 using magnetic field ‘on’ (B-on) and magnetic field ‘on’ – ‘ off’ (background subtracted) data. First three columns from left to right show MMUS images derived using FPL, BSS-FPL with kernel length = λ, and 4*λ, respectively and fourth column shows difference between FPL and BSS-FPL with kernel length 4*λ derived images. First and second rows show MMUS images generated using B-on data. Third and fourth rows show MMUS images generated using background subtracted data. Ensemble length (EL) of 1.0 s or 7.5 s was used to derive MMUS images. White dashed lines indicate the inclusion boundaries. Measured contrast is listed above each corresponding image.

Similarly, Fig. 5 qualitatively compares MMUS images derived using FPL versus BSS-FPL algorithms in phantom #2 with the stiff SPIO-laden inclusion. Results were generally consistent with the observations made in phantom #1 (Fig. 4). However, one difference is notable. When the background subtracted data was used, the BSS-FPL algorithm provided a better match to the true inclusion shape than the FPL algorithm for 1.0 s ensemble length. The FPL algorithm is unable to remove background motion in the right side of the inclusion (panel i).

Fig. 5.

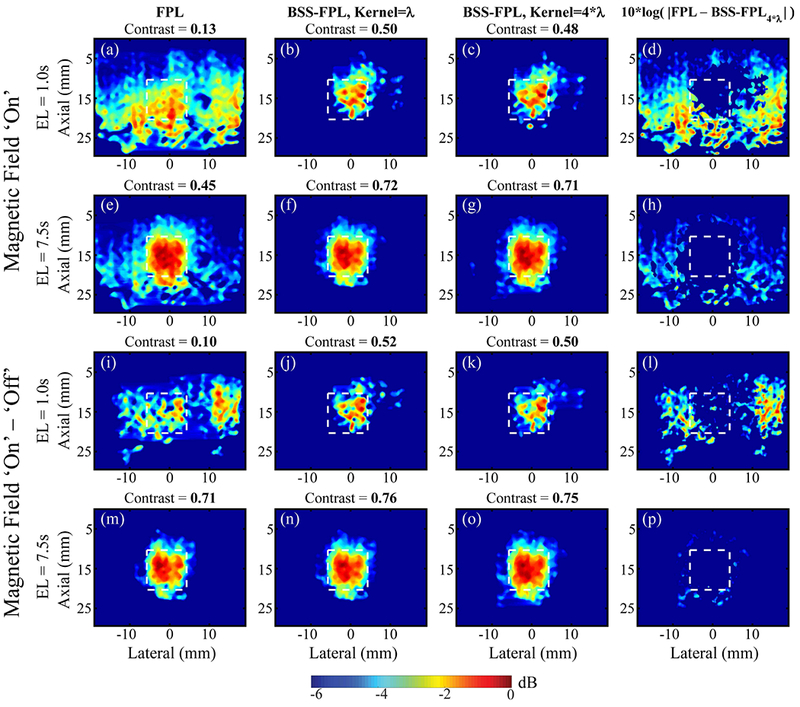
FPL and BSS-FPL derived MMUS images of phantom #2 using magnetic field ‘on’ (B-on) and magnetic field ‘on’ – ‘off’ (background subtracted) data. First three columns from left to right show MMUS images derived using FPL, BSS-FPL with kernel length = λ, and 4*λ, respectively and fourth column shows difference between FPL and BSS-FPL with kernel length 4*λ derived images. First and second rows show MMUS images derived using B-on data, whereas third and fourth rows show MMUS images derived using background subtracted data. Ensemble length (EL) of 1.0 s or 7.5 s was used to generate MMUS images. White dashed lines indicate the inclusion boundaries. Measured contrast is listed above each corresponding image.

A comparison of FPL and BSS-FPL in terms of contrast and CNR is provided in Fig. 6. Four observations are notable. First, when B-on data was used, contrast and CNR were significantly higher in the BSS-FPL versus FPL derived MMUS images irrespective of axial kernel lengths, phantoms, or ensemble lengths (except for 1.0 s ensemble lengths in panels a and c, and of 2.5 s in panel d). Second, when background subtracted was used, contrast and CNR were significantly higher (*) in the BSS-FPL than FPL derived images for ensemble length of 2.0, 2.5, and 5.5 s in phantom # 1 and of 1.0 and 1.5 s in phantom # 2. Third, contrast and CNR were significantly higher (Δ) when background subtracted versus B-on data was used for FPL algorithm irrespective of phantoms or ensemble lengths (except 2.0 and 2.5 s ensemble length in panel a, c and 1.0 and 1.5s ensemble length in panel d). Fourth, contrast and CNR of BSS-FPL algorithm were not significantly different when background subtracted versus B-on data was used irrespective of axial kernel length, phantom or ensemble length (except 4.5 s ensemble length in panel b and d).

Fig. 6.

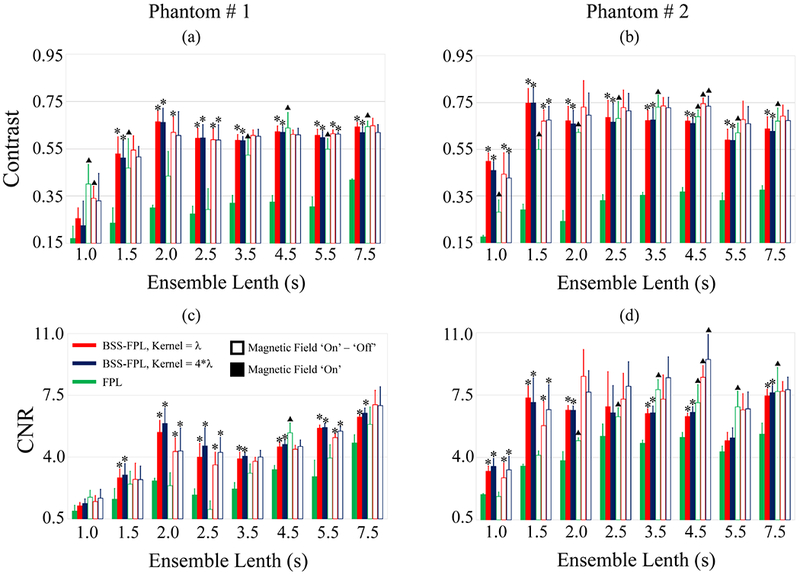
Contrast (top row) and CNR (bottom row) of inclusions in phantoms #1 (a, c) and #2 (b, d) as a function of ensemble lengths. Data are plotted as median + 0.5 × interquartile range over 5 acquisitions in different elevational planes in each phantom. Green, red, and blue represent FPL, BSS-FPL with kernel length = λ, and 4*λ, respectively. Filled and open bars represent magnetic field ‘on’ (B-on) and magnetic field ‘on’ – ‘off’ (background subtracted) data, respectively. Asterisks (*) represents significantly different (p ≤ 0.05) values between FPL versus BSS-FPL with kernel length = λ and 4λ. Triangles (Δ) represent significantly different (p ≤ 0.05) values between magnetic field B-on versus background subtracted data.

Fig. 7 quantitatively compares the performance of FPL and BSS-FPL algorithms in terms of estimated height and width of inclusions. Six observations are notable. First, estimated height and width were significantly higher (*) for FPL versus the BSS-FPL algorithm when B-on data used irrespective of axial kernel lengths, phantom stiffness, or ensemble lengths. Second, when background subtracted data was used, the estimated height and width of the inclusion was not significantly different between the FPL and BSS-FPL algorithms for the majority of ensemble lengths. Third, estimated height and width were larger for kernel length = 4*λ versus λ for the BSS-FPL algorithm. Fourth, the estimated height and width found using the FPL algorithm was significantly higher (Δ) irrespective of phantom stiffness or ensemble length when B-on versus background subtracted data was used. Fifth, the estimated height and width found using the BSS-FPL algorithm with kernel length = 4*λ was not significantly different when using background subtracted versus B-on data (except for 4.5 and 5.5s ensemble lengths in panel a). Sixth, the estimated width of the inclusions was higher than the height of inclusions for both algorithms, although true height and width were equal.

Fig. 7.

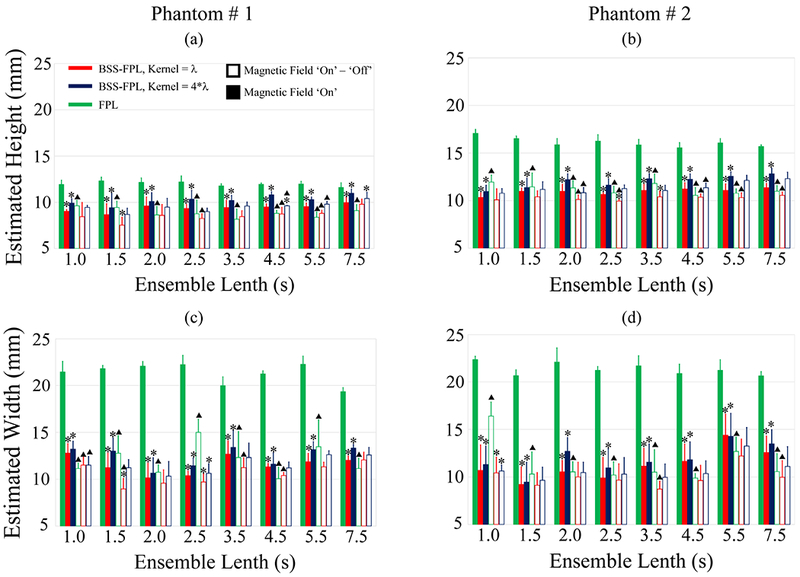
Estimated height (top row) and width (bottom row) of inclusions in phantoms #1 (a, c) and #2 (b, d) as a function of ensemble lengths. Data are plotted as median + 0.5 × interquartile range over 5 acquisitions in different elevational planes in each phantom. Green, red, and blue represent FPL, BSS-FPL with kernel length = λ, and BSS-FPL with kernel length = 4*λ, respectively. Filled and open bars represent magnetic field ‘on’ (B-on) and magnetic field ‘on’ – ‘off’ (background subtracted) data. Black dash-dot line represents the true height and width of the inclusion. Asterisks (*) represent statistically different (p ≤ 0.05) values between FPL versus BSS-FPL with kernel length = λ and 4*λ. Triangles (Δ) represent statistically different (p ≤ 0.05) values between B-on versus background subtracted data.

IV. Discussion

This manuscript describes the development and experimental demonstration of a novel BSS based motion detector for MMUS imaging using our open-air MMUS imaging system [6]. The open air system is advantageous over other closed MMUS systems [3], [5] because translation to in vivo animal imaging is feasible. In the open-air system, the ultrasound transducer and magnets are placed on the same side of the imaging objects, whereas imaging objects are placed in between the transducer and the magnet in other MMUS imaging systems.

While the open-air design supports live animal imaging, the magnetic field strength and induced displacement are lower in open-air versus closed MMUS systems, making induced motion detection more challenging [6]. For example, using a closed MMUS imaging system, Evertsson et al. reported induced average displacement of 150-250 nm when the magnetic field strength and concentration of magnetic particles were 0.18 T and 0.45 mg Fe/mL, respectively [3]. Mehrmohammadi et al. reported induced displacement of 50 μm using their pulsed magneto-motive system with a magnetic field strength and concentration of magnetic particles of 0.6 T and 3.5 μ mol Fe/mL, respectively [5]. The magnetic field gradient of our MMUS system was 0.02 T²/m, which induced approximately 20–30 nm displacements in the inclusion.

As described above, low amplitude induced motion is difficult to discern from motion estimation noise. Moreover, motion arising from mechanical vibration of the electromagnet cores could translate through the table to the imaging object and cause false positives. Despite these challenges, Fig. 3 shows that both FPL and BSS-FPL algorithms detected MMUS motion, which enabled delineation of an SPIO-laden inclusion in a tissue mimicking phantom. Notably, a sham inclusion containing no SPIO was not detected. This result suggests that the detected motion was due to the magnetically-induced motion of the SPIO particles rather than noise, and that the electromagnet vibration is effectively decoupled from the sample in our MMUS system.

Previously developed FPL approaches to MMUS motion detection subtracted B-off data from the B-on data. As described above, this strategy is not effective when the imaging object moves between B-on and B-off data acquisitions. Moreover, twice the data acquisition and processing time is needed. Ideally, an MMUS motion detector should not require subtraction of the B-off data. As Fig. 4 and Fig. 5 illustrate, the BSS-FPL algorithm performed comparably with regard to inclusion detection in the B-on and background subtracted cases. On the contrary, the FPL algorithm overestimated the inclusion boundaries in Fig. 4 and Fig. 5 when only the B-on data was used because the FPL algorithm was not able to isolate inclusion motion from background noise. Using the background subtracted data with a 7.5 s ensemble length, the FPL algorithm isolated inclusion motion from background noise and the performance of both FPL and BSS-FPL algorithms was similar. Interestingly, using the background subtracted data with a 1.0 s ensemble length, the performance of both FPL and BSS-FPL were similar in the soft phantom (Fig. 4 panels i-k), but the FPL algorithm overestimated the inclusion boundaries than BSS-FPL algorithm in the stiff phantom (Fig. 5 panels i versus j-k). This could be due to the difference in inclusion stiffnesses. In Fig. 4, the phantom contains a soft inclusion relative to the background, whereas in Fig. 5, the inclusion is stiff. Inclusion motion was higher in the soft inclusion, which enabled the FPL algorithm to isolate the inclusion from background using a 1.0 s ensemble length (Fig. 5 panel i). However, the BSS-FPL algorithm isolated inclusions in both phantoms (panels’ j-k in Fig. 4 and Fig. 5).

Comparing Fig. 4 and Fig. 5 enables one to consider another potential impact of stiffness on inclusion delineation. The width of the soft inclusion (Fig. 4) was overestimated by both the BSS-FPL and the FPL algorithms. This result could be due to higher inclusion motion in the soft phantom inducing motion in the surrounding background. More experiments are needed to fully understand the impact of inclusion motion and stiffness on the surrounding background. It is important to consider that the first order speckle statistics (μ/σ) of the inclusion and background were 1.67 and 1.82 in phantom #1 (containing the soft inclusion) and 1.83 and 1.91 in phantom #2 (containing the stiff inclusion), respectively. The potential impact of such subtle differences in first order speckle statistics on motion detection in MMUS imaging is a topic of future investigation.

By qualitative visual inspection of Fig. 4 and Fig. 5, using a λ versus a 4*λ axial kernel length in the BSS decomposition has little impact on the overall inclusion delineation. However, Fig. 6 suggests that contrast is higher for the shorter kernel length, while CNR is higher for the longer kernel length. This result is consistent with the expectation that a larger kernel will blur detail while reducing noise. The kernel size determines the axial range of data considered collectively for source separation. When motion is uniform over a large axial range, a large kernel size is beneficial because it offers more realizations of the 2 Hz motion. However, when the motion is not uniform (such as at the inclusion boundaries), a large kernel size may be detrimental because the limited number of sources must span more forms of motion and noise, which could result in incomplete MMUS signal isolation. The generally comparable performances of the λ and 4*λ kernel lengths employed in this study suggests that both kernels provided sufficient realizations of the 2 Hz motion for successful MMUS signal isolation without corrupting the decomposition at the boundaries.

Fig. 6 demonstrates that contrast and CNR were statistically higher in the BSS-FPL than FPL case irrespective of axial kernel lengths, phantom stiffness, or ensemble lengths when B-on data was used. More specifically, contrast and CNR were 1.94 ± 0.21 (median ± 0.5*IQR) and 1.56 ± 0.28 times higher in BSS-FPL versus FPL derived images over all ensemble lengths. In general, the 7.5 s ensemble length substantially improved contrast and CNR relative to the 1 s case, especially in FPL derived images. This performance improvement is attributable to more realization of the 2 Hz signal available for detection by the Goertzel algorithm.

When background subtracted data was used, contrast and CNR were 1.20 ± 0.20 and 1.56 ± 0.34 times higher in BSS-FPL versus FPL derived images for ensemble lengths less than 3.5 s. However, contrast and CNR were similar for BSS-FPL and FPL for ensemble lengths greater than or equal to 3.5 s. Interestingly, using background subtracted data, contrast, and CNR in phantom #1 were not statistically different between FPL versus BSS-FPL for ensemble lengths of 1.0 and 1.5 s but were statistically different for ensemble lengths of 2.0 and 2.5 s (panels a and c). Contrast and CNR plateaued after 1.5 s and 1.0 s ensemble lengths in phantoms # 1 and # 2, respectively. Further, contrast and CNR achieved using B-on data and the BSS-FPL algorithm were similar to the contrast and CNR achieved using background subtracted data and the FPL algorithm. This result is meaningful because it suggests that shorter data acquisitions are required when the BSS-FPL algorithm is used, which expedites data acquisition and reduces computational overhead. One limitation of the current statistical analysis is that only five measurements were used in the statistical analysis at each ensemble.

In terms of delineating inclusion size, Fig. 7 shows that when B-on data was used, the percent error in the inclusion’s height and width was 39.30 ± 19.98 % and 110.37 ± 6.5 %, respectively for FPL and was 7.30±7.6 % and 16.21 ± 10.29 %, respectively for BSS-FPL algorithm. The BSS-FPL method more closely estimates the soft inclusion’s height and width, relative to the FPL algorithm. When background subtracted data was used, percent error in inclusio’s height and width was reduced to 0.88 ± 11.20 % and 9.40 ± 1.16 % for FPL and 0.20 ± 8.70 % and 4.40 ± 7.90 %, for BSS-FPL algorithm. The inclusio’s size was overestimated by both algorithms. This may due to inclusion motion introducing vibration in the surrounding mediums. In future, finite element method simulation will be performed to understand the impact of inclusion motion in the surrounding backgrounds. The concentration of SPIO particles was comparable to the study of imaging SPIO-labeled platelets using MMUS [6]. The present study did not explore the BSS-FPL algorith’s potential for detecting MMUS motion induced in materials with lower concentrations of SPIO particles. Future work will investigate the lowest concentration of SPIO particles that are needed to detect presence of inclusion using BSS-FPL algorithm.

A limitation of the proposed BSS-FPL method is the assumption that SPIO motion is spanned by the most energetic basis function. In the examined cases of stationary phantoms, this assumption is reasonable because the magnetically induced SPIO motion is the only motion present. However, during in vivo imaging with the potential for physiological and/or hand-held user motion, this assumption may break down. For example, if an echo-bright tissue region moves independently of the magnetic field, then SPIO motion will likely be spanned by a lower energy basis function. In such a case, it will be necessary to evaluate each basis function to identify which spans SPIO motion. Fortunately, the phase and frequency of SPIO motion are known, and this a priori information may be exploited to adaptively identify the basis function spanning the MMUS signal. In the future, BSS-FPL methods will be improved by adaptively identifying basis functions that represent SPIO motion.

Another limitation of the presented BSS-FPL motion detection method is the additional processing time required for BSS decomposition. It took 2 minutes and 30 seconds to perform complex PCA decomposition of 1568 × 255 samples (axial × lateral) with an ensemble length of 2.5 s and kernel length of 4*λ using a core i7 processor and 8 GB of RAM. However, parallel processing and other expediting methods could be implemented to perform the complex PCA decomposition faster. Note that it took 2 minutes and 40 seconds to perform the FPL algorithm of 1568 × 255 samples (axial × lateral) with an ensemble length of 2.5 s using the same computer.

V. Conclusion

In this work, a BSS based motion tracking algorithm to detect nanometer scale, periodic motion in an open-air MMUS imaging setting is presented. Parametric MMUS images of gelatin tissue mimicking phantoms containing inclusions laden with SPIO were rendered using FPL and BSS-FPL algorithms. Inclusion contrast, CNR, height, and width in BSS-FPL derived MMUS images were superior as compared to FPL when only B-on data was used, suggesting that the BSS-FPL algorithm obviates the need to collect data with the B-field off. Similarly, the BSS-FPL algorithm outperformed the FPL method for short ensemble lengths, suggesting that faster data acquisition is enabled by BSS-FPL. This research achieves a major step towards translating MMUS imaging for in vivo animal imaging.