Effect of Head Motion on MRI B₀ Field Distribution

Abstract

Purpose

To identify and characterize the sources of B₀ field changes due to head motion to reduce motion sensitivity in human brain MRI.

Methods

B₀ fields were measured in five healthy human volunteers at various head poses. After measurement of the total field (TF), the field originating from the subject (SF) was calculated by subtracting the external field (EF) generated by the magnet and shims. A subject-specific susceptibility model was created to quantify the contribution of the head and torso. The spatial complexity of the field changes was analyzed using spherical harmonic expansion.

Results

Minor head pose changes can cause substantial and spatially complex field changes in the brain. For rotations and translations of about 5° and 5 mm respectively at 7 T, the SF component alone generates a resonance frequency shift over the brain with a standard deviation of about 10 Hz. The stationary torso contributes to the SF significantly with a standard deviation of about 5 Hz. These SF change leads to image-corrupting phase errors in multi-shot T₂*-weighted acquisitions.

Conclusion

The B₀ field changes arising from head motion are problematic for multi-shot T₂*-weighted imaging. Characterization of the underlying sources provides new insights into mitigation strategies, which may benefit from individualized predictive field models in addition to real-time field monitoring and correction strategies.

INTRODUCTION

Subject motion is a common source of artifacts in brain MRI. Typical anatomical MRI acquisitions last for several minutes during which the data for image reconstruction is collected. Any head motion during this period can corrupt the data and affect image quality. Often, and especially during scanning of patients and children, motion related artifacts in the form of blurring and ghosting are severe enough to affect clinical diagnosis (1).

Over the years, a variety of methods have been developed to mitigate motion artifacts (2,3). These have optimized the MRI acquisition process to reduce motion sensitivity or corrected for motion during image reconstruction. For example, fast acquisition schemes such as single-shot methods (4–7), can be utilized to “freeze” motion or to limit the amount of motion during the image acquisition time. This however limits the flexibility of manipulating image contrast, optimizing the signal-to-noise ratio (SNR) in the images, as well as the maximum attainable spatial resolution.

Alternatively, the incorrect spatial encoding of the object due to motion during the scan can be corrected using estimates of the motion parameters. These can be measured in real time with an external measurement device, such as an optical camera (8,9) or magnetic field probes together with off-resonance frequency markers (10), or from MR signal itself in the form of so called “navigators” (11–16). The estimated motion can then be used to dynamically adjust the slice location and orientation of an ongoing scan (prospective motion correction) (17) or correct the motion artifacts at the reconstruction stage (retrospective motion correction) (16,18,19). In some of these methods (14,15), beyond the spatial correction scheme, effect of motion-induced changes of the MRI main magnetic field (B₀) was partially corrected based on the measured navigators and will be mentioned in more details later in this section.

While these methods often decrease the sensitivity of brain MRI to motion, they may be inadequate under specific circumstances. For example, brain MRI based on magnetic susceptibility contrast requires a long echo time (TE) and generally cannot be performed with single-shot methods, making such methods particularly sensitive to motion artifacts, even with the application of correction schemes. This sensitivity is attributed in part to the complex effects of motion on the B₀ field, which typically are not or inadequately considered in motion correction approaches. This is particularly problematic at high magnetic field strength, where susceptibility contrast is increased and has promising applications for the study of brain structure and function (20,21). In fact, to achieve consistent high image quality for these applications, motion appears to be a major impediment.

The complexity of the relationship between head pose (i.e. position and orientation) and the B₀ field results from an interplay of several effects. As the head moves, there are two main sources of B₀ field inhomogeneity that contribute to the total field (TF) changes in the brain. The first is the external field (EF), which is the combined field from the main magnet and the B₀ shim coils of the MRI system. A second contribution comes from the subject’s inhomogeneous magnetization (the subject’s field or SF), which consists of a (mostly) static component due to the magnetization of the immobile torso and a dynamic one from the head and neck. At the start of an MRI exam, typically the B₀ shim fields are adjusted to homogenize the TF in the head. With motion, however, the head will experience a changed SF due to the reorientation of the magnetization of the head in the main field direction, and a change due to a changed position in the inhomogeneous EF and the SF from the torso. Note that although the EF component can be determined on a scanner-specific basis, the subject-specific SF remains unknown. A third, temporally varying contribution comes from the respiratory motion of the chest. The latter may introduce spatially varying changes with a peak-to-peak amplitude of about 3 Hz at 7 T with a strong dependency on location in the inferior-superior (z) direction (22). Real-time shimming may counteract this field fluctuation using the chest displacement data as input (23). In the current study, this respiration-related field fluctuation was corrected for during image reconstruction and not further investigated.

Changes in B₀ alter phase and frequency of the MRI signal, which can lead to geometric distortions, image intensity dropouts, and ghosting artifacts. These effects can be minimized by acquiring all image data very rapidly relative to the time scale of head motion, as is done in single-shot MRI. While these techniques remain sensitive to the (static) B₀ distribution across the head, correction is possible retrospectively by, for example, estimating this distribution from the image phase (24). For multi-shot techniques, however, additional dynamic field estimation and correction methods are required to correct the B₀ errors across the phase encoding steps. For low-order spatial variations of B₀, these may include three one-dimensional projections (14,25) or volumetric navigators (26,27) combined with adjustment of the shims in real time. However, the effectiveness of these approaches depends on the spatial complexity of the motion-induced field changes in the brain and the extent to which they can be accurately measured and compensated for with the available shim hardware, which may not be straightforward. In this regard, measurement of the field outside the head with e.g. field probes is theoretically not sufficient to estimate the field inside the head, as was recently confirmed in a study that combined measurement data from sixteen field probes placed around the head (28). The alternative approach of navigators can be demanding in scan time for mapping complex field changes. Furthermore, even if such information were available, the real-time field shimming capability of standard clinical scanners is generally insufficient to compensate for the dynamic changes that may have second- or higher-order spatial dependencies. In previous studies (17,29,30), the spatial pattern and magnitude of the TF changes were reported in several subjects, but the contributions to the TF from different magnetization components and the complexity of its spatial pattern were not quantified. Based on these earlier findings, we hypothesized that the spatial complexity of the head motion-induced B₀ change is beyond the measuring capacity of the conventional navigators that can be easily inserted into MRI sequences, and the magnitude of this change is significant enough to cause severe image artifacts in T₂*-weighted MRI or at high field. In order to ultimately correct its impact, it is important to develop a better understanding of the magnitude, complexity and contribution from the various sources, including the EF and the SF of the head and torso. To address this, we performed MR-based measurements of the B₀ field at various head poses and numerical simulation based on a subject-specific model of the susceptibility distribution of the head and torso.

METHODS

Human experiments

Anatomical images and B₀ field map data were acquired from five healthy human subjects under a human subject research protocol approved by the Institutional Review Board at the National Institutes of Health. Head scans were obtained at 7 T (scanner: Magnetom, Siemens, Erlangen, Germany). One subject was also scanned at 3 T (scanner: Magnetom Prisma, Siemens, Erlangen, Germany). This scanner was equipped with a transmit-receive body radiofrequency (RF) coil which could be used to image the neck and torso for modeling of their effect on the SF in the head. For head scans at 3 T, a 32-channel receive head coil (Nova Medical, Wilmington, MA, USA) was used. At 7 T, either a 32-channel receive head coil (Nova Medical, Wilmington, MA, USA) or a home-built birdcage transmit-receive head coil (31) was used.

During the experiments, the subjects were instructed to move their head to various poses and remain still during the following scan period when the B₀ field was measured. After an initial scan (“reference”), head poses employed were, “right”, “left”, “up” and “down”. The same B₀ shim parameters were used across different head poses. The field map data at each pose were acquired with a 2D gradient-echo (GRE) sequence with five echoes spaced by 1.2 ms and a 2 mm isotropic resolution. In this sequence, a first-order navigator echo along the read-out direction was acquired for each shot (i.e. RF excitation) to allow for correction of the dynamic frequency changes due to scanner instability or respiration. The field maps were calculated based on the unwrapped phase difference between echoes (32). The frequency data acquired in different poses were detrended based on the average frequency in a 3×3×3 voxel³ region at the center of the brain to reduce the field drift effect of the scanner. Note that this is an approximation of the field drift from the scanner since the pose change is likely to cause a global field shift. The head poses were determined based on an inter-pose, rigid-body co-registration of the GRE magnitude images. This procedure returned the 6-parameter rotation and translation information.

To generate the susceptibility model, anatomical data were acquired from the subject in the 3 T experiment using a proton density-weighted 2D GRE sequence (TE=3.4 ms, TR= 500 ms, flip angle=35°) covering a range of 50 cm from the top of the head to the chest. This was done in three stages with table positions at head, neck and chest and isotropic resolutions of 2, 4 and 4 mm, respectively. The combined image was interpolated to 2 mm resolution for generating a susceptibility model of the subject.

Estimation of the EF

To estimate the EF, which originates from the MRI system, field maps were also acquired on a spherical oil phantom with a diameter of 164 mm. Choice of this phantom was based on the theoretical notion that a sphere of uniform magnetic susceptibility does not change the resonance frequency within it. After each scan session on a human subject, this phantom was placed in a position that closely matched that of the head. A different B₀ shim configuration was utilized in the phantom experiment to optimize the B₀ homogeneity and the data quality. The measured field maps in the phantom were fitted to polynomials up to the third order to compensate for the location mismatch between the phantom and the head. In addition, shim calibration was performed by acquiring field maps at various magnetic field shim settings using the spherical phantom. Based on these data, the EF was calculated as the sum of the measured field in the phantom and the difference of the shim fields, essentially the field from the magnet and the shim coils. The calculated EF was subtracted from the measured TF of each subject to obtain the SF.

Simulation of B₀ field

To further elucidate the mechanisms of the effects of head pose on the SF (and thus the TF) in the brain, a model-based field simulation was performed. A susceptibility model was constructed based on the proton density-weighted GRE image of the subject in the 3 T experiment. The GRE image was manually segmented into air cavities, lung and other tissues, the former including sinuses, ear canals, nasal cavity, esophagus and air way and the latter including bone and soft tissues, in reference to visual descriptions of the gross anatomy of human head and torso (33,34). The susceptibility value of air (0.36 ppm) was assigned to the background and air cavities in the model, and that of water (−9 ppm) to bone and soft tissues. Lung was assigned a mixed value with an air-to-water ratio of 8:2 (35). The value of ear canals and upper nasal cavity were assigned empirical air-to-water ratios of 5:5 and 7:3, respectively, to account for the ear plugs and circuitous nasal air path. Field simulation was performed using a custom program implementing the Fourier-based method as described in (36). Simulated field distributions for various head poses were calculated by changing the head pose of the model using the six motion parameters from the experimental data. The simulated field in various poses was then transformed to the reference pose.

Quantification of the magnitude and complexity of the B₀ field changes

The B₀ maps were filtered to reduce the Gibbs ringing artifact, using a 3D Gaussian filter of which the standard deviation was 0.6 voxels and the kernel size was 5 voxels. Analysis about the B₀ field changes was performed in a region of interest (ROI) covering the cerebrum and part of the cerebellum and midbrain for each subject. The ROI was obtained using manual segmentation of the GRE images used for B₀ mapping. The edge of the brain was excluded in the analysis by shrinking the ROI by two voxels—half of the Gaussian filter kernel width—to avoid partial volume effects near the brain-skull interface. An example of the ROIs is shown in Sup. Fig. S1 in the Supporting Information.

The standard deviations (SD) of the SF and TF were analyzed within the ROIs to measure the magnitude of the motion-induced field changes. Because the field drift of the scanner cannot be completely separated from the motion-induced global field changes, the mean value of the field changes was only analyzed in the simulation data. B₀ field data from a phantom experiment showed that the scanner field drift was mostly spatially uniform.

The spatial complexity of the B₀ field changes was evaluated based on the residual of the spherical harmonic expansion. The expansion of the field changes was performed in the laboratory frame and the head frame, respectively, i.e., the field data was re-aligned by co-registration in the latter case.

Evaluating the SF effect

In order to estimate the significance of the pose-dependent SF on image quality, simulations were performed based on a T₂*-weighted GRE dataset with a TE of 25 ms, acquired with a single, constant head pose. For a selected slice, n consecutive k-space lines were modified based on the measured SF from a different head pose, starting at varying k-space location p. This simulated the field effects of moving from the reference pose to the new pose at k-space line p and returning to the reference pose at line p+n. The artifact level in the resultant “field-corrupted” image was then evaluated using the normalized root-mean-square error (NRMSE) of its magnitude relative to the uncorrupted image magnitude. Note that this particular simulation isolates the effects of field changes with pose changes and avoids confounding effects from gradient encoding errors resulting from pose changes. The latter may be correctable with dedicated strategies based on estimation of the motion parameters. It also isolates the change of the EF in the head frame which can be determined on a scanner-specific basis as shown earlier and further corrected with estimated motion parameters.

The impact of the phase error on the image resolution was further analyzed based on the fractional energy of the side lobes (FESL) of the point spread function (PSF) when n k-space lines (TE=25 ms) were modified with a spatially constant frequency offset Δf. Note that the location of the n lines does not change the magnitude of the PSF based on the Fourier Shift Theorem. FESL is defined as $\mathit{FESL}=1-\frac{{\left|{\mathit{PSF}}_0\right|}^2}{{\displaystyle \sum _j}{\left|{\mathit{PSF}}_j\right|}^2}$, with j being the spatial index of the discrete PSF relative to the central position. Based on the Convolution Theorem, FESL can be derived as

$$\mathit{FESL}=1-{\left|1+r\left(e^{2\pi i\mathrm{\Delta }\mathit{fTE}}-1\right)\right|}^2$$ (1)

where r is the ratio between the numbers of the corrupted lines and the total phase-encoded lines.

RESULTS

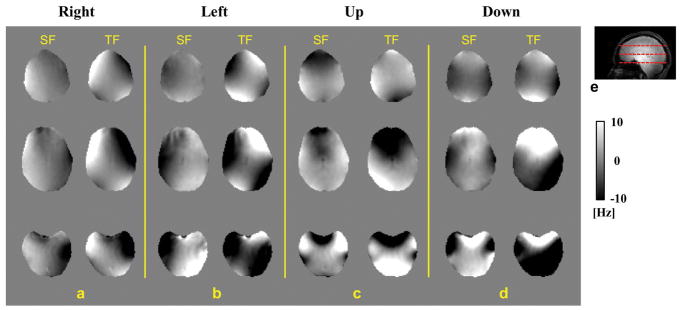
An example of the effects of head pose on the SF and TF in the brain is shown in Fig. 1, where B₀ field maps from different poses (a–d) were aligned with that of the reference pose, i.e., in the head frame. The ROI used for analyzing the data of this subject is shown in Sup. Fig. S1 in the Supporting Information. The corresponding motion parameters are listed in Table 1. Even for small pose changes (a few degrees rotation and a few mms translation), robust and highly inhomogeneous field shifts are observed that reach levels of +/− 10 Hz for both SF and TF. The spatial patterns are complicated and, as would be expected, show opposing directions of field shift with respect to the directions of pose change (i.e. “left” versus “right” and “up” versus “down”). Histograms showing the distribution of the SF change in the brain of the same subject are shown in Fig. 2, indicating that observed frequency shifts range from −10 to 10 Hz. The SDs of both SF and TF changes are summarized, with the pose parameters, in Table 1.

FIG. 1.

a–d: Field difference in the brain of subject #1 in four poses relative to the field in the reference pose in the head frame. The results on the left of each panel are the SF change while the TF change is shown on the right. e: A sagittal image of the subject. Dashed lines indicate the positions of the slices shown in a–d. The field map is presented in the unit of Hz offset from the resonance frequency at 7 T.

TABLE 1.

Estimated head orientation and position changes of subject #1 and the standard deviation of the field change inside the brain in the head frame.

	Rotation*/°			Translation/mm			SD/Hz
	x**	y	z	x	y	z	SF	TF
Right	−0.7	−1.3	−7.2	6.6	−1.4	−0.3	5.0	8.3
Left	1.7	−0.6	8.7	−5.0	0.5	−1.2	7.8	10.8
Up	−5.2	−0.8	2.1	−0.5	−2.6	−4.2	7.9	12.7
Down	4.9	−1.5	3.0	1.2	0.6	0.6	8.6	16.6

^*: The center of the rotation is on the center of the FOV.

^**: The positive directions of x, y and z axes are towards the left, posterior and head direction of the subject, respectively.

FIG. 2.

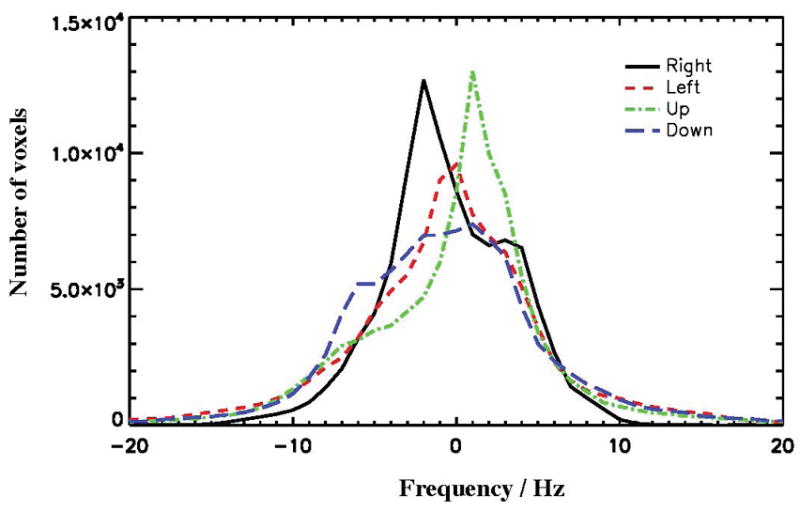
Distribution of the SF change in the head frame of subject #1 for the four poses relative to the reference.

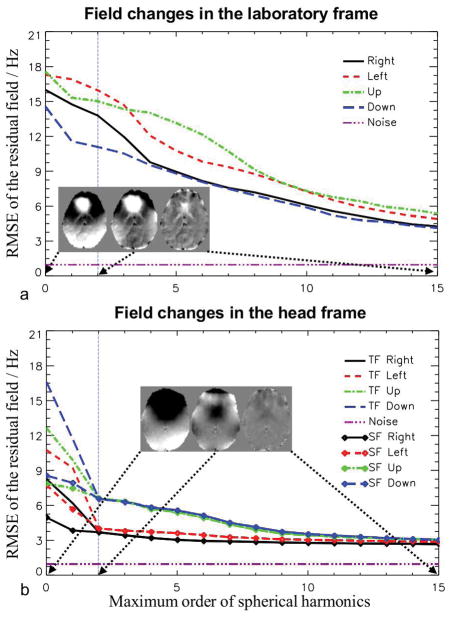
The complexity of the spatial patterns of the field changes was first analyzed in the laboratory frame (i.e. prior to registering the field maps to the reference) based on fitting with spherical harmonics. As shown in Fig. 3a, the root-mean-square error (RMSE) of the residual field decays only slowly as a function of the maximum order of the harmonics. Even with high-order expansions up to 15, RMSE of the residual field is still around 5 Hz, well above the noise threshold derived from the noise scan data (37). In contrast, in the head frame as shown in Fig. 3b, the TF and SF changes have fewer high-order components and their residuals merge with each other after the second order expansion. This can be explained by the fact that the field changes due to the change of head pose in the inhomogeneous EF are mostly composed of low-order spatial components while the higher-order changes mainly originate from the moved susceptibility distribution of the subject. By tracking the SF curves alone, it can be noticed that in the “Right” and “Left” poses, the residuals reached the flat part of the curves earlier than the “Up” and “Down” poses, suggesting predominantly low-order SF changes in the former two cases, which are mostly from the low-order inhomogeneous field of the torso. As suggested by the residual curves and the maps (inserts), it still needs shims beyond the commonly available second order to counteract the field changes in the head frame.

FIG. 3.

RMSEs of the residual, when the field changes in the laboratory frame (a) and head frame (b) were modeled as spherical harmonic expansions, as a function of the maximum order of the harmonics. For the head frame, both TF and SF changes were analyzed. The purple dashed line shows the level of noise in the field measurement. The vertical dashed line marks the second order expansion, illustrating the maximum order of the shim coils on a typical high-field MRI system. The inserts show the TF residual fields of pose “Up” in a slice after the expansions of 0th, 2nd and 15th orders, respectively. The gray scale of the maps ranges from −10 to 10 Hz.

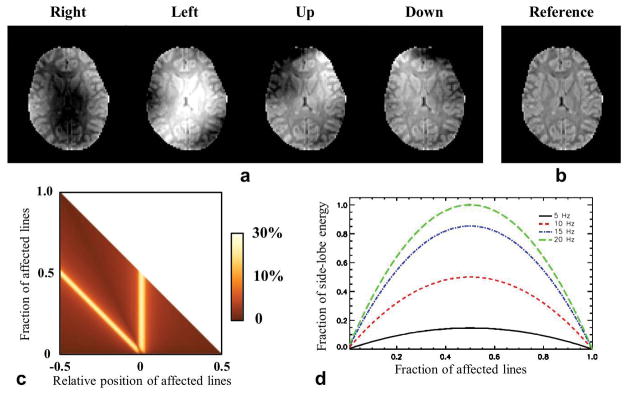
The motion-induced changes in the SF during MRI image acquisition are strong enough to cause substantial image artifacts. To illustrate this, we simulated the effect using T₂*-weighted GRE data acquired at 7 T with TE=25 ms, based on the observed SF change in the central slice shown in Fig. 1. As expected, the worst-case scenario should occur when pose changes happen during acquisition of the central lines in the k-space. To illustrate this, we replaced two central lines (p=-2 and n=2) of the k-space data with “field-corrupted” data (Fig. 4). The NMRSE values of the corrupted images are 9.7%, 12.9%, 16.7% and 16.0% for “Right”, “Left”, “Up”, and “Down” head poses, respectively. The NMRSE values resulting from replacing n consecutive k-space lines starting from k-space location p are shown in Fig. 4c. The largest NMRSEs occur when the pose transition (one of the two borders of the group of n-lines) occurs at the center of the k-space, resulting in two peaks at each y-axis location. Although smaller NRMSE values are observed when the outer k-space lines are corrupted, the phase error may still cause strong deterioration on the detailed structure in the image. To evaluate this, in Fig. 4d, the calculated FESL of the PSF based on Eq. 1 as a function of the frequency change Δf (TE=25 ms) and the fraction r of the corrupted lines suggests that even a small Δf such as 10 Hz can relocate significant energy to a pixel from the other pixels. As expected, this effect is the most significant when the k-space lines are divided into two halves of different frequency states and the resultant phase difference is 180º.

FIG. 4.

Impact of the motion-induced SF change on the synthetic GRE image with TE=25 ms. a: Resultant image magnitudes after two central k-space lines of the reference image (b, in the same color map as a) were replaced by the corresponding lines of the “field-corrupted” images. The data of field change was obtained from the measurement in the middle slice as shown in Fig. 1. c: Summary of NRMSE of corrupted image magnitude as a function of the fraction of affected lines and their relative position in the k-space. d: The FESL curves of the PSF as a function of the fraction of the affected lines and the frequency change.

Results of the simulations investigating the contributions to the SF changes as a function of head poses are shown in Fig. 6 based on the extracted susceptibility model as shown in Fig. 5. The measured and simulated SF changes in the head frame of reference were converted to the corresponding frequency at 7 T. It can be seen that the simulated SF changes based on the full model (head and torso) closely matched the experimentally observed changes. Reassuringly, field patterns for different poses in this subject were similar to those in subject 1 (Fig. 1). This was also the case for the SD values of the measured and simulated field changes (Table 3, compare with Table 2). Importantly, Figure 5 also shows that the contributions from both the head and the torso are significant in explaining the observed field changes with pose changes. Field calculation using the head-only model resulted in noticeable differences from both the experimental data and the head-torso model, indicated by the yellow arrows in Fig. 6. This difference, which is equivalent to the field change originating from the susceptibility of the torso, is shown in the bottom row of Fig. 6 for “right”, “left” and “up” poses. Corresponding torso-originated field changes in the brain were 0.2±4.1, −0.4±5.0 and −1.8±5.8 Hz, respectively, which are substantial portions of the total SF changes reported in Table 3. Note that these SD values are comparable to the SD values when head rotation is predominantly around the z-axis as shown in Table 2. It can be understood that when the head only rotates around the z-axis, the main source driving the SF change is the non-uniform field from the stationary torso. To confirm the adverse consequence of neglecting the torso in the model, the distribution of prediction error against measurement data is illustrated in Fig. 7, showing broadened error distributions in all three poses based on the head-only model.

FIG. 6.

Comparison of model-predicated field changes with experiment data in three head poses. The subject did not move as expected in the step of “Down” pose. The field data was converted to the resonance frequency at 7 T.

FIG. 5.

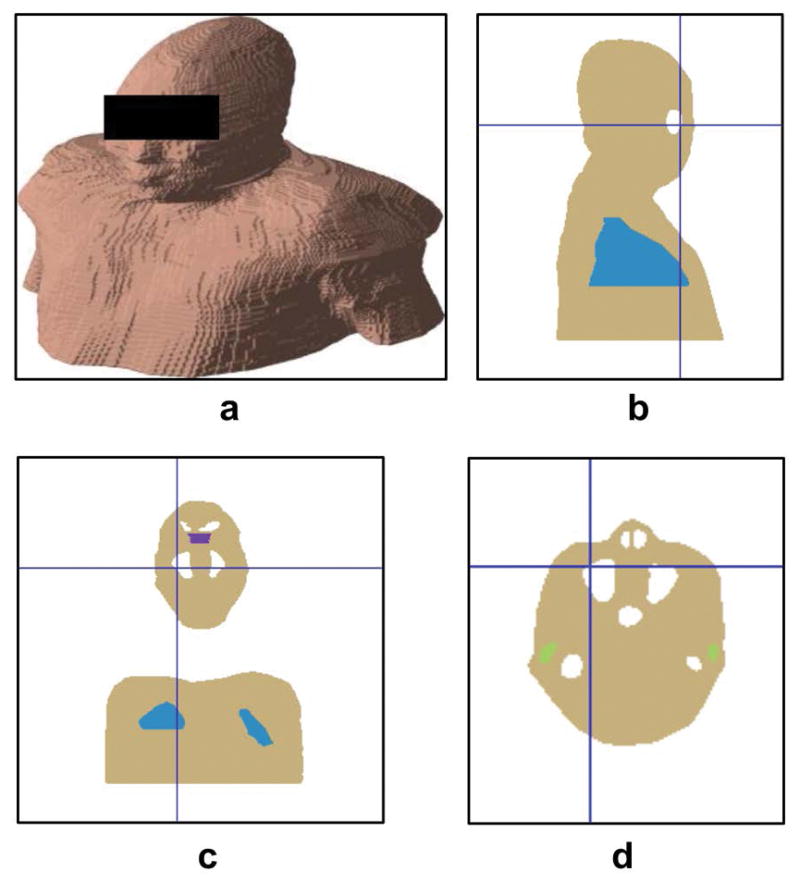
The extracted susceptibility model of subject #5 in the simulation study. a: Surface view of the model. b–d: Sagittal, coronal and axial view of the model, respectively. Blue, white, green and purple regions indicate lung, air cavity, ear canal and upper nasal pathway, respectively.

TABLE 3.

Estimated head pose change of subject #5 in the 3 T experiment and the statistics of the measured and simulated SF change equivalently at 7 T in the brain in the head frame.

	Rotation/°			Translation/mm			SD of Measurement/Hz (7T)	Mean±SD of Simulation/Hz (7T)
	x	y	z	x	y	z
Right	−0.6	−2.1	−10.6	3.5	−1.0	0.0	11.1	0.4±8.2
Left	−2.5	3.7	7.3	−3.0	−0.2	−1.5	14.1	4.5±12.3
Up	−7.3	1.1	0.5	−1.0	−1.2	4.0	17.9	12.0±17.3

TABLE 2.

Standard deviation of the SF change inside the brain of four subjects in the 7 T experiments. Maximum displacement is measured among four locations at the forehead, the back of the head and above the ears, respectively.

Subject	Motion			SD/Hz
	Maximum displacement/mm	Rotation/° (x, y and z)	Translation/mm (x, y and z)	SF	TF
#2	12.0	−4.4, 1.2, 3.0	−0.9, −0.9, 4.7	8.7	15.8
	15.1	1.0, 1.3, 7.8	−1.4, −0.1, 2.4	5.2	8.2
#3	11.8	6.3, 2.7, 0.0	−1.3, 1.4, −0.5	12.0	21.1
	14.5	−7.4, 2.8, −2.5	−0.8, −2.7, −0.6	14.2	18.9
	22.9	−0.2, 5.4, 9.9	−4.4, −1.5, −1.7	10.3	15.4
#4	12.2	−2.8, −0.9, 4.4	−2.3, −0.3, 5.2	8.3	15.5
	15.4	−5.1, −0.8,2.7	−1.5, −0.1, 5.3	12.5	21.4
#5	12.6	−5.0, −1.1, −3.8	−0.2, −2.4, −2.4	13.6	14.3
	11.9	−6.2, −0.2, 0.6	0.2, −2.7, −0.9	14.3	15.7
	9.9	−2.1, −0.3, 3.8	1.3, −0.5, 1.0	6.0	8.4

FIG. 7.

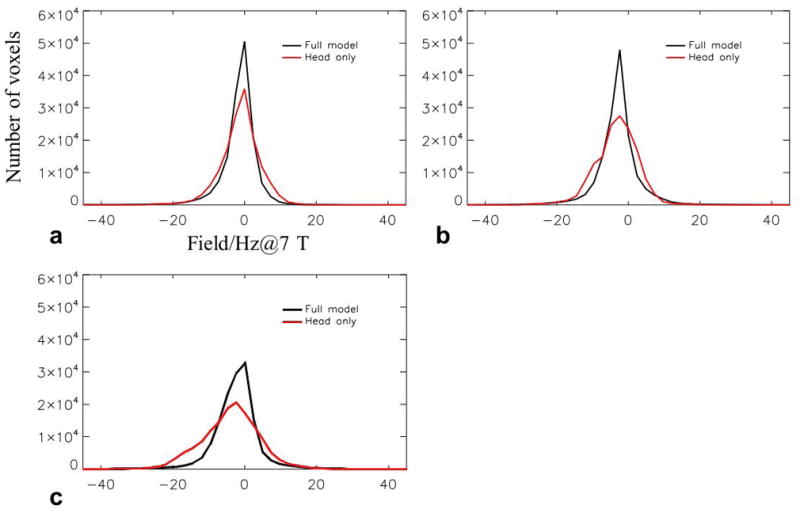
Histograms of the difference between calculated field change and experimental data for the head-only (red) and full (black) models. The head-only model shows increased error compared with the full model. a–c: Error distribution corresponding to “Right”, “Left” and “Up” poses, respectively.

DISCUSSION

Head motion-induced changes in the TF during susceptibility-weighted MRI can form a major source of image artifacts. Two distinct sources contribute to the TF changes in the head: a change in the head pose in the inhomogeneous external field from the MRI magnet and its shims, and a change in the SF originating from the susceptibility of the subject. The latter can originate from, in the reference frame of the head, a static component from the torso (ignoring respiratory motion of the chest), and a dynamic motion-related component from head and neck. Quantification of these contributions in five healthy human volunteers showed that inhomogeneity of the external background field and the magnetization of the human subject both contribute significantly to the TF change following head motion. Although the amplitude of field changes is relatively minor compared to the background inhomogeneity and therefore less likely to cause severe additional distortion in either the read-out direction or the phase-encoding direction of EPI data, we have shown that it is significant enough to cause significant phase-encoding errors in multi-shot MRI, during which head motion tends to occur, especially when the TE is long. The metric FESL was proposed to quantify the energy displacement over pixels due to the phase error happening across the phase encoding steps. The field changes were also found to be spatially complex, making them difficult to correct with conventional phase correction schemes based on navigator echoes.

Several previous studies have reported on the magnitude of the B₀ field changes caused by head motion based on either measurement or simulation (17,29,30,38,28). The values were either similar, or substantially higher than the values found here. For example, in (17), the maximum field change was reported to be 160 Hz at 3 T at the front of the brain, albeit with a much larger (12.5º pitch rotation, i.e., rotation around the left-right axis) pose change than used here. In (29), the maximum field change was in excess of 50 Hz at 3 T with a 5º pitch rotation. In another experimental study using a 2 mm resolution at 7 T (30), with rotations less than 10º, the field changes in several representative ROIs were in the range of 10–20 Hz, close to the SD value of the TF changes (Table 1 and 2) in the current study. In another study performed under similar conditions (38), reported field changes were substantially higher and in the range of 20–40 Hz with a higher resolution of 1 mm. Lastly, a simulation study (28) showed that the average absolute shifts of the SF were in the 10–20 Hz range at 7 T when the head model was rotated by about 5º, again similar to the SD value of the SF changes reported here (Table 1, 2 and 3). In summary, while there is a significant variation in the reported field changes associated with head motion, these studies confirm the notion that the effects are substantial.

While it is possible to estimate the EF from a calibration scan (e.g. by using a spherical phantom), correcting for the SF is more challenging as it depends on the subject-specific susceptibility distribution in both head and torso, and their relative orientation and position. The shim field in the EF is partially optimized to reduce the inhomogeneity of the SF in the original pose. Therefore, it is necessary to understand the contributions from both the head and torso to obtain a full picture of the B₀ effect. As shown in the tables, the motion-induced SF change is a substantial portion of the TF change, which is furthermore dependent on the type of motion. For example, in the cases when the pitch rotation dominates, the SD of the SF is 12.4 Hz compared to 7.7 Hz for the case when the yaw rotation around the z-axis dominates. This is in agreement with the expectation that SF in the brain is most severely affected by air-tissue interfaces in the head and their change in orientation relative to the main field direction. Nevertheless, as shown in Fig. 6, the torso contributes considerably to SF, with a SD around 5 Hz at 7 T. These field variations are larger than the commonly seen respiration-related field fluctuation (~ 3 Hz at 7 T) as mentioned above. Based on the result shown in Fig. 4d, with a 5 Hz field offset, up to 15% of the total energy of the T₂*-weighted signal (TE=25 ms) in a voxel can be generated from its neighbors.

The spatial complexity of the motion induced changes in the TF (Fig. 3) makes real-time monitoring challenging For example, the use of external field probes (39) to detect these changes is inadequate, as fields external to the head provide insufficient information to reconstruct those inside the head. Likewise, navigators-based correction (27) needs to be sophisticated enough to provide sufficient spatial information for field correction, especially for 3D imaging. While previous studies have shown the feasibility of using navigators to compensate for simple spatial patterns of field change (14,26,27), proper correction of the high-order pattern of the TF changes will require a sophisticated navigator at the cost of significant additional scan time. Design of such navigators with time-efficient encoding schemes will be important to develop a practical solution for T₂*-weighted MRI in the presence of motion.

A potential alternative to navigator-based field correction may be to establish a predictive model incorporating the relationship between the SF and head motion parameters. Regression analysis of the acquired and simulated field data suggests a highly linear relationship between the two in regions other than the vicinity of air-tissue interfaces. This model could be constructed for each individual using pre-measured field data acquired from different head poses. It may not be practical to establish a generalized model across subjects due to the multitude of factors contributing to this issue. Even within the same subject, SF patterns may vary across different sessions because of their initial head-torso posture or physiological condition (e.g. absence or presence of sinus congestion). An alternative way is based on a subject-specific model of susceptibility. In fact, this approach has been proposed to correct the EPI distortion of a moving phantom (40). For human subjects, anatomical scans revealing the air cavities against bone and soft tissue may support this predictive model, e.g., scans based on ultrashort or zero echo-time designs (41–43). The influence of the neck and torso can potentially be modeled using simplified geometry with appropriate susceptibility values (41). Future work is needed to validate the feasibility of such an approach.

Because of the spatial complexity of the field change, prospective field correction is not practical with the state-of-the-art spherical harmonic (SH) shim systems due to either the limited order of the shim systems or the slow response of the nonlinear shim coils. Recently, high-order shim systems with multiple local non-spherical-harmonic (NSH) coils have been proposed to improve the homogeneity of the main field in the human brain dynamically (44,45). Based on the result in Fig. 3, although it is not feasible to completely eliminate the B₀ field inhomogeneity in the brain (Fig. 3a), it might be possible to dynamically counteract the motion-induced B₀ field changes in the head frame (Fig. 3b) using the NSH shim coils and the head pose information as an input while the shim coils are kept static in space. The previous studies (44,45) suggest that the NSH coils can compensate the B₀ field inhomogeneity to about the fifth order. Alternatively, the field effect can be corrected retrospectively in the image reconstruction integrating the estimated and/or measured information of the field change. As mentioned earlier, this information can potentially be obtained by field measurement, predictive models or a combination of both.

In summary, changes of head pose can cause significant changes of B₀ in the brain with a high-order spatial complexity and contributions from multiple factors, including inhomogeneities in the field of the MRI magnet and shims, and field effects from both head and torso. Quantitative analysis shows that all these factors need to be considered in the design of correction approaches, which will likely need to include sophisticated navigators and field probe systems or predictive field modeling.

Supplementary Material

Supp info

Sup. FIG. S1 Purple color indicates the region of interest in which the standard deviation, complexity and distribution of the field changes were analyzed.