Inter-method Reproducibility of Biexponential R2 Magnetic Resonance Relaxometry for Estimation of Liver Iron Concentration

Abstract

Purpose

To assess the reproducibility of biexponential R2-relaxometry magnetic resonance imaging (MRI) for estimation of liver iron concentration (LIC) between proprietary and nonproprietary analysis methods.

Methods

This single-center retrospective study, approved by Investigational Review Board and compliant with Health Insurance Portability and Accountability Act, included 40 liver MRI exams in 38 subjects with suspected or known iron overload. From spin-echo images of the liver, acquired at 5 different echo times (TE = 6 – 18 ms), biexponential R2-maps were calculated using a proprietary (FerriScan^®) and three nonproprietary (simulated annealing, nonlinear least squares, dictionary search) analysis methods. Each subject’s average liver R2 value was converted to LIC using a previously validated calibration curve. Inter-method reproducibility for liver R2 and LIC were assessed for linearity using linear regression analysis and absolute agreement using intraclass correlation (ICC) and Bland-Altman analysis. For point estimates, 95% confidence intervals (CI) were calculated; P-values < 0.05 were considered statistically significant.

Results

Linearity between the proprietary and nonproprietary methods was excellent across the observed range for R2 (20 – 312 s⁻¹) and LIC (0.4 – 52.2 mg/g), with all coefficients of determination (R²) ≥0.95. No statistically significant bias was found (slope estimates ~ 1; intercept estimates ~ 0; P-values > 0.05). Agreement between the four methods was excellent for both liver R2 and LIC (ICCs ≥0.97). Bland-Altman 95% limits of agreement in %-difference between the proprietary and nonproprietary methods were ≤9% and ≤16% for R2 and LIC, respectively.

Conclusion

Biexponential R2-relaxometry MRI for LIC estimation is reproducible between proprietary and nonproprietary analysis methods.

Introduction

Excessive accumulation of iron in the body is toxic and occurs in patients with hereditary hemochromatosis and in those with chronic anemias requiring repeated red-cell transfusion (e.g. sickle cell disease, thalassemia). If untreated, iron toxicity can result in liver cirrhosis, cardiomyopathy, endocrine dysfunction, and ultimately premature death (1–4). To prevent these complications, periodic quantitative assessment of the body iron burden is needed for clinical management of at-risk patients, to guide iron-reduction therapy (5–8). Liver is the primary storage organ of excess body iron and correlates very closely to total body iron stores (9). For this reason, liver iron concentration (LIC) is widely accepted as the reference standard to assess the overall body iron burden and the prognosis for end-organ damage and long-term mortality risk (8,10–12). Historically, invasive liver tissue sampling (i.e. biopsy) was once considered the gold standard of LIC measurement. However, the sampling variability and the procedural risks associated with this biopsy are major limitations in these patients, many of whom may need lifelong LIC monitoring (13–15).

As an alternative for longitudinal LIC monitoring by biopsy, R2-relaxometry magnetic resonance imaging (R2-MRI) was developed for noninvasive LIC estimation and validated against liver biopsy (16,17). Currently, the only R2-MRI method to estimate LIC with regulatory clearance (e.g. from the U.S. Food and Drug Administration) is FerriScan^® (Resonance Health Ltd., Claremont WA, Australia). This proprietary method has been used in multicenter clinical trials as study endpoints, adopted in several professional societies’ practice guidelines, and become a de facto reference standard for LIC in patients with iron overload (18–20). To date, FerriScan^® analyses reported in the literature have been performed using a single proprietary biexponential R2-MRI method by Resonance Health or its associate centers. An external, third-party validation of any analysis tool in clinical use would be highly desirable, to confirm its independence from commercial bias, methodological robustness and generalizability. To our knowledge, however, the reproducibility of biexponential R2-MRI has not been independently validated using nonproprietary methods. Therefore, the purpose of this study was to assess the reproducibility of biexponential R2-MRI for LIC estimation in patients with known or suspected liver iron overload, using proprietary and nonproprietary methods.

Methods

Patient Population

Institutional Review Board (IRB) approval was obtained, and all patient data were handled in compliance with the U.S. Health Insurance Portability and Accountability Act. Standardized spin-echo (SE) MRI exams performed per FerriScan^® protocol (details below) between August 2013 and September 2017 were eligible for this retrospective study. Thirty-eight (38) consecutive subjects were referred for MRI from our institution’s hepatology and hematology clinics based on suspected or known iron overload: Twenty-eight (28) MRI exams in 28 subjects were performed as part of a research study (ClinicalTrial.gov ID blinded for review), and informed consent was obtained from each subject. Twelve (12) exams in 10 subjects were performed as part of standard clinical care, and IRB waived the need for informed consent for this group; two subjects in this group each had two MRI exams during the study period.

Image Acquisition

All MRI exams were performed on one of two 1.5T scanners (Philips Ingenia or Philips Achieva, Philips Healthcare, Eindhoven, The Netherlands), using a multichannel anterior torso array coil (16 and 8 channels for Ingenia and Achieva, respectively) and a posterior built-in table coil (12 and 8 channels, respectively). Quality assurance approval for FerriScan^®-protocol MRI was obtained for both scanners from Resonance Health Ltd. Axial, free-breathing, SE acquisitions without parallel imaging were performed at five different echo times (TEs) through the liver, as per the standardized FerriScan^® imaging protocol (Table 1).

Table 1. Image Acquisition Protocol.

Standardized imaging acquisition parameters as approved by Resonance Health for the proprietary analysis (FerriScan^®), with placement of a 1-liter saline bag under the left axilla. The axial spin-echo acquisition was repeated at the listed TEs during free-breathing. TR = repetition time; TE = echo time.

Field of view	# of slices	TR (ms)	Slice thickness / gap (mm)	Acquisition Matrix	Flip Angle (deg)	TE (ms)
Entire cross section of abdomen plus 2.5 cm of surrounding background	11	1000	5 / 5	256 x N (≤ 256) adjusted to subject size	90	6, 9, 12, 15, 18

Image and Data Analysis

Biexponential R2-relaxometry was performed by fitting the signal intensity data, S(t) measured at different echo time (t), to a signal model with a slow (R2_s) and a fast (R2_f) relaxation components (21),

$$S(t)\propto D[p{e}^{-R{2}_{s}t}+(1-p)e^{-R{2}_{f}t}],$$ (Eqn. 1)

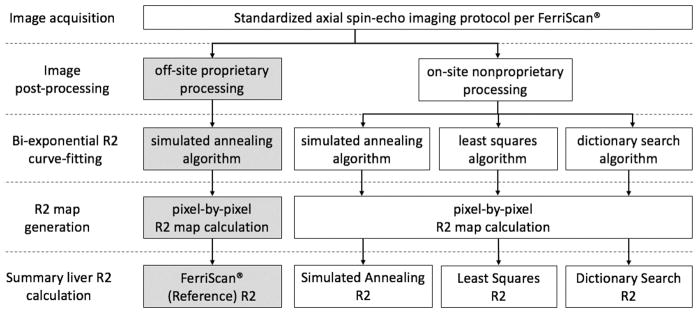
where p is the slow-component fraction and D is the spin-density. The proprietary analysis, performed off-site by Resonance Health (FerriScan^®, herein referred to as the proprietary method), utilizes a simulated annealing algorithm for curve-fitting (22). In this study, we tested whether more widely-available or simpler curve-fitting algorithms can reproduce the proprietary analysis’ results. To this end, we implemented three nonproprietary methods: (1) simulated annealing algorithm as used in the proprietary analysis, (2) standard nonlinear least squares algorithm, and (3) recently-introduced dictionary search algorithm (details below). Figure 1 illustrates the SE data analysis flow using these four biexponential R2-relaxometry methods.

Figure 1.

Flowchart describes the R2-MRI relaxometry procedures step-by-step from image acquisition to summary liver R2 calculation. The proprietary procedures performed off-site by Resonance Health are indicated by gray boxes. Open boxes represent on-site procedures. The three nonproprietary methods differ in the curve-fitting algorithm but share an identical image post-processing step. The on-site image processing was independently implemented following the general principles of those used in the proprietary method.

Proprietary R2-relaxometry

SE data were securely transmitted to Resonance Health for off-site post-processing and analysis via the proprietary method, the general principles of which have been described previously (21,23,24) and have the following components: (1) correction for scanner gain drift, respiratory motion artifact, and subtraction of background noise offset, (2) radiofrequency field intensity-weighted spin-density projection, followed by (3) biexponential curve-fitting using a simulated annealing algorithm. Using the report generated by the proprietary analysis, the mean of pixel-by-pixel R2 fit of a single segmented liver section was extracted. The corresponding estimated LIC (in mg Fe/g dry liver tissue, herein reported as mg/g) were calculated using the conversion formula developed for the proprietary method (16).

Nonproprietary R2-relaxometry

SE data were also post-processed and analyzed on-site using three fitting algorithms written in MATLAB^™ (The MathWorks, Inc., Natick, MA), following the general principles of the proprietary analysis as described previously (21,23,24), unless otherwise stated. The liver was manually segmented by a fellowship-trained abdominal radiologist (__, 10 years of experience interpreting liver MRI), on the same axial slice approximating the same region of interest (ROI) as used in the proprietary analysis. The SE data were corrected for scanner gain drift, background noise offset, and respiratory motion artifacts as previously described (21,23,24).

The radiofrequency (RF) field intensity-weighting and spin-density projection procedures were reproduced, to the best of our knowledge, as loosely described previously (21). RF field intensity-weighting is intended to normalize all pixels to a uniform intensity scale by estimating and correcting for the spatial variation of the RF field and receiver coil sensitivities. The spin-density projection controls the spin density estimate (D in Eqn. 1) to take physiologically plausible values and prevent spurious fits in cases of extremely rapid R2 signal decay. A combination of these procedures has been shown to improve robustness and minimize bias of biexponential R2 estimates in phantoms having both fast and slow R2 components (21).

The RF field intensity weighting was implemented as follows: On the shortest-TE image (TE=6 ms), the outer boundary of the subcutaneous fat was automatically contoured, and the signal intensity was recorded along the closed boundary. The boundary’s signal intensity was fitted to an 8^th order Fourier series using MATLAB’s fit function with the ‘fourier8’ option. The local maxima (up to 8) were analytically determined based on the first and second derivatives of the fitted Fourier series. These local maxima were set as the point sources for their respective local RF field (i.e. points closest to the receive coil elements). At each point source location, a point spread function (PSF) was defined as a 2D radially-symmetric mono-exponential decay, parameterized by a location-specific amplitude and a common spatial decay constant. The boundary signal data was modeled as the sum of these PSFs, and the PSF parameters of all point source locations were simultaneously estimated by nonlinear least squares algorithm. The map of RF field intensity weights was constructed by extrapolating the sum of the fitted PSFs into the boundary interior, i.e. inside the body. The gain-, noise- and motion-corrected image at each TE was normalized (divided) by the estimated RF field intensity weights, to generate RF field intensity-corrected multi-TE data.

The spin-density projection procedure was implemented as follows. In a sub-cohort of subjects with normal LIC (<1.8 mg/g) by the proprietary R2 method (16), the spin-density (D) was estimated in the subcutaneous fat and in the liver, respectively, by projecting the RF field intensity-corrected multi-TE data to TE=0 ms according to monoexponential nonlinear least squares fit. The liver-to-fat spin-density ratio was calculated as the ratio of estimated spin-density of the liver and that of the subcutaneous fat. The observed range of the liver-to-fat spin-density ratio in normal subjects was subsequently used to inform the biexponential R2 fit in all subjects, including those with iron overload.

The gain-, noise-, motion-, and RF field intensity-corrected signal data, S(t), were fitted pixel-by-pixel according to Eqn. 1, using the (1) simulated annealing algorithm, simulannealbnd, included in MATLAB’s Global Optimization Toolbox; (2) MATLAB’s Levenberg–Marquardt nonlinear least squares algorithm, lsqcurvefit; and (3) recently-introduced dictionary search algorithm (described below). The parameter ranges were set as: p = 0.1 – 0.3; R2_s = 1 – 100 s⁻¹; R2_f = R2_s + Δ, where Δ = 1 – 250 s⁻¹, based on previously validated parameter ranges of biexponential fitting used in the proprietary method (21). The fast R2 component was therefore always faster than the slow R2 component by design, to avoid potential degeneracy in the simultaneous dual-component fitting. For simulated annealing and least-square algorithms, spin-density projection was implemented by bounding the liver-to-fat spin-density ratio range to the observed values in normal subjects. Spin-density projection was not implemented for dictionary search algorithm as explained in the next section. For each pixel, the weighted average of the slow and fast R2 components were calculated as: R2 = p × R2_s + (1 – p) × R2_f. Finally, the average liver R2 was calculated by averaging the pixel R2 values of the ROI as done in the proprietary method. Each average liver R2 was converted to LIC using the validated formula developed for the proprietary method (16). The computation time for each ROI and the number of pixels in the ROI were recorded for both fitting algorithms, on a standard desktop 2.5 GHz single-core central processing unit (CPU) with 16 GB of random access memory (RAM).

Dictionary search Fitting Algorithm

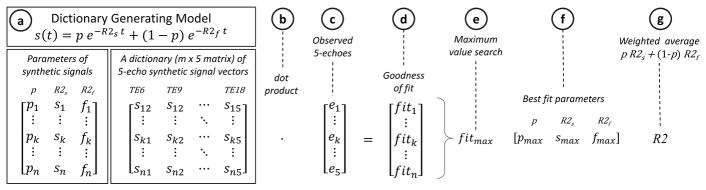
A dictionary search method for curve fitting was recently introduced to quantitative MR imaging in the context of liver fat quantification by multi-echo chemical shift imaging (reference blinded for review purposes). The general principle of this method was applied for biexponential R2 fitting as illustrated in Figure 2. Briefly, this method utilized a database, or a dictionary, of time-dependent signal vector, S(t) at t = 6, 9, 12, 15, and 18 ms, in a manner akin to MR fingerprinting (25). Each synthetic signal vector was calculated a priori based on the biexponential model (Eqn. 1) on each point on a 100 × 250 × 40 parameter grid: p = [0.1:0.01:0.3]; R2_s = [1:1:100] s⁻¹; R2_f = R2_s + Δ, where Δ = [1:1:250] s⁻¹. The resulting dictionary of synthetic signals was stored as a 750,000 × 5 matrix, and each row vector (i.e. over variable t) was normalized to unit length by Euclidean norm. The observed signal intensity values from the SE images at five TEs were also normalized to unit length, and then compared to each synthetic vector in the dictionary by the dot product operation. The dot product between two unit vectors measures their “closeness” (i.e. goodness-of-fit) and is mathematically equivalent to the linear least squares procedure (26). Therefore, the synthetic signal resulting in the highest dot-product value with the observed signal was identified as the best fit, and the corresponding best-fit parameter values were recorded. The conceptual advantage of the dictionary search strategy is that the nonlinear function evaluations are performed only once a priori at the time of dictionary generation and saved for future use. The repeated pixel-by-pixel curve-fitting can then be implemented using computationally-efficient dot-product operation and a simple array search, without the need for iterative nonlinear function evaluations for each pixel. Spin-density projection could not be incorporated for the dictionary search algorithm, because the normalization to unit vectors renders the algorithm insensitive to any scaling factor, including the spin-density ratio D in Eqn. 1. All other post-processing procedures were identical to the simulated annealing and least squares algorithms.

Figure 2.

Overview of the dictionary search method to estimate the slow R2 component (R2_s), fast R2 component (R2_f), and slow-component fraction (p) for the time-dependent signal intensities S(t) (equation, a). For a given 5-TE spin-echo imaging protocol, a dictionary of a large number (n) of unit-length synthetic signal vectors (an n × 5 matrix) is calculated a priori, using a dictionary-generating model on a 3-dimensional grid: p = [0.1:0.01:0.3]; R2_s = [1:1:100] s⁻¹; and R2_f = R2_s + Δ, where Δ = [1:1:250] s⁻¹ (a). Each row of this dictionary is a signal vector with a different signal model parameter combination (p, R2_s, R2_f). (b & c) An observed 5-TE signal vector at each pixel location is compared to all synthetic signal vectors in the dictionary by matrix-vector dot product operation. (d) The resulting dot product values serve as goodness-of-fit metric. (e) A search for the maximum goodness-of-fit value identifies the synthetic signal “closest” to the observed signal, i.e. “the best fit.” (f) The best-fit model parameters are extracted, and (g) the final R2 value is calculated as a weighted average of R2_s and R2_f.

Statistical Analysis

All statistical analyses were performed using the MATLAB statistical toolbox. Reproducibility of average liver R2 and LIC calculated using the three different implementations of biexponential R2-relaxometry was compared in terms of linearity and agreement. Inter-method linearity was assessed by linear regression analysis. To permit the inclusion of subjects who had repeated MRI exams, mixed effects model regression was used to account for potential intra-subject correlation. The coefficient of determination (R², i.e. the goodness of fit) as well as the slope and intercept point estimates with respective 95% confidence intervals (CIs) were calculated. The inter-method bias was assessed by paired t-test for R2 and LIC. The inter-method agreement was assessed for absolute agreement by intraclass correlation (ICC) and its 95% CI, for R2 and LIC. The inter-method %-disagreement was graphically assessed by Bland-Altman analysis, where the average %-difference (i.e. mean %-bias) and 95% limits of agreement (LOA) were calculated. For the on-site analyses, the relative computational efficiency of the three fitting algorithms was calculated by taking the ratio of the computation times. P-values < 0.05 were considered statistically significant.

Results

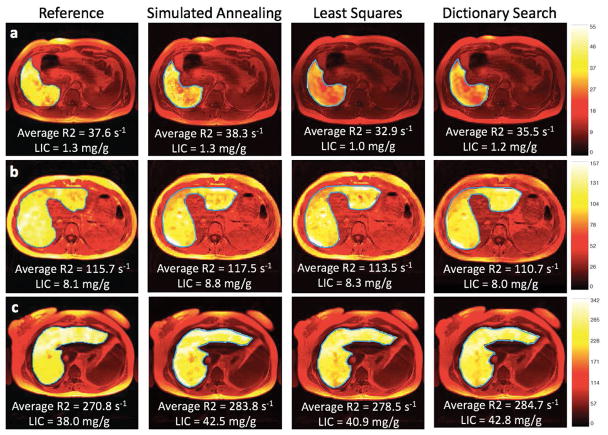
All eligible 40 MRIs in 38 subjects (25 men and 13 women) were included in the analysis. The etiology of iron overload (number of subjects) in the study population was as follows: primary hemochromatosis (n=16), beta thalassemia (n=5), hyperferritinemia of indeterminate etiology (n=4), sickle cell disease (n=4), autoimmune hemolytic anemia (n=2), acute myelogenous leukemia (n=1), acute promyelocytic leukemia (n=1), pancytopenia (n=1), end-stage renal disease (n=1), hemoglobin constant spring (n=1), Diamond-Blackfan anemia (n=1), and aplastic anemia (n=1). Figure 3 illustrates examples of generated R2 maps as well as the average liver R2 and LIC by the four different relaxometry methods. Average number of pixels per ROI (range) was 3398 (997 – 8496). Average liver R2 (range) by the proprietary, and the three nonproprietary relaxometry methods in the study population were respectively 86 s⁻¹ (20 – 312), 87 s⁻¹ (21 – 310), 84 s⁻¹ (22 – 304), and 84 s⁻¹ (23 – 292). The corresponding average LICs (range) were respectively 8.3 mg/g (0.4 – 52.2), 8.7 mg/g (0.4 – 51.8), 7.9 mg/g (0.5 – 49.4), and 8.1 mg/g (0.5 – 45.2). Eighteen (18) subjects had normal LIC < 1.8 mg/g by the proprietary methods, and the mean [range] of the observed liver-to-fat spin-density ratio was 0.56 [0.37 – 0.83].

Figure 3. Liver R2 maps.

Liver R2 maps generated by the proprietary (reference) and the three nonproprietary R2-relaxometry methods (simulated annealing, least squares, dictionary search) in three representative subjects: (a) a 36-year-old man with primary hemochromatosis, (c) a 24-year-old woman with Diamond-Blackfan anemia, and (b) a 31-year-old woman with sickle cell anemia. The proprietary R2 maps subjectively appear more homogeneous than the nonproprietary R2 maps, potentially due to differences in smoothing techniques used by off-site and on-site analyses; however, the average R2 and LIC values are similar across different R2 methods. LIC = liver iron concentration, reported in mg of iron per g dry liver tissue (mg/g).

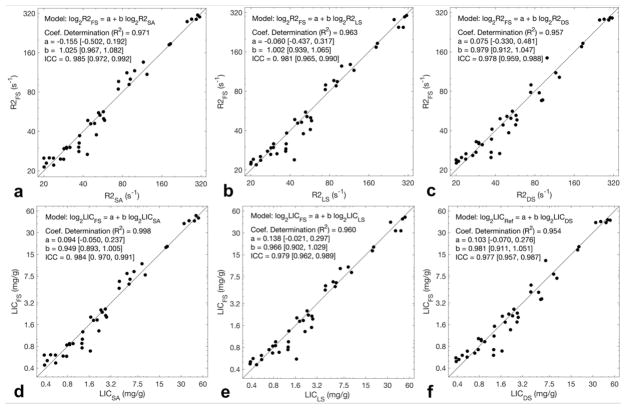
Figure 4 illustrates the linear relationship between the proprietary method and the three nonproprietary methods for R2 and for LIC. Of note, near-identical appearance of the R2 and LIC scatterplots was expected, as R2-to-LIC conversion for all three methods was performed using the same monotonic nonlinear transformation (16); as both R2 and LIC are relevant to the aims of this study, both plots were presented. Tables 2 and 3 summarizes the estimated slopes, intercepts, coefficients of determination (R²), and ICCs for R2 and for LIC, respectively, comparing all pairs of R2 methods, including nonproprietary method pairs. Overall, linearity was excellent with R² exceeding 0.95 in all pairwise comparisons with no statistically significant differences found in the estimated slopes or intercepts from unity and zero, respectively (all P values > 0.05). Agreement between the proprietary and nonproprietary methods was excellent, with all ICCs ≥0.97 for both R2 and LIC, and ≥ 0.99 between the three nonproprietary methods.

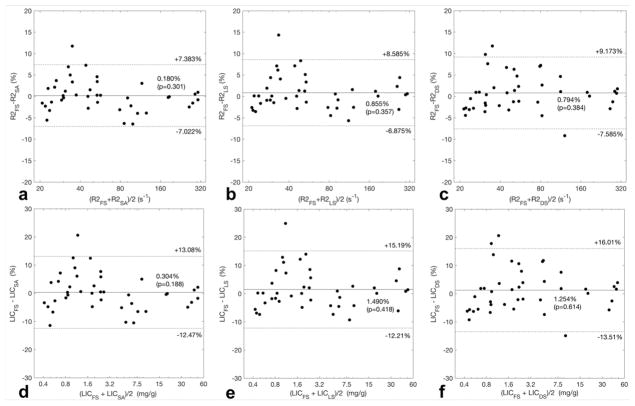
Figure 4. Linear regression analysis.

Scatterplots (a – c) respectively illustrate the strong linearity of the nonproprietary methods (simulated annealing, least squares, dictionary search) against proprietary (FerriScan^®) reference R2, on a logarithmic scale (coefficients of determination R² ≥ 0.95). Solid lines in each plot represent the diagonal with slope = 1 and intercept = 0. Best fit lines are not shown as they closely overlap the diagonal line, however, fitted parameters are shown in Table 2. Scatterplots (d – f) illustrate the linearity of LICs corresponding to the R2 values in (a – c), respectively. Near-identical appearance of the top row plots to the bottom row plots is expected, as the R2-to-LIC conversion is a monotonic nonlinear transformation. Subscripts correspond to the R2-relaxometry method utilized to obtain the value; FS = FerriScan^®, SA = simulated annealing, LS = least squares, DS = dictionary search.

Table 2.

Comparison Between R2 Estimation Methods

	FS vs. SA	FS vs. LS	FS vs. DS	SA vs. LS	SA vs. DS	LS vs.DS
R2	0.971	0.963	0.957	0.990	0.978	0.983
Intercept	−0.155 [−0.502, 0.192]	−0.060 [−0.437, 0.317]	0.075 [−0.330, 0.481]	0.099 [−0.087, 0.284]	0.246 [−0.033, 0.524]	0.162 [−0.087, 0.411]
Slope	1.025 [0.967, 1.082]	1.002 [0.939, 1.065]	0.979 [0.912, 1.047]	0.977 [0.946, 1.007]	0.952 [0.906, 0.999]	0.973 [0.931, 1.015]
ICC	0. 985 [0.972, 0.992]	0. 981 [0.965, 0.990]	0.978 [0.959, 0.988]	0.995 [0.990, 0.997]	0.988 [0.978, 0.994]	0.991 [0.984, 0.995]
ΔR2% 95% LOA	0.180 [−7.022, 7.383]	0.855 [−6.875, 8.585]	0.794 [−7.585, 9.173]	0.681 [−3.427, 4.789]	0.611 [−5.682, 6.905]	−0.068 [−5.465, 5.330]

The proprietary FerriScan^® method (FS) and the non-propriety methods (SA = simulated annealing, LS = least squares, DS = dictionary search) are compared using linear regression analysis. R² = coefficient of determination of a linear fit; Intercept/Slope are coefficients of fitted linear model; ICC = intraclass coefficient; ΔR2% = mean %-difference of summary R2 by Bland-Altman Analysis; [ ] indicates 95% confidence intervals for point estimates. LOA = limits of agreement.

Table 3.

Comparison Between LIC Estimation Methods

	FS vs. SA	FS vs. LS	FS vs. DS	SA vs. LS	SA vs. DS	LS vs.DS
R2	0.968	0.960	0.954	0.989	0.978	0.982
Intercept	0.094 [−0.050, 0.237]	0.138 [−0.021, 0.297]	0.103 [−0.070, 0.276]	0.049 [−0.037, 0.135]	0.0149 [−0.108. 0.137]	−0.029 [−0.137, 0.080]
Slope	0.949 [0.893, 1.005]	0.966 [0.902, 1.029]	0.981 [0.911, 1.051]	1.016 [0.982, 1.051]	1.0297 [0.980, 1.0792]	1.010 [0.966, 1.054]
ICC	0. 984 [0. 970, 0.991]	0.979 [0.962, 0.989]	0.977 [0.957, 0.987]	0.993 [0.988, 0.997]	0.988 [0.978, 0.994]	0.991 [0.983, 0.995]
ΔLIC% 95% LOA	0.304 [−12.47, 13.08]	1.490 [−12.21, 15.19]	1.254 [−13.51, 16.01]	1.223 [−6.363, 8.810]	0.948 [−9.792, 1.688]	−0.267 [−9.737, 9.203]

The proprietary FerriScan^® method (FS) and the non-propriety methods (SA = simulated annealing, LS = least squares, DS = dictionary search) are compared using linear regression analysis. R² = coefficient of determination of a linear fit; Intercept/Slope are coefficients of fitted linear model; ICC = intraclass coefficient; ΔLIC = mean %-difference of Liver Iron Concentration (LIC) by Bland-Altman Analysis; [ ] indicates 95% confidence intervals for point estimates. LOA = limits of agreement.

Bland-Altman analysis (Figure 5) between the proprietary and nonproprietary methods showed a mean %-bias within ±1.0% for R2 and ±1.5% for LIC, and the differences were not statistically significant (p>0.05). The 95% limits of agreement was ≤9% for R2 and ≤16% for LIC. Based on previously reported threshold values for normal LIC range (LIC < 1.8 mg/g) (16), a greater %-difference was observed in a few subjects in the normal LIC range than in those with iron overload. Bland-Altman analysis (Table 2 and 3) between the nonproprietary methods (simulated annealing, least squares, dictionary search) showed slightly narrower 95%-LOA for R2 and LIC within ±7% and ±10%, respectively (Table 2 & 3).

Figure 5. Bland-Altman Analysis.

Scatterplots illustrate the agreement in average liver R2 (a – c) and LIC (d – f) between the proprietary R2 method (FerriScan^®) and three nonproprietary R2 methods, calculated in %-difference across the observed range in the study population. The mean %-difference is shown as the horizontal solid line, with the corresponding p-values of paired t-test; 95% limits of agreement are shown in horizontal dotted lines. A greater %-difference between the proprietary and nonproprietary methods among those with normal LIC, i.e. LIC < 1.8 mg/g (d – f), than in those with iron overload, i.e. LIC > 1.8 mg/g. R2 = average liver R2, LIC = liver iron concentration in mg/g; subscripts correspond to the R2-relaxometry method utilized to obtain the value; FS = FerriScan^®, SA = simulated annealing, LS = least squares, DS = dictionary search.

The average (range) computation time for R2 map calculation was 1.6 s (1.3 – 2.3) per 1000 pixels for the dictionary search algorithm (using the 750,000-element parameter grid described earlier). The corresponding average (range) computation time for least squares and simulated annealing algorithms for the same ROI data were 12.3 s (6.7 – 15.5) and 42.0 s (26.7 – 60.6) per 1000 pixels, respectively. The average relative computation efficiency for dictionary search method was a 8-fold compared to least squares and 27-fold compared to simulated annealing, suggesting considerable computational advantage of the dictionary search algorithm over to the two nonlinear fitting algorithms.

Discussion and Conclusions

Biexponential R2-relaxometry MRI has been validated for liver iron concentration (LIC) estimation and shown to be reproducible across different 1.5T scanners (17). However, this highly complex analysis is currently only available through a commercial data processing center using a proprietary method. Thus, the reproducibility across different implementations of R2-MRI has not been independently or externally validated using nonproprietary methods. To address this gap in knowledge, we investigated the inter-method reproducibility between four different biexponential R2-relaxometry methods: the proprietary off-site analysis (FerriScan^®), and three on-site nonproprietary analyses using simulated annealing, nonlinear least squares, and dictionary search algorithms.

In this single-center retrospective study of 40 liver MRIs in 38 unique subjects spanning a wide range of liver iron overload (0.4 – 52.2 mg/g), we demonstrated an excellent reproducibility between the proprietary and the nonproprietary methods for liver R2 and LIC, despite different implementation of R2-relaxometry. The observed mean %-bias within ±1% between the proprietary and nonproprietary R2 is unlikely to be clinically meaningful. The Bland-Altman 95% LOA of approximately ±9% between the proprietary and nonproprietary R2 is similar to the previously reported inter-scanner reproducibility of ±10.9% for the proprietary method (calculated 95% LOA based on reported standard-deviation of 7.7%) (16). While this study was not designed to separately measure and compare different variance components (i.e. between different scanners, analysis methods, ROI placement), this degree of inter-method variability in R2 measurement may be expected in our study that utilized two different 1.5T scanners.

Overall, these results support methodological robustness and generalizability of the biexponential R2-MRI approach to LIC estimation. To our knowledge, the biexponential R2-relaxometry methods implemented in this study are the first independent and external replications of the proprietary R2-MRI for LIC estimation. Availability of such nonproprietary methods can facilitate future research by independent non-commercial investigators. Potential research areas may include incorporation of fat suppression (27), motion-desensitizing techniques such as non-Cartesian k-space acquisitions (28), and acquisition speed improvement such as echo train acquisitions (29) and compressed sensing (30).

While all four investigated R2-relaxometry methods are designed for optimization of the biexponential model parameters (R2_s, R2_f, and p), the proprietary method is implemented with an unconventional criterion function (fit error raised to the 8^th power) for simulated annealing algorithm (21,22). In addition to simulated annealing, we also implemented the more widely-available nonlinear least squares Levenberg-Marquardt algorithm using conventional criterion function (square error). The dictionary search algorithm used vector dot product as the criterion function, which is mathematically equivalent to the well-understood linear least squares procedure (26). All four methods showed high degree of agreement suggesting robustness against the choice of a specific fitting algorithm.

This study also reports a successful example of applying a dictionary search method to a complicated nonlinear curve-fitting for quantitative MRI. The results of dictionary search fitting are expected to be close to those by other nonlinear optimization algorithms, depending on the resolution of the parameter search grid. Dictionary search approach takes advantage of the fact that clinically relevant range of R2 is wide (approx. 20 s⁻¹ to 300 s⁻¹ in our data), and any potential for estimation error by a few s⁻¹ points is unlikely to be clinically meaningful or necessary. Dictionary search approach trades off the estimation precision for computational simplicity and efficiency with x27 speed gain over simulated annealing and x8 over nonlinear least squares, for the specific dictionary size (750,000 elements). The computation time is expected to increase linearly with the number of elements in the dictionary, which is determined by the parameter range and step size. For applications in which clinically-meaningful parameter range and acceptable precision levels are known, dictionary search may provide a substantial computational advantage over nonlinear optimization algorithms. This general approach to nonlinear curve-fitting may also be applicable to other fitting problems in quantitative MRI, such as intra-voxel incoherent motion (IVIM), which uses a similar biexponential model as the one used in this study.

Limitations of this study include a small sample size and retrospective design. While this study population covered a wide range of LIC values (0.4 – 52.2 mg/g), representative of those observed in clinical studies of liver iron overload (13,17), only 15 subjects were included with clinically significant iron overload (LIC > 3.2 mg/g). Larger, multi-center studies are necessary to assess the generalizability of these results. We did not evaluate intra-subject reproducibility of R2 and estimated LIC (e.g. between different axial images and/or different Couinaud segments), as this study was focused on inter-method reproducibility, with the proprietary method as the reference. However, encouraged by the results of this study, we are in the process of evaluating inter-observer (i.e. differences caused by ROI size/shape) and intra-subject reproducibility (i.e. heterogeneity of iron overload) throughout the liver. Another limitation of the study is the potential differences between the off-site and on-site post-processing procedures, although we followed previously described general principles to the best of our abilities (21,23,24). In particular, co-localization of the ROIs between the proprietary and nonproprietary methods may have been imperfect and introduced a source of variability. To our knowledge, there is no published data to inform on this potential variability due to ROI placement using the proprietary R2 method. In addition, image post-processing procedures, such as smoothing, may not have been identical between the proprietary and nonproprietary methods. These potential sources of variability may explain better inter-method reproducibility between the nonproprietary methods (which used identical liver ROI and post-processing) than that between the proprietary and nonproprietary methods. These differences in the technical details may also explain the slight differences in the appearances of the R2 maps generated by the proprietary and nonproprietary methods, however, they did not result in significant bias in the average R2 values in majority of cases, demonstrated by excellent statistical agreement between these methods. Lastly, up to 15% disagreement in R2 value was observed in a minority of subjects between the proprietary and nonproprietary methods. While this variability may be related to the inherent imperfections of the reference standard method as a surrogate of LIC, this study was not designed to ascertain the cause of this variability. It is currently unclear whether these nonproprietary techniques could replace the reference technique in clinical care, to guide per-patient management decisions, especially given a small size of this single center study. However, this work may facilitate future development and validation of improved liver R2 relaxometry techniques, as discussed above.

In summary, R2-MRI for LIC estimation is highly reproducible between proprietary and nonproprietary biexponential R2-relaxometry methods. These results suggest generalizability of R2-MRI approach to noninvasive LIC estimation in patients with suspected or known liver iron overload.