Clustering and Variable Selection in the Presence of Mixed Variable Types and Missing Data

Abstract

We consider the problem of model-based clustering in the presence of many correlated, mixed continuous and discrete variables, some of which may have missing values. Discrete variables are treated with a latent continuous variable approach and the Dirichlet process is used to construct a mixture model with an unknown number of components. Variable selection is also performed to identify the variables that are most influential for determining cluster membership. The work is motivated by the need to cluster patients thought to potentially have autism spectrum disorder (ASD) on the basis of many cognitive and/or behavioral test scores. There are a modest number of patients (486) in the data set along with many (55) test score variables (many of which are discrete valued and/or missing). The goal of the work is to (i) cluster these patients into similar groups to help identify those with similar clinical presentation, and (ii) identify a sparse subset of tests that inform the clusters in order to eliminate unnecessary testing. The proposed approach compares very favorably to other methods via simulation of problems of this type. The results of the ASD analysis suggested three clusters to be most likely, while only four test scores had high (> 0.5) posterior probability of being informative. This will result in much more efficient and informative testing. The need to cluster observations on the basis of many correlated, continuous/discrete variables with missing values, is a common problem in the health sciences as well as in many other disciplines.

1 Introduction

Model-based clustering has become a very popular means for unsupervised learning^1–4. This is due in part to the ability to use the model likelihood to inform, not only the cluster membership, but also the number of clusters M which has been a heavily researched problem for many years. The most widely used model-based approach is the normal mixture model which is not suitable for mixed continuous/discrete variables. For example, this work is motivated by the need to cluster patients thought to potentially have autism spectrum disorder (ASD) on the basis of many correlated test scores. There are a modest number of patients (486) in the data set along with many (55) test score/self-report variables, many of which are discrete valued or have left or right boundaries. Figure 1 provides a look at the data across three of the variables; Beery_standard is discrete valued and ABC_irritability is continuous, but with significant mass at the left boundary of zero. The goals of this problem are to (i) cluster these patients into similar groups to help identify those with similar clinical presentation, and (ii) identify a sparse subset of tests that inform the clusters in an effort to eliminate redundant testing. This problem is also complicated by the fact that many patients in the data have missing test scores. The need to cluster incomplete observations on the basis of many correlated continuous/discrete variables is a common problem in the health sciences as well as in many other disciplines.

Figure 1.

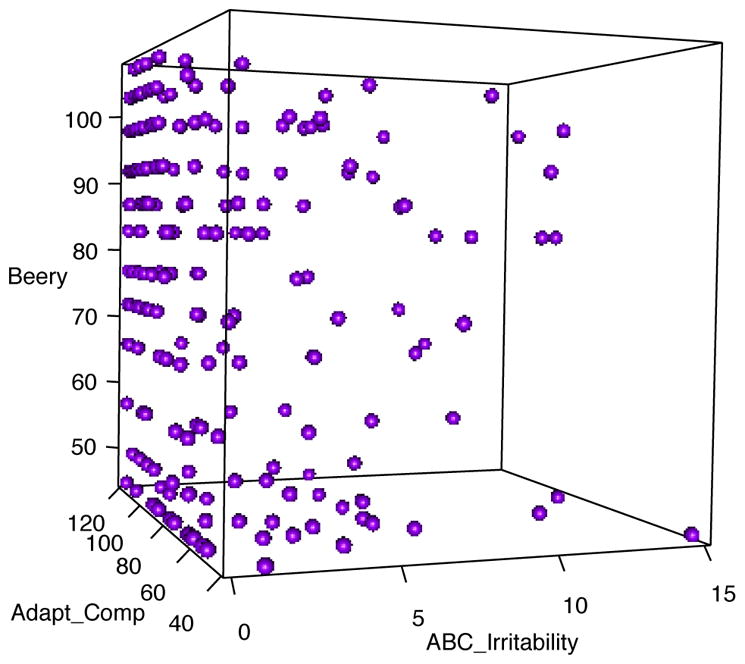
3D scatter plot of three of the test score variables for potential ASD subjects.

When clustering in high dimensions, it becomes critically important to use some form of dimension reduction or variable selection to achieve accurate cluster formation. A common approach to deal with this is a principal components or factor approach⁵. However, such a solution does not address goal (ii) above for the ASD clustering problem. The problem of variable selection in regression or conditional density estimation has been well studied from both the L₁ penalization^6–8 and Bayesian perspectives^9–11. However, variable selection in clustering is more challenging than that in regression as there is no response to guide (supervise) the selection. Still, there have been several articles considering this topic; see Fop and Murphy¹² for a review. For example, Raftery and Dean¹³ propose a partition of the variables into informative (dependent on cluster membership even after conditioning on all of the other variables) and non-informative (conditionally independent of cluster membership given the values of the other variables). They use BIC to accomplish variable selection with a greedy search which is implemented in the R package clustvarsel. Similar approaches are used by Maugis et al.¹⁴ and Fop et al.¹⁵. An efficient algorithm for identifying the optimal set of informative variables is provided by Marbac and Sedki¹⁶ and implemented in the R package VarSelLCM. Their approach also allows for mixed data types and missing data, however, it assumes both local and global independence (i.e., independence of variables within a cluster and unconditional independence of informative and non-informative variables, respectively). The popular LASSO or L1 type penalization has also been applied to shrink cluster means together for variable selection^17–19. There have also been several approaches developed for sparse K-means and distance based clustering^20–22.

In the Bayesian literature Tadesse et al.⁴ consider variable selection in the finite normal mixture model using reversible jump (RJ) Markov chain Monte Carlo (MCMC)²³. Kim et al.²⁴ extend that work to the nonparametric Bayesian mixture model via the Dirichlet process model (DPM)^25–28. The DPM has the advantage of allowing for a countably infinite number of possible components (thus making it nonparametric), while providing a posterior distribution for how many components have been observed in the data set at hand. Both Tadesse et al.⁴ and Kim et al.²⁴ use a point mass prior to achieve sparse representation of the informative variables. However, for simplicity they assume all non-informative variables are (unconditionally) independent of the informative variables. This assumption is frequently violated in practice and it is particularly problematic in the case of the ASD analysis as it would force far too many variables to be included into the informative set as is demonstrated later in this paper.

There is not a generally accepted best practice to clustering with mixed discrete and continuous variables. Hunt and Jorgensen²⁹, Biernacki et al.³⁰, and Murray and Reiter³¹ meld mixtures of independent multinomials for the categorical variables and mixtures of Gaussian for the continuous variables. However, it may not be desirable for the dependency between the discrete variables to be entirely represented by mixture components when clustering is the primary objective. As pointed out in Hennig and Liao³², mixture models can approximate any distribution arbitrarily well so care must be taken to ensure the mixtures fall in line with the goals of clustering. When using mixtures of Gaussian combined with independent multinomials, a data set with many correlated discrete variables will tend to result in more clusters than a comparable dataset with mostly continuous variables. A discrete variable measure of some quantity instead of the continuous version could therefore result in very different clusters. Thus, a Gaussian latent variable approach^33–37 would seem more appropriate for treating discrete variables when clustering is the goal. An observed ordinal variable x_j, for example, is assumed to be the result of thresholding a latent Gaussian variable z_j. For binary variables, this reduces to the multivariate probit model^38,39. There are also extensions of this approach to allow for unordered categorical variables.

In this paper, we propose a Bayesian nonparametric approach to perform simultaneous estimation of the number of clusters, cluster membership, and variable selection while explicitly accounting for discrete variables and partially observed data. The discrete variables as well as continuous variables with boundaries are treated with a Gaussian latent variable approach. The informative variable construct of Raftery and Dean¹³ for normal mixtures is then adopted. However, in order to effectively handle the missing values and account for uncertainty in the variable selection and number of clusters, the proposed model is cast in a fully Bayesian framework via the Dirichlet process. This is then similar to the work of Kim et al.²⁴, however, they did not consider discrete variables or missing data. Further, a key result of this paper is a solution to allow for dependence between informative and non-informative variables in the nonparametric Bayesian mixture model. Thus, this work overcomes the assumption of (global) independence between informative and non-informative variables. Furthermore, by using the latent variable approach it also overcomes the (local) independence assumption among the informative/clustering variables often assumed when clustering data of mixed type¹².

The solution takes a particularly simple form and also provides an intuitive means with which to define the prior distribution in a manner that decreases prior sensitivity. The component parameters are marginalized out to facilitate more efficient MCMC sampling via a modified version of the split-merge algorithm of Jain and Neal⁴⁰. Finally, missing data is then handled in a principled manner by treating missing values as unknown parameters in the Bayesian framework^41,42. This approach implicitly assumes a missing at random (MAR) mechanism⁴³, which implies that the likelihood of a missing value can depend on the value of the unobserved variable(s), marginally, just not after conditioning on the observed variables.

The rest of the paper is laid out as follows. Section 2 describes the proposed nonparametric Bayesian approach to clustering observations of mixed discrete and continuous variables with variable selection. Section 3 evaluates the performance of this approach when compared to other methods on several simulation cases. The approach is then applied to the problem for which it was designed in Section 4 where a comprehensive analysis of the ASD problem is presented. Section 5 concludes the paper. This paper also has supplementary material which contains derivations, full exposition of the proposed MCMC algorithm, and MCMC trace plots.

2 Methodology

2.1 Dirichlet Process Mixture Models

As discussed above, the proposed model for clustering uses mixture distributions with a countably infinite number of components via the Dirichlet process prior^25,44,45. Let y = (y₁, . . . , y_p) be a p-variate random vector and let y_i, i = 1, . . . , n, denote the i^th observation of y. It is assumed that y_i are independent random vectors coming from distribution F (θ_i). The model parameters θ_i are assumed to come from a mixing distribution G which has a Dirichlet process prior, i.e., the familiar model,

$${\mathit{y}}_i\mid {\theta }_i~F({\theta }_i),{\theta }_i~G,G~\text{DP}(G_0,\alpha ),$$ (1)

where DP represents a Dirichlet Process distribution, G₀ is the base distribution and α is a precision parameter, determining the concentration of the prior for G about G₀ ⁴⁴. The prior distribution for θ_i in terms of successive conditional distributions is obtained by integrating over G, i.e.,

$${\theta }_i\mid {\theta }_1,\dots ,{\theta }_{i-1}~\frac{1}{i-1+\alpha }\sum _{i^{\prime }=1}^{i-1}\delta ({\theta }_{i^{\prime }})+\frac{\alpha }{i-1+\alpha }{G}_0,$$ (2)

where δ(θ) is a point mass distribution at θ. The representation in (2) makes it clear that (1) can be viewed as a countably infinite mixture model. Alternatively, let Ω = [ω₁, ω₂, . . . ] denote the unique values of the θ_i and let ϕ_i be the index for the component to which observation i belongs, i.e., so that ω_ϕi = θ_i. The following model²⁶ is equivalent to (2)

$$P({\varphi }_i=m\mid {\varphi }_1,\dots ,{\varphi }_{i-1})=\{\begin{array}{ll}1\hfill & \text{if}i=1\text{and}m=1.\hfill \\ \frac{n_{i,m}}{i-1+\alpha }\hfill & \text{if}{\varphi }_{i^{\prime }}=m\text{for}\text{any}{i}^{\prime }<i.\hfill \\ \frac{\alpha }{i-1+\alpha }\hfill & \text{if}m=max({\varphi }_1,\dots ,{\varphi }_{i-1})+1.\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}$$ (3)

with y_i | ϕ_i, Ω ~ F(ω_ϕi), ω_m ~ G₀ and n_i,m is the number of ϕ_i′ = m for i′ < i. Thus, a new observation i is allocated to an existing cluster with probability proportional to the cluster size or it is assigned to a new cluster with probability proportional to α. This is often called the Chinese restaurant representation of the Dirichlet process. It is common to assume that F is a normal distribution in which case ω_m = (μ_m, Σ_m) describes the mean and covariance of the m^th component. This results in a normal mixture model with a countably infinite number of components.

2.2 Discrete Variables and Boundaries/Censoring

Normal mixture models are not effective for clustering when some of the variables are too discretized as demonstrated in Section 3. This is also a problem when the data have left or right boundaries that can be achieved (e.g., several people score the minimum or maximum on a test). However, a Gaussian latent variable approach can be used to circumvent these issues. Suppose that variables y_j for j ∈ 𝒟 are discrete, ordinal variables taking on possible values d_j = {d_j,1, . . . , d_j,_Lj} and that y_j for j ∈ 𝒞 = 𝒟^c are continuous variables with lower and upper limits of b_j and c_j, which could be infinite. Assume for some latent, p-variate, continuous random vector z that

$$y_j=\{\begin{array}{ll}{\sum }_{l=1}^{L_j}{d}_{j,l}{I}_{\{a_{j,l-1}<z_j\le a_{j,l}\}}\hfill & \text{for}j\in \mathcal{D}\hfill \\ z_j{I}_{\{b_j\le z_j\le c_j\}}+b_j{I}_{\{z_j<b_j\}}+c_j{I}_{\{z_j>c_j\}}\hfill & \text{for}j\in \mathcal{C}\hfill \end{array}$$ (4)

where I_A is the indicator function equal to 1 if A and 0 otherwise, a_j,0 = −∞, a_j,_Lj= ∞, and a_j,l = d_j,l for l = 1, . . . , L_j − 1. That is, the discrete y_j are the result of thresholding the latent variable z_j on the respective cut-points. The continuous y_j variables are simply equal to the z_j unless the z_j cross the left or right boundary of what can be observed for y_j. That is, if there are finite limits for y_j, then y_j is assumed to be a left and/or right censored version of z_j, thus producing a positive mass at the boundary values of y_j.

A joint mixture model for mixed discrete and continuous variables is then,

$${\mathit{z}}_i\mid {\varphi }_i,\mathrm{\Omega }~N({\mathit{\mu }}_{{\varphi }_i},{\mathbf{\sum }}_{{\varphi }_i}),$$ (5)

with prior distributions for ω_m and ϕ = [ϕ₁, . . . , ϕ_n]′ as in (3).

Binary y_j such as gender can be accommodated by setting d_j = {0, 1}. However, if there is only one cut-point then the model must be restricted for identifiability³⁹; namely, if y_j is binary, then we must set Σ_m(j, j) = 1. The restriction that Σ_m(j, j) = 1 for binary y_j complicates posterior inference, however, this problem has been relatively well studied in the multinomial probit setting and various proposed solutions exist⁴⁶. It is also straight-forward to use the latent Gaussian variable approach to allow for unordered categorical variables^47,46,48,49, however, inclusion of categorical variables also complicates notation and there are no such variables in the ASD data. For brevity, attention is restricted here to continuous and ordinal discrete variables.

2.3 Variable Selection

Variable selection in clustering problems is more challenging than in regression problems due to the lack of targeted information with which to guide the selection. Using model-based clustering allows a likelihood based approach to model selection, but exactly how the parameter space should be restricted when a variable is “out of the model” requires some care. Raftery and Dean¹³ defined a variable y_j to be non-informative if conditional on the values of the other variables, it is independent of cluster membership. This implies that a non-informative y_j may still be quite dependent on cluster membership through its dependency with other variables. They assumed a Gaussian mixture distribution for the informative variables, with a conditional Gaussian distribution for the non-informative variables and used maximum likelihood to obtain the change in BIC between candidate models. Thus, they accomplished variable selection with a greedy search to minimize BIC. They further considered restricted covariance parameterizations to reduce the parameter dimensionality (e.g., diagonal, common volume, common shape, common orientation, etc.). We instead take a Bayesian approach to this problem via Stochastic Search Variable Selection (SSVS)^9,50 as this allows for straight-forward treatment of uncertainty in the selected variables and that due to missing values. Kim et al.²⁴ used such an approach with a DPM for infinite normal mixtures, however, due to the difficulty imposed they did not use the same definition as Raftery and Dean¹³ for a non-informative variable. They defined a non-informative variable to be one that is (unconditionally) independent of cluster membership and all other variables. This is not reasonable in many cases, particularly in the ASD problem, and can result in negative consequences as seen in Section 3. Below, we layout a more flexible model specification akin to that taken in Raftery and Dean¹³ to allow for (global) dependence between informative and non-informative variables in a DPM.

Let the informative variables be represented by the model γ, a vector of binary values such that {y_j : γ_j = 1} is the set of informative variables. A priori it is assumed that Pr(γ_j = 1) = ρ_j. Without loss of generality assume that y has elements ordered such that y = [y⁽¹⁾, y⁽²⁾], with y⁽¹⁾ = {y_j : γ_j = 1} and y⁽²⁾ = {y_j : γ_j = 0}, and similarly for z⁽¹⁾ and z⁽²⁾. The model in (5) becomes,

$${\mathit{z}}_i\mid \mathit{\gamma },{\varphi }_i,\mathrm{\Omega }~N({\mathit{\mu }}_{{\varphi }_i},{\mathbf{\sum }}_{{\varphi }_i}),$$ (6)

with

$${\mathit{\mu }}_m=\left(\begin{array}{c}{\mathit{\mu }}_{m1}\\ {\mathit{\mu }}_{m2}\end{array}\right),{\mathbf{\sum }}_m=\left(\begin{array}{cc}{\mathbf{\sum }}_{m11}& {\mathbf{\sum }}_{m12}\\ {\mathbf{\sum }}_{m21}& {\mathbf{\sum }}_{m22}\end{array}\right).$$ (7)

From standard multivariate normal theory, [z⁽²⁾ | z⁽¹⁾, ϕ = m] ~ N(μ_2|1, Σ_2|1) with ${\mathit{\mu }}_{2\mid 1}={\mathit{\mu }}_{m2}+{\mathbf{\sum }}_{m21}{\mathbf{\sum }}_{m11}^{-1}({\mathit{z}}^{(1)}-{\mathit{\mu }}_{m1})$ and ${\mathbf{\sum }}_{2\mid 1}={\mathbf{\sum }}_{m22}-{\mathbf{\sum }}_{m21}{\mathbf{\sum }}_{m11}^{-1}{\mathbf{\sum }}_{m12}$. Now in order for the non-informative variables to follow the definition of Raftery and Dean¹³, the μ_m and Σ_m must be parameterized so that μ_2|1, Σ_2|1 do not depend on m. In order to accomplish this, it is helpful to make use of the canonical parameterization of the Gaussian⁵¹,

$$\mathit{z}\mid \mathit{\gamma },\mathrm{\Omega },\varphi =m~{\mathcal{N}}_C({\mathit{b}}_m,{\mathit{Q}}_m),$$

with precision ${\mathit{Q}}_m={\mathbf{\sum }}_m^{-1}$ and b_m = Q_mμ_m. Partition the canonical parameters as,

$${\mathit{b}}_m=\left(\begin{array}{c}{\mathit{b}}_{m1}\\ {\mathit{b}}_2\end{array}\right),{\mathit{Q}}_m=\left(\begin{array}{cc}{\mathit{Q}}_{m11}& {\mathit{Q}}_{12}\\ {\mathit{Q}}_{21}& {\mathit{Q}}_{22}\end{array}\right).$$ (8)

Result 1

The parameterization in (8) results in (μ_2|1, Σ_2|1) that does not depend on m.

Proof

The inverse of a partitioned matrix directly implies that ${\mathbf{\sum }}_{2\mid 1}={\mathit{Q}}_{22}^{-1}$, which does not depend on m. It also implies that $-{\mathit{Q}}_{22}^{-1}{\mathit{Q}}_{21}={\mathbf{\sum }}_{m21}{\mathbf{\sum }}_{m11}^{-1}$, and substituting Σ_mb_m for μ_m in μ_2|1 gives ${\mathit{\mu }}_{2\mid 1}={\mathit{Q}}_{22}^{-1}({\mathit{b}}_2-{\mathit{Q}}_{21}{\mathit{z}}^{(1)})$, which also does not depend on m.

The Q₂₁ does not depend on m which implies the same dependency structure across the mixture components. This is a necessary assumption in order for z⁽²⁾ to be non-informative variables, i.e., so that cluster membership conditional on z⁽¹⁾ is independent of z⁽²⁾.

Now the problem reduces to defining a prior distribution for Ω, i.e., ω_m = {b_m, Q_m}, m = 1, 2, . . . , conditional on the model γ, that maintains the form of (8). Let ${\omega }_m^{(1)}=\{{\mathit{b}}_{m1},{\mathit{Q}}_{m11}\}$ and ${\omega }_m^{(2)}={\omega }^{(2)}=\{{\mathit{b}}_2,{\mathit{Q}}_{21},{\mathit{Q}}_{22}\}$. The prior distribution for Ω will be defined first unconditionally for ω⁽²⁾ and then for ${\omega }_m^{(1)}$, m = 1, 2, . . . , conditional on ω⁽²⁾. There are several considerations in defining these distributions: (i) the resulting Q_m must be positive definite, (ii) it is desirable for the marginal distribution of (μ_m, Σ_m) to remain unchanged for any model γ to limit the influence of the prior for ω_m on variable selection, and (iii) it is desirable for them to be conjugate to facilitate MCMC sampling^26,40.

Let Ψ be a p × p positive definite matrix, partitioned just as Q_m, and for a given γ assume the following distribution for ω⁽²⁾,

$$\begin{gathered} {\mathit{Q}}_{22}~\mathcal{W}({\mathbf{\Psi }}_{22\mid 1}^{-1},\eta ),{\mathit{b}}_2\mid {\mathit{Q}}_{22}~\mathcal{N}(\mathbf{0},\frac{1}{\lambda }{\mathit{Q}}_{22}), \\ {\mathit{Q}}_{21}\mid {\mathit{Q}}_{22}~ℳ\mathcal{N}(-{\mathit{Q}}_{22}{\mathbf{\Psi }}_{21}{\mathbf{\Psi }}_{11}^{-1},{\mathit{Q}}_{22},{\mathbf{\Psi }}_{11}^{-1}), \end{gathered}$$ (9)

where 𝒲 denotes the Wishart distribution, and ℳ𝒩 denotes the matrix normal distribution.

The distribution of ${\omega }_m^{(1)}$, conditional on ω⁽²⁾ is defined implicitly below. A prior distribution is not placed on (b_m1, Q_m11), directly. It is helpful to reparameterize from (b₂, Q₂₂, Q₂₁, b_m1, Q_m11) to (b₂, Q₂₂, Q₂₁, μ_m1, Σ_m11). By doing this, independent priors can be placed on (b₂, Q₂₂, Q₂₁) and (μ_m1, Σ_m11) and still maintain all of the desired properties as will be seen in Results 2 and 3.

The prior distribution of (μ_m1, Σ_m11) is

$${\mathbf{\sum }}_{m11}\stackrel{\mathit{iid}}{\sim }{\mathcal{W}}^{-1}({\mathbf{\Psi }}_{11},\eta -p_2),{\mathit{\mu }}_{m1}\mid {\mathbf{\sum }}_{m11}\stackrel{\mathit{ind}}{\sim }\mathcal{N}(\mathbf{0},\frac{1}{\lambda }{\mathbf{\sum }}_{m11}),$$ (10)

where 𝒲⁻¹ denotes the inverse-Wishart distribution and (μ_m1, Σ_m11) are independent of ω⁽²⁾. The resulting distribution of (b_m1, Q_m11) conditional on (b₂, Q₂₂, Q₂₁) is not a common or named distribution, but it is well defined via the relations, ${\mathit{b}}_{m1}={\mathbf{\sum }}_{m11}^{-1}{\mathit{\mu }}_{m1}+{\mathit{Q}}_{12}{\mathit{Q}}_{22}^{-1}{\mathit{b}}_2$, and ${\mathit{Q}}_{m11}={\mathbf{\sum }}_{m11}^{-1}+{\mathit{Q}}_{12}{\mathit{Q}}_{22}^{-1}{\mathit{Q}}_{21}$.

Result 2

The prior distribution defined in (9) and (10) results in a marginal distribution for (μ_m, Σ_m) of 𝒩 ℐ 𝒲 (0, λ, Ψ, η),i.e.,the same normal-inverse-Wishart regardless of γ.

Proof

It follows from Theorem 3 of Bodnar and Okhrin⁵² that Σ_m ~ ℐ 𝒲 (η, Ψ). It remains to show μ_m | Σ_m ~ 𝒩 (0, (1/λ) Σ_m). However, according to (9) and (10) and the independence assumption,

$$\left(\begin{array}{c}{\mathit{\mu }}_{m1}\\ {\mathit{b}}_2\end{array}\right)|{\mathbf{\sum }}_m~\mathcal{N}\left(\left(\begin{array}{c}\mathbf{0}\\ \mathbf{0}\end{array}\right),\frac{1}{\lambda }\left(\begin{array}{cc}{\mathbf{\sum }}_{m11}& \mathbf{0}\\ \mathbf{0}& {\mathit{Q}}_{22}\end{array}\right)\right).$$

Also, b_m = Q_mμ_m implies,

$$\left(\begin{array}{c}{\mathit{\mu }}_{m1}\\ {\mathit{\mu }}_{m2}\end{array}\right)=\left(\begin{array}{cc}\mathit{I}& \mathbf{0}\\ -{\mathit{Q}}_{22}^{-1}{\mathit{Q}}_{21}& {\mathit{Q}}_{22}^{-1}\end{array}\right)\left(\begin{array}{c}{\mathit{\mu }}_{m1}\\ {\mathit{b}}_2\end{array}\right).$$

Using the relation Ax ~ 𝒩(Aμ, AΣA′) for x ~ 𝒩 (μ, Σ) gives the desired result.

As mentioned above, the normal-inverse-Wishart distribution is conjugate for ω_m in the unrestricted (no variable selection) setting. It turns out that the distribution defined in (9) and (10) is conjugate for the parameterization in (8) as well, so that the component parameters can be integrated out of the likelihood. Let the (latent) observations be denoted as $\mathit{Z}={[{\mathit{z}}_1^{\prime },\dots ,{\mathit{z}}_n^{\prime }]}^{\prime }$, and the data likelihood as f(Z | γ, ϕ, Ω).

Result 3

The marginal likelihood of Z is given by

$$\begin{gathered} f(\mathit{Z}\mid \mathit{\gamma },\mathit{\varphi })=\int f(\mathit{Z}\mid \mathit{\gamma },\mathit{\varphi },\mathrm{\Omega })f(\mathrm{\Omega }\mid \mathit{\gamma })d\mathrm{\Omega } \\ ={\pi }^{-\frac{np}{2}}\prod _{m=1}^M\left[{\left(\frac{\lambda }{n_m+\lambda }\right)}^{\frac{p_1}{2}}\frac{{\mid {\mathbf{\Psi }}_{11}\mid }^{\frac{\eta -p_2}{2}}{\mathrm{\Gamma }}_{p_1}\left(\frac{n_m+\eta -p_2}{2}\right)}{{\mid {\mathit{V}}_{m11}\mid }^{\frac{n_m+\eta -p_2}{2}}{\mathrm{\Gamma }}_{p_1}\left(\frac{\eta -p_2}{2}\right)}\right]\left[{\left(\frac{\lambda }{n+\lambda }\right)}^{\frac{p_2}{2}}\frac{{\mid {\mathbf{\Psi }}_{11}\mid }^{\frac{p_2}{2}}{\mid {\mathbf{\Psi }}_{2\mid 1}\mid }^{\frac{\eta }{2}}{\mathrm{\Gamma }}_{p_2}\left(\frac{n+\eta }{2}\right)}{{\mid {\mathit{V}}_{11}\mid }^{\frac{p_2}{2}}{\mid {\mathit{V}}_{2\mid 1}\mid }^{\frac{n+\eta }{2}}{\mathrm{\Gamma }}_{p_2}\left(\frac{\eta }{2}\right)}\right], \end{gathered}$$

where (i) M = max(ϕ), i.e., the number of observed components, (ii) p₁ = Σγ_j is the number of informative variables, (iii) p₂ = p − p₁, (iv) n_m is the number of ϕ_i = m, (v) Γ_p(·) is the multivariate gamma function, and (vi) V_m11, V₁₁, V_2|1 are defined as,

$$\begin{gathered} {\mathit{V}}_{m11}=\sum _{{\varphi }_i=m}({\mathit{z}}_i^{(1)}-{\overline{\mathit{z}}}_{m1}){({\mathit{z}}_i^{(1)}-{\overline{\mathit{z}}}_{m1})}^{\prime }+\frac{n_m\lambda }{n_m+\lambda }{\overline{\mathit{z}}}_{m1}{\overline{\mathit{z}}}_{m1}^{\prime }+{\mathbf{\Psi }}_{11}, \\ {\mathit{V}}_{11}=\sum _{i=1}^n({\mathit{z}}_i^{(1)}-{\overline{\mathit{z}}}_1){({\mathit{z}}_i^{(1)}-{\overline{\mathit{z}}}_1)}^{\prime }+\frac{n\lambda }{n+\lambda }{\overline{\mathit{z}}}_1{\overline{\mathit{z}}}_1^{\prime }+{\mathbf{\Psi }}_{11}, \\ {\mathit{V}}_{2\mid 1}={\mathit{V}}_{22}-{\mathit{V}}_{21}{\mathit{V}}_{11}^{-1}{\mathit{V}}_{21}^{\prime }, \end{gathered}$$

with ${\overline{\mathit{z}}}_{m1}=\frac{1}{n_m}{\sum }_{{\varphi }_i=m}{\mathit{z}}_i^{(1)},{\overline{\mathit{z}}}_1=\frac{1}{n}{\sum }_{i=1}^n{\mathit{z}}_i^{(1)},{\overline{\mathit{z}}}_2=\frac{1}{n}{\sum }_{i=1}^n{\mathit{z}}_i^{(2)}$,

$$\begin{gathered} {\mathit{V}}_{22}=\sum _{i=1}^n({\mathit{z}}_i^{(2)}-{\overline{\mathit{z}}}_2){({\mathit{z}}_i^{(2)}-{\overline{\mathit{z}}}_2)}^{\prime }+\frac{n\lambda }{n+\lambda }{\overline{\mathit{z}}}_2{\overline{\mathit{z}}}_2^{\prime }+{\mathbf{\Psi }}_{22},\mathit{and} \\ {\mathit{V}}_{21}=\sum _{i=1}^n({\mathit{z}}_i^{(2)}-{\overline{\mathit{z}}}_2){({\mathit{z}}_i^{(1)}-{\overline{\mathit{z}}}_1)}^{\prime }+\frac{n\lambda }{n+\lambda }{\overline{\mathit{z}}}_2{\overline{\mathit{z}}}_1^{\prime }+{\mathbf{\Psi }}_{21}. \end{gathered}$$ (11)

The derivation of Result 3 is provided in Web Appendix B.

2.4 Hyper-Prior Distributions

Kim et al.²⁴ found there to be a lot of prior sensitivity due to the choice of prior for the component parameters. This is in part due to the separate prior specification for the parameters corresponding to informative and non-informative variables, respectively. The specification above treats all component parameters collectively, in a single prior, so that the choice will not be sensitive to the interplay between the priors chosen for informative and non-informative variables. A further stabilization can be obtained by rationale similar to that used in Raftery and Dean¹³ for restricted forms of the covariance (such as equal shape, orientation, etc.). We do not enforce such restrictions exactly, but one might expect the components to have similar covariances or similar means for some of the components. Thus it makes sense to put hierarchical priors on λ, Ψ, and η, to encourage such similarity if warranted by the data. A Gamma prior is also placed on the concentration parameter α, i.e.,

$$\begin{array}{ll}\hfill \lambda ~\text{Gamma}(A_{\lambda },B_{\lambda }),& \mathbf{\Psi }~\mathcal{W}(\mathit{P},N),\hfill \\ \hfill \eta -(p+1)~\text{Gamma}(A_{\eta },B_{\eta }),& \alpha ~\text{Gamma}(A_{\alpha },B_{\alpha }).\hfill \end{array}$$ (12)

In the analyses below, relatively vague priors were used with A_λ = B_λ = A_η = B_η = 2. The prior for α was set to A_α = 2, B_α = 2, to encourage anywhere from 1 to 15 clusters from 100 observations. The results still have some sensitivity to the choice of P. In addition, there are some drawbacks to Wishart priors which can be exaggerated when applied to variables of differing scale^53,54. In order to alleviate these issues, we recommend first standardizing the columns of the data to mean zero and unit variance, then using N = p + 2, P = (1/N)I. Finally, the prior probability for variable inclusion was set to ρ_j =0.5 for all j. The data model in (4) and (6), the component prior distribution in (9) and (10), along with the hyper-priors in (12), completes the model specification.

2.5 MCMC Algorithm

Complete MCMC details are provided in the Web Appendix C. However, an overview is provided here to illustrate the main idea. The complete list of parameters to be sampled in the MCMC are Θ = {γ, ϕ, λ, η, Ψ, α, Z̃}, where Z̃ contains any latent element of Z (i.e., either corresponding to missing data, discrete variable, or boundary/censored observation). The only update that depends on the raw observed data $\mathit{Y}={[{\mathit{y}}_1^{\prime },\dots ,{\mathit{y}}_n^{\prime }]}^{\prime }$ is the update of Z̃ . All other parameters, when conditioned on Y and Z, only depend on Z. The Z̃ are block updated, each with a MH step, but with a proposal that looks almost conjugate, and is therefore accepted with high probability; the block size can be adjusted to trade-off between acceptance and speed (e.g., acceptance ~ 40%). A similar strategy is taken with the Ψ update, i.e., a nearly conjugate update is proposed and accepted/rejected via an MH step. Because the component parameters are integrated out, the ϕ_i can be updated with simple Gibbs sampling²⁶, however, this approach has known mixing issues^40,55. Thus, a modified split-merge algorithm⁴⁰ similar to that used in²⁴ was developed to sample from the posterior distribution of ϕ. The remaining parameters are updated in a hybrid Gibbs, Metropolis Hastings (MH) fashion. The γ vector is updated with MH by proposing an add, delete, or swap move⁵⁰. The λ, η, α parameters have standard MH random walk updates on log-scale. The MCMC routine then consists of applying each of the above updates in turn to complete a single MCMC iteration, with the exception that the γ update be applied L_g times each iteration.

Two modifications were also made to the above strategy to improve mixing. The algorithm above would at times have trouble breaking away from local modes when proposing ϕ and γ updates separately. Thus, an additional joint update is proposed for ϕ and γ each iteration which substantially improved the chance of a move each iteration. Also, as described in more detail in Web Appendix C, the traditional split merge algorithm proposes an update by first selecting two points, i and i′, at random. If they are from the same cluster (according to the current ϕ) it then assigns them to separate clusters and assigns the remaining points from that cluster to each of the two new clusters at random. It then conducts several (L) restricted (to one of the two clusters) Gibbs sampling updates to the remaining ϕ_h from the original cluster. The resulting ϕ^* then becomes the proposal for a split move. We found that the following adjustment resulted in better acceptance of split/merge moves. Instead of assigning the remaining points to the two clusters at random, simply assign them to the closest of the two observations i or i′. Then conduct L restricted Gibbs sample updates to produce the proposal. We found little performance gain beyond L = 3. Lastly, it would be possible to instead use a finite mixture approximation via the kernel stick breaking representation of a DPM^56,55. However, this approach would be complicated by the dependency between γ and the structure and dimensionality of the component parameters. This issue is entirely avoided with the proposed approach as the component parameters are integrated out. The code to perform the MCMC for this model has been made available in a GitHub repository at https://github.com/cbstorlie/DPM-vs.git.

2.6 Inference for ϕ and γ

The estimated cluster membership ϕ̂ for all of the methods was taken to be the respective mode of the estimated cluster membership probabilities. For the DPM methods, the cluster membership probability matrix P (which is an n× ∞ matrix in principle) is not sampled in the MCMC, and is not identified due to many symmetric modes (thus their can be label switching in the posterior samples). However, the information theoretic approach of Stephens⁵⁷ (applied to the DPM in Fu et al.⁵⁸) can be used to address this issue and relabel the posterior samples of ϕ to provide an estimate of P. The resulting estimate P̂ has i^th row, m^th column that can be thought of as the proportion of the relabeled posterior samples of ϕ_i that have the value m. While technically P is an n × ∞ matrix, all columns after M^* have zero entries in P̂, where M^* is the maximum number of clusters observed in the posterior. For the results below, the point estimate of γ̂ is determined by γ̂_j = 1 if Pr(γ_j = 1) > ρ_j = 0.5, and γ̂_j = 0 otherwise.

3 Simulation Results

In this section the performance of the proposed approach for clustering is evaluated on two simulation cases similar in nature to the ASD clustering problem. Each of the cases is examined (i) without missing data or discrete variables/censoring, (ii) with missing data, but no discrete variables/censoring, (iii) with missing data and several discrete and/or censored variables.

The approaches to be compared are listed below.

DPM-vs –	the proposed method.
DPM-cont –	the proposed method without accounting for discrete variables/censoring (i.e., assuming all continuous variables).
DPM –	the proposed method with variable selection turned off (i.e., a prior probability ρj = 1).
DPM-ind –	the approach of Kim et al.24 when all variables are continuous (i.e., assuming non-informative variables are independent of the rest), but modified to treat discrete variables/censoring and missing data when applicable just as the proposed approach.
Mclust-vs –	the approach of Raftery and Dean13 implemented with the clustvarsel package in R. When there are missing data, Random Forest Imputation59 implemented with the missForest package in R is used prior to application of clustvarsel. However, the Mclust-vs approach does not treat discrete variables differently and thus treats all variables as continuous and uncensored.
VarSelLCM –	the approach of Marbac and Sedki16 implemented in the R package VarSelLCM. It allows for mixed data types and missing data, however, it assumes both local independence of variables within cluster and global independence between informative and non-informative variables.

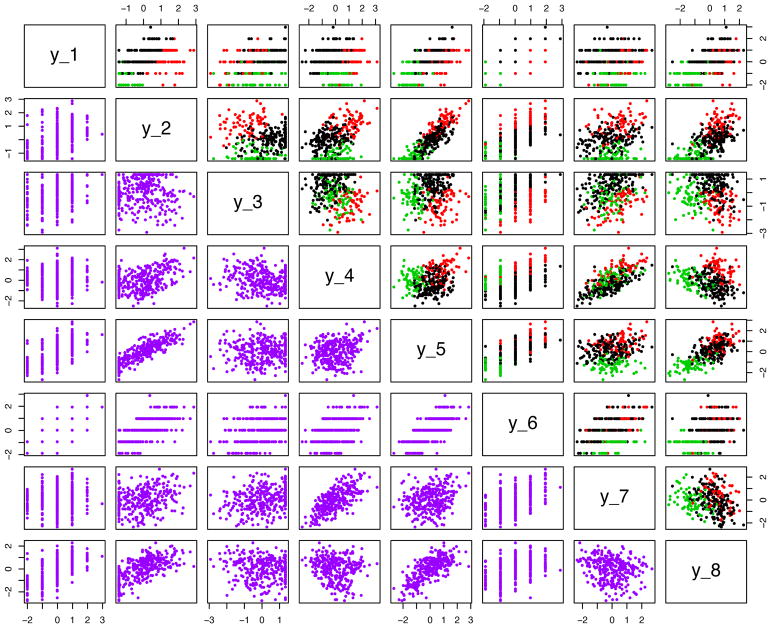
Each simulation case is described below. Figure 2 provides a graphical depiction of the problem for the first eight variables from the first of the 100 realizations of Case 2(c). Case 1 simulations resulted in very similar data patterns as well.

Figure 2.

Pairwise scatter plots of the first eight variables for simulation Case 2(c).

Case 1(a) –	n = 150, p = 10. The true model has M = 3 components with mixing proportions 0.5, 0.25, 0.25, respectively, and y | ϕ is a multivariate normal with no censoring nor missing data. Only two variables y(1) = [y1, y2]′ are informative, with means of (2, 0), (0, 2), (−1.5, −1.5), unit variances, and correlations of 0.5, 0.5, −0.5 in each component, respectively. The non-informative variables y(2) = [y3, . . . , y10]′ are generated as iid 𝒩(0, 1).
Case 1(b) –	Same as the setup in 1(a) only the non-informative variables y(2) are correlated with y(1) through the relation y(2) = By(1) + ε, where B is a 8 × 2 matrix whose elements are distributed as iid 𝒩(0, 0.3), and $\mathit{\epsilon }~\mathcal{N}(0,Q_{22}^{-1})$, with Q22 ~ 𝒲(I, 10).
Case 1(c) –	Same as in 1(b), but variables y1, y6 are discretized to the closest integer, variables y2, y9 are left censored at −1.4 (~8% of the observations), and y3, y10 are right censored at 1.4.
Case 1(d) –	Same as 1(c), but the even numbered yj have ~ 30% of the observations MAR.
Case 2(a) –	n = 300, p = 30. The true model has M = 3 components with mixing proportions 0.5, 0.25, 0.25, respectively, y|ϕ is a multivariate normal with no censoring nor missing data. Only four variables (y1, y2, y3, y4) are informative, with means of (0.6, 0, 1.2, 0), (0, 1.5, −0.6, 1.9), (−2, −2, 0, 0.6) and all variables with unit variance for each of the three components, respectively. All correlations among informative variables are equal to 0.5 in components 1 and 2, while component 3 has correlation matrix, Σ311(i, j) = 0.5(−1)||i+j|| I{i ≠ j} +I{i=j}. The non-informative variables y(2) = [y5, . . . , y30]′ are generated as iid 𝒩(0, 1).
Case 2(b) –	Same as the setup in Case 2(a) only the non-informative variables y(2) are correlated with y(1) through the relation y(2) = By(1) + ε, where B is a 26 × 4 matrix whose elements are distributed as iid 𝒩(0, 0.3), and $\mathit{\epsilon }~\mathcal{N}(0,Q_{22}^{-1})$, with Q22 ~ 𝒲(I, 30).
Case 2(c) –	Same setup as in Case 2(b), but now variables y1, y6, y11 are discretized to the closest integer, variables y2, y9, y10, y11 are left censored at −1.4 (~8% of the observations), and variables y3, y12, y13, y14 are right censored at 1.4.
Case 2(d) –	Same as Case 2(c), but the even numbered yj have ~ 30% MAR.

For each of the eight simulation cases, 100 data sets were randomly generated and each of the five methods above was fit to each data set. The methods are compared on the basis of the following statistics.

Acc –	Accuracy calculated as the proportion of observations in the estimated clusters that are in the same group as they are in the true clusters, when put in the arrangement (relabeling) that best matches the true clusters.
FI –	Fowlkes-Mallows index of ϕ̂ relative to the true clusters.
ARI –	Adjusted Rand index.
M –	The number of estimated clusters. The estimated number of clusters for the Mclust-vs and VarSelLCM methods was chosen as the best of the possible M = 1, . . . 8 cluster models via BIC. The number of clusters for the Bayesian methods is chosen as the posterior mode and is inherently allowed to be as large as n.
p1 –	The model size, p1 = Σj γ̂j.
PVC –	The proportion of variables correctly included/excluded from the model, PVC = (1/p)ΣjI{γ̂j = γj}.
CompT –	The computation time in minutes (using 20,000 MCMC iterations for the Bayesian methods).

These measures are summarized in the columns of the tables below by their mean (and standard deviation) over the 100 data sets. It appeared that 20,000 iterations (10,000 burn in and 10,000 posterior samples) was sufficient for the Bayesian methods to summarize the posterior in the simulation cases via several trial runs, however not every simulation result was inspected for convergence.

The simulation results from Cases 1(a)–(d) are summarized in Table 1. The summary score for the best method for each summary is in bold along with that for any other method that was not statistically different from the best method on the basis of the 100 trials (via an uncorrected paired t-test with α = 0.05). As would be expected, DPM-ind is one of the best methods on Case 1(a), however, it is not significantly better than DPM-vs or Mclust-vs on any of the metrics. VarSelLCM performs slightly worse than the top three methods in this case since the local independence assumption is being violated. All of the other methods solidly outperform DPM though, which had a difficult time finding more than a single cluster since it had to include all 10 variables. In Case 1(b) the assumptions of DPM-ind are now being violated and it is unable to perform adequate variable selection. It must include far too many non-informative variables due to the correlation within y⁽²⁾ and between y⁽¹⁾ and y⁽²⁾. The clustering performance suffers as a result and like DPM, it has difficulty finding more than a single cluster. VarSelLCM also struggles in this case for the same reason; the global independence assumption is being violated. Mclust-vs still performs well in this case, but DPM-vs (and DPM-cont) is significantly better on two of the metrics. In case 1(c) DPM-vs is now explicitly accounting for the discrete and left/right censored variables, while DPM-cont does not. When the discrete variables are incorrectly assumed to be continuous it tends to create separate clusters at some of the unique values of the discrete variables. This is because a very high likelihood can be obtained by normal distributions that are almost singular along the direction of the discrete variables. Thus, DPM-vs substantially outperforms DPM-cont and Mclust-vs, demonstrating the importance of explicitly treating the discrete nature of the data when clustering. Finally, Case 1(d) shows that the loss of 30% of the data for half of the variables (including an informative variable) does not degrade the performance of DPM-vs by much. In this case Mclust-vs uses Random Forest Imputation to first impute the data, then cluster. The imputation procedure does not explicitly take into account of the cluster structure of the data, rather it could mask this structure. This is another reason that the performance is worse than the proposed approach which incorporates the missingness directly into the clustering model. Mclust-vs and VarSelLCM both have much faster run-times than the Bayesian methods, however, when there are local or global correlations and discrete variables and/or missing data, they did not perform nearly as well as DPM-vs.

Table 1.

Simulation Case 1 Results.

Method	Acc	FI	ARI	M	p1	PVC	CompT
Case 1(a)
DPM-vs*	0.91 (0.11)	0.86 (0.07)	0.78 (0.16)	2.9 (0.4)	2.0 (0.3)	0.99 (0.04)	296 (18)
DPM	0.37 (0.02)	0.58 (0.00)	0.00 (0.00)	1.0 (0.1)	10.0 (0.0)	0.20 (0.00)	341 (28)
DPM-ind	0.90 (0.13)	0.86 (0.08)	0.76 (0.20)	3.0 (0.6)	1.9 (0.4)	0.99 (0.04)	295 (23)
Mclust-vs	0.91 (0.10)	0.86 (0.07)	0.78 (0.15)	3.0 (0.4)	2.0 (0.2)	0.99 (0.06)	1 (0)
VarSelLCM	0.74 (0.21)	0.73 (0.10)	0.52 (0.29)	2.9 (1.2)	3.5 (3.2)	0.84 (0.32)	6 (2)
Case 1(b)
DPM-vs*	0.89 (0.14)	0.85 (0.08)	0.76 (0.20)	3.0 (0.7)	1.9 (0.4)	0.98 (0.05)	267 (19)
DPM	0.37 (0.02)	0.58 (0.00)	0.00 (0.00)	1.0 (0.0)	10.0 (0.0)	0.20 (0.00)	292 (15)
DPM-ind	0.37 (0.02)	0.58 (0.00)	0.00 (0.00)	1.0 (0.0)	8.5 (0.8)	0.35 (0.08)	243 (18)
Mclust-vs	0.87 (0.12)	0.83 (0.10)	0.72 (0.19)	2.8 (0.4)	2.0 (0.1)	0.94 (0.12)	1 (0)
VarSelLCM	0.52 (0.06)	0.57 (0.05)	0.40 (0.06)	6.7 (0.9)	9.1 (0.8)	0.29 (0.08)	11 (2)
Case 1(c)
DPM-vs	0.85 (0.14)	0.81 (0.08)	0.68 (0.20)	2.8 (0.6)	1.9 (0.4)	0.97 (0.07)	254 (18)
DPM-cont	0.62 (0.06)	0.52 (0.06)	0.31 (0.07)	4.9 (0.7)	2.0 (0.5)	0.89 (0.11)	296 (25)
DPM	0.37 (0.02)	0.58 (0.00)	0.00 (0.00)	1.0 (0.0)	10.0 (0.0)	0.20 (0.00)	285 (19)
DPM-ind	0.37 (0.02)	0.58 (0.00)	0.00 (0.00)	1.0 (0.0)	8.2 (1.0)	0.38 (0.10)	243 (24)
Mclust-vs	0.49 (0.10)	0.43 (0.09)	0.19 (0.12)	6.7 (1.5)	2.7 (0.8)	0.67 (0.14)	1 (0)
VarSelLCM	0.48 (0.08)	0.51 (0.06)	0.34 (0.07)	6.8 (1.1)	8.4 (0.8)	0.36 (0.08)	10 (1)
Case 1(d)
DPM-vs	0.77 (0.19)	0.76 (0.10)	0.57 (0.25)	2.6 (0.8)	1.9 (0.6)	0.95 (0.09)	304 (21)
DPM-cont	0.62 (0.04)	0.52 (0.05)	0.31 (0.06)	4.8 (0.8)	1.9 (0.5)	0.89 (0.11)	355 (29)
DPM	0.37 (0.02)	0.58 (0.00)	0.00 (0.00)	1.0 (0.1)	10.0 (0.0)	0.20 (0.00)	343 (29)
DPM-ind	0.37 (0.02)	0.58 (0.00)	0.00 (0.00)	1.0 (0.0)	7.6 (1.3)	0.44 (0.13)	277 (40)
Mclust-vs	0.50 (0.10)	0.43 (0.08)	0.20 (0.11)	7.0 (1.1)	3.1 (0.9)	0.64 (0.14)	1 (0)
VarSelLCM	0.50 (0.08)	0.51 (0.06)	0.34 (0.07)	6.5 (1.1)	8.3 (0.8)	0.36 (0.08)	12 (9)
True	1.00 (0.00)	1.00 (0.00)	1.00 (0.00)	3.0 (0.0)	2.0 (0.0)	1.00 (0.00)	–

^*DPM-cont is identical to DPM-vs for cases 1(a) and 1(b) and is therefore not listed separately.

The simulation results from Cases 2(a)–(d) are summarized in Table 2. A similar story line carries over into Case 2 where there are now p = 30 (four informative) variables and n = 300 observations. Namely, DPM-vs is not significantly different from DPM-ind or Mclust-vs on any of the summary measures for Case 2(a), with the exception of computation time. DPM-vs is the best method on all summary statistics (except CompT) by a sizeable margin on the remaining cases. While Mclust is much faster than DPM-vs, the cases of the most interest in this paper are those with discrete variables, censoring and/or missing data (i.e., Cases 1(c), 1(d), 2(c), and 2(d)). In these cases, the additional computation time of DPM-vs might seem inconsequential relative to the enormous gain in accuracy. It is interesting that DPM-vs suffers far less from the missing values when moving from Case 2(c) to 2(d) than it did from Case 1(c) to 1(d). This is likely due to the fact that there are a larger number of observations to offset the additional complexity of a larger p. However, it is also likely that the additional (correlated) variables may help to reduce the posterior variance of the imputed values.

Table 2.

Simulation Case 2 Results.

Method	Acc	FI	ARI	M	p1	PVC	CompT
Case 2(a)
DPM-vs*	0.89 (0.11)	0.85 (0.09)	0.74 (0.20)	3.0 (0.6)	3.8 (0.7)	0.99 (0.02)	544 (45)
DPM	0.50 (0.03)	0.61 (0.01)	0.00 (0.00)	1.4 (0.8)	30.0 (0.0)	0.13 (0.00)	1158 (120)
DPM-ind	0.90 (0.10)	0.85 (0.08)	0.75 (0.17)	3.1 (0.6)	3.9 (0.4)	1.00 (0.02)	543 (36)
Mclust-vs	0.91 (0.12)	0.88 (0.09)	0.78 (0.23)	2.9 (0.5)	4.0 (0.8)	0.98 (0.07)	8 (3)
VarSelLCM	0.68 (0.07)	0.68 (0.04)	0.53 (0.06)	4.7 (0.6)	4.0 (0.0)	1.00 (0.00)	25 (1)
Case 2(b)
DPM-vs*	0.90 (0.10)	0.85 (0.08)	0.75 (0.17)	3.1 (0.6)	3.9 (0.5)	0.99 (0.03)	557 (27)
DPM	0.50 (0.03)	0.61 (0.01)	0.00 (0.00)	1.0 (0.0)	30.0 (0.0)	0.13 (0.00)	1009 (67)
DPM-ind	0.50 (0.03)	0.61 (0.01)	0.00 (0.00)	1.0 (0.0)	28.9 (0.2)	0.17 (0.01)	966 (71)
Mclust-vs	0.83 (0.14)	0.80 (0.12)	0.63 (0.24)	2.6 (0.5)	3.4 (0.8)	0.91 (0.10)	8 (3)
VarSelLCM	0.43 (0.04)	0.46 (0.04)	0.26 (0.05)	7.3 (0.6)	27.3 (1.4)	0.22 (0.05)	53 (3)
Case 2(c)
DPM-vs	0.93 (0.03)	0.89 (0.05)	0.82 (0.07)	3.3 (0.6)	4.0 (0.2)	1.00 (0.02)	589 (47)
DPM-cont	0.62 (0.16)	0.57 (0.14)	0.34 (0.20)	4.4 (1.2)	3.4 (1.4)	0.87 (0.05)	597 (49)
DPM	0.50 (0.03)	0.61 (0.01)	0.00 (0.00)	1.0 (0.0)	30.0 (0.0)	0.13 (0.00)	1078 (54)
DPM-ind	0.50 (0.03)	0.61 (0.01)	0.00 (0.00)	1.0 (0.0)	28.8 (0.5)	0.17 (0.02)	1060 (101)
Mclust-vs	0.45 (0.06)	0.40 (0.04)	0.13 (0.06)	6.4 (1.3)	2.8 (1.0)	0.81 (0.04)	8 (24)
VarSelLCM	0.42 (0.05)	0.43 (0.05)	0.21 (0.06)	7.3 (0.8)	26.6 (1.5)	0.24 (0.05)	59 (3)
Case 2(d)
DPM-vs	0.91 (0.08)	0.86 (0.08)	0.78 (0.14)	3.2 (0.6)	3.9 (0.4)	0.99 (0.03)	577 (54)
DPM-cont	0.61 (0.16)	0.55 (0.14)	0.32 (0.19)	4.3 (1.1)	3.2 (1.2)	0.87 (0.05)	581 (41)
DPM	0.50 (0.03)	0.61 (0.01)	0.00 (0.00)	1.3 (0.5)	30.0 (0.0)	0.13 (0.00)	1028 (85)
DPM-ind	0.50 (0.03)	0.61 (0.01)	0.00 (0.00)	1.0 (0.0)	28.2 (1.1)	0.19 (0.04)	958 (81)
Mclust-vs	0.46 (0.06)	0.41 (0.04)	0.14 (0.05)	6.7 (1.4)	3.0 (1.2)	0.81 (0.04)	6 (7)
VarSelLCM	0.43 (0.05)	0.43 (0.05)	0.20 (0.06)	7.0 (1.0)	26.0 (1.8)	0.26 (0.06)	73 (19)
True	1.00 (0.00)	1.00 (0.00)	1.00 (0.00)	3.0 (0.0)	4.0 (0.0)	1.00 (0.00)	–

^*DPM-cont is identical to DPM-vs for cases 1(a) and 1(b) and is therefore not listed separately.

4 Application to Autism and Related Disorders

The cohort for this study consists of subjects falling in the criteria for “potential ASD” (PASD) on the basis of various combinations of developmental and psychiatric diagnoses obtained from comprehensive medical and educational records as described in Katusic et al.⁶⁰. The population of individuals with PASD is important because this group represents the pool of patients with developmental/behavioral symptoms from which clinicians have to determine who has ASD and/or other disorders. Subjects 18 years of age or older were invited to participate in a face-to-face session to complete psychometrist-administered assessments of autism symptoms, cognition/intelligence, memory/learning, speech and language, adaptive functions, and maladaptive behavior. In addition, guardians were asked to complete several self-reported, validated questionnaires. The goal is to describe how the patients’ test scores separate them in terms of clinical presentation and which test scores are the most useful for this purpose. This falls in line with the new Research Domain Criteria (RDoC) philosophy that has gained traction in the field of mental health research. RDoC is a new research framework for studying mental disorders. It aims to integrate many levels of information (cognitive/self-report tests, imaging, genetics) to understand how all of these might be related to similar clinical presentations.

A total of 87 test scores measuring cognitive and/or behavioral characteristics were considered from a broad list of commonly used tests for assessing such disorders. A complete list of the individual tests considered is provided in Web Appendix A. Using expert judgment to include several commonly used aggregates in place of individual subtest scores, this list was reduced to 55 test score variables to be considered in the clustering procedure. Five of the 55 variables have fewer than 15 possible values and are treated here as discrete, ordinal variables. A majority (46) of the 55 variables also have a lower bound, which is attained by a significant portion of the individuals, and are treated as left censored. Five of the variables have an upper bound that is attained by many of the individuals and are thus treated as right censored. There are 486 observations (individuals) in the dataset, however, only 67 individuals have complete data, i.e., a complete case analysis would throw out 86% of the observations.

DPM-vs was applied to these data; four chains with random starting points were run in parallel for 85,000 iterations each, which took ~ 40 hours on a 2.2GHz processor. The first 10,000 iterations were discarded as burn-in. More iterations were used here than in the simulation cases due to the fact that this analysis is slightly more complicated (e.g., more variables and observations) and it only needed to be performed once. MCMC trace plots are provided in Web Appendix D. All chains converged to the same distribution (aside from relabeling) and were thus combined.Four of the tests (Beery standard, CompTsc_ol, WJ_Pass_Comprehen, and Adaptive Composite) had a high (> 0.88) posterior probability of being informative (Table 3). There is also evidence that Ach_abc_Attention and Ach_abc_AnxDep are informative. The posterior samples were split on which of these two should be included in the model (they were only informative together for 0.1% of the MCMC samples). The next highest posterior inclusion probability for any of the remaining variables was 0.17 and the sum of the inclusion probabilities for all remaining variables was only 0.28. Thus, there is strong evidence to suggest that only five of the 55 variables are sufficient to inform the cluster membership.

Table 3.

Posterior inclusion probabilities and sample means for the six most informative tests.

Variable	Pr(γj = 1)	Cluster Means
		1	2	3
Beery_standard	1.000	0.77	−1.02	−0.44
CompTsc_ol	1.000	0.46	−1.21	−0.01
WJ_Pass_Comprehen	0.944	0.38	−1.26	0.30
Adaptive_Composite	0.889	0.44	−0.68	0.16
ach_abc_Attention	0.460	−0.18	0.21	0.04
ach_abc_AnxDep	0.427	−0.04	0.06	−0.01

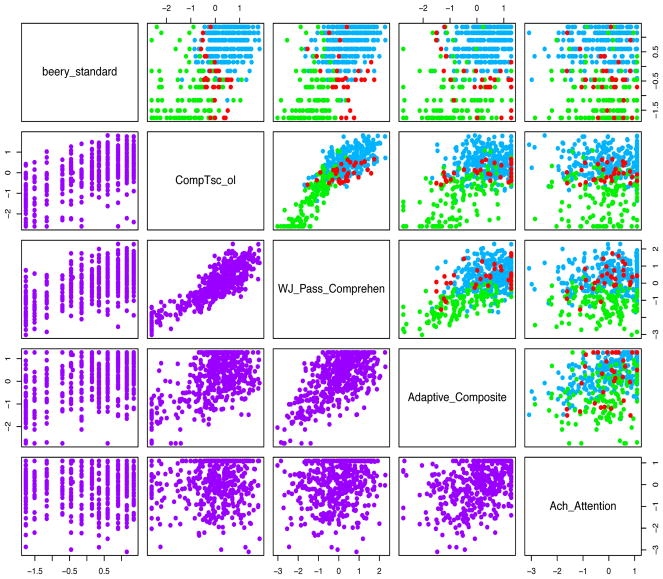
A majority (54%) of the posterior samples identified three components/clusters, with 0.12 and 0.25 posterior probability of two and four clusters, respectively. The calculation of ϕ̂ also resulted in three components. Figure 3 displays the estimated cluster membership via pairwise scatterplots of the five most informative variables on a standardized scale. Ach_abc_Attention has also been multiplied by minus one so that higher values imply better functioning for all tests. The corresponding mean vectors of the three main components are also provided in Table 3. There are two groups that are very distinct (i.e., Clusters 1 and 2 are the “high” and “low” groups, respectively), but there is also a “middle” group (Cluster 3). Cluster 3 subjects generally have medium-to-high Adaptive_Composite, WJ_Pass_Comprehen, and Ach_abc_Attention scores, but low-to-medium Beery_standard and WJ_Pass_Comprehen.

Figure 3.

Pairwise scatter plots of the standardized version of the five most informative variables in Table 3 with estimated cluster membership above the diagonal and the raw data below.

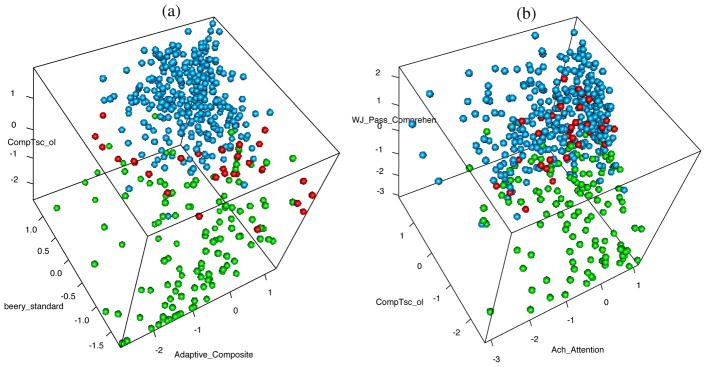
Figure 4(a) provides a 3D scatter plot on the three most informative variables, highlighting separation between Cluster 1 and Clusters 2 and 3. However, Clusters 2 and 3 are not well differentiated in this plot. Figure 4(b) shows a 3D scatter plot on the variables CompTsc_ol, WJ_Pass_Comprehen, and Ach_Attention, illustrating differentiation between Clusters 2 and 3.

Figure 4.

Three dimensional scatter plots of the tests on standardized scale: (a) The most informative three variables with estimated cluster membership. (b) Observations plotted on the variables CompTsc_ol, WJ_Pass_Comprehen, and Ach_abc_Attention, to better illustrate the separation of clusters 2 and 3.

The goal of this work is not necessarily to identify clusters that align with clinical diagnosis of ASD, i.e., it is not a classification problem. The Research Domain Criteria (RDoC) philosophy is to get away from subjective based diagnosis of disease. The hope is that these clusters provide groups of similar patients that may have similar underlying physiological causes and can be treated similarly (whether the clinical diagnosis was ASD or not). That being said, the “high” cluster aligned with no clinical diagnosis of ASD for 92% of its subjects, while the “low” cluster aligned with positive clinical ASD diagnosis for 50% of its subjects. As these clusters result from a bottom-up, data-driven method, they may prove useful to determine imaging biomarkers that correspond better with cluster assignment than a more subjective diagnosis provided by a physician. This will be the subject of future work.

5 Conclusions & Further Work

In this paper we developed a general approach to clustering via a Dirichlet process model that explicitly allows for discrete and censored variables via a latent variable approach, and missing data. This approach overcomes the assumption of (global) independence between informative and non-informative variables and the assumption of (local) independence of variables within cluster often assumed when clustering data of mixed type. The MCMC computation proceeds via a split/merge algorithm by integrating out the component parameters. This approach was shown to perform markedly better than other approaches on several simulated test cases. The approach was developed for moderate p in the range of ~10–300. The computation is 𝒪(p³), which makes it ill-suited for extremely large dimensions. However, it may be possible to use a graphical model^61,62 within the proposed framework to alleviate this burden for large p.

The approach was used to analyze test scores of individuals with potential ASD and identified three clusters. Further, it was determined that only five of the 55 variables were informative to assess the cluster membership of an observation. This could have a large impact for diagnosis of ASD as there are currently ~100 tests/subtest scores that could be used, and there is no universal standard. Further, the clustering results have served to generate hypotheses about what might show up in brain imaging to explain some of the differences between potential ASD patients. A follow-up study has been planned to investigate these possible connections.