Assessment of the generalization of learned image reconstruction and the potential for transfer learning

Abstract

Purpose

While deep learning has shown great promise for MR image reconstruction, an open question regarding the success of this approach is the robustness in the case of deviations between training and test data. The goal of this study is to assess the influence of image contrast, SNR and image content on the generalization of learned image reconstruction, and to demonstrate the potential for transfer learning.

Methods

Reconstructions were trained from undersampled data using data sets with varying SNR, sampling pattern, image contrast and synthetic data generated from a public image database. The performance of the trained reconstructions was evaluated on 10 in-vivo patient knee MRI acquisitions from two different pulse sequences that were not used during training. Transfer learning was evaluated by fine-tuning baseline trainings from synthetic data with a small subset of in-vivo MR training data.

Results

Deviations in SNR between training and testing lead to substantial decreases in reconstruction image quality, while image contrast was less relevant. Trainings from heterogeneous training data generalized well towards test data with a range of acquisition parameters. Trainings from synthetic non-MR image data showed residual aliasing artifacts, which could be removed by transfer learning inspired fine-tuning.

Conclusion

This study presents insights into the generalization ability of learned image reconstruction with respect to deviations in the acquisition settings between training and testing. It also provides an outlook for the potential of transfer learning to fine-tune trainings to a particular target application using only a small number of training cases.

Introduction

The use of deep learning [1] for medical image reconstruction is a new and emerging field. The first early stage developments were reported in 2016. Wang et al. proposed to augment a conventional compressed sensing reconstruction with a regularizer that is based on a convolutional neural network [2]. Kwon et al. proposed to learn a parallel imaging reconstruction without explicit use of coil sensitivity maps that operates entirely within image space [3,4]. We proposed a learning approach based on the framework of variational optimization with the goal of learning the complete reconstruction procedure, which maps from multi-channel k-space rawdata to image space, and the associated numerical procedure [5,6]. Since then, a substantial increase of developments occurred around the world. At the 2017 annual meeting of ISMRM, work was shown that employed learning for image reconstruction for angiography [7], multi-contrast MRI [8], cardiac imaging [9], MR fingerprinting [10], manifold learning [11], partial Fourier imaging [12], projection reconstruction [13] and compressed sensing using residual learning [14]. Our own recent developments presented at ISMRM 2017 included a preliminary investigation of the influence of sampling patterns on the training procedure [15], the influence of different loss functions that are used in the training [16], and a first clinical reader study with the goal of evaluating the diagnostic content of accelerated images that were reconstructed using a variational network [17].

One of the biggest open questions regarding the success of these technologies in practice is generalization. To what degree can the test data deviate from the data that was used during training? This is important for several reasons. First, one of the key strengths of MRI is the flexibility during data acquisition. Due to the range of available MR-systems and protocols, images from different institutions commonly vary with respect to acquisition parameters. A learned reconstruction procedure that works only for a specific set of imaging parameters would therefore be only of limited practical use, since it would require re-training for every new setup. Second, collecting large data sets for training is usually expensive in medical imaging. In some cases, it is even impossible, for example in in the case of time-resolved imaging, where a high spatial and temporal resolution ground truth cannot be obtained. The necessity to collect separate training data for all protocol versions of a particular sequence would put substantial restrictions on clinical translation of these new technologies.

The main goal of this study is to assess the influence of image contrast, SNR, sampling pattern and image content on the generalization of a learned image reconstruction. These design parameters were chosen for investigation because the goal of learning a reconstruction for accelerated data is the separation of aliasing artifacts and true image content. These parameters have a strong influence on the structure of the aliasing artifacts and consequently, the conditioning of the reconstruction problem.

The additional goal, which is also related to the question of generalization and the issue of limited training data is to investigate the potential for transfer learning [18] for image reconstruction using our proposed variational network architecture [6]. This particular topic was recently investigated for MR-image reconstruction of brain data (Dar and Cukur arXiv, 2017) with a deep CNN architecture recently proposed in [9]. In the context of image processing and computer vision, the general hypothesis behind transfer learning is that low level image features, for example edges and simple geometrical structures, are independent of the actual image content of the target application. As a consequence, they can be learned from arbitrary data sets where large amounts of training data are available. These pre-trained models then serve as a baseline, which is then fine-tuned to the target domain using less training data than what would be required when training from scratch. This concept is appealing for MR image reconstruction because non-medical image data are easily available [19],[20], which can be used to simulate synthetic k-space data. In contrast, large amounts of true measurement training data are often challenging to obtain.

Methods

We used a combination of true measurement k-space data from clinical patients, additionally processed k-space data and completely synthetic data for the experiments in this study. For in-vivo data acquisition 40 consecutive patients referred for diagnostic knee MRI to evaluate for internal derangement were enrolled in the study, which was approved by the IRB. Fully sampled rawdata were acquired on a clinical 3T system (Siemens Magnetom Skyra) with a standard 15 channel knee coil. We acquired data with the conventional 2D TSE protocol that is used clinically at our institution. Coronal proton-density weighted (PD_w) sequences with and without fat suppression (FS) were acquired. Technologists were instructed to keep the following sequence parameters constant during the study:

• PD_w: TR=2750ms, TE=27ms, echo-train-length 4, matrix size 320×288, in-plane resolution 0.49×0.44mm², slice thickness 3mm.

• PD_w FS: TR=2870ms, TE=33ms, echo-train-length 4, matrix size 320×288, in-plane resolution 0.49×0.44mm², slice thickness 3mm.

The number of acquired slices varied depending on the size of the patient. 20 cases were acquired for both the PD_w (5 female / 15 male, age 15–76, BMI 20–33) and the PD_w FS (10 female / 10 male, age 30–80, BMI 20–34) sequence. The data was split equally in two categories. The first 10 acquisitions were used for training, the remaining half was used for validation. A selection of slices reconstructed by an inverse Fourier transform followed by a sum-of-squares combination of the individual coil elements is shown in Supporting Information Figure S1. These data show strong similarities in terms of the actual image content, but have fundamentally different contrast and SNR. The noise level σ_est of the two sequences was estimated from an off-center slice that showed only background u_σ. The estimation was performed by averaging the standard deviation from the real and imaginary channels of the uncombined multi-channel data, and then averaging over all N_k training data cases n: ${\sigma }_{\mathit{est}}(u_{\sigma })=\frac{1}{N_k}{\mathrm{\sum }}_{n=1}^{N_k}(\mathit{std}(Re(u_{\sigma }))+\mathit{std}(Im(u_{\sigma })))$. This resulted in an estimated noise level of σ_est = 10⁻⁵, which was identical for both the fat-suppressed and the non-fat-suppressed sequence. The signal level μ_est was then estimated by calculating the l2 norm of the complex multi-channel k-space data f, averaged over the central N_sl = 20 slices of all training data cases: ${\mu }_{\mathit{est}}(f)=\frac{1}{N_k}{\mathrm{\sum }}_{n=1}^{N_k}\left(\frac{1}{N_{sl}}{\mathrm{\sum }}_{sl=1}^{N_{sl}}\frac{{\Vert f\Vert }_2}{\mathit{length}(f)}\right)$. The central 20 slices were selected to ensure that no slices that contained no signal because they were outside the imaged anatomy were included in this analysis. In this definition f is organized as single stacked column vector of the data from all receive coils. The estimated $\mathit{SNR}=\frac{{\mu }_{\mathit{est}}}{{\sigma }_{\mathit{est}}}$ of the PD_w data was approximately 80, that of the PD_w FS data was approximately 20. A third dataset was then generated by adding additional complex Gaussian noise to the PD_w data such that the SNR corresponded to the PD_w FS data. These datasets allow to study the generalization influences of SNR and image contrast independently from each other.

Synthetic k-space data were generated using 200 images from the Berkeley segmentation database (BSDS) [19]. Images were cropped according to the matrix size of the knee k-space data, including readout oversampling. The images were modulated with a synthetic sinusoidal phase using different randomly selected frequencies. After point-wise multiplication with randomly selected coil sensitivity maps estimated from our knee training data, the images were Fourier transformed. Complex Gaussian noise was then added to this synthetic k-space data according to the noise levels of our knee imaging data. We generated three different versions of this data. The first was generated at the SNR level of the PD_w data, the second at the SNR level of the PD_w FS data. The third was generated with a randomly selected level of SNR for every single image using the PD_w FS data as the lower and the PD_w data as the upper bound of SNR.

K-space data were undersampled by a factor of 4, according to a regular Cartesian undersampling pattern as implemented by the scanner vendor for accelerated acquisitions using parallel imaging, and variable density pseudorandom sampling according to [21]. The same random sampling pattern was used in all experiments. 24 reference lines at the center of k-space were used for the estimation of coil sensitivity maps in both cases, using ESPIRiT [22].

We followed the learned image reconstruction procedure using a variational network described in [5] for this study. In this approach a regularized iterative image reconstruction defined by:

$$E(u)=R(u)+\frac{\lambda }{2}{\Vert Au-f\Vert }_2^2$$ (1)

is learned from the training data. The input of the variational network is the undersampled k-space rawdata f and the corresponding coil sensitivity maps (included in the forward sampling operator A in Eq. 1), the output is a complex-valued coil-combined image u. All computations are performed accounting for the complex valued data with exception of the application of the regularizer on the image u, where the image is split up into the real and imaginary part. The regularizer is defined as:

$$R(u)={\mathrm{\sum }}_{i=1}^{N_k}{\rho }_i(k_i\ast u),k_i\ast u=k_{i,Re}\ast u_{Re}+k_{i,Im}\ast u_{Im}.$$ (2)

It consists of a set of N_k spatial filter kernels k for the real and imaginary component of an MR image and potential functions ρ, which are learned from the data together with the regularization parameter λ. Inserting this regularizer in an iterative image reconstruction yields the following update:

$$u_{t+1}=u_t-\sum _{i=1}^{N_k}{\overline{k}}_i^{\mathrm{t}}\ast {\mathrm{\rho }}_{i,t}^{\prime }(k_i^t\ast u_t)-{\lambda }_t{A}^{\ast }(A{u}_t-f),{\lambda }_t>0,0\le t\le T-1$$

where ${\overline{k}}_i^t$ denote the filter kernels $k_i^t$ rotated by 180°. ${\mathrm{\rho }}_{i,t}^{\prime }$ are the first derivatives of the potential functions ρ_{i, t}. Unfolding several iterations of the above scheme, leads to the variational network structure depicted in Figure 1 [6]. Essentially, one gradient step GD of an iterative reconstruction can be related to one stage t in a network with a total of T stages. For reference, the used network architecture is shown in Figure 1. 10 stages were used, each consisting of 24 convolution kernels of size 11×11. The iPalm optimizer and the variational network architecture were implemented and trained using Tensorflow [23], which was extended with additional operators such as the trainable activation functions and (inverse) Fourier shift operations. Source code of our extended Tensorflow library will be provided online (https://github.com/VLOGroup/tensorflow-icg). In addition, example training and testing code for MRI reconstruction will be provided online as well (https://github.com/VLOGroup/mri-variationalnetwork). Trainings were performed slice by slice. During both training and testing each slice u was normalized between 0 and $1\left(u=\frac{u_{\mathit{orig}}}{\mathit{max}(\mid u_{\mathit{orig}}\mid )}\right)$ for the application of the learned regularizer. The pixel-by-pixel mean-squared-error to the fully sampled reference was used as the error metric that was minimized during the training process. All trainings were performed with 150 epochs with a batch-size of 5, using the iPalm algorithm [24]. One epoch is being defined as a sequence of updates of the network parameters when all training examples have been used exactly once. Trainings were performed using the following training data:

Figure 1.

Overview of the variational network architecture used in this work.

First set of experiments: Assessment of generalization with respect to contrast and SNR

• 1PD_w using the central 20 slices from 10 patients (total of N=200 slices).
• 2PD_w FS using the central 20 slices from 10 patients (total of N=200 slices).
• 3PD_w using the central 20 slices from 10 patients (total of N=200 slices) with additional noise added to the complex multi-channel k-space data such that the SNR corresponds to the SNR level of the FS sequence.
• 4Joint PD_w (5 patients) and PD_w FS (5 patients) training, each using the central 20 slices (total of N=200 slices).
• 5Joint PD_w (5 patients) and PD_w with additional noise added (5 patients) training, each using the central 20 slices (total of N=200 slices).

Second set of experiments: Influence of the number of training samples and the heterogeneity of the training data

• 1Joint PD_w (10 patients) and PD_w FS (10 patients) training, each using the central 20 slices (total of N=400 slices).
• 7PD_w using the central 20 slices from the 5 patients used in the joint training in experiment Nr. 4 in the first set of experiments (total of N=100 slices).
• 8PD_w FS using the central 20 slices from the 5 patients used in the joint training in experiment Nr. 4 in the first set of experiments (total of N=100 slices).

Third set of experiments: Assessment of generalization with respect to the sampling pattern

• 9Training with regular sampling, testing with regular sampling.
• 10Training with random sampling, testing with regular sampling.
• 11Training with regular sampling, testing with random sampling.
• 12Training with random sampling, testing with regular sampling.
• 13Joint training with regular and random sampling, testing with regular sampling.
• 14Joint training with regular and random sampling, testing with random sampling.

Fourth set of experiments: Training with synthetic data

• 15Synthetic BSDS data (total of N=200 images) with (high) SNR level of PD_w, regular sampling.
• 16Synthetic BSDS data (total of N=200 images) with (low) SNR level of PD_w FS, regular sampling.
• 17Synthetic BSDS data (total of N=200 images) with variable SNR, regular sampling.
• 18Synthetic BSDS data (total of N=200 images) with variable SNR, random sampling.

Transfer learning experiments: Fine-tuning the regular sampling variable SNR synthetic BSDS model for another 150 epochs

• 19Fine-tuning using a subset of N=20 slices selected from all PD_w cases.
• 20Fine-tuning using a subset of N=20 slices selected from all PD_w FS cases.

In addition, trainings using only the reduced subsets that were used for fine-tuning were performed as a reference for the transfer learning experiments.

The remaining 10 knee measurement datasets of both sequences and the dataset with additional noise added were used to test the performance of the different learned image reconstruction networks. Quantitative evaluation was performed by calculating the root-mean-squared-error $\mathit{RMSE}\left(u,u_{\mathit{ref}}\right)=\frac{{\Vert u_{\mathit{ref}}-u\Vert }_2}{{\Vert u_{\mathit{ref}}\Vert }_2}$ and the structural similarity index $\mathit{SSIM}\left(u,u_{\mathit{ref}}\right)=\frac{\left(2\mathit{mean}(u_{\mathit{ref}})\mathit{mean}(u)+C_1\right)\left(2\mathit{cov}(u,u_{\mathit{ref}})+C_2\right)}{\left(\mathit{mean}{(u_{\mathit{ref}})}^2+\mathit{mean}{(u)}^2+C_1\right)\left(\mathit{std}{(u_{\mathit{ref}})}^2+\mathit{std}{(u)}^2+C_2\right)}$ to the fully sampled reference u_ref for all test slices (378 slices in the case of PD_w and 365 slices in the case of PD_w FS). In the definition of the SSIM, C₁ = (0.01L)² and C₂ = (0.03L)², with L being the dynamic range of the input images, are regularization parameters that are used to avoid instabilities in regions of the image where the local mean or standard deviation is close to zero [25]. Finally, in order to obtain insight into the fine-tuning process in transfer learning, the learned network parameters before and after fine-tuning were visualized together with those from the corresponding in-vivo training.

Results

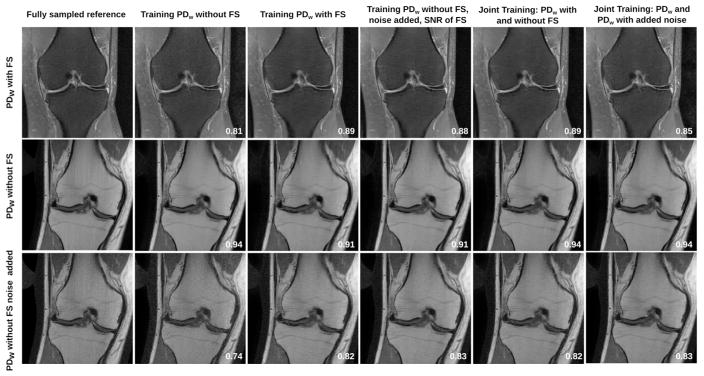
Results of the assessment of generalization with respect to contrast, and SNR are shown in Figure 2. A zoomed view to a region of interest that includes complex image texture due to bone trabeculae and fine details due to ligaments and cartilage is shown in Supporting Information Figure S2. Unsurprisingly, the best results can be achieved when applying the network to test data from the same sequence that it was trained on. When applying the network trained from high SNR PD_w data to the lower SNR fat-suppressed data, a substantial level of noise is present in the reconstructed images. This leads to a reduction of SSIM from 0.89 to 0.81 for this particular slice. In contrast, applying the network trained from low SNR PD_w FS data to higher SNR PD_w data leads to slightly blurred images with some residual artifacts, leading to a SSIM reduction from 0.94 to 0.91. The behavior of the network trained from PD_w data with additional noise is comparable to the network trained from the lower SNR PD_w FS data. In particular, the SSIM is 0.88 for PD_w FS test data in comparison to 0.89 when training with data from the same sequence. In case of the PD_w data test, the SSIM is identical (0.91). The PD_w test data with additional noise results in substantially lower quality in case of the PD_w training (SSIM of 0.74) in comparison to all other trainings, including the individual training from PD_w FS data (SSIM of 0.82). The results from the joint training using data from both contrasts are identical to using the same sequence for training and testing. (SSIM of 0.89 for PD_w FS and 0.94 for PD_w). The joint training from PD_w data with and without additional noise leads to identical results for the PD_w and noisy PD_w test data. For the PD_w FS test data, SSIM is reduced slightly (0.85 in comparison to 0.88 for training with noisy PD_w). The visual impression and the SSIM values of the individual slices shown for the different experiments are confirmed by the quantitative SSIM and RMSE analysis over all cases in the test set (Supporting Information Table S1).

Figure 2.

Assessment of generalization with respect to contrast and SNR. SSIM to the fully sampled reference is shown for the corresponding slices. When applying a network from high SNR PD_w data to lower SNR PD_w FS data, a substantial level of noise is present in the reconstructions. Applying the low SNR PD_w FS network to higher SNR PD_w data leads to slightly blurred images with residual aliasing artifacts. The behavior of the network trained from PD_w data with additional noise was comparable to the network trained from the lower SNR PD_w FS data. The PD_w test data with additional noise results in substantially lower quality in case of the PD_w training in comparison to all other trainings. The results from the joint training using data from both contrasts are identical to using the same sequence for training and testing. The joint training from PD_w data with and without additional noise leads to identical results for the PD_w and noisy PD_w test data and slightly reduced SSIM for the PD_w FS test data. A zoomed view of these results is included in the supporting information.

The influence of the number of training data points in relation to their heterogeneity is shown in Figure 3. No substantial differences in image quality can be observed between the results of these trainings and the individual trainings in Figure 2. A small improvement of 0.01 in the SSIM can be observed in the quantitative analysis (Supporting Information Table S2) for the largest training data set that includes all trainings samples from both sequences.

Figure 3.

Influence of the number of training data points in relation to their heterogeneity. No substantial differences in image quality can be observed between the results of these trainings and the individual trainings in Figure 2.

Figures 4 and 5 show the results of the assessment of generalization with respect to the sampling pattern. When the sampling pattern is consistent between training and testing, results without aliasing artifacts and preservation of fine details are obtained. Applying a network that was trained from random undersampled data to regular undersampling leads to subtle residual artifacts. With the exception of application of a network that was trained from regular undersampling to random undersampling, which shows a small SSIM drop from 0.96 to 0.95 for PD_w test data, quantitative image metrics were identical for all other combinations of training and test data. A joint training with data from both sampling patterns leads to results that are comparable to individual trainings with no deviations in acquisition parameters. This behavior is identical to the experiments with image contrast and SNR. Quantitative SSIM and RMSE analysis over all cases in the test set are also shown in Supporting Information Table S3 for this experiment.

Figure 4.

Assessment of generalization with respect to the sampling pattern for the higher SNR non-fat-suppressed data. When the sampling pattern is consistent between training and testing, results without aliasing artifacts and preservation of fine details are obtained. Applying a network that was trained from regular undersampling to random undersampling leads to subtle over-smoothing, which is also reflected in a slight drop of the SSIM from 0.96 to 0.95. Applying a network that was trained from random undersampled data to regular undersampling leads to residual artifacts. Identical to the experiments with image contrast and SNR, a joint training with data from both sampling patterns leads to results that are comparable to individual trainings with no deviations in acquisition parameters.

Figure 5.

Assessment of generalization with respect to the sampling pattern for the lower SNR fat suppressed data shows the same behavior as the experiments with non-fat-suppressed data (Figure 4). However, residual aliasing artifacts are subtler because the image corruption is mainly dominated by noise amplification in this lower SNR case and aliasing artifacts are buried under the noise level.

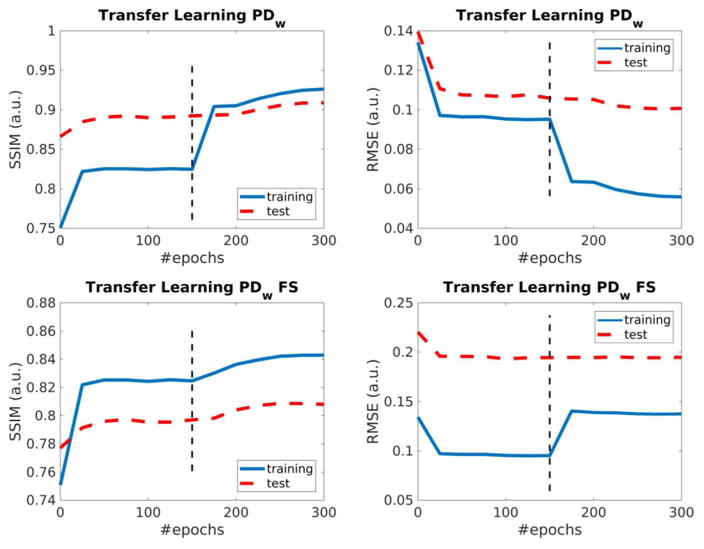
To demonstrate that the trainings are properly converged, plots of RMSE and SSIM of the training and test sets over the training epochs are shown in Figure 6 for the experiments shown in Figures 3, 5 and 6.

Figure 6.

Plots of RMSE and SSIM of the training and test sets over the training epochs for: (a) SNR and contrast generalization experiments in Figure 3. (b) Experiments with changes of the sampling pattern from figures 5 and 6.

The results of the trainings that were performed on synthetic k-space data generated from the BSDS database are shown in Figure 7. The most substantial difference to the experiments when training with true in-vivo MR-data from the same anatomical area is the presence of residual aliasing artifacts in the results (indicated by red arrowheads in Figure 3). The effects of the influence of SNR can be reproduced with the synthetic data. Training data with a substantially higher SNR level leads to noise amplification. This effect is strongest in the case of no additional noise, where the SSIM drops to 0.65 for this particular slice of PD_w FS test data. Training with substantially lower SNR leads to blurring and residual artifacts. This effect is strongest when using the network trained at the noise level of the PD_w FS data for non-fat-suppressed test cases. Again, training with a range of SNR values leads to results that are comparable to training with data that is consistent to the test data in terms of SNR. The corresponding quantitative analysis is shown in Supporting Information Table S4.

Figure 7.

Trainings from synthetic, regularly undersampled, k-space data generated from the BSDS database. SSIM to the fully sampled reference is shown for the corresponding slices. Reconstructions show a larger degree of residual aliasing artifacts (red arrowheads) in comparison to trainings with in-vivo knee data. The effects of the influence of SNR can be reproduced with the synthetic data. Experiments with deviating SNR levels between training and test data again lead to either noise amplification or blurring and residual artifacts. Again, training with a range of SNR values leads to results that are comparable to training with data that is consistent to the test data in terms of SNR. This particular training was also performed and tested with random sampling, with comparable behavior.

The results from the transfer learning experiments are shown in Figure 8. For data of both sequences, results from fine-tuned networks outperform both baseline trainings using only synthetic data, as well as reference trainings using the same subset of knee MRI data that was used during fine-tuning in terms of removal of residual artifacts. Quantitative SSIM and RMSE analysis are shown in Supporting Information Table S5. In particular, with the exception of SSIM for training and testing with non-fat-suppressed PD_W data (0.96, vs. 0.95 for the corresponding transfer learning experiment), results for transfer learning lead to the same SSIM values as the corresponding trainings with in-vivo MRI data from the same sequence. Figure 9 shows plots of RMSE and SSIM for the transfer learning experiments. The first 150 epochs are baseline training and the training error is shown for synthetic data. Epochs 151 to 300 are fine-tuning and the training error is shown for the corresponding subset of in-vivo data. The test error is shown for the in-vivo test cases that were used for all experiments in this study. A substantial jump in the training error can be observed at the transition between baseline training and fine tuning. This is to be expected, because the dataset that is used to obtain the error metric changes at this point. The effect is more subtle for the test error, but it can still be seen that the baseline training reached a plateau and is then improved further during the fine-tuning period.

Figure 8.

Transfer learning experiments. For both PD_w and PD_w FS data, results from fine-tuned networks outperform baseline trainings using only synthetic data, as well as reference trainings using the same subset of knee MRI data that was used during fine-tuning in terms of removal of residual artifacts. This indicates the possibility of fine-tuning networks that were pre-trained from generic data with only a very small number of training cases for a particular target application.

Figure 9.

Plots of RMSE and SSIM of the training and test sets over the training epochs for the transfer learning experiments. The first 150 epochs are baseline training and the training error is shown for synthetic data. Epochs 151 to 300 are fine-tuning and the training error is shown for the corresponding subset of in-vivo data. The test error is shown for the in-vivo test cases that were used for all experiments in this study. The dashed line illustrates the epoch where the training changes from baseline training to fine-tuning.

Discussion

The results from this study demonstrate that a deviation of SNR between training and test data leads to a substantial reduction of image quality when using a trained variational network for image reconstruction. This can be related to the influence of two design parameters in image reconstruction, which are usually tuned by hand in a conventional image reconstruction approach. The number of iterations in an iterative reconstruction [26] and the regularization parameter in compressed sensing [21]. These parameters determine the tradeoff between resolution, g-factor based noise amplification and residual aliasing artifacts. In a machine learning approach, the parameter that balances the data consistency term and the regularization term, as well as the step size of the numerical algorithm, is learned from the training data. Interestingly, reconstructed test case images showed the same behavior when an SNR deviation occurred due to a change of the pulse sequence that was used between training and testing, and when data from the same pulse sequence was retrospectively corrupted by additional noise. In particular, lower SNR PD_w FS test data showed comparable image quality for trainings from PD_w FS data and PD_w data with additionally added noise. PD_w test data with additionally added noise showed substantially higher image quality for trainings from PD_w FS data, with different contrast but matched SNR, than for trainings from PD_w data, with matched contrast but different SNR. This demonstrates that while SNR is a critical parameter that has to be consistent between training and testing, image contrast is a less critical factor. It should be noted that this particular behavior can only be interpreted for our particular network architecture, implementation of the training procedure and the difficulty of the reconstruction problem defined by the acceleration factor, SNR and the quality of the particular multi-channel receive coil.

As expected, since the structure of the aliasing artifacts is influenced by the used sampling pattern, deviations between training and testing influence the quality of the reconstructions. However, it is important to note that our approach does not learn a particular aliasing pattern by heart. Elimination of artifacts is performed locally, by spatial convolution of learned filter kernels in image space. This explains why the negative effects on the reconstruction quality are relatively benign. However, it cannot be expected that these results generalize to more substantial changes in the trajectory, e.g. 3D pseudorandom sampling or non-Cartesian trajectories like radial or spirals, which have fundamentally different aliasing properties.

Training a reconstruction from heterogeneous data lead to the same results as training from data that were consistent between training and testing. This behavior was consistent for both contrast, SNR and multiple sampling patterns. These experiments demonstrate that a reconstruction can be learned that generalizes with respect to changes in acquisition parameters, under the condition that the corresponding heterogeneity is included in the training data. It is currently an open question to what degree an increase of heterogeneity in the training data also requires an increase of the total samples to achieve generalization. The experiments in this study did not show substantial deviations in performance when varying the number of training samples. However, the goal of these experiments was not a large-scale analysis of the influence of the number of training data sets in learned image reconstruction. The goal was to study the cases where the exact same data sets are used in single-contrast and heterogeneous multi-contrast trainings (N=100 to N=400 slices). An analysis of the influence of the number of training samples in the context of transfer learning for the network architecture proposed in [9] is presented in an arXiv preprint by Dar and Cukur (“A Transfer-Learning Approach for Accelerated MRI using Deep Neural Networks,” arXiv, 2017). The authors report improvements of SSIM from 0.93 to 0.96 when increasing the number of baseline training images by a factor of eight and the number of fine-tuning images by a factor of four. While the acquisition of large datasets with sufficient heterogeneity can be challenging in practice, the results from this study indicate that data augmentation can potentially be used successfully. Given the availability of fully sampled training k-space data, experiments with different sampling patterns and acceleration factors can be performed without the need to acquire additional measurements. The influence of SNR vs. image contrast further supports this strategy. Different levels of SNR can easily be achieved with data augmentation, while a change of image contrast would require either additional acquisitions or the use of synthetic data and numerical simulations of the MR signal of different pulse sequence and sequence parameters.

The influence of SNR that was observed in the generalization experiments with knee data from different sequences can be reproduced entirely with experiments using synthetic data. This again shows that SNR plays a more critical role than image content in the context of learned image reconstruction. However, results from trainings with synthetic data showed a substantially higher level of residual aliasing artifacts, illustrating that both the sampling pattern and the actual image content define the structure of the introduced aliasing. It should be noted that our experiments were designed around the two extreme ends of the spectrum of training and test data consistency: Training from the same anatomy and scan orientation, and training from arbitrary non-medical images. Future work should be conducted to investigate training from the same anatomical structure but different scan orientations and scans from different anatomical areas. Also, the particular choice of using natural camera images to generate synthetic k-space data, and the particular image database was only one of several possible experiment design choices in this study. Another topic of future research is the use of dedicated numerical simulation data that are designed specifically with the idea of training an image reconstruction procedure. This is particularly interesting for dynamic imaging applications, where the acquisition of high spatial and temporal resolution training data is even more challenging.

Transfer learning inspired fine-tuning with a substantially smaller size of target domain knee MR images reduced the effect of residual aliasing artifacts. The results were close to the optimal case of using MR imaging data from the same anatomical area and pulse sequence for training and testing. These results are not only in line with studies in computer vision, where transfer learning was used to classify class labels that were not present in the original training data set [27], they are also comparable to transfer learning for a neural network architecture for MR reconstruction proposed in [9] evaluated on brain MR datasets (Dar and Cukur, arXiv, 2017) Visualizing the parameters of the learned network provides some additional insight into the fine-tuning procedure. Figure 10 shows a visualization of the learned filter kernels k_RE and k_IM for the real and imaginary plane of the regularizer together with the learned nonlinear activation functions ρ′. The fine-tuned kernels closely resemble the kernels from the baseline training, indicating that they are not updated substantially during the fine-tuning process. Larger updates can be observed for the learned influence functions. They still bear closer resemblance to the baseline trainings than the corresponding in-vivo trainings. However, a direct comparison between the trainings is challenging because they do not necessarily perform the same operations on the images at the same stage in the network. The reason for this is that the training process is a highly non-convex optimization problem. The parameters of the whole network are trained simultaneously and the error metric is the final output after the last stage. This means that the result of each training is one of multiple local minima that lead to approximately the same result, a property that is known from deep learning [1].

Figure 10.

Visualization of a selection of learned nonlinear activation functions ρ′ and filter kernels k_RE and k_IM for the real and imaginary plane of the regularizer. The fine-tuned kernels closely resemble the kernels from the baseline training, indicating that they are not updated substantially during the fine-tuning process. Larger updates can be observed for the learned influence functions.

The relation of the number of training data samples that was used for fine-tuning in comparison to the full trainings (one tenth) was chosen empirically for this study. A more systematic comparison of the influence of the relation between the number of samples for baseline training and for fine-tuning is presented by Dar and Cukur (Dar and Cukur arXiv, 2017). Also, while the particular network architecture that was used in this study can be trained successfully from datasets in the order of several hundred samples, it is a topic for further research if additional performance benefits can be achieved by training different architectures with a larger number of free parameters using synthetic data followed by a fine-tuning step using real MR data.

Conclusion

This study presents insights into the general properties and the generalization ability of a learned variational network for MR image reconstruction with respect to deviations in the acquisition settings between training and testing for a clinically representative set of test cases. Our results show that mismatches in SNR have the most severe influence. Our experiments also demonstrate that by increasing the heterogeneity of the training data set, trained networks can be obtained that generalize towards wide range acquisition settings, including contrast, SNR and the particular k-space sampling pattern. Finally, our study provides an outlook for the potential of transfer learning to fine-tune trainings of our variational network to a particular target application using only a small number of training cases.

Supplementary Material

Supp info

Supporting Figure S1: Overview of the training data that was used in this study: a) Data from a coronal proton density weighted (PD_w) 2D TSE sequence for knee imaging with and without fat-suppression. These two datasets show substantial differences in terms of image contrast and SNR. b) Knee data from the PD_w sequence without fat-suppression with additional noise added to the complex multi-channel k-space data, such that the SNR is comparable to the lower SNR fat-suppressed data. Completely synthetic k-space data generated from images from the Berkeley segmentation database.

Supporting Information Figure S2: Zoomed ROIs from the results shown in Figure 2, further demonstrating the noise amplification and blurring in cases of SNR mismatch between training and test data and the effects of joint training with heterogeneous data. The selected ROI highlights these effects in an anatomical region that includes complex image texture due to bone trabeculae and fine details due to ligaments and cartilage.

Supporting Information Table S1: Table of the quantitative analysis of SSIM and RMSE to the fully sampled reference for the generalization experiments with respect to contrast and SNR. Mean and standard deviations are shown over all cases in the test set, consisting of 378 slices for PD_w and PD_w with additional noise. The PD_w FS test set consisted of 365 slices. Highest image quality values are achieved when data from the same sequence is used for both training and testing. Drops can be observed when the SNR level deviates between training and testing. Results for trainings with PD_w FS data and PD_w data with added noise are comparable. Joint trainings from multiple contrasts and SNR levels show comparable performance to using consistent data between training and testing.

Supporting Information Table S2: Table of the quantitative analysis of SSIM and RMSE to the fully sampled reference for the experiments with different numbers of training examples for joint training. Mean and standard deviations are shown over all cases in the test set, consisting of 378 slices for PD_w and 365 slices for PD_w FS.

Supporting Information Table S3: Table of the quantitative analysis of SSIM and RMSE to the fully sampled reference for the generalization experiments with respect to the sampling pattern. Mean and standard deviations are shown over all cases in the test set, consisting of 378 slices for PD_w and 365 slices for PD_w FS. Trainings show good generalization ability with respect to changes in the sampling pattern. In particular, for non-fat-suppressed test cases, the SSIM values are identical for all combinations of sampling patterns in training and testing.

Supporting Information Table S4: Table of the quantitative analysis of SSIM and RMSE to the fully sampled reference for the trainings with synthetic data. Mean and standard deviations are shown over all cases in the test set, consisting of 378 slices for PD_w and 365 slices for PD_w FS. A slight drop in image quality values can be observed in comparison to trainings with in-vivo data. The experiments show the same behavior in terms of SNR dependency.

Supporting Information Table S5: Table of the quantitative analysis of SSIM and RMSE to the fully sampled reference for the experiments with different numbers of training examples for the transfer learning experiments. Mean and standard deviations are shown over all cases in the test set, consisting of 378 slices for PD_w and 365 slices for PD_w FS. Transfer learning fine-tuned transfer learning results outperform both baseline trainings using only synthetic data, as well as reference trainings using the same subset of knee MRI data that was used during fine-tuning. Quantitative image quality values are close to trainings with consistent in-vivo data.