Absolute Binding Free Energies for the SAMPL6 Cucurbit[8]uril Host-Guest Challenge via the AMOEBA Polarizable Force Field

Abstract

As part of the SAMPL6 host-guest blind challenge, the AMOEBA force field was applied to calculate the absolute binding free energy for a cucurbit[8]uril host complexed with 14 diverse guests, ranging from small, rigid structures to drug molecules. The AMOEBA results from the initial submission prompted an investigation into aspects of the methodology and parameterization employed. Lessons learned from the blind challenge include: a double annihilation scheme (electrostatics and van der Waals) is needed to obtain proper sampling of guest conformations, annihilation of key torsion parameters of the guest are recommended for flexible guests, and a more thorough analysis of torsion parameters is warranted. When put in to practice with the AMOEBA model, the lessons learned improved the MUE from 2.63 to 1.20 kcal/mol and the RMSE from 3.62 to 1.68 kcal/mol, respectively. Overall, the AMOEBA protocol for determining absolute binding free energies benefitted from participation in the SAMPL6 host-guest blind challenge and the results suggest the implementation of the methodology in future host-guest calculations.

Introduction

The development of accurate methodologies for the prediction of protein-ligand binding free energies is a central goal within computational drug design. Accurate prediction of the interaction between a protein and a ligand affords the pharmaceutical industry the opportunity to design a variety of compounds to bind to their primary target and then focus synthesis efforts on a small subset of computationally promising candidates.[1] The cost of designing an approved drug has increased remarkably in recent decades. It is estimated that by achieving an accuracy of 2 kcal/mol or better in computed relative binding free energies, structure-based drug designers could greatly improve the lead optimization phase of the discovery process.[2]

Blind challenges provide a mechanism to rigorously evaluate computational protocols for the prediction of protein-ligand binding free energies. The D3R/SAMPL6 challenge included a host-guest component, where methodologies could be applied to test systems selected based on their similarity to possible pharmaceutical problems, e.g. hydrophobicity, polarity, charged species, drug-like molecules, etc. Host-guest systems are an excellent tool to examine the accuracy and efficacy of computational models in the prediction of binding affinities. These small, well characterized systems are used to calibrate and optimize computational algorithms with the ultimate goal of application of the methods to large proteins and drug-receptor interactions. Past SAMPL contests have utilized cucurbit[7]uril (CB[7]),[3,4] and a cucurbituril clip[5] as the hosts of interest. This CB series of macromolecules are possible tools for drug delivery, with a hydrophobic core and a ring of carbonyls around the top and the bottom of the cylinder. [6] The complementing guests often contain protonated or alkylated amines, and vary in size, complexity, and total charge.

Efforts to design an optimal procedure to tackle these binding free energy calculations range from quantum mechanical approaches to molecular mechanical force fields to empirical docking algorithms. Selection of a methodology involves striking a balance between computational efficiency and model accuracy that proves useful in applications such as drug design. Force fields employed within molecular dynamics simulations provide an excellent means to effectively sample a variety of configurations and energetics for interacting systems. Classical force fields, such as Amber,[7] CHARMM,[8] and OPLS-AA,[9] are fixed-charge models, where point charges and Coulomb’s law are used to describe the electrostatics in combination with a van der Waals term for the intermolecular interactions. These fixed-charged models only crudely describe the electrostatic potential around a molecule and neglect the electrostatic response of the system to its surroundings. These shortcomings can be addressed through the inclusion of higher-order atomic multipole moments and an explicit treatment of electronic polarization. The AMOEBA force field is a prime example of a fully polarizable model, with permanent atomic multipole moments through the quadrupole and induced dipole polarization. [10] The polarizable force field affords the prediction of more accurate thermodynamic properties, is more transferable, and the parameters can be directly optimized against high-level ab initio results. AMOEBA force field parameters have been developed for water,[11,12] organic molecules,[13] proteins,[14] transition metals,[15] and nucleic acids,[16] while there has been demonstrated success of the force field for calculating properties, such as binding free energies[17] and helix stability. [18]

In this work, the cucurbit[8]uril ring (CB[8]) from the SAMPL6 host-guest challenge was examined. The corresponding guests ranged from small organic systems to approved drug molecules. This test set represented a diverse group of 14 structures, ranging in size, structure, charge, and rigidity. [19] The polarizable atomic multipole AMOEBA force field, in conjunction with free energy perturbation calculations, was applied to this host-guest set as part of the blind challenge. After the unveiling of the experimental results, flaws in the AMOEBA binding free energy protocol were identified and modifications to the methodology were explored.

Methodology

The SAMPL6 host-guest challenge included a cucurbit[8]ril ring, CB[8], in complex with a series of 14 guests. In order to calculate the absolute binding free energies for the host-guest systems, AMOEBA force field parameters were needed. AMOEBA parameters for CB[8] and individual guests were developed following the standard protocol,[13] as described here briefly. Ab initio calculations were utilized in order to derive the electrostatic parameters. Initial structures were optimized with a “low-level” of theory [MP2/6-311G(1d,1p)] via the Gaussian 09 software package[20] or the Psi4 software package. [21] The optimized structures were then used as input for a single-point “high-level” calculation at the MP2/aug-cc-pVTZ level. Distributed Multipole Analysis via the GDMA program[22,23] determined initial atomic multipole estimates, including the charge, x-, y-, and z-components of the dipole, and the quadrupole tensor, from the low-level ab initio results. Keeping the partial charges fixed, the atomic dipole components and quadrupole values were fit to the electrostatic potential generated from the high-level ab initio calculation. A Thole damping value[24,25] of 0.39 was used for each atom, in combination with AMOEBA atomic polarizabilities as defined in previous iterations of the AMOEBA force field. Polarization groups, defined by the rotatable bonds within the molecule, were used to describe the intra- and inter-molecular polarization. For each guest, symmetry was imposed during parameterization. Electrostatic parameter generation utilized the poledit and potential programs from the Tinker 8 software. [26] Valence parameters were determined by fitting to the QM-optimized structure, transferred from previous AMOEBA parameters,[13,14] or taken from the corresponding MMFF parameters. [27–31]

Initial host-guest starting structures were obtained by orienting the guest within the binding cavity of the host based on chemical intuition and/or utilizing the structures provided by the contest organizers. If necessary, multiple binding poses were examined. CB hosts tightly bind organic ammonium guests with the charged nitrogen atom interacting with carbonyl oxygens of the host, which limits the number of poses to be considered. For calculation of absolute binding free energies, two independent free energies legs must be evaluated: the guest molecule solvated in explicit water and the host-guest complex solvated in explicit water. The binding free energy is then estimated as the difference between these two legs. All free energies were calculated via free energy perturbation (FEP)[32] and Bennett’s Acceptance Ratio (BAR) method.[33] The molecular dynamics (MD) simulations employed a 40.0 A explicit water box and were run for 10 ns, at 298 Kelvin, and 1 atm via a Bussi thermostat[34–36] and Monte Carlo barostat, [37,38] respectively. Particle mesh Ewald summation (PME) with a real space cutoff at 7 A was used to compute electrostatic and polarization energies and forces. The induced dipoles were converged to 1.0E-5 Debye per atom RMS. The van der Waals (vdW) interactions were splined to zero over a 1.2 Å window ending at 12 Å. The NPT simulations were propagated by using a two-stage RESPA integrator[39–41] with an inner time step of 0.25 fs and a 2 fs outer time step. The first 10% of the trajectory samples were discarded prior to the BAR calculations. All dynamic simulations and BAR were calculated by Tinker-OpenMM[42] using the dynamic_omm and bar_omm programs. The 10 ns MD simulations used for both guest solvation and host-guest complexes required approximately 12 hours to complete on prior generation NVIDIA GTX 1070 GPU cards. BAR calculations, again run on GPUs, require less than an hour. Since all solvation and host-guest windows can be run independently, the turnaround time needed to compute a single binding free energy is easily less than one day given sufficient GPU resources.

Within the simulations the electrostatics of the guest molecule were first annihilated, followed by the annihilation of the van der Waals interactions of the guest molecule. For the initial submission, the van der Waals terms were decoupled. Soft core van der Waals was used for both decoupling and annihilation protocols to avoid sampling issues near vdW λ values of zero.[43] A lambda value spacing of 0.1 was used for an initial set of windows within the electrostatics and the van der Waals, with additional intermediate windows run if there was hysteresis observed between the forward and backward FEP energies. This protocol was followed for both the guest solvation and the host-guest solvation legs.

For the host-guest simulations a flat-bottom harmonic restraint potential was added between the host and guest. The flat-bottomed parabolic function u(r) adopts the following form:

$$u(r)=\{\begin{array}{cc}\hfill k_1{(r-r_1)}^2\hfill & \hfill 0<r<r_1\hfill \\ \hfill 0\hfill & \hfill r_1\le r\le r_2.\hfill \\ \hfill k_2{(r-r_2)}^2\hfill & \hfill r>r_2\hfill \end{array}\phantom{\}}$$

where k is the force constant, r is the distance between the centers of mass of atom subsets of the host and guest, and r₁ and r₂ define the inner and outer range of the flat-bottom. According to Hamelberg and McCammon,[44] the analytical correction for removal of the geometric restraint is ΔG_corr = k_BT ln(c°V) where c° is the unit concentration and V is equal to the integral ${\int }_0^{\infty }4\pi r^2{e}^{-\beta u(r)}dr.$ The free energy, enthalpy and entropy for the constraint correction were computed via the Tinker freefix utility. To determine parameters for the geometric restraint, an initial unrestrained host-guest simulation was run for 40 ns. Analysis was carried out to determine the length of the flat-bottom and the sets of host and guest atoms to tether via the restraint. Restraint parameters were selected such that the chosen restraint is never violated in a fully coupled, unrestrained host-guest simulation. Thus, there is no free energy consequence for the initial introduction of the restraint. The atoms or groups of atoms restrained as well as the inner and outer distance cutoffs used for each host-guest system are provided in Table 1. For all calculations reported here, the restraint harmonic force constants were set to k₁ = k₂ = 5.0 kcal/mol/Ų.

Table 1.

The restraint-group defining atoms and flat-bottom defining distances r₁ and r₂. Distance units are Å. Restraint force constants k were set to 5.0 kcal/mol/Ų.

Guest	r1	r2	r1 Atoms (Guest)	r2 Atoms (Host)
G0	0.0	3.0	All atoms	Oxygen atoms on one side
G1	0.0	5.0	All atoms	Oxygen atoms around top ring
G2	1.0	4.0	All atoms	All atoms
G3	0.0	3.5	Carbons and nitrogens of quinine	All atoms
G4	0.0	3.0	Central nitrogen	All atoms
G5	0.0	2.0	All atoms	All atoms
G6	0.0	3.0	All atoms	All atoms
G7	0.0	3.0	All atoms	All atoms
G8	0.0	2.5	Carbons within ring	All atoms
G9	0.0	2.5	All atoms	All atoms
G10	0.0	2.5	All atoms	All atoms
G11	0.0	3.0	Carbons of cyclohexane ring	All atoms
G12	0.0	3.0	Aromatic carbons	Oxygen atoms around top ring
G12b	0.0	5.0	Aromatic carbons on guest 1	Aromatic carbons on guest 2
G13	0.0	3.0	Platinum atom	Oxygen atoms around top ring

Results and Discussion

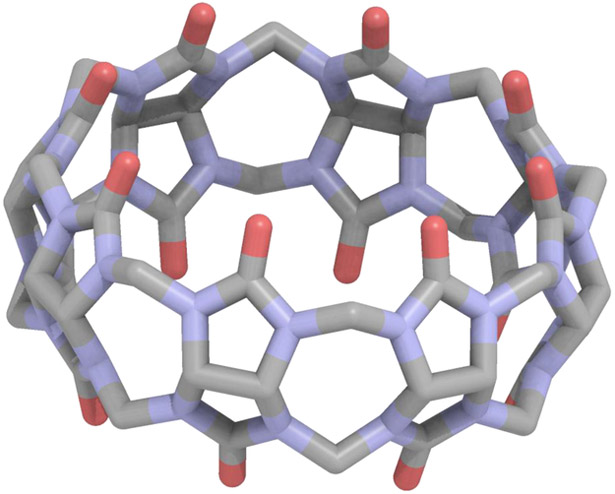
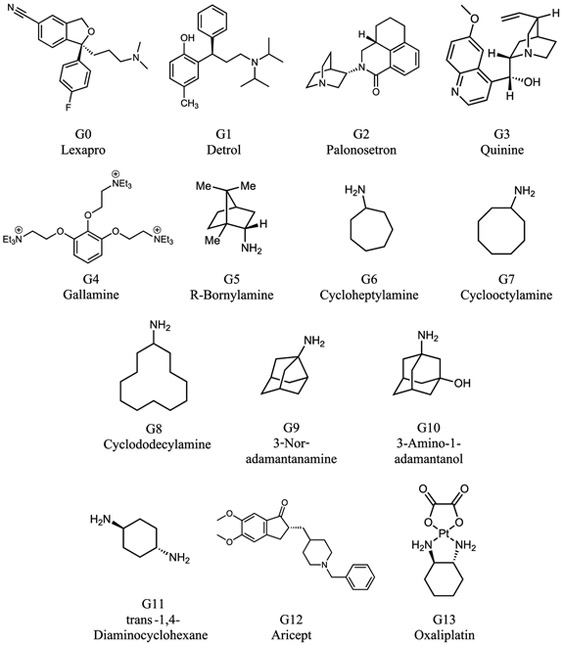
Overall the absolute binding free energies were determined via the AMOEBA force field for 14 host-guest systems as part of the SAMPL6 challenge. The cucurbit[8]uril host is shown in Figure 1 and the fourteen guests, ranging in size from small monofunctional organic structures to larger drug molecules, are shown in Figure 2. Due to the diversity of the guest molecule set, an absolute binding free energy approach is preferred. The CB[8] host is comprised of a hydrophobic core and polar exterior, with carbonyl oxygen rings circling the top and bottom of the structure. The big contrast in environmental conditions is best modeled via a polarizable model.

Figure 1.

The Cucurbit[8]uril (CB[8]) host as part of the SAMPL6 host-guest challenge.

Figure 2.

Chemical structures of the CB[8] guests.

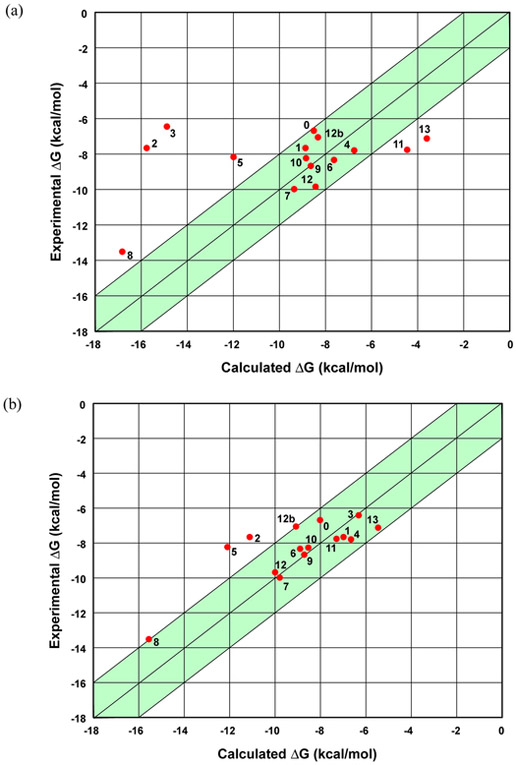
As part of the challenge the blind predictions via AMOEBA were submitted and, after the experimental results were made available, shortcomings in the computational protocol were identified. The initial AMOEBA submission yielded an MUE of 2.63 kcal/mol and an RMSE of 3.62 kcal/mol. These initial AMOEBA results are represented in Figure 3a. Three of the guests were identified by the organizers as “bonus” problems due to their questionable host-guest ratio (guests 11 and 12) or their inclusion of a transition metal (guest 13). The AMOEBA model accurately identified the correct host-guest ratio for both guests 11 and 12, 1:1 and 1:2, respectively. Examination of the initial AMOEBA submission revealed a gross over-estimation of the absolute binding free energy for two of the drug molecules, with the large errors being observed for guest 2 (Palonosetron) and guest 3 (Quinine). The deviations of the calculated results from experiment warranted a further investigation, and two distinct possibilities leading to possible errors were observed: (1) the AMOEBA parameters for the CB[8] host resulted in stochastic indentations of the ring system during the host-guest simulations, and (2) the less rigid guests had a tendency to lock in different conformations during solvation in pure water vs. binding in a solvated host-guest complex.

Figure 3.

(a) A plot of the initial AMOEBA predictions for the host-guest binding free energies. (b) A plot of the revised AMOEBA results for the CB[8] host and guests. The shaded green regions represent deviations within 2 kcal/mol from experiment. In both plots, the 12b point is the binding of a second guest 12 molecule to an existing 1:1 CB[8]/guest 12 complex.

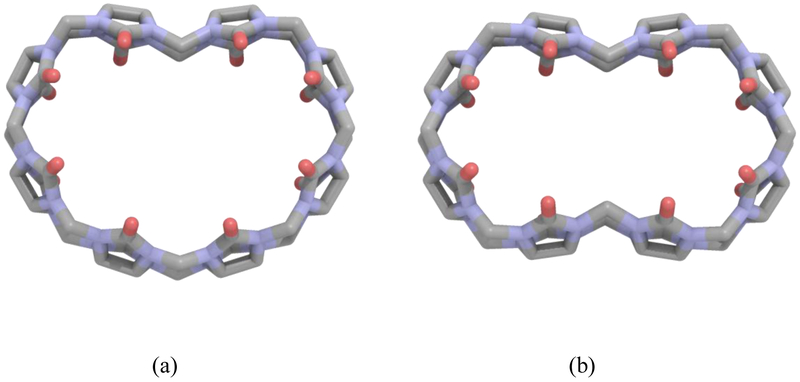
A common phenomenon observed in the initial host-guest simulations was the indentation(s) of the CB[8] host. In addition to the starting ring structure, singly or doubly indented structures were observed during the host-guest simulations, as depicted in Figure 4. These indentations appeared randomly throughout the simulations, even though the starting host structures were circular or slightly oval in shape. Such indented conformations have not been reported and are not observed in known CB-containing crystal structures. The most obvious difference in the structures was a rotated C(N)—C–amide N—carbonyl C torsional angle that varies from 117.8° (circular) to −149.1° (indented). The extreme fluctuation in this torsion angle prompted an examination of the associated three-fold torsional parameter.

Figure 4.

The Cucurbit[8]uril host with single (a) and double (b) indentation.

The fluctuations of the CB[8] host suggests the value of the key torsion parameter may be too weak. In order to assess the 3-fold torsion parameter, ab initio calculations were carried out for different CB[n] conformations. Conformations considered were the single and double indentation of CB[8] and CB[7], as well as three constrained elliptical shapes produced by varying the major/minor axis ratio of the CB[8]. CB[7] was included to improve the description of the flexibility of the ring system. The initial CB[n] 3-fold amplitude parameter for the torsion of interest was −0.25 kcal/mol. The AMOEBA energetics were computed for each conformation at varying torsional values, as tabulated in Tables 2 and 3. In comparison to the ab initio results, it was evident that the initial torsional value was too weak to inhibit indentation during room temperature MD simulation, and the preferred 3-fold torsional value was −1.60 kcal/mol. When this new parameter was put into practice, the indentations of the CB[8] were no longer observed in the host-guest simulations, suggesting a more accurate description of the host-guest interaction.

Table 2.

Single point energy differences between the circular CB[n] (n = 7 or 8) and singly or doubly indented CB[n] (denoted by CB[n]-1 and CB[n]-2, respectively), from ωB97X-D/6-311(1d,1p) level of theory (QM), and different 3-fold parameters for the C(N)—C—amide N—carbonyl C torsional angle. Units are kcal/mol.

		Three-Fold Torsional Parameter
Structure	QM	−0.25	−1.50	−1.60	−1.70
CB[8]–1	13.91	6.84	12.99	13.45	13.91
CB[8]–2	23.35	11.41	22.04	22.83	23.61
CB[7]–1	20.89	12.49	19.91	20.46	21.01

Table 3.

Single point energy differences between the circular CB[8] and three different elliptical CB[8] from ωB97X-D/6-311(1d,1p) level of theory (QM) and different 3-fold torsional parameters. The column “R” denotes the length (in Å) of the longest axis of the CB[8] molecule. Units are kcal/mol.

Ellipse Major Axis		Three-Fold Torsional Parameter
R	QM	−0.25	−1.50	−1.60	−1.70
14.885	8.78	5.50	8.58	8.88	9.61
16.946	65.61	46.83	64.15	65.51	66.91
18.399	233.61	186.44	211.57	213.75	215.580

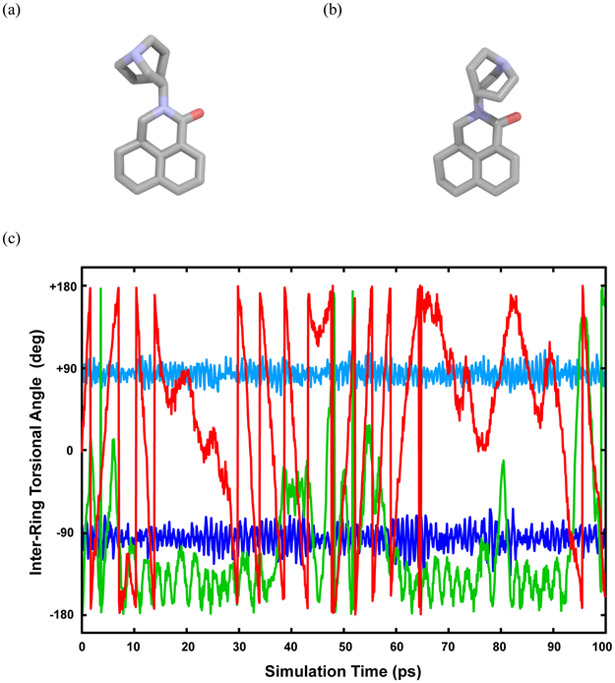
Further examination of the AMOEBA host-guest deviations revealed a difference in the guest conformation between the solvated guest simulations and the host-guest simulations at the fully decoupled level where λ = (0,0) for both electrostatic and vdW interactions. Within the annihilation-decoupling scheme, at the λ = (0,0) level the electrostatic contribution and intermolecular van der Waals of the guest are completely turned off, but the intramolecular van der Waals of the guest remain. During this final lambda window, the conformation of guest 2, palonosetron, in solution differed from the conformation of the same guest in the host-guest simulation, as shown in Figure 5. In order to accurately complete the thermodynamic cycle to compute the absolute binding free energy, there must be equal sampling of the guest conformations in these final, fully decoupled states.

Figure 5.

Palonosetron sampled in: the solvation λ= 0,0 state (a), and the host-guest λ= 0,0 state (b). (c) The inter-ring torsional angle value for C(N)—C–amide N–carbonyl C of palonosetron at the λ= 0,0 state as sampled in a 100 ps MD simulation. Blue curves: both intramolecular van der Waals and key torsion present; Green curve: intramolecular van der Waals annihilated; Red curve: both intramolecular van der Waals and key torsion annihilated.

To rectify the guest sampling issue within the van der Waals windows, annihilation of all guest van der Waals interactions was examined in place of the decoupling. To further increase the sampling, the possibility of annihilating key torsions was also explored. For example, we select the key torsions in flexible guests as those involving bonds between two large substituent groups. The key torsion chosen in guest 2 is identified in Figure 5. The results of these different approaches are represented in Figure 5c. When the van der Waals are fully decoupled, two distinct conformations are observed. The change to annihilation of the van der Waals exhibited an increase in the sampling of the two alternative conformations. The additional annihilation of key guest torsions yields even greatest conformational sampling, suggesting that the AMOEBA absolute binding free energy protocol should be a double annihilation scheme (i.e., electrostatic and vdW), with consideration given to annihilation of key guest torsions value on the structure and flexibility of the guest.

The revised AMOEBA results are presented in Figure 3b. There is the distinct observation that the previous outlier drug molecules, guests 2 and 3, are now in better agreement with experiment, in addition to modest improvements overall for many of the remaining guests. The RMSE of the revised AMOEBA results was 1.68 kcal/mol and the MUE was 1.20 kcal/mol. Additional statistical metrics are provided in Table 4. For the full set of host-guest combinations, eight of the 15 predicted absolute binding free energies fall within 0.65 kcal/mol of experiment.

Table 4.

Initial and revised predictions of CB[8] host-guest binding free energies compared to the experimental values. Units are kcal/mol. The standard error for all calculated values is close to +/− 0.4 kcal/mol.

Guest	Initial	Revised	Expt.
G0	−8.51	−8.03	−6.69
G1	−8.88	−7.01	−7.65
G2	−15.76	−11.13	−7.66
G3	−14.89	−6.34	−6.45
G4	−6.76	−6.62	−7.80
G5	−11.98	−12.10	−8.18
G6	−7.63	−8.92	−8.34
G7	−9.37	−9.71	−9.98
G8	−16.81	−15.55	−13.50
G9	−8.64	−8.71	−8.68
G10	−8.85	−8.54	−8.22
G11	−4.46	−7.30	−7.77
G12	−8.33	−9.99	−9.86
G12b	−8.43	−9.05	−7.05
G13	−3.61	−5.64	−7.11
MUE	2.63	1.20
RMSE	3.62	1.68
Pearson’s R	0.382	0.783
Kendall’s τ	0.12	0.47

Additional consideration was given to the use of the flat-bottom harmonic restraint within the host-guest simulations. When implementing the restraint, there is a decision to be made about which host atoms and which guest atoms to tether. An analysis was carried out for two of the guests (8 and 13), alternatively setting the restraint between a single guest atom and the host, or from the center-of-mass of all guest atoms and the host. For guest 8, the AMOEBA absolute binding free energies were −16.3 and −15.6 kcal/mol for a single atom vs. collection of atoms restraint, respectively. For guest 13, the AMOEBA the analogous results were −5.6 vs. −4.8 kcal/mol. Examination of further host-guest combinations is warranted in order before drawing any conclusion regarding the impact of restraint atom selection on the binding energy.

As part of the thermodynamic cycle to compute the absolute binding free energies, the guest is solvated and the electrostatics and van der Waals are annihilated. Additional gas phase simulations were carried out in order to calculate the guest solvation energies, see Table 5. The more highly charged molecules clearly have much more favorable aqueous solvation free energies. Within the singly charged guests, larger hydrophobic substituents positively correlate with less favorable solvation energies.

Table 5.

The guest solvation energies, ΔG_solv, for the 14 guests as part of the SAMPL6 CB[8] host-guest challenge. Units are kcal/mol. The standard error for all values is between +/− 0.15 and 0.26 kcal/mol.

Guest	ΔGsolv	Guest	ΔGsolv
G0	−46.33	G7	−53.80
G1	−32.37	G8	−60.07
G2	−46.90	G9	−52.34
G3	−64.63	G10	−59.12
G4	−215.98	G11	−178.16
G5	−53.18	G12	−49.14
G6	−54.39	G13	−24.32

The AMOEBA calculations provide a bootstrap error estimate from the BAR procedure. For host-guest binding energies reported in Table 4, the statistical standard error is approximately 0.4 kcal/mol for all guests. For the aqueous solvation free energies vs. gas phase listed in Table 5, the error is in the range from 0.15 to 0.25 kcal/mol. In addition, we performed multiple total binding free energy runs for the CB[8]/guest 9 complex, which suggested inherent error of roughly 0.25 kcal/mol.

Conclusion

Blind challenges, such as the D3R/SAMPL exercise, present an excellent opportunity for members of the computer-aided drug design community to test and compare their models and technology, and learn ways to improve their approaches in order to advance the field. Overall, our AMOEBA-based protocol benefited significantly from participation in the SAMPL6 host-guest challenge. The initial AMOEBA submission benefitted from the inclusion of annihilation of the van der Waals, annihilation of key torsion(s) within the guest, and re-optimization of a CB[n] torsion parameter in order to achieve a better description of the host flexibility. After correcting these two issues with our original, the AMOEBA absolute binding free energies for the full set of CB[8] complexes had an MUE of 1.20 kcal/mol, and an excellent correlation was observed between theory and experiment.

It is important to note that the improvements in the results and the modifications in the methodology were not made solely to obtain better agreement with experiment in this specific system. The double annihilation scheme will be put into practice in future AMOEBA predictions within our lab and is the recommend scheme for similar host-guest systems. The more thorough examination of the torsional parameters demonstrates a common hurdle in the field, where the accurate description of torsional angles and relative conformational energetics plays a crucial role in the accuracy of a model. Future work will include an examination of various host-guest restraints, calculation of enthalpy and entropy for binding processes, and application of the AMOEBA model to larger protein-ligand complexes.

Based on the AMOEBA results for the SAMPL6 host-guest challenge, the double annihilation scheme in conjunction with annihilating key guest torsions is recommended for use with the AMOEBA force field and there is a great promise that this approach will make meaningful contributions to the field of computer-aided drug design.