Force Field for Water Based on Neural Network

Abstract

We developed a novel neural network-based force field for water based on training with high-level ab initio theory. The force field was built based on an electrostatically embedded many-body expansion method truncated at binary interactions. The many-body expansion method is a common strategy to partition the total Hamiltonian of large systems into a hierarchy of few-body terms. Neural networks were trained to represent electrostatically embedded one-body and two-body interactions, which require as input only one and two water molecule calculations at the level of ab initio electronic structure method CCSD/aug-cc-pVDZ embedded in the molecular mechanics water environment, making it efficient as a general force field construction approach. Structural and dynamic properties of liquid water calculated with our force field show good agreement with experimental results. We constructed two sets of neural network based force fields: nonpolarizable and polarizable force fields. Simulation results show that the nonpolarizable force field using fixed TIP3P charges has already behaved well, since polarization effects and many-body effects are implicitly included due to the electrostatic embedding scheme. Our results demonstrate that the electrostatically embedded many-body expansion combined with neural network provides a promising and systematic way to build next-generation force fields at high accuracy and low computational costs, especially for large systems.

Graphical Abstract

Water is one of the most important solvents for many chemical and biological processes. Although water molecules have simple geometric structures, they show various interesting and peculiar phenomena, such as the density maximum at 4° C. In the past few decades, much effort from the molecular dynamics (MD) simulation community has been devoted to simulating water accurately and efficiently. The earliest water models are SPC¹⁴ and TIP3P.⁴⁰ Both SPC and TIP3P adopt three-site structures and fixed atomic charges. Though simple, these two models achieve great success in recovering many bulk properties of water,⁶⁹ and they are still widely used today. However, they fail to predict intermolecular interactions well. Going beyond these two models, various classical water models have been developed, including TIP4P,⁴¹ TIP4P-FQ,⁶¹ AMOEBA,^60,71 COS/D2,^8,45 and SWM4-NDP.⁴⁶ These models add either more interaction sites or explicit polarization effects to further improve the accuracy, and show a significant improvement over SPC and TIP3P not only for bulk properties but for molecular interactions. However, conventional molecular mechanics (MM) force fields fail to give the predictive quantitative accuracy needed for some of the questions of interest.^9,57 To a large extent, the inaccuracy is due to the limited form of the classical MM force fields.

Direct ab initio MD (AIMD)^15,37 simulations can give highly accurate results but at high computational costs. Thus, AIMD is limited to relatively small systems, and the majority of AIMD simulations of water in the literature is at the level of density functional approximations (DFAs),^{28,31,42,51,52,56,75,76} which currently have certain limitations.¹⁷ Various approximations have been developed to alleviate the highly demanding quantum mechanical (QM) computational costs without significant loss of accuracy. Fragment-based methods have been designed for large systems, such as the divide-and-conquer approach,⁷³ molecular fractionation with conjugate caps,⁷⁷ systematic molecular fragmentation,^2,18,23 and the generalized energy-based fragmentation approach.^36,47 Another frequently used approximation is to expand the system energy as a sum of many-body expansions and truncate it after the first several terms.^20,32,58 The simplest expansion is to use only two-body interactions. The scheme of many-body expansion can systematically improve the accuracy by including more and more terms. However, the computational costs increase quickly as more terms are added. In order to improve the accuracy and convergence of many-body expansions, electrostatic embedding from background atoms can be added into the Hamiltonian. Electrostatic interactions with background molecular charges may be added in different forms, such as the pair interaction molecular orbital method⁴⁴ and the fragment molecular orbital method of Kitaura and coworkers.^25,26,43,55 However, all these require direct QM calculations, and none of these schemes are in force field form.

Author: Please verify the changes made to the above reference.Author: Please verify the changes made to the above reference.The conventional force field has its limited forms and associated limitation in accuracy. It is possible to go beyond the conventional force field with a neural network (NN), because of its flexibility and low computational costs. It has been shown that NNs are able to approximate unknown functions to, in principle, any desired accuracy.^12,19,49,50 NNs have many applications in chemistry, such as the analysis of spectra,⁶⁸ quantitative structure-activity relationship studies⁶⁶ and free energy corrections of chemical reactions.⁶⁵ The development of NN-based potential energy surface has seen tremendous progress in the past few years. In early applications, NN-based potentials are restricted to low-dimensional systems due to its rapidly increasing complexity with system size. Recently, high-dimensional NN-based potentials was developed by Behler and Parrinello.¹³ They expressed the molecular energy as the sum of atomic energies, and each atomic energy is represented by a set of NNs. It turns out that this strategy simplifies the NN structure of molecular systems studied and can achieve very high accuracy.^12,13,53 However, their procedure of building NN-based potentials for water can be expensive, since it requires QM calculations of large water clusters.⁵³ Parkhill and co-workers recently combined NNs with many-body expansion to predict energy of methanol clusters at the level of second-order Møller-Plesset perturbation theory (MP2).⁷⁴ But again, this was not developed for the force field purpose. Paesani and co-workers built a high-precision water force field based on many-body expansion using carefully designed polynomial fitting without electrostatic embedding.^6,7,59 On top of classical intermolecular interactions (electrostatic and dispersion energy), they added short-range two-body and three-body corrections at the level of CCSD(T)/CBS. Their model contains higher-order many-body effects due to polarization.^7,59 Some studies have shown that electrostatic embedding can accelerate the convergence of fragment-based method, especially for polarizable systems, such as water.^{20,18,29,30,47} Electrostatically embedded two-body expansion includes many-body effects beyond two-body interactions due to the electrostatic embedding. It has been demonstrated that electrostatically embedded two-body expansion show similar accuracy with three-body expansion in gas phase for water clusters.^20,21 Since Paesani and co-workers successfully developed a high-precision water force field by many-body expansion in the gas phase, we are particularly interested in modeling electrostatically embedded energy of water monomers and dimers with a high-level ab initio method as a reference to predict bulk properties of water. The idea of modeling electrostatically embedded two-body expansion is appealing since it significantly reduces the computational costs compared with higher-order many-body expansion.

In the present work, our aim is to develop a general NN force field for water with high level QM accuracy and low computational costs. Inspired by quantum mechanics/molecular mechanics (QM/MM) approaches,^27,35,48,78 our NN force field uses the many-body expansion up to binary interactions and NN representation of atomic energies, employing an electrostatic embedding scheme. For each electrostatically embedded one-body or two-body term, only water molecules in the QM regions use NN representation, and water molecules in the MM regions only serve as background charges to provide the electrostatic embedding. To properly represent the atomic environment, many different descriptors have been developed including Coulomb matrix,^24,33,62 symmetry functions,^12,13 bispectrum,^10,11 permutation invariant polynomial,^38,39 metric finger-print^63,64,79 and Fourier series of atomic radial distribution functions.⁷⁰ In this work, the atomic environment feature we used is the power spectrum, which is a subset of the bispectrum developed by Csányi and co-workers.^10,11 Although power spectrum is not a one-to-one mapping between geometric configurations of molecules and output value, we find it sufficient to represent an atomic environment for our purpose. Molecular dynamics simulations were performed with our in-house program QM4D.³⁴

We use the following form of potential energy for the whole system:

$$E=\sum _{i=1}^N{E}_1[i;Q_i]+\sum _{i>j}^{R_{ij}<R_{\text{QM}}}(E_2\left[i,j;Q_i\cup Q_j\right]-E_1\left[i;j\cup Q_i\cup Q_j\right]-E_1\left[j;i\cup Q_i\cup Q_j\right])-\sum _{i>j}^{R_{\text{QM}}<R_{ij}<R_{\text{sR}}}\frac{q_i{q}_j}{R_{ij}}+\sum _{i>j}^{R_{\text{SR}}<R_{ij}<R_{\text{LR}}}\frac{q_i{q}_j}{R_{ij}}$$ (1)

Two-body interactions within R_QM are evaluated with NNs at QM level. R_SR is the short-range electrostatic interactions cutoff and R_LR is the long-range electrostatic interactions cutoff. Q_i represents background charges within R_SR of QM molecule i. q_i in the last two terms is either TIP3P charges (for nonpolarizable NN force field) or electrostatic potential (ESP) derived atomic charges (for polarizable NN force field). E₁ and E₂ are electrostatically embedded one-body and two-body energies, respectively. This expansion scheme was used by Hirata and coworkers.⁷² In their case, they ran AIMD for small water clusters at the level of MP2. In our work, instead of carrying out repeated ab initio electronic structure calculations for the small water clusters, we develop NNs to describe the electrostatically embedded one-body and two-body energy terms, using feed-forward NNs for atomic energies in the QM region. For both one-body and two-body terms, each chemical element shares one common set of NNs (i.e., oxygen atoms use one set of NNs and hydrogen atoms use another set of NNs.). The atomic energy e_a represented by two hidden-layer NNs is given as

$${\text{e}}_{\text{a}}=\sum _{k=1}^{N_2}{w}_k^{23}\tanh \left[\sum _{j=1}^{N_1}{w}_{jk}^{12}\tanh \left(\sum _{i=1}^{N_0}{w}_{ij}^{01}{G}_i+b_j^1\right)+b_k^2\right]+b_0$$ (2)

where G_i is the input variable for node i, $w_{ij}^{01}\left(w_{jk}^{12}\right)$ is the weight parameter that connects node i (j) in the previous layer and node j (k) in the current layer, $w_k^{23}$ is the weight parameter that connects node k in the second hidden layer and output layer, $b_j^1$ and $b_k^2$ are bias weight parameters of two hidden layers, b₀ is the bias weight parameter of output layer, N₀ is the number of nodes in input layer, and N₁ and N₂ are the number of nodes in two hidden layers. Energy of electrostatically embedded one-body and two-body terms is the sum of atomic energies in the QM region (Figure 1),

$$E_{1/2}=\sum _a{\text{e}}_{\text{a}}$$ (3)

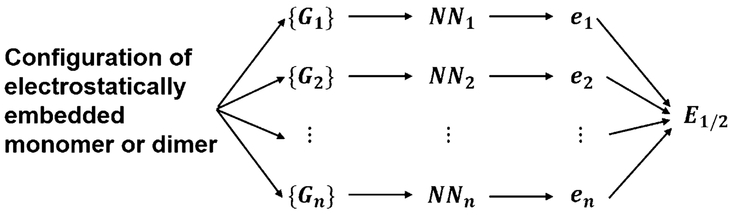
Figure 1.

Schematic representation of neural network structure for electrostatically embedded water monomer and dimer. {G_i} represents power spectrum of atom i including both QM and MM environment. NN_i represents atomic neural network for atom i. e_i represents the atomic energy of atom i. E_1/2 is the energy of electrostatically embedded water monomer or dimer.

To construct a power spectrum, we project the discrete charge density ρ(r) = ∑_i δ(r − r_i)q_i, including both QM charges and MM charges, onto selected radial functions and spherical harmonic functions:

$$\rho (r)=\sum _{l=0}\sum _{m=-l}^l{c}_{nlm}{g}_n(r)Y_{lm}(\theta ,\varphi )$$ (4)

After obtaining the coefficients c_nlm, the corresponding power spectrum can then be calculated as

$$c_{nl}^{†}{c}_{nl}=\sum _i\sum _j\sum _{m=-l}^l{g}_n\left(r_i\right)g_n\left(r_j\right)q_i{q}_j{Y}_{{}_{lm}}^{*}\left({\theta }_i,{\varphi }_i\right)Y_{lm}\left({\theta }_j,{\varphi }_j\right)$$ (5)

Details of the structures of our NNs can be found in the Supporting Information.

Due to large system size and high computational costs of ab initio methods, the majority of AIMD simulations of water in the literature is at the level of DFAs.^{28,31,42,51,52,56,75,76} However, most DFAs suffer from delocalization and strong correlation error and lack accurate van der Waals interactions.¹⁶ This leads to inaccurate simulations of water, in which van der Waals interactions are believed to play an important role. Although some van der Waals density functionals were adopted for AIMD simulations of water, they still cannot fully represent the van der Waals interactions in water.^42,76 Therefore, we developed NNs for electrostatically embedded water monomers and dimers representing coupled cluster singles doubles (CCSD) results.

The reference CCSD was calculated with the basis set aug-ccpVDZ. Compared with using NNs to predict the whole system directly,⁵³ NNs combined with many-body expansions provide a possible way of simulating water with higher-level QM methods. This is because a smaller size of water clusters is needed for training NNs in the many-body scheme.

The NN optimization object function, in weighted mean squared deviation (MSD), for one-body (E₁[i;Q_i]) and two-body terms (E₂[i,j;Q_i∪Q_j] − E₁[i;j∪Q_i∪Q_j] − E₁[j;i∪Q_i∪Q_j]) is defined as

$$L=\sum _i(\left|E_{\text{ref},i}-E_i{|}^2+\frac{\alpha }{3N_{\text{qm}}}\right|F_{\text{ref},i}-F_i{|}^2)+\beta \sum _i{w}_i^2$$ (6)

where α is the relative weight of force with respect to energy and is set to be 0.1 in the current study. The last term is a regularization penalty added to prevent overfitting, and {w_i} are parameters of the NN. β is a small number and is set to be 1 × 10⁻⁶. N_qm is the number of atoms in the QM region. Only force components of atoms in the QM region are accounted for in the object function. NNs are constructed in the following iterative way:⁴ First, several rough NN potentials were built based on snapshots taken from MD simulations. Then, one NN potential was used to run MD simulations, and other NN potentials monitored configurations sampled in this process. When two sets of NN potentials deviated from each other by more than a predetermined value for some configuration, this configuration was then selected out and added into the training set. This process was iterated until one set of satisfying NN was generated. We used 1904 configurations for training and 445 configurations for testing for water monomer model, and 1646 configurations for training and 948 configurations for testing for water dimer model. The embedding cutoff is 12 Å for both training and testing set. There are more than 200 embedding MM water molecules for a typical configuration, which makes it very challenging to model for virial-related calculations. This will be discussed in more details later. The accuracy of our NNs is summarized in Table 1. The energy root mean squared error (RMSE) of the monomer is 0.16 kcal/mol for the training set and 0.22 kcal/mol for the testing set, and the force RMSE of the monomer is 0.77 kcal/mol/Å for the training set and 0.86 kcal/mol/Å for the testing set. The energy RMSE of the dimer is 0.06 kcal/mol/H₂O for the training set and 0.05 kcal/mol/H₂O for the testing set, and the force RMSE of the dimer is 0.66 kcal/mol/Å for the training set and 0.54 kcal/mol/Å. As we can see from Table 1, the error of the testing sets is of comparable accuracy with the training sets.

Table 1.

Accuracy of Neural Networks for Electrostatically Embedded Water Monomers and Dimers^a

	energy (kcal/mol/H2O)		force (kcal/mol/Å)
NN	training set	testing set	training set	testing set
monomer	0.16	0.22	0.77	0.86
dimer	0.06	0.05	0.66	0.54

^aRoot mean squared deviation of energy and force for monomer (E₁[i;Q_i]) and dimer (E₂[i,j;Q_i∪Q_j]−E₁[i;j∪Q_i∪Q_j]−E₁[j;i∪Q_i∪Q_j]).

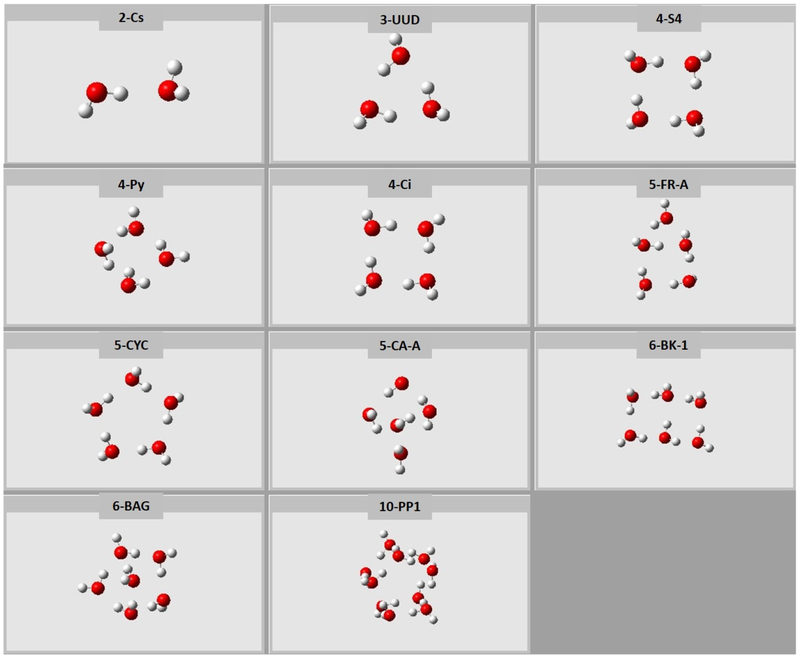
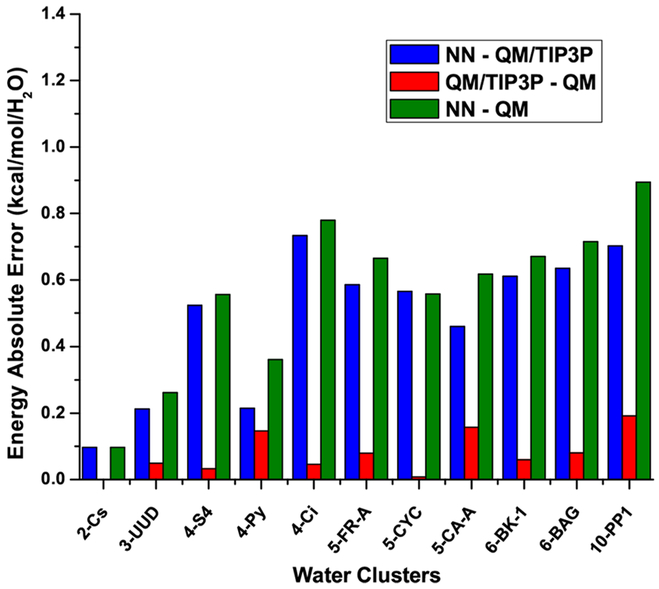
We developed two sets of NN force fields: one using nonpolarizable TIP3P charges as the electrostatic embedding charges, and the other using polarizable ESP charges as the electrostatic embedding charges. Accurate representation of electrostatic embedding is important for reliable energy prediction. As demonstrated in Truhlar’s work,²⁰ TIP3P background charges with electrostatically embedded two-body expansion show very low energy error for water clusters among different point-charge embedding schemes. Thus, we used TIP3P embedding charges for our nonpolarizable force fields. In the polarizable NN force field, a different set of NN was used to predict atomic ESP charges. Before the many-body expansion calculations, atomic ESP charges converge in a self-consistent way. In order to satisfy neutral charge condition for each single water molecule, only the hydrogen atomic charge was predicted by the NN and the oxygen atomic charge was calculated by −q(H₁)−q(H₂). The accuracy of NN charge prediction for a hydrogen atom is 0.03 electron. Artrith et al. applied the idea of environment-dependent charges to the zinc oxide system.⁵ However, there are two major differences between their work and ours. First, in their method, environment-dependent charges are predicted using a cutoff of 6 Å, which only partially reflect the contribution of environment. This is fine since their total energy of the bulk system is the sum of atomic energy, and the energy remainder is absorbed into NN. However, in our case, our total energy is the sum of electrostatically embedded energy. To represent electrostatic interactions well, we have to take into account all the contribution from the MM embedding charges within 12 Å. The chemical complexity in our case is higher. Second, direct application of symmetry functions to represent chemical environment of embedding charges within 12 Å (more than 200 water molecules for a typical configuration) is very expensive. We developed the use of embedding charge density to construct a power spectrum to efficiently represent electrostatically embedded energy. To verify the accuracy of our force fields, we first tested it for water clusters of different size (Figure 2). Geometric coordinates of these water clusters were obtained from the Benchmark Energy and Geometry Database.¹ The corresponding absolute error of binding energy is shown in Figure 3, where we compared electrostatically embedded two-body expansion using TIP3P charges with NN force fields, electrostatically embedded two-body expansion using TIP3P charges at the level of CCSD/aug-cc-pVDZ, and full QM calculations at the level of CCSD/aug-cc-pVDZ. The absolute error of binding energy for our NN force field is stable as the size of water clusters increases. It is larger than our training accuracy for monomer and dimer but is still of chemical accuracy. The red bar confirms that electrostatically embedded two-body expansion provides an accurate reference for our force fields.

Figure 2.

Geometric structure of water clusters used to test an NN force field with TIP3P embedding charges.

Figure 3.

Absolute error of binding energy for water clusters of different size. NN represents an NN force field with TIP3P embedding charges. QM/TIP3P represents electrostatically embedded two-body expansion at the level of CCSD/aug-cc-pVDZ using TIP3P charges. QM represents full quantum mechanical calculations at the level of CCSD/aug-cc-pVDZ.

We now apply the NN force fields to determine bulk water properties using MD simulations. The radial distribution function (RDF) is one of the most important properties reflecting the local structure of water. Experimental data are available for comparison.⁶⁷ We calculated the oxygen‒oxygen (OO), oxygen‒hydrogen (OH) and hydrogen‒hydrogen (HH) RDF, which are shown in Figure 4. As we can see, our predicted OO RDF shows excellent agreement with experimental data for the whole range. Here we emphasize that our NN force fields are constructed only from QM calculations of electrostatically embedded one and two water molecules, and are not fitted to any experimental results. We therefore conclude that our NN force fields provide an accurate description of structural features of liquid water. OO RDF obtained with MP2 using electrostatically embedded two-body expansion shows a much higher first peak.⁷² We believe this is because van der Waals interactions are not correctly accounted for in MP2. Some studies pointed out that nuclear quantum effects are important for hydrogen atoms in water.⁵⁴ The subtle mismatch of the first peak in OO RDF may be due to the lack of consideration of nuclear quantum effects in the current NN force fields or the error of NN representation. We observed that OH and HH RDF do not match experimental results as well as OO RDF. This may affect the prediction of other water properties. Our OH and HH RDF show comparable accuracy with those of TIP3P (not shown here). Compared with TIP3P, our force fields do not improve OH and HH RDF much.

Figure 4.

Radial distribution function of oxygen‒oxygen, oxygen‒hydrogen, and hydrogen‒hydrogen (from left to right) with nonpolarizable (NN) and polarizable NN (PNN) force fields are compared with experimental results.

The self-diffusion coefficient (D) measures the dynamical properties of liquids. The self-diffusion coefficient was calculated by Einstein’s formula:²²

$$D_{\text{PBC}}=\underset{t\to \infty }{\lim }\frac{|r(t)-r(0){|}^2}{6t}$$ (7)

The self-diffusion coefficient is related to the MSD of atomic positions. MSD as a function of time t is plotted in Figure 5, and our calculated self-diffusion coefficient is compared with experimental data and TIP3P results in Table 2. From Table 2 we can conclude that NN force fields compares favorably with experimental data and describe the dynamical property of liquid water properly.

Figure 5.

Average mean squared deviation of atomic positions with nonpolarizable (NN) and polarizable (PNN) neural network force fields.

Table 2.

Self-Diffusion Coefficient

	experiment	TIP3P	NNa	PNNb
D (Å2/ps)	0.23	0.52	0.23	0.16

^aNonpolarizable neural network force field.

^bPolarizable neural network force field.

The shear viscosity was calculated by the integration over the autocorrelation function (ACF) of stress tensor elements,³

$$\eta =\frac{V}{k_{\text{B}}T}\underset{0}{\overset{\infty }{\int }}\langle \delta P_{\alpha \beta }(t)\delta P_{\alpha \beta }(0)\rangle \text{d}t$$ (8)

where δP_αβ(t) = P_αβ(t) − ⟨P_αβ(t)⟩. There are in total five independent components P_xy, P_xz, P_yz, $\frac{1}{2}\left(P_{xx}-P_{yy}\right)$, and $\frac{1}{2}\left(P_{yy}-P_{zz}\right)$. Simulation results are shown in Table 3 and Figure 6. Compared with ACF of TIP3P, both nonpolarizable and polarizable NN force fields show longer correlation time and do not show negative correlation. These two factors together make the shear viscosity of NN force fields relatively large. The inaccurate prediction of shear viscosity, or more general virial-related properties, are likely due to two reasons. First, virial-related properties put a higher demand on force accuracy between largely separated molecules. Second, in many-body expansion with electrostatic embedding, forces on one molecule consist of contributions from more terms, i.e., each MM embedding charge contributes to the forces on QM atoms. These two reasons together will amplify small force errors in virial-related calculations in the current scheme. Modeling electrostatically embedded many-body expansion is challenging especially for virial-related properties. Virial calculations are directly related to pressure estimation in MD simulations. Poor virial calculations will limit the ability of the current force field to predict density, heat of vaporization, heat capacity, thermal expansion coefficient, and isothermal compressibility. One possible solution to overcome this difficulty is to use shorter cutoff of embedding charges to construct input features for NN while keeping QM calculations with original long embedding cutoff. For example, suppose all the QM calculations of snapshots in the training set are with 12 Å cutoff of MM charges. When we construct a power spectrum to represent an MM environment, embedding charges are cut at 5 Å. This means embedding charges between 5 Å and 12 Å are treated in mean field. We call this method partial mean field for NN representation of an MM environment. The partial mean field method will reduce both the number of pairwise interactions and the need to calculate forces between largely separated molecules. Thus, it may improve the virial calculations.

Table 3.

Shear Viscosity of TIP3P, Nonpolarizable NN, and Polarizable NN Force Fields^a

shear viscosity (mPa·s)	TIP3P	NNb	PNNc	experiment
				0.85
average	0.39	3.05	6.41
0.5*(xx − yy)	0.23	2.30	6.10
0.5*(yy − zz)	0.30	2.40	7.95
xy	0.39	3.48	7.95
xz	0.41	3.60	4.60
yz	0.54	3.31	5.65

^aFive independent components and average results are shown.

^bNonpolarizable NN force fields.

^cPolarizable NN force fields.

Figure 6.

Stress tensor autocorrelation function and shear viscosity. Top: the left one is the autocorrelation function of the stress tensor element for nonpolarizable NN force field; the right one is the shear viscosity changing with time for nonpolarizable NN force field. Middle: the left one is the autocorrelation function of the stress tensor element for polarizable NN force field; the right one is the shear viscosity changing with time for polarizable NN force field. Bottom: the left one is the autocorrelation function of the stress tensor element for TIP3P; the right one is the shear viscosity changing with time for TIP3P.

In summary, a novel NN force field for water was built based on an electrostatically embedded two-body expansion scheme. The new NN force field is not limited by the Hamiltonian form as classical force fields and is efficient for applications. It was developed at low cost using high-level electronic structure calculations only for one and two water molecules embedded in MM water molecules and showed high accuracy compared with high-level QM results. Our NN force fields show good structural and dynamical properties of water. Compared with the force field of Paesani and co-workers,^6,7,59 we provide an alternative way to build a water force field. The electrostatically embedded two-body expansion includes many-body effects due to the electrostatic embedding scheme, while in the force field of Paesani and co-workers many-body effects are accounted by long-range classical polarization. The idea of electrostatically embedded two-body expansion is appealing since it significantly reduces the computational costs compared with higher-order many-body expansion. We made progress in modeling electro-statically embedded two-body expansion for bulk systems with high-level QM reference. However, challenges still exist for virial-related calculations in modeling electrostatic embedding. Our work provides a general way of building high accuracy force fields, based on only the high-level QM calculations for small electrostatically embedded clusters, which can be easily extended to the force field construction of other systems.