Multivariate left-censored Bayesian model for predicting exposure using multiple chemical predictors

Abstract

Environmental health exposures to airborne chemicals often originate from chemical mixtures. Environmental health professionals may be interested in assessing exposure to one or more of the chemicals in these mixtures, but often exposure measurement data are not available, either because measurements were not collected/assessed for all exposure scenarios of interest or because some of the measurements were below the analytical methods’ limits of detection (i.e. censored). In some cases, based on chemical laws, two or more components may have linear relationships with one another, whether in a single or in multiple mixtures. Although bivariate analyses can be used if the correlation is high, often correlations are low. To serve this need, this paper develops a multivariate framework for assessing exposure using relationships of the chemicals present in these mixtures. This framework accounts for censored measurements in all chemicals, allowing us to develop unbiased exposure estimates. We assessed our model’s performance against simpler models at a variety of censoring levels and assessed our model’s 95% coverage. We applied our model to assess vapor exposure from measurements of three chemicals in crude oil taken on the Ocean Intervention III during the Deepwater Horizon oil spill response and clean-up.

1 Introduction

Frequently, vapor emissions from multiple sources contribute to workers’ overall airborne exposure. When the sources are mixtures with varying composition, they may share common chemical components that are correlated. In other situations, only a single mixture may be present (either as a single source or from multiple sources and the temperature of the mixture varies between sources over time, such that these are actually different mixtures) with its components having high or low correlations. For brevity, in the remainder of this paper, this second situation, will not be referred to in the text below, but should be considered to have the same characteristics as multiple mixtures.

In either instance, some chemicals may have been measured in only some of the groups of interest resulting in missing data or measurement results may be below the analytical method’s limit of detection (LOD, described as left-censored), adding uncertainty about the exposure of interest. A LOD is a threshold below which exposure cannot be quantified with a given analytical method to the degree of accuracy and precision deemed adequate to estimate exposure. Measurements below the LOD cannot be distinguished from each other or quantified. Since exposure assessors aim to provide exposure estimates that are as unbiased as possible, these measurements below the LOD must be considered. Not including measurements below the LOD can result in a biased estimate that overestimates exposure metrics typically used in epidemiology studies, such as the arithmetic average (AM) or geometric mean (GM), which can lead to an underestimation of the disease risk.

Assessing exposures from mixtures with missing data is dependent on the correlation of the components. If there is high correlation among two components of one or more mixtures, one may use a simple linear regression between the two highly correlated components to estimate exposure when measurements of one component are missing for some scenarios, while accounting for censoring (Groth et al., 2017). If the correlation among components is low, however, the relationships of two or more components in measured scenarios can help us estimate exposure to a third component that is missing information or is highly censored. In particular, in the presence of multiple mixtures, one source may allow for the strong prediction of the chemical of interest using a chemical X₍₁₎ where another source would use a chemical predictor X₍₂₎. As a result, a multiple linear regression framework with both chemicals as predictors may be useful.

To account for multiple mixtures of common chemicals, this paper extends the work of Groth et al. (2017) to a multiple linear regression framework for estimation of a chemical of interest while accounting for censoring in multiple predictors (X) and in the primary chemical response of interest (Y). Due to the multivariate framework (which allows us to derive a multiple linear regression equation for each chemical using the other chemicals in the model as predictors), this model also allows us obtain exposure estimates for both the chemical of interest and the chemical predictors simultaneously.

In the next section, we briefly discuss the chemical and the statistical background of censored data methods in environmental health. Next, we describe a multivariate model to predict low correlated components of multiple mixtures, as well as a method for comparing it to other models with different numbers of predictors. Then, we discuss the results of several simulations that compare our model to simpler models with fewer chemical covariates and that test our model’s coverage, i.e. the ability to encompass the true parameter values (values we set for the dataset) in the model’s 95% credible intervals (CI). Finally, we conclude with an example using air measurement data collected from a vessel that participated in the Deepwater Horizon oil spill response and clean-up efforts, the Ocean Intervention III.

2 Chemical and statistical background

When assessing exposures in a workplace, particularly in an epidemiologic study, measurements may be missing or nondetectable (due to levels below the LOD) for some workers of interest for a particular chemical. These workers, however, may have been measured for other exposures. If there is a relationship between the observed measurements, it may be possible to use that knowledge to inform the exposure of interest of the measured workers. In this paper, we assume the primary interest is assessing exposure to one chemical, using other exposures experienced at the time.

The bases for linear relationships of air concentrations among components of mixtures such as oil are the Ideal Gas Law, Raoult’s Law and Henrys Law (Stenzel & Arnold, 2015). The vapor concentration (VC) of a pure chemical in the air above the chemical’s liquid surface at a specific liquid temperature is the ratio of the chemical’s vapor pressure (VP) divided by atmospheric pressure. With mixtures, the VP of each component in the mixture is lower than if it were the pure chemical. The degree of lowering is proportional to the chemical’s molar concentration in the mixture. This lower VP is called the chemical’s adjusted vapor pressure (AVP). Once the AVP is determined, it can be divided by atmospheric pressure to estimate the VC of the chemical in the air above the mixture surface. If the composition of the mixture (in mass percent) is constant, the relative VCs of the components of the mixture will be constant (Stenzel & Arnold, 2015). This concept then is the basis for estimating unmeasured exposures using correlational analyses (linear relationships).

Workplaces can be very complex and contain multiple mixtures with common components. It is seldom possible or practical to measure a significant portion of exposure scenarios that exist in a workplace; therefore, decisions regarding exposure must be made with data collected on only a fraction of the possible exposure scenarios. Industrial hygienists have simplified this complexity and the lack of measurements by developing exposure groups. The definition of an exposure group depends on the purpose of the exposure assessment, but generally, it is a group of individuals who are exposed to the same inventory of chemicals and perform the same tasks or activities under similar exposure conditions at a comparable frequency and duration, resulting in a similar exposure distribution in each chemical.

In this work, we focus on estimating exposure in the a situation characterized by multiple mixtures containing some common chemicals at different concentrations. Because the components are at different concentrations in the various mixtures, they are not likely to be highly correlated in the air. If the workplace is under “pseudo”-equilibrium conditions, multivariate correlation among the components from the multiple sources is expected to be observed. Therefore, this approach can be used to estimate exposures to the chemicals from these multiple mixtures, either when the mixtures are present in exposure groups that were not measured or when one of the chemicals is more highly censored than the others (Stenzel & Arnold, 2015).

2.1 Limits of detection

An analytical method’s inability to quantify exposures below a measurement’s LODs provides uncertainty to exposure estimation. LODs vary based on the duration of the measurement and the chemical’s analytical method. In our setting values of the LOD are known and observable (rather than absent and thus not observable).

Scientifically, it is important to account for these values below LOD. It is possible that exposures below the LOD may be associated with detrimental health effects that cannot be investigated because we do not know the concentration of the exposure below the LOD. By accounting for censored values, we may be better able to investigate if such an association exists. In addition, low exposures may have additive or synergistic effects with other exposures experienced simultaneously. Furthermore, often exposure-based health effect studies quantify exposure for a low exposed or unexposed reference group to which higher exposed groups are compared. This reference group may be more likely to have measurements below the LOD. Perhaps most importantly, omitting values below the LOD may lead to a bias of the mean estimate. By not including values below the LOD, the mean estimate (AM or GM) is likely to be higher than was actually experienced because the lower values are not included in the calculation of the mean to pull the mean estimate down to its true value. Furthermore, as described by Groth et al. (2017), one may come to fundamentally different statistical conclusions if censored data are ignored compared to when they are included in an analysis.

2.2 Left-censored statistical methods

Scientists have proposed a variety of different statistical methods to account for left-censored variables. For occupational health studies with left-censoring, Huynh et al. (2014) compared several classical approaches including β-substitution, reverse-Kaplan Meier, and maximum likelihood. Of these approaches, the β-substitution method had the lowest RMSE and bias. However, Huynh et al. (2016) suggested that Bayesian models have advantages over classical methods such as β-substitution (Ganser & Hewett, 2010). Huynh et al. (2016) concluded that while the β-substitution method performed similarly to Bayesian methods (for bias and root mean squared error), Bayesian models provided variance estimates (important for uncertainty characterization) whereas formulas for calculating confidence intervals on the imputed β were not available for the β-substitution method.

In Groth et al. (2017), researchers expanded the results of Huynh et al. (2016), developing a method for regression where either a predictor, a response, or both, may be censored. When analyzing data from the Deepwater Horizon oil spill response and clean-up efforts, Groth et al. (2017) found that linear relationships between THC and xylene (one of the BTEXH chemicals; BTEXH stands for benzene, toluene, ethylbenzene, xylene, and n-hexane), as measured using dosimeters worn by workers, were present in many groups of workers on the Development Driller III from May 15 to July 15, 2010. As indicated above (section 2), chemical laws suggest that the relationship between the exposures to THC and each of the BTEXH chemicals should be linear in nature if there is a single source, such as crude oil. The Development Driller III was in the immediate area of the leaking wellhead and crude oil was being continuously released, so it was expected that crude oil was the primary source of exposure and a “pseudo” equilibrium existed. That is, as the volatiles in the crude oil evaporated, new crude oil surfaced to provide a new supply of volatiles. Using a hierarchical Bayesian structure, Groth et al. (2017) estimated the exposure of multiple groups of workers simultaneously to each of the BTEXH chemicals using THC as the chemical predictor. This method allowed groups with higher censoring levels or lower sample sizes to gain inference from the overall relationship in the dataset. This paper focuses on extending this method to allow for more than one chemical predictor with values below the LOD.

2.3 Multivariate Modeling

Another benefit of our modeling structure is it allows us to assess exposure to multiple chemicals through one model. If it is known that several chemicals could have linear relationships among themselves, we may gain a significant amount of knowledge from modeling all chemicals and their correlations into one modeling framework. The multivariate framework allows us to model simultaneously correlations between all chemicals included in the model. As a result, multiple linear regression equations for each chemical in the model can be derived, along with estimates of exposure to all chemicals in the model. This structure avoids the need to fit additional models to assess exposure to a chemical already included in the model.

However, using a single multivariate model to develop exposure estimates for all chemicals in the model may not be useful in all scenarios. For example, for one chemical, it may be appropriate to include two particular chemicals as predictors. But in another model of one of the chemical predictors, other chemicals not in the original model may be useful in predicting exposure. Therefore, in this paper, we assume we are primarily interested in a chemical Y given the predictors (X). But, if the multivariate model is structured in a way such that the groups of chemicals are good predictors of each other, one could use this model to generate exposure estimates for multiple chemicals simultaneously.

2.4 Multicollinearity

In this paper, we seek to use multiple predictors that are correlated with one another to estimate exposures. This situation, however, presents a potential problem because our model is parameterized based on conditional relationships and regression expressions. The inclusion of multiple highly correlated predictors in a linear regression setting creates a commonly known problem called multicollinearity (also called collinearity). High correlations among at least two predictors can lead to misleading regression estimates and inflated standard errors. Inflated standard errors are a significant problem as they may lead us to conclude that the linear relationships are not significant by inflating slope estimates. Similarly, the inflated standard errors are likely to inflate the uncertainty in the mean posterior distribution. Dormann et al. (2013) found that variables with greater than 0.7 correlation will likely create problems with statistical inference if included as predictors in a model. While 0.7 is the generally accepted threshold, others argue that researchers should try to avoid correlations above 0.5 if possible (Dormann et al., 2013; Kutner et al., 2004).

To further understand how multicollinearity may influence our model, we preformed a simulation study described in our simulation study section. For more information on multicollinearity, see Dormann et al. (2013) and Kutner et al. (2004).

3 Statistical methods

We will assume that we are primarily interested in assessing exposure estimates to a single chemical Y given several other chemicals (X). To build our model, we start with a simple linear Bayesian regression framework. Let Y_i be the natural log of the primary chemical of interest and X_i,(1) be the natural log of the first predictor of interest for observation i with i = 1, … N. Later on, we will add multiple chemical covariates, so we denote this first chemical covariate with a subscript (1) (Distribution of air measurements in the occupational setting are lognormal). We assume X_i,(1) follows a normal distribution with mean β₀,₍₁₎ and variance ${\sigma }_{(1)}^2$. Let the regression coefficient vector β_(Y|X) be the slope (β₁,_(Y|X)) and intercept (β₀,_(Y|X)) for Y | X₍₁₎. Therefore, we assume Y_i follows a normal distribution with mean β₀,_(Y|X) + β₁,_(Y|X)X_i,(1) and conditional variance ${\sigma }_{(Y|X)}^2$. To this structure, we place priors on the variance components $({\sigma }_{(Y|X)}^2,{\sigma }_{(1)}^2)$ and mean components (β₀,₍₁₎,β_(Y|X)). With traditional definitions of inverse gamma (IG()) and normal (N()) distributions as described in Gelman et al. (2013), we arrive at the following joint distribution

$$\begin{gathered} IG({\sigma }_{Y|X}^2|a,b)\times IG({\sigma }_{(1)}^2|c,d)\times N({\beta }_{0,(1)}|\theta ,{\sigma }_{\mu }^2)\times N({\mathit{\beta }}_{(Y|X)}|{\mathit{\mu }}_{\beta },{\mathbf{V}}_{\beta }) \\ \times {\displaystyle \prod _{i=1}^{N}N(Y_i|{\beta }_{0,(Y|X)}+{\beta }_{1,(Y|X)}{X}_{i,(1)},{\sigma }_{Y|X}^2)\times {\displaystyle \prod _{i=1}^{N}N(X_{i,(1)}|{\beta }_{0,(1)},{\sigma }_{(1)}^2)}}. \end{gathered}$$ (1)

In this framework, we used inverse gamma priors (IG()) on the variance components and normal priors on the mean components. Other priors are possible, and the above priors are used to allow for weakly informative priors and conjugate relationships to be used. In the above model, we also specify the values mean θ_μ and variance ${\sigma }_u^2$ in the prior for β₀,₍₁₎. Finally, we specify the values of the mean (μ_β) and variance-covariance matrix (V_β) for our prior on the regression coefficients β_(Y|X). Alternatively, one may set hyperpriors on this mean and variance-covariance matrix for β_(Y|X) to allow these parameters to be estimated. It may be of particular interest to estimate these parameters for more than one exposure group. But, for simplicity, we focus on modeling one group’s exposures.

To account for censored observations in both the response and predictor, we adjust the above model’s likelihood. Let LOD_i(X₍₁₎) be the LOD on the natural log (ln) scale for the ith observation for chemical predictor X₍₁₎ and LOD_i(Y) be the LOD for the ith observation of Y. These LODs are fixed and known prior to modeling and supplied to the model as data. Then, we separate the N observations for each variable into censored and observed sets. Define C₍₁₎ = {i : X_i,(1) ≤ LOD_i(X₍₁₎)} and C_(Y) = {i : Y_i ≤ LOD_i(Y)} as the censored sets of observations of X_i,(1) and Y respectively. Let O₍₁₎ and O_(Y) be the observed values. Using the same definitions of parameters and variables defined in equation (1), the resulting joint distribution of all model parameters including censored values is

$$\begin{gathered} IG({\sigma }_{Y|X}^2|a,b)\times IG({\sigma }_{(1)}^2|c,d)\times N({\beta }_{0,(1)}|{\theta }_{\mu },{\sigma }_{\mu }^2)\times N({\mathit{\beta }}_{(Y|X)}|{\mathit{\mu }}_{\beta },{\mathbf{V}}_{\beta }) \\ \times {\displaystyle \prod _{i\in O_{(Y)}}N(Y_i|{\beta }_{0,(Y|X)}+{\beta }_{1,(Y|X)}{X}_{i,(1)}),{\sigma }_{Y|X}^2)} \\ \times {\displaystyle \prod _{i\in C_{(Y)}}\mathrm{\Phi }\left(\frac{LO{D}_i(Y)-({\beta }_{0,(Y|X)}+{\beta }_{1,(Y|X)}{X}_{i(1)})}{{\sigma }_{Y|X}}\right)} \\ \times {\displaystyle \prod _{i\in O_{(1)}}N(X_{i,(1)}|{\beta }_{0,(1)},{\sigma }_{(1)}^2)}\times {\displaystyle \prod _{i\in C_{(1)}}\mathrm{\Phi }\left(\frac{LO{D}_i(X_{(1)})-{\beta }_{0,(1)}}{{\sigma }_{(1)}}\right)}, \end{gathered}$$ (2)

where Φ(u) denotes the cumulative density function (cdf) of a standard normal random variable at u.

To this bivariate situation described in Groth et al. (2017), we add additional chemical covariates with potential censoring. Our ultimate goal is to model a chemical response Y that is dependent on all chemical predictors (X). We will consider p chemical predictors (which are arbitrarily called X₍₁₎, X₍₂₎, etc). Let X_(k) represent one of the chemical predictors of interest (natural log scale) where k = 1, … p. We model each additional X_(k), where k = 2, … p, as conditional on the set of all X_(l), where l = 1 … k − 1, to generate multivariate model framework. Due to the conditional distributions, this model can also be written using a multivariate normal distribution framework.

To adjust the likelihood for multiple chemical covariates when modeling Y, we divide our likelihood into three likelihood components that when multiplied form the full likelihood of this multivariate model. The first component is the likelihood of our chemical response Y which is dependent on all chemical predictors X. Like in equations (1) and (2), let β_(Y|X) and ${\sigma }_{Y|\mathbf{X}}^2$ represent the vector of regression coefficients and the conditional variance respectively for the conditional expression of Y | X where now we have multiple X components. To simplify notation of the conditional means, let D_i,(Y|X) represent the row of the design matrix for the i-th observation for Y. Here the design matrix would consist of a column of 1s for the intercept and X₍₁₎, … X_(k) in columns. Therefore, we can abbreviate the mean expression for Y_i | X_i (β₀,_(Y|X) +β₁,_(Y|X)X_i,(1)+·⋯·+β_p,(Y|X)X_i,(p)) as D_i,(Y|X)β_(Y|X). To account for censored Y values, this likelihood of Y will contain a censored set C_(Y) (dependent on the LOD_i(Y)) and observed set O_(Y) as previously defined in equation (2). The second component is the likelihood of all chemical predictors other than X₍₁₎. Here each chemical X_(k) is modeled as conditional on X₍₁₎ and other chemical predictors X_(l) where l = 2, … k − 1. Let β_(k) represent the vector of all regression coefficients for the conditional expression on X_(k). Like we did for Y_i, we let D_i,(k) represent the row of the design matrix for the i-th observation for X_(k), The design matrix for X_(k) is a column of 1s followed by columns of each X_(l) where l = 1, … k − 1. This allows us to abbreviate the conditional mean of X_i,(k) as D_i,(k)β_(k). Then, we define the conditional variance of X_(k) | X₍₁₎, … X_(k−1) as ${\sigma }_{(k|1,\dots k-1)}^2$. Again as in equation (2), we consider a censored set C_(k) (with LOD_i(X_(k))) and observed set O_(k) in the likelihoods of each X_(k). Finally, the third component is the likelihood of X₍₁₎ which is dependent on its mean β₍₁₎ and variance ${\sigma }_{(1)}^2$ as previously defined in equations (1) and (2). In order to account for censoring, we use previous definitions of the observed set O₍₁₎, the censored set C₍₁₎, and LOD_i(X₍₁₎) from equation (2).

From these likelihood components, we obtain the following joint distribution of all model parameters and censored values

$$\begin{gathered} N({\beta }_{(1)}|{\mu }_{\beta ,(1)},{\gamma }_{\beta ,(1)})\times IG({\sigma }_{(1)}^2|a_{(1)},b_{(1)})\times N_{(p+1)}({\mathit{\beta }}_{(Y|\mathbf{X})}|{\mathit{\mu }}_{\beta ,(Y|\mathbf{X})},{\mathbf{V}}_{\beta (Y|\mathbf{X})}) \\ \times IG({\sigma }_{(Y|\mathbf{X})}^2|a_{(Y)},b_{(Y)})\times {\displaystyle \prod _{k=2}^{p}IG({\sigma }_{(k|1,\dots k-1)}^2|a_{(k)},b_{(k)})}\times {\displaystyle \prod _{k=2}^p{N}_k({\mathit{\beta }}_{(k)}|{\mathit{\mu }}_{\beta ,(k)},{\mathbf{V}}_{\beta ,(k)})} \\ \times {\displaystyle \prod _{i\in O_{(Y)}}N(Y_i|{\mathbf{D}}_{i,(Y|\mathbf{X})}{\mathit{\beta }}_{(Y|\mathbf{X})},{\sigma }_{(Y|\mathbf{X})}^2)}\times {\displaystyle \prod _{i\in C_{(Y)}}\mathrm{\Phi }\left(\frac{LO{D}_i(Y)-{\mathbf{D}}_{i,(Y|\mathbf{X})}{\mathit{\beta }}_{(Y|\mathbf{X})}}{{\sigma }_{(Y|\mathbf{X})}}\right)} \\ \times {\displaystyle \prod _{k=2}^p{\displaystyle \prod _{i\in O_{(Y)}}N(X_{i(k)}|{\mathbf{D}}_{i,(k)}{\mathit{\beta }}_{(k)},{\sigma }_{(k|1,\dots k-1)}^2)}}\times {\displaystyle \prod _{k=2}^p{\displaystyle \prod _{i\in C_{(k)}}\mathrm{\Phi }\left(\frac{LO{D}_i(X_{(k)})-{\mathbf{D}}_{i(k)}{\mathit{\beta }}_{(k)}}{{\sigma }_{(k|1,\dots k-1)}}\right)}} \\ \times {\displaystyle \prod _{i\in O_{(1)}}N(X_{i(1)}|{\beta }_{(1)},{\sigma }_{(1)}^2)}\times {\displaystyle \prod _{i\in C_{(1)}}\mathrm{\Phi }\left(\frac{LO{D}_i(X_{(1)}-{\beta }_{(1)})}{{\sigma }_{(1)}}\right)}, \end{gathered}$$ (3)

where μ_β,(1) and γ_β,(1) are the mean and variance respectively of β₍₁₎. We let all variances and conditional variances follow inverse gamma distributions with shape parameters a₍₁₎, a₍₂₎, … a_(k), a_(Y) and scale parameters b₍₁₎, b₍₂₎, … b_(k), b_(Y). In practice, we usually use the same prior for each variance or conditional variance, though the estimated values of each variance are allowed to be different from each other (i.e. we do not assume all chemicals have the same variance). We define μ_β,(Y|X) as the mean vector for regression coefficients β_(Y|X) (of length p + 1) and V_β,(Y|X) as the (p + 1) × (p + 1) variance-covariance matrix for β_(Y|X). Finally, we define each μ_β,(k) as the mean vector for the regression coefficients β_(k) and V_β,(k) as the k × k variance-covariance matrix of β_(k). For β_(k), we will consider k = 2, … p, and define a separate variance-covariance matrix and mean vector for each k.

In both our simulation and real data analysis, we set shape and scale parameters for all variance terms (a₍₁₎, … a_(p), b − (1), … b_(p) or a, b, c, and d in the bivariate framework of equations (1 or 2)) to 0.01 within our inverse gamma priors on the variances $({\sigma }_{(Y|X)}^2,{\sigma }_{(k|1,\dots k-1)}^2)$ for k = 2, … p and ${\sigma }_{(1)}^2$). We assume all regression coefficients are independent with variances of 100,000 (i.e. γ_β,(1), V_β,(k) with k = 2, … p, and V_β,(Y|X) are equal to the identity matrix times 100,000). We also assume that the regression coefficients are sampled from the normal distribution with mean of 0 (i.e.μ_β,(1), μ_β,(k) for k = 1, … p, and μ_β,(Y|X) are set to vectors of 0) for all regression parameters and mean estimates (β₍₁₎, β_(k) where k = 2, … p, and β_(Y|X)). These weekly informative prior settings allow the data to drive the inference.

Many possible extensions of (3) exist. For example, if we were interested in modeling more than one group of workers at the same time and allowing groups with minimal information (e.g. smaller sample sizes and/or high censoring) to be informed by an overall regression relationship, we may add a hierarchical structure and hyperpriors across each set of β coefficients. Furthermore, researchers may be interested in modeling individual level variability if subjects had more than one measurement. The flexible nature of the Bayesian regression framework allows us easily to add in random effects for the individual to the above model.

3.1 Posterior inference

In a non-censored setting, all posterior inference of marginal means and variances extends from conditional means and variance formulas. As previously mentioned, this model with p chemical predictors and primary response Y may be represented through multivariate normal framework. Let μ_Y and ${\sigma }_{(Y)}^2$ be the marginal mean and variance respectively of Y. Similarly, for each X_(k) with k = 1, … p, let X_(k) have marginal mean μ_(k) and marginal variance ${\sigma }_{(k)}^2$. Then, the set of all X and Y would be modeled multivariate normal with a (p + 1) length vector of marginal means (μ₍₁₎, μ₍₂₎, … μ_(p), μ_(Y)), and a (p + 1) × (p + 1) variance-covariance matrix. This symmetric variance-covariance matrix would have marginal variances of all Xs followed by the marginal variance of $Y({\sigma }_{(1)}^2,{\sigma }_{(2)}^2,\dots ,{\sigma }_{(p)}^2,{\sigma }_{(Y)}^2)$ on the diagonal. Covariances between each set of variables would be found on the off-diagonals.

From this framework, it is easy to derive relationships between conditional and marginal variables. For example, for the response Y, let μ_(Y|X) be the conditional mean of Y|X. Therefore, the marginal mean (μ_(Y)) and variance ( ${\sigma }_{(Y)}^2$) for the response Y are defined by

$$\mu (Y)={\mu }_{(Y|\mathbf{X})}-{\mathbf{B}}^T{\sum }_{(\mathbf{X})}{ }^{-1}(\mathbf{X}-{\mathit{\mu }}_{(X)}){\sigma }_{(Y)}^2={\sigma }_{(Y|\mathbf{X})}^2+{\mathbf{B}}^T{\sum }_{(\mathbf{X})}{ }^{-1}\mathbf{B}$$ (4)

where B is a vector of length p of the covariances of Y with each X and Σ_(X) is an p × p variance-covariance matrix with variances of all Xs on the diagonal and covariances on the off-diagonals. It should be noted that we can obtain marginal means and variances for each chemical in the model, not just Y. Therefore, we can obtain a multiple linear regression expression for every chemical included in the model (with all other chemicals as predictors). This allows us to estimate exposure to multiple chemicals simultaneously while accounting for correlations among chemicals.

Posterior inference for the parameters of interest in the censored setting uses an overarching Gibbs sampler as described in Gelfand et al. (1992). In the Bayesian setting, we treat the censored values as parameters in our model. Therefore, within each iteration j (j = 1, … M), we can first sample these censored values using the full conditionals (with parameters defined by the previous iteration) of each X_(k) and Y. This fills in the censored values, giving us a full dataset. Second, using the full dataset (including the previously censored X_(k) values), we can sample the conditional means and variances using full conditional distributions. We repeat these steps within each iteration until convergence of the parameters is met.

Convergence of this model is immediate (well within 5,000 iterations) as assessed by Gelman Rubin diagnostics, trace plots, and Monte Carlo standard error (MCSE). To account for additional uncertainty where higher censoring levels exist, we recommend running the chain long enough to allow the model to fully explore the parameter space. In all cases, we provide 25,000 iterations after 5,000 iterations of burn-in to ensure convergence of our model. A more formal description of the convergence of our model including assessments of autocorrelation, is provided in the supplementary materials.

Inference for GMs, AMs, and geometric standard deviations (GSDs) stem from the posterior samples of the marginal means and variances. First, through the conditional formulas, we calculate the marginal means and variances for each iteration. Then, we obtain inference on the GM of each chemical by exponentiating the posterior samples of the marginal means previously found for each chemical. The variances reported in the model are for the natural log of each variable. Once marginal standard deviations are found, we simply exponentiate them to find the GSD. The AMs are derived using the posterior samples of the GSD and GM of each variable and calculated using $AM=GM\times e^{\frac{1}{2}{(\mathit{log}(\mathit{GSD}))}^2}$.

The above framework can be easily coded in Openbugs or RJAGS for a specific number of chemicals. A sample RJAGS code for 3 chemicals is provided in the supplementary materials (Plummer, 2014). The Gibbs sampler for any specific number of chemicals written in R described above is also provided in the supplementary materials.

3.2 Posterior predictive model comparisons: WAIC

In any model, there may be multiple chemicals to consider as chemical covariates. We need a method to decide if we should add an additional chemical covariate to the model. We want to compare the ability of each model (with different number of chemical covariates) to predict the real data provided to the model. This method must account for censoring in any of the predictors, in the chemical response of interest, or in both the predictions and the response.

Watanabe (2010) developed a criteria known as widely applicable information criterion (WAIC) that is based on the likelihood of each observation (i) over a set of iterations j (j = 1, …, M) that can be used to compare models fit to the same datasets. The use of the likelihood allows us to also account for censored observations. Other methods such as Gelfand and Ghosh’s D-statistic does not allow us to account for censored observations because it relies on a statistic that compares points generated from the model to the true data values (Gelfand & Ghosh, 1998). The true censored measurements are not known in our case, so using this statistic would require us to ignore censored response values.

In the multivariate framework, the full likelihood of each observation consists of three primary components as modeled in equation (3). Again, the components include the likelihood for of Y | X, the likelihoods for each X_i,(k) | X_i,(k−1), … X_i,(1), and the likelihood of X_i,(1). These likelihood components when multiplied form the full likelihood for a particular observation i. As in equation (3), a censored Y_i would have likelihood $\mathrm{\Phi }\left(\frac{LO{D}_i(Y)-{\mathbf{D}}_{i,(Y|\mathbf{X})}{\mathit{\beta }}_{(Y|\mathbf{X})}}{{\sigma }_{(Y|\mathbf{X})}}\right)$ while an observed values in set O_Y would have likelihood $N(Y_i|{\mathbf{D}}_{i,(Y|\mathbf{X})}{\mathit{\beta }}_{(Y|\mathbf{X})},{\sigma }_{Y|\mathbf{X}}^2)$. Similarly, the likelihood of a censored X_i,(k) for any k, k = 2, … p, would be $\mathrm{\Phi }\left(\frac{LO{D}_i(X_{(p)}-{\mathbf{D}}_{i,(k)}{\mathit{\beta }}_{(k)})}{{\sigma }_{k|k-1,\dots 1}}\right)$. The likelihood for an observed X_i,(k) would be $N(X_{i,(k)}|{\mathbf{D}}_{i,(k)}{\mathit{\beta }}_{(k)},{\sigma }_{(k|k-1,\dots 1)}^2)$. Finally, the likelihood for a censored X_i,(1) is $\mathrm{\Phi }\left(\frac{LO{D}_i(X_{(1)})-{\mathit{\beta }}_{0,(1)}}{{\sigma }_1}\right)$ while an observed X_i,(1) would have likelihood $N(X_{i,(1)}|{\beta }_{0,(1)},{\sigma }_{(1)}^2)$.

The full likelihood is calculated using parameter estimates at each iteration j, where M is the total iterations sampled after burn-in (the number of posterior samples of each parameter). These parameter estimates include censored X_i, regression coefficients (β₀,₍₁₎, β₀,₍₂₎ etc.), and variances $({\sigma }_{(1)}^2,{\sigma }_{(2|1)}^2,\dots ,{\sigma }_{(p|p-1,\dots 1)}^2,{\sigma }_{(Y|\mathbf{X})}^2)$. A censored chemical measurement X_i,(k) may depend on likelihoods of other X_i for observation i as well as other parameters.

3.2.1 WAIC of full likelihood

WAIC involves two statistics that rely off the likelihoods, known as LPPD, or the log posterior predictive density, and P, the penalty term. The quantity LPPD can be thought of as the goodness of fit term. P is the penalty for more model parameters and greater variation in the likelihoods. Let L_ij be the full likelihood formed using the three components previously defined for a particular measurement i calculated using parameter estimates at iteration j. Then, LPPD and P are defined as follows:

$$\mathit{LPPD}={\displaystyle \sum _{i=1}^N\log \left(\frac{1}{M}{\displaystyle \sum _{j=1}^M{L}_{ij}}\right)}P={\displaystyle \sum _{i=1}^N\text{Var}(\log (L_{ij}))},$$ (5)

where here we provide the penalty term (which we call P₂ to distinguish it with the penalty defined by Watanabe (2010)) recommended by Gelman et al. (2014). The variance (Var) is over the M iterations for each observation i. The penalty developed by Watanabe (2010), which we will call P₁ is defined as ${\displaystyle {\sum }_{i=1}^{N}2\left(\log (\frac{1}{M}{\displaystyle {\sum }_{j=1}^M{L}_{ij}})-\frac{1}{M}{\displaystyle {\sum }_{j=1}^M\log (L_{ij}})\right)}$ but usually is close to that defined by Gelman et al. (2014).

Since we want to maximize the mean likelihood for each observation, we want to maximize LPPD. We want to minimize the penalty term P since we want variability in parameter estimates to be small, leading to lower variability in the likelihood of each observation. To develop a deviance-like statistic, WAIC is calculated using the expression WAIC=−2(LPPDP). Lower values of WAIC are preferred (Watanabe, 2010).

In the supplementary materials, we describe an additional type of WAIC, the WAIC of Y. The WAIC of Y may be particularly useful if the primary interest is in modeling the response. See the supplementary materials for more information.

3.2.2 Model Comparisons

Since the components in the likelihood vary slightly between WAIC and WAIC_Y of the full likelihood, we perform two different model comparisons in this paper, one with each WAIC form. WAIC of the full likelihood allows us to identify if the multivariate nature of the model is beneficial for all chemicals included in the model (not just Y) whereas WAIC_Y focuses on if the model is beneficial/preferred when modeling Y only.

In practice, one may want to compare the multivariate model to a bivariate model or ANOVA model (here defined as an intercept only regression model) accounting for censoring (or a combination of models). The calculations of WAIC remain the same, but the likelihood changes for these models. We will assume similar notation for censored and observed values (like in equation (2) and (3)). For a bivariate model of Y and X, let μ_Y |_Xi be the expression for Y_i | X_i (mean expression is α₀ + α₁X_i) where α₀ is an intercept, α₁ is the slope, and X_i is the chemical covariate at observation i. Let ${\sigma }_{Y|X}^2$ be the variance of Y | X under the bivariate model. Then, the likelihood of a censored Y is $\mathrm{\Phi }\left(\frac{LO{D}_i(Y)-{\mu }_{Y|X_i}}{{\sigma }_{Y|X}}\right)$ while an observed observation in set O_Y would have likelihood $N(Y_i\text{|}{\mu }_{Y|X_i}\text{,}{\sigma }_{Y|X}^2)$. Then X would be modelled like the X₍₁₎ component above with an mean estimate β₀,₍₁₎ and variance estimate ${\sigma }_{(1)}^2$. For an ANOVA famework (an intercept only regression model), let μ_Y and ${\sigma }_Y^2$ are the marginal mean and marginal variance of Y respectively. Then the likelihood of a censored Y would be $\mathrm{\Phi }\left(\frac{LO{D}_i(Y)-{\mu }_Y}{{\sigma }_Y}\right)$ and the observed likelihood of Y would be $N(Y_i|{\mu }_Y\text{, }{\sigma }_Y^2)$. Modeling other variables as ANOVAs would have similar forms for the likelihood components.

4 Simulation studies

In practice, it is important to assess if additional chemical predictors will add meaningful information. In order to formally test if our multivariate model provides more meaningful information with additional covariates, we performed a series of simulation studies where we compare our multivariate modeling framework to simpler models.

In addition to comparing models, we also tested the multivariate model’s 95% coverage and observed the 95% width of various parameters. As part of this simulation, we also investigated how multicollinearity may influence the 95% CI width and coverage rates.

4.1 Data development

In all simulation studies, we assume the true model contains three chemicals. The response Y would be best modeled by two chemical covariates. To generate data to fit this modeling scenario, we generated 100 observations (i; N=100) for each X₍₁₎, X₍₂₎ and Y. Specifically, we modeled $X_{i(1)}\stackrel{\mathit{iid}}{~}N(2.6,2.25)$, $X_{i(2)}\stackrel{\mathit{iid}}{~}N(2.75+0\ast X_{i(1)},0.64)$, and $Y_i\stackrel{\mathit{iid}}{~}N(1.25+0.35X_{i,(1)}+0.25X_{i,(2)},0.36)$. This particular dataset assumes that both X₍₁₎ and X₍₂₎ contribute significantly to the estimation of Y, but X₍₁₎ and X₍₂₎ are not correlated to avoid multicollinearity concerns (in our multicollinearity simulation we change this). We also assume that X₍₁₎ contributes slightly more than X₍₂₎. The coefficients chosen here were made based on data commonly presented in environmental health studies (variables on natural log scale).

After developing the raw data, we imposed censoring on each variable by censoring all values below particular quantiles of each variable. In this context, censoring values means labeling an indicator as censored, and changing the value to missing. We imposed censoring on the raw dataset using all possible combinations of 25, 50 and 75 percent censoring for Y, X₍₁₎, and X₍₂₎. We selected this range of censoring levels to reflect typical censoring values seen in industrial hygiene. For example, censoring of airborne chemical exposures during the Deepwater Horizon oil spill response and clean up varied from 0 to as much as 100%. We consider each of these datasets with different imposed censoring levels to be a separate modeling scenario.

As indicated earlier, the LOD of a measurement depends on the analytical method and the duration. In practice, measurements are taken over a variety of durations; thus for a single chemical analyzed by a single method, multiple LODs may be observed across measurements. We also developed LODs for each chemical by sampling the LODs from a uniform distribution defined by the chemical’s censoring status. For a given variable Z at observation i we determined its censored status. For censored values, we sampled from Unif(Z_i + 0.1, quantile(Z) + 0.2) and for observed values, we sampled from Unif(min(Z) −0.1, Z_i −0.1). For censored values, we chose the upper bound to be a value slightly above the quantile of Z (quantile: value below which censoring occurs). This allowed LODs to occur roughly in a band below a censoring value which provides a range of LODs in each chemical (allowing for multiple LODs). Censored values had LODs higher than the original simulated datapoint while observed values had LODs below the real simulated datapoint values. LODs are not used in our model formulation if the values are observed, so this definition of LODs is sufficient for our purposes as long as the LODs are less than the real datapoint values we simulated (and classified as observed).

We also ran a completely non-censored modeling scenario to ensure our model would be preferred to simpler models under a completely observed data scenario. We maintained the same sampling strategy for LODs here, but using only the observed LOD sampling strategy.

4.2 Model comparison simulation

We have two primary purposes of this modeling framework. First, we are interested if our multivariate model is preferred over simpler model combinations with respect to WAIC for all chemicals included in the model (both Y and all X). Secondly, we are interested if the multivariate framework leads to lower WAIC_Y compared to simpler models with fewer covariates. We consider the best model as the model with the lowest WAIC and/or WAIC_Y, reflecting that the model is a good fit to the data while not adding unnecessary complexity. To test how well our model meets these two goals, we performed two sets of model comparisons. On our first set of models, we calculated WAIC for the full likelihood including all chemical predictors and responses. On a second set of models, we assessed WAIC_Y. The methods and results of the simulation with WAIC_Y are included in the supplementary materials.

4.2.1 WAIC for full likelihood

To each unique dataset, we fit a series of five separate modeling frameworks that each account for censored observations. The first model was the (true) multivariate model as described above (in section 4.1). We will call this the 3-variable model. Frameworks 2, 3, and 4 involved a bivariate model and an ANOVA (intercept only regression) that when multiplied allowed us to model all three variables. Framework 2 modeled X₍₁₎ and Y using a bivariate model and modeled X₍₂₎ using an ANOVA modeling framework. Modeling framework 3 modeled X₍₂₎ and Y with a bivariate model, and used an ANOVA model for X₍₁₎. Modeling framework 4 modeled X₍₁₎ and X₍₂₎ using a bivariate model and used an ANOVA model for Y. Framework 5 used an ANOVA model for each variable individually and multiplied them to form the full modeling framework. Modeling frameworks 2-5 assume that the models for the different components are independent.

We calculated WAIC for each of these frameworks by calculating the likelihood components (for X₍₁₎, X₍₂₎, and Y) as described above (section 3.2).

4.2.2 Model comparison simulation results

WAIC values for the full likelihood model comparison are shown in Table 1. WAIC values should only be compared to models fit to the same dataset, and therefore WAIC values should only be compared across a given row of Table 1.

Table 1.

WAIC statistics for the full likelihood by model type for various different datasets with different degrees of censoring in X₍₁₎, X₍₂₎, and Y. WAIC of the full likelihood values are reported using the same model seed.

			WAIC of Full Likelihood
Modeling Framework			1	2	3	4	5
Percent Censoring			3-Variable Model	Bivariate ANOVA	Bivariate ANOVA	Bivariate ANOVA	ANOVAs
X(1)	X(1)	Y	(X(1),X(2),Y)	(X(1),Y)×(X(2))	(X(2),Y)×(X(1))	(X(1),X(2))×(Y)	(X(1))×(X(2))×(Y)
0	0	0	799.3	814.5	865.5	874.3	875.7
25	25	25	762.3	776.2	819.6	828.1	826.3
25	25	50	736.6	749.3	795.0	802.3	800.5
25	25	75	691.4	699.0	735.0	739.5	737.6
25	50	25	737.9	752.3	797.2	803.9	802.4
25	50	50	712.6	725.4	772.5	778.1	776.6
25	50	75	666.1	675.1	711.7	715.3	713.8
25	75	25	688.4	695.3	742.2	747.3	745.5
25	75	50	659.2	668.5	715.9	721.5	719.7
25	75	75	612.0	618.2	655.1	658.7	656.8
50	25	25	715.4	728.0	766.0	774.2	772.6
50	25	50	685.8	695.6	741.3	748.4	746.8
50	25	75	641.8	648.3	681.2	685.6	684.0
50	50	25	691.6	704.1	743.5	749.7	748.7
50	50	50	660.5	671.7	718.8	723.9	722.9
50	50	75	616.5	624.4	658.0	661.0	660.1
50	75	25	641.3	647.2	688.5	693.6	691.8
50	75	50	607.1	614.8	662.3	667.8	666.0
50	75	75	561.9	567.5	601.4	605.0	603.1
75	25	25	619.1	628.7	667.3	675.9	673.8
75	25	50	594.0	601.9	642.5	650.1	648.0
75	25	75	538.1	544.0	582.5	587.2	585.2
75	50	25	593.9	604.8	644.7	651.4	649.9
75	50	50	569.6	578.1	620.0	625.6	624.2
75	50	75	513.4	520.1	559.2	562.8	561.3
75	75	25	540.3	547.8	589.8	594.7	593.0
75	75	50	513.2	521.1	563.5	569.0	567.2
75	75	75	456.9	463.2	502.7	506.1	504.3

To ensure our model framework was set up correctly, we ran WAIC for the completely observed scenario (percent censoring of 0). The WAIC values in this scenario indicated that our 3-variable model would be preferred as expected and designed. Similarly, results of our model comparison across the scenarios with different percent censoring levels showed that the 3-variable model consistently had the lowest WAIC of the modeling frameworks tested. This result demonstrated that the multivariate model had the best fit given the complexity of the models tested (which matches how we designed the simulation), even under various censoring levels.

As expected, modeling framework 2 (Bivariate (X₍₁₎,Y) ANOVA(X₍₂₎)) had the second lowest WAIC across all model scenarios. Modeling frameworks 4 and 5 performed poorly, as expected, since the modeling frameworks failed to account for correlation between either chemical predictor and response Y.

4.3 Coverage and multicollinearity simulation

In order to understand our model’s ability to develop parameter estimates that resemble the true parameters we set, we ran a simulation study to estimate the 95% coverage of the regression coefficients for (β₀,₍₁₎, β₀,₍₂₎,β₁,₍₂₎, β₀,_(Y|X), β₁,_(Y|X), β₂,_(Y|X)) and variances $({\sigma }_{(1)}^2,{\sigma }_{(2|1)}^2,{\sigma }_{(Y|\mathbf{X})}^2)$. First, we generated 1000 different datasets for each censored combination (including a scenario with no censored observations), using the characteristics described in section 4.1 (i.e. β₀,₍₁₎ = 2.6, β₀,₍₂₎=2.75, β₁,₍₂₎ = 0, β₀,_(Y|X) = 1.25, β₁,_(Y|X) = 0.35, β₂,(Y|X)=0.25, ${\sigma }_{(1)}^2=2.25$, ${\sigma }_{(2|1)}^2=0.64$, and ${\sigma }_{(Y|\mathbf{X})}^2=0.36$). Then, we fit our 3-variable multivariate model to each dataset and obtained 95% CIs for the regression coefficients and variances. For each of the 1000 runs, we identified whether the true value of each parameter of interest was contained within the 95% CI. 95% coverage was defined as the percentage of these CIs that contained the true parameter value. We repeated this process for each separate dataset (with different censored combinations of X₍₁₎, X₍₂₎,and Y).

4.3.1 Multicollinearity simulation

To test how our 3-variable model responded to the presence of multicollinearity, we repeated the coverage analysis on several different modeling scenarios with different correlations between X₍₁₎ and X₍₂₎. In the initial simulation study described above, the correlation between X₍₁₎ and X₍₂₎ was assumed to be 0. In addition to these results, we also ran a series of scenarios using all of the earlier censoring combinations of X₍₁₎, X₍₂₎,and Y with the correlation between X₍₁₎ and X₍₂₎ adjusted to 0.25, 0.50, and 0.75. Only the β₁,₍₂₎ was altered to adjust for the different correlations.

For each unique censoring level and correlation level combination, we assessed 95% coverage of the regression coefficients and variances using 1000 different generated datasets. In addition, we obtained the median posterior 95% CI width of each of the regression coefficients.

4.3.2 Coverage and multicollinearity simulation results

Coverage probability are provided in Table 2. To show our model worked correctly, we reported the coverage probability for a scenario with no censored data points (completely observed data). All coverage levels, as expected were near 95% in all parameters.

Table 2.

Coverage and median 95% CI width for different degrees of censoring in X₍₁₎, X₍₂₎, and Y when the correlation between X₍₁₎ and X₍₂₎ is 0.00

Percent Censoring			95% Coverage Probabilities									Median Posterior 95% CI Width
			Regression Coefficients						Variances			Regression Coefficients
Y	X(1)	X(2)	β0,(1)	β0,(2)	β1,(2)	β0,(Y|X)	β1,(Y|X)	β2,(Y|X)	${\sigma }_{(1)}^2$	${\sigma }_{(2|1)}^2$	${\sigma }_{(Y|\mathbf{X})}^2$	β0,(1)	β0,(2)	β1,(2)	β0,(Y|X)	β1,(Y|X)	β2,(Y|X)
0	0	0	94.3	95.8	95.3	94.2	94.6	94.3	95.2	94.9	94.0	0.59	0.64	0.22	0.94	0.16	0.29
25	25	25	92.6	95.8	94.9	95.7	95.2	95.4	83.0	90.2	91.7	0.68	0.66	0.22	1.12	0.19	0.33
25	25	50	92.6	89.4	95.5	94.5	95.9	94.6	82.9	47.1	93.0	0.68	0.86	0.28	1.04	0.19	0.31
25	25	75	92.6	40.5	95.5	74.1	95.8	80.0	83.2	1.1	94.6	0.68	1.62	0.47	0.90	0.19	0.27
25	50	25	62.7	95.2	95.2	92.9	87.1	95.9	33.5	89.9	93.8	0.91	0.58	0.20	1.13	0.18	0.34
25	50	50	61.9	86.5	95.2	84.6	86.9	94.5	33.8	48.3	94.0	0.91	0.76	0.25	1.05	0.18	0.32
25	50	75	62.3	27.3	95.9	44.8	86.6	81.2	33.9	1.5	94.9	0.91	1.48	0.42	0.91	0.19	0.28
25	75	25	1.0	95.5	95.2	62.9	40.4	95.1	1.9	91.2	95.8	1.85	0.45	0.18	1.21	0.18	0.37
25	75	50	1.0	78.9	95.0	43.1	39.4	95.6	1.9	50.1	95.0	1.85	0.60	0.22	1.13	0.18	0.35
25	75	75	1.1	7.7	94.1	8.8	41.5	83.2	1.7	1.8	95.3	1.85	1.26	0.36	0.96	0.18	0.31
50	25	25	92.7	95.7	95.2	79.1	82.5	91.8	81.2	89.7	65.5	0.68	0.66	0.22	1.56	0.25	0.43
50	25	50	92.4	89.4	95.6	88.1	82.2	94.8	81.2	46.7	68.9	0.68	0.86	0.28	1.46	0.26	0.40
50	25	75	92.7	39.8	95.1	97.2	84.2	92.6	82.1	1.2	73.5	0.68	1.63	0.47	1.26	0.26	0.35
50	50	25	58.7	94.9	95.6	92.7	96.4	92.5	29.7	89.9	72.4	0.94	0.57	0.20	1.54	0.24	0.43
50	50	50	58.8	85.7	94.3	95.8	97.1	95.7	29.5	47.7	74.8	0.94	0.75	0.25	1.44	0.24	0.40
50	50	75	58.4	25.1	96.3	94.2	96.1	92.3	30.0	1.6	79.7	0.94	1.48	0.42	1.23	0.25	0.35
50	75	25	0.8	95.0	95.1	94.5	84.9	92.4	1.0	90.9	84.6	1.94	0.44	0.17	1.56	0.22	0.46
50	75	50	0.9	77.5	94.9	87.5	84.6	94.2	0.9	50.4	86.2	1.94	0.59	0.22	1.45	0.23	0.43
50	75	75	0.6	4.9	94.8	54.1	85.0	91.7	0.9	1.8	89.2	1.94	1.26	0.36	1.22	0.23	0.37
75	25	25	92.5	95.7	94.9	23.0	40.2	83.8	81.7	89.8	16.8	0.68	0.66	0.22	3.18	0.48	0.73
75	25	50	92.6	89.4	95.1	27.7	40.3	88.3	82.1	47.0	17.9	0.68	0.86	0.28	3.02	0.48	0.68
75	25	75	92.6	39.1	95.1	43.6	43.0	95.5	81.8	1.1	24.3	0.68	1.65	0.47	2.62	0.49	0.58
75	50	25	56.5	95.4	95.7	38.6	59.3	84.3	29.1	90.0	22.2	0.96	0.57	0.20	3.11	0.45	0.74
75	50	50	56.7	85.7	94.8	44.8	59.7	88.6	29.0	46.7	24.0	0.96	0.75	0.25	2.92	0.46	0.69
75	50	75	56.4	24.6	95.8	68.3	61.7	95.6	29.3	1.1	30.5	0.96	1.49	0.43	2.52	0.46	0.58
75	75	25	0.4	95.1	95.0	81.9	95.4	85.6	0.5	90.8	37.5	2.04	0.43	0.17	2.94	0.40	0.77
75	75	50	0.4	77.9	95.3	88.6	95.2	89.9	0.6	50.2	40.2	2.04	0.58	0.22	2.74	0.39	0.72
75	75	75	0.3	4.4	94.6	98.4	95.8	96.2	0.5	1.8	47.7	2.05	1.26	0.36	2.32	0.40	0.61

Results when censoring was introduced revealed that as censoring levels increased, coverage decreased for the intercepts. As censoring in X₍₁₎ increased (holding censoring constant in both X₍₂₎ and Y) for example, we saw coverage of β₀,₍₁₎ decrease. Similarly, as censoring in X₍₂₎ increased (holding censoring constant in both X₍₁₎ and Y), the coverage for the intercept β₀,₍₂₎ decreased.

Trends in coverage for the regression coefficients associated with Y (β_(Y|X)) are related to the graphical region of the plot of Y and X where the censored points are being estimated. To better understand the influence of the estimated censored values, Figure 1 shows a scatter plot with predictor X and response Y. In this graphic, we assume that the LODs of X and LODs of Y were each at a particular value, represented by the dark solid lines. These lines divide our graphic into 4 regions, and each region corresponds to a different censored and observed combination of the variables X and Y. For example, the upper right hand region contains observed X and Y coordinate pairs while the lower left region contains coordinate pairs where both X and Y are censored. From this graphic, it is easy to see that the region where points are estimated will influence the overall regression estimates. For example, if we estimate many censored values for Y where X is observed (for a range of observed X values), and don’t estimate many points in other regions, we are likely to see the regression line become flatter.

Figure 1.

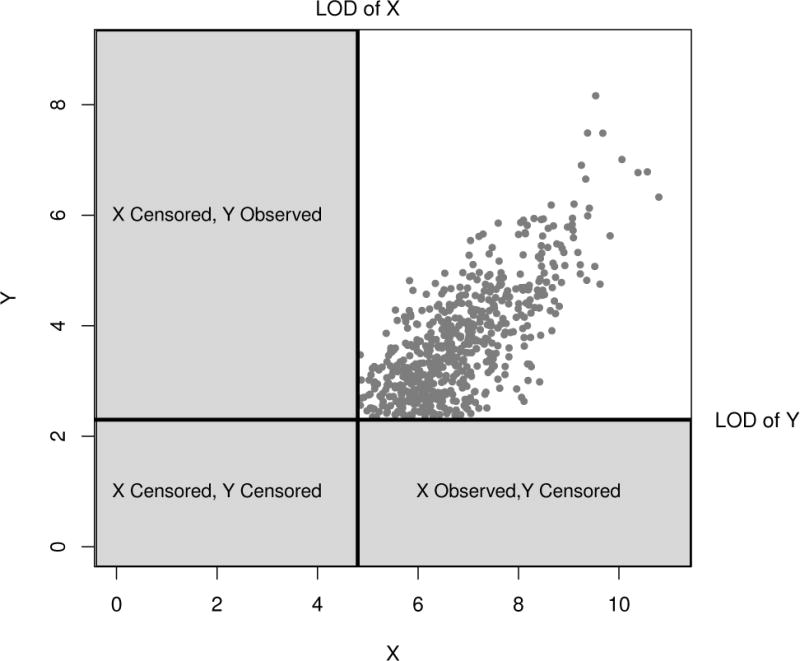
Graphical representation of regression with censoring in both X and Y. This graphic demonstrates that knowing the censoring status of both the predictor X and response Y allows us to know the region in which censored data points will be estimated. The locations where points will be estimated are important because it will influence the slope and intercept of the regression line.

Coverage of β₁,_(Y|X), the slope coefficient for X₍₁₎ depended greatly on the censoring of both X₍₁₎ and Y (Table 2). If X₍₁₎ and Y had the same censoring levels, coverage of this coefficient was around 95% regardless of the amount of censoring. However, when there were differences in the censoring levels, coverage increasingly dropped the further apart the censoring became. Referring again to Figure 1, if censoring levels were different in X and Y, we would be more likely to estimate points in the region where only X₍₁₎ is censored (Y observed) or only Y is censored (X₍₁₎ observed)in the coordinate pair. Estimating values in these two regions will be likely pull the regression line (either up or down depending on the region) and therefore lead to regression estimates that differ from the true values. Coverage of β₂,_(Y|X), the slope coefficient for X₍₂₎ performed similarly and was dependent on censoring in both X₍₂₎ and Y. Since, an intercept coefficient changes with any changes in the slope, whenever either of the slopes coverage dropped, we also saw drops in coverage for β₀,_(Y|X).

The variances also showed reduced coverage at higher censoring levels in the chemical of interest. For example, as censoring increased in X₍₂₎, the coverage of ${\sigma }_{(2|1)}^2$ decreased. This result is expected because we expect greater uncertainty when we have to estimate more censored values. All median posterior estimates of the variances when CIs did not contain the true variance were higher than the true variance (not shown). The conditional variance for Y | X did not decrease as quickly. This result is likely related to information being provided from each X, and therefore, this statistic is partially dependent on censoring in each X.

The coverage for the slope of X₍₁₎ in the equation for X₍₂₎ (β₁,₍₂₎), remained relatively constant regardless of censoring. The slope we used to generate the original data was a slope of 0. As censoring increased, the CI width became larger (due to increased variances). When the censoring differed, resulting in one region in Figure 1 to have more influence on the slope than the other region, the center of the CI changed and the width of the CI increased, leading us to still capture 0 most of the time. This led to the high coverage.

While coverage may suffer greatly at high censoring levels, we do not necessarily expect that the estimates from the model to be close to the truth with high levels of censoring. With increased censoring, we fundamentally change the dataset and introduce additional parameters (the censored values) we need to estimate. With each censored value, we also introduce an LOD. These LODs greatly limit the values that can be estimated and may lead to changes in the model parameters. Therefore, our the CIs will be unable to capture the original true model parameters.

Tables of the 95% CI width and coverage probabilities for different correlation levels between X₍₁₎ and X₍₂₎ are provided in the supplementary materials. Results indicate that the 95% CI width for the regression coefficients of β₁,_(Y|X) and β₂,_(Y|X) inflated as the correlation increased. While censoring did increase the width of the 95% CI, the increase in the width of the 95% CI from multicollinearity (increasing the correlation between X₍₁₎ and X₍₂₎) did not appear to be moderated by censoring level. Coverage probabilities were not dramatically different between correlation levels.

5 Preliminary analysis: Deepwater Horizon oil spill response and clean-up efforts

Approximately 5 million barrels of oil were released into the Gulf of Mexico as a result of the Deepwater Horizon oil spill. In the months following the spill, over 50,000 workers were involved in the response and clean-up efforts. Crude oil releases potentially harmful chemicals into the air including the THC group of chemicals, specifically the BTEXH chemicals. In this illustration, crude oil is expected to be the primary source of exposure to these chemicals. As a part of the National Institutes for Environmental Health Science’s Gulf Longterm Follow-up Study (GuLF STUDY), researchers are working to quantify several of these airborne chemical exposures for these workers, and investigate if any association exists with detrimental health outcomes in this population (Kwok et al., 2017).

In this data example, we are interested in developing a model to estimate hexane exposure from July 16, 2010 to September 30, 2010 on the Ocean Intervention III, a vessel involved in the response and clean-up effort by deploying a remotely operated vehicle (ROV). One of the BTEXH chemicals is n-hexane (called hexane from now on) which is important to estimate because hexane has been associated with neuropathology (Ritchie et al., 2001). Furthermore, in the GuLF STUDY, hexane was not always measured for many scenarios that were measured for THC and BTEX, so it’s exposure level needs to be approximated using these other chemicals. Also of interest are exposures for toluene and xylene, as these chemicals have also been associated with detrimental health effects (U.S. Department of Health and Human Services, 2017,U.S. Department of Health and Human Services, 2007). Although crude oil is a single mixture, because of evaporation of the volatile components over time, it is actually several mixtures, thus meeting our criteria of multiple mixtures.

This dataset consists of 60 4-18 hour air measurements that were collected using passive dosimeters worn by workers who worked on the outside of the vessel (compared to the living quarters inside). Each sample was analyzed for a variety of chemicals including THC, BTEX, and in some cases hexane. Censoring in this sample for hexane, toluene, and xylene was generally low, with censoring levels ≤ 25% (Table 3).

Table 3.

Characteristics of Ocean Intervention III measurements (N=60) from July 16 to September 30. We report count, percent censoring, and non-censored correlations between hexane, toluene, and xylene.

Chemical	Count Non-censored	Percent Censored	Non-censored Correlations
			Hexane	Toluene	Xylene
Hexane (Y)	53	12		0.42 (N=40)	0.25 (N=44)
Toluene	45	25			0.01 (N=38)
Xylene	48	20

We performed two model comparisons using the two forms of WAIC as defined above (section 3.2). Under model comparison 1, we compared model fit for all 3 chemicals (toluene, xylene, and hexane), using WAIC for the full likelihood. For model comparison 2, we compared model fit for hexane only using WAIC_Y. Results of model comparison 2 are included in the online supplementary materials.

5.1 Model comparison 1

First, we assessed how well our model fit the toluene, xylene, and hexane data accounting for complexity. As in the simulation study (section 4), framework 1 was the multivariate model and frameworks 2, 3, and 4 used a bivariate model multiplied by an ANOVA model. In framework 2, we modeled hexane and toluene using a bivariate model and modeled xylene using an ANOVA model. In framework 3, we modeled hexane and xylene using a bivariate model and used an ANOVA model for toluene. In framework 4, we modeled xylene and toluene using a bivariate model and used an ANOVA model for hexane. Framework 5 used separate ANOVAs for hexane, toluene, and xylene and assumed these chemicals were not correlated with each other (overall once accounting for censoring). Models were compared using WAIC for the full likelihood (which includes likelihood components for toluene, xylene and hexane). Variability in WAIC was assessed by changing model seeds and doing 100 runs for each model type.

5.2 General results

Results of our first model comparison are shown in Table 4. These results revealed that the 3-variable model (the multivariate model) had the lowest WAIC of the modeling frameworks tested. An assessment of variability of WAIC indicated that this difference was significant (at alpha of 0.10) even though the magnitude of the differences in the 5 models’ WAIC was minimal. Modeling frameworks 4 and 5 had the highest WAIC reported of all models tested. This result indicates that modeling frameworks accounting for the correlation between hexane and toluene or hexane and xylene were preferred to modeling frameworks that did not account for this correlation.

Table 4.

Model comparison for the Ocean Intervention III Data. Comparing WAIC with full likelihood values for modeling frameworks 1–5. WAIC estimates are reported for the same model seed of the program. The 5th and 95th percentiles of 100 runs with different model seeds are reported for WAIC.

Modeling Framework	Model Types	LPPD Estimate	P2 Estimate	WAIC
				Estimate	(5%, 95%)
1	3-Variable (Hexane, Toluene, Xylene)	−277.7	9.2	573.9	(573.9, 574.2)
2	Bivariate × ANOVA (Hexane, Toluene) × (Xylene)	−280.7	7.0	575.3	(575.0, 575.2)
3	Bivariate × ANOVA (Hexane, Xylene) × (Toluene)	−283.7	6.9	581.3	(581.1, 581.3)
4	Bivariate × ANOVA (Toluene, Xylene) × (Hexane)	−285.7	6.3	584.0	(583.8, 584.0)
5	ANOVAs (Hexane)× (Xylene)× (Toluene)	−286.7	5.2	583.7	(583.6, 583.7)

We also saw consistent trends in both LPPD and P₂. LPPD was highest for the 3-variable model indicating strong goodness of fit. P₂ also was highest for the 3-variable model because this model contained more model parameters (increased model complexity). However, the improvement in the goodness of fit measure LPPD outweighed the increased complexity of the 3-variable model (hence the lower WAIC).

Next, we examined the estimates from the 3-variable model framework since it was preferred in both model comparisons. Table 5 contains the median posterior estimates and 95% CI of the GMs, GSDs, and AMs for hexane, toluene, and xylene. We also report the median posterior estimates and 95% CIs for the correlations among hexane, toluene, and xylene and the regression coefficients defined for hexane as Y (toluene was X₍₁₎ and xylene was X₍₂₎).

Table 5.

Exposure estimates and parameter estimates from the 3-variable multivariate model for samples taken outside on the Ocean Intervention III from July 16–September 30, 2010. The median and 95% CI (2.5 and 97.5 quantiles) are reported for each parameter.

	Parameter	Median	2.5 Quantile	97.5 Quantile
Geometric Mean (ppb)	Hexane Toluene Xylene	9.66 9.16 10.89	7.08 5.29 7.73	13.03 15.34 15.01
Geometric Standard Deviations	Hexane Toluene Xylene	3.21 7.16 3.48	2.63 4.98 2.77	4.20 11.93 4.82
Arithmetic Means (ppb)	Hexane Toluene Xylene	19.06 63.72 23.82	13.47 29.87 16.30	30.51 209.35 40.59
Correlations	ρ(ln(Hexane), ln(Toluene)) ρ(ln(Hexane), ln(Xylene)) ρ(ln(Toluene), ln(Xylene))	0.41 0.29 0.18	0.17 0.03 −0.08	0.61 0.52 0.43
Regression Coefficients	β0,(1) β0,(2) β1,(2) β0,(Y|X) β1,(Y|X) β2,(Y|X)	2.21 2.13 0.12 1.29 0.22 0.21	1.67 1.61 −0.05 0.62 0.08 −0.02	2.73 2.62 0.29 1.92 0.37 0.44

Results of the 3-variable model demonstrated that the 3-variable model was preferred in the model comparisons. The intercepts for hexane (β₀,_(Y|X)), toluene (β₀,₍₁₎), and xylene (β₀,₍₂₎) were all significantly positive. The regression coefficient corresponding to the slope between hexane and toluene (β₁,_(Y|X)) was statistically significant (median posterior estimate:0.22, 95% CI: (0.08,0.37)) and the correlation coefficient was moderate with a median posterior estimate of 0.41. In contrast, the slope coefficient (β₂,_(Y|X)) of xylene when modeling hexane was insignificant (median posterior estimate: 0.21; 95% CI: (−0.02,0.44)). The lack of significance in this regression coefficient implied that xylene did not explain a significant amount of the variation in hexane when toluene was already a predictor in the model. However, xylene was related to hexane as demonstrated by the significant correlation coefficient (median posterior estimate: 0.29, 95% CI= (0.03,0.52)). So while the model containing toluene and xylene as predictors had a slightly better fit than a model only containing toluene as a predictor, the improvement in fit (for all variables and for hexane) was not substantial, leading to a minimal difference in WAIC and WAIC_Y (Table 4 and the supplementary materials). Finally, the slope and correlation estimates between toluene and xylene (β₁,₍₂₎) were slightly positive, but insignificant.

There was little difference in the median posterior estimates of the GM exposure estimates (in parts per billion, ppb). The GSD estimates were reasonable for hexane and xylene, but higher for toluene, but the 95% CIs were within the range commonly observed for the GuLF STUDY data (1.01 to 12). Hexane was slightly less variable than xylene. The AM estimates were greatly influenced by the GSDs. The median posterior estimates for the AMs of hexane, toluene, and xylene were 19.06 ppb, 63.72 ppb, and 23.82 ppb respectively. The increased variability in toluene led to a higher AM estimate for toluene. Since hexane had a lower GSD and GM, a lower AM of hexane was found.

6 Discussion

This model provides a statistical framework for exposure estimation when measurements are not available (due to not being measured or being censored) for a chemical in one or more mixtures but that measurements are available on other common chemicals. The simulation study and data analysis example both showed that we can use the linear relationships in chemical mixtures to better inform exposure estimates when data are missing or censoring is present.

Results of our simulation study in section 4 indicated that we could correctly identify when both particular covariates (X₍₁₎ and X₍₂₎) may be useful in a model setting under a variety of censoring levels. We were able to correctly identify that both X₍₁₎ and X₍₂₎ contributed significantly to the model regardless of the censoring levels in the variables in the model.

Results of our coverage simulation demonstrated that coverage generally decreased as censoring became more different in the covariate and response. This result is expected because censored points would be estimated in a region on Figure 1 which will pull the regression line down or up. This change in the regression line will change, therefore, the slope and intercept estimates. Results also indicated that with increased censoring, variability was generally higher.

Results of the multicollinearity simulation study showed that as the correlation increases between X₍₁₎ and X₍₂₎, the width of the 95% CIs increases for the slope coefficients in the conditional expression of Y | X₍₁₎, X₍₂₎. However, while censoring increased the CI width overall, the inflation in the width of the CI did not appear to be moderated by censoring levels. In the context of environmental exposure assessment, this inflation in the width of the CI could be concerning because it would affect the uncertainty quantification in the estimates. Since the conditional mean expression is used in the calculation of the GMs and AMs, the inflated width of the 95% CI could lead to greater uncertainty on the mean of Y and therefore greater uncertainty in the final exposure estimate. Such an increase in uncertainty may be undesirable, because in an epidemiologic study, the uncertainty would cause an exposure-disease association to be missed due to misclassification. Therefore, it is recommended that correlations between chemical covariates be kept to less than 0.5 to decrease the likelihood of this increase in uncertainty. One may be able to reduce the increase in width of the 95% CI with introducing shrinkage priors. The impact of shrinkage priors in this setting should be further investigated at different censoring levels.

Results of our analysis of hexane exposure from July 16-September 30, 2010 on the Ocean Intervention III indicated that the 3-variable model was preferred over other simpler models. Both xylene and toluene were moderately correlated with hexane in the final model (r=0.2–0.4). Models with only toluene or only xylene as a predictor for hexane (i.e. frameworks 2 and 3; models 2 and 3), did not fit the data quite as well, given the model complexity, as the multivariate model. Together, however, the correlations provided enough information to our model to allow us to develop reasonable estimates for hexane when hexane measurements were missing either because the measurements were not collected or because the measurement results were below the LOD. In addition, we used the model to better inform toluene and xylene estimates using the available but limited hexane data.

This model assumes that there is a clear linear relationship between the logarithms of the response and each predictor. Other relationships were not explored. This model also relies the assumptions of linear regression including independence of observations, equal variances, and normality of the residuals. Other distributions or violations of these assumptions were not investigated. Departures from these assumptions should be further investigated. We also did not investigate censoring levels greater than 75%. Furthermore, we did not assess the impact of influential points or outlying observations in this work. Future work similar to that of Bayes et al. (2012), should investigate methods for dealing with potential outlying observations.

Additional information and supporting material for this article is available online at the journal’s website.