Motion Sequence Alignment for A Kinect-Based In-Home Exercise System for Lymphatic Health and Lymphedema Intervention

Abstract

Using Kinect sensors to monitor and provide feedback to patients performing intervention or rehabilitation exercises is an upcoming trend in healthcare. However, the users’ motion sequences differ significantly even when doing the same exercise and are not temporally aligned, making the evaluation of the correctness of their movement challenging. We have developed a method to divide the long motion sequence for each exercise into multiple subsequences, each corresponding to the transition of one key pose to another. We also developed a subsequence-based dynamic time warping algorithm that can automatically detect the endpoint of each subsequence with minimum delay, while simultaneously aligning the detected subsequence to the reference subsequence for the exercise. These methods have been integrated into a prototype system for guiding patients at risks for breast-cancer related lymphedema to perform a set of lymphatic exercises in order to promote lymphatic health and reduce the risk of lymphedema. The system can provide relevant feedback to the patient performing an exercise in real time.

I. INTRODUCTION

Having patients performing prescribed exercises is an important clinical intervention for many health conditions such as chronic pain, post-surgery rehab, and physical therapy after a sports injury. Using sensor-based systems to automatically track patients’ movements during their exercises and to provide instant feedback to the patients regarding the “correctness” of their movements holds great promise in reducing the cost for such interventions and increasing their effectiveness.

To evaluate the performance of the user’s motion against a reference motion derived from a training dataset of motion sequences captured from an lymphatic exercise expert, Alexiadis et al. [1] proposed to use the maximum cross correlation (MCC) to calculate a global shift between user’s motion sequence and a ground truth sequence. Then, by applying this shift to the user’s motion data, the two sequences are aligned and their similarity can be calculated. However this method applies one shift to the whole sequence and can not deal with the situation where users may have inconsistent speed when performing different parts of an exercise. Yurtman et al. [2] applies the dynamic time warping to detect and identify correct and incorrect implementations of a physical therapy exercise. However, this system requires the user to attach wearable motion sensors, which is very expensive and inconvenient for the user. Wei et al. [3] consider a cloud based system, where a user can download the exercise video from the cloud database to a local device. Then, the user employs a Kinect sensor to capture his/her motion data and upload the data back to the cloud for a remote server to evaluate the correctness of the exercise and provide feedback. They proposed a gesture-based dynamic time warping algorithm to align the patient motion with a reference motion. In their work, the exercise is relatively easy and only focuses on one joint, so the remote motion analysis algorithm only needs to consider one joint. Our system is developed to handle complicated exercises where multiple joints need to be analyzed, both for temporal alignment and for assessment of motion correctness.

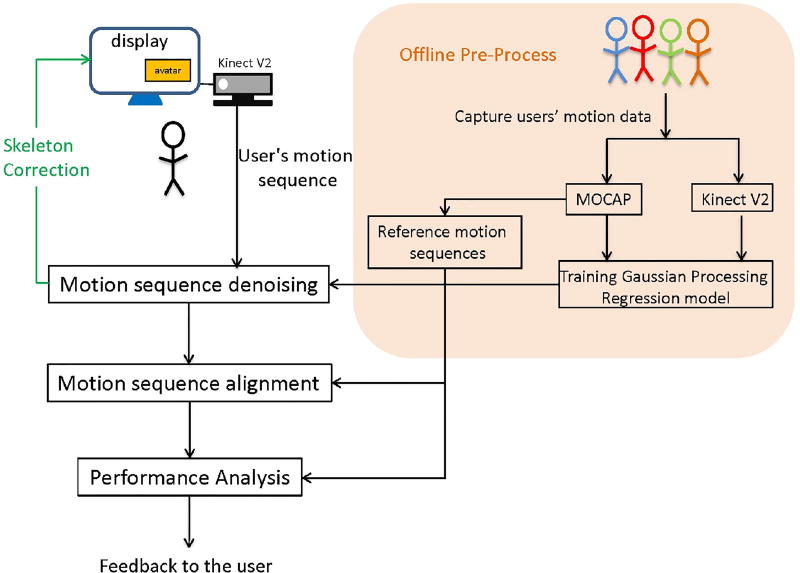
The proposed intervention system has two major parts, as shown in Fig. 1. The first part is the training stage, during which we capture the joint positions using both a motion capture (MOCAP) system and a Kinect sensor. This enables us to develop a Gaussian process regression model to denoise the Kinect data to be similar to the MOCAP data, after both types of data are mapped to a standard domain to eliminate the bias due to different body sizes of the users [4]. Also we use the MOCAP data recorded from an expert to generate the reference sequence for each exercise. The second part is for the live session when a patient (to be referred to as a user) is performing the intervention exercises and the Kinect sensor captures both an RGB video of the user and the joint motion. The system has a display screen (see Fig. 1 and Fig. 2) that shows an avatar performing a target exercise and the live captured video of the user with an overlay of the skeleton connecting the joint positions. First, the Kinect data will be denoised using the trained Gaussian process regression model [4]. Then the system will compare the denoised motion sequence with the reference sequence established during the training stage, and provide instantaneous feedback to the user regarding the improvement needed after processing each subsequence. The system will also provide constructive feedback at the end of an exercise. We have developed a prototype system, which can operate in real time while a user is performing an exercise.

Fig. 1.

Proposed system flowchart

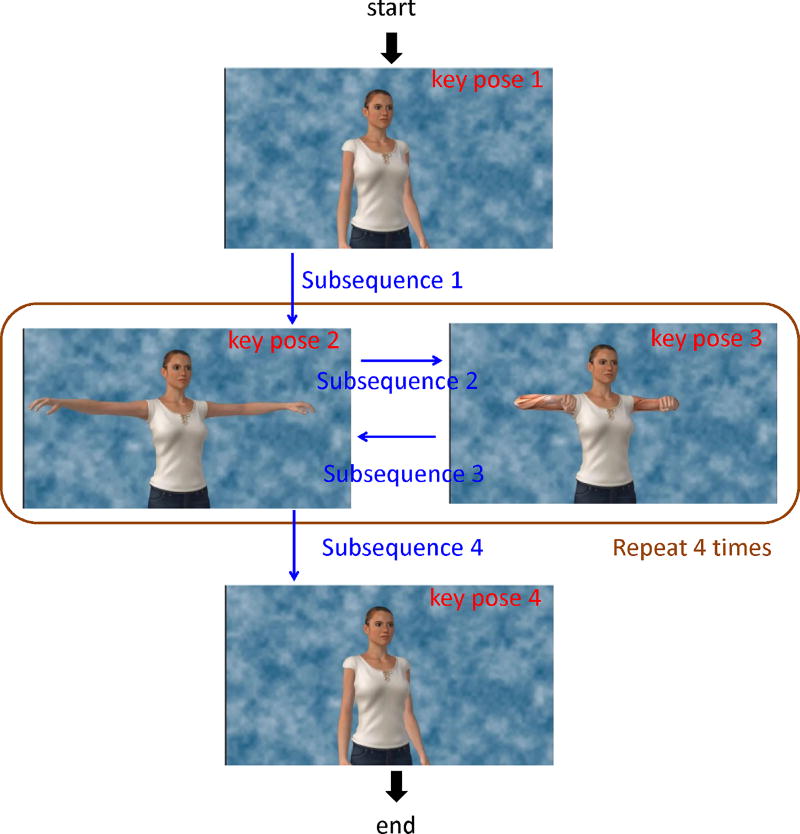
Fig. 2.

The subsequences and repetitions in “horizontal pumping” exercise

To enable the comparison of a user’s motion sequence against the reference sequence, we recognize that each exercise can be divided into multiple subsequences. We develop a dynamic time warping approach that can automatically recognize the endpoints of different subsequences, and furthermore temporally align the detected subsequences with the corresponding reference subsequences.

The rest of this paper is organized as follows. In Sec. II, we briefly discuss the structure of the lymphatic exercises and explain how to generate the reference subsequence. In Sec. III, we discuss our gradient-weighted dynamic time warping algorithm for temporal alignment of the motion sequence with a reference sequence. We conclude this paper in Sec. IV.

II. EXERCISE SEQUENCE DECOMPOSITION AND REFERENCE SEQUENCE GENERATION

The lymphatic exercise is developed by Dr. Mei R. Fu and her research team and is called The-Optimal-Lymph-Flow™ (TOLF) exercise. It contains a set of exercises that have been shown to improve lymph flow, lessen symptom severity, and reduce the risk for chronic breast-cancer-related lymphedema [5][6][7]. Currently, we only focused on a subset of the TOLF exercises that require the tracking of seven upper body joints, specifically left/right shoulder, left/right elbow, left/right wrist and spine shoulder. The Institutional Review Board approved the project procedures involving human subjects as part of a larger research study.

A. Decomposition of a motion sequence

An exercise contains a series of movements. Here, we define one exercise as a time sequence, and each time sample is one static pose, defined by the 3D positions of multiple joints. Many poses exist in one exercise, but usually we will focus on a few key poses. Each original exercise can be decomposed into several key poses and the transition between two key poses. We define the transition from one key pose to the next key pose as a subsequence. Futhermore, an exercise usually contains several repetitions of the same set of ordered subsequences. For example, the exercise “horizontal pumping”, contains four subsequences. During the exercise, users do the first subsequence at the beginning (from ”hands-down” to ”T-pose”). Then, they do the subsequence 2 (from “T-pose” to “hands close to the chest”) and subsequence 3 (from “hands close to the chest” to “T-pose”) repeatedly four times. This will be followed by subsequence 4 (from “T-pose” to “hands down”), which finishes the whole exercise. The subsequence decomposition for four exercises are summarized in Table I.

TABLE I.

Decomposition for Four Lymphatic Exercises

Name of the data set	Number of key poses	Number of subsequences
muscle-tightening deep breathing (Exercise 1)	3	2
over the head pumping (Exercise 2)	3	2
push down pumpingg (Exercise 3)	4	4
horizontal pumping (Exercise 4)	4	4

B. Reference sequence generation for each exercise

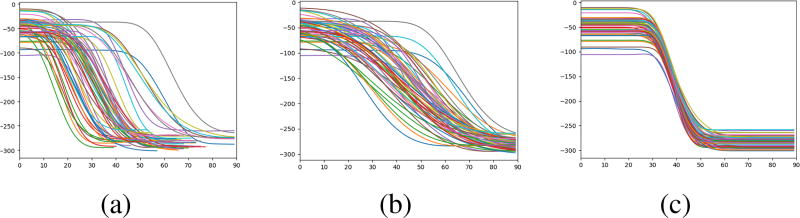
For each exercise, we generate a reference sequence, which consists of multiple subsequences and repetitions, and each repetition further consists of multiple subsequences. We ask an expert for the lymphatic exercises to perform each exercise several times and record the Kinect and MOCAP motion traces for each exercise. We use the MOCAP data to create the reference sequence. We divide original MOCAP sequence into several subsequences by considering the weighted sum of the temporal gradient magnitudes of the joint positions. The raw MOCAP data in one subsequence are shown as Fig. 3(a). Note that, although all the subsequences are captured from the same expert, each subsequence has different length. This is because it is hard to use the same speed every time when one does the exercise. To deal with this problem, we need to normalize the raw MOCAP data to the same length before we average these data to create a single reference. Although we can just interpolate all the raw data to the same length, as shown in Fig. 3(b), they are not aligned in where the transition occurs. To circumvent this problem, we evaluate the second order derivative of the raw data and find two turning points.

Fig. 3.

Traces of the left wrist x-coordinate while users performing a subsequence in the ”Horizontal Pumping” exercise. (a) Standardized MOCAP traces; (b) Aligned traces by stretching all traces to the same length; (c) Aligned traces by aligning at two key transition points.

According to these two turning points, we divide the subsequence into three parts. We map each part to an assigned length and then combine three parts together to get our aligned subsequences as shown in Fig. 3(c). Finally we use the mean of the aligned subsequences from multiple expert traces performing the same subsequence to generate the reference sequence for this subsequence.

C. Evaluation of a user’s movement against the reference sequence

For each exercise, we predefine a series of subsequences. When a user performs an exercise, her joint motion sequence will be captured by the Kinect sensor. Our system compares the user sequence with the reference subsequences sequentially, to determine the endpoint of each subsequence. The system will further analyze the difference between each identified user subsequence with the corresponding reference subsequence, to determine what feedback to provide to the user.

III. Temporal alignment using Low-delay dynamic time warping

A. Human Reaction Delay and Motion Variability

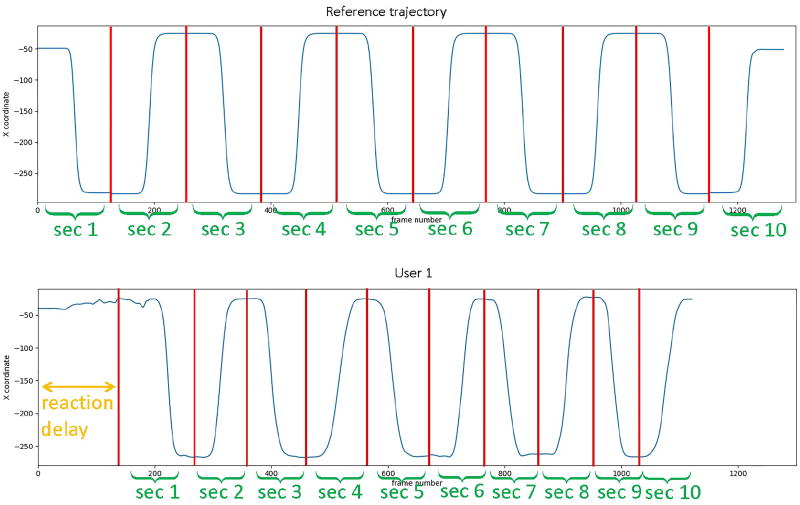
In our system, a user is supposed to follow the movement of the avatar shown on the display during each exercise. Usually, at the beginning of an exercise, the user may take a few seconds to understand what should she do before starting to follow the avatar’s movement. Fig. 4 shows the reference sequence and a user’s motion sequence during the exercise. We can see that the user takes some reaction time to figure out what kind of motion she needs to follow in the beginning. After the user has learned what to do in each repeat, the user tends to spend less reaction time to do the following subsequences. Also, once a user learns what to do, she may do each repeat faster or slower than the avartar. Also, different users will perform the same exercise or each subsequence with different speeds. We will discuss how to deal with these problems in the following subsections.

Fig. 4.

The reference sequence and a user’s motion sequence of the x coordinate of the left wrist during Exercise 4. Each “sec” indicate a subsequence.

B. Dynamic time warping for motion sequences

In the time sequence analysis, dynamic time warping (DTW) is a useful algorithm for measuring the similarity between two temporal sequences, which may vary in their temporal dynamics. DTW are widely used in temporal sequence matching for audio data processing [8]. DTW measures the similarity between two given sequences by finding the optimal correspondence between sampling points in the two sequences with certain restrictions. The original DTW method was developed for aligning two sequences of scalar variables (e.g. audio signal intensity). Here, we extend it to align two sequences of vector variables A = [a₁, a₂, …, a_M], and B = [b₁, b₂, …, b_N], where a_i and b_i each represents the 3D positions of 7 joints at time sample i. We define a M × N distance matrix with the (m, n)-th entry being the Euclidean distance between a_m and b_n is, i.e., d(m, n) = ‖a_m − b_n‖₂. To find the best way to map sequence A to sequence B, a continuous warping path is found by minimizing the summation of the distance on the path. The final DTW path is defined as P = [p₁, p₂, …, p_q], where max(M, N) ≤ q ≤ M + N − 1 and p_k = (m_k, n_k) indicates that a_mk is mapped to b_nk in the path. The optimal DTW distance is

$$S(M,N)=\sum _{(i,j)\in \mathit{\text{path}}}d(i,j)$$ (1)

Directly using the DTW on two sequences to evaluate their similarity can be affected by the absolute difference in the data amplitude of the two sequences. Following [3], given two sequences A = [a₁, a₂, …, a_M] and B = [b₁, b₂, …, b_N], we first find the difference c between the two initial elements in sequence A and B, where c = a₁ − b₁. We then generate the normalized sequence B′ with B′ = B + c. We will apply DTW to A and B’ to find the optimal correspondence path, and use the resulting path to align A and B.

C. DTW for Sub-sequence Detection and Alignment

As introduced in Sec. II-A, each exercise can be divided into multiple subsequences. It is better to give some feedback after a user has just finished each subsequence, rather than after the user has finished the entire exercise. Therefore, we need to develop an algorithm that can automatically detect the end of each subsequence soon after it is done, and furthermore align this subsequence with its corresponding reference subsequence. We accomplish this goal by modifying the original DTW to a subsequence-based DTW. Assume that the reference motion sequence for this exercise contains K subsequences and is denoted as A = [A₁, A₂, …, A_K], with A_k = [a_k,1, a_k,2, …, a_k,Mk] and the user’s motion sequence for this exercise is B = [b₁, b₂, …, b_N]. To determine the endpoint, q, of the first subsequence of the user, we compute the DTW distance between each candidate subsequence [b₁, b₂, …, b_q](q = 2, 3…, N) with the first subsequence A₁ = [a_1,1, …, a_1,M1] of the reference sequence and find q that minimizes the distance S(M₁, q). Directly solving this equation means that the endpoint of the first subsequence can not be decided until we go through the entire user sequence, which is very time consuming and prevents us from giving instantaneous feedback to the user. To overcome this problem, we propose a sequential decision approach. Let the initial time when the recording of an exercise starts to be 0. We continuously calculate the DTW distance between A₁ and the user’s current sequence up to time t. We keep capturing the user sequence until a certain time t* + 1 when we find the DTW distance S(M₁, t*) between A₁ and sequence B = [b₀, b₁, …, b_t*] reaches a local minimum value at t*. That is S(M₁, t*) < S(M₁, t* + 1) and S(M₁, t*) < S(M₁, t* − 1). To ensure the current point t* is not a poor local minimum due to noise, we will continue to compare the DTW distance in the following T frames (in this paper we set T as 15). If there is no DTW distance less than the DTW distance at time t*, then we set time t* as the endpoint of subsequence 1. Otherwise, we will keep looking for the local minimum in the following time points beyond the T frames. Then we reset the current time to 0, and start to compare the second subsequence A₂ of the reference sequence with the new samples of the user’s sequence, to identify the endpoint of the second subsequence.

D. Speed up of DTW

The DTW algorithm’s complexity for subsequence k is O(M_kN_k), which is proportional to the length of the user’s subsequence N_k. Therefore, the slower the user’s motion, the more computation time the system will spend. To deal with this problem and to accelerate the algorithm, we first apply the DTW algorithm every L frames. That is we downsample both the reference subsequence and the user sequence by a factor of L. In our work, we set L as 10. After the system finds the initial endpoint at time t* following the approach described in Sec. III-C, we will further check the time points between t* − L to t* in the the original sequences to find the best endpoint. Instead of using the DTW distance to decide on the optimal endpoint, we look for a mid point in this duration that has the least amount of joint motion. We measure the joint motion by the weighted sum of the temporal gradient magnitudes of the joint positions. That is, we find the end time point using

$$t^{†}=\text{arg }\underset{t\in (t^{\ast }-L,t^{\ast })}{\text{min}}\sum _{i\in \mathit{\text{joints}}}{w}_{{\mathit{\text{exercise}}}_n}(i)\ast {\Vert b_{t,i}-b_{t-1,i}\Vert }_2$$ (2)

We assign different weights for different joints based on the characteristics of each exercise.

E. Detection of Repetitions and Robustness to Repetition Variability

Usually in an exercise, the user is told to do several repetitions. For example, do “T-pose” to “ hand close to chest” and “ hand close to chest” to “T-pose” four times as shown in Fig. 2. In reality, users may forget how many repetitions they have already done, so they may do more or less repetitions than the reference sequence, which also can cause alignment error. We add a feature in the current system, which let the system choose what are the possible candidate subsequence after the current subsequence according to the user’s motion input. For example, in Fig. 2, when the user is in key pose 2 (end of subsequence 3), the user can either do subsequence 2 again to go to key pose 3 or do subsequence 4 to go to key pose 4. When the user finishes subsequence 3, the system will compare the user’s subsequent motion data with both reference subsequence 2 and reference subsequence 4, and find out the subsequence with the minimal matching error. Furthermore, the system detects the completion of one repetition upon the identification of subsequence 3 followed by subsequence 2. After the detection of each repetition, the system will display a message regarding how many more repetitions the user should do. At the end of this exercise, the system will give a friendly message to the user if the user did fewer or more repetitions.

IV. Conclusion

We have developed an exercise guidance system, which can automatically detect whether a user is performing a set of exercises properly, based on the joint positions captured by a Kinect sensor. The main contribution is a low-delay dynamic time warping algorithm that can automatically detect the end of each exercise subsequence while simultaneously aligning the detected subsequence with a reference subsequence. Our prototype can accurately align a user’s motion sequence with the reference sequence, and evaluate the “correctness” of user’s movements in real time, enabling instantaneous feedbacks to the user while the user is performing an exercise.