Development of Multivariable Models to Predict and Benchmark Transfusion in Elective Surgery Supporting Patient Blood Management

Summary

Background: Blood transfusion is a highly prevalent procedure in hospitalized patients and in some clinical scenarios it has lifesaving potential. However, in most cases transfusion is administered to hemodynamically stable patients with no benefit, but increased odds of adverse patient outcomes and substantial direct and indirect cost. Therefore, the concept of Patient Blood Management has increasingly gained importance to pre-empt and reduce transfusion and to identify the optimal transfusion volume for an individual patient when transfusion is indicated.

Objectives: It was our aim to describe, how predictive modeling and machine learning tools applied on pre-operative data can be used to predict the amount of red blood cells to be transfused during surgery and to prospectively optimize blood ordering schedules. In addition, the data derived from the predictive models should be used to benchmark different hospitals concerning their blood transfusion patterns.

Methods: 6,530 case records obtained for elective surgeries from 16 centers taking part in two studies conducted in 2004–2005 and 2009–2010 were analyzed. Transfused red blood cell volume was predicted using random forests. Separate models were trained for overall data, for each center and for each of the two studies. Important characteristics of different models were compared with one another.

Results: Our results indicate that predictive modeling applied prior surgery can predict the transfused volume of red blood cells more accurately (correlation coefficient cc = 0.61) than state of the art algorithms (cc = 0.39). We found significantly different patterns of feature importance a) in different hospitals and b) between study 1 and study 2.

Conclusion: We conclude that predictive modeling can be used to benchmark the importance of different features on the models derived with data from different hospitals. This might help to optimize crucial processes in a specific hospital, even in other scenarios beyond Patient Blood Management.

Citation: Hayn D, Kreiner K, Ebner H, Kastner P, Breznik N, Rzepka A, Hofmann A, Gombotz H, Schreier G. Development of multivariable models to predict and benchmark transfusion in elective surgery supporting patient blood management. Appl Clin Inform 2017; 8: 617–631 https://doi.org/10.4338/ACI-2016-11-RA-0195

1. Background and Significance

1.1 Patient Blood Management (PBM)

Red blood cell (RBC) transfusion is a highly prevalent procedure in surgery, obstetrics, gynecology, intensive care, trauma and other clinical specialties. In some clinical scenarios it has lifesaving potential. However, in most cases transfusion is administered to hemodynamically stable patients with no measurable benefit, but increased odds of adverse patient outcomes and substantial direct and indirect costs. Therefore, transfusion is now identified as one of the most overused treatments in modern medicine [ 1 ]. This phenomenon is well described by a high inter-hospital variability of transfusion rates (number of transfused patients per patient population) and transfusion indices (RBC volume transfused per patient) for matched patients. Additionally, transfusion is associated in a dose-dependent relationship with adverse outcomes including morbidity (infections, myocardial infarction, stroke, thrombotic events and others), hospital length of stay and mortality [ 2 ]. Therefore, a growing number of clinicians are now applying treatment modalities to optimize and preserve the patients’ own blood rather than resorting to donor blood. In the current literature this concept is referred to as Patient Blood Management (PBM). It is based on three pillars:

• Detection and correction of anemia before (elective) surgery

• Peri -surgical minimization of blood loss and

• Optimization and harnessing of patient specific physiological tolerance to anemia [ 2 , 3 ]

In combination with the rational use of blood products according to guidelines, PBM leads to significant improvement of patient outcomes and reductions in blood product utilization [ 4 ].

In Austria, two benchmark studies for blood use in elective surgery were commissioned by the Austrian Federal Ministry of Health and conducted from 2004 to 2005 [ 3 ] and from 2009 to 2010 [ 5 ]. The aims were to measure the key variables of transfusion practice in elective surgery, to determine the current situation, to identify predictors of transfusion, and to use the data for developing strategies to optimize transfusion practices across Austrian hospitals. After completion, the investigators provided a final report to the contracting authority and individual benchmark reports to the participating hospitals [ 6 ], including detailed and overall findings, as well as all relevant data. In terms of predictive aspects, the data were analyzed using logistic regression on all collected variables to identify the main blood transfusion drivers, which were gender in all types of surgeries analyzed, relative preoperative hemoglobin, volume of RBC lost, lowest relative postoperative hemoglobin. In coronary artery bypass graft (CABG) surgery, also age, body mass index, American Society of Anaesthesiology (ASA) score, and platelet aggregation inhibitors were identified to be independent predictors of RBC transfusion [ 5 ].

1.2 Number of Red Blood Cell (RBC) Units to Order – The Mercuriali Algorithm

In elective surgical patients with a high risk for significant blood loss, and in compliance with current transfusion guidelines, physicians need to order an appropriate number of RBC units prior to surgery . This number would closely resemble the number of units actually transfused in an logistically optimized, cost-effective setting. The required RBC volume ( TEV _required ), which determines the number of RBC units to order, can be calculated according to an algorithm published by Mercuriali and Inghilleri in 1996 [ 7 ] ( Equation 1 ).

with

EV _preop .............. individual patient’s current erythrocyte volume [L]

EV _{min acceptable} .... individual lower limit of EV that the patient is expected to tolerate [L] LEV _anticipated ..... expected loss of erythrocyte volume (LEV) during the surgery [L]

EVp _reop can be estimated from the current blood volume ( BV [L]), the preoperative venous hematocrit ( Hct [ 1 ]) and the correction factor 0.91 [ 1 ], as shown in Equation 2 (the correction factor had not been used in the original formula).

According to Equation 3 and Equation 4 , BV [L] can be estimated from body weight ( BW [kg]) and body height ( BH [m]), by applying gender specific empirical factors.

Based on clinical assessment, the physician estimates EV _{min, acceptable} , which is derived from the lowest Hct each individual patient is expected to tolerate without significant symptoms.

LEV _anticipated is derived as the 80 % quantile of LEV from previous similar surgeries within the respective hospital, not taking into account any individual parameters of the patient [ 2 ].

1.3 Predictive Modelling for Blood Transfusion Prediction

Various attempts have been made to provide clinicians with prognostic estimates and predictions of RBC needs in specific situations [ 8 ]. However, when it comes to elective surgeries, very few efforts have been made, although information on RBC needs for specific surgeries could be of high value. Recently, following the success in different industries, the application of machine learning methods and decision support has gained momentum in healthcare settings in general with some emerging activities in blood transfusion as well. Goodnough et al. have shown that digital decision support systems can reduce RBC transfusions and save costs [ 9 , 10 ]. Murphree et al. applied a large number of different model approaches to a related topic, i.e. the prediction of complications after blood transfusion [ 11 ]. Their results indicate that most models give good results if applied alone and that combining those models with a “majority vote” strategy did not yield a significant improvement.

In a recent publication [ 12 ], we re-evaluated the data from the Austrian Benchmarking Studies by going beyond the previous analysis attempting to predict blood transfusion related outcomes. The objective was to predict TEV based on different feature sets formed by patient-level pre-, intra and post-surgical parameters. However, the effects leading to the findings of the paper remained unclear and required additional research. Additionally, these initial analyses indicated that center specific patterns might have a significant influence on the predictive models, aspects which had not been investigated yet.

2. Objectives

The present paper describes the development of a novel approach for data driven benchmarking based on prognostic predictive modeling, which was applied retrospectively to analyze different transfusion patterns in different hospitals in Austria. It was our aim a) to prospectively predict the RBC volume transfused during surgery based on pre-surgical data and b) to identify differences in transfusion patterns between different centers in between two subsequent clinical trials.

3. Methods

Reporting of our approach was done according to the Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis (TRIPOD) Statement [ 13 ].

3.1 Source of data and study setting

Our dataset comprised of 6,530 case records from 16 centers (408 ± 222 records per center, min 164, max 907), obtained for elective surgeries of one of the following procedures: total hip replacement (2,570 cases), total knee replacement (2,469 cases) and coronary artery bypass grafting (1,491 cases). 3,465 cases (53 %) concerned female patients. Patient age was 67.8 ± 10.2 years (mean ± standard deviation). 63 % of the patients were older than 65 years. The data were recorded during the first [ 3 ] and second [ 5 ] Austrian Benchmarking Study. Only data from 16 centers taking part in both studies were considered (7 centers taking part in only one study were excluded).

3.2 Outcome

It was the aim to predict the RBC volume transfused during and after surgery ( transfused erythrocyte volume, TEV ). Data of our model were compared to the actual numbers of transfused units as recorded during the Austrian Benchmarking Studies.

3.3 Feature Matrix/Predictors

► Table 1 summarizes the features used for prediction of TEV . We selected all features that were recorded prior to elective surgeries, which were available in our dataset. Only preoperative data were used since those will be available for prospective determination of the optimal number of RBC units prior to surgery in a real world application. All data were recorded during the Austrian Benchmarking Studies except for LEV _mean , TEV _mean , LEV _qu80 , TEV _qu80 , and TEV _predicted which were estimated as described in chapter 3.4. The information, whether a patient received tranexamic acid (a drug which can be used in cardiac surgery) was only available in 62 % of all patients. However, even such incomplete cases were included in our analyses.

Table 1.

The Feature Set used for predictions of transfused erythrocyte volume TEV.

Name	Description	Type	Unit	Data availability [%]
OPtype	Type of surgery	THR/TKR/CABG	-	100
OPtechn	Surgical technique	open/endoscopic	-	100
CellSaver	Cell saver used	boolean	-	100
Gender	Gender	m/f	-	100
Age	Age	integer	years	100
ASA	American Society of Anesthesiologists (ASA) physical status classification	1 /2/3/4/5/6	-	100
Wgt	Body weight	decimal	kg	100
Hgt	Body height	integer	cm	100
BMI	Body mass index	decimal	kg/m 2	100
BSA	Body surface area	decimal	m 2	100
Hb	Preoperative Hemoglobin	decimal	g/dl	100
Hct	Preoperative Hematocrit	integer	%	100
Aggrlnh	Type of aggregation inhibitors	none/yes unspecified/acetylsalicylic acid/plavix with or without ASS	-	100
Tranex	Tranexamic acid	boolean	-	62
BV	Blood volume	integer	ml	100
EV	Preoperative circulating erythrocyte-volume	integer	ml	100
LEVmean	Mean LEV per center and type of surgery	integer	ml	100
LEVqu80	80 % quantile of LEV per center and type of surgery	integer	ml	100
TEVmean	Mean TEV per center and type of surgery	integer	ml	100
TEVqu80	80 % quantile of TEV per center and type of surgery	integer	ml	100
EVordered	Erythrocyte volume ordered	integer	ml	100
TEVpredicted	Predicted TEV accordinq to Mercuriali	inteqer	ml	100

LEV…Lost Erythrocyte Volume; TEV…Transfused Erythrocyte Volume; Hb…Hemoglobin concentration; Hct…Hemato-crit; THR…Total hip replacement; TKR Total Knee Replacement; CABG…Coronary artery Bypass grafting

3.4 Estimation of missing data

The Mercuriali algorithm requires a) centre- and surgery-specific historical data of LEV and b) patient-level data for EV _{min acceptable} [L]. Since these data were not available within our datasets, specific estimators were used instead:

These values were estimated by calculating a) the 80 % quantile and b) the mean value of all data for a specific center and type of surgery available in the database, independent on the time point (the 80 % quantile was expected to correlate with the amount of ordered RBC units, while the mean value is more accurate to predict the actual values). Separate quantiles/mean values per center were calculated for data from the first and from the second study, since we assumed that blood transfusion procedures did change during the five years in between.

EV _{min acceptable} was computed based on all data stored in the datasets, by assuming a constant minimum acceptable Hct value of 25 % for all patients. This estimator was used for comparison of our model results with the performance of the Mercuriali algorithm, as described in chapter 1.2.

TEV _predicted was calculated based on the Mercuriali algorithm, using mean values of LEV instead of 80 % quantiles for historical data.

3.5 Predictive Modelling Pipeline

Our predictive modelling pipeline is based on MATLAB R2016a (The Mathworks, Inc, Natik, NE) and consists of the following main modules:

Feature Set Compiler – an extract, transform, load (ETL) module for importing data from a variety of sources (databases, EXCEL or CSV files, output of preprocessing components e.g. from Biosignal analysis, etc.) governed by a Source Data Definition File and converting the data into a MATLAB datasets object for memory efficient computing based on a Feature Set Definition File.

Model Generator – utilizing the MATLAB Statistics and Machine Learning Toolbox and a Modelling Set Definition File, a variety of different models can be generated from the feature sets, including General Linear Models, Bagged Trees, etc. Observations in the feature set can arbitrarily be divided into subsets for training, testing and validation with corresponding predictions being computed automatically.

Model Evaluator – allows visualizing and evaluating model based predictions using methods like Receiver Operating Characteristics (ROC) and a variety of standard key performance indicators like correlation coefficients, root means square error, sensitivity, predictive values, etc.

The predictive modelling pipeline guarantees reproducibility and has a number of additional features useful for processing large scale and heterogeneous healthcare data, from clinical codes to bio signals. Previous projects utilized the predictive modelling pipeline on different healthcare data sets, e.g. to predict the number of future days in hospital based on health insurance claims [ 14 ], to evaluate the utility of groups of features in given models by applying statistical tests on a set of related models build from observational subspaces (leave 10% out) [ 15 ] and to predict future events using time series approaches [ 16 ].

3.6 Random forest

Each model was trained with a random forest type regression tree [ 17 ] using MATLABs TreeBagger functionality with default settings except for OOBPred = on, NPrint = 1, MinLeaf = 10, Method = regression, Surrogate = off, PredictorSelection = interaction-curvature , and OOBVarImp = onPrediction . The modelling result of each sub-model was compared to the actual target parameters and Pearson’s correlation coefficient was calculated for each sub-model as a “goodness of fit” measure between observed and predicted values.

3.7 Feature importance analysis

For each feature used in our model, we calculated the feature importance according to the algorithm described by Breiman and Cutler [ 17 ]. Therefore, for each tree, the model was trained with 2/3 of all observations and the model accuracy for the remaining 1/3 of observations was calculated a) considering all features and b) replacing the values of one feature after the other with random values. The degree to which this procedure reduced the model accuracy was inversely related to the feature importance. Important features, if substituted by random values, severely reduced the model accuracy, while features with little influence of random values on the outcome were considered “unimportant”.

3.8 Leave 10 % out

As already published in [ 12 ], we used the “Leave 10 % out” approach for training and testing our models. This resulted in 10 different sub-models based on a training set of 90 % of the whole data set each, which was applied to the remaining 10 % as a test set. Statistical parameters of the correlation coefficients of the ten sub-models were visualized using boxplots. We further extended this approach by applying the leave-10%-out approach to feature importance. We calculated the feature importance of all features in our model in order to identify, which features have the most impact on blood transfusions. Boxplots were used for visualization of the results from different models. Since TEV was 0 ml for a significant number of surgeries, the median TEV was 0 ml in many analyses. Therefore, boxplots for TEV were extended by markers for mean values.

► Figure 1 illustrates the leave 10 % out approach and the corresponding visualization.

Fig. 1.

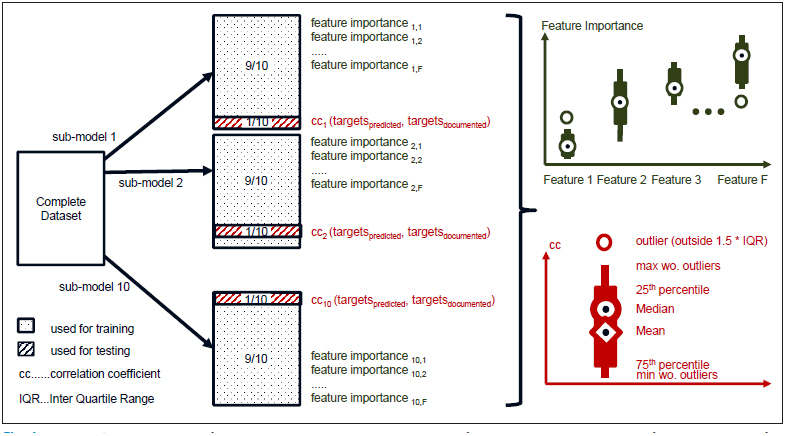
Leave 10% out approach used for training, prediction and statistical evaluation of each model, including calculation of model accuracy and feature importance.

3.9 Centre specific analyses and benchmarking

We developed separate models for each of the centers included in our dataset. We then compared the feature importance as calculated with models using data from different centers with one another, in order to identify potential center-specific patterns in PBM. Feature importance values derived for a specific center were compared to the respective values derived from other centers (► Figure 2 ).

Fig. 2.

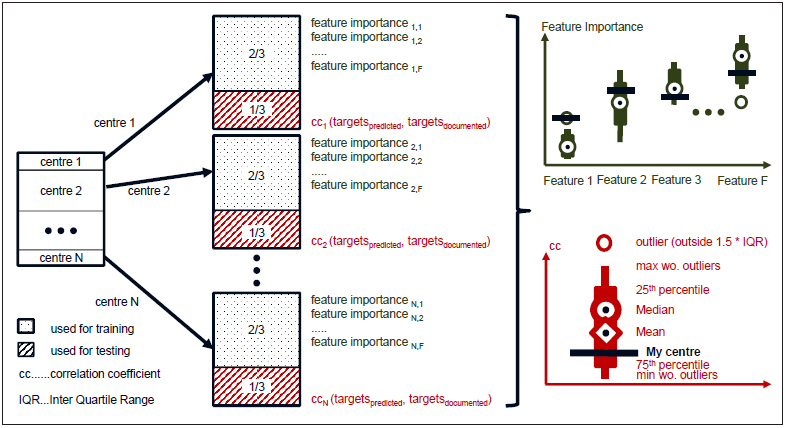
Centre specific model design for benchmarking feature importance across centers.

4. Results

4.1 Model accuracy

We compared TEV as predicted by our model with the actual values available in our datasets. Correlation coefficients are summarized in ► Table 2 .

Table 2.

Pearson’s correlation coefficient between predicted and actual amount of blood transfused, based on different prediction methods

Prediction method	Correlation coefficient	p value
Number of ordered units	0.21	<0.0001
Mean transfused volume of the current center	0.34	<0.0001
Mercuriali algorithm	0.39	<0.0001
Predictive modelling	0.61	<0.0001

The correlation coefficient between predicted and actual values was 0.61, which was notably higher than correlation values achieved with predictors based on ordered units, the mean value of the respective center, and based on the Mercuriali algorithm ( TEV _predicted ). The root mean square error was 277 ml.

TEV _predicted was evaluated using different key performance indicators. Therefore, TEV > 0 was used as a threshold value for the actual TEV . The following results were achieved: area under the receiver operating curve: 0.88; optimal threshold for predicted TEV : 162,81 ml, leading to sensitivity: 81 %; specificity: 80 %; positive predictive value: 72 %; negative predictive value: 86 %; kappa: 58 %; accuracy: 79 %; F-score: 75 %.

4.2 Overall Feature Importance

Comparison of the feature importance of different features revealed that the most important feature for predicting TEV was the center- and surgery-specific mean value of TEV (TEV _mean ). This feature was even more important than the predicted value according to Mercuriali, the individual hematocrit, hemoglobin value and the individual erythrocyte volume ( Figure 3 ). The amount of RBC units ordered was only a weak predictor, too.

Fig. 3.

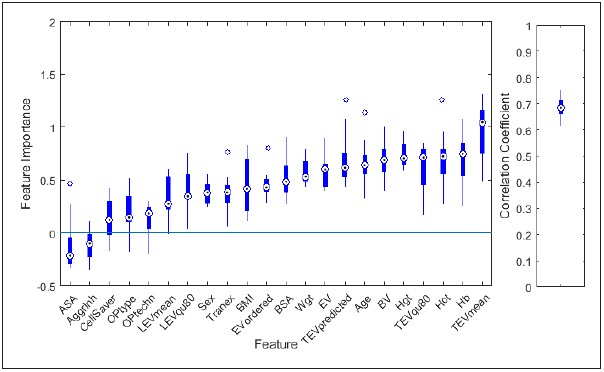
Feature importance (left) of the 22 features used during modelling (see table 1 for a description of the features) and correlation coefficient between actual and predicted transfused red blood cell (RBC) volume (right). 10 models were built applying a leave-10%-out approach. Boxplots summarize the results achieved for these 10 models.

4.3 Centre Specific Feature Importance

For each center, a separate model was trained and feature importance values for all features were calculated and compared with one another. For visualization, box plots representing feature importance values of all but one center were plotted and compared to the results of the remaining center.

Comparison of mean value and standard deviation of the feature importance of different centers showed, that some features show a high dependence on the respective center while other features are rather equally distributed for different centers (► Figure 4 ).

Fig. 4.

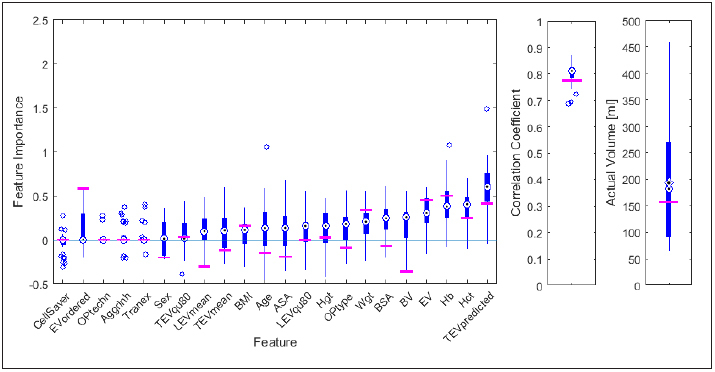
Example of a visualization of benchmarking data for the feature importance as achieved for a single center (center 8 of the Austrian Benchmarking Study 1, horizontal lines) with the respective values of all other centers represented by boxplots (left). Correlation coefficients between predicted an actual transfused (RBC) volume and actual transfused RBC volume are shown on the right. 32 models were built (one per center). Boxplots summarize the results achieved for each single center.

4.4 Differences between First and Second Austrian Benchmarking Study

For both studies (First and Second Austrian Benchmarking Study), separate models were trained and validated using the leave-10%-out approach described above. Feature importance was derived for all models. Results are shown in ► Figure 5 .

Fig. 5.

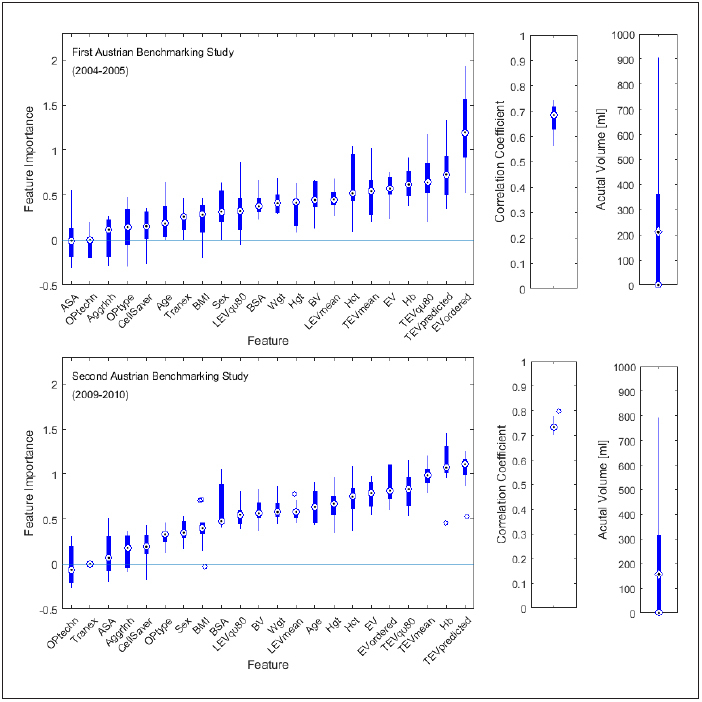
Comparison of feature importance (left), correlation coefficient in between predicted and actual value of transfused RBC volume (middle) and actual transfused red blood cell (RBC) volume (right) as achieved for the first (top) and the second (bottom) Austrian Benchmarking Study. Results of ten submodels – each developed and validated with a leave 10 % out approach – are shown as boxplots.

For some features, feature importance changed between the two studies. The RBC volume ordered was the most important feature in study one, while in study two, it ranked number 5. Other features such as age (rank 17 vs. rank 9) and ASA score (rank 22 vs. rank 20) gained importance in study two. Model accuracy was slightly higher in study two. The mean actual RBC volume transfused decreased from 211 ml to 184 ml.

5. Discussion

Predictive modeling is expected to play an increasing role in healthcare processes. Besides prospectively predicting future values of various parameters of interest, retrospective analyses can be used to identify the major drivers for a certain outcome parameter, even in case of complicated bundles of confounders. The present paper describes how feature importance can be used for benchmarking in PBM. However, this method is also applicable to various other scenarios in healthcare.

5.1 Model accuracy

Our results indicate that TEV can be predicted more precisely when considering individual pre-surgical parameters than currently done in clinical routine.

The number of ordered RBC units is a measure of the number of RBC units to transfuse, as estimated by the physician prior surgery. We found that the correlation between TEV and the number of RBC units ordered was a modest 0.21. Comparison of the model’s predictions with the number of ordered units is not perfectly “fair”, since ordered units reflect an upper limit of units needed rather than the estimated value (which is reflected by the use of a 80 % quantile of historic data). However, since the upper limit is expected to correlate with the expected value, even the upper limit should show a high correlation with the actual values. For comparison of our model performance with the Mercuriali algorithm, we re-engineered the minimum accepted EV of a specific patient, assuming a minimum acceptable hematocrit of 25 % for all patients. Actually, this value depends on the current status of the individual patient. Therefore, the correlation between transfusion needs based on Mercuriali and actual transfused volume might be slightly higher than in our estimation. However, with a correlation coefficient (cc) of 0.61, predictive modelling still seems likely to outperform current praxis in RBC unit ordering (cc = 0.21), mean transfused volume per center (cc = 0.34) and the Mercuriali algorithm (cc = 0.39) in terms of transfusion needs estimation.

5.2 Feature importance analysis for patient blood management (PBM) benchmarking

The importance of features for predicting different outcome parameters has been estimated for models derived from data of different centers. These feature importance values can be used for benchmarking centers in terms of “which factors influence the amount of blood transfused”. Since Random Forests are used for modelling, important features do not need to correlate with the outcome variable (as required e.g. for multiple regression analyses), but even non-linear and non-continuous relations can be identified and non-ordinary features (such as the type of surgery) can be explored. By comparing feature importance values of a specific center with data from reference centers serving as role models, i.e. “Best Practice Centers”, centers may be able to identify critical factors (“low hanging fruits”) for optimizing their processes in PBM. An example of how feature importance benchmarking could be visualized is shown in ► Figure 4 .

Feature importance does not directly reflect any cause-effect-relationships. Therefore, as in all benchmarking scenarios, the data need to be interpreted with care. Differences between hospitals may either result from different processes or other factors like different patient populations. Nevertheless, predictive modeling might guide a more detailed analysis in a second step. . Particulary in the transfusion setting it would be important to identify practice gaps in the application of the various PBM modalities and the reasons therefore.

The type of surgery as plotted in ► Figure 3 – 5 seems to be of little importance. However, this parameter is already considered in historic data such as LEV _mean and TEV _mean . Additionally, the influence of the type of surgery might increase if the number of different types (currently three) is increased. In a recent publication, Meier et al. [ 18 ] showed that in a cohort of 5,803 patients in 126 European countries, TEV was rather depending on LEV _anticipated than on TEV _required . This finding could not be verified in our model, as LEV _anticipated (estimated from LEV _mean ) was less important than TEV _required . However, this might change when better estimations for LEV _anticipated are available.

Tranexamic acid is a drug which can be applied during cardiac surger. In the First Austrian Benchmarking study, this parameter was not determined (however, it was set to “no” for hip and knee surgeries). Therefore, this feature was only available in 62 % of all patients. Therefore, feature importance of this feature might increase if the information is available for all patients.

Feature importance of random forests can be influenced by a) the number of distinct values for a specific feature and b) correlated features [ 19 , 20 ]. Features with more distinct values (e.g. ordinary features) receive higher feature importance than features with less distinct values (e.g. boolean features) and highly correlated features receive lower feature importance than independent features. Both aspects are relevant for our dataset, since there are both, ordinary and boolean, features included and since some of the features are highly correlated (e.g. Hb, Hct, and EV). In order to reduce this effect, we used MATLAB’s property PredictorSelection = interaction-curvature , which applies chi-square tests of the association between each predictor or each pair of predictors and the response as a split criterion. It can be seen in ► Figure 3 – Figure 5 , that even highly correlated features showed high feature importance. However, feature importance should still be interpreted with care.As described in chapter 3.3, TEV _predicted was a derived from various other features based on the Mercuriali algorithm. In order to better understand the effect of this special parameter, we compared model performance with and without TEV _predicted . Results showed that exclusion of only this chance to validate the present results with an independent, single parameter did not significantly reduce the model performance. We assume that correlated features could well replace TEV _predicted .

Feature importance of ordered RBC volume varies a lot depending on the model used. This feature was most important in study one and had rank 5 in study two. Still, it is only on rank 21 (center specific analysis)/12 (overall analysis) when combining both studies. These differences indicate, that the underlying mechanisms changed in between study one and two and, therefore, machine learning algorithms could not discover these mechanisms when data from both studies were combined. This assumption can also be supported by the fact, that the correlation in between number of ordered RBC units and TEV changed from study one (0.13) to study two (0.33), and that the mean number of units ordered decreased from 2.42 units in study one to 2.12 in study two.

5.3 Outlook

The present paper describes how predictive modeling tools can be used for benchmarking in PBM. However, these tools are applicable for various scenarios in healthcare. Any topic, where benchmarking and/or predictive modeling are currently explored, might benefit from our approach, such as the management of discharges, re-admissions, length of stay optimization, intensive care units, OPs, number of complications, nosocomial infections, and many more.

There are various possibilities to further improve our model performance. One example would be alternative learning algorithms, including Gradient Boosted Machines (BGM) or advanced ensemble methods. We expect that model optimization could further improve prediction. However, the general concept of how to interpret the results in benchmarking scenarios would remain the same.

Sex was a weak feature in our models. However, transfusion rate and volume are higher in women compared to men. In a recent publication we assumed that this is due to clinicians applying the same absolute transfusion thresholds irrespective of a patient’s gender. This, together with the common use of a liberal transfusion strategy despite the recommendations in relevant guidelines, may lead to over-transfusion in women [ 21 ]. These findings will be applied to future predictive models in order to further optimize PBM in women.

Currently, the EU project EU-PBM Patient Blood Management [ 22 ] is in its final phase in which similar data are collected from five centers in five European Union member states. Once this project has been concluded, there will be a chance to validate the present results with an independent, prospectively collected dataset. Also, these data are expected to allow to look at the impact of factors related to the three pillars of the PBM strategy. Future work will also focus on aspects of providing prediction results to health care professionals in a way which is easy to access and comprehend anywhere in their institution and anytime when decisions need to be made.

6. Conclusion

There exists an immediate need for patient blood management (PBM) in elective surgery. Predictive modeling, together with other measures, can support PBM, since it presents a powerful tool not only for prospective prediction of events and outcomes, but also for retrospective analyses of the current state of a specific topic. Analyses of the importance of various features during prediction of different outcomes has the potential to give new insights even into complicated and non-linear processes within a hospital and can be useful e.g. for benchmarking.

7. Multiple Choice Question

Which of the following is an aim of patient blood management and can benefit from predictive modeling:

1. Optimization of blood ordering schedules

2. Increase of post-surgical erythrocyte volume

3. Prevention of transfusion-transmissible infections in blood components

4. Reduction of waiting times prior to elective surgery

Right answer: A) One of the aims of patient blood management (PBM) is optimization of blood ordering schedules. Therefore, algorithms such as the Mercuriali algorithm can be applied. We presented a method for predicting the amount of blood which will be transfused via machine learning techniques. Such methods allow to benchmark ordering schedules and transfusion patterns in different hospitals.

PBM does not aim at increasing post-surgical erythrocyte volume, but rather on harnessing the physiological tolerance of anaemia. Prevention of transusion-transmissible infections in blood components is an aim of donor blood management rather than PBM. PBM aims at optimising pre-operative red cell mass. Therefore, in case of elective surgeries without urgency, a delayed surgery with less blood transfusion due to preceding anaemia treatment would be preferred over an early surgery performed at an anaemic patient.

Clinical Relevance Statement

Blood transfusion is one of the most common procedures in hospitalized patients and in some clinical scenarios it has lifesaving potential, however, it is also considered to be one of the most overused interventions. Previous research showed that blood product ordering and transfusion patterns vary significantly from center to center. The present paper demonstrates, how predictive modelling can not only be applied to prospectively optimize ordering procedures prior to elective surgery, but also to retrospectively analyze such center-specific patterns, which both has the potential to reduce adverse events and costs related to blood transfusion in the future.

Funding Statement

Funding The research leading to these results has received funding from Austrian Research Promotion Agency under the project HIS-PREMO, grant agreement number 853264.