Abstract
A new diffusion model of decision making in continuous space is presented and tested. The model is a sequential sampling model in which both spatially continuously distributed evidence and noise are accumulated up to a decision criterion (a 1D line or a 2D plane). There are two major advances represented in this research. The first is to use spatially continuously distributed Gaussian noise in the decision process (Gaussian process or Gaussian random field noise) which allows the model to represent truly spatially continuous processes. The second is a series of experiments that collect data from a variety of tasks and response modes to provide the basis for testing the model. The model accounts for the distributions of responses over position and response time distributions for the choices. The model applies to tasks in which the stimulus and the response coincide (moving eyes or fingers to brightened areas in a field of pixels) and ones in which they do not (color, motion, and direction identification). The model also applies to tasks in which the response is made with eye movements, finger movements, or mouse movements. This modeling offers a wide potential scope of applications including application to any device or scale in which responses are made on a 1D continuous scale or in a 2D spatial field.
Keywords: Diffusion model, spatially continuous scale, response time, Gaussian process noise, distributed representations
Stimuli in laboratory research and in the real world are often continuous in space and, in the real world, responses to them are often made on continuous scales, sometimes one dimensional (1D) and sometimes two dimensional (2D). I present a new spatially continuous diffusion model (SCDM), a quantitative sequential-processing model, and show that it can explain how decisions are made about such stimuli, how decisions are expressed on continuous scales, and how decisions evolve over the time between onset of a stimulus and execution of a response.
Continuous response scales may be better suited than discrete ones in some situations for clinical patients, children, or older adults in that they remove the requirement of dividing the knowledge on which their decisions are based into discrete categories. There is also a broad range of potential applications in cognitive psychology including visual search and coordinate systems (e.g., Golomb et al., 2014), psychometric item response theory (e.g., Noel & Dauvier, 2007; Muller, 1987; Ferrando, 1999), working memory (e.g., Hardman et al., 2017; van den Berg et al., 2014), number line tasks in numerical cognition (e.g., Thompson & Siegler, 2010), relationships between binary responses, confidence judgments, and responses on continuous scales in perception and memory (e.g., Province & Rouder, 2012), fuzzy set theory (e.g., Smithson & Verkuilen, 2006), visual attention (e.g., Itti & Koch, 2001), and dynamical systems models of movements (e.g., Klaes et al., 2012; Wilimzig et al., 2006). Many of this list of studies used representations of stimuli and responses on continuous scales but did not examine or model the time course of processing, something that is essential to understanding decision making. This modeling approach also fits naturally with models of neural population codes (e.g., Beck et al., 2008; Deneve et al., 1999; Georgopoulos et al., 1986; Jazayeri & Movshon, 2006; Liu & Wang, 2008; Nichols & Newsome, 2002; see the review and challenge for diffusion modeling in Pouget et al., 2013). The SCDM can also be seen as an extension of dynamical systems and population code models that allows them to account for both response choices and the distributions of response times (RTs).
The SCDM is also an extension of one of the most successful models of simple decision making, the sequential sampling, diffusion decision model for two-choice decisions (Ratcliff, 1978; Ratcliff & McKoon, 2008; Ratcliff, Smith, Brown, & McKoon, 2016). That model explains the choices individuals make and the time taken to make them by assuming that noisy evidence is accumulated over time to one of two decision criteria. This and related models have been influential in many domains, including clinical research (Ratcliff & Smith, 2015; White, Ratcliff, Vasey, & McKoon, 2010), neuroscience research, and neuroeconomics research (Gold & Shadlen, 2001, 2007; Krajbich, Armel, & Rangel, 2010; Smith & Ratcliff, 2004). There is also a growing body of evidence that diffusion models provide a reasonable account of the mappings between behavioral measures and neurophysiological measures (e.g., EEG, fMRI, and single-cell recordings in animals; see the review by Forstmann, Ratcliff, & Wagenmakers, 2016). The model is also being used as a psychometric tool in studies of differences among individuals (e.g., Ratcliff, Thapar & McKoon, 2010, 2011; Ratcliff, Thompson, & McKoon, 2015: Schmiedek et al., 2007; Pe, Vandekerckhove, & Kuppens, 2013).
Historically, the earliest models for two-choice decisions were random walk models or counter models (LaBerge, 1962; Laming, 1968; Link & Heath, 1975; Stone, 1960; Smith & Vickers, 1988; Vickers, Caudrey, & Willson, 1971) in which evidence entered the decision process at discrete times (see Ratcliff & Smith, 2004, for an evaluation of model architectures). The advance from discrete random walk processes to continuous diffusion processes resulted in an explosion of theoretical and applied research (much of it in the last 15 to 20 years). I believe that the advance from modeling the time course of discrete decisions to the time course of decisions in continuous space could have the same theoretical and applied impact.
Diffusion models have also been used for multi-choice decisions. For example, Roe, Busemeyer, & Townsend (2001; Busemeyer & Townsend, 1993) developed decision field theory and applied it to tasks with multi-alternative decisions and multi-attribute stimuli. According to the theory, at each moment in time, options are compared in terms of advantages and disadvantages with respect to an attribute and these evaluations are accumulated across time until a threshold is reached. The first option to cross the threshold determines the choice that is made. The theory accounts for a number of findings that seem paradoxical from the perspective of rational choice theory. Another domain that has been studied intensively involves confidence judgments. When individuals are asked to indicate how confident they are in the correctness of a decision, they typically do so by choosing one of several categorical responses (e.g., very confident, somewhat confident, etc.). Like the two-choice model, multi-choice diffusion models have provided a detailed explanation of choices and RTs (Leite & Ratcliff, 2010; Niwa & Ditterich, 2008; Pleskac & Busemeyer, 2011; Ratcliff & Starns, 2009, 2013; Voskuilen & Ratcliff, 2016). However, despite the tradition in which confidence judgments are measured in discrete categories, confidence should be seen as a continuous dimension in some situations, not a discrete categorical one, and the modeling presented here might apply to such confidence judgments made on a continuous scale.
The Spatially Continuous Diffusion Model
The core of the SCDM is conceptually simple: It is a sequential sampling model in which information from a stimulus is represented on a continuous line or plane and evidence from it is accumulated up to a decision criterion, which is also a continuous line or plane. Key to the model’s success is that the noise added to the accumulation process is spatially continuously distributed. To demonstrate the potential of the model, the experiments below tested it across a range of tasks, stimuli, and response modalities. The tasks were brightness, color, and direction-of-motion discriminations with static and dynamic displays with responses made on the same scale as stimuli were displayed or with responses and stimuli decoupled. Responses were made on 1D circles, arcs, and lines and 2D planes and they were given by eye, finger, and mouse movements. The effects of each independent variable were measured in at least two experiments to address the replicability of the effects.
Figure 1 illustrates the model for a 1D task for which subjects move their eyes from a central fixation point to the location on a circle (actually an annulus) that is the brightest, that is, the greatest concentration of white pixels (Figure 1A). The heavy line in Figure 1B shows the representation of a stimulus for which the center of a bright patch is at an angle of 180 degrees from an arbitrary zero point. The dashed and dotted lines show variability across trials, which is discussed later. A Gaussian distribution is used for the representation because 2D Gaussian distributions were used to generate the patches, but a circular Gaussian von Mises distribution, traditionally used in modeling tasks with circular response fields (Smith, 2016; Zhang & Luck, 2008), could also be used. Gaussian and von Mises distributions are probably indistinguishable in the applications presented here. The representation of the stimulus determines the rate (drift rate) at which evidence is accumulated toward a criterion, with the highest drift rates at and near the center of the distribution and decreasing with distance from the center. A response is executed when the amount of accumulated evidence reaches the criterion. In tasks with more than one stimulus (e.g., two or more patches of bright pixels, or more than one motion direction), the stimulus distribution has two or more Gaussian distributions, one for each stimulus.
Figure 1.
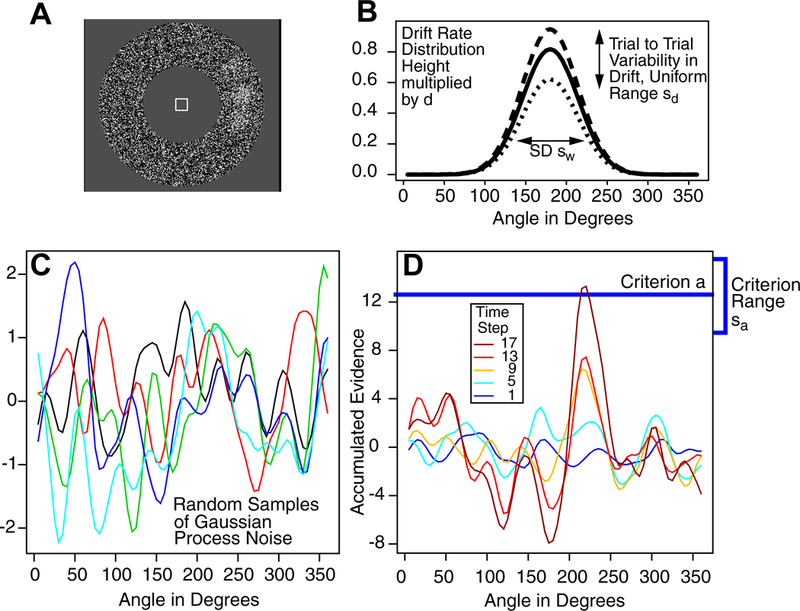
(A) An example stimulus display for a task in which the subject moves his or her eyes from the central fixation square to the brightest area on the surrounding annulus. (B) A representation of the normally distributed stimulus representation. (C) Six examples of random Gaussian process noise. (D) Five samples of accumulated information with the last reaching the decision criterion (the blue horizontal line).
Noise in the accumulation of evidence for a 1D stimulus is represented by a spatially continuously distributed Gaussian process. For a Gaussian process, at any point on the spatial dimension, noise in the evidence dimension has a Gaussian distribution. There is a correlation between nearby points on the spatial dimension and there is a kernel parameter of the model that determines the range of this correlation. The SD in the evidence dimension (within-trial variability or diffusion coefficient) is set to 1 per 10 ms step and it acts as a scaling parameter in the same way as within-trial noise in the two-choice diffusion model. For tasks with circular displays, I have not attempted to make the Gaussian process noise continuous over the 360 degree to 0 degree boundary that is present in the current modeling. Until this becomes an issue that is critical in modeling data, it is left for future modeling.
Figure 1C shows examples of Gaussian process noise for 1D stimuli; the five lines show noise across angles, horizontally, and across time, vertically. The distribution of noise is added to the evidence from the representation of the stimulus (Figure 1D) and the evidence from the sum of the two proceeds through time until it reaches criterion at some location on the circle (the blue line in 1D). For 2D stimuli, the idea is the same except that variability is represented by Gaussian random field noise. Gaussian processes and Gaussian random fields are active areas of research in machine learning (Lord, Powell, & Shardlow, 2014; Powell, 2014). For example, because random Gaussian processes are summed (along with the signal), the accumulation process can be seen as a time autoregressive spatial model (Storvik, Frigessi, & Hirst, 2002).
The accumulation process is assumed to be continuous in space and time but to simulate it, discrete time steps and discrete spatial locations are used. For any simulation of a continuous process on a digital computer, the continuous process must be approximated by a discrete one. A later section in this article presents a discussion of how to scale the process to change the sizes of the steps in space and time to approach continuous processes with smaller time steps and more points on the continuous spatial dimension.
It is assumed that evidence for one location is evidence against the others such that the total amount of accumulated evidence is constant across time (normalized to zero at each time step; e.g., Audley & Pike, 1965; Bogacz et al., 2006; Ditterich, 2006; Niwa & Ditterich, 2008; Ratcliff & Starns, 2013; Roe, Busemeyer, & Townsend, 2001; Shadlen & Newsome, 2001). Ratcliff and Starns (2013), in their confidence and multichoice model, showed that normalization of the evidence (so that the mean over all the accumulators was zero) on each time step allowed the model to account for shifts in RT distributions that occur for about half of the subjects in their experiments.
It is also assumed that the amounts of accumulated evidence for nearby angles are correlated (because the angles are close together). Because of the noise in the accumulation process, the time it takes for evidence to reach the criterion varies and sometimes the accumulated evidence reaches the wrong location. Total RT is the time to reach criterion plus the time to encode the stimulus into decision-relevant information and the time to execute a response. The latter two, which are outside the decision process itself, are added together in one component of the model that is called nondecision time.
The assumptions that there is noise in the process of accumulating evidence and that the amount of accumulated evidence is constant across time are shared with the two-choice diffusion model. There are three other shared assumptions: One is that the three components of processing (drift rate, criterion, and nondecision time) are independent of each other. Another is that the value of the criterion is under an individual’s control; setting it higher means longer RTs and better accuracy and setting it lower means shorter RTs and lower accuracy. The independence of drift rate and criterion means that an individual can set the criterion to value speed over accuracy (or accuracy over speed), no matter what his or her drift rate, and an individual with high drift rate (or low drift rate) can respond more or less quickly, depending on where he or she sets the criterion. The third shared assumption is that there is variability across trials in drift rate, criterion setting, and nondecision time, reflecting individuals’ inability to hold processing exactly constant from one trial of a stimulus to another. Variability in drift rate is represented by random variation in the height of the drift-rate distribution, illustrated by the three lines in Figure 1B. When there is more than one stimulus in the display, trial to trial variability in the height of the drift rate distributions can act to make the internal representation of a weaker stimulus stronger than a strong stimulus. This acts like an attentional mechanism with a focus on a weaker stimulus on some trials (though random noise is the major determinant of choices of weaker stimuli and random responding away from any stimuli).
The most important feature of the SCDM is that the stimulus representation (which determines drift rates), the noise in the accumulation of evidence, and the response criteria are all continuous in space. That representations of stimuli have a Gaussian distribution is straightforward. However, the assumption about noise is less so because theoretical assumptions about continuously distributed noise across space have received almost no attention in psychology. Earlier versions of my approach, since discarded, assumed multiple accumulators, but this always raised the issue of granularity (e.g., how many accumulators for a circle, 36, 360, 3600?) and the question of scaling the number of accumulators. Moving to continuous noise makes accumulation in continuous space possible. As mentioned, for fitting the model to data, the continuous functions are approximated with discrete functions but there is a simple transformation of model parameters to vary the number of discrete points.
In Figure 1C, for any angle, a straight vertical line drawn through samples for that angle (five are shown) would produce a Gaussian distribution on the vertical line. A smooth continuous function across angles (on the x-axis) is generated by a kernel function; a standard one was used here, a squared exponential, (K(x,x’)=exp(−(x-x’)2/(2r2)), where x and x’ are two points, K is a matrix, and r is a (kernel) length parameter that determines how smooth the function is. If r is varied from small to large, the correlation in noise between nearby points starts small and becomes larger. A small value of r would give a function with more peaks and troughs and larger value of r would give a function with fewer peaks and troughs. (The precise form of the kernel function is likely to be unimportant as long as it is unimodal because samples are accumulated.)
To obtain random numbers from the Gaussian process, the square root (R) of the kernel matrix, K (K=R’R, where R is an upper triangular matrix), is multiplied by a vector of independent Gaussian distributed random numbers (with SD 1) to produce the smooth random function (Lord et al., 2014). If r is relatively small, the matrix R will have only a few values off the diagonal and only points close together in the random vector will be smoothed together resulting in a jagged Gaussian process function. If r is relatively large, the matrix R will have many off-diagonal elements that are not small and the Gaussian process function will be smooth with few peaks and troughs. In Figure 1C, r is 10 degrees.
Figure 1D shows the amounts of accumulated evidence at each angle for time steps from 1 to 17, with the process terminating at the 17th time step at an angle of about 215 degrees. The peak emerges gradually with the spread of activity around the peak determined by the standard deviation (SD) of the drift-rate distribution and the kernel length parameter.
The parameters of the model that are common across tasks are nondecision time (Ter), the range of nondecision times (st, uniformly distributed), criterion (or boundary) setting (a), the range of the boundary setting (sa, uniformly distributed), the Gaussian process kernel parameter (r), the across-trial range in the height of the drift-rate distribution (sd, uniformly distributed), and the standard deviation in the drift-rate normal distribution (sw). In addition, there is one parameter for each of the conditions in an experiment that differ in difficulty, where the parameter (di) represents the mean height of the drift-rate distribution. The appendix shows how each of these parameters affects RT and accuracy. The parameters of the 2D model are described in the section on that model.
Fitting the Model to Data
I do not know of any exact solutions for DIXCthe probabilities of responses across the criterion line (i.e., the probabilities of responses at each angle) or for the distributions of RTs, so simulations are used (usually 10,000 simulated trials) to generate predictions. The data generated from the simulations are compared to the empirically obtained data and then the generating parameters are adjusted with a SIMPLEX fitting routine to obtain the best match between simulated and empirical data. The data for all the conditions of an experiment are fit to the model simultaneously and the data for each subject are fit individually. In this article, my aim was not to explore model fitting methods to find an optimal method but rather to use a fairly straightforward and robust method to show that the model can fit the data. Other methods might produce better fits but this is a topic for future investigation.
In order to generate predictions and fit the model, both time and space have to be made discrete. We fit the model using 10 ms time steps and 5 degree spatial divisions. The model parameters are presented in terms of 10 ms time steps and 1 degree spatial divisions. The equation for the update to a spatial position at each 10 ms time step is the standard Δxi=viΔt + σηi √Δt, where σ(=1) is the SD in within-trial noise, vi is the height of the drift rate location at spatial position i, xi is the evidence, and ηi is a normally-distributed random variable with mean zero and SD 1. Note that the samples of noise are not correlated across time steps, but they are correlated across spatial position (as in Gaussian process noise). This means that the samples of noise are not independent across spatial locations.
To fit the model, the data are grouped into three categories: the area around the central peak (the A area in Figure 2); the two areas just outside the central peak (B’s in Figure 2), and the combination of all the other areas (T’s - for tail - in Figure 2). Two areas, A and B, were needed for the center because when only one area was used, there was an identifiability problem because a high narrow central peak mimicked the lower wider peak shown in Figure 2. Using the two areas (A and B) solved the problem because the two areas constrained the fitting method to produce responses across the range around the peak. In experiments with more than one response location, two areas A and B were used for the strongest peak but only one area (C, D, etc.) was needed for each of the weaker peaks. The cutoffs that defined the areas A and B were selected based on the mean experimental results with a check that each individual had a B area that contained some of the tail of the distribution around the central peak.
Figure 2.
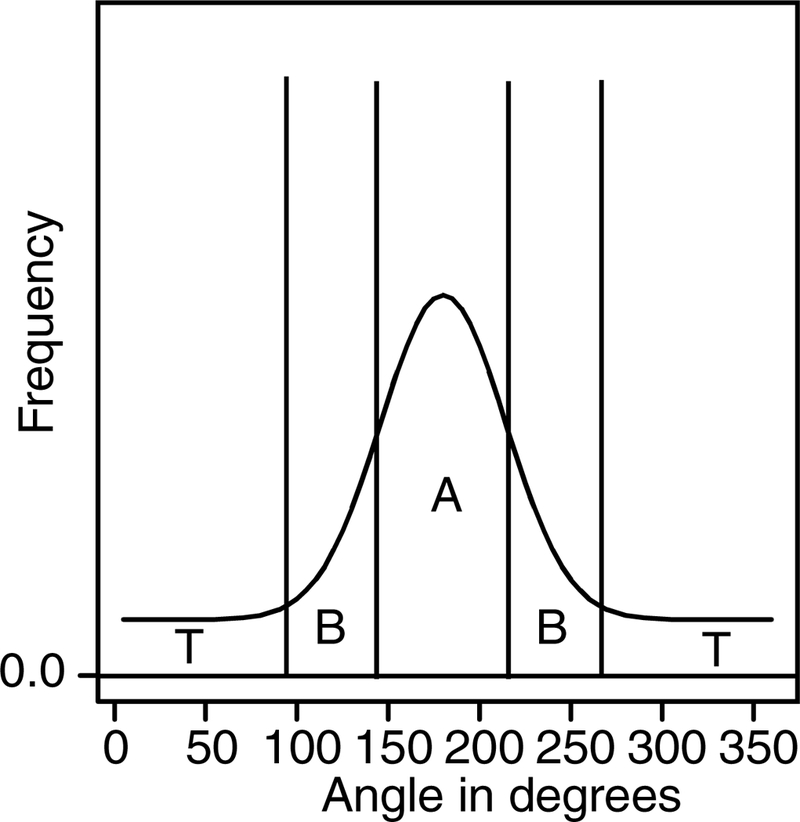
A plot of a hypothetical distribution of responses showing how they are divided into the central proportion (A), the side lobes (B), and responses outside the stimulus range (T). This division is used to group the data to provide RT distributions for model fitting. When there were two or more possible targets, areas C, D, etc. were added for the weaker targets and these represented areas A and B combined for those stimuli.
For fitting the model and for displaying data and model predictions, RT distributions are represented by 5 quantiles, the .1, .3, .5, .7, and .9 quantiles. The quantiles and the probabilities of responses for each region for each condition of an experiment are entered into a minimization routine and the model is used to generate the predicted cumulative probability of a response occurring by each quantile RT. Subtracting the cumulative probabilities for each successive quantile from the next higher quantile gives the proportion of responses between adjacent quantiles. For a G-square computation, these are the expected proportions, to be compared to the observed proportions of responses between the quantiles (i.e., the proportions between 0, .1, .3, .5, .7, .9, and 1.0, which are .1, .2, .2, .2, .2, and .1). The proportions for the observed (po) and expected (pe) frequencies and summing over 2Npolog(po/pe) for all conditions gives a single G-square (log multinomial likelihood) value to be minimized (where N is the number of observations for the condition). A standard SIMPLEX minimization routine was used to adjust the model parameters to minimize G-square. To avoid the possibility that the fitting process ended up in a local minimum, the SIMPLEX routine was restarted 8 times with 40 iterations per run and then finally run with 200 iterations (for the last 100 to 150 iterations, usually there was no change in the model parameters).
Besides the possibility of local minima in fitting the model to data, there were some other problems. In fitting the model (and in two-choice modeling), if nondecision time is too large and across-trial variability in nondecision time is small, it is possible for there to be no overlap between the predicted and data distributions at the lower quantiles. This means that a probability cannot be assigned to the lower quantile RTs and this produces numerical overflow in the programs. To deal with this, a value of nondecision time at the low end of the range for successful fits to data was selected along with a large value of across-trial variability in nondecision time. These were fixed for the first two runs of the SIMPLEX routine. This allowed other parameters to move to values nearer their best-fitting values. For the third iteration, all the parameters were free to vary which allowed nondecision time to move to a value near the best-fitting value for those data. The fourth iteration started with the across-trial range in nondecision time divided by 2.5 to counteract the large value used in the initial runs (without this adjustment, it took a lot of restarts of the SIMPLEX routine for this parameter to move to a stable lower value). Also, nondecision time was not allowed to become shorter than 175 ms because a value much lower than this is implausible given the encoding and response output processes and translation between the stimulus representation and the decision variable processes that were needed (this is discussed later). Initial values of the parameters were near the mean of those from a first run of the model fitting program and were the same for each subject, i.e., they were not adjusted for each subject. The method described above was robust to moderate changes in the initial values (e.g., a 30–50% change in them).
Experiments
There is little guidance in the literature on how to design experiments to examine performance on tasks with responses on continuous scales while at the same time measuring RTs. There are paradigms with responses on continuous scales but none that I know of that are designed to provide RT measures, especially with the constraint that decision processing should be completed prior to initiating a response.
RTs were measured from the onset of a stimulus until subjects’ eyes, finger, or mouse left a resting location. Reducing the possibility of movement before a decision was a major constraint on the development of the paradigms used here. To do this, in all the tasks, subjects were instructed to make movements only after they had made their decision. Furthermore, they were instructed to move directly to the response area to make their response. Feedback was provided if the movement from the resting point to the response location was too slow. There were some false starts with experiments that did not control or give feedback on the duration of the movement. In these, some subjects clearly lifted their finger or moved their eyes very quickly after stimulus presentation and before they made their decision, and then moved to make the response (often with slow movement times). In tasks with eye movements, eye position was recorded every millisecond and this allowed tracks to be examined. In some cases, tracks to intermediate points with a fixation at that earlier point were recorded (Kowler & Pavel, 2013). Then the eyes moved to make a response. The experiments reported here eliminated the majority of these behaviors with careful instructions, monitoring, and feedback if movement times were too long.
Recently there has been concern about the lack of replicability of studies in psychology and, historically, there has been concern that models or empirical results apply only to the specific design of a single experiment. To address these concerns, nine experiments were performed with four kinds of tasks. Each major empirical and modeling result was replicated at least once. The tasks allowed generalization over response modes, types of stimuli, and types of decisions.
Data and model fits are presented from a series of experiments with manipulations that involve the task, the stimulus, the response mode, and the mapping from stimulus to response. The first six experiments use different response methods, namely, eye fixations and touch-screen finger movements. The question was whether these modalities produce qualitatively similar or different patterns of results. The first two experiments present a patch of colored pixels in a central location, with one color dominant, and the task is to move the eyes or finger (usually the index finger) to the position on a color annulus or color half annulus that matches the dominant color in the stimulus. The second two experiments present an annulus or half annulus of black and white pixels with some areas brighter or darker than the background (more white or more dark pixels respectively) and the task is to move the eyes or finger to the brightest or darkest area (alternating from trial block to trial block). In the experiment with black and white pixels, the stimulus and response are physically the same whereas in the color experiment, the subject has to map between a degraded central color stimulus and the non-degraded response area. The next two experiments use quite different stimuli and the task is to respond by moving hand or eyes to a point on a surrounding annulus that best matches the stimulus. The fifth experiment uses stimuli that are a collection of arrows with some proportion pointing in the same direction. The task is to move the eyes to a position on the response annulus corresponding to the dominant direction. The sixth experiment is a moving dots experiment with three directions of motion and with one stronger than the others. The task is to move the finger to the position on a response annulus that corresponds to the dominant direction of motion. The next two experiments are mouse based versions of Experiment 1 and the last experiment is a version of Experiment 3 but with stimuli presented in a rectangular 2D array and requiring a touch screen response in the 2D space.
All the subjects were Ohio State University students in an introductory psychology class who participated for class credit. A small proportion (less than 5%) finished only a few trials in an experiment before deciding to leave and were eliminated. A few others had trouble with the eye-movement apparatus (e.g., excessive blinking, inability of the system to provide accurate eye fixation data) and were also eliminated. The aim was to collect data from 16 subjects in each experiment but in a few cases, the number who signed up for an experiment was more than 16 and data from all of them was used.
The data and predictions of the model for them are displayed in two ways, illustrated with the data from Experiment 1. The stimuli (Figure 3A) were center patches surrounded by a circular annulus and a subject’s task was to move his or her eyes from the center patch to the location on the annulus that matched the most dominant color in the center patch. The data were aligned so that the correct response was at 180 degrees. Then, as in Figure 2, the annulus was divided into the region around the (180 degree) location that best matched the center patch (the A region, Figure 2), the regions immediately on each side of it (the B regions), and all the other regions (the T regions).
Figure 3.
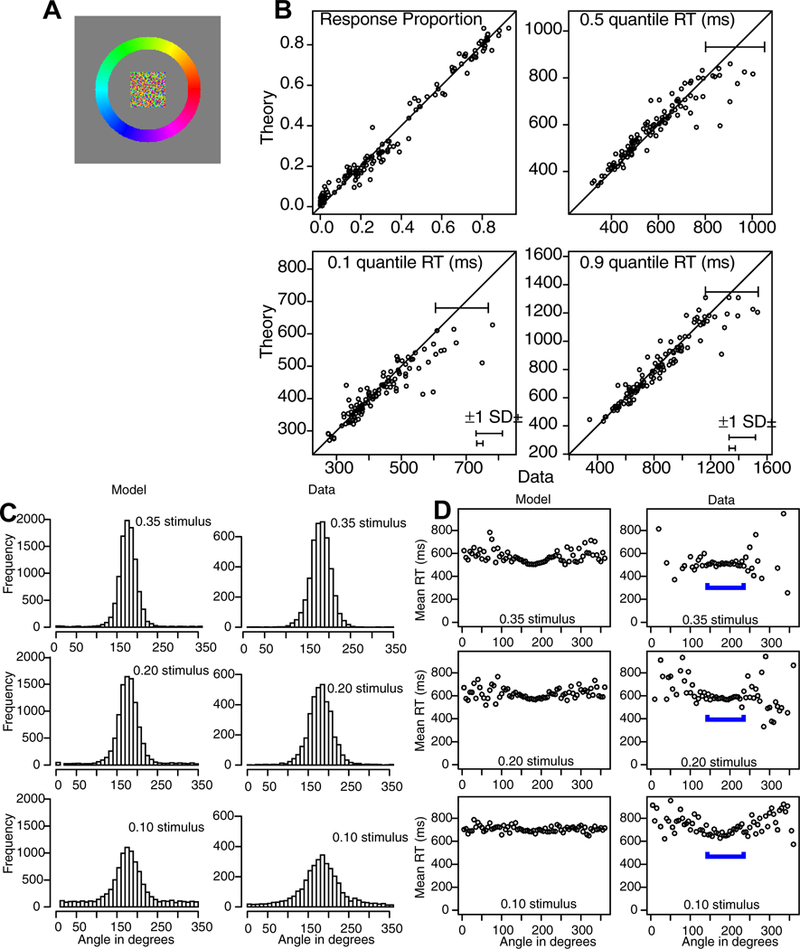
Stimulus and results for Experiment 1. A: An example of the stimulus and response configuration. B: Plots of model predictions plotted against data of the proportion of A, B, and T responses (see Figure 2) and the 0.1, 0.5 (median) and 0.9 quantile RTs for all the conditions for data from each individual subject. The horizontal error bars in the bottom right corner represent the minimum and maximum 1 SDs in the quantile RTs derived from a bootstrap analysis. The error bars in the top right show a 2 SD error bar from the maximum of the error bars in the bottom right corner. This provides an upper bound of the variability in the quantile RTs. C: Histograms of responses for the model and data as a function of angle for all data from subjects combined with the stimulus aligned on 180 degrees. D: Plots of mean RT for theory and data as a function of angle averaged over subjects. The blue brackets show the angles with most responses as shown in Panel C (and hence with lowest variability).
Figure 3B shows the data and the predictions plotted against each other. The upper left panel shows response probabilities, ranging from 0.0 (for T regions) to 0.8 (for A regions). There are 144 points on the function: the three regions for each of the three conditions (different levels of difficulty, defined later) in the experiment for each of the 16 subjects. The fact that the data and predictions fall tightly around the straight line indicates a reasonably good fit of the model to the data. The other three panels of Figure 3B show predictions against data for the 0.1, 0.5, and 0.9 quantile RTs (quantiles with less than 10 observations are not shown). Again, the tight fit of predications to data indicates a reasonably good fit.
The second way predictions and data are displayed is to plot response probabilities and RTs across angles. Figure 3C shows histograms for response probabilities for the three conditions for all the data from all the subjects and the predictions match the data well. Figure 3D shows similar plots for mean RTs.
Apparatus
For the eye-movement experiments, stimuli and response fields were presented on a CRT monitor 40 cm wide (640 pixels) and 30 cm high (480 pixels). At the standard viewing distance used (69.5 cm), the whole screen subtends a visual angle of 32×24 degrees. For the touch screen experiments, the CRT monitor was 32 cm wide and 24 cm high, which, at a standard viewing distance of 55.8 cm, gave a visual angle of 32×24 degrees. The screen phosphors for the CRT monitors are not known so the precise decay characteristics of the displays are not known and the relative intensities of the three color guns are not known. However, most of the manipulations were within-subjects with moderately short presentation durations (250–300 ms) and differences among individual subjects were so large that any assumptions about stimulus duration that might be affected by slow decay of a stimulus on the screen over 20 or 40 ms was not important.
For the eye-movement experiments, the eye tracker was an EyeLink 1000 from SR Research. The system was desktop-mounted with a chin and forehead rest. The measurements were monocular (left eye) sampling at a rate of 1000 Hz. Every trial began with a fixation point (details are presented for each experiment). After some amount of time (e.g., 500 ms) of fixation, the trial began. A response was recorded when the eyes moved from the fixation position to a response location and remained fixated at the response location for 500 ms. Response time was defined as the time from stimulus presentation to the time at which the eyes moved from the fixation position.
A few times in an experiment, calibration in the eye tracker drifted, that is, the eye tracker recorded a location systematically away from the location to which the eyes were looking. The first part of each experimental trial involved the subject fixating on a box prior to stimulus presentation (usually for 500 ms). During this time, and only this time, the position of the eye was shown on the screen by a dot drawn at every screen refresh. Both experimenter and subject could see the dots as they were drawn and the experimenter could hit a game controller button during the fixation period to tell the system that the subject was fixated in the box if the system was recording fixations outside the box. The eye tracker was then recalibrated. This happened no more than 5 or 10 times per experimental session.
The touch screen (CRT) was an ELO Entuitive 1725C with dimensions 40 cm wide and 30 cm high. Because there is considerable arm fatigue in using a touch screen horizontally on a desk, a mount was constructed so that the screen was at almost horizontal and was located between the knees of subject. This eliminated arm fatigue. A trial began when subjects hit a starting box on the screen (details are presented in each experiment). They were required to lift their finger and place it at the response location and not slide it.
There were some complicating factors with the touch-screen system used in these experiments. It uses a “surface wave” technology that detects an event based on detection of an ultrasonic wave that is generated when a finger hits or leaves the glass of the touch screen. The first measurements of the duration of the movement from finger lift to response placement produced some delays of only 20–40 ms, too short to be legitimate measurements of movement time.
In light of this, calibration tests were conducted. A piezoelectric sensor was used to measure the time at which the finger lifted, which gave an immediate measurement of lift time. This was compared to the time at which the touch screen recorded the lift. In the calibration procedure, the screen was programmed to turn an all-black screen display to an all-white one when the finger lift was recorded. A photodiode was used to record the time of this all-black to all-white change. An oscilloscope displayed the two events and results showed a 110 ms delay from when the piezoelectric sensor detected the change (finger lift) until the screen turned white. The same setup was used to record the time from a finger press to detection of the finger press event from the touch screen. As before, the finger press turned the black screen white and the photodiode was used to record this change. A delay between the finger press and recording the event of about 48 ms was found. These numbers were verified by recording the events on a video camera at a 60Hz frame rate in a completely independent set of measurements. The number of frames between lift of the finger to the screen changing from black to white replicated the 110 ms measurement (as did the finger press measurement). These delays were added into the measurements in Experiments 2, 4, 6, and 9. It is important to perform such measurements if touch-screen devices, such as tablets, phones, or laptop screens, are to be used in RT experiments.
In the mouse-based experiments, subjects placed the mouse pointer in a starting box on the screen and after some delay (so long as the pointer remained in the box), the trial began. The position of the mouse was displayed on the screen every 16.7 ms as a small dot to subjects.
RTs were measured from the onset of the stimulus/response display to the eye leaving the fixation point, a finger leaving the resting box, or the mouse leaving the starting box. Responses that were too slow (specific to each task) and movements off the response dimension (e.g., off an arc) were considered spoiled trials. To minimize visual search of the display, the stimulus was usually presented for only 250 ms for finger and mouse movements. For eye movements, the stimulus and response field remained on the screen until the eye left the fixation point, at which time the screen was blanked. To provide feedback to participants, correct responses were defined as responses within a 50-pixel square box of the peak of the target; responses outside that box were followed by an error message.
The eye tracker experiments were more finicky than the others. With touch or mouse responses, when a trial ended, the next trial could begin. With the eye tracker, the next trial began only when the camera sensed the subject’s eyes on the central fixation point. For some subjects this was a smooth process, but for others it took a few extra seconds for the fixation point to register. Over the course of the entire experiment, if this happened with regularity then those subjects were not able to complete the full sessions of trials. Additionally, some subjects calibrated easily in the initial calibration process and for others, there were problems that required the experimenter to perform the calibration process several times. Sometimes the subjects also had difficulty in fixating on the target (without moving back to the central location). Also, for some subjects, there were problems in calibration due to glasses and contact lens. A session was planned to be the number of trials that could be completed in 50 minutes if everything ran without problems, but sometimes only a little more than half the trials could be obtained from a subject.
Experiment 1
The stimuli were central patches of colored pixels surrounded by a circular annulus also made up of colored pixels (Figure 3A). Subjects responded by moving their eyes from the central patch to the location on the annulus that best matched the dominant color in the patch. There were three levels of difficulty; the proportion of pixels of the dominant color in the central patch was 0.35, 0.20, or 0.10. Subjects were instructed to make their decisions as quickly and accurately as possible and to move their eyes only after they had made their decision.
Method
At the beginning of each trial of the experiment, subjects were asked to fixate on a 20×20 pixel white box at the center of the CRT screen. After 500 ms of fixation, the central patch replaced the box and simultaneously the annulus was displayed. RTs were measured from the onset of the display to when the eyes moved outside a 30 pixel (1.5 degree) radius from the fixation point.
The central patches were 44×44 pixels. They were created by placing pixels of random colors (out of 253 possible colors) at random locations on the patch. One color was selected randomly and then a proportion of the pixels, 0.35, 0.20, or 0.10, was changed so that each pixel was changed to the target color or one within 10 of the target. The color selected was one of 21 from a uniform distribution with range minus 10 to plus 10 of the target.
The annulus contained all 253 colors. Its central radius was 60 pixels (3.0 degrees) from the center of the screen and it was 16 pixels (0.75 degrees) wide. The pixels changed from red (at angle zero, horizontal right) counter-clockwise through all 253 colors with yellow at 60 degrees, green at 120 degrees, teal at 180 degrees, dark blue at 240 degrees, and violet at 300 degrees (Figure 3A).
There were 16 subjects in the experiment. They were instructed to move their eyes away from the central patch only when they had made a decision about where the central patch’s dominant color was located on the surround. To discourage moving the eyes in more than a single step, the display of the central patch and surround was blanked when the eye moved outside two degrees from the fixation point. This meant that once the eyes moved, there was no more stimulus or response information available from the display.
There were 10 blocks of 72 trials each, preceded by two practice blocks. Each block contained 24 trials for each of the conditions, randomly ordered. A session was 50 min. long. Many subjects did not finish all 10 blocks: There was an average of 560 observations per subject out of a possible 720.
Target locations were measured in terms of their x/y coordinates in the 640 by 480 screen of pixels. The center of a target location was at a radius midway between the inner and outer radii of the surrounding annulus and its size was a 2-degree-by-2-degree (40-by-40 pixel) invisible box centered on the target color. The box was not rotated based on stimulus angle, so the box had a narrower angular extent at 0, 90, 180, 270 degrees than at other angles.
To indicate whether a response was correct, if a subject’s eyes moved to a location in the box, a “1” was displayed in the invisible box location; if not, a “0” was displayed at the position to which the eyes had moved. “1”s and “0”s remained on the screen for 300 ms. If the movement started later than 1250 ms after the onset of the display, “TOO SLOW” was presented for 500 ms in the center of the display. If it started earlier than 150 ms, “TOO FAST” was presented. There was a 40 ms blank screen between the feedback messages and the fixation point for the next trial. Generally, the task became routine and subjects rarely received “TOO SLOW” or “TOO FAST” messages after the practice blocks.
Results
The stimuli were aligned to set the zero point at 180 degrees. The A area corresponded to 150–210 degrees, the B area to 100–150 and 210–260 degrees, and the T area to the rest. Figure 3B, top left panel, shows the data and predictions from the model for response probabilities for the three difficulty conditions for the three response categories for the 16 subjects (144 points). There were a few misses as large as 10%, but misses of this size are only a little larger than the maximum expected. (If there were 200 observations per difficulty level, then for a proportion of 0.2, the SD is sqrt(.2*.8/200)=0.028, which means that 2SD’s are almost plus or minus 0.06.)
The other panels of the figure show the 0.1, 0.5 (median) and 0.9 quantile RTs. There are only 111 points on these plots because only data for which there were more than 10 observations per condition per response category are plotted. In the bottom right corner of each quantile plot are two plus and minus 1 SD error bars (horizontal because the data are on the x-axis). To construct the error bars, a bootstrap method was used. For each condition and response category for each subject, a bootstrap sample was obtained by sampling with replacement from all the responses for that condition. This was repeated for 100 samples and then the SDs in the RT quantiles were obtained for that subject, condition, and response category from the 100 bootstrap data sets. The SDs for the three conditions and the three response categories with the largest and smallest SDs were then averaged across subjects and it is these two SDs that are at the bottom right corners (this excluded T quantiles from the two easier conditions, 0.35 and 0.20, because most subjects had less than 10 responses in those categories, and sometime zero, with 10 the minimum number of observations we used for displaying quantiles). On the diagonal line of equality, a 2-SD error bar computed from the larger SD at the bottom right is shown. This 2-SD error bar provides an upper bound on deviations that would be expected between the predictions and data if the model fit the data perfectly.
The results for the quantile RTs show a good match between predictions and data; almost all of the data points fall within the two-SD error bars. The largest misses are four values of the 0.1 quantile that show longer RTs than predicted (by about 100–200 ms). These are for single conditions and single response categories for single subjects. If they represented a systematic miss, then the 0.1 quantile RTs should miss for all the A, B, and T responses (and perhaps all the conditions) but they do not.
Tables 1 and 2 show the values of the parameters that produced the best fits of the model to data for all the experiments, averaged over subjects. The SDs in the model parameters across subjects are shown in Tables 3 and 4. For this experiment, the height of the normal distribution of drift rates decreased with difficulty, as would be expected. Discussion of the other parameters is presented after Experiment 1–8.
Table 1:
SCDM parameters
| Task | Exp. | Ter | St | a | sa | sw | r | Sd | G2 | df | χ2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Color 72 eye | 1 | 177.5 | 33.1 | 15.4 | 5.9 | 37.0 | 14.0 | 0.859 | 89.2 | 41 | 56.9 |
| Color 72 touch | 2 | 272.4 | 25.1 | 11.0 | 3.0 | 24.9 | 11.8 | 1.082 | 98.8 | 41 | 56.9 |
| Dynamic bright eye | 3 | 177.7 | 48.1 | 12.3 | 5.5 | 26.0 | 34.0 | 0.821 | 102.0 | 35 | 49.8 |
| Static bright touch | 4 | 221.5 | 59.3 | 7.5 | 2.7 | 17.5 | 18.1 | 0.761 | 92.6 | 35 | 49.8 |
| Arrows 72 eye | 5 | 186.0 | 22.6 | 11.4 | 5.7 | 26.5 | 24.1 | 0.839 | 82.4 | 41 | 56.9 |
| Moving dots touch | 6 | 301.6 | 34.4 | 9.3 | 3.4 | 31.0 | 21.7 | 0.925 | 185.2 | 71 | 91.7 |
| Color 72 mouse | 7 | 235.9 | 26.3 | 15.4 | 2.9 | 32.0 | 5.4 | 1.047 | 93.0 | 41 | 56.9 |
| Color sp/acc mouse | 8 | 225.6 | 23.4 | 13.6 15.3 |
2.4 | 33.7 | 9.8 | 0.897 | 133.6 | 58 | 76.7 |
| 2D brightness | 9 | 179.1 | 26.0 | 8.8 | 4.0 | 16.4 | 18.2 | 0.528 | 282.4 | 48 | 65.2 |
Ter is nondecision time, st is the range in nondecision time, a is the boundary setting, sa is the range in the boundary setting, sw is the SD in the drift rate distribution, r is the Gaussian process kernel parameter, sd is the range in the height of the drift rate distribution, G2 is the multinomial maximum likelihood statistic, df is the number of degrees of freedom, and χ2 is the critical chi-square value. Exp. means Experiment.
Table 2:
SCDM drift rates
| Task | Exp. | Conditions | d1 | d2 | d3 |
|---|---|---|---|---|---|
| Color 72 eye | 1 | 0.35, 0.20, 0.10 | 42.7 | 31.3 | 16.7 |
| Color 72 touch | 2 | 0.35, 0.20, 0.10 | 29.3 | 25.8 | 19.4 |
| Dynamic bright eye | 3 | 0.62, 0.58 | 26.2 | 12.2 | |
| 0.58, 0.54 | 14.6 | 5.1 | |||
| Static bright touch | 4 | 0.75, 0.65 | 26.7 | 13.4 | |
| 0.65, 0.60 | 20.6 | 12.2 | |||
| Arrows 72 eye | 5 | 0.60, 0.40, 0.20 | 31.1 | 23.4 | 13.2 |
| Moving dots touch | 6 | 0.5, 0.1,0.1 | 33.6 | 5.6 | 6.0 |
| 0.4, 0.2, 0.1 | 25.3 | 9.6 | 3.3 | ||
| 0.4, 0.2, 0.2 | 21.9 | 6.9 | 5.6 | ||
| Color 72 mouse | 7 | 0.35, 0.20, 0.10 | 30.0 | 25.8 | 18.0 |
| Color sp/acc mouse | 8 | 0.25, 0.10 | 32.1 | 21.4 | |
| 2D brightness touch | 9 | 0.70, 0.50, 0.40 | 18.1 | 10.6 | 6.6 |
| 0.60, 0.50, 0.40 | 16.3 | 12.1 | 8.3 |
di is the height of the drift rate distribution. Exp. means Experiment.
Table 3:
SDs in SCDM parameters
| Task | Exp. | Ter | St | a | sa | sw | r | Sd |
|---|---|---|---|---|---|---|---|---|
| Color 72 eye | 1 | 12.4 | 13.2 | 2.6 | 2.5 | 2.4 | 10.0 | 0.47 |
| Color 72 touch | 2 | 81.8 | 3.8 | 1.3 | 1.9 | 2.9 | 6.0 | 0.46 |
| Dynamic bright eye | 3 | 20.7 | 15.7 | 1.8 | 0.9 | 2.2 | 5.5 | 0.25 |
| Static bright touch | 4 | 39.3 | 6.6 | 1.4 | 0.7 | 3.5 | 5.7 | 0.11 |
| Arrows 72 eye | 5 | 12.6 | 2.0 | 1.3 | 0.6 | 1.7 | 4.9 | 0.13 |
| Moving dots touch | 6 | 57.4 | 14.2 | 1.5 | 0.6 | 2.9 | 5.8 | 0.22 |
| Color 72 mouse | 7 | 41.7 | 6.3 | 2.6 | 1.3 | 3.9 | 0.3 | 0.46 |
| Color sp/acc mouse | 8 | 30.6 | 1.8 | 2.3 3.2 |
0.8 | 3.7 | 0.9 | 0.28 |
| 2D brightness | 9 | 6.9 | 4.0 | 0.9 | 0.4 | 1.8 | 17.2 | 0.05 |
Table 4:
SDs in SCDM drift rates
| Task | Exp. | Conditions | d1 | d2 | d3 |
|---|---|---|---|---|---|
| Color 72 eye | 1 | 0.35, 0.20, 0.10 | 11.2 | 5.9 | 3.9 |
| Color 72 touch | 2 | 0.35, 0.20, 0.10 | 4.6 | 3.5 | 3.7 |
| Dynamic bright eye | 3 | 0.62, 0.58 | 3.2 | 2.6 | |
| 3 | 0.58, 0.54 | 2.8 | 2.4 | ||
| Static bright touch | 4 | 0.75, 0.65 | 2.4 | 1.3 | |
| 4 | 0.65, 0.60 | 2.3 | 1.8 | ||
| Arrows 72 | 5 | 0.60, 0.40, 0.20 | 3.1 | 2.7 | 1.9 |
| Moving dots | 6 | 0.5, 0.1,0.1 | 4.3 | 2.8 | 3.4 |
| 6 | 0.4, 0.2, 0.1 | 4.4 | 2.4 | 1.9 | |
| 6 | 0.4, 0.2, 0.2 | 4.3 | 1.8 | 1.8 | |
| Color 72 mouse | 7 | 0.35, 0.20, 0.10 | 5.4 | 5.1 | 4.5 |
| Color sp/acc mouse | 8 | 0.25, 0.10 | 5.3 | 4.4 | |
| 2D brightness | 9 | 0.70, 0.50, 0.40 | 1.4 | 1.1 | 1.1 |
| 9 | 0.60, 0.50, 0.40 | 1.3 | 1.1 | 0.9 |
For Figures 3C and 3D, predictions and data are plotted as a function of angle, with the target locations aligned at 180 degrees. The predictions were generated by simulation using the parameter values in Table 1 with 10,000 simulations for each condition. For Figure 3C, response probabilities, the data and predictions were grouped into bins of 10 degrees. The predicted and data distribution peaks and spreads qualitatively match each other. This is especially impressive because the predictions were generated from the model parameters derived from fits to the response probabilities and quantiles (Figure 2B) and not from fits to the distributions of data directly. One deviation between predictions and data is the wider distribution of responses for the data relative to the model for the 0.1 stimulus. This suggests that a weak stimulus has greater variability (less precision) and this could be accommodated by assuming the SD in the drift rate distribution is larger for weak stimuli. Another deviation between theory and data is in the response proportions for conditions with values near zero for the data. The model predicts values larger than zero and there are systematic misses for some of these. In the discussion the possibility that the Gaussian process noise is stimulus location dependent and larger near the stimulus is considered.
For Figure 3D, RTs, the data and predictions also match well (5 degree angles per bin). The responses nearest the target angle (180 degrees) represent the A category, responses a little farther away represent the B categories, and all the others represent the T category. The blue bars in the figure show the responses in the A and B categories. The data show higher variability in the tails away from 180 degrees for the data than the predictions because there were low numbers of observations for the data but 10,000 observations in the simulated values. There was little difference in RTs across angles (i.e., across the A, B, and T response categories). However, RTs increased with difficulty, from a mean of 507 ms for the 0.35 condition to 576 ms for the 0.20 condition to 693 for the 0.10 condition (these means represent the vertical shifts from responses in one condition to another in Figure 3D). These are large effects and ones that the model captures well.
Experiment 2
This experiment was similar to Experiment 1 except that the display used a half annulus surround and the response modality was a finger movement to the target color. Apart from this, the geometry of the display was the same as for Experiment 1. Figure 4A shows the central patch and the response half annulus. Responses were made by finger movements on the touch screen system. A half annulus was used because the resting position of the arm would have obscured part of a full annulus. Difficulty was manipulated in the same way as for Experiment 1. To anticipate, response modality (eye movements or finger movements) did not affect the patterns of results.
Figure 4.
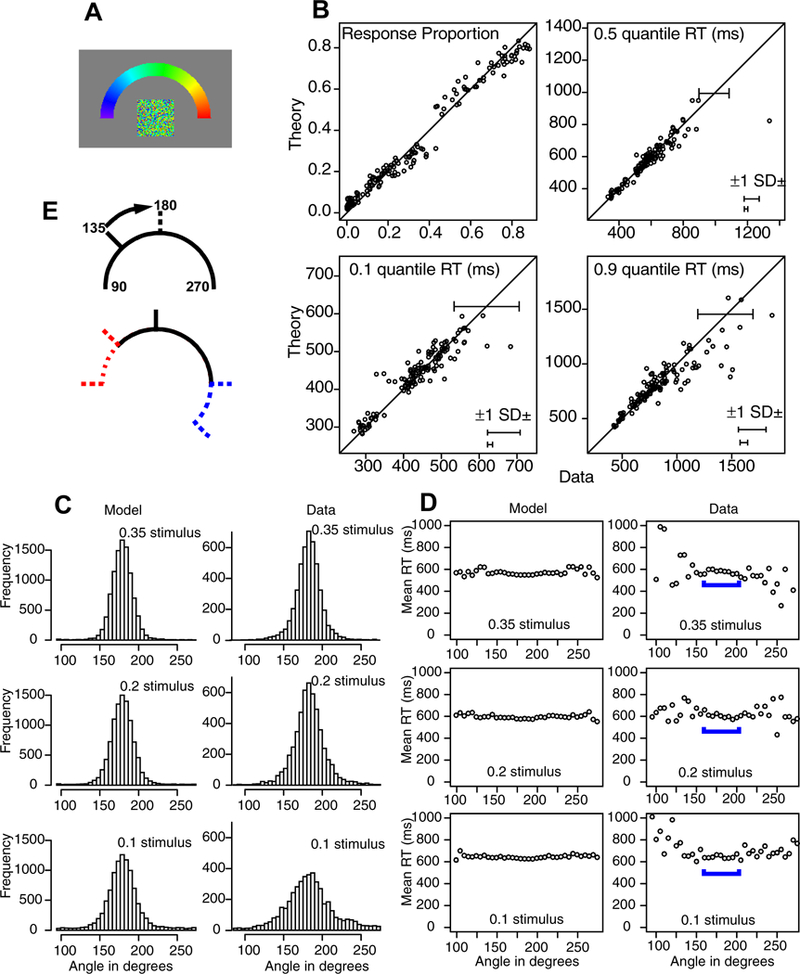
The same analysis as in Figure 3 for Experiment 2. Panel E shows the result of aligning the stimuli at a common angle (180 degrees). Responses are lost (blue dashed line to the right) and areas contain no responses (red dashed line to the right). For full details, see the text.
Method
There were 12 blocks of 72 trials each, 24 of each condition in each block ordered randomly. Like Experiment 1, a session was 50 min. long but, without the need for eyetracker calibration, there were more responses, an average of 823 out of a possible 864. There were 16 subjects.
The central patches were constructed in the same way as for Experiment 1 except that only colors between 10 degrees and 170 degrees were used in order to avoid end effects. The central patch was displayed at the center of the half annulus (Figure 4A) and it was 16 pixels (.75 degrees) square. The half annulus contained 190 out of the possible 253 colors and its colors began at purple on the far left and ended at red on the right.
Subjects began each trial by touching their index fingers to a square that was located 9.5 degrees below the central patch. 250 ms after the touch, a plus sign appeared at the location at which the central patch would be displayed and it remained on the screen for 500 ms. 240 ms after that, the central patch and the half annulus were displayed. Subjects were instructed to move their fingers and touch the location on the half annulus that best matched the dominant color in the central patch. To discourage subjects from changing the target locations they had chosen during the finger movement, the central patch was turned off as soon as the finger was lifted but, unlike Experiment 1, the half annulus remained on the screen until the finger touch. This seemed to be more natural than turning it off as in the eye movement experiments. In the eye movement experiments, many of the eye movements were ballistic and turning off the response annulus did not affect the response. Following a response, feedback of the same kind as for Experiment 1 was presented for 300 ms, followed by the 40-ms blank screen. Response time was measured from onset of the patch and half-annulus to the time at which the finger lifted from the resting square.
Results
The stimuli were aligned to set the zero point at 180 degrees. The A area corresponded to 70–110 degrees, the B area to 45–70 and 110–145, and the T area to the rest. The results are quite similar to those of Experiment 1. The best-fitting parameter values are shown in Tables 1 and 2, with the heights of the distributions of drift rates decreasing with difficulty.
Figure 4B shows response probabilities and the 0.1, 0.5, and 0.9 quantile RTs for the three difficulty conditions for the three response categories for each subject, and for the quantiles, SDs constructed by the same method as for Experiment 1. There are 144 points on the probability plot and only 124 for the quantiles because conditions with fewer than 10 observations were excluded. There are no remarkable deviations between predictions and data for the response probabilities. For RTs, there are perhaps two large deviations in the 0.1 quantile, one in the 0.5 quantile and four or five in the 0.9 quantile. As in Experiment 1, these deviations are not consistent across conditions for an individual subject.
Figures 4C and 4D show predictions and data as a function of angle. The predictions were generated in the same manner as for Experiment 1 and they match the data well. As for Experiment 1, there was little change in RTs across angles, RTs increased with difficulty, and there was more variability in the tails away from 180 degrees for the predictions than the data. RTs increased from a mean of 536 ms for the 0.35 condition to 555 ms for the 0.20 condition to 579 ms for the 0.10 condition and the model fit these differences well.
There is one issue to note and that is that to produce the plots in Figures 4C and 4D, the stimulus location was repositioned to 180 degrees (with a range from 100 to 260 degrees). In Experiment 1, this was accomplished by simple rotation, but in this experiment there is a problem because there are separate end points for the half annulus. To illustrate this problem, suppose the central patch had a color that was at 135 degrees (with the center of the half annulus at 180 degrees) and the stimulus location was rotated by 45 degrees from 135 to 180 degrees as in Figure 4E. Then responses that were at 270 degrees move to 270+45=315 degrees which is outside the 100–260 degree range (the blue dashed line to the right in the bottom panel). Stimuli at 90 degrees rotate to 135 degrees which means that are no responses in the range from 90 to 135 (red dashed line to the left in the bottom panel).
For the responses in Figure 4C, frequencies at 135 degrees are out of 75% of the possible frequencies at 180 degrees. This means that the histograms in Figure 4C (for the data) underestimate the frequencies in the tails away from 180 degrees. This does not change the results for the 0.35 and 0.20 stimulus conditions because there are few responses in the tails, but for the 0.1 stimulus condition, the extreme tails are lower than they would be with equiprobable histograms. In the model predictions, the stimulus position is set to 180 degrees only so all the other angles from 100–260 degrees are equiprobable.
In the later experiments, two or more stimuli occur at random positions and in order to provide plots of the responses around the peak of both stimuli and between them, it is necessary to compensate for missing responses by moving responses that are outside the range to inside the range that would otherwise contain no responses, i.e., responses in regions that do not correspond to stimuli are filled in with responses that would be discarded.
The width of the histogram for the 0.10 stimulus condition is larger than that for the predictions. As for Experiment 1, one way to address this is to assume more variability (less precision) in weak stimuli which would require increasing the SD in the drift rate distribution (instead of keeping it constant as it was done in the fits).
Experiment 3
The aim for this experiment was to examine a task in which stimulus and response coincided, as they might for many devices such as cell phones and touch screens. Each stimulus was an annulus made up of black and white pixels (Figure 5A). The pixels were randomly distributed across the annulus except that there were two patches with more white than black pixels, one with a higher proportion of white pixels than the other, and two patches with more black than white, one with a higher proportion of black pixels than the other. On some blocks of trials, subjects were instructed to move their eyes from a center fixation point to the location on the annulus that was the brightest (the largest proportion of white pixels) and on the other blocks of trials, to the darkest (largest proportion of black pixels). It turned out that dark responses to dark patches were symmetric with bright responses to bright targets and so the two were collapsed. Also, when responding to bright targets there was no evidence that subjects were avoiding dark patches (and vice versa) and so the status of the patches of the other polarity was ignored in the method and analyses presented below. Collapsing conditions produced two conditions at different levels of difficulty with two stimulus patches for each condition. The circular annulus was dynamic: a new randomly generated annulus was displayed on each frame of the display with the same brighter and darker locations.
Figure 5.
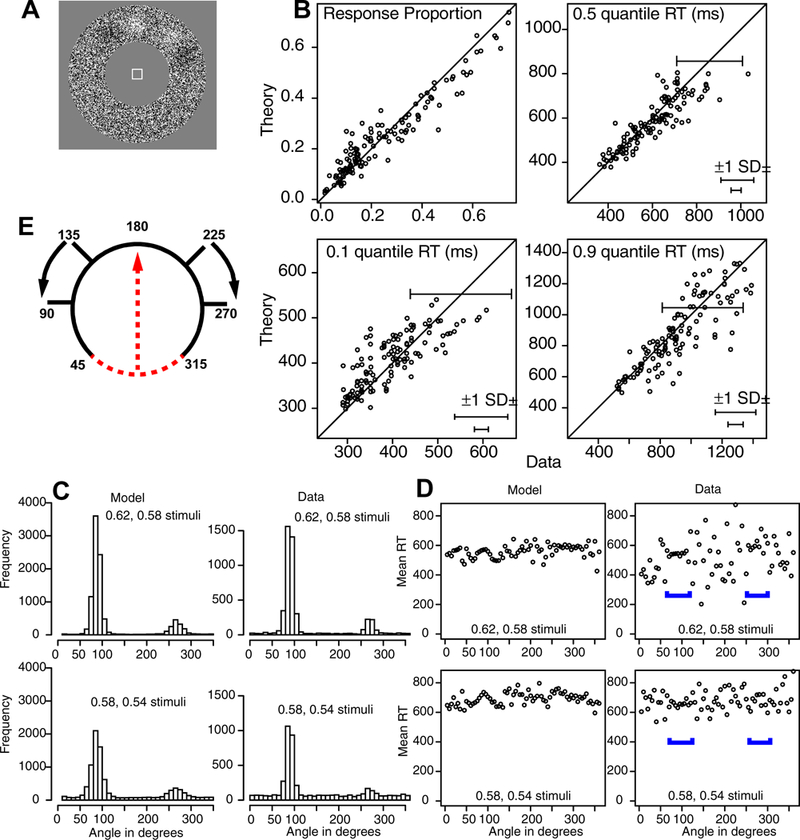
The same analysis as in Figure 3 for Experiment 3. Panel E shows the result of aligning the stimuli at common angles (90 and 270 degrees). When stimuli are moved apart, areas are left with no responses (e.g., 135 to 225 degrees - what was at 179 moves to 134 and what was at 181 moves to 226), and to compensate, responses in areas in which there may be responses but disappear, e.g., 45–0-315, the red dashed area, are moved to the 135–225 range.
Method
The circular annulus stimuli were constructed in the following way: first, pixels were randomly set so that 50% of them were white and 50% black. Then four locations on the annulus (at the center radius) were randomly selected with the limitation that they were at least 36 pixels apart (about 1.8 degrees of visual angle and 21 radial degrees around the annulus). Then some proportion of the pixels at two of the locations were changed to white and at the other two, changed to black. These locations served as the centers of 2D normal distributions with SD 6 pixels. The proportions that were flipped to white or to black in the patches were obtained from the height of the normal distributions. The proportions of white or black pixels at the peak of the normal distribution (center of the patch) were 0.62 and 0.58 for the easier condition and 0.58 and 0.54 for the more difficult condition. The radius of the center of the annulus was 100 pixels (5 degrees of visual angle) and it was 72 pixels wide.
The displays were dynamic. Every 10 ms (determined by the refresh rate of the CRT monitors), a new random sample of noise was generated and new patches were generated in the same locations with different random samples of pixels changed from black to white or white to black.
There were 12 blocks of 72 trials, preceded by 45 practice trials. In each block, there were two conditions for the bright or dark targets, one with the easier proportions and one with the more difficult ones, in random order. For half of the blocks, subjects were instructed at the beginning of the block to move their eyes to the brightest location and for the other half, to the darkest location. These blocks alternated through the experiment. Subjects found this task more difficult than that for Experiment 1 in terms of staying on task and so very few subjects completed the experiment. This produced an average of 457 observations per subject out of 819 total trials.
At the beginning of a trial, subjects fixated on a white square (20 pixels square - about 1 degree) at the center of where the annulus was to appear (Figure 5A); then the annulus appeared with random assignment of 50% black and 50% white pixels for 500 ms with a new random assignment of black and white pixels presented every 10 ms (the frame rate of the display); then as a signal that the stimulus appeared, the fixation rectangle changed to all black pixels and the pixels at the four locations on the annulus changed to the appropriate proportions of black and white pixels. RTs were recorded from the onset of the bright and dark patches to when eyes moved 30 pixels from the center of the fixation box. When the eyes had moved 70 pixels from the center of the fixation box, the screen blanked. Feedback was provided with “2” presented for a response at the strongest peak, “1” at the weaker peak, and “0” for the other locations. The regions around the peak used to determine the feedback were boxes that had side lengths of 40 pixels. During the period that feedback was presented, the next set of images for the stimuli was loaded into the computer memory and this took about 1.4 seconds.
Results
“Bright” responses to bright stimuli were collapsed with “dark” responses to dark stimuli because there was less than a 1% difference in accuracy between them and only a 21 ms difference in mean RTs between them. Furthermore, subjects did not avoid responding to the opposite parity (e.g., they were not less likely to respond to a dark region when the task was to respond to a bright region). Therefore the data were collapsed across dark and bright conditions and so modeling and data are in terms of two conditions, stronger (higher proportion of black or white pixels) and weaker (lower proportions).
Because the locations of the bright and dark patches were randomly generated, it was necessary to align their positions in order to group data appropriately for model fitting. The peaks of the locations were aligned such that the stronger peak was rotated to 90 degrees and the weaker rotated to 270 degrees. The two peaks were usually closer than 180 degrees which means that after aligning the peaks, the numbers of observations between the two would be under-represented. For example, if the locations were at 135 and 225 degrees and responses were moved along with the locations, then responses 135–180 would move to 90–135 and responses 180–225 would move to 225–270. Thus there would be a gap between 135 and 225 degrees. To compensate, these positions were filled with responses from 45–0-315 degree range on the opposite side (the red dashed line moving up as in Figure 5E). An analysis showed that there were no differences in response proportions from those in the shorter distance between two peaks versus those in the larger distance between two peaks which shows that this alignment method did not distort results.
Responses were divided into four areas (cf., Figure 4): the A area was 83–97 degrees with the center of the strongest location at 90 degrees, the B area was from 69–82 and from 98–111 degrees, the C area was from 249–291 degrees (with the center of the weaker location at 270 degrees), and the T area was all the rest.
Figure 5B shows response probabilities and the 0.1, 0.5, and 0.9 quantile RTs for the two levels of difficulty and the four categories of responses (A, B, C, and T) for each subject. For the quantiles, only conditions and areas with more than 10 observations per subject are plotted. The number of points for response probabilities was 128 and the number for quantiles was 123.
There is a good match between predictions and data. The SD bars in the lower right of the panels and the SD bar around the diagonal line were computed as for the other experiments. For the response probabilities, there were few large non-systematic outliers. For the quantiles, there were fewer observations than for the earlier experiments, so variability was larger and there were deviations in the 0.1 quantile RTs between theory and data as large as 100 ms. But the large variability in the data made these large deviations less than 2 SD’s outside the predictions. There seems to be less deviation between theory and data in the median RTs (0.5 quantiles), but the x-axis and y-axis scales are twice that for the 0.1 quantiles and the deviations are as large numerically. As before, the deviations in the 0.9 quantiles (tails of the distributions) are large also.
Figure 5C shows the proportions of responses combined over subjects plotted as a function of angle. To construct these plots from the data, the data are aligned as described above with the strongest stimulus at 90 degrees and the weaker one at 270 degrees then all responses are combined over subjects and plotted. Predictions are generated from the mean parameter values from Table 1 and then plotted in the same way as for the data. The comparisons between data and the model predictions are good especially keeping in mind that the details of the shape of the function are not fitted, rather only the A, B, C, and T groups of trials as in Figure 2.
Figure 5D shows mean RTs as a function of angle. There was little difference in mean RTs across the angles, but there was a large effect of difficulty with the mean RT 549 ms for the easier condition and 665 ms for the more difficult one.
Experiment 4
The display was a half annulus of black and white pixels (Figure 6A) and subjects were to move their index finger to the brightest or darkest area. Like Experiment 3, there were two locations with more white than black pixels, one with a higher proportion of white than the other, and two locations with more black than white pixels, one with a higher proportion of black than the other. As for Experiment 3, bright responses to bright stimuli were symmetric with dark responses to dark stimuli and when responding to bright stimuli, the dark patches were not avoided and vices versa (and so patches of the opposite polarity could be ignored). This led to two conditions with two levels of difficulty (brightness levels) with two patches in each of them. Unlike Experiment 3, the displays were static.
Figure 6.
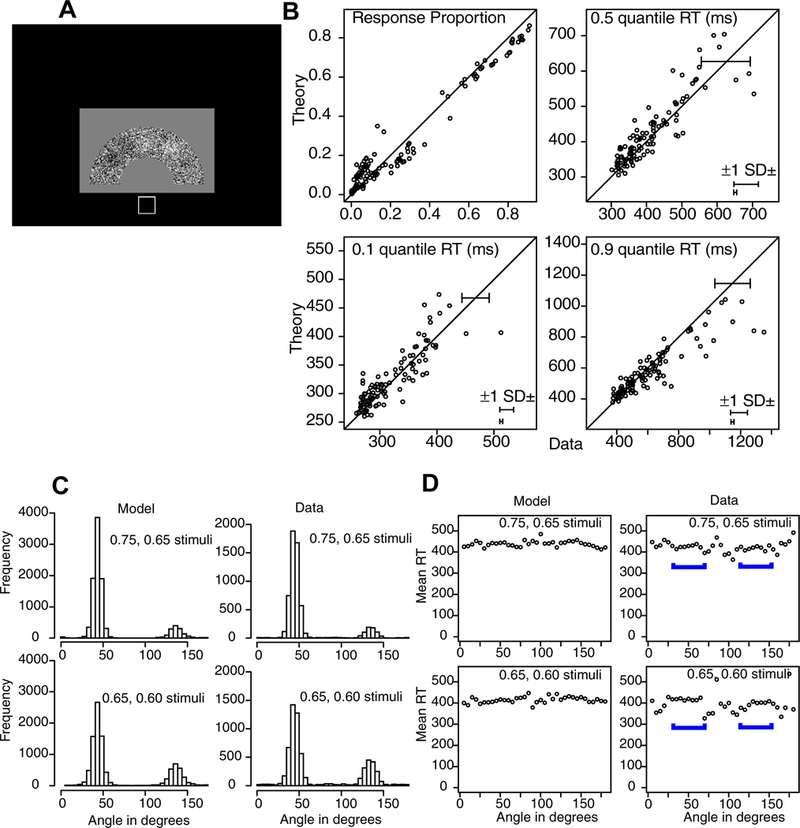
The same analysis as in Figure 3 for Experiment 4.
Method
The half annulus stimuli were constructed in the same way as for the annulus stimuli in Experiment 3. To construct the stimuli, a half annulus of 50% randomly placed black and white pixels was constructed with a center radius of 100 pixels (5 degrees of visual angle) and width of 72 pixels. The patches were 2D Gaussians with SD of 12 pixels. The patches were constrained to be at least 36 pixels apart (about 1.8 degrees of visual angle). There were two levels of difficulty with 0.75 and 0.65 proportions of white (or black) pixels at the strongest peak of the Gaussian and with 0.65 and 0.60 proportions at the weaker peak (the shorthand strong and weak stimuli within the easy and difficult conditions is used below). In the task, subjects placed a finger in a start box 190 pixels (9.5 degrees of visual angle) below the center of the half annulus (Figure 6A), the stimulus appeared and then the task was to move the finger to the brightest patch (or the darkest patch in different blocks of trials).
The proportions of pixels changed were much larger and the SDs in the Gaussians were twice as large as those for Experiment 3. This is because Experiment 3 used dynamic stimuli which tended to average out variability leading to more visible differences at lower values of the proportions (e.g., Ratcliff & Smith, 2010).
The apparatus was the same as in Experiment 2 and there were 16 undergraduate subjects. Subjects touched their finger in a square corresponding to the fixation square in Experiment 3 (as in Experiment 2) which was located at the center of the screen. After the touch there was a 250 ms period where the square remained on, then it was erased and a + sign came on for 500 ms in the center of the half annulus, then it went off and 250 ms later the stimulus in the response annulus was presented. The annulus remained on until a finger lift was detected. After the response, feedback was presented for 250 ms with “2” presented for the stronger peak, “1” for the weaker peak, and “0” otherwise. The regions around the peak used to determine the feedback were boxes that had side lengths of 50 pixels. Response time was measured from stimulus presentation to the time at which the finger lifted from the resting square to move to the target.
For modeling and data analysis, the strong and weak stimuli were aligned on 45 degrees and 135 degrees respectively on the half annulus (which subtended 180 degrees). The stimuli were randomly placed in the display which leads to the problems discussed in Experiments 2 and 3: how to align responses and deal with those that were outside the patches. Also, because the stimuli were presented on the half annulus, there was the same problem as for Experiment 2 with alignment outside the 180 degree range. In the design of the experiment, first, no patch could be more than 90 degrees away from the others, second, patches were 3 SDs away from the ends of the half annulus (i.e., between 21 and 159 radial degrees), and third, patches could be no closer than 3 SDs, i.e., 21 radial degrees.
To align the stimuli, the stimuli were moved in a way analogous to Figure 5E and areas analogous to the blue area in Figure 4E and the red area in Figure 5E were moved to fill in the empty ranges. As for Experiment 3, there was no systematic difference between the proportions of responses in the areas that were moved from those that were rotated (Figure 4E).
As for Experiments 1 and 2, the touch screen task was easier to perform than Experiment 3 with eye movements. There were 12 blocks of 72 trials as for Experiment 3 preceded by 45 practice trials. Trials proceeded more quickly than in Experiment 1 and many subjects completed all trials. There was a mean of 812 observations per subject out of 819 total.
Results
As in Experiment 3, bright responses to bright stimuli were reasonably symmetric with dark responses to dark stimuli (for strong stimuli, the difference is 3% in accuracy and 9 ms in mean RT and for weak stimuli the difference is 4% in accuracy and 5 ms in mean RT) and so they were grouped into strong versus weak. The angles used to specify the areas used to group data to produce quantile RTs as in Figure 2 are: A 36–54 degrees, B 18–35 and 55–72 degrees, C (the area for the second peak) 126–172 degrees, and T the rest. Also, as in Experiment 3, when the task was to respond to bright areas, responses at dark areas were no lower than the background (and vice versa).
Figure 6B shows plots of the model fit to the response proportions and 0.1, 0.5, and 0.9 quantile RTs for each individual subject for each condition of the experiment (there are 168 points in the response proportion plot and 154 in the quantile plots, i.e., those with greater than 10 observations in the condition.
Figures 6C and 6D show plots of the data and model for response proportions and mean RTs. As for the other experiments, these show good matches between theory and data. There are responses to the brightest and next brightest peak in the stimulus and the model matches the data as for Experiment 3. The RT results show little effect of difficulty on performance with only a 10 ms effect of difficulty (0.75/0.65 versus 0.65/0.60 stimuli). Also, the weak peak has mean RT only 5 ms shorter than the strong peak. This lack of any difference as a function of difficulty is quite different from the results from Experiments 1 and 2 which show quite large differences in RTs for easy and difficult stimuli. However, the model captures all these accuracy and RT effects.
Experiment 5
In Experiments 1 and 2, there was a direct 1–1 correspondence between the dominant color in the central patch and the target location in the surrounding annulus. In other words, if red was the dominant color in the patch, then red was the target location. In Experiments 3 and 4, there was also a 1–1 correspondence: the brightest (or darkest) location on the circular or half-circular annulus was the location to which eyes or fingers moved. Experiment 5 broke these direct perceptual correspondences. The central patches were made up of arrows (Figure 7A) with a proportion of them pointing in the same general direction and the others in random directions. The surrounding response annulus was also made up of arrows, with their directions moving around the circle from pointing upward at the top of the circle to downward at the bottom. Subjects were to move their eyes from the central patch to the location on the circle that matched the dominant direction of the arrows in the patch. This requires determining the dominant direction in the patch and only after that has been accomplished can the target location on the surround be determined. There were three different conditions with different proportions of arrows pointing in the target direction.
Figure 7.
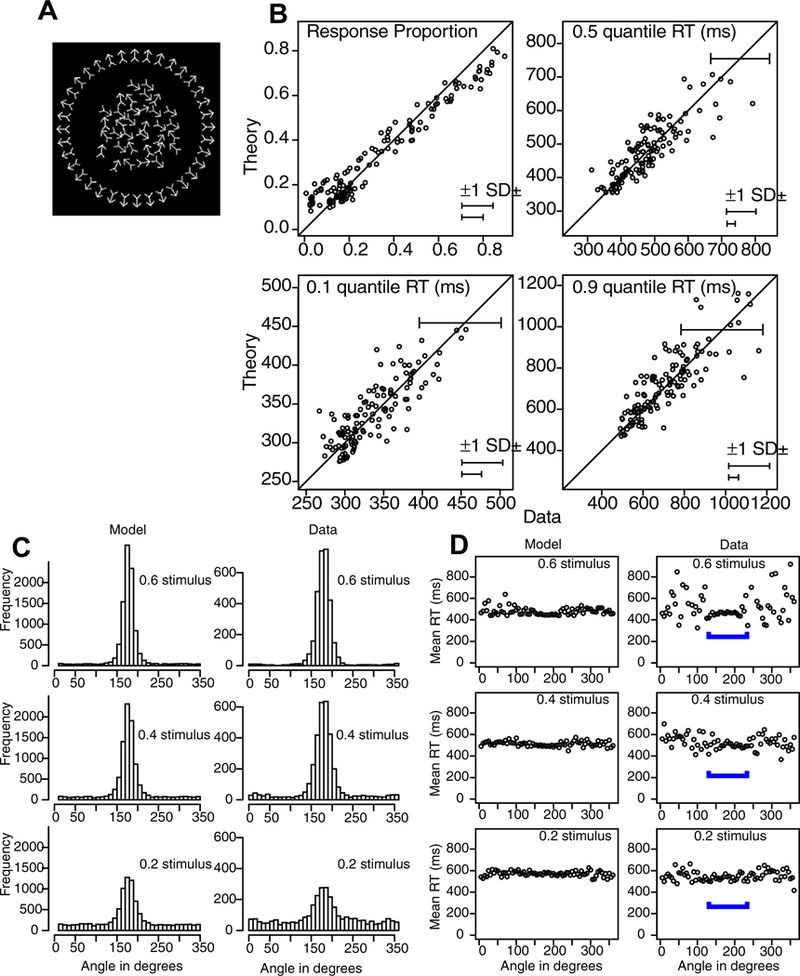
The same analysis as in Figure 3 for Experiment 5.
Method
At the beginning of each trial, subjects were asked to fixate on a white 20×20 pixel square at the center of the screen. After 500 ms of fixation, the central patch and the circular annulus surrounding it were displayed; these remained on the screen until a subject’s eyes moved 40 pixels (2 degrees) away from the fixation point, at which point the screen cleared.
Feedback was presented for 300 ms (“1” for a response in the target location which was a box 40 pixels around the target location and “0” otherwise). Feedback for fast or slow responses or slow movement time was the same as for Experiment 1.
The central patch was a disk with radius 50 pixels (2.5 degrees of visual angle) and contained 32 non-overlapping arrows. The circular response annulus was 4 degrees of visual angle (80 pixels) from the fixation point with a width of 0.65 degrees. In both the central patch and the surrounding annulus, the arrows were 13 pixels (0.65 degrees) long and 7 pixels (0.35 degrees) wide. The arrows had heads and tails to minimize the possibility of using the density of the head relative to the tail if only heads were used. There were 36 arrows in the response annulus, one for each 10 degrees of rotation, as in Figure 7A.
In the stimulus patch, some proportion of the arrows pointed within plus or minus 10 degrees of the target direction. Difficulty was manipulated by the proportion that pointed in the same direction: the proportions were 0.6, 0.4, and 0.2.
There were 16 subjects. The experiment was composed of 12 blocks of 72 trials each, with 24 trials in each block for each of the three conditions, ordered randomly. The first 90 trials were used as practice. As for the other eye tracking experiments, few subjects finished the 50 min. session; the average number of observations per subject was 520 out of 774.
Results
The target direction on the response annulus was rotated to 180 degrees. The A area was 161–200 degrees, B was 141–160 and 201–220 degrees, and T was the rest.
There were 144 data points for response probabilities and 127 for the RT quantiles (data points for which there were more than 10 observations). There were no systematic deviations of predictions from data and only two serious deviations for the 0.5 quantile and three for the 0.9 quantile (Figure 7B). The fit of the model was also good for the histograms of response probabilities and mean RTs in Figures 7C and 7D. For response probabilities, the only miss is a slightly lower peak for the data than the predictions for the condition with 0.2 of the central arrows pointing in the same direction and a slightly higher level of responses away from the peak. As before, if different SDs in the stimulus distribution were used for the different difficulty conditions, the model would produce a much smaller miss. The RT functions are flat across angles and increase with difficulty, from 469 ms to 519 ms to 543 ms. As before, the predicted RTs are less variable in regions off the center of the functions (blue brackets) than the data because they had fewer observations.
Experiment 6
This experiment was designed to connect to a frequently-used task in research on motion discrimination (Ball & Sekuler, 1982; Britten, Shadlen, Newsome, & Movshon, 1992; Newsome & Pare, 1988; Roitman & Shadlen, 2002; Salzman, Murasugi, Britten, & Newsome, 1992). In the standard task, the stimuli are displays of moving dots and there is a subset of them in which the dots are moving in the same direction. The subjects’ task is to decide in which direction the dots of the subset are moving and the response categories are discrete (usually, 2, 3, or 4 choices). Subjects are required to respond on a continuous scale.
On each trial, there were four subsets of dots, each of three of the subsets with the dots in it moving together (coherently) in the same direction with the three subsets moving at 120 degrees to each other. The other subset had the dots redrawn between frames in random positions (cf. Niwa & Ditterich, 2008). Stimuli were presented in a circle 100 pixels in diameter and were composed of white dots on a black background. Responses were made to a circle 140 pixels in diameter concentric with the stimulus circle. In the three subsets with coherent motion, a direction for a dominant direction was chosen, and the two other directions for the other two subsets of dots were at 120 radial degrees from the others (Figure 8A). Fixed orientations were used because if motion directions become close together, as they might if random directions were chosen, they become difficult to discriminate and fuse together. Difficulty was varied with the proportions of dots that moved coherently in each of the three subsets: in one condition, the proportions were 0.5, 0.1, and 0.1, in another they were 0.4, 0.2, and 0.2, and in the third, they were 0.4, 0.2, and 0.1 (e.g., Figure 8A). Subjects were to move their fingers from a start box below the response circle to the location on the surrounding circle that matched the direction in which the largest proportion of dots was moving.
Figure 8.
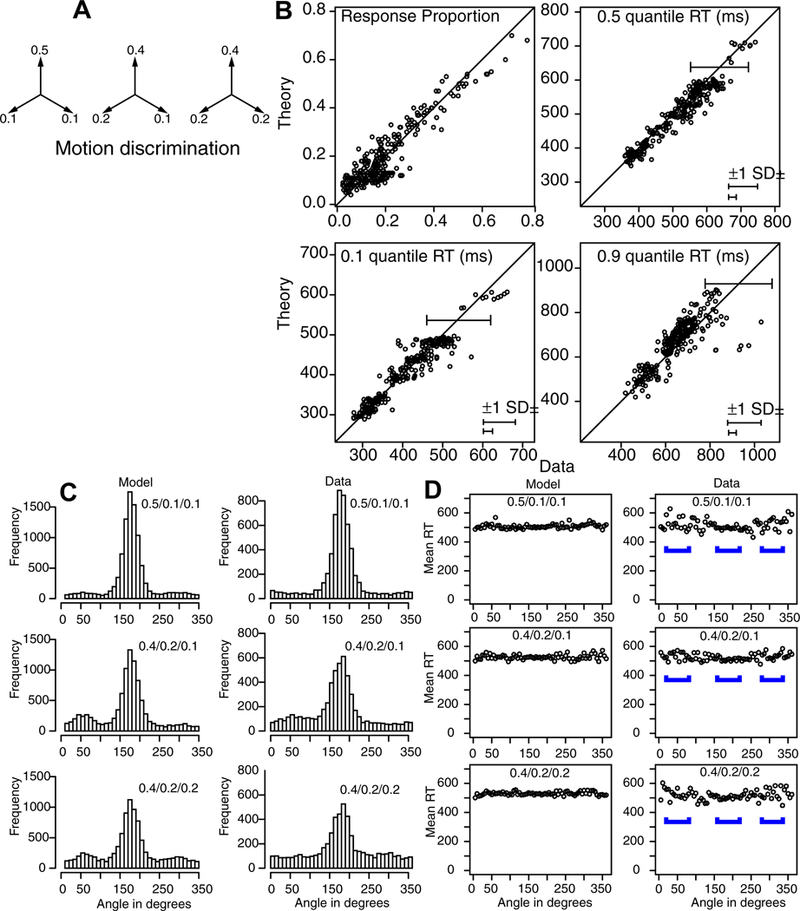
The same analysis as in Figure 3 for Experiment 6.
Method
To begin each trial, a subject placed the first finger of her or his dominant hand on a square at the bottom center of the screen. Subjects were to keep their finger on the square for 250 ms, after which the response circle and a plus sign in the center of the screen were displayed for 500 ms. Then the central patch was added to the display and it remained on the screen for 350 ms. RTs were measured from the onset of the patch to the time at which the finger was lifted from the resting square.
There were 36 directions in which dots could move, separated from each other by 10 degrees. The direction of the largest proportion of coherently moving dots (0.4, 0.5) was chosen randomly from the 36 directions and the directions of the other two, smaller, proportions (0.1, 0.2) were each located at 120 degrees from the direction of the largest proportion.
Each block of 108 stimuli had each of these 36 directions (for the strong coherences) presented 3 times. The coherences were: 0.5/0.1/0.1 for 1/3 of trials, 0.4/0.2/0.1 for 1/3 of trials, and 0.4/0.2/0.2 for 1/3 of trials.
The size of each dot was 2×2 pixels. The central patch was a circle 100 pixels in diameter. When a dot in a coherent set moved off the circle, it was placed back on the circle 180 degrees from the position at which it had moved off. The dot motions were presented in different frames of the display and the method followed that in Niwa and Ditterich (2008; also Ratcliff & Starns, 2013, Experiment 2). The first 5 dots were placed at random positions in the patch in the first frame and these were assigned to one of four groups probabilistically. For the 0.5/0.1/0.1 condition, for example, a dot was assigned to the 0.5 condition (“1”) with probability 0.5, the 0.1 conditions (“2” and “3”) with probability 0.1 each, and to the random condition (“4”) with probability 0.3. On frame 2, the “1” dots moved coherently, the “4” dots moved randomly, and the others remained in place. On frame 3, the “2” dots moved coherently and on frame 4, the “3” dots moved coherently. On frame 5, the dots were randomly reassigned to conditions (so a dot could remain in condition 1 or it could be reassigned to one of the other conditions) and dots in the newly assigned conditions “1” and “4” moved, and so on.
The location of a correct response was determined by the intersection of a line pointing in the direction of the strongest coherence from the center to the surround. It was a box 50 pixels square at that location. If the response was to the correct location, “correct” appeared 35 pixels above the response location (so the hand did not obscure it) for 250 ms and if the response was outside the 50 pixel square, “ERROR” appeared 35 pixels above the response location for 250 ms. RTs were measured from the onset of the first frame to the point at which the finger left the resting point. For RTs longer than 1250 ms, a “TOO SLOW” message was displayed for 500 ms. For RTs shorter than 150 ms, a “TOO FAST” message was displayed for 500 ms.
The experiment was composed of 10 blocks of 108 trials with 36 trials for each of the three conditions in random order. Many of the subjects finished the whole experiment and the mean number of trials per subject was 943.
Results
Because the movement directions were at 120 degrees from each other, it was easy to rotate the data so that the strong stimulus direction was at 180 degrees and the two weaker directions were at 60 and 300 degrees. For the 0.4/0.2/0.1 condition, half the time the conditions were in this order and half the time they were in the 0.4/0.1/0.2 order (clockwise). In these cases, one of them was reflected to align the 0.2 condition on 60 degrees. The A, B, C, D, and T areas (A and B for the dominant direction, and C and D for the other two directions) were 161–200 degrees, 141–160 and 201–220 degrees, 21–100 degrees, 261–340 degrees, and T responses were the rest.
The model fit reasonably well with only a few mismatches for the 0.9 quantile. There were 270 points for response probabilities and there were 258 points with greater than 10 observations for the quantiles.
Figures 8C and 8D show plots of response proportions and mean RT as a function of angle that are constructed in the same way as earlier experiments. The response proportion plots match quite well with one exception: the secondary peaks for the model have more pronounced peaks than the data. One possible interpretation is that low coherent motion in the competing directions has less precision and provides much poorer directional information leading to a smearing of the responses over position. As for the earlier experiments, this could be addressed by increasing the SD in the drift rate distributions for those lower coherence stimuli.
As for the earlier experiments, mean RTs across angles show little difference. Unlike the earlier experiments, averaging over all angles, mean RTs differ by a small amount, namely 18 ms, between the 0.5/0.1/0.1 and the 0.4/0.2/0.2 conditions (the values for the 0.5/0.1/0.1, 0.4/0.2/0.1, and 0.4/0.2/0.2 conditions were 506, 518, and 525 ms respectively). This difference is smaller than the difference as a function of difficulty for Experiment 3 and is much smaller than the difference observed in Experiment 1 as a function of difficulty. The small difference is likely because the difference in the dominant motion coherence is relatively small for this task (0.5 versus 0.4).
Experiment 7
With this experiment, the computer-mouse response modality was examined. The experiment was the same as Experiment 1 in that central patches of colored pixels were surrounded by a circular response annulus and subjects were to indicate the color on the response annulus that matched the dominant color of the central patch. Subjects indicated the color by moving a mouse from a central resting square in which the stimulus appeared to a location on a surrounding response annulus that corresponded to the dominant color in the stimulus square (Figure 9A). There were the same three conditions as in Experiment 1; the proportion of pixels of the dominant color was 0.35, 0.2, or 0.1.
Figure 9.
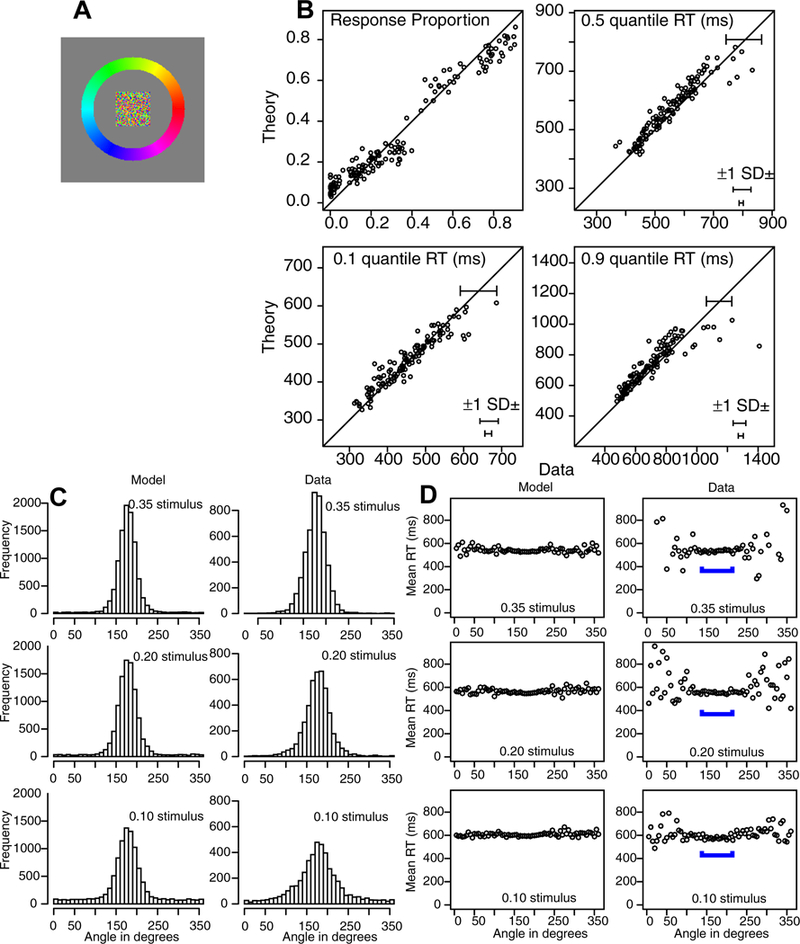
The same analysis as in Figure 3 for Experiment 7.
The main finding from this experiment was that the results replicated those of Experiment 1. From a practical perspective, eye trackers are expensive and touch screens are specialized (though they are common in tablets and cell phones). Almost every PC or laptop system has a mouse or is capable of adding a mouse and has software to use a mouse. This allows more general opportunities to conduct experiments with continuous stimuli and response scales with standard PC based experimental systems. However, just prior to submitting a revision of this article, we have implemented our real-time system on cheap chromebook laptop convertibles ($250 each) and can collect data from finger movements on these. Because movement times are much shorter than for mouse-based experiments (see the analysis later in the article) and training for the touch-screen tasks is easier for populations such as older adults, we now lean to using touch-screen experiments on chromebooks.
Method
The experiment was composed of 10 blocks of 72 trials (24 for each condition in random order) preceded by two practice blocks. There were 16 subjects and the mean number of observations per subject was 719.
At the beginning of each trial, a fixation box was presented at the center of the display and subjects had to move the mouse into the box and click it. Immediately after the click, the box disappeared and was replaced by the stimulus patch and the response annulus. After 250 ms the patch turned off but the response annulus remained on the screen until the subject made a response by clicking the mouse when he or she had moved it to the intended location. The central patch was displayed for only 250 ms instead of remaining on the screen until a movement was initiated as in Experiment 1. This was because in a pilot study, subjects were found to start to move the mouse before they had made a decision which lead to curved mouse tracks instead of tracks that went directly to the response location. RT was measured from stimulus presentation time to the time the mouse had moved 10 pixels away from the position clicked on to initiate the trial.
The position of the mouse was explicitly displayed on the screen as it was moved; it was a 3×3-pixel black cross (with white pixels in the corners of the 3×3 array) with its location refreshed every 10 ms. The track began when the mouse position moved outside a 10-pixel radius from the click position and stopped when the mouse was clicked to indicate the response. After the response click, the screen cleared to 50% gray and feedback appeared as in Experiment 1, with a “1” for a correct response and “0” for an incorrect response presented for 300 ms. If initiation of the mouse motion was too fast, beginning within 300 ms of stimulus onset or with duration less than 250 ms, a TOO FAST message appeared at the center of the screen for 1000 ms, shown before the “1/0” feedback. If the mouse motion was too slow, started over 1250 ms after stimulus presentation or with duration greater than 1250 ms, a TOO SLOW message appeared at the center of the screen for 500 ms before the “1/0” feedback. After feedback, the screen cleared to 50% gray for 20 ms.
Results
The locations of the target colors were aligned in the same way as for Experiment 1, with the central location at 180 degrees. Responses were also grouped in the same way, into A, B, and T areas. The match between the data and predictions for response probabilities and RT quantiles (Figure 9B) was good with few serious outliers except for 0.9 quantile RTs that were longer than those predicted. There were 144 points for the response proportions (16 subjects by the A, B, and T response areas, and 3 levels of difficulty) and 114 observations for the quantiles (conditions with more than 10 observations). A careful examination of response proportions shows a number with experimental values close to zero, but predicted values from the model were in the 0.02 to 0.1 range. As noted earlier, this might be accommodated with stimulus location dependent noise and this is examined in the discussion.
The distributions of responses and mean RTs over position showed similar results as for Experiments 1 and 2. The one noticeable difference between predictions and data was that the histogram for response probabilities for the most difficult condition (Figure 9C) had a wider distribution for the data than the predictions which suggests that the SD in the drift-rate distribution increases with difficulty as discussed earlier. Mean RTs for the three difficulty levels were 532 ms, 554 ms, and 588 ms.
Experiment 8
A key manipulation in experimental and theoretical work in perceptual and cognitive decision-making is a manipulation of instructions about speed and accuracy. On some trials, subjects are asked to make their responses as quickly as possible and on other trials, as accurately as possible. This manipulation gives considerable leverage for testing the model because it is assumed in the model that the criteria subjects set to achieve their desired speed and accuracy are independent of the information upon which their decisions are based. In other words, the only parameter that should change as a function of instructions is the decision boundary setting (though in two-choice tasks, there is some evidence that nondecision time also changes). The manipulation is also of practical importance because in real-world decision making, it is sometimes necessary to respond quickly and sometimes to be sure to make the correct decision.
This experiment was the same as Experiment 7 except for the speed-accuracy manipulation and a reduction in the number of levels of difficulty from three to two (to give more observations per condition).
Method
The experiment was composed of 12 blocks of 72 trials each with the first 45 trials of the first block used as practice. There were 16 subjects. Instructions for speed versus accuracy alternated across the blocks; for half the subjects, the first block was an accuracy block and for the other half, it was a speed block. There was a mean of 653 observations per subject. In the easier condition, 0.25 of the pixels in the central patch were of the dominant color and in the more difficult condition, 0.1 of them were.
Results
To apply the model to the data, the only parameter allowed to change between speed and accuracy instructions was the decision boundary.
There were two levels of difficulty, speed and accuracy instructions, and three response areas (A, B, and T, Figure 2), so there were 192 data points for the 16 subjects, which is the number plotted for response proportions in Figure 10B. Quantile RTs were plotted for the 164 conditions with greater than 10 observations. There are few data points that lay outside the maximum 2SD error bars.
Figure 10.
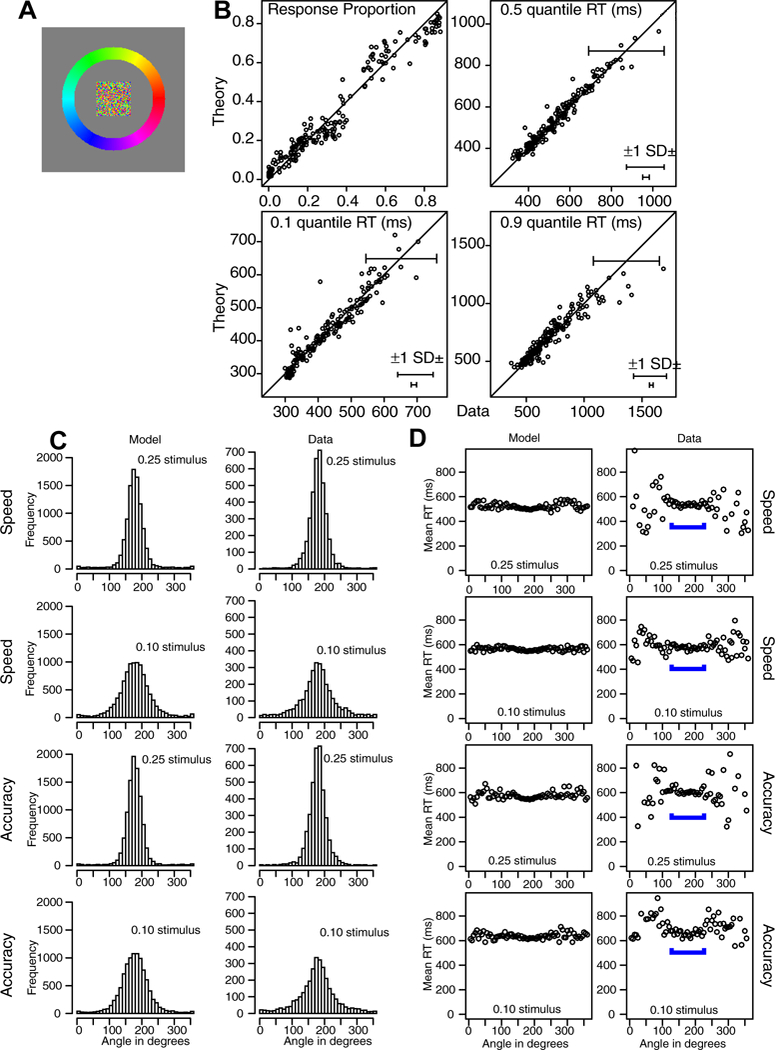
The same analysis as in Figure 3 for Experiment 8.
Accuracy was little different with speed instructions than accuracy instructions, about 1%. Specifically, the proportions of correct responses (the A and B areas combined) with speed instructions were 0.98 and 0.86 for the 0.25 and 0.1 levels of difficulty, respectively, and 0.99 and 0.87 with accuracy instructions. Mean RTs differed by about 70 ms: with speed instructions, the means were 523 and 557 ms for the two levels of difficulty, respectively, and with accuracy instructions, they were 557 and 639 ms, respectively (for the model, the four values were 525, 565, 578, and 637 ms respectively). The smaller difference as a function of difficulty with speed than accuracy instructions is captured by the model. The predictions of the model for the distribution of responses across angle and mean RT across angle matched this well (Figures 10C and 10D).
Model parameters are shown in Tables 1 and 2. The boundary parameters (13.6 and 15.3) were significantly different across the 16 subjects, t(15)=5.1, p<0.05.
In this task, it seems that subjects are reluctant to adopt more lax speed-accuracy criteria settings that would produce a significant increase in random errors. They are capable of slowing down or speeding up a little, but this does not materially change the location at which they make their response or the spread in responses over angles. The instructions in this experiment were similar to those used in standard two-choice tasks. But they were not strong enough to make accuracy fall as it does in standard tasks (Ratcliff, Thapar, & McKoon, 2001, 2003, 2004; Thapar, Ratcliff, & McKoon, 2003). If more extreme speed-stress instructions were used (see Starns, Ratcliff, & McKoon, 2012), subjects might start to move the mouse (or eyes in eye movement tasks or their finger in the touch screen tasks) before the decision has been made or they might guess and simply move to a random location. If more extreme accuracy-stress instructions were given, subjects might make multiple attempts at processing the stimulus. Probably the main difference between the continuous response scale and two-choice tasks is that errors in two choice tasks involve one alternative that is well defined. But in the continuous task, there is only one small range of correct responses but a large number of directions for errors. Subjects are unlikely to want to produce a high proportion of completely random responses that could be a large distance from the correct response location when waiting a few tens of ms longer will produce higher accuracy. These considerations suggest that manipulating speed-accuracy stress in these kinds of tasks might not be as straightforward as for two-choice tasks.
Color Biases
The subjects in our experiments showed a bias to respond with primary and additive colors and a bias against colors between them. To show this, data from Experiments 1 and 7 are used in which the central patches and response annuli were colored pixels and the response annulus was a full circle. Responses in Experiment 1 were made by eye movements and in Experiment 7, by mouse movements. This bias has rarely been reported in other tasks using color response scales because researchers have collapsed over colors when analyzing data. However, it is likely present in all experiments in which responses are made on a continuous color circle.
Biases like these have been observed in long-term memory for objects (Persaud & Hemmer, 2016) and in the visual working memory task (Hardman, Vergauwe, & Ricker, 2017). In Persaud and Hemmer’s (2016) experiments, colored shapes were presented for study and at test, a colored shape was presented and the subject had to decide whether the color was the same or different as that in the studied shape. There was a bias to respond “same” when the color was a primary or additive color. They also performed experiments that involved naming colors and experiments that involved, given a color name, locating the color on a color wheel. Both these tasks showed color biases. Hardman et al. also found biases toward primary and additive colors. They used the standard visual working memory task (see discussion of this task later). Subjects were given several colored squares to remember and then they were probed with one square colored grey and were to indicate the color that square had appeared in on a color wheel. They modeled the accuracy data with a model with both continuous and discrete components with a multinomial model guiding which components were used with what probability.
In Experiments 1 and 7, the biases in the data were as large as 3:1. Figure 11A shows responses from all the subjects and all of the conditions as a function of the stimulus and the response (positions on the color circle). There are some vertical gaps (which are partially hidden because of the size of the circles that plot the data) because our colors were from the 0–253 palette and we plotted in 1-degree increments. Figure 11B shows the distribution of stimuli averaged over subjects and conditions. Ideally, this distribution would have been flat, that is, the probability of a target at each angle would have been the same, but the sampling method used to construct stimuli did not produce this. Figure 11C shows the distribution of responses averaged over subjects and conditions and this shows the color biases. There are more responses at red, purple, blue, teal, green, and yellow (the vertical dashed lines on the figure) than the colors between them. These biases were hidden when the response angles were aligned at 180 degrees and averaged over color for the analyses presented earlier in the article. The biases in responses were not due to differences in the stimulus probabilities because the peaks of the response frequencies do not correspond to the peaks of the stimulus frequencies (Figures 11B and 11C).
Figure 11.
A: plots of response angle versus stimulus angle for all responses from all subjects for Experiments 1 and 7. The horizontal blobs show a bias to respond within certain ranges. B: plot of the number of stimuli as a function of angle. C: a plot of the number of responses as a function of angle. The vertical dashed lines show the center of the primary and additive colors (red, yellow, green, teal, blue, and purple). The color scale at the bottom and right side shows the colors that corresponds to the angle.
In order to examine groups of responses, the data were divided into two groups, in one the stimuli are preferred colors and in the other the stimuli are non-preferred. The A, B, C, and D panels of Figure 12 illustrate how biases with these two groups of data can be modeled. For this illustration, the distributions of evidence from stimuli are assumed to be back-to-back exponentials rather than the normal distributions in the model, the boundary setting is sinusoidal, there is no noise, and the stimulus distribution is multiplied by the boundary to give a distribution of responses. This is a simple way of illustrating the main features of the data. Figure 12A shows the distribution for an angle at a primary color and 12B shows it for angles that are not at primary or additive colors (the dashed lines align on the peak of the evidence distribution). Multiplying the exponentials by the sinusoid gives the distributions in 12C and 12D. When a peak of the exponentials aligns with a peak of the sinusoid, the result is a flattened response at the peak and a wider distribution (Figure 12C). This is because (in the SCDM), when the peak of the drift rate distribution is at the peak, there is a greater tendency for processes to hit the sinusoidal boundaries on the left and right of the peak which decreases probabilities at the peak and increases them to the sides of the peak. Similarly, when a trough of the exponentials aligns with the peak of the sinusoid (Figure 12B), the result is a more peaked function (Figure 12D) because processes close to the peak of the stimulus distribution tend to hit at the trough of the decision boundary. This also produces high side lobes that correspond to the next trough of the boundary sinusoid (Figure 12D).
Figure 12.
A shows plot of a sinusoidal decision boundary centered on a peak in sinusoid and an illustrative stimulus distribution (this is not based on the model). B is an illustrative plot of the responses produced by multiplying the stimulus representation by the decision bound which shows a flat wide peak. C shows the same plot for the decision boundary centered on a trough. D shows that resulting response distribution is highly peaked with side lobes. E shows the same accumulation of information as in Figure 1C, but with a blue sinusoidal decision boundary (which is equivalent to a constant boundary but with a sinusoidal starting point (the green starting point and red constant boundary).
The full model, with normal distributions of evidence and continuous noise, is illustrated in Figure 12E. The blue line shows the sinusoidal line as the decision criterion. The same results would be achieved if the starting points were sinusoidal (the green sinusoid) and the decision criterion was a straight line because the model is a linear one and thus the two are mathematically equivalent.
To generate predictions for the color biases, the only change in the model is that the decision criterion function (or the starting point function) is sinusoidal. Because the primary and additive colors are 60 degrees apart on the color wheel, the period of the sinusoidal boundary or starting point is fixed. Thus, the only parameter added to the model is the amplitude (height) of the sinusoid. To model the data for Experiment 1 and 7, the mean values of the best-fitting parameters across subjects were used along with the sinusoidal starting point function (the green line in Figure 12E). The amplitude of the sinusoidal was determined by trial and error using simulations of the model. For color bias analyses, for Experiment 1, the decision criterion was 15.2 and the peak-to-peak height of the starting point sinusoid was 3.2 and for Experiment 7, the decision boundary was at 15.4 with the peak-to-peak height of the sinusoid 2.0. Two sets of predictions were generated, one with sinusoid aligned so that the peak was at the peak position of the drift rate distribution (e.g., 180 degrees) and the other with the peak at a trough of the drift rate distribution.
Figure 13 shows the observed and predicted response probabilities as a function of angle for the two experiments for the preferred angles (the primary and additive ones) and the non-preferred ones. The results for Experiment 1 are on the left and those for Experiment 7 are on the right. When the trough of the sinusoid is in the preferred direction (i.e., the trough aligns with a primary or additive color), both theory and data show peaked functions with side lobes (especially in the most difficult, 10%, stimulus condition). When the peak of the sinusoid is in the preferred direction, both theory and data show wider functions with flatter peaks.
Figure 13.
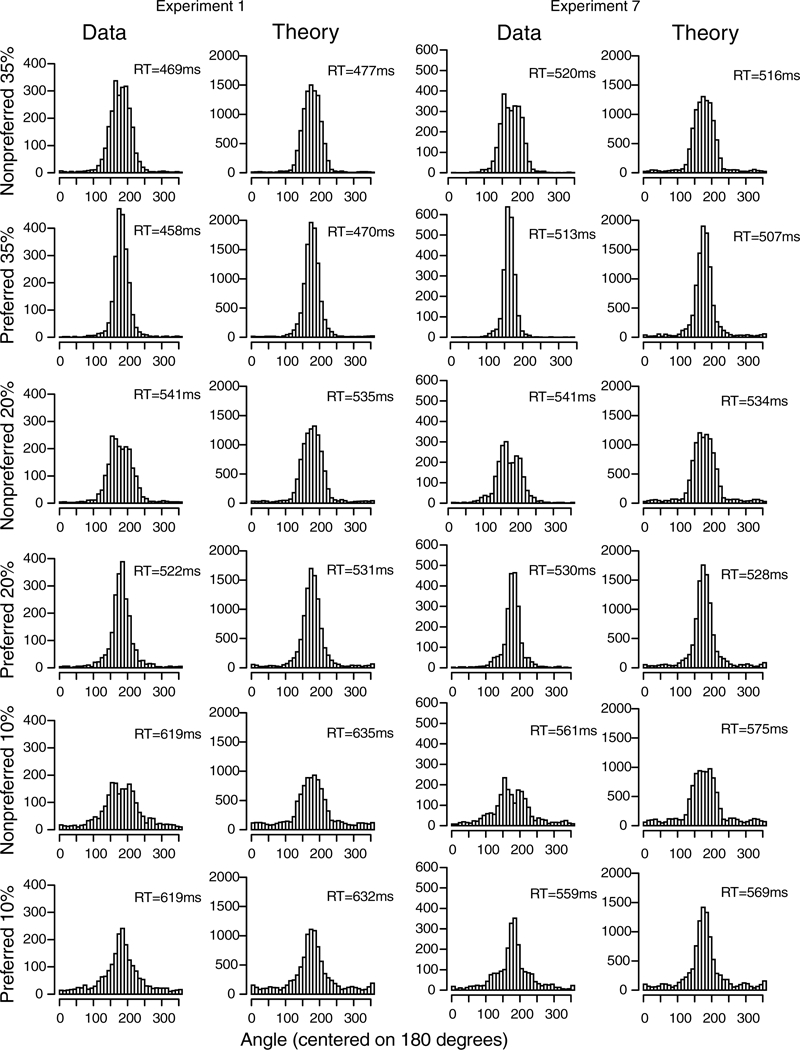
Plots of the frequency of responses for responses centered on the primary and additive colors (“preferred” plots) and those between the primary and additive colors (“nonpreferred” plots) for all responses from all subjects for Experiments 1 and 7 for data and model predictions. Mean RTs are shown as insets. The data are shown for the two more difficult conditions because the easy condition does not show much difference between the two sets of plots. Results show the same kind of peaked versus flat response functions as shown in Figures 12A and B.
Median RTs are also shown in the figures and the correspondence between them is remarkably good with a maximum difference between theory and data of 14 ms. Although the shape of the frequency versus angle functions differs quite considerably for preferred versus non-preferred directions, median RTs differ little between the two; averaging over all levels of difficulty for both experiments, the mean RT difference in preferred and non-preferred directions for data is 8 ms and for the model 5 ms.
As before, the data in Figure 13 were not fit directly. Choice proportions and RT quantiles for Areas A, B, and T (see Figure 2) were fit (earlier) for Experiments 1 and 7 and then one additional parameter was added (the amplitude of the sinusoidal starting point) and this produced the predictions for the distributions of responses over angle and mean RT in Figure 13.
The results presented in Figure 13 provide another explanation of why the distributions of responses over angle are wider in the data for difficult conditions than for easy conditions for the color experiments. For easy conditions, the side lobes for the preferred condition are quite small, but for the difficult condition, they are wider and higher. Combining the preferred and non-preferred distributions leads to a wider distribution for the difficult conditions (bottom two rows) than for the easy conditions (top two rows). However it might be that this is not enough and there is additional variability (less precision) in processing difficult stimuli which leads to wider distributions of drift rates (which would be needed in the non-color experiments).
Hardman et al. (2017) developed a 4-state multinomial model to account for similar effects in their visual working memory task. They assumed that responses are a probability mixture of stimulus-driven responses and guesses. First, processing a stimulus either finds an item in working memory or it does not. If the item is in working memory, then either a response is made based on continuous information or it is based on categorical information. If the item is not in working memory, either a categorical guess is made or a random guess. There are different probabilities of these states and a common noise term. For different set sizes, some of these parameters are the same which produces some parameter invariance over conditions.
A major problem with the model is that it makes no predictions about RTs and their distributions. In a multistate model like that of Hardman et al., it is extremely unlikely that different categories of responses have exactly the same RT distributions. Guesses are not the same thing as stimulus-driven responses and it is unlikely that the time course of making a categorical or random guess has exactly the same time course as a response to an item that is in working memory. One would expect that the processing time for a strong item would be shorter than a weak item and detecting absence from working memory would be a slower process. The advantage of the SCDM is that only one process is required to account for what is argued by Hardman et al. to be a multistate or multicomponent process (see also Zhang & Luck, 2008; Bays et al., 2011; van den Berg et al., 2012, 2014).
To further examine color biases, a number of issues could be explored that involve examination of perceptual properties of stimuli. First, in Figure 10C, yellow has a smaller number of responses than green. These differences might be able to be modeled with modulation of the height of the sinusoidal starting point distribution (e.g., the peak for yellow would be lower than the peak for green). However, it may be that the yellow stimuli are perceptually more difficult, that is, harder to identify, than red or blue in the experimental apparatus used here. This would mean that perceptual properties of our stimuli would have to be examined and this would lead into issues of perceptual properties of color vision which is beyond the scope of the topic of this article. However, in applications that use responses on color scales such as the visual working memory domain, such issues need to be examined. Second, if the differences across colors resulted from differences in perceptual properties of the stimuli such as luminance, then stimuli with equiluminant stimuli might be used instead of the colors used in the experiments presented here. For example, color wheels of CIELUV-space stimuli could be used. These have the added advantage of making the colors more difficult to name which would reduce possible naming biases. Third, an alternative hypothesis is that instead of decision biases, the results in Figure 10 could be explained by differences in drift rates so that for a primary or additive color, drift rate might be higher than for one in between. However, this assumption would not produce the difference in the shapes of the response functions in Figure 12 (peaked for on a primary or additive color and flattened for between these colors as in Figure 11) and so the bias explanation is the one most consistent with the data.
Model-Based Analyses and Experimental Designs
There are four points to discuss about the data and modeling for the 1D tasks for Experiments 1–8. First, only few experiments similar to those presented here have been conducted in related domains and these few have not collected RT data and have not considered modeling the time course of the decision process.
Second, significant effort was put into designing tasks in this article to be “natural,” easy to instruct, and easy for a subject to perform. One focus has been on minimizing the initiation of responding before the decision has been made. In early versions of several of the tasks, many of the movements away from the resting position took hundreds of milliseconds and where the tracks could be measured, they were often to intermediate points that were not on a line from the fixation to the eventual response (i.e., curved tracks). In some mouse-based two-choice tasks, such slow movement is a design target (see discussion in Ratcliff, Smith, Brown, & McKoon, 2016), but data from such tasks are not appropriate for the SCDM. (In fact, examining movement times in eye-movement tasks is a separate research domain, cf., Kowler & Pavel, 2013).
Third, the fitting methods used here have not been shown to be optimal in any sense and more research would be needed to produce better fitting methods. However, the important point is that the fitting method produces fits that generate the predictions shown in the experimental sections. Better fitting methods might produce better fits and predictions than those shown here, but the methods used here show that the model fits data at least as well as is shown above. If alternative models are developed (e.g., Smith, 2016) that make qualitatively and quantitatively similar predictions, then fitting methods and the properties of fitting methods will become important in comparisons among models. Parameter recovery studies are presented in the Appendix.
Fourth, the parameter space of the model has not been explored in much detail. For example, adding across-trial variability parameters improved the fit, but not in any dramatic qualitative way (see the appendix for how the different parameters affect model predictions). As more data from more paradigms are collected and the SCDM and related models are fit to data, a more comprehensive view of the models and the detailed assumptions in each of the models will begin to appear.
Model Parameters, Scaling, and Numerical Goodness-of-Fit
Tables 1 and 2 show the best-fitting model parameters, averaged across subjects, for Experiments 1–8. Tables 3 and 4 show SDs across subjects in the model parameters. The values of the model parameters are defined in terms of 10 ms time steps and one degree spatial steps. To change this scaling of time steps or spatial distance, several model parameters need to be adjusted. These changes can be understood by examining the units of the various model parameters. For example, drift rate is evidence per unit time so changes in time steps will require changes in drift rate. The diffusion coefficient (σ2) has units of evidence per unit time and so σ has units of (time)−1/2. Thus the value of σ will be changed if the time step is changed. The kernel parameter has units of spatial distance and so changes in the number of spatial divisions will change this parameter.
For changing the spatial distance by a factor of x, e.g., moving from 72 5-degree divisions in angle to 360 1-degree divisions, x=5, these parameters are adjusted:
SD in noise added on each time step in the accumulation process (the parameters are scaled to this value) is divided by x.
The boundary value and the range in the boundary (a and sa) are divided by x.
The SD in the drift rate distribution (sw) and the SD in Gaussian process noise (the kernel parameter, r) are both multiplied by x.
Drift rate parameter and SD in that parameter (d and sd) stay the same, BUT, because they multiply the height of the drift rate distribution and because the width is increased (the SD, sw, is increased and multiplied by x), the height of normal drift rate function is x times lower (as is the range of heights), which means that d and sd do not change.
For changing the time step by a factor of t, e.g., moving from 10 ms steps to 5 ms steps (t=1/ 2), these parameters are adjusted:
Drift rate peak and range in the peak (d and sd) are divided by t.
SD in noise added on each time step (σ) in the accumulation process is divided by the square root of t.
Boundary parameters, SD in the drift rate distribution and the SD in Gaussian process noise (the kernel parameter) all remain the same.
Nondecision times in some of the experiments are close to the minimum that was set in the fitting program, namely 175 ms. It is implausible for nondecision time to be less than this value because it is close to the time taken for neural signals to be transmitted from the eyes to frontal cortex plus the time for signals to be transmitted from frontal cortex to the motor system (the sum is about 150 ms). The values for the moving dots and mouse-based experiments are larger than 175 ms (Table 1).
Across the experiments presented in this article, boundary settings are between 7 and 15 units (i.e., a 2:1 ratio) and across-trial range in boundary setting is between 2 and 5 times smaller than the value of the boundary setting. The Gaussian process parameter is between 5 and 30 degrees and the SD in the drift-rate distribution is between 17 and 36 degrees. The peak height of the drift-rate distributions varies between 2:1 and 8:1 for the strongest stimulus versus the weakest stimulus. These differences in parameter values across tasks are similar to the size of differences across tasks in related parameters for the two-choice diffusion model.
Generally, the G-square goodness of fit values are acceptable, with values about twice the critical value of chi-square. This is consistent with acceptable fits of the two-choice and confidence judgment models to data (Ratcliff, Thapar, Gomez, & McKoon, 2004; Ratcliff & Starns, 2013).
Parameter Recovery and Correlations Among Model Parameters
In the appendix, parameter recovery simulations are presented and these provide parameter values that allow tradeoffs among parameters to be examined. It is important to understand tradeoffs among parameters because if there is a difference in one parameter between two groups (e.g., a group with a disease or clinical disorder and a control group), it is important to know whether this is a real difference or whether it is the result of another parameter covarying with it, with no real difference in processing between the two groups.
Parameter recovery with 200 observations per condition (about the same number as in an experiment) produces parameter values that are relatively unbiased. There are correlations in some of the model parameters so that if one is higher than the value used to generate the simulated data, another is lower to compensate. Most of these correlations are readily interpretable as is discussed in the Appendix (and in Ratcliff & Tuerlinckx, 2002, for the two-choice model). The impact of these correlations on interpreting the behavior of model parameters is qualified by the relative sizes of the SDs in parameters relative to the SDs in model parameters across subjects, i.e., individual differences. The SDs across subjects were two times or more larger than the SDs in model parameters in the simulations presented in the Appendix. This means that the dependencies in the model structure that allow parameters to trade off are not likely to be a problem in interpretation of individual or group differences, although this issue will have to be examined using simulation methods in any application of the model to individual differences.
Are the Across-Trial Variability Parameters Needed and is Normalization Needed?
In modeling two-choice tasks, incorrect responses are sometimes slower than correct responses and sometimes faster, depending on the task (see the review in Ratcliff & McKoon, 2008). A successful way to model this is to let the components of processing, drift rates and starting point, vary from trial to trial. In contrast, the results from Experiments 1–8 (as well as Experiment 9 described below) show little change in RTs across spatial position (angle); that is, correct and incorrect responses have similar RTs. Thus it might seem that variability across trials is not needed by the SCDM. However, as shown in the appendix, there are values of parameters that produce either slow or fast error responses relative to correct responses (area T versus A in Figure 2) and the combinations of all the parameters are needed to produce the observed behavior.
The original motivation for including across-trial variability in model components is the belief that individuals cannot hold components of processing constant across trials. For memory, Ratcliff (1978) followed signal detection theory in assuming that memory strength (drift rate) varied from trial to trial. Although it was known that this assumption produced slow errors, only later was it found that this allowed the model to produce high-quality quantitative fits to experimental data (Ratcliff & Rouder, 1998; Ratcliff, Van Zandt, & McKoon, 1999). Recently, direct evidence has been presented for such variability using a double pass procedure in which exact copies of stimuli were repeated in widely separated tests (Ratcliff, Voskuilen, & McKoon, 2018). Furthermore, in numerosity discrimination tasks, across-trial variability in drift rate is needed to account for otherwise puzzling patterns of results in which RTs decrease as difficulty increases and accuracy decreases (Ratcliff & McKoon, 2018).
Setting the across-trial variability parameters in the SCDM to zero produced a poorer goodness-of-fit. The model was fit to the data from Experiments 1, 3, and 5 (chosen because they used different tasks: color, brightness, and arrows) with across-trial variability in drift rate and boundary setting set to zero. Results showed that goodness-of-fit, as measured by G-square and AIC, was worse than fits with non-zero across-trial variability parameters. For Experiments 1, 3, and 5, with across-trial variability, the G-square values were 79.8, 82.4, 102.0, respectively, and without it, the G-square values were 94.4, 99.0, and 135.8. These are large and significant differences. The difference in G-square values has to be at least 6.0 (chi-square with 2 degrees of freedom) and the difference in AIC values has to be at least 4.0 for the fit to be improved with the additional parameters. Thus, across-trial variability in drift rates and boundary improves the model’s ability to match data. However, there were no visible qualitative differences between the models with and without across-trial variability. Thus, this issue needs to be explored when more data sets become available from different tasks and when competing models are considered.
To examine whether normalization of evidence was needed, a similar analysis was carried out for the data from Experiment 1. Taking out the normalization of evidence at each time step allowed evidence to increase or decrease at each location, with the summed evidence increasing over time. The G-square value was 93.1 as opposed to 79.8 with normalization in the model. As above, the difference in G-squares and in AIC were both large and supported the model with normalization. Later we discuss another scheme for normalization.
The Shapes of RT Distributions
The SCDM produces RT distributions that have the same shape across conditions of the experiments, across experiments, and the same shape as data from two-choice tasks. Furthermore, the SCDM and two-choice models produce RT distributions of the same shape. Figure 14A and 14B show examples of predicted RT distributions from the model for one condition from Experiment 1 and one condition from Experiment 4. The histogram shape is what is usually seen in the majority of simple perceptual and memory tasks. Figure 14C shows mean quantiles averaged over subjects from RT distributions from Experiment 1 with quantiles from each condition plotted against one of the others (the one marked “1” is the standard plotted against itself, i.e,. a straight line). There are 7 instead of 9 for the 9 conditions because some subjects had no responses in the “T” conditions (Figure 2) for the high accuracy conditions (0.35 and 0.20) and so mean quantiles could not be computed. The result is a series of straight lines showing that the RT distributions have the same shape. Figure 14D shows one of many possible examples in which six of the quantiles from Experiment 1 (from those in Figure 14C) are plotted against quantiles of RT distributions from the two-choice motion discrimination task in Ratcliff and McKoon (2008, Experiment 1). The quantile-quantile plots are largely linear showing similar shaped RT distributions. These results show once again remarkable invariance in RT distribution shape across conditions and tasks (Ratcliff, Smith, & McKoon, 2015). This suggests a general finding and that is that models that assume accumulation of evidence to decision criteria naturally produce RT distributions of a shape that matches experimental data (Figures 3D–10D).
Figure 14.
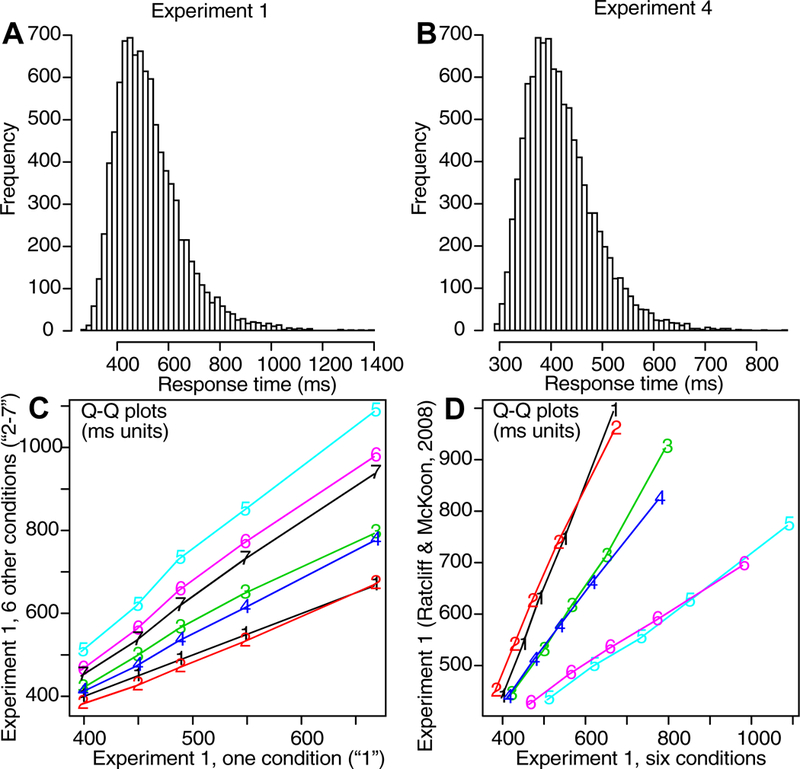
A and B show sample RT distributions predicted from the model for Experiments 1 and 4 for the easiest condition for correct responses. C shows plots of quantiles from Experiment 1 from the 7 conditions with enough responses to form quantiles plotted against the quantiles from the easiest condition. Results show straight lines which shows similar distribution shapes across condition. D shows plots of quantile RTs averaged over subjects for 6 conditions from Experiment 1 (a continuous color identification task) plotted against 6 conditions from Experiment 1 in Ratcliff and McKoon (2008 - a two choice motion discrimination task) which again show straight lines which suggests similar distribution shapes between tasks and subjects.
Modeling Responses in Two Dimensions
The generalization of the one dimensional SCDM to two dimensions represents the decision making process as a growth of evidence in a 2D plane to a criterion. This process is consistent with neurophysiological results in motor and saccadic systems. In motor cortex, evidence accumulation can be viewed as growth of activity in a 2D motor map that represents the possible choices. In the saccadic system, evidence accumulation can be seen as growth in a 2D motor map in areas such as LIP, FEF, and SC.
For responses on a line or circle, the theoretical advance is to represent noise in the decision process as a continuous 1D variable, and in this case, Gaussian process noise is a natural choice. In the 2D case, the natural choice is a Gaussian random field. Just like the Gaussian process, the distribution at any point in a Gaussian random field is Gaussian and nearby points are correlated with each other.
A Gaussian random field is a simple generalization of the Gaussian process to two dimensions (Lord, et al., 2014; Powell, 2014). Gaussian random fields can be generated using the same Cholesky decomposition method used in the 1D model but in two dimensions. However, this method is quite inefficient: Cholesky decomposition of a NxN matrix takes on the order of N3 operations and the matrix-vector multiplication takes on the order of N2 operations. A more efficient method is termed circulant embedding which uses a property of stationary Gaussian processes: the covariance matrix is invariant under translations. This means that the covariance matrix is fully determined by the first row or column (hence “circulant”). The method uses Fourier transforms to compute eigenvalues and the method takes on the order of Nlog(N) operations. The matlab code in Kroese and Botev (2014, page 8) was translated into Fortran for use with the Intel MKL toolkit and parallelized the code using openmp. Our parallelization has each simulated decision performed on a different core of the workstation. The 2D program takes about 8 hours per subject on a 64 core AMD workstation with a 160×100 matrix compared with about 20 minutes per subject for the 1D model with a 72 element vector.
The model is illustrated in Figure 15 and is a straightforward generalization of the 1D model. Figure 15A shows a decision plane, Figure 15B shows a single Gaussian stimulus, and Figure 15C shows a single realization of a Gaussian random field. (Any line though the plane will produce a realization of Gaussian process.) Figures 15D to 15F show three Gaussian random fields with different SD kernel parameters that represent the spatial range of the correlations. In the experiment there are three response areas and so there are three Gaussian stimuli (there would be three peaks in Figure 15B). In our simulation of this process, on each time step (10 ms as for the 1D case), there is an evidence array that represents accumulated evidence and to this is added the stimulus (three peaks instead of the one in Figure 15B) plus a new realization of the Gaussian random field. This is repeated until one point on the evidence array hits the decision plane (if more than one point hits, the one with the largest distance above the decision plane is chosen).
Figure 15.
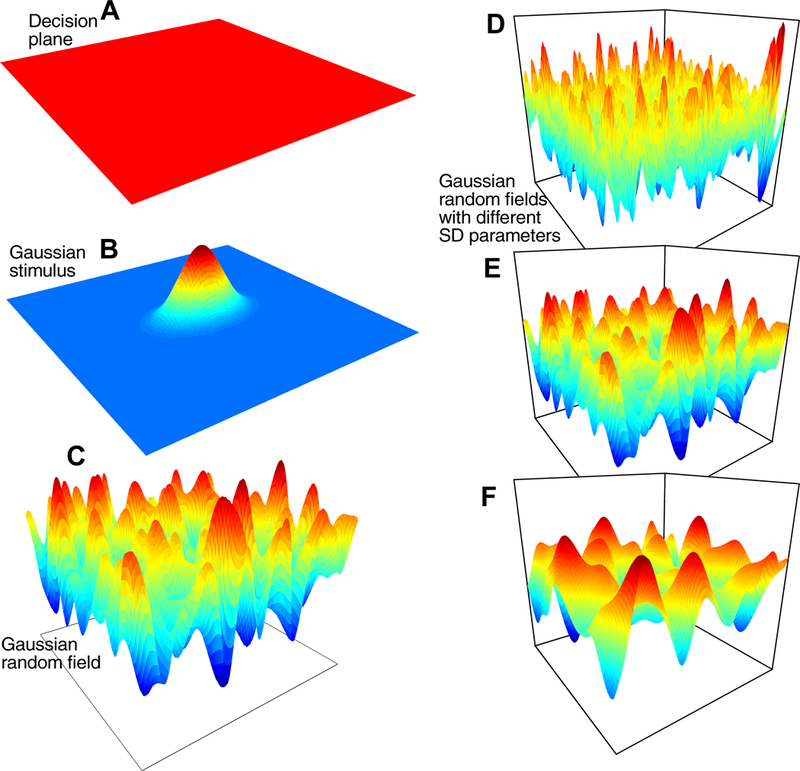
A representation of the 2D model. A shows a decision plane, B shows a 2D normal distribution of drift rates, and C shows the Gaussian random field noise distribution (by analogy to the Gaussian process distributions in Figure 1). D-E show examples of Gaussian random field with different kernel SD parameters.
The model is fit to data in the same way as for Experiments 1–8. An area around the peak of the strongest stimulus is defined as A as in Figure 2. Then an area surrounding that is designated B. Other stimuli are designated C and D and the remaining area is designated T (tail). The model is used to generate predicted choices and RTs as for Experiments 1–8 and plots are shown in Figure 16.
Figure 16.
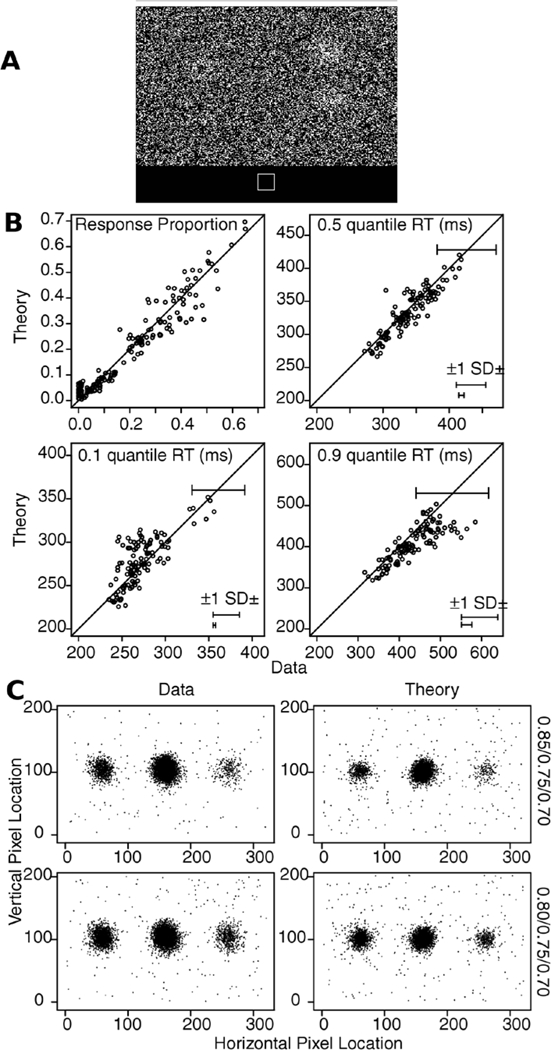
A shows an example stimulus with three bright patches. B shows plot of response proportions and quantile RTs for theory plotted against data with error bars produced in the same way as for Figure 3. C shows plots of the data and theoretical predicted responses for all subjects for each condition with the data aligned with the strongest stimulus patch in the middle (100×180), the next strongest at 100×60, and the weakest at 100×270.
Experiment 9
In this experiment, the stimulus was presented in a 2D plane of black and white pixels. The background was 50% white and 50% black pixels and the stimulus was composed of three bright patches or three dark patches randomly placed in the plane (Figure 16A). The task used a touch screen display and subjects were required to move their index finger from a resting box to the brightest or darkest patch in the display. This is the 2D analog of Experiment 4 in which the response was to the brightest or darkest patch on a half annulus.
Method
The same display and apparatus as Experiment 4 were used in this experiment. Sixteen undergraduates from the same pool as the other experiments were tested. The stimulus was presented in a 320 by 200 array of black and white pixels in a 640 by 480 pixel screen. The background was set to 50% black and 50% white pixels. Then three points in the stimulus array were randomly selected and a 2D Gaussian with SD radius of 12 pixels was used to provide values for the probability of flipping pixels in the stimulus array. There were two levels of difficulty with three patches in each difficulty condition. The probability of flipping a pixel (from black to white or white to black) at the centers of the three Gaussians was either 0.7, 0.5, and 0.4 or 0.6, 0.5, and 0.4. This led to the proportion of white or black pixels at the peak of 0.85, 0.75, and 0.70 or 0.80, 0.75, and 0.70. The centers of these patches were selected with the restriction that they could not be less than 64 pixels from the left and right edges of the stimulus array and 40 pixels from the top and bottom. The peaks of the three patches were not closer than 36 pixels.
In the task, a starting box was presented (Figure 16A) below the stimulus at a location centered at 320×430 pixels that was 40×40 pixels square. The subject was instructed to place their finger in the box to initiate the trial. After a delay of 250 ms, a + sign was presented at the center of the stimulus rectangle which remained on for 500 ms, then the screen was blanked for 250 ms and then the stimulus array was presented until the finger was lifted from the box. Following this, the stimulus array was cleared from the screen.
After the stimulus was presented, the subject moved their finger and placed it at the position in the stimulus rectangle corresponding to their decision. If the delay before finger lift after stimulus presentation was greater than 600 ms, then a message “TOO SLOW” was presented for 500 ms. If the delay between lifting the finger and responding was greater than 300 ms, then a “TOO SLOW MOVEMENT” message was presented for 500 ms. If a finger lift occurred earlier than 220 ms after the stimulus turned on, the message “TOO FAST” appeared for 500 ms. If the subject responded by placing their finger in a square 50 pixels on each side centered on the strongest stimulus peak, “2” was presented, if the response was on one of the weaker peaks, “1” was presented, and “0” otherwise. Feedback was presented for 250 ms and 30 pixels above their response.
The stimulus was presented until the finger was lifted which suggests that the subjects could have searched the array strategically for the brightest location. But the time limits were made short, with the warning “TOO SLOW” after 600 ms and the stimulus display turning off after 800 ms, and these encouraged very fast responding. The median RTs were almost all below 400 ms which is relatively little time for anything more than a couple of eye fixations. In retrospect, the design of this experiment could be improved, but this is what we had at this stage of development.
Results
Because the number of combinations of positions of the three stimuli is very large (infinite), they were aligned in a similar way to as was done in Experiments 3 and 4. The strongest stimulus was placed at 160×100, the next strongest at 50×100 and the weakest at 210×100. Responses at a circular radius of 40 pixels were moved to consistent positions around these locations and responses outside the three areas were randomly placed in the rest of the space. In future designs, it would be better to select several configurations in terms of the angle and separations of the stimuli and use them in some proportion of the trials (e.g., three configurations in 40% of the trials) with the configurations rotated and translated from trial to trial (e.g., Experiment 6). This would allow specific questions about the distribution of responses between stimuli and away from stimuli to be examined, for example, to see if stimulus location dependent noise is required.
The model was fit to data from each individual subject in the same way as for Experiments 1–8. An area around the peak of the strongest stimulus was defined as A as in Figure 2. Then an area surrounding that was designated B. Other stimuli were designated C and D and the remaining area was designated T (tail). The A region was a 10.8 pixel radius around the central peak, the B region was an annulus with inner radius 10.8 pixels and outer radius 39 pixels.The same SIMPLEX minimization routine was used as in the fits to earlier experiments and the same G-square statistic was minimized using choice proportions and quantile RTs.
The predicted choice proportions and RT quantiles are plotted against the data in Figure 16B. The quality of the fits looks similar to those in the earlier experiments, but there are some systematic misses. At the bottom left of the response proportion plot there is a vertical stack of points in which the theory predicts between 0 and 0.05 proportion of responses, but in the data the proportion is near zero for many of the conditions by subjects. Second, there are misses in the leading edge of the RT distribution for some conditions and subjects. The model predicts larger values than the data especially those in which the 0.1 quantile RTs for the data are in the 250–270 ms range. The median RTs fit quite well, and there are a few longer 0.9 quantile RTs than the model predicts.
Figure 16C shows plots of the choice proportions for the aligned data for each subject and choice. The data around the central peak have too many observations to display, but the range and density of the secondary peaks show correspondence between theory and data.
The parameters for Experiment 1–8 are defined in terms of angular distance, while the parameters for Experiment 9 are in terms of number of pixels divided by two in the array. This means that the parameters sw, r, and sd are not directly comparable unless the scaling from pixels to angle is examined.
The 2D model fit the data adequately but not as well as the 1D model fits data from 1D tasks. The main issue seems to be that the model predicts more responses at larger distances from the stimuli than occur in data. This suggests that noise is too large away from stimuli which suggests that one way to deal with this is to make noise larger around the stimuli and smaller at larger distances away from the stimuli (cf., something like Poisson noise). The main problem in exploring this model is the high computational cost. But with additional computational resources, variants of this model (such as assuming that noise varies as a function of the distance from stimuli) will be able to be examined. This model and fits should be viewed as highly suggestive, but the fits are not quite good enough yet. Thus, the application of this model structure to tasks using responses in 2D space appears promising.
Saccade, Mouse, and Finger Movement Durations
Subjects were asked in our experiments to make rapid one-shot decisions and to make their decisions before beginning to move their eyes, fingers, or mice to the target location. In contrast to decision times, measured as the time between stimulus onset and movement, movement times are defined as the time between the eyes, fingers, or mice moving away from their resting position to a response (eyes fixating on a response location, fingers pressing on a response location, or a button on a mouse being pressed). We examined the distributions of movement times for each experiment and looked to see whether fast versus slow movement times affected the accuracy or RTs of decisions. If short decision RTs were associated with long movement times and vice versa, then it might be that the decision was during the movement time rather than prior to the movement. Thus, analyses of movement times provide some evidence as to whether our instructions were sufficient to ensure that the decision process was finished before movement began (at least, on most trials).
Figure 17 shows the distributions of movement times for the nine experiments. The first thing to notice is that eye movements have differently shaped distributions than finger and mouse movements. For Experiments 1 and 3, most of the eye movements were rapid (20–60 ms) and a few were from a wide distribution that started at about 200 ms. The slower ones came from movements to an intermediate position and then a corrective movement to the target. For Experiment 5, again most movement times were fast, but a greater number of them than for Experiments 1 and 3 were 200 ms and above. (Note that for these experiments, the stimulus was erased as soon as the eyes left the fixation point so moving early did not allow additional information to be gathered from the stimulus.)
Figure 17.
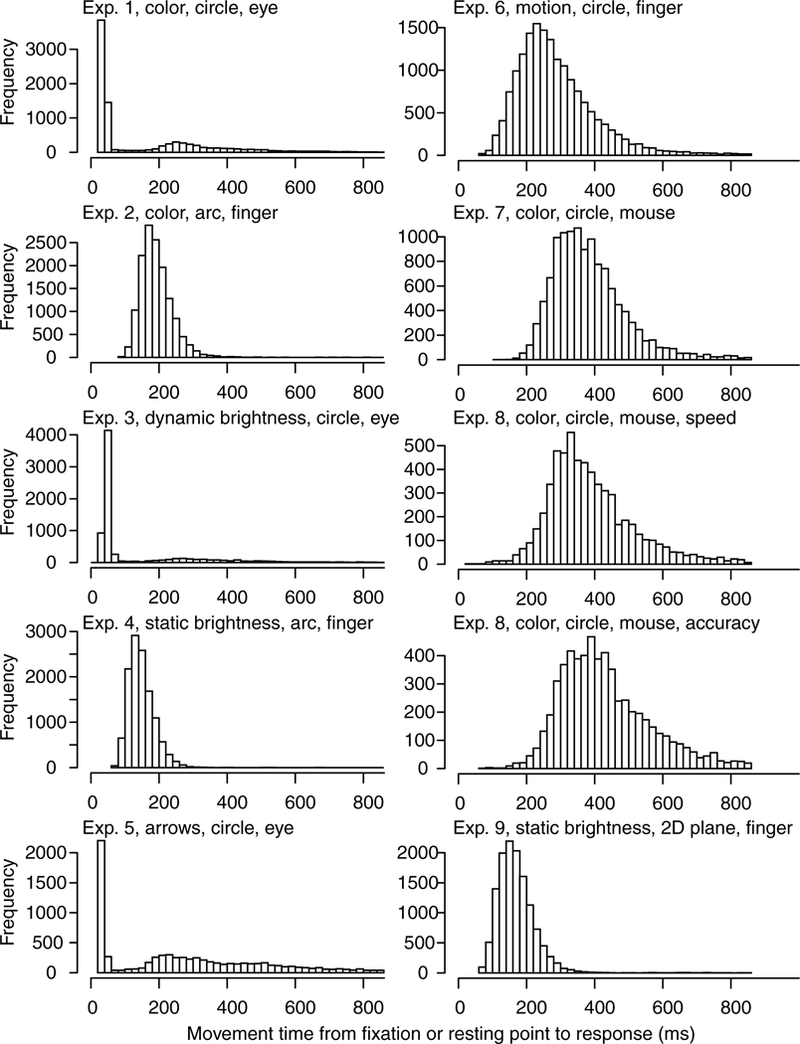
Plots of the movement times from the time at which the eyes, finger or mouse left the resting/fixation point until it reached the response target for all the experiments. Exp. means Experiment.
Finger movements on the touch screen have quite narrow distributions of movement times (Experiments 2, 4, and 9), consistent with a roughly ballistic movement with the decision made before the movement. Movement time is slower for Experiment 6, most likely because the finger resting point was farther from the response circle than for the other experiments. This would also explain why the distribution is wider than for those from Experiments 2, 4, and 9.
The two experiments with mouse responses (Experiments 7 and 8) show considerably wider distributions of movement times. This is to be expected because moving and clicking a mouse is more complicated than moving eyes or fingers. For Experiment 8, the movement distributions for speed instructions largely overlapped with those for accuracy instructions, so subjects were not trading the speed and accuracy of decisions against movement time. (The much larger movement times for mouse experiments relative to touch screen experiments is one reason we now favor touch screen tasks with chromebooks mentioned earlier.)
For each experiment, we calculated the mean RTs for the data averaged over all the conditions of the experiment and conditionalized on the movement time, namely the half of the RT data based on the fastest half of the movement times and the half based on the slowest half of the movement times. For Experiments 1 through 9 respectively, the mean RT for the fastest half of the movement times minus the mean for the slowest half was +10 ms, +32 ms, +1 ms, +15 ms, −71 ms, −42 ms, +21 ms, +4 (for the speed instruction condition and −31 ms for the accuracy instruction condition), and +19 ms. The positive numbers are relatively small and show that almost all decisions are made prior to movements. The negative numbers are larger and show that slow movement times are associated with slow decisions. The largest difference is for Experiment 5, the arrow task. This may represent decisions being made after movement begins. But generally, movement times are only weakly related to RTs.
For Experiment 6, the finger resting point was below the response circle so that movement distance was larger than for the other experiments. The movement times were divided into near (bottom half of the response circle) and far (top half). The mean differences in movement time (from leaving the resting square to hitting a point on the response annulus) were different by about 53 ms, consistent with the distance traveled.
Saccadic eye movements have different properties than finger and mouse movements, which may explain why subjects wanted to move their eyes to intermediate locations before a final decision. Saccadic eye movements have lower processing costs and in natural situations are generated by systems that seem to set global rates of production (Kowler & Pavel, 2013). This means that it costs the processing system relatively little effort to make saccades to low information targets or even to targets with no useful information. In some paradigms, many saccades to low information targets are followed by brief fixations (e.g., 100 ms) that are too fast for much useful information to be extracted (Araujo, Kowler, & Pavel, 2001). Although this is suboptimal in some laboratory tasks, it may be an important strategy in viewing natural scenes in which cognitive operations are decoupled to some degree from the current fixation (Kowler & Pavel, 2013). When designing experiments with eye movements, this complication should be kept in mind, but in the experiments reported in this article, these complications were minimized by the instructions and paradigms, which, except for Experiment 5, produced mainly direct eye movements.
Discussion
Previously there have been no models that explain how decisions are made about stimulus representations that are continuous in space with responses on continuous dimensions and that explain both the accuracy of decisions and the time taken to make them. To construct the SCDM (Figure 1), spatially continuously distributed noise represented within-trial variability in the decision process (spatially continuous Gaussian process noise or Gaussian random field noise for responses in 1D and 2D spaces, respectively). The combination of this continuously distributed noise and a continuously distributed stimulus representation allowed the model to explain the results from the experiments. Across the experiments, the stimuli were displays of black and white and colored arrays of pixels, arrays of arrows, and arrays of moving dots, with static and dynamic displays. Responses were made by eye, finger, and mouse movements. In each experiment, there were several levels of difficulty. The model accounted for accuracy and RT distributions for all the experiments quite well with relatively few outlier responses per experiment. The model captured the spatial distributions of responses and the full distributions of RTs.
To fit the model to the data, responses and the model’s predictions were grouped into the A, B, and T categories (plus a C or D category for some of the experiments), which approximately correspond to correct responses, near-correct responses, and errors (Figure 2). Predictions from the model were generated by simulation and a SIMPLEX minimization routine was used to find the values of the model’s parameters that provided the best fit of the model to the data, that is, to the proportions of responses and the RTs for each of the categories. The model was successfully fit to the data from each individual subject, which offers the possibility of using the parameters of the model in future studies of differences among individuals (e.g., IQ, assessing neuropsychological and clinical deficits).
Surprisingly, there were only small to nonexistent differences in RTs across positions on the response dimension (Figures 3D–10D), even when there were competing stimuli (e.g., two patches of bright pixels). In other words, incorrect responses had about the same RTs as correct ones, a contrast with the two-choice decision model for which RTs are usually significantly different for correct and incorrect responses (the differences are explained by the two-choice model’s assumptions of across-trial variability in drift rates and starting point). This is not to say that there were no RT effects in the experiments here: as difficulty increased, RTs increased by over 100 ms in some tasks. For the more difficult conditions in some of the experiments, the model’s predictions for the distributions of responses over spatial location were wider than the data. However, only one SD in the drift rate distribution(s) was used for all the levels of difficulty in an experiment (sw); if the SD differed between levels of difficulty (in other words, there was precision and more uncertainty in location for weaker stimuli), the model would produce wider distributions. For the experiments with colored stimuli, there was an additional salient result; subjects were biased in their responses toward primary and additive colors over other colors. These biases were explained by assuming a sinusoidal boundary or starting point function so that less evidence was needed for a primary or additive color decision than colors between them.
The model fit all the features of the data with relatively few parameters: nondecision time and the across-trial variability in it, the response boundary and the across-trial variability in it, the Gaussian-process kernel parameter for the continuous distribution of noise in the process of accumulating evidence, the across-trial variability in the height of the distributions of drift rates, and the SD in the drift-rate distributions, plus a drift-rate parameter for each level of difficulty. For the color biases, there was one additional parameter for the amplitude of the sinusoidal response boundary (or starting point). Overall, this is a dramatic reduction from the number of degrees of freedom that would be needed to fit the full distributions of responses and RTs across spatial locations.
At this point the question might arise: why have theories about decision making for continuous stimulus and response dimensions not been developed and fit to RT and choice proportion data before this? There are a number of tasks for which the stimulus and response dimensions are continuous, but there appear to be no attempts to model choice proportions and RT data. Such tasks include working memory tasks (e.g., Zhang & Luck, 2008), number line tasks (e.g., Thompson & Siegler, 2010), and tasks for which individuals indicate how confident they are in their decisions on a continuous scale (e.g., how confident they are in their decision about whether or not a test item had been previously presented in an experiment; e.g., Province & Rouder, 2012). One possible answer is that assumptions about spatially continuous noise and stimulus representations have not been considered in attempting to model such tasks.
An important direction for further research is to link the SCDM to models of perceptual processing. In all of the experiments reported here, precise control was not exerted over color, luminance, or other physical characteristics of the stimuli. At this point of theory development, I was not concerned with the link between precise quantitative perceptual characteristics of stimuli and the information actually used in the decision process. The aim in this article was to develop and test a model of decision processes. In future research, it will be important to link perceptual properties to the distributions of evidence used to make decisions, both their heights and their SDs. For example, it might be that perceptual template models that specify the representations of perceptual stimuli (Lu & Dosher, 2008) or Smith and Ratcliff’s (2009) integrated systems model of attention and perceptual processing could be adapted to add the SCDM to account for RTs and choices on continuous scales.
Examining the Structure of the Model and Alternative Assumptions
A number of variants of the SCDM can be explored. First, stimulus variability from trial to trial has been represented as variability in the height of the drift-rate function driving the decision process. An alternative would be to have the same height, but have the function vary from trial to trial in its location on the angle axis. Second, a normal distribution of drift rates has been assumed. However, other distributions are possible such as back-to-back exponentials or circular Gaussian von Mises distributions (which are similar to normal distributions). Third, different distributions for the across-trial variability parameters are possible, but it may be that choices of these distributions are not critical and produce similar patterns of results to the choices in the model implemented here (e.g., Ratcliff, 2013). Fourth, instead of normalizing evidence, perhaps the drift rate distributions could be normalized so the average drift is zero. In Figure 1D, this would mean that zero drift would be at about 0.3 on the y-axis and drift rates between 120 and 240 degrees would be positive and drift rates outside this range would be negative. Then mean evidence would not be set to zero after each time step. I have implemented this model and found that it provides somewhat better numerical fits for some but not all experiments. But a more comprehensive evaluation is needed before it could be used as an alternative to the model used to fit the experiments. These examples show that there may be tweaks to the structure of the model presented in this article that might provide a better description of the data.
One issue that has not been addressed for circular response dimensions is how to generate Gaussian process noise that is continuous across the 360–0 degrees boundary. This is because a line was used to represent the circle and Gaussian process was assumed on the line. For a circle, the function should be continuous from one end of the line to the other, for example, in Figure 1C, each function at 0 degrees should be the same as the value at 360 degrees. This is specific to the SCDM and applications to responses on a circular scale. However, this is probably not too important because the stimulus was placed away from the 0 and 360 degree end points and so would only affect model predictions for a relatively small number of responses in distances far away from the stimulus.
In several of the experiments, there were two kinds of small but consistent misses between the model and data. First, the model overpredicts the probability of responses at distances far away from the stimulus. One way to improve the fits would be to change the assumption that noise comes from a Gaussian process with constant amplitude. The modification would be to assume that the Gaussian process noise is stimulus location dependent so that the amplitude of noise is larger at the stimulus location and decreases as a function of distance to a constant level outside the range of the drift rate distribution (e.g., constant in the tails outside 100–260 degrees in Figure 1B). This would lead to fewer responses in locations away from the stimulus. The behavior of RTs across spatial position would be a key measure that would indicate whether this assumption was reasonable or not. A second issue is that the distribution of responses over angle is often wider for the low accuracy conditions than the model predicts. It was assumed that the SD in the drift-rate distribution is constant over levels of difficulty. But, if that assumption were relaxed and it was assumed that weaker stimuli have more variability and wider distributions (less precision), the model would fit the data better. These two additional assumptions were not made in the fits presented in this article because the aim was to present the simplest model with the fewest degrees of freedom, to show how it accounted for data, and to show deviations and suggest what assumptions might be needed to accommodate them (because there may be alternatives to the ones suggested here).
The Appendix contains examples of how changes in each of the model parameters affects the predictions of the model for choices and mean RTs across spatial position as well as RT distributions. One prominent finding is that across-trial variability in drift rate and boundary setting affect the relative speed of correct and error responses (A and B vs. T in Figure 2) in the same way as for the two-choice model: Across-trial variability in drift rate and boundary setting produces errors slower than correct responses and errors faster than correct responses respectively.
The appendix also shows that for four examples using simulated data, the fitting method recovers the parameter values with SDs lower than the SDs across individuals. For two of the simulated data sets, tradeoffs among parameter values are examined, and these suggest that although there are some large tradeoffs, these are readily interpretable. These results mean that the fitting method (at least for these and those with similar parameter values) does not introduce biases into the parameter estimates and produces estimates that are sufficient for individual difference analyses. In the future, alternative fitting methods can be explored (cf., the efforts to develop methods for the two-choice diffusion model, Lerche, Voss, & Nagler, 2016; Ratcliff & Childers, 2015; Ratcliff & Tuerlinckx, 2002; Vandekerckhove & Tuerlinckx, 2007; Voss & Voss, 2008; Wiecki, Sofer, Frank, 2013). Such studies are important if the model is to be applied to examine differences in performance in different populations, such as those with cognitive deficits, disease, or development or aging. Using the best method for estimating model parameters will be especially important for examining differences among individuals or diagnostic tools.
Cognitive Models that Use Distributed Representations
Spatially continuous distributions of stimulus information like the ones used in this model have been used in letter matching and confidence judgment tasks with discrete response choices. For tasks in which subjects are asked to decide if one string of letters matches another one, it has been assumed that the letter representation for an item just studied is distributed over spatial position. Thus, when several letters are presented, the representations overlap and this allows the model to account for low accuracy and long RTs when adjacent letters are switched in position compared to higher accuracy and shorter RTs when non-adjacent letters are switched in position. In some models for confidence judgments about memory, it has been assumed that memory strength, which determines confidence, is continuously distributed.
In the letter-matching task used by Gomez et al. (2008) and Ratcliff (1981, 1987), a string of 3–7 letters was presented then erased and a second string was presented and the task was to respond “same” or “different”. If two adjacent letters were switched in position it was more difficult to respond different than if two farther-apart letters were switched. To model this, letters in the first string were assumed to be distributed over position. Criteria were placed between the letters and the areas between the criteria were summed to provide a measure of the degree of match between the first string and the second. This model accounted for all combinations of transpositions of letters (adjacent and non-adjacent), replacements of letters with new letters, repeated letters, strings of different lengths, letter migrations, and transpositions with words and nonwords. Ratcliff (1981) found a linear relationship between drift rates from the two-choice diffusion model and overlap in the model, which suggested that a combination of these models might explain both accuracy and response time measures in this paradigm. The assumption of distributed representations is consistent with the assumption in the SCDM.
In a typical confidence judgment procedure, subjects choose which of some small number of categories best describes their degree of confidence (e.g., “sure,” “very sure,” and so on). To model confidence judgments about memory (the RTCON and RTCON2 models, Ratcliff & Starns, 2009, 2013; Voskuilen & Ratcliff, 2016), memory strength was assumed to be distributed and confidence criteria were placed on the strength dimension. The area under the strength distribution between the criteria provided the drift rate for an accumulator for that confidence category. The model accounted well for the proportions of responses for each category and their RT distributions.
In an earlier approach, I attempted to use a version of the RTCON model to approximate continuous response dimensions with discrete accumulators, one for each small range on the continuous scale. If the stimulus distribution was such that the evidence at nearby points was correlated, then this might approximate a continuous process. The problem is that there is no proof that the limiting version of this would be a continuous process and it is difficult to see how to go about developing a proof. In the SCDM, discrete values are used for time steps, stimulus representations, and response dimensions, which might make the model appear to be discrete. But the same results are produced (subject to numerical approximation) if the size of the discrete steps is made small with appropriate scaling of the model’s parameters. In the limit as the step sizes approach zero, the process is continuous.
The stimulus representation used in the RTCON model is similar to the representations used in the SCDM and so the combination could be used to compare modeling confidence judgments recorded on both continuous and discrete scales.
The Circular Diffusion Model
Smith’s (2016) circular diffusion model was designed to model tasks in which a stimulus is presented and a response is made on an annulus (e.g., Experiments 1, 3, 5, 6, 7, and 8). In the circular model, a diffusion process in two dimensions begins at the center of a circle and evidence is accumulated in two dimensions until the process hits the circumference of the circle, which is the decision boundary. The stimulus determines a drift rate which is represented by a distribution that causes the process to drift towards one position on the edge of the circle. Smith derived exact predictions from the model for the distributions of choices at the boundary and their RT distributions and tested them by examining predictions for the qualitative effects of standard manipulations of experimental variables in this task (although he did not fit data directly). Plots of the model’s predictions for RT quantiles from conditions with different drift rates, boundary values, and across-trial variability parameters were plotted against the quantiles for one reference condition (Q-Q plots). The results were a straight line which indicates that the distribution shape was the same over these different conditions (cf. Figure 14 in this article).
The SCDM is more general than Smith’s because it can be applied to a wider range of tasks. However, direct comparisons between the two models across a range of tasks and manipulations will provide fertile questions for future research. For example, one issue will be whether the circular model can account for results when two or more stimuli are presented in the same display (e.g., the several bright/dark patches in Experiment 3). The simplest assumption would be to combine information from the several stimuli into a single, bimodal distribution of drift rates but, contra our data, this would produce an increase in the number of responses between the stimuli. Another possibility would be to assume that on each trial only one stimulus is encoded so that responses would be a probability mixture of responses to the two (or more) individual stimuli.
Population Code and Neural Models
The SCDM can be seen as an implementation of population code models in neuroscience (e.g., Beck et al., 2008; Deneve, Latham, & Pouget 1999; Jazayeri & Movshon, 2006; Liu & Wang, 2008; Nichols & Newsome, 2002; Pouget et al., 2013). Population code models assume that activity is distributed over an array of elements (neurons) and a response to a stimulus is a weighted average of the activity in the population. The SCDM extends population code models by using a spatially continuous distribution of noise in the decision process and by using this, it is able to fit response choices and RTs across spatial locations, including the distributions of RTs. None of these population code models have yet dealt with choice proportions and RT distributions from experiments with responses on a continuous scale such as the ones here.
Beck et al.’s (2008) Bayesian population code model is similar in many ways to the SCDM. It was developed to explain computations carried out in the motion system with assumptions about the representation and processing in MT (middle temporal), LIP (lateral intraparietal), and SCb (superior colliculus - motor burst neurons). They assume these represent an input layer, an evidence accumulation layer, and a readout layer where motor output is generated. LIP units accumulate input activity from MT cells that fire in response to a continuously changing moving-dot stimulus. Activity is accumulated in a series of accumulators along a line and the amounts accumulated are correlated between nearby accumulators (nearby locations in the stimulus and noise are also correlated).
The Beck et al. model makes assumptions about short-range activation and long-range inhibition within the LIP accumulation layer. However, Ratcliff, Hasegawa, Hasegawa, Smith, & Segraves (2011) used simultaneous recordings of pairs of neurons and found no evidence of long-range inhibition in buildup neurons in the SC (activity that should mirror activity in LIP). The SCDM assumes no such inhibitory interactions. In the Beck et al. model, a decision is initiated in the SCb layer which implements a winner-take-all network based on an estimate of the probability of firing as opposed to the actual firing rate of a neuron.
The Beck et al. model was applied to motion discrimination tasks like our Experiment 6 in which subjects decided if the direction of coherently moving dots was to the left or the right (or left, right, up or down). The model accounted for choices and mean RTs for correct responses in discrete two-choice and four-choice tasks, but it has not accounted for the full distributions of RTs or RTs for incorrect responses.
Beck et al. argued that their model can be extended to time-varying stimuli. The model assumes that when a stimulus is turned off, the accumulation process stops and evidence begins to decay with a some time constant). However, Ratcliff and Rouder (2000; see Ratcliff, Smith, et al., 2016 for further discussion) showed that when a stimulus is presented briefly, the best model is one in which drift rate is constant; it does not rise with stimulus onset and fall to zero with stimulus offset. This is consistent with the Beck et al. proposal if their time constant is large (e.g., over 500 ms). Smith and Ratcliff (2009) developed a model that accounts for manipulations of attention, contrast, and stimulus duration for briefly presented perceptual stimuli. In that model, stimulus information is encoded into a visual working memory and a constant output from working memory is used to drive the decision process. In the SCDM, brief presentations (e.g., 200–300 ms) are assumed to produce constant drift rates, and this can be justified by assuming a stationary drift rate produced from a distributed working-memory representation. A related question is whether the model should allow drift rate to ramp up over a few 10’s of ms. Ratcliff (2002) showed such ramping up is mimicked by a constant drift model and so a constant drift model accommodates a model with drift rate ramping up.
The SCDM is simpler and more general than the Beck et al. model, but it does not deal with details of neurophysiology as the Beck model does. It is unclear whether the Beck model can account for the aspects of the behavioral data that the SCDM can and whether it can be modified to account for decision-making in tasks like those presented in this article. However, the similarities between the two models outweigh the differences.
Liu and Wang (2008) developed a model for motion discrimination with (normally distributed) evidence from a stimulus driving populations of direction-sensitive neurons. The dynamics of evidence accumulation were based on synaptic currents for several types of neurotransmitters. As far as I know, this model is too complicated to be explicitly fit to RTs and choice probabilities to produce estimates of model parameters. However, the model provides a plausible detailed neural implementation of an evidence-accumulation process. Liu and Wang generated predictions from the model for accuracy and RT distributions for a two-choice task, but the model was not actually fit to data. It was also used to account for results from microstimulation experiments in which electrical current is injected into MT neurons. At this point it would be a daunting task to fit the Liu and Wang model to data. However, in the future, it might be possible to develop a simplified version of the model, as Wong and Wang (2006) did for another model for two-choice decisions, and use such a simplified model to account for experimental data from the kinds of tasks and data in this article.
There are also models in which collections of accumulators are used to represent neural population codes (Zandbelt, Purcell, Palmeri, Logan, & Schall, 2014). Such collections show similar behavior to single accumulators if there is a modest correlation in firing rates between the individual accumulators in the collection. Also, collections with different numbers of accumulators show similarities to each other. Early in development of the SCDM, models were developed that used arrays of separate accumulators, but as discussed above, models with spatially continuous evidence and noise provide a more natural account of processing in the tasks used here. However, by using neurophysiological constraints and the kinds of models developed by Zandbelt et al. (2014), it might be that a model with plausible assumptions about collections of accumulators would show similar behavior to the SCDM.
Dynamical-Systems Neural Field Models
Klaes et al. (2012) developed a model that represents activity in a series of 1D continuous maps that are similar to those used in our 1D model. The maps proceed from an input map to an association field to premotor and motor maps. The motor map is similar to the accumulated evidence in the SCDM and the input mapped through the association field is similar to our drift rate distribution. The mapping from the stimulus through the association field highlights the important insight that a stimulus has to be transformed to a decision-related representation. For example, the color stimuli in Experiment 1 have to be mapped onto a 1D decision representation. The model was applied to reaching data for monkeys (but not to RTs). A related model by Wilimzig et al. (2006) was applied to saccadic decision making in simple saccadic tasks. As in Klaes et al., there was a field representing the input, an initiation field, and a selection field. One difference between their models and ours is that noise in the Klaes and Wilimzig models is represented as independent Gaussians in the units of the model whereas ours is continuously distributed and correlated across position. The Klaes et al. and Wilimzig et al. models are closely related to the SCDM and so the insights from those models and similarities between the two kinds of models can help guide future modeling.
Visual Search Models
The SCDM is also relevant to visual search models (e.g., Thornton & Gilden, 2007; Wolfe, 2007) that are applied to tasks for which an array of objects is displayed and subjects decide whether there is or is not a particular target object in the array. A common assumption is that the objects in an array each have a diffusion process and the processes for all of the objects race to a threshold. For the SCDM, it could be assumed that objects are represented in continuous space with a peak of activity corresponding to each object in the array. However, there are two important questions that this implementation of the SDCM would not address. The first is how the system constructs representations of the objects in terms of the dimension on which decisions are made. For example, in an array of letters, the task might be to choose the letter “x” or it might be to choose the object that was red. Hence, the activities for the objects in an array would need to be dependent on the dimension being searched for, something the SCDM does not address. An example of how this may be accomplished is using a salience map (Klaes et al., 2012) that modulates the 2D representation of the stimulus so that only objects with the right color or shape produce activation. But this would not answer the questions of why some features are integrated in search while others are separable (Garner, 1974) and why some stimuli pop out and others do not.
The second question is how the system can make a judgment that the target is not in the array. This has been problematic for visual search models and search models in general and the SCDM does not address it. However, for a task requiring a present/absent judgment for stimuli in a 2D array, the stimuli could be represented by a Gaussian peak for each item in the display that has the desired property (brightness, color, shapes, etc.), as in Figure 15B. Then a horizontal plane through the representation of the array could be used to separate present versus absent stimuli. The integrated activity or peak activity above or below the plane could be used as drift rate in a two-choice diffusion model.
The main point is that to produce a reasonably comprehensive model, the relationship between stimulus and decision representations has to be understood. This is taken up later in this discussion.
Complications in Relationships Between Domains
The relationship between population code models and the SCDM and tasks used to test the model was discussed above. However, in research that examines responses on continuous scales in neuroscience, there is a great deal of complexity and models of the kind proposed here (including population code models and the SCDM) will be only part of the story. Two examples that suggest that the relationships are more complicated are presented below.
Early research found that response areas in motor cortex and in movement-related oculomotor areas have maps that represent 2D space. If an individual is to make an arm movement to a position in space, then an area in motor cortex corresponding to the direction of movement increases its firing rate (e.g., Georgopoulos et al., 1986). Also, if an eye movement is to be made to a position in space, then buildup cells in a corresponding area on a retinotopic map in the superior colliculus (SC) increase their firing rates (e.g., Wurtz & Optican, 1994) and when the firing rates reach a criterial level, burst cells fire and the eyes move. Results in both these domains have suggested that winner-take-all networks select the reaching or saccade goal. It might seem that it would be relatively easy to add mechanisms to population code and winner-take-all models based on these observations to account for RTs and choice probabilities.
However, more recent research makes clear that some aspects of the decision processes are much more complex. For example, Optican (2009) pointed out that the SC contains a spatially coded map, but feedback (the motor error) is temporally coded and so SC output must be converted to a temporal code and this has not yet been modeled. Likewise, Churchland et al. (2012) argued that reaching should be viewed as a dynamical process represented in a state space rather than a simple population code. When the SCDM is at least somewhat mature and validated against data, hypotheses about possible relationships between it and neural models can be generated and tested and used to examine wider issues about neural representations and processes.
Visual Working Memory
The task in Experiment 1 is similar to one that has been used to study visual working-memory (VWM; Zhang & Luck, 2008, and subsequent studies). In these studies, several colored squares were presented briefly at locations around a fixation point. They were followed by squares in the same locations but without colors. The lines of one of them were bold and for that square, subjects were to move their eyes to the color that that square had contained on a circular color wheel. Zhang and Luck proposed that the probability of reporting the correct color is a combination of a von Mises distribution over angle on the color wheel and guessing. Later models (e.g., Bays et al., 2011) assumed a mixture of von Mises distributions or a continuous mixture of them (Bays, 2014; Bays et al., 2011; Zhang & Luck, 2008). On some trials of the task, the stimulus was only a single colored square so, to prevent subjects anticipating where the color was located on the circular color wheel, the wheel was randomly rotated from trial to trial. However, rotating the color wheel means that, in addition to making a decision about what color was in the box, there is also a search process to find the color. This is why in our color wheel tasks, the wheel was fixed across all trials to eliminate search time and avoid having to model that combination of processes.
As just described, patterns of results for VWM tasks have often been modeled with a mixture of processes, specifically a process based on memory for the stimulus and a guessing process (e.g., Zhang & Luck, 2008). In other domains, it is usually found that guessing processes have different time courses from stimulus-based processes (e.g., Luce, 1986; Ratcliff & Tuerlinckx, 2002). In fact, it would be highly unlikely that stimulus-based and guessing processes had identical time courses. However, in the experiments in this article, the RT distributions for processes away from the stimulus and the RT distributions for processes near the stimulus were quite similar (Figures 3, 4, 9, and 10). This makes mixture models implausible for the experiments presented here. Results from experiments in the VWM domain similar to Experiments 1, 2, 7, and 8 in this article have been explained with these guessing mixture models, but RT results for the experiments have not been reported. In using the SCDM to model these processes, search processes mentioned above would have to be eliminated as in Experiments 1 and 2 for example, by fixing the color wheel across trials. If results with such a modification to the paradigm were produced and if the RT functions were flat across position, then the single process SCDM might explain the decision process used in the task with only a single process with continuously varying evidence. But if error RTs (in the T area of distributions, Figure 2) were shorter or longer than those around the peak, then a mixture model might be more appropriate with some proportion of responses based on a zero drift process or some other kind of guess. Such an analysis would lead to an explanation of both the spatial distribution of choices and RTs and would provide a more complete explanation of processing in this kind of paradigm.
There are other model-based analyses of VWM but these have been based on two-choice tasks and not on tasks with responses on continuous scales. For example, Donkin et al. (2013) and Pearson et al. (2014) have applied the LBA and LATER models (respectively) to two-choice VWM tasks. However, there is some dispute as to whether such two-choice tasks are appropriate for examining VWM and it has been argued that continuous scales are necessary because they can provide information about the contents of VWM that discrete responses cannot (Fougnie et al., 2012; Ma et al., 2014; van den Berg et al., 2012, 2014).
Mapping Between Stimulus and Decision Representations
When a stimulus is presented to the processing system for a decision, information relevant to the decision must be extracted from the representation of the stimulus. For example, with a letter string as a stimulus, decision tasks with different mappings might be was the string a word or nonword, was studied earlier or not, was upper or lower case, was red or green, was large or small, etc. Some of these dimensions might be separable (Garner, 1974) in that the value on one dimension (e.g., red vs. green) may have no effect on a decision made on another dimension (e.g., word vs. nonword), but others may be integral (e.g., a previously studied letter string may produce more “word” responses in a word vs. nonword task than an unstudied string). For Experiment 3 above, it is the brightest or darkest of the patches that is relevant, not whether the brightness of a patch is greater or less than 60% white pixels or whether the patches are on the same or different sides of the stimulus annulus. The process by which information on the relevant dimension is extracted from the stimulus must take some amount of time and in the SCDM that time is part of nondecision time. Neurophysiological estimates of encoding and response output put their duration at about 150 ms so if the translation of the stimulus to a decision variable is more complicated than identifying a bright patch on a display, nondecision time should be somewhat larger than 150 ms.
Studies using EEG measures provide evidence for differences in the representations that occur over the time course of processing. Philiastides, Ratcliff, and Sajda (2006) used a face/car discrimination task with briefly displayed degraded pictures. They recorded EEGs from multiple electrodes and combined (weighted) the signals to obtain a single number (a regressor) for each trial that best discriminated between faces and cars. This single-trial regressor was significant at two times, around 180 ms and around 380 ms. Ratcliff, Philiastides, and Sajda (2009) reasoned the regressor was an index of how car-like or how face-like each stimulus was. So, in each condition of the experiment, subjects’ behavioral responses (“car” or “face”) were sorted based on the EEG regressor into ones that were closer to faces and ones that were closer to cars. The two-choice diffusion model was fit to the two halves of the behavioral data and the drift rates for them differed substantially but only for the later component, 380 ms. This shows that the later EEG signal indexes difficulty across trials prior to the onset of the decision process (estimated to be at 350–400 ms by fits of the model). With these results, it appears that the earlier signal represents perceptual encoding from which decision-related information must be extracted. Ratcliff, Sederberg, et al. (2016) performed a similar analysis of EEG data from a recognition memory task. In this domain, an argument has been made for an early frontal familiarity signal and a later parietal recollection signal. However, only the later parietal signal (peaking around 600 ms following stimulus presentation) was implicated in decision making because it, and not the earlier signal, affected drift rate.
The estimated duration of nondecision time is quite short in some of the tasks, as low as the 175 ms lower limit placed on the model fitting process. This value is lower than for other perceptual tasks with two-choice decisions (e.g., 270 ms, Smith & Ratcliff, 2009 and as low as 330 ms over several perceptual tasks in Ratcliff, 2014). It may be that for tasks in which the subject is to move his or her eyes or fingers to a location at which the stimulus appears, less translation of the stimulus representation is involved, but even so, the short duration of nondecision time estimated in some of the experiments presented here is a concern.
The more general issue is that computing a decision representation (sometimes called a decision variable) is a key issue that is implicit in much of the current work on decision making. In conflict tasks (e.g., the Stroop task, the Simon task, the flanker task), models explicitly represent the opposition of different sources of information. But for other tasks, memory or perceptual variables are sometimes simply assumed to be available or directly mapped from perceptual representations.
An example of how stimulus representations must be transformed to decision representations is given by Sperling’s centroid computation task (Drew, Sun, & Sperling, 2010; Sun, Chubb, Wright, & Sperling, 2016). In this task, dots of different luminances or sizes are displayed in a 2D plane and the task of the subject is to point to the centroid.
The model that best explains how the center of mass is computed uses a weighted sum of the coordinates of the dots or patches. The x-coordinate is a weighted sum of the x-coordinates of the items and the y coordinate is a weighted sum of the y-coordinates. This model could be easily integrated with the SCDM by assuming that the representation driving the decision process is a weighted sum of stimuli instead of a direct representation of the stimuli themselves (as is used for the brightness tasks in Experiments 3 and 4). As discussed earlier, this suggests that the decision variable is a function of the stimulus and the task requirements.
Population Code Models and the Two-Choice Diffusion Model
On the face of it, there appears to be a conflict between population code models and standard two-choice diffusion models. Population code models and the SCDM require a distribution of drift rates to drive the decision process on each trial, but the two-choice models have only a single drift rate for each trial. However, for the two-choice models, it could simply be assumed that trial-to-trial variability in drift rate represents a distribution of drift rates used to drive the decision process instead of a distribution from which a single drift rate is selected. The mathematics of the diffusion model is indifferent to these two possible accounts of variability in the two-choice model.
This population code assumption would require an identical distribution of drift rate on each trial. However, there has to be variability from trial to trial in the stimulus representation (Ratcliff, 1978). To have such variability and a population code, a population code distribution could be assumed with a mean that varied from trial to trial so the combined SD was the across-trial SD in drift rate (as in the RTCON2 model for confidence and multichoice decision making; Ratcliff & Starns, 2009, their Figure 2; Ratcliff & Starns, 2013; Voskuilen & Ratcliff, 2016; Voskuilen, Ratcliff, & McKoon, 2018).
Conclusions
SCDM can be viewed in three ways. For one, it is a generalization of the successful two-choice diffusion model and it provides a new domain of study for modeling decision processes. For another, it adds a decision component to dynamical systems models of decisions in a continuous space (eye movements and arm movements). For a third, it adds a spatially continuous decision process to neural population code models and so is consistent with population code interpretations of neurophysiological data from motor cortex and areas involved in generating eye movements. In such neurophysiological data, activity rises in 2D planes with the position of the maximum activity corresponding to a movement in space and the 2D SCDM can be seen as representing this activity and the process of selecting a response.
The SCDM was designed to account for both choice proportions and RT distributions in a variety of tasks, but at this point, there has been no attempt to model perceptual processes and the processes that translate encoded stimulus information to decision-related information (see Klaes et al., 2012, for an example of such modeling in which the mapping is 1:1). Integrating models of perception with the SCDM (as in Smith & Ratcliff, 2009, with the two-choice diffusion model) will potentially be a fertile domain for understanding the transformation of stimulus representations to decision-related representations on continuous dimensions.
There are three major features of this research that provide a basis for advancing theory. The first is to take continuous spatial dimensions seriously by using continuously distributed representations of stimuli. The second is to represent variability in the decision process with continuously distributed Gaussian noise (Gaussian process noise for 1D and Gaussian random field noise for 2D). The properties of Gaussian processes and Gaussian random fields are active areas of research in machine learning (Lord et al., 2014) and so the SCDM offers the possibility of linking research in machine learning with modeling decision-making on continuous scales. The third feature is a set of experiments that collect RTs and choices on continuous dimensions with a variety of stimulus and response types and tasks. These provide a template for paradigms that can be used to collect RT and choice data, but more importantly show that patterns of results generalize across stimulus and response modes.
The SCDM also offers the possibility of applications in domains that go beyond simple perceptual tasks, including psychometric tasks on continuous scales, any simple rating scale judgment (such as preferences for items), and confidence judgments. More generally, it offers the possibility of being applied in a wide range of tasks that require responses in a continuous 1D or 2D space.
Acknowledgments
Preparation of this article was supported by NIA grants R01-AG041176 and R56-AG057841. I would like to thank Geoff Gordon for motivating this project and helping point me in the right direction for some of the technical details. I would also like to thank Gail McKoon for forcing some serious rewrites of part of the article. Talks on this model were presented at the 2017 Annual Mathematical Psychology meeting and the 2017 Australian Mathematical Psychology Meeting.
Appendix
Parameter Behavior, Parameter Recovery, SDs in Model Parameters, and Covariance in Model Parameters
In this appendix I show how each of the parameters of the SCDM model affects predictions of the model, how well the fitting method recovers model parameters, and how the model parameters trade off against each other. Because the SCDM is a new model with no existing guidelines for how to fit it, the method I chose to use is one that is robust and has had success in other applications (e.g., Ratcliff & Starns, 2013). There is one critical fact to stress in evaluating results produced by the fitting method: the model fits the data at least as well as is reported in the figures for each experiment and alternative methods can only improve on these.
The Effects of Changing Single Parameters
Figure A1 shows predictions from the model for the mean parameter values from Experiment 1 (Tables 1, 2, and A1) with the second drift rate (31.3). The plots show the results of changing single model parameters to a high and a low value (except mean nondecision time which only produces a shift in RTs). The terms correct responses and error responses are shorthands for the regions A and T respectively in Figure 2.
Figure A1.
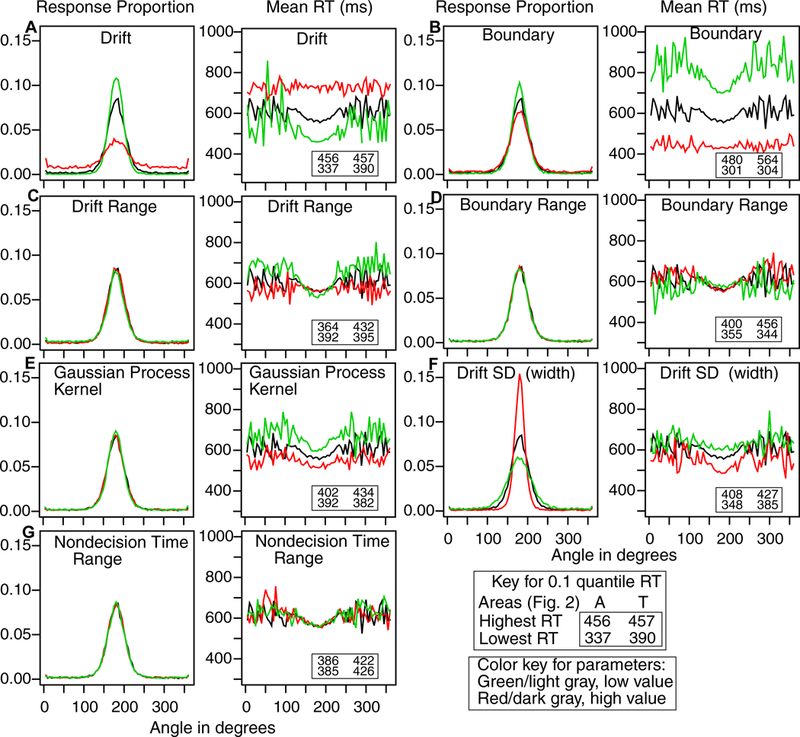
Predictions for the parameter values in top line of Table A1 with the value of one parameter changed per panel. The values of the parameters changed are presented in the text. For each panel, the distribution of responses over position and mean RTs over position are shown. The inset for the mean RT plots show quantile RTs. The black lines in the plots are predictions for the parameter values in the top line of Table A1, the green/light gray lines are for low values of the parameter and the dark gray/red lines are for the high values of the parameter.
Table A1:
Mean and SDs in SCDM parameters from simulation studies
| Data set | Param | Ter | St | a | sa | sw | r | Sd | d1 | d2 | d3 | d4 | G2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Experiment 1 | Mean | 177.5 | 33.1 | 15.4 | 5.9 | 37.0 | 14.0 | 0.859 | 42.7 | 31.3 | 16.7 | 89.2 | |
| Sim. data N=4000 | 176.0 | 26.6 | 14.1 | 4.2 | 36.7 | 20.6 | 0.721 | 44.8 | 33.5 | 18.5 | 54.4 | ||
| Sim. data N=200 | 181.0 | 25.1 | 13.8 | 4.4 | 37.6 | 22.9 | 0.761 | 46.4 | 34.5 | 18.8 | 37.2 | ||
| Experiment 3 | 177.7 | 48.1 | 12.3 | 5.5 | 26.0 | 34.0 | 0.821 | 26.3 | 12.2 | 14.6 | 5.1 | 102.1 | |
| Sim. data N=4000 | 179.9 | 58.3 | 12.7 | 6.3 | 25.8 | 31.5 | 0.917 | 27.2 | 13.1 | 15.1 | 6.0 | 46.2 | |
| Sim. data N=200 | 182.8 | 55.7 | 12.7 | 6.3 | 26.0 | 31.1 | 0.945 | 28.3 | 14.2 | 15.7 | 6.6 | 34.4 | |
| Experiment 1 | SD | 12.4 | 13.2 | 2.6 | 2.5 | 2.4 | 10.0 | 0.47 | 11.2 | 5.9 | 3.9 | ||
| Sim. data N=4000 | 2.0 | 1.9 | 0.2 | 0.4 | 0.5 | 1.0 | 0.06 | 1.0 | 0.8 | 0.5 | |||
| Sim. data N=200 | 4.9 | 2.6 | 0.3 | 0.5 | 1.5 | 2.0 | 0.10 | 2.7 | 2.3 | 1.6 | |||
| Experiment 3 | 20.7 | 15.7 | 1.8 | 0.9 | 2.2 | 5.5 | 0.25 | 3.2 | 2.6 | 2.8 | 2.4 | ||
| Sim. data N=4000 | 4.9 | 5.0 | 0.2 | 0.2 | 0.6 | 1.6 | 0.07 | 1.1 | 0.9 | 0.6 | 0.5 | ||
| Sim. data N=200 | 8.4 | 5.5 | 0.4 | 0.2 | 1.2 | 3.2 | 0.13 | 2.1 | 2.1 | 1.2 | 1.4 |
Ter is nondecision time, st is the range in nondecision time, a is the boundary setting, sa is the range in the boundary setting, sw is the SD in the drift rate distribution, r is the Gaussian process kernel parameter, sd is the range in the height of the drift rate distribution, dt is the height of the drift rate function, and G2 is the multinomial maximum likelihood statistic.
Drift rate, d (the values were 10 and 50): Increases in drift rate produced more peaked distribution of responses over position with more responses in the tail. There was also an increase in mean RT over position by over 200 ms. Errors were slower than correct responses for the high drift rate but errors were about as fast as correct responses for the low drift rate. The change in the 0.1 quantile RT was modest relative to the 200–300 ms change in mean RT.
Boundary setting, a (the values were 11.2 and 19.2): Increasing the value of a produced a modest increase in the peak of the distribution of responses over position but a large increase in mean RT. The 0.1 quantile RT increased substantially, by over 200 ms, and mean RT changed by over 300 ms. Errors were slower than correct responses for the high boundary setting, but about as fast for the low boundary setting. Boundary setting and drift rate affect performance in the same way as the corresponding parameters for the two-choice model.
Across-trial variability (the range) in drift rate, sd (the values were 0.01 and 1.80): Increases in the range produced similar behavior as for the two-choice model. Error responses became slower than correct responses with little change in the distribution of choices over position (cf., accuracy in the two-choice model).
Across-trial variability in boundary setting, sa (the values were 1. and 60.): Greater trial-to-trial variability in the boundary setting produced shorter error RTs relative to correct RTs, again, similar to the two-choice model. Because the SCDM is a linear model, trial-to-trial variability in the boundary with a fixed starting point produces identical behavior to the same trial-to-trial variability in the starting point with a fixed boundary.
Gaussian process kernel parameter, r (the values were 9.0 and 19.0 degrees): Increases in this parameter had little effect on the distribution of responses across position, but produced longer RTs for larger values of the parameter. If there is greater spatial variability (more peaks and troughs, the 1D analog of Figure 15D), there is more chance for a process at some small range of locations to hit the boundary relative to processes with less spatial variability (fewer peaks and troughs, the 1D analog of Figure 15F). As the kernel parameter became larger, errors tended to become slower than correct responses.
Width of the drift rate distribution, sw (the values were 5.0 and 9.0): As this became larger, the distribution of responses across position became wider with a smaller peak and RTs became longer (because the height became smaller).
Range in nondecision time, st (the values were 3 and 73 ms): this had little effect on performance and could possibly be dropped from modeling for the tasks with short RTs in this article (especially those with nondecision time restricted to be no smaller than 175 ms). However, tasks with longer RTs may need the st parameter to model the behavior of the leading edge of RT distributions (cf., Ratcliff, Gomez, & McKoon, 2004). But more importantly, this parameter is included because I subscribe to the view that encoding and response output times could not be identical from trial to trial.
Parameter Recovery
To examine parameter recovery, mean parameter values from Experiments 1 and 3 were used to generate simulated data and then the model was fit to these simulated data. These experiments were chosen because the first had one central stimulus and the second had two stimulus patches. Table A1 shows results from parameter-recovery simulations. The mean model parameters were used to generate 32 sets of simulated data with either 4000 observations per condition or 200 observations per condition. The latter mirrors the number of observations in the data per individual subject and reflects what I consider close to the minimum number needed for model fitting. Table 1A shows the mean recovered parameter values and the SDs in those parameter values. These can be compared with the SDs across individuals (which represent individual differences) which are reproduced from Tables 3 and 4. The simulated data sets are generated with identical parameter values for each set.
First, there are few consistent biases in recovered model parameters across the two sets of parameter values. Drift rates are sightly overestimated, but what might be a bias for some of the parameters for Experiment 1 has an opposite bias for Experiment 2.
Second, the SDs in recovered parameters from the simulations with identical input parameter values and 200 observations per condition are (with a couple of exceptions) between 2 and 5 times smaller that the SDs across subjects, i.e., individual differences. For 4000 observations per condition in the simulated data, the SD’s halve in most cases. It might be expected that the SD should be reduced as the ratio of square root of the number of observations, then most of the SDs should be reduced by a factor of 4.5. However, the model is fit with predictions generated with 10,000 sets of simulated data per condition and the variability in the predicted values adds variability in the recovered parameter values reducing the ratio.
There does appear to be a systematic bias in nondecision time for 200 observations per condition. But this is artificial because the lowest value of nondecision time that I allow is 175 ms. Thus, if moderately large variability in this parameter occurs because of low numbers of observations, fits of the model would attempt to produce a wide difference in the nondecision time. But truncation at 175 ms would only allow values of 175 ms and higher to be produced and this would result in a value higher than the parameter used to generate the simulated data (e.g., 177.5 and 177.9 for Experiments 1 and 3 respectively).
Scaling
In the standard two-choice diffusion model, the parameters are not all identifiable. For drift rate, boundary, starting point, and within-trial noise (diffusion coefficient) parameters, increasing one by some proportion and increasing or decreasing the others by the same proportion produces identical fits. Thus, one of the model parameters, usually the diffusion coefficient, is chosen as a scaling parameter and fixed to some value and then the other parameters are identifiable. The diffusion coefficient is usually chosen because it reflects noise in the accumulation process that is typically assumed not to change with the strength of the stimulus (cf., Smith & Ratcliff, 2009).
In the SCDM, I have chosen the same parameter to scale the other parameters against, namely the value of within-trial noise. There are two dimensions for Gaussian process noise, the evidence dimension (vertical) and spatial dimension (horizontal, which is controlled by the kernel parameter). The model parameters are scaled with respect to the evidence dimension. A different issue that is related to the scaling issue is how to change the spatial and temporal step sizes in the model simulation. Model parameters can be scaled so that if the steps are made smaller, parameters can be adjusted to produce the same fits subject to variability in the simulations that generate predictions. Note that there may be some small biases if the time or spatial step sizes are too large.
It is plausible that other parameters are subject to scaling issues. I tried fixing some of these (such as the kernel parameter, r, or the SD in the evidence distributions, sw), but this resulted in fits that got considerably worse as the value of the parameter moved away from the value in Table 1A. In fact, changing the kernel parameter to half the value in Table 1A produced goodness-of-fit values that were numerically 10 times worse. This suggests that it is not possible to replace a pair of model parameters with one parameter that has the same function as both of them.
Correlations Among Parameter Values
In interpreting results from model fitting, it is important to understand covariation among model parameters that are characterized by correlations in the parameters across sets of simulated data. Random variation in data can lead to changes in two or more parameters to compensate and this can lead to correlations in the parameters. An example of compensation be seen in linear regression. Figure 5 (Ratcliff & Tuerlinckx, 2002) shows how random variation in data (bottom panel), especially at the two ends of the line, produces increasing intercept and decreasing slope (or vice versa) which produces a high negative correlation (−0.85) between slope and intercept (top panel). In the two-choice diffusion model, Ratcliff and Tuerlinckx (2002, Figure 7) show how random variation in one quantile RT would produce compensatory changes in other model parameters. Table 3 and Figure 6 (Ratcliff & Tuerlinckx, 2002) show some quite large correlations between different two-choice diffusion model parameters. However, they point out that the SDs in the recovered parameter values are much smaller than the SDs across individuals and so they have little impact on parameter estimates for the group means and for individual difference analyses for the two-choice diffusion model.
Figure A2 and A3 show correlations and scatter plots of parameter values for fits of the model to the two simulated data sets in the second and third lines of Table A1. For these simulations, there were three stimuli as in the experiment (three drift rates), and 4000 observations per stimulus condition, and 200 observations per condition.
Figure A2.
Scatter plots, histograms, and correlations for SCDM model parameters for fits to simulated data with 40,000 observations per condition. Each dot represents the parameter values for one of the 32 simulated data sets. The identity of the comparison in each off-diagonal plot or correlation is obtained from the task labels in the corresponding horizontal and vertical diagonal plots. The lines in the scatter plots are lowess smoothers (from the R package).
Figure A3.
The same plots as in Figure A2 but for simulated data with 200 observations per condition.
For the fits to the 4000-observation simulated data, there were large correlations between the boundary setting (also trial-to-trial variability in the boundary setting), the Gaussian process kernel parameter, and between-trial variability in the height of the drift-rate distribution. The interpretation of these is straightforward: Decreasing the kernel parameter makes noise more bumpy over spatial position and so provides more opportunities for the process to hit the boundary quickly at some point, because there are more points or regions on the function fluctuating randomly. To compensate for this decrease in RT, boundary setting has to be higher. Also, more variability (height) in the drift rate function can produce more faster responses and to compensate, the boundary setting has to be higher. Although these examples have one direction of causality, bidirectional explanations can be shown for each pair of the three parameters. In addition to these correlations, there are two other large correlations, between the boundary setting and trial-to-trial variability in the boundary setting, and between the width of the drift rate distribution and the value of its height. The first of these can be seen as a multiplicative scaling effect (the higher the boundary, the more variability). The second results from the requirement that probability density has to be assigned to the A, B, and T areas. If the width of the drift rate function increased, there would be less probability density in the A area and the height of the drift rate function would be increased to compensate.
For the fits to the 200-observation simulated data, some of the correlations that were large for the 4000-observation simulated data are small. The only large ones are the correlations between boundary setting and the kernel parameter and between the drift rate function height and width. The interpretations are the same as above. Also, because of the lower numbers of observations, there is increased variability in parameter estimates and this might be partly responsible for the reductions in the correlations.
Similar results were obtained for the simulations with the parameters values for Experiment 3. High correlations between the kernel parameter and boundary setting and between the height and width of the drift rate function were obtained. The correlation between the kernel parameter and trial-to-trial variability in the drift rate function was small for both simulated data sets.
Only one drift rate is shown in Figures A2 and A3. However, for Experiments 1 and 3 respectively, the means over the combinations of pairs of the three drift rates correlate 0.52 and 0.77 with the 4000 observations per condition and 0.36 and 0.34 with 200 observations per condition.
Summary
In conclusion, the parameters of the model have identifiable effects on behavioral data. Error RTs (T areas, Figure 2) can be longer than correct RTs if across-trial variability in the height of the drift rate distribution is large and they can be shorter than correct RTs if across-trial variability in the boundary setting is large. This is similar to the behavior of the two-choice model with changes in the sizes of analogous parameters. Parameter recovery with 200 observations per condition (about the same number as in an experiment) is relatively unbiased and variability in model parameters is moderately to much lower than variability across individuals. Finally, there are correlations between model parameters that are readily interpretable, but because the variability across individuals is larger than the variability in the parameter from simulated data, these tradeoffs are not of major concern. The most important point here is that the model is fit to data of individual subjects and the fits show the matches between theory and data for these individuals.
References
- Araujo C, Kowler E, & Pavel M (2001). Eye movements during visual search: the costs of choosing the optimal path. Vision Research, 41, 3513–3625. [DOI] [PubMed] [Google Scholar]
- Audley RJ & Pike AR (1965). Some alternative stochastic models of choice. The British Journal of Mathematical and Statistical Psychology, 18, 207–225. [DOI] [PubMed] [Google Scholar]
- Ball K, & Sekuler R (1982). A specific and enduring improvement in visual motion discrimination. Science, 218, 697–698. [DOI] [PubMed] [Google Scholar]
- Bays PM (2014). Noise in neural populations accounts for errors in working memory. Journal of Neuroscience, 34, 3632–3645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bays PM, Wu EY, & Husain M (2011). Storage and binding of object features in visual working memory. Neuropsychologia, 49, 1622–1631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck JM, Ma WJ, Kiani R, Hanks T, Churchland AK, Roitman J, Shadlen MN, Latham PE, & Pouget A (2008). Probabilistic population codes for Bayesian decision making. Neuron, 60, 1142–1152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bogacz R, Brown E, Moehlis J, Holmes P & Cohen JD (2006). The physics of optimal decision making: A formal analysis of models of performance in two-alternative forced choice tasks. Psychological Review, 113, 700–765. [DOI] [PubMed] [Google Scholar]
- Britten KH, Shadlen MN, Newsome WT, & Movshon JA (1992). The analysis of visual motion: A comparison of neuronal and psychophysical performance. Journal of Neuroscience, 12, 4745–4765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Busemeyer JR, & Townsend JT (1993). Decision field theory: A dynamic-cognitive approach to decision making in an uncertain environment. Psychological Review, 100, 432–459. [DOI] [PubMed] [Google Scholar]
- Churchland MM, Cunningham JP, Kaufman MT, Nuyujukian P, Foster JD, Ryu SI, & Shenoy KV (2012). Structure of neural population dynamics during reading. Nature, 487, 51–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deneve S, Latham PE, & Pouget A (1999). Reading population codes: a neural implementation of ideal observers. Nature Neuroscience, 2, 740–745. [DOI] [PubMed] [Google Scholar]
- Ditterich J (2006). Stochastic models of decisions about motion direction: Behavior and physiology. Neural Networks, 19, 981–1012. [DOI] [PubMed] [Google Scholar]
- Donkin C, Nosofsky RM, Gold J, & Shiffrin R (2013). Discrete-slots models of visual working-memory response times. Psychological Review, 120, 873–902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drew SA, Chubb CF, & Sperling G (2010). Precise attention filters for Weber contrast derived from centroid estimations. Journal of Vision, 10, 1–16. [DOI] [PubMed] [Google Scholar]
- Ferrando PJ (1999). Likert scaling using continuous, censored, and graded response models: Effects on criterion-rated validity. Applied Psychological Measurement, 23, 161–175. [Google Scholar]
- Forstmann BU, Ratcliff R, & Wagenmakers E-J (2016). Sequential sampling models in cognitive neuroscience: Advantages, applications, and extensions. Annual Review of Psychology, 67, 641–666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fougnie D, Suchow JW, & Alvarez GA (2012). Variability in the quality of visual working memory. Nature Communications, 3, 1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garner WR (1974). The processing of information and structure. Potomac, MD: Lawrence Erlbaum Associates. [Google Scholar]
- Georgopoulos AP, Schwartz AB, & Kettner RE (1986). Neuronal population coding of movement direction. Science, 233, 1416–1419. [DOI] [PubMed] [Google Scholar]
- Gold JI, & Shadlen MN (2001). Neural computations that underlie decisions about sensory stimuli. Trends in Cognitive Science, 5, 10–16. [DOI] [PubMed] [Google Scholar]
- Gold JI, & Shadlen MN (2007). The neural basis of decision making. Annual Review of Neuroscience, 30, 535–574. [DOI] [PubMed] [Google Scholar]
- Golomb JD, L’Heureux ZE, & Kanwisher N (2014). Feature-binding errors after eye movements and shifts of attention. Psychological Science, 25, 1067–1078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gomez P, Ratcliff R, & Perea M (2008). A model of letter position coding: The overlap model. Psychological Review, 115, 577–601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardman K, Vergauwe E, & Ricker T (2017). Categorical working memory representations are used in delayed estimation of continuous colors. Journal of Experimental Psychology: Human Perception and Performance, 43, 30–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Itti L, & Koch C (2001). Computational modelling of visual attention. Nature Reviews Neuroscience, 2, 194–203. [DOI] [PubMed] [Google Scholar]
- Jazayeri M, & Movshon JA (2006). Optimal representation of sensory information by neural populations. Nature Neuroscience, 9, 690–696. [DOI] [PubMed] [Google Scholar]
- Klaes C, Schneegans S, Schoner G, & Gail A (2012). Sensorimotor learning biases choice behavior: A learning neural field model for decision making. PLoS Computational Biology, 8, e1002774. doi:10.1371/journal.pcbi.1002774 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kowler E, & Pavel M (2013). Strategies of saccadic planning In Chubb C, Dosher BA, Lu Z-L, & Shiffrin RM (Eds.), Human information processing: Vision, memory, and attention. American Psychological Association. doi:10.1037/14135-009 [Google Scholar]
- Krajbich I, Armel C, & Rangel A (2010). Visual fixations and the computation and comparison of value in simple choice. Nature Neuroscience, 13, 1292–1298. [DOI] [PubMed] [Google Scholar]
- Kroese DP, & Botev ZI (2014). Spatial process generation In Schmidt V (Ed.), Lectures on stochastic geometry, spatial statistics and random fields, Volume II: Analysis, modeling and simulation of complex structures. Berlin: Springer-Verlag; arXiv: 1308.0399 [Google Scholar]
- LaBerge DA (1962). A recruitment theory of simple behavior. Psychometrika, 27, 375–396. [Google Scholar]
- Laming DRJ (1968). Information theory of choice reaction time. New York: Wiley. [Google Scholar]
- Leite FP, & Ratcliff R (2010). Modeling reaction time and accuracy of multiple-alternative decisions. Attention, Perception and Psychophysics, 72, 246–273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lerche V, Voss A, & Nagler M (2016). How many trials are required for robust parameter estimation in diffusion modeling? A comparison of different estimation algorithms. Behavior Research Methods, 1–25. doi: 10.3758/s13428-016-0740-2 [DOI] [PubMed] [Google Scholar]
- Link SW & Heath RA (1975). A sequential theory of psychological discrimination. Psychometrika, 40, 77–105. [Google Scholar]
- Liu F, & Wang X-J (2008). A common cortical circuit mechanism for perceptual categorical discrimination and veridical judgment. PLoS Computational Biology, 4:e1000253. doi:10.1371/journal.pcbi.1000253 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lord GJ, Powell CE, & Shardlow T (2014). An introduction to computational stochastic PDEs (Cambridge Texts in Applied Mathematics, 1st Edition). New York: Cambridge University Press. [Google Scholar]
- Lu Z-L, & Dosher BA (2008). Characterizing observer states using external noise and observer models: Assessing internal representations with external noise. Psychological Review, 115, 44–82. [DOI] [PubMed] [Google Scholar]
- Luce RD (1986). Response times. New York: Oxford University Press. [Google Scholar]
- Ma WJ, Husain M, & Bays PM (2014). Changing concepts of working memory. Nature Neuroscience, 17, 347–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller H (1987). A Rasch model for continuous ratings. Psychometrika, 52, 165–181. [Google Scholar]
- Newsome WT, & Pare EB (1988). A selective impairment of motion perception following lesions of the middle temporal visual area (MT). Journal of Neuroscience, 8, 2201–2211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols MJ, & Newsome WT (2002). Middle temporal visual area microstimulation influences veridical judgments of motion direction. Journal of Neuroscience, 22, 9530–9540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niwa M, & Ditterich J (2008). Perceptual decisions between multiple directions of visual motion. Journal of Neuroscience, 28, 4435–4445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noel Y, & Dauvier B (2007). A beta item response model for continuous bounded responses. Applied Psychological Measurement, 31, 47–73. [Google Scholar]
- Optican LM (2009). Oculomotor System: Models. Encyclopedia of Neuroscience, 7, 25–34. [Google Scholar]
- Pe ML, Vandekerckhove J, & Kuppens P (2013). A diffusion model account of the relationship between the emotional flanker task and rumination and depression. Emotion, 13, 739–747. [DOI] [PubMed] [Google Scholar]
- Pearson B, Raskevicius J, Bays PM, Pertzov Y, & Husain M (2014). Working memory retrieval as a decision process. Journal of Vision, 14, 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Persaud K, & Hemmer P (2014). The influence of knowledge and expectations for color on episodic memory. In, Proceedings of the 36th Annual Conference of the Cognitive Science Society (Bello P, Guarini M, McShane M, & Scassellati B, Eds.) Quebec City, CA: Cognitive Science Society. [Google Scholar]
- Philiastides MG, Ratcliff R, & Sajda P (2006). Neural representation of task difficulty and decision making during perceptual categorization: A timing diagram. Journal of Neuroscience, 26, 8965–8975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pleskac TJ, & Busemeyer JR (2011). Two-stage dynamic signal detection: a theory of choice, decision time, and confidence. Psychological Review, 117, 864–901. [DOI] [PubMed] [Google Scholar]
- Pouget A, Beck JM, Wei JM, & Latham PE (2013). Probabilistic brains: knowns and unknowns. Nature Neuroscience, 16, 1170–1178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powell C (2014). Lecture notes on: Numerical Methods for generating Gaussian random fields. Presentation. Retrieved from http://www.icms.org.uk/downloads/PMPM2014/PowellPart1.pdf and www.icms.org.uk/downloads/PMPM2014/PowellPart2.pdf on January 30, 2017.
- Province JM, & Rouder JN (2012). Evidence for discrete-state processing in recognition memory. Proceedings of the National Academy of Sciences, 109, 14357–14362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R (1978). A theory of memory retrieval. Psychological Review, 85, 59–108. [Google Scholar]
- Ratcliff R (1981). A theory of order relations in perceptual matching. Psychological Review, 88, 552–572. [Google Scholar]
- Ratcliff R (1987). More on the speed and accuracy of positive and negative responses. Psychological Review, 94, 277–280. [PubMed] [Google Scholar]
- Ratcliff R (2002). A diffusion model account of reaction time and accuracy in a two choice brightness discrimination task: Fitting real data and failing to fit fake but plausible data. Psychonomic Bulletin and Review, 9, 278–291. [DOI] [PubMed] [Google Scholar]
- Ratcliff R (2013). Parameter variability and distributional assumptions in the diffusion model. Psychological Review, 120, 281–292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R & Childers R (2015). Individual differences and fitting methods for the two-choice diffusion model. Decision, 2, 237–279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Gomez P, & McKoon G (2004). A diffusion model account of the lexical-decision task. Psychological Review, 111, 159–182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Hasegawa YT, Hasegawa YP, Childers R, Smith PL, & Segraves MA (2011). Inhibition in superior colliculus neurons in a brightness discrimination task? Neural Computation, 23, 1790–1820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, & McKoon G (2008). The diffusion decision model: Theory and data for two-choice decision tasks. Neural Computation, 20, 873–922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, & McKoon G (in press). Modeling numeracy representation with an integrated diffusion model. Psychological Review. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Philiastides MG, & Sajda P (2009). Quality of evidence for perceptual decision making is indexed by trial-to-trial variability of the EEG. Proceedings of the National Academy of Sciences, 106, 6539–6544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, & Rouder JN (1998). Modeling response times for two-choice decisions. Psychological Science, 9, 347–356. [Google Scholar]
- Ratcliff R, & Rouder JN (2000). A diffusion model account of masking in letter identification. Journal of Experimental Psychology: Human Perception and Performance, 26, 127–140. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Sederberg P, Smith T, & Childers R (2016). A single trial analysis of EEG in recognition memory: Tracking the neural correlates of memory strength. Neuropsychologia, 93, 128–141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R & Smith PL (2004). A comparison of sequential sampling models for two-choice reaction time. Psychological Review, 111, 333–367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, & Smith PL (2010). Perceptual discrimination in static and dynamic noise: the temporal relation between perceptual encoding and decision making. Journal of Experimental Psychology: General, 139, 70–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R & Smith PL (2015). Modeling simple decisions and applications using a diffusion model In Busemeyer JR, Wang Z, Townsend JT, & Eidels A (Eds.), Oxford Handbook of Computational and Mathematical Psychology. New York, NY: Oxford University Press. [Google Scholar]
- Ratcliff R, Smith PL, Brown SD, & McKoon G (2016). Diffusion decision model: Current issues and history. Trends in Cognitive Science, 20, 260–281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Smith PL, & McKoon G (2015). Modeling regularities in response time and accuracy data with the diffusion model. Current Directions in Psychological Science, 24, 458–470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, & Starns JJ (2009). Modeling confidence and response time in recognition memory. Psychological Review, 116, 59–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, & Starns JJ (2013). Modeling response times, choices, and confidence judgments in decision making: recognition memory and motion discrimination. Psychological Review, 120, 697–719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, Gomez P & McKoon G (2004). A diffusion model analysis of the effects of aging in the lexical-decision task. Psychology and Aging, 19, 278–289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, & McKoon G (2001). The effects of aging on reaction time in a signal detection task. Psychology and Aging, 16, 323–341. [PubMed] [Google Scholar]
- Ratcliff R, Thapar A & McKoon G (2003). A diffusion model analysis of the effects of aging on brightness discrimination. Perception and Psychophysics, 65, 523–535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, & McKoon G (2004). A diffusion model analysis of the effects of aging on recognition memory. Journal of Memory and Language, 50, 408–424. [Google Scholar]
- Ratcliff R, Thapar A, & McKoon G (2010). Individual differences, aging, and IQ in two-choice tasks. Cognitive Psychology, 60, 127–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, & McKoon G (2011). Effects of aging and IQ on item and associative memory. Journal of Experimental Psychology: General, 140, 46–487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thompson CA, & McKoon G (2015). Modeling individual differences in response time and accuracy in numeracy. Cognition, 137, 115–136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, & Tuerlinckx F (2002). Estimating the parameters of the diffusion model: Approaches to dealing with contaminant reaction times and parameter variability. Psychonomic Bulletin and Review, 9, 438–481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Van Zandt T, & McKoon G (1999). Connectionist and diffusion models of reaction time. Psychological Review, 106, 261–300. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Voskuilen C, & McKoon G (2018). Internal and external sources of variability in perceptual decision-making. Psychological Review, 125, 33–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roe RM, Busemeyer JR, & Townsend JT (2001). Multialternative decision field theory: A dynamic connectionist model of decision-making. Psychological Review, 108, 370–392. [DOI] [PubMed] [Google Scholar]
- Roitman JD & Shadlen MN (2002). Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. Journal of Neuroscience, 22, 9475–9489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salzman CD, Murasugi CM, Britten KH, & Newsome WT (1992). Microstimulation in visual area MT: Effects on direction discrimination performance. Journal of Neuroscience, 12, 2331–2355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmiedek F, Oberauer K, Wilhelm O, Suβ H-M, & Wittmann W (2007). Individual differences in components of reaction time distributions and their relations to working memory and intelligence. Journal of Experimental Psychology: General, 136, 414–429. [DOI] [PubMed] [Google Scholar]
- Shadlen MN & Newsome WT (2001). Neural basis of a perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. Journal of Neurophysiology, 86, 1916–1935. [DOI] [PubMed] [Google Scholar]
- Smith PL (2016). Diffusion theory of decision making in continuous report. Psychological Review, 123, 425–451. [DOI] [PubMed] [Google Scholar]
- Smith PL, & Ratcliff R (2004). The psychology and neurobiology of simple decisions, Trends in Neuroscience, 27, 161–168. [DOI] [PubMed] [Google Scholar]
- Smith PL, & Ratcliff R (2009). An integrated theory of attention and decision making in visual signal detection. Psychological Review, 116, 283–317. [DOI] [PubMed] [Google Scholar]
- Smith PL, & Vickers D (1988). The accumulator model of two-choice discrimination. Journal of Mathematical Psychology, 32, 135–168. [Google Scholar]
- Smithson M, & Verkuilen J (2006). Fuzzy set theory: Applications in the social sciences Quantitative Applications in the Social Sciences Series, Thousand Oaks, CA: Sage. [Google Scholar]
- Starns JJ, Ratcliff R, & McKoon G (2012). Evaluating the unequal-variability and dual-process explanations of zROC slopes with response time data and the diffusion model. Cognitive Psychology, 64, 1–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stone M (1960). Models for choice reaction time. Psychometrika, 25, 251–260. [Google Scholar]
- Storvik G, Frigessi A, & Hirst D (2002). Stationary Space Time Gaussian Fields and their time autoregressive representation. Statistical Modelling, 2, 139–161. [Google Scholar]
- Sun P, Chubb C, Wright C,E, & Sperling G (2016). Quantifying feature-based attention in terms of attention filters. Attention, Perception, and Psychophysics, 78, 474–515. [DOI] [PubMed] [Google Scholar]
- Thapar A, Ratcliff R, & McKoon G (2003). A diffusion model analysis of the effects of aging on letter discrimination. Psychology and Aging, 18, 415–429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson CA, & Siegler RS (2010). Linear numerical magnitude representations aid children’s memory for numbers. Psychological Science, 21, 1274–1281. [DOI] [PubMed] [Google Scholar]
- Thornton TL, & Gilden DL (2007). Parallel and serial processes in visual search. Psychological Review, 114, 71–103. [DOI] [PubMed] [Google Scholar]
- van den Berg R, Shin H, Chou W-C, George R, & Ma WJ (2012). Variability in encoding precision accounts for visual short-term memory limitations. Proceedings of the National Academy of Sciences, 109, 8780–8785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Berg R, Awh E, & Ma WJ (2014). Factorial comparison of working memory models. Psychological Review, 121, 124–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vandekerckhove J & Tuerlinckx F (2007). Fitting the Ratcliff diffusion model to experimental data. Psychonomic Bulletin & Review, 14, 1011–1026. [DOI] [PubMed] [Google Scholar]
- Vickers D, Caudrey D, & Willson RJ (1971). Discriminating between the frequency of occurrence of two alternative events. Acta Psychologica, 35, 151–172. [Google Scholar]
- Voskuilen C, & Ratcliff R (2016). Modeling confidence and response time in associative recognition. Journal of Memory and Language, 86, 60–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voskuilen C, Ratcliff R, & McKoon G (2018). Aging and confidence judgments in item recognition. Journal of Experimental Psychology: Learning, Memory, and Cognition, 44, 1–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voss A, & Voss J (2008). A Fast Numerical Algorithm for the Estimation of Diffusion-Model Parameters. Journal of Mathematical Psychology, 52, 1–9. [Google Scholar]
- White CN, Ratcliff R, Vasey MW, & McKoon G (2010). Anxiety enhances threat processing without competition among multiple inputs: A diffusion model analysis. Emotion, 10, 662–677. [DOI] [PubMed] [Google Scholar]
- Wiecki TV, Sofer I and Frank MJ (2013). HDDM: Hierarchical Bayesian estimation of the Drift-Diffusion Model in Python. Frontiers in Neuroinformatics, 7, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilimzig C, Schnieder S & Schoner G (2006). The time course of saccadic decision making: Dynamic field theory. Neural Networks, 19, 1059–1074. [DOI] [PubMed] [Google Scholar]
- Wolfe JM (2007). Guided Search 4.0: Current Progress with a model of visual search In Gray W (Ed.), Integrated Models of Cognitive Systems (pp. 99–119). New York: Oxford. [Google Scholar]
- Wong K-F, & Wang X-J (2006). A recurrent network mechanism for time integration in perceptual decisions. Journal of Neuroscience, 26, 1314–1328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wurtz RH, & Optican LM (1994). Superior colliculus cell types and models of saccade generation. Current Opinion in Neurobiology, 4, 857–861. [DOI] [PubMed] [Google Scholar]
- Zandbelt B, Purcell BA, Palmeri TJ, Logan GD, & Schall JD (2014). Response times from ensembles of accumulators. Proceedings of the National Academy of Sciences, 111, 2848–2853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W, & Luck SJ (2008). Discrete fixed-resolution representations in visual working memory. Nature, 453, 233–235. [DOI] [PMC free article] [PubMed] [Google Scholar]


