Simple and Fast Adaptive Nonlocal Multispectral Filtering Algorithm for Efficient Noise Reduction in Magnetic Resonance Imaging

Abstract

Purpose:

We recently introduced a multispectral (MS) nonlocal (NL) filter based on maximum likelihood estimation (MLE) of voxel intensities, termed MS-NLML. While MS-NLML provides excellent noise reduction and improved image feature preservation as compared to other NL or MS filters, it requires considerable processing time, limiting its application in routine analyses. In this work, we introduced a fast, simple, and robust filter, termed nonlocal estimation of multispectral magnitudes (NESMA), for noise reduction in multispectral (MS) magnetic resonance imaging (MRI).

Methods:

Through extensive simulation and in-vivo analyses, we compared the performance of NESMA and MS-NLML in terms of noise reduction and processing efficiency. Further, we introduce two simple adaptive methods that permit spatial variation of similar voxel, R, used in the filtering. The first method is semi-adaptive and permits variation of R across the image by using a relative Euclidean distance (RED) similarity threshold. The second method is fully adaptive and filters the raw data with several RED similarity thresholds to spatially determine the optimal threshold value using an unbiased criterion.

Results:

NESMA shows very similar filtering performance as compared to MS-NLML, however, with much simple implementation and very fast processing time. Further, for both filters, the adaptive methods were shown to further reduce noise in comparison with the conventional non-adaptive method in which R is set to a constant value throughout the image.

Conclusions:

NESMA is fast, robust, and straightforward to implement filter. These features render it suitable for routine clinical use and analysis of large MRI datasets.

1-. INTRODUCTION

Image filtering for noise reduction has been broadly applied in magnetic resonance imaging (MRI) to improve diagnostic accuracy, quality of image registration and segmentation (1), and parameter estimation (2–6). The enhancement in signal-to-noise ratio (SNR) can be used to improve temporal or spatial resolution. Local image filtering methods estimate the true intensity of a given voxel using neighboring voxels. A popular method of local filtering is based on local kernel convolution with the original image to provide a weighted-average estimate of the intensity for the voxel of interest (i.e. index voxel). Unlike local kernel methods such as boxcar or Gaussian averaging, nonlocal (NL) filtering algorithms permit the inclusion of non-neighboring voxels in the intensity estimation of an index voxel (7–9). Rather than using spatial proximity as a criterion for inclusion in the intensity estimate, NL filters use the similarity of signal intensities between voxels (7–10). This increases the number of similar voxels available while not forcing inclusion of dissimilar ones, leading to improved denoising and feature preservation.

MRI studies often involve acquiring multispectral (MS) images, e.g. images obtained at different echo times (TEs), repetition times (TRs), flip angles, or diffusion b-values (9–19). These image sets provide varying contrast that reflect the evolution of the MR signal for different tissues with respect to the varied acquisition parameter. While noise may make two dissimilar tissues appear similar within a given image, the overall evolution of intensity across MS images improves discrimination between different tissue types leading to improved filtering (9–11).

We have recently introduced a new MS nonlocal maximum likelihood (MS-NLML) filter (9) and demonstrated its superior performance as compared to current advanced filters in terms of noise reduction and feature preservation. This filter restores the amplitude of an index voxel using a maximum likelihood estimation (MLE) based on R pre-selected voxels with similar MS signal patterns. However, the MS-NLML filter is relatively complex to implement and requires lengthy processing times, especially for large datasets, due to the MLE calculation. Here, we introduce a new filter, termed nonlocal estimation of multispectral magnitudes (NESMA), which replaces the MLE with a mean estimate of R similar voxels; this greatly simplifies implementation and accelerates processing time. Note that the MS-NLML and NESMA filters are similar in that they are both non-local estimates of index voxel intensity based on incorporating data from voxels deemed similar to the index voxel. However, in practical terms, they are very different, due to the use of simple averaging in NESMA as opposed to maximum likelihood estimation in MS-NLML.

The number of similar voxels used in nonlocal MLE filters, including in our previous MS-NLML filter, is conventionally set to a fixed value, R, throughout the image (8, 9, 20). In many instances this includes too many or too few voxels, depending upon the local structure of the image. For example, if there are relatively few voxels similar to the index voxel, as is the case for heterogeneous regions and near object edges, fixing R may force inclusion of dissimilar voxels and cause blurring. In contrast, if R is too small for an index voxel in which there are many similar voxels, as in homogenous regions, the denoising process will be suboptimal. Previous implementations of adaptive filtering have used different approaches to overcome this limitation. Rajan et al. introduced a method to compare the MLE of local noise variance, based on a progressively increasing number of NL voxels, to the noise variance estimated from the image background. The optimal value of R for each index voxel was then defined as the value yielding the closest match (21). The same authors proposed a method to replace the Euclidean distance with a Kolgomorov-Smirnov test to evaluate the difference between the neighborhoods surrounding the index voxel, i, and a candidate voxel, j, to determine if the difference was Gaussian-distributed (22). However, these approaches involve a complex definition of voxel similarity or lengthy processing times. Here we introduce two new, easy-to-implement, adaptive methods that permit spatial variation of R. We term these methods semi-adaptive (SA) and fully-adaptive (FA).

The plan of the paper is as follows. First, we describe and detail the implementation of the MS-NLML and NESMA filters. We then outline the two new adaptive methods for determining R. Finally, we present the results and discuss the filtering performance of the MSNLML and NESMA filters. Analyses were performed on both synthetic and in vivo datasets.

2-. THEORY

We assume that the data consists of a multispectral set of registered images S defined on a discrete grid I, given by $S=\left\{S_k\left(i\right)|i\in I,S_k\left(i\right)\in {ℝ}^K\right\},$ where K is the total number of images in the spectral dimension. Each measured signal intensity S_k(i) and true intensity A_k(i) for index voxel i and spectral image k follows a Rician-distributed conditional probability density function P(S_k(i)|A_k(i),σ) given by

$$P\left(S_k|A_k,\sigma \right)==\frac{S_k}{{\sigma }^2}\text{\hspace{0.17em}exp\hspace{0.17em}}\left(-\frac{S_k^2+A_k^2}{2{\sigma }^2}\right).I_0\left(\frac{S_k{A}_k}{{\sigma }^2}\right),$$ (1)

where S_k represents the measured signal intensity in spectral image k, A_k represents the underlying true signal intensity of spectral image k, σ is the standard deviation (SD) of the noise, and I₀ is the modified zero-order Bessel function of the first kind. We assume that the images include background regions with zero signal intensity from which σ can be accurately estimated through the Rayleigh distribution (9, 23, 24), and that σ is stationary and constant throughout S.

2.1. The multispectral nonlocal maximum likelihood (MS-NLML) filter

The NLML filter was introduced by He et al. (8) and extended by Bouhrara et al. (9) to incorporate multispectral information (MS-NLML). Voxel similarity for the MS-NLML filter is defined according to:

$$d\left(i,j\right)=\sum _{k=1}^K{\left(S_k\left(i\right)-S_k\left(j\right)\right)}^2,$$ (2)

where d(i,j) is the distance in signal intensity between the index voxel i and candidate voxel j. The search for candidate voxels is restricted to a large search window, W, centered on the index voxel. d(i,j) between i and each candidate voxel j belonging to W is calculated and arranged in ascending order, with the R voxels having the smallest distance being incorporated into the MLE of its true intensity through

$${\widehat{A}}_k\left(i\right)=\arg {\max }_{A_k}\left\{\sum _{i=1}^R\log \frac{S_k\left(i\right)}{{\sigma }^2}-\sum _i^R\frac{S_k{}^2\left(i\right)+A_k{}^2}{2{\sigma }^2}+\sum _{i=1}^R\log I_0\left[\frac{S_k\left(i\right)\cdot A_k}{{\sigma }^2}\right]\right\}.$$ (3)

where ${\widehat{A}}_k\left(i\right)$ is the estimated true intensity of spectral image k and index voxel i. The size of the window W must be sufficiently large to ensure inclusion of an adequate number of similar voxels, and sufficiently restricted to ensure that the transmission and reception B₁ fields is approximately constant within the window (25, 26).

2.2. The nonlocal estimation of multispectral magnitudes (NESMA) filter

As previously mentioned, the NESMA filter utilizes the nonlocal filtering paradigm, but replaces the MLE with Rician-corrected average estimates given by

$${\widehat{A}}_k\left(i\right)=\sqrt{\max \left\{\frac{{\sum }_{j=1}^R{S}_k{}^2\left(j\right)}{R}-2{\sigma }^2,0\right\}}.$$ (4)

This correction scheme follows from the second moment of the Rician distribution given by

$$S^2=A^2+2{\sigma }^2,$$ (5)

where S is the measured signal intensity and A is the true intensity (23, 27, 28). As in MSNLML, NESMA uses Eq. 2 to define voxel similarity, with the R voxels with the smallest distances d(i,j) used for averaging. The NESMA and MS-NLML filters using this non-adaptive (NA) method for selecting similar voxels are termed NA-NESMA and NA-MS-NLML respectively.

2.3. Adaptive selection of similar voxels

In both the MS-NLML and NESMA filters described above, the true underlying intensity for each voxel is estimated based on a set of R similar voxels. We introduce two methods for defining R according to the local image structure, and compare the results to those obtained with the conventional NA approach where R is predefined and spatially fixed (8, 9, 20). Note that these adaptive methods apply to both the MS-NLML and NESMA filters.

Semi-adaptive method:

We normalize the distance between the index voxel i and a candidate voxel j (Eq. 2) by the sum over the squared multispectral intensities of the index voxel to create a relative distance. The relative Euclidean distance (RED) metric is therefore defined as

$$\text{RED}\left(i,j\right)=\frac{{\sum }_{k=1}^K{\left(S_k\left(i\right)-S_k\left(j\right)\right)}^2}{{\sum }_{k=1}^K{S}_k{\left(i\right)}^2}.$$ (6)

A global threshold value t for the RED is then specified as a cutoff, with voxels exhibiting RED < t considered as being sufficiently similar to the index voxel and incorporated into its filtered value according to Eq. 4. This method is termed semi-adaptive (SA), with the threshold value t specified by the user. Note that while t is global, the resulting value of R, calculated for each voxel based on t, varies across the image. The NESMA and MS-NLML filters using this semi-adaptive (SA) method for selecting similar voxels are termed SA-NESMA and SA-MS-NLML, respectively.

Fully-adaptive method:

A fully-adaptive (FA) implementation of this approach seeks to eliminate the requirement for the user to select an RED threshold as described in the SA method above. Instead, an optimal threshold T for each index voxel is defined by

$$T(i)=\underset{t}{\text{min}}\left\{\frac{1}{R\cdot K}\sum _{k=1}^K\left|\sum _{j=1}^R{S}_k{(j)}^2-{\widehat{A}}_{k,t}{(j)}^2-2{\sigma }^2\right|\right\}$$ (7)

where ${\widehat{A}}_{k,t}\left(j\right)$ is the estimated signal intensity of the voxel j within the search window W of spectral image k using threshold t. This criterion for an optimal threshold arises from the fact that for each voxel, the relationship between the observed intensity and the true underlying intensity follows the second moment of the Rician distribution (Eq. 5) (23, 27, 28). As t approaches the optimal value, ${\widehat{A}}_{k,t}\left(i\right)$ approaches the true underlying intensity value, and the objective function in Eq. 7 is minimized. In this manner, Eq. 7 is used to evaluate the quality of filtering and determine the optimal value of T. Specifically, for each index voxel i, the objective function, given by the Eq. 7, was calculated for several values of t, and the threshold for which T(i) = 0 is found by linear interpolation. For each t, the number of similar voxels, R, are defined according to the procedure outlined above for the SA method. The NESMA and MS-NLML filters using this FA method for selecting similar voxels are termed FA-NESMA and FA-MS-NLML, respectively.

3-. METHODS

3.1. Simulation datasets

Synthetic multislice T₂-weighted (T₂W) brain datasets were obtained from BrainWeb, (29) from which a T₂ map was generated. Representative T₂ values for white matter, gray matter, and cerebrospinal fluid were chosen as 60 ms, 85 ms, and 180 ms, respectively. T₂W brain images were then generated with twenty values of TE ranging uniformly from 10 ms to 200 ms. Rician-distributed noise was incorporated into the noise-free images to create datasets with SNR values of 10 or 25 (30). SNR was defined as the peak signal intensity at TE = 0 ms divided by σ.

3.2. In vivo datasets

Experimental analyses were performed on an in vivo brain dataset acquired from a healthy 23-year-old female using a 3T whole-body MRI system (Achieva, Phillips Medical Systems, Best, Netherlands) equipped with an internal quadrature body coil for transmission and reception. An axial brain T₂W dataset was acquired using a single-slice spin-echo imaging sequence with repetition time of 1300 ms, 32 echo times ranging uniformly from 7 ms to 224 ms, field of view 22 cm x 19.2 cm, matrix size of 448 × 440, and slice thickness of 2 mm. The total acquisition time was 10 minutes. σ was determined from background regions (23).

3.3. Filtering analysis

NA, SA, and FA methods were implemented using a search window size of 15 × 15 × 3 for the multislice synthetic images and 25 × 25 × 1 for the single-slice in vivo images. For the NA and SA methods, we used a conservative value for R and RED threshold, t, respectively. While this may penalize homogenous regions where large values of R or t would provide further increase in SNR, our analysis showed that larger values led to blurring in regions with smaller structures. R was fixed to 50 for the NA filtering, while for SA filtering the RED thresholds were fixed to 10% and 4% for SNRs of 10 and 25 respectively. The FA filters were evaluated using 2%, 3%, 4%, 5% thresholds for the synthetic dataset with SNR = 25, and 0%, 4%, 8%, 15%, 20% thresholds for the in vivo dataset. For analysis of simulated images, all filters were evaluated using the known input σ, while for in vivo analysis σ was calculated from image background regions (23).

Evaluation of filtering performance was based upon the extent of noise reduction and feature preservation. Mean squared error (MSE) and structural similarity (SSIM) index values (31) were calculated for synthetic images. Voxels from the image background were not included in the MSE or SSIM calculations. In vivo datasets were evaluated by visual inspection of filtered images since there was no ground truth to calculate SSIM or MSE. Maps showing the spatial variation of R, termed R-maps, were calculated for the SA and FA methods, while maps of the threshold T, termed T-maps, were constructed for the FA method. For further comparison, a reference R-map was determined by finding the true number of similar voxels at each point in the noise-free image.

Computation time was compared for the NESMA and MS-NLML filters for images of different sizes. The computation times reported represent the cumulative time taken to complete filtering for the specified number of voxels. For the FA method, this includes the time required to calculate the optimal threshold for each voxel. All calculations were performed using MATLAB R2016a (MathWorks, Natick, MA) on a computer with an Intel Xeon E5–2680 CPU, NVIDIA Quadro K2200 GPU, and 128 GB RAM.

4-. RESULTS

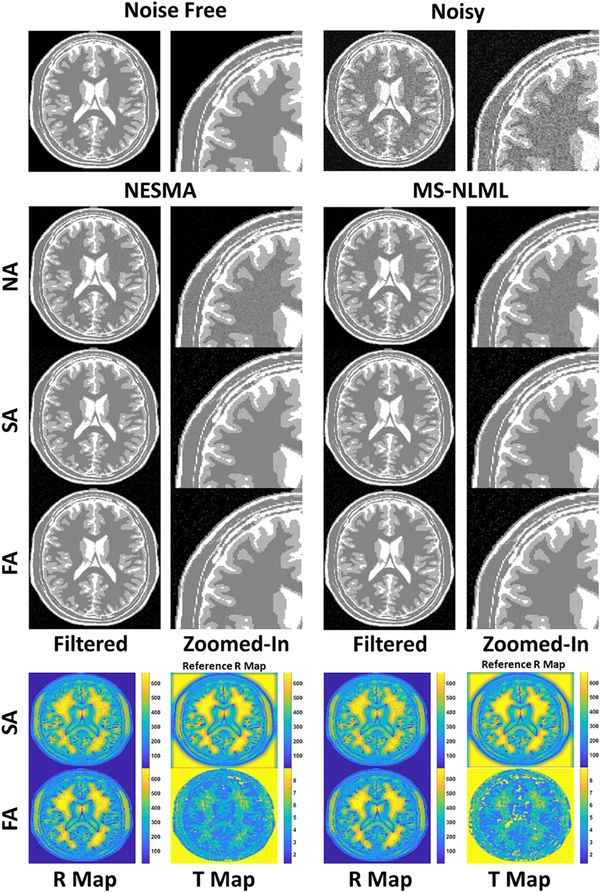
Fig. 1 shows a comparison of the filtering performance of the NA, SA, and FA NESMA and MSNLML filters on a synthetic T₂W dataset generated with SNR = 25. NA-NESMA and NA-MS-NLML filtered images showed comparable levels of noise reduction and have nearly identical MSE values, 0.027 and 0.029, respectively, and identical SSIM values (0.95) (Table 1). However, the zoomed-in images in Fig. 1 show that noise reduction for both filters is not optimal in white matter regions. While noise reduction could be improved in these regions by increasing R, this would come at the expense of blurring of fine structures in inhomogeneous regions by incorporating dissimilar voxels in the estimation of their true intensity. Improved noise reduction was achieved using the SA method (Fig. 1). The filtered images clearly show reduced random variation, especially in the white matter regions. This was supported by the identical SSIM and nearly identical MSE values for SA-NESMA and SA-MS-NLML (Table I). The improved performance can be attributed to the spatial variation of R as seen in the R-maps (Fig. 1). Indeed, the R-maps show that the value of R can be substantially greater than 50 in homogenous regions (e.g. white matter regions), while remaining in the range of 10–50 in inhomogeneous regions (e.g. gray matter regions) (Fig. 1). Finally, nearly identical MSE values and identical SSIM values were obtained with the FA and SA methods across both NESMA and MS-NLML filters (Table 1).

Figure 1.

Filtering performance of non-adaptive (NA), semi-adaptive (SA), and fully-adaptive (FA) NESMA and MS-NLML filters on a synthetic T₂W dataset generated with SNR = 25. Results are shown for TE = 60 ms. The grayscale is consistent across all filtered and zoomed-in images. R-maps and T-maps show the respective values of the number of voxels and threshold selected at each location for the NESMA and MS-NLML filters. The reference R-map represents the optimal number of voxels selected at each point in the image. The filtered images demonstrate the nearly identical noise reduction and feature preservation of the NESMA filter as compared to the MSNLML filter for NA, SA, and FA methods. Further, both adaptive methods demonstrate superior noise reduction compared to their NA counterparts for both the NESMA and MS-NLML filters.

Table 1.

PERFORMANCE OF FILTERS AND ADAPTIVE METHODS. The MSE and SSIM values demonstrate that the NESMA and MS-NLML filters have nearly identical filtering performance for the NA, SA, and FA methods. Further, both adaptive methods exhibit better filtering performance than the NA method.

	MSE		SSIM
Method	NESMA	MS-NLML	NESMA	MS-NLML
NA	0.027	0.029	0.95	0.95
SA	0.003	0.004	0.99	0.99
FA	0.004	0.006	0.99	0.99

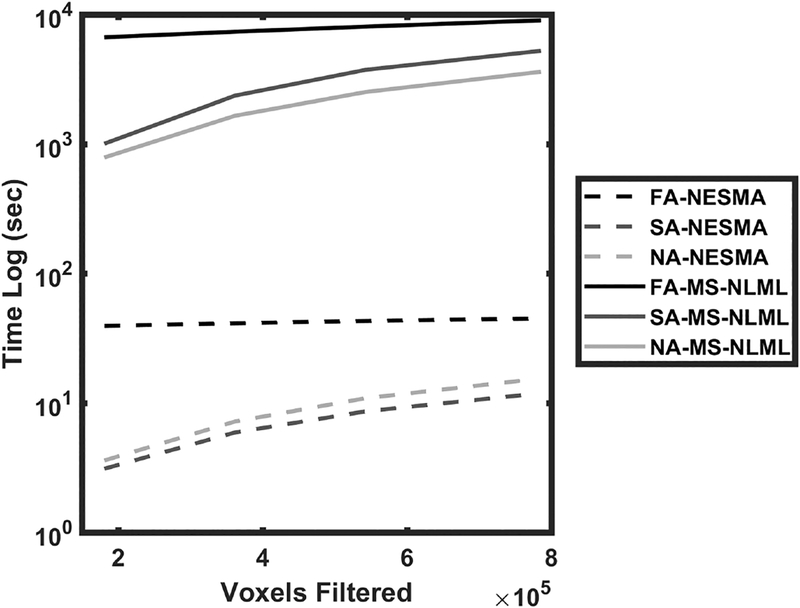
Fig. 2 shows the computation time required for filtering a multispectral dataset as a function of image size measured in voxels. As shown, the NESMA filters require about two orders of magnitude less computational time than the corresponding MS-NLML filters. Each implementation of the FA method requires several implementations of the SA method to establish the optimal threshold for each voxel. This time-consuming process, with computation time roughly proportional to the number of thresholds evaluated, represents the bulk of the implementation time for the FA filter, rendering it relatively insensitive to image size.

Figure 2.

Computation time of the non-adaptive (NA), semi-adaptive (SA), and fully-adaptive (FA) NESMA and MS-NLML filters. Computation time is plotted as a function of the number of voxels. It is evident that the NESMA filters require two orders of magnitude less computation time than the MS-NLML filters.

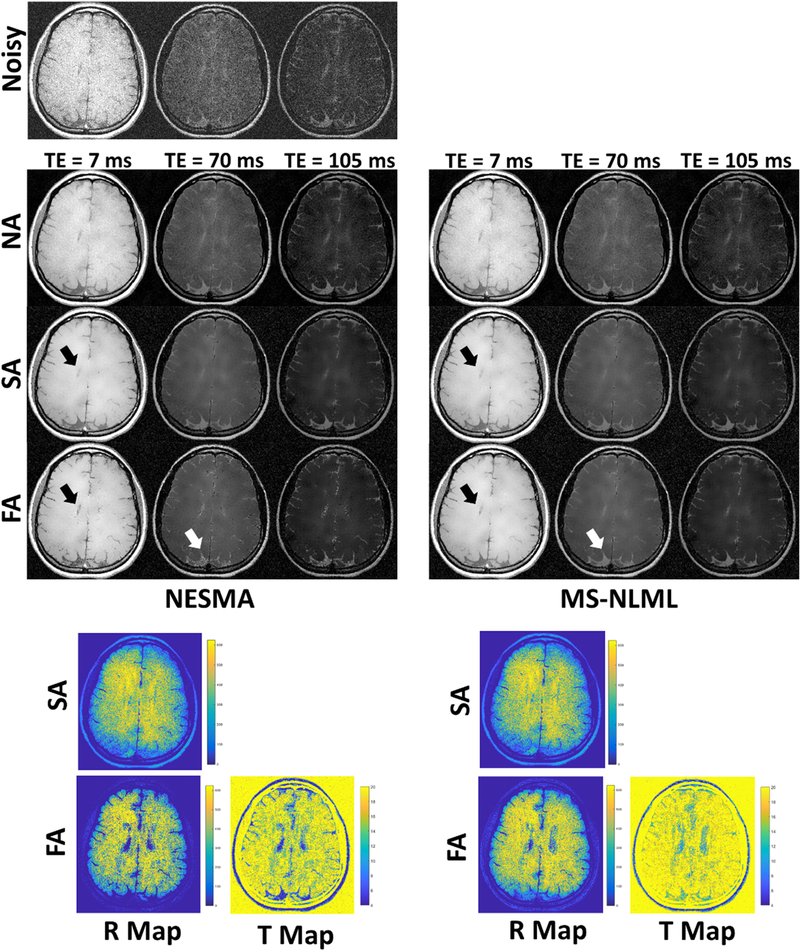
Fig. 3 shows the filtering performance of the NA, SA, and FA methods for both NESMA and MS-NLML on an in vivo T₂W dataset. Consistent with the synthetic dataset analyses (Fig. 2), the NA and SA implementations of NESMA show nearly the same level of noise reduction as their MS-NLML counterparts. However, the filtered images for the FA-MS-NLML and FANESMA filters differed in the posterior gray matter regions (white arrows). This was attributed to the FA-NESMA filter selecting fewer voxels in these regions. Further, both FA filters selected noticeably different values for R compared to their respective SA filters; most visible in the ventricles (black arrows).

Figure 3.

Filtering performance of non-adaptive (NA), semi-adaptive (SA), and fully-adaptive (FA) NESMA and MS-NLML filters on an in vivo T₂W dataset. Results are shown for three different TEs. The grayscale is consistent across filtered images and across TEs. Noisy images are shown for comparison. R-maps and T-maps show, respectively, number of voxels and threshold selected at each location for the NESMA and MS-NLML filters. SA-NESMA and SAMS-NLML filtered images show similar noise reduction. However, FA-NESMA and FA-MSNLML show slight differences in filtering, which can be attributed to the FA method selecting different values for R (white arrows). Also, it can be seen in the ventricles that the FA method selected fewer voxels compared to the SA method, leading to less blurring (black arrows).

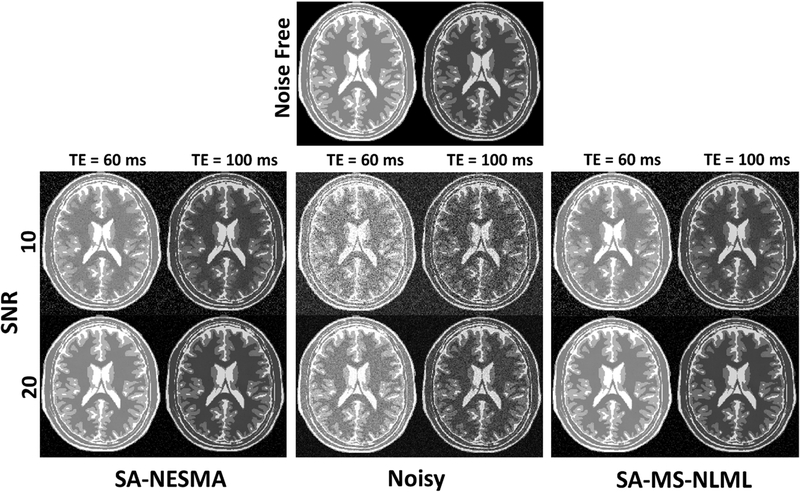
Fig. 4 compares the filtering performance of the SA-NESMA and SA-MS-NLML filters for different SNR values. The SA method was selected to show optimal filtering performance using identical values for R at each location in the image. This permits direct comparison between the denoising algorithms used in NESMA and MS-NLML. Filtered images from the SA-NESMA and SA-MS-NLML filters show similar levels of noise reduction and feature preservation. This is highlighted by the nearly identical SSIM and MSE values (Table 2) for both SNR = 10 and SNR = 25. This shows that, even in the setting of low SNR, NESMA provides essentially indistinguishable denoising performance compared to the MS-NLML filter.

Figure 4.

Filtering performance of SA-NESMA and SA-MS-NLML on synthetic datasets of SNR 10 and 25. Two TEs are shown to illustrate each filter’s performance at different contrasts. The grayscale is consistent across filtered images and across TEs. Noisy images are shown for comparison. The thresholds used for both filters were 10% and 5% for SNR 10 and 25 respectively. The filtered images demonstrate that the NESMA and MS-MLML denoising methods differ minutely, if at all, even at very low SNR.

Table 2.

FILTERING PERFORMANCE FOR DIFFERENT SNR LEVELS. The MSE and SSIM values demonstrate that these filters have nearly identical performance even at very low SNR.

	MSE		SSIM
SNR	NESMA	MS-NLML	NESMA	MS-NLML
10	0.079	0.079	0.91	0.91
25	0.003	0.004	0.99	0.99

5-. DISCUSSION

We present a new nonlocal multispectral filter, NESMA, which greatly simplifies implementation and reduces computational time as compared with MLE-based filters, including the MS-NLML filter. We show that filtering quality is retained with respect to noise reduction and feature preservation. Furthermore, we propose two simple approaches for spatially varying the number of similar voxels, R, used in denoising. Our analyses of synthetic and in vivo data show that the SA method provides an improvement over the NA method due to the spatial variation in the number of voxels included in the denoising process. However, in the SA method, selection of the threshold is crucial. In the expression for RED (Eq. 6), we can see that for an index voxel of high intensity and a given difference between itself and a candidate voxel (i.e. constant numerator), the distance d(i,j) will be smaller than for an index voxel of low intensity, due to the magnitude of the respective denominator. The effect of this can be seen in the T-maps in Fig.1 where the FA method selected lower thresholds in the ventricles (white arrows) compared to the white matter, despite having similar values of R. This effect also means that it is not possible to choose a threshold (i.e. RED) that is optimal across the entire image. Depending on the threshold chosen, high signal-intensity regions may be susceptible to blurring while low signal-intensity regions may be susceptible to suboptimal noise reduction. While this is not always an issue, improved performance may be obtained by permitting spatial variation in the RED threshold. This can be seen in Fig. 3 where the FA filters selected smaller values for R in the ventricles than their respective SA filters, thereby further reducing the small amount of blurring (black arrows).

The simple averaging process that forms the basis of NESMA greatly reduces the computational burden as compared to MLE-based filters (Eq. 3). This permits the processing of large datasets, including those incorporating the multiple contrast mechanisms often obtained in a clinical setting. Thus, the NESMA filter may be widely applicable, rather than useful only for specialized applications. As noted above, there are fundamental operational differences between the MS-NLML and NESMA filters. We have summarized these in the following table (Table 3). Note that these differences in basic filter design lead overall to near-equivalent performance with over three orders of magnitude more rapid processing with NESMA, permitting routine clinical application.

Table 3.

MS-NLML vs. NESMA. Feature comparison of the MS-NLML and NESMA filters.

	MS-NLML	NESMA
Performance	High	High
Computational speed	Slow	Fast
Spatially adaptive	Yes	Yes
Implementation	Complex	Simple

Differences in computation time for the SA method relative to the NA method for each filter can be attributed to two factors: the inclusion of more voxels in the denoising process, and thresholding the distances as opposed to sorting them to find the R smallest distances. The SA method permits much higher values for R in homogeneous regions, while maintaining relatively similar values of R for heterogeneous regions, as compared to the NA method. This leads to the inclusion of many more voxels in the denoising process as compared to the NA method (Figs. 1 and 3) and an overall increase in computation time. The number of calculations required to select voxels based on a RED threshold value, as is required for the SA method, increases linearly, O(n), with respect to the number of voxels n within the search window. The number of computations required for sorting, as required for the NA method in which distances are calculated for all voxels in the search window and then sorted, increases by O(n·log(n)). This difference is particularly evident for larger window sizes and dominates the relative speed of the NA and SA methods. The SA and FA methods increase values of R as compared to the NA method in homogeneous image regions, while maintaining low values of R for regions with small structures. The superior filtering quality is due to the adaptive and appropriate selection of R for each voxel individually.

In our analysis, image noise is assumed to be spatially stationary. In multi-channel acquisitions, such as parallel imaging or phased array acquisition (24), this assumption does not hold. However, even in this setting, using one of several methods that have been introduced to estimate local background noise (21, 32, 33) would permit application of the NESMA and MSNLML filters through incorporating spatially varying noise. In addition to relaxing the stationary noise assumption, local noise estimation would allow for filtering of images that lack available background for noise estimation.

6-. CONCLUSION

We have introduced a new fast multispectral nonlocal filter, NESMA, and two adaptive variants, for filtering magnitude MR images. In addition to its robust filtering performance, NESMA is straightforward to implement and requires minimal user-defined parameters. These features render it suitable for routine clinical use and analysis of large datasets.