Structural consequences of hereditary spastic paraplegia disease-related mutations in kinesin

Significance

Motor proteins are important biological machines responsible for cellular transport. Malfunctioning of them causes several neurodegenerative diseases. We searched for a molecular-level answer for malfunctioning kinesin, which causes hereditary spastic paraplegia (HSP) disease. Using explicit solvent simulation, the thermodynamic integration (TI) method, and bioinformatics analysis, we explored how four HSP mutants of kinesin perturb microtubule (MT) binding and motor dimerization. Taking these observations into account, we developed a coarse-grained structure-based model to reveal the effect of these mutations on kinesin’s order–disorder transition, which leads to the processivity and directionality of kinesin. Our study potentially uncovers a molecular-level picture of the role of some HSP mutants and its broad aspect in kinesin mechanochemistry.

Abstract

A wide range of mutations in the kinesin motor Kif5A have been linked to a neuronal disorder called hereditary spastic paraplegia (HSP). The position of these mutations can vary, and a range of different motile behaviors have been observed, indicating that the HSP mutants can alter distinct aspects of kinesin mechanochemistry. While focusing on four key HSP-associated mutants, this study examined the structural and dynamic perturbations that arise from these mutations using a series of different computational methods, ranging from bioinformatics analyses to all-atom simulations, that account for solvent effects explicitly. We show that two catalytic domain mutations (R280S and K253N) reduce the microtubule (MT) binding affinity of the kinesin head domains appreciably, while N256S has a much smaller impact. Bioinformatics analysis suggests that the stalk mutation A361V perturbs motor dimerization. Subsequent integration of these effects into a coarse-grained structure-based model of dimeric kinesin revealed that the order–disorder transition of the neck linker is substantially affected, indicating a hampered directionality and processivity of kinesin. The present analyses therefore suggest that, in addition to kinesin-MT binding and coiled-coil dimerization, HSP mutations affecting motor stepping transitions and processivity can lead to disease.

Cytoskeletal motors are an important class of proteins that drive the transport of materials in the cytoplasm by converting the chemical energy available from ATP hydrolysis into mechanical work (1–5). Kinesin-1 (Kif5) is a widely expressed, but neuron-enriched, microtubule (MT) motor that drives the outward, plus-end-directed, cytoplasmic transport of numerous vesicles and organelles and signaling complexes (6). Kinesin is a heterotetrameric protein containing two dimerized heavy chains and two light chains. The heavy chains contain the MT binding and catalytic or motor domain. This domain is linked to a dimerizing coiled-coil stalk domain via a flexible neck-linker domain (7). This structural organization allows kinesin to coordinate the hydrolytic and MT binding activities of its head domains and to advance along the MT via a “hand-over-hand” mechanism (8). Conformational changes and a strain-sensing mechanism within the neck linkers connecting the motor domains are critical to this coordination, which, overall, allows kinesin to transport cargos rapidly (∼1 μm⋅s⁻¹) and processively over long transport distances (∼1 μm), even as a single, noninteracting motor.

Mutations in the kinesin family proteins have been associated with several diseases (9, 10). Specially, mutations in the kinesin-1 family motor Kif5A have been reported to occur in ∼10% of patients identified with hereditary spastic paraplegia (HSP) (11). HSP is a genetically and clinically heterogeneous illness that causes progressive damage of axons in the corticospinal tract (10, 12). At least 25 different HSP-causing Kif5A mutations have been discovered. They are associated with the more complicated forms of the disease. The vast majority of these mutations (23 of 25) occur in highly evolutionally conserved residues of the motor domain. The remaining two mutations occur within the coiled-coil stalk (13–15).

A recent comprehensive survey by Jennings et al. (15) indicates that kinesin motor dysfunction in HSP is often linked to a combination of impaired ATP hydrolysis rates and/or decreased motility. Other analyses by Ebbing et al. (16) characterized the hydrolytic, motile, and force-producing properties of four selected mutants within the L11 and L12 loops of the MT binding domain (K253N, R280S, and N256S), as well as a mutation in the motor stalk (A361V). A spectrum of different effects was also observed with these constructs. The R280S mutation was shown to primarily impair MT binding affinity. MT gliding velocities were only slightly impaired, but achieving this motility required more than 10-fold higher motor surface concentrations. MT affinities were apparently too low for measurements of the rates of MT-stimulated ATP hydrolysis. The remaining two MT binding domain mutants (K253N and N256S) both showed appreciable drops in MT gliding velocity and diminished ATPase activity. The A361V neck-linker mutation resulted in slightly lower hydrolysis rates and may affect heavy chain dimerization. Together, these results suggest the HSP mutations can induce a range of different forms and strengths of mechanochemical perturbations to the kinesin functions in cells. Resolving the structural basis of these different perturbations is therefore important for understating and potentially managing the effects of kinesin mutations in HSP.

Herein, we explore structural determinants of mutant perturbations in Kif5A motors. This work builds upon theoretical frameworks our group has developed to model cytoskeletal motors (kinesin, Ncd, myosin, and dynein) and explores properties of their mechanochemical cycle (17–22). Models of motor states are built using structural data available from the protein database as initial information. Simulation methods based on the energy landscape theory of protein folding (23–27) are then employed to model motor–MT interactions and the transition behaviors of key intermediate states of motors along their mechanochemical cycle. This framework allowed us to uncover the unidirectional movement and processivity of kinesin-1 depend on nucleotide-dependent, structural order–disorder transitions within the motor neck linker (28, 29). The present study builds upon this framework to examine how HSP mutations affect motor interactions with MTs. Using a combination of all-atom and explicit solvent simulations that calculate the binding free energies of MT-bound kinesins, as well as coarse-grained (CG) structure-based modeling approaches to characterize the effect of HSP mutations on motor stepping directionality and processivity, the present study provides a structural basis for the full range of different observations that some HSP mutations primarily affect the kinesin-MT binding affinity, while others affect coiled-coil dimerization or motor stepping transitions. Furthermore, our CG simulation shows that HSP mutations can impair kinesin stepping directionality and processivity by specifically altering the order–disorder transition of the motor neck linker.

Results

A recent experimental study by Jennings et al. (15) examined 25 kinesin mutants related to HSP disease. Biochemical analyses of the mutations within the switch I domains (six of 25) show that these mutations alter quite different aspects of the kinesin mechanochemistry (ATPase activity, MT affinity, gliding velocity, etc.). An earlier experimental study by Ebbing et al. (16) examined four selected mutants related to HSP disease (K253N, N256S, R280S, and A361V) in comprehensive detail. A range of different perturbations to MT binding affinity, ATPase activity, and MT gliding velocity were observed from these mutations as well. The four mutations examined by Ebbing et al. (16) occur within different regions of the kinesin motor (Fig. 1). The A361V is located at the coiled-coil stalk region and can possibly affect the dimerization of the kinesin motor. The other three mutations, K253N, N256S, and R280S, are present in the motor head domain. Among them, K253N and N256S are found to be close to the nucleotide binding domain (distances of the Cα atom of the residues from the third phosphate atom of ATP are 1.8 nm for K253 and 1.4 nm for N256, respectively), indicating their possible role in affecting nucleotide binding, hydrolysis, or release of hydrolysis products. R280S is far from the nucleotide binding domain (distance of the Cα atom of the residue from the third phosphate atom of ATP is 2.7 nm for R280), suggesting that it may have no significant effect in those processes.

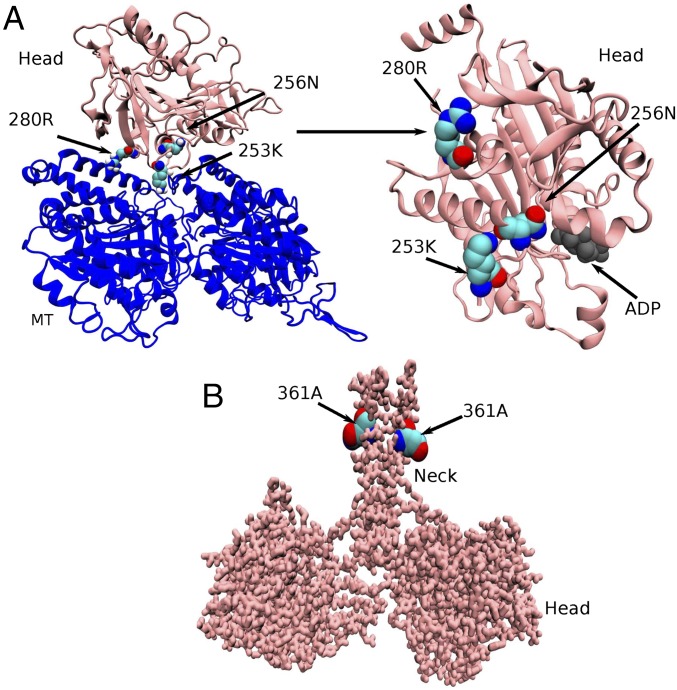
Fig. 1.

Location of four mutants responsible for HSP. (A) MT-bound single-head domain of kinesin. The head domain residues 253Lys and 256Asn are close to the nucleotide binding pocket; however, 280Arg is distant from it. (B) Head domain residue 361Ala is located at the coiled-coil stalk region.

Changes in the MT Binding Affinity due to Head Domain Mutations.

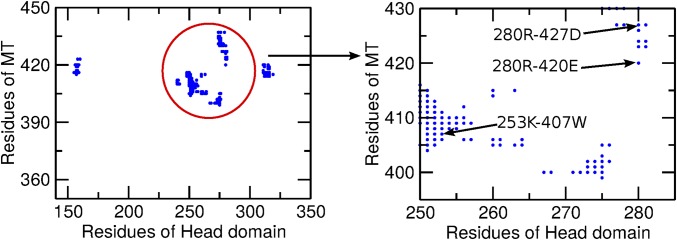
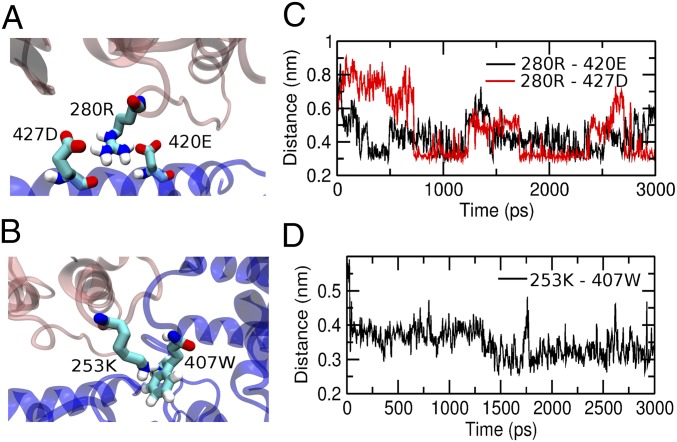
To determine whether the 280Arg, 253Lys, and 256Asn head domain residues have any direct contact with the MT, we examined contact maps of the MT–head interface with a cutoff distance of 10 Å (Fig. 2) between the Cα atoms using the SMOG@ctbp online server (30–32). Both the 280Arg and 253Lys residues are found to interact with the MT within the cutoff distance. The 280Arg makes a double-salt bridge type of contact with the 427Asp and 420Glu residues of the MT. The 253Lys makes contact with the 407Trp of the MT, which indicates a π-cation type of interaction between them. From the equilibrium simulations of the MT-bound kinesin, we determined that the 280Arg does not break the double salt bridges with 427Asp and 420Glu of the MT and that the distances between them remain around 0.4 nm. A representative configuration showing the salt bridges is illustrated in Fig. 3A. Similarly, the distances between 253Lys and 407Trp are also found to equilibrate around 0.35 nm, indicating a strong π-cation type of interaction between them (Fig. 3B). In contrast, significant contact interactions are not found between the 256Asn and the MT, neither in the contact map nor during equilibrium simulations.

Fig. 2.

Contact map of the head–MT interface. The zoomed-in graph clearly shows that 280Arg makes contact with 427Asp and 420Glu and that 253Lys makes contact with 407Trp.

Fig. 3.

Interactions of the MT with 280Arg and 253Lys. (A) Head domain residue 280Arg makes double salt bridges with 427Asp and 420Glu. (B) Head domain residue 253Lys makes a π-cation type of interaction with 407Trp. (C and D) Time evolution of contact pair distances from equilibrium simulations.

We next calculated binding free-energy changes for mutants with respect to the wild-type kinesin using the thermodynamic integration (TI) method (33–37) as a way to clarify the effect of the mutations of these residues (R280S, K253N, and N256S) in the head domain on the affinity of MT binding. In this calculation, the 280Arg residue is gradually mutated to Ser by perturbing the interaction parameter λ in both the MT-bound complex and the free head states in explicit solvent molecular dynamics (MD) simulations. Calculation of the binding free energy was performed using Eq. 1. Similarly, we mutated the 253Lys and the 256Asn to Asn and Ser, respectively, and then calculated free energies using same technique (SI Appendix, Fig. S1). Table 1 summarizes the free-energy (ΔG) values for each mutation in bound and free conditions and the changes in binding free-energy (ΔΔG) values due to different mutations. For a control simulation, we mutated the 60Glu to Val, which was far from the MT in the head domain. The change in the ΔΔG value is found to be very small (1.8 ± 1.7 kJ/mol) for the 60Glu mutation. This result validates the method used for binding energy calculation. For the 280Arg, the ΔΔG value is 30.10 ± 6.8 kJ/mol, which indicates that this mutation affects the head domain affinity toward the MT significantly. The ΔΔG value for the 253Lys mutation is found to be 16.69 ± 4.8 kJ/mol, which is also significant and suggests a weakening of the affinity toward the MT.

Table 1.

Change in the MT binding free energy due to mutation on kinesin obtained from the thermodynamic calculations

Mutants	Complex ΔG, kJ/mol	Solvent ΔG, kJ/mol	ΔΔG, kJ/mol
R280S	−83.87 ± 4.7	−113.97 ± 3.6	30.10 ± 6.8
K253N	−156.68 ± 4.3	−173.37 ± 1.7	16.69 ± 4.8
N256S	32.69 ± 1.3	26.19 ± 0.9	6.50 ± 1.79
E60V	390.33 ± 1.7	388.53 ± 0.2	1.8 ± 1.7

For the 256Asn mutation, the value of ΔΔG is relatively small (6.50 ± 1.79 kJ/mol), indicating that the 256Asn mutation may not have a significant role in MT binding and probably changes the motility of kinesin by affecting nucleotide binding or chemistry or by other means, since the distance between the active site for hydrolysis and this residue is the lowest among the three head domain residues.

Changes in Dimerization Interactions due to Stalk Domain Mutation.

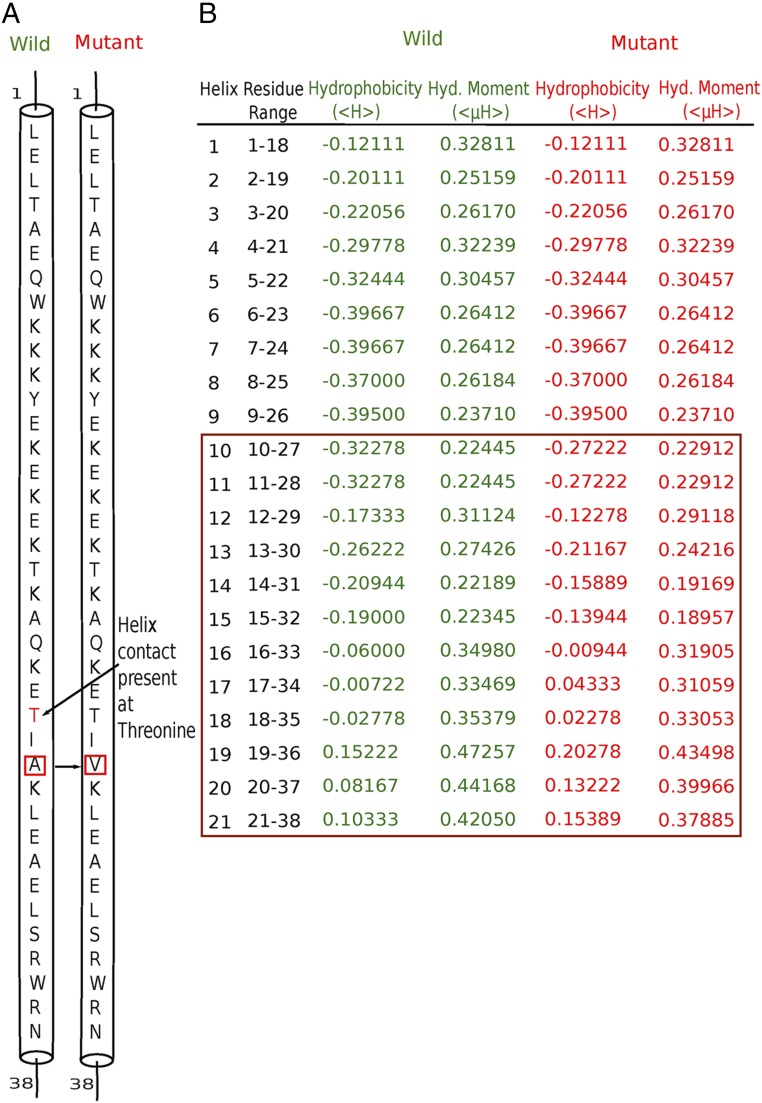
We also investigated the role of the mutant present in neck domain A361V using two bioinformatics software packages: RHYTHM (38) and HELIQUEST (39). From RHYTHM, we observed that a contact in the coiled-coil region of the wild-type kinesin disappears upon the A361V mutation (Fig. 4A). HELIQUEST produced changes in hydrophobicity and of the hydrophobic moment of each coil after mutations. From this information, we may infer that the hydrophobic mutation of Ala to Val introduces a steric effect in the system. This steric effect changes the helix packing, which leads to a change in the hydrophobic moment of each coil and the breakage of contacts between two coil-coiled stalks (Fig. 4B). Results from both methods imply disruption/reduction of the dimerization interactions between coiled-coil helices.

Fig. 4.

Hydrophobic mutation A361V leads to change in helix packing and the breaking of helix contact. (A) Result obtained from RHYTHM indicates disappearance of the helix contact at threonine. (B) Data collected from HELIQUEST software. Green and red colors indicate hydrophobicity and the hydrophobic (Hyd.) moment for the wild-type and mutant proteins, respectively. The brown box signifies the change in hydrophobicity and the hydrophobic moment from wild type to mutant.

Alteration of Order–Disorder Transition of Neck Linker due to Head and Stalk Domain Mutations.

Our explicit simulation results have indicated that some mutations affect the MT binding affinity, and bioinformatics analysis suggests that another mutation causes the destabilization of the coiled-coil dimerization of the dimeric kinesin. To further explore how these two changes affect the kinesin motility, we mimicked the effect of these mutations in our previously developed CG model of dimeric kinesin on the MT. The model was built using structural information whenever available or from homology modeling otherwise (40, 41). The key result was that in the two-head–bound state of dimeric kinesin on the MT, the symmetry of the free dimeric crystal structure is broken and the two heads become different. While the trailing head remains closed to the crystal structure, the apparent strain on the neck linker of the leading kinesin monomer propagates to the leading head. As a result, its radius of gyration and also its root mean square deviation (rmsd) become larger than for the trailing head. This difference between the two heads was suggested to be important for kinesin motility (42–45). As long as the trailing head is bound to the MT, the strain on the neck linker on the leading head is not released, and therefore it cannot bind to ATP. Thus, the trailing head needs to be released before ATP binding to the leading head can take place. This causes the docking of the neck linker of the leading head and the forward motion of the trailing head, with the kinesin walking toward the positive end of the MT (46–48). It has been shown recently that a major portion of the kinesin stepping (16 nm along the MT) occurs through Brownian motion and that docking of the neck linker plays an important role in biasing the Brownian search of the trailing head to the binding site on the MT toward the positive direction (49).

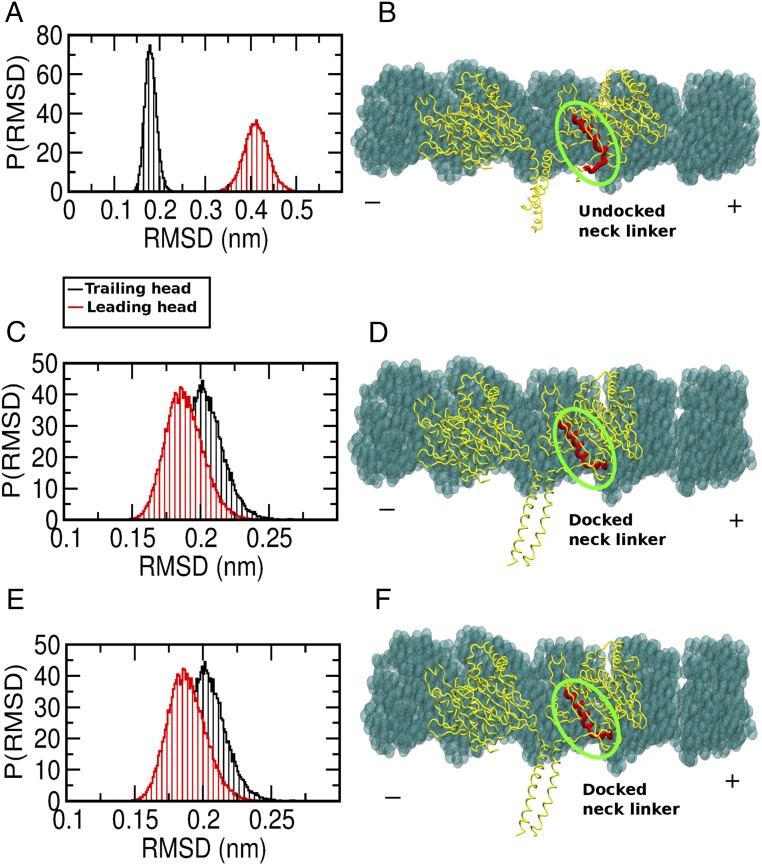
To explore the alteration of the above-mentioned mechanism through the structural order–disorder transition of the neck linker of kinesin, we first reproduced the asymmetrical fluctuation of the two heads of kinesin using the CG structure-based model simulation for the wild-type kinesin bound to MT. Fig. 5A shows the distribution of the rmsd of the trailing and leading heads of the kinesin bound to the MT determined via CG simulations. Note that the leading head has a larger rmsd (∼0.4 nm) than the trailing head (∼0.2 nm). This is a signature of the structural changes in the leading head. In Fig. 5B, we show a representative configuration of the dimeric kinesin on the MT. Note the strained/undocked configuration of the neck linker in the leading head.

Fig. 5.

Mutation affects the structural asymmetry between two motor heads. (A) Distribution of the rmsds of the two motor heads of wild-type kinesin bound to the MT. Note the asymmetry of the rmsds between the two heads. (B) Structural representation showing an undocked neck linker of the leading head. (C) Distribution of the rmsds of the two motor heads of MT binding mutant kinesin bound to the MT. Note that the asymmetry of the rmsds between two heads has disappeared. (D) Structural representation showing the docked neck linker of the leading head. (E) Distribution of the rmsds of the two motor heads of the dimerization mutant kinesin bound to the MT. Note that the rmsds of the two heads are similar. (F) Structural representation showing the docked neck linker of the leading head. P(RMSD) indicates probability distribution of RMSD.

Next, we explore the effect of the mutations on the motility of kinesin. We categorized the mutations in two different groups. Some mutations are found to decrease the affinity of the head toward the MT. They are mimicked in our CG model by decreasing the strength of MT–kinesin interface surface contacts. For another mutation that affects the coiled-coil dimerization, the coiled-coil dimerization contact strength has been reduced. We performed simulations with only the kinesin–MT interface interaction defect, with only the dimerization interaction defect, and with both the defects.

In Fig. 5C, we present the distribution of the rmsd of the two heads from the CG simulations where the mutation affecting kinesin–MT interaction was introduced. We observed that the asymmetry of the rmsd between the two heads vanishes and that both of them showed similar values of the rmsd (∼0.2 nm). We show a representative configuration of the kinesin on the MT from the trajectory in Fig. 5D. In this case, note that the neck linker of the leading head is now docked and, as a result, the fluctuation of the leading head decreases.

We observed a similar effect on the rmsd of the two heads of kinesin bound to the MT when only a dimerization mutation was introduced in the CG model, as shown in Fig. 5E. Fig. 5F is a representative structure from the simulation trajectory showing a docked neck linker. When both of the mutations are introduced in the CG simulations, similar rmsds and leading heads with the docked neck linker are observed. In the wild-type kinesin bound to the MT, the balance between interactions of the kinesin–MT interface and the dimerization region introduces a strain on the neck-linker region that propagates to the leading head and establishes asymmetry in the structural fluctuations between the two heads of kinesin. When either of the interactions (or both) is reduced, then the two heads of kinesin can adjust to release the strain on the neck linker, and this essentially removes the asymmetry between the two heads, therefore affecting processivity and motion directionality.

Discussion

HSP is a debilitating neuronal disease that has been associated with 25 different mutations in the kinesin-1/Kif5 motor. Of these 25 mutations, 23 occur within the catalytic motor domain and the other two are in the coiled-coil stalk region (15). Several of the 23 head domain mutations occur within the MT binding interface of the motor domain, while others are proximal to the nucleotide binding site and likely affect allosteric communication inside kinesin. The other two stalk domain mutants are expected to influence dimerization of the coiled-coil stalk region. Similar to the wide distribution of position of these mutations in the kinesin structure, they modulate a wide range of mechanochemical properties of kinesin, including MT binding affinity, ATPase activity, MT gliding velocity, and force production. Experiments by Ebbing et al. (16) have provided a comprehensive analysis of these properties for four selected HSP-related mutants (K253N, N256S, R280S, and A361V). Three of them (K253N, N256S, and R280S) are at the kinesin head domain, and one (A361V) is at the coiled-coil region. From their biochemical assays, these researchers inferred that R280S showed reduced MT affinity, N256S showed reduced velocity, K253N showed a reduction in both of these the quantities, and A361V does not seem to alter either of these quantities appreciably. In the present study, we interrogate the effects of these four mutants on the motility of kinesin using several computational tools to provide a structural interpretation of the observed effects. Bioinformatics-based analysis [RHYTHM (38) and HELIQUEST (39)] was performed to examine the change in helix contact and packing in the coiled-coil stalk region on mutation. All-atom explicit solvent simulations, contact map analysis, and the TI method have been used to instigate the modulation of MT binding affinity upon mutation. CG structure-based model (SBM) simulations of dimeric kinesin-bound MT, incorporating the effect of mutations, have been performed to investigate modification of the order–disorder transition of the neck linker. Based on these studies, we have classified the role of these mutations in HSP disease in two ways.

Mutations Affecting Order–Disorder Transition of Neck Linker.

The study by Ebbing et al. (16) indicates that MT binding affinity reduction is highest for R280S, moderate for K253N, and lowest for N256S among the head domain mutants. The values of binding free energies (ΔΔG) calculated from the TI method are 30.10 kJ/mol, 16.69 kJ/mol, and 6.50 kJ/mol upon mutation of R280S, K253N, and N256S, respectively, showing good agreement with experiments (Table 1). In the case of the coiled-coil stalk domain mutation, A361V, experimental results did not provide conclusive effects. Nevertheless, our bioinformatics analysis suggests disruption of helix contacts and modulations of the helix packing in the coiled-coil region, implicating a weakening of the dimeric interactions (Fig. 4). When the effect of these mutations was incorporated in our CG SBM simulations, the order–disorder transition of the linker region was affected and the asymmetry between the leading head and trailing head disappeared in the two-head–bound configuration. It has already been suggested by Hyeon and Onuchic (50) that this asymmetry is important for kinesin movement and processivity. These results also implicate a delicate balance between these two types of interactions (MT–kinesin and dimerization) in the kinesin mechanochemical cycle that may be disrupted by the A361V mutation.

Mutations Affecting ATPase Activity and MT Gliding Velocity.

The N256S mutation is found to cause the largest reduction of the kinesin velocity of the head domain mutants experimentally, followed by K253N and then R280S. The A361V mutant moves with near-equivalent velocities to the wild-type kinesin. Since A361V is located in the coiled-coil region of the kinesin, which is far away from the nucleotide binding domain (Fig. 1B), its insensitivity for the ATPase activity and gliding velocity is therefore expected. N256S is notably positioned closest to the nucleotide binding pocket (1.4 nm), followed by K253N (1.8 nm) and then R280S (2.7 nm) (Fig. 1A). While additional calculations are ultimately needed, the reduction of ATPase activity and gliding velocity should be in the following order: N256S > K253N > R280S, based on their distance from the active site.

Our work therefore provides evidence that several HSP mutations affect the kinesin velocity by altering the motor–MT interaction binding energies and interfering with an order–disorder transition that is critical to the coordination of the motor head domains and resultant processivity. While we provide a structural rationale for the impaired kinesin motility by the above-mentioned mechanism for these four mutants, such behavior may be more general and could influence the stepping mechanism of other HSP mutations studied by Jennings et al. (15) For example, several other HSP-related mutations occur in the switch I region of kinesin (M198T, S202N, S203C, R204Q, R204W, and E251K). As switch I is an important element for ATP hydrolysis (they are all close to the active site) and allosteric communication, modification of the ATPase activity and the gliding velocity is therefore expected. Indeed, reduced motility is observed for all these mutants. Moreover, the R204Q/W and E251K mutants have significantly reduced MT affinity, which we now hypothesize stems, at least in part, from the disruption of the order–disorder transition of the neck-linker region.

Conclusion

In summary, our structural analyses show that HSP disease-related mutations can affect kinesin motility via at least two different mechanisms: mutations affecting the order–disorder transition of the neck linker and mutations affecting ATPase activity/MT gliding velocity. These mechanisms would likely alter MT-dependent transport and net outward-directed fluxes of cargos by reducing either the proportion of cargos engaged in active transport or their transport velocity. Slow kinesins may also serve as “roadblocks” for other MT motors. HSP-associated transport defects can therefore stem from a range of structural perturbations and effects. This circumstance probably reflects the importance and sensitivity of neuron physiology to kinesin-1 functions. Moreover, HSP is a heterozygous disease, and there will be a mixture of normal kinesin along with homodimer and heterodimer kinesins with disease mutation. One therefore needs to characterize the perturbation strengths of mutations in homodimers and heterodimers to fully capture the complexity of kinesin behaviors in HSP.

Materials and Methods

Explicit Solvent MD Simulations.

The initial structure of kinesin/KIF5A was obtained from the crystal structure [Protein Data Bank (PDB) ID code 3KIN] (51). The MT structure comes from PDB ID code 2HXF (52). Both PDB structures originated from a mouse organ. Missing residues were built using SWISS-MODEL homology modeling software (40, 41). The head domain was attached to the MT by superimposing structures using PyMOL (53) Both the MT-bound head and the free head simulations were performed using the GROMOS96 53a6 force field (54, 55) and the simple point charge (SPC) water model (56) using the GROMACS simulation package (57). The MT-bound complex was placed in a simulation box sized 7.16 × 11.01 × 11.01 nm³ and filled with 22,817 water molecules. The free head system, however, was kept in a box of sized 6.60 × 6.53 × 7.38 nm³, and 8,789 water molecules were added. The energy minimization was carried out using steepest descent. To relax water molecules, a 100-ps simulation was carried out restraining the initial positions of the protein atoms by a harmonic potential. Finally, the solvated protein was equilibrated for 3 ns using a constant-temperature bath at 300 K and a constant-pressure bath at 1 atm. The SHAKE algorithm was used to keep all bonds rigid (58). Nonbonded interactions were calculated using the PME cutoff scheme (59).

Binding Free-Energy Calculation.

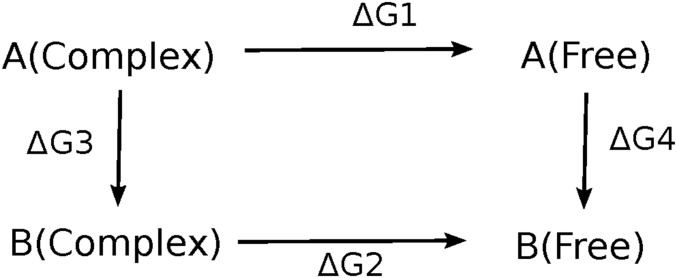
Motor–MT binding interactions were investigated using a TI method (33–37). It was used to investigate the changes in binding free energies between the head and the MT upon perturbing three residues in the head domain: 253Lys, 256Asn, and 280Arg. In this method, a thermodynamic cycle was considered, as shown in Fig. 6. The wild-type system is perturbed toward the mutant for both cases: the solvated complex formed by MT-bound head domain and the free, solvated head domain. The alchemical method uses a coupling parameter λ for transitioning between states. The total energy of each system is described by a given Hamiltonian H, and an alchemical transformation between states is controlled by the coupling parameter λ (60). The two states of a system are defined as follows: state A: H_A = H(λ = 0) and state B: H_B = H(λ = 1). The coupling parameter λ constructs a path that connects these two Hamiltonians between state A and state B. This perturbation was performed in discrete steps. The Hamiltonians at intermediate states are defined as follows: H(λ) = H_A(1−λ) + H_B(λ). The free-energy difference between the two states, ΔG_AB, can be calculated by integrating along any path from state A to state B using Eq. 1:

$$\mathrm{\Delta }{G}_{AB}={\displaystyle \underset{0}{\overset{1}{\int }}\frac{\delta G\left(\lambda \right)}{\delta \lambda }}d\lambda ={{\displaystyle \underset{0}{\overset{1}{\int }}\langle \frac{\partial H\left(\lambda \right)}{\partial \lambda }\rangle }}_{\lambda }.$$ [1]

Fig. 6.

Thermodynamic cycle to calculate binding free energy.

The term in the angular bracket represents the ensemble average of a derivative of the Hamiltonian H with respect to λ. Separate MD simulations were performed at different λ values, and integrations over λ values were carried out using a trapezoidal integration method to calculate the final free-energy difference between states A and B.

In our study, four MD trajectories were generated for each λ value and the three residues 253Lys, 256Asn, and 280Arg were gradually mutated into Asn, Ser, and Ser, respectively, for both the MT-bound head complex and the free head one. Since the free energy is a state function, ΔΔG = ΔG1 − ΔG2 = ΔG3 − ΔG4.

Mutation of a particular residue such as K253N was done by switching off the nonbonded interaction of the 253K side chain–CH₂–CH₂–CH₂–CH₂–NH₂ and switching on of the nonbonded interaction of the mutated 253N side chain–CH₂–CONH₂. Eleven equally spaced simulations were performed from λ = 0 to λ = 1. At each point, the system was equilibrated for 1,000 ps and data were collected for another 7,000 ps.

Bioinformatics Analysis.

To explore the possibility of affecting the dimerization interactions at the coiled-coil stalk region of kinesin by stalk domain mutation A361V, we have used two bioinformatics software packages, RHYTHM (38) and HELIQUEST (39), to obtain information about changes of the secondary and tertiary structures and of the helix packing of the coiled-coil domain. RHYTHM predicts helix–helix contacts, particularly for transmembrane protein. We have therefore applied the prediction tool to identify a possible change in a helix–helix contact based on the primary sequence information of a protein. The propensity matrices were derived from a nonredundant dataset containing 310 and 179 transmembrane helices. The helix was defined by the algorithm of Kabsch and Sander (61). Those helix pairs were removed from the dataset when the interhelical distances were high, as evident from visual inspection. The type of contact of a specific residue was then identified by counting its atomic contacts with the neighboring helix or with a virtual membrane or water. The propensity matrices were derived for residues in contact with another helix or the membrane, and the propensities of all neighboring amino acids were also stored in the same matrix. Finally, scores were calculated by adding the residue propensities for a given residue length. HELIQUEST predicts, using amino acid composition, the physicochemical properties of a protein and identifies protein segments with similar properties. Starting from the protein sequence, it considers a sliding window with a helical wheel of 18 amino acids. It provides a net charge (z) at pH 7.4, mean hydrophobicity (<H>), and the hydrophobic moment (<μH>). Mutations in any characterized helix can be done manually or automatically by a genetic algorithm. The values of z, <H>, and <μH> are modified independently or simultaneously using a genetic algorithm-based module.

The Kinesin Structure-Based Model.

Structure-based models were developed to evaluate the alteration of the structural order–disorder transition of the neck-linker region of the kinesin by the HSP-related mutants. These models are constructed using the native structure available in the PDB (ID code 3KIN) (51) by considering each amino acid as a single bead located at the Cα position (coarse graining) using SMOG@ctbp (30–32). The Hamiltonian is

$$H_{SBM}\overrightarrow{\left\{\left(r_i\right)\right\}}=H_B+H_{NB},$$

where H_B and H_NB are the local bonded and nonbonded components, respectively:

$$H_B={\displaystyle \sum _{i=1}^{N-1}\frac{K_r}{2}}{\left(r_{i,i+1}-r_{i,i+1}^0\right)}^2+{\displaystyle \sum _{i=1}^{N-2}\frac{K_{\theta }}{2}}{\left({\theta }_i-{\theta }_i^0\right)}^2+{\displaystyle \sum _{i=1}^{N-3}{\displaystyle \sum _{n=\mathrm{1,3}}{K}_{\varphi }^{\left(n\right)}}}\left(1-\cos \left[n\left({\varphi }_i-{\varphi }_i^0\right)\right]\right).$$

The first term, $r_{i,i+1}$, represents the distance between residues i and i + 1 and is constrained harmonically with respect to the native distance $r_{i,i+1}^0$ by a spring constant K_r = 200 (kJ⋅mol⁻¹⋅Å⁻²). The angle between the residues of i, i + 1 and i + 2, is represented by the second term ${\theta }_i$, and it is constrained with respect to native value ${\theta }_i^0$ by a harmonic spring constant $K_{\theta }$ with a value of 40 (kJ⋅mol⁻¹⋅rad⁻²). The third term is a dihedral angle potential that describes the rotation of the backbone involving successive residues from i to i + 3 with K_φ⁽¹⁾ = 2K_φ⁽³⁾, where K_φ⁽¹⁾ = 1 (kJ⋅mol⁻¹).

The nonbonded part of the Hamiltonian $\left(H_{NB}^O\right)$ is represented by

$$H_{NB}^O={\displaystyle \sum _{i=1}^{N-4}{\displaystyle \sum _{j=i+4}^N\left[{\epsilon }^O\left(5{\left(\frac{r_{ij}^0}{r_{ij}}\right)}^{12}-6{\left(\frac{r_{ij}^0}{r_{ij}}\right)}^{10}\right){\mathrm{\Delta }}_{ij}^O+{\epsilon }_r{\left(\frac{\sigma }{r_{ij}}\right)}^{12}\left(1-{\mathrm{\Delta }}_{ij}^O\right)\right]}}.$$

If i and j residues are in contact, then ${\mathrm{\Delta }}_{ij}^O\mathrm{=1}$; otherwise,${\mathrm{\Delta }}_{ij}^O\mathrm{=0}$. Nonnative pairs $\left({\mathrm{\Delta }}_{ij}^O\mathrm{=0}\right)$ feel repulsive potential. To incorporate the mutation in the SBM, we control the value of ε to decrease the strength between the MT and the kinesin surface contacts and the coiled-coil dimerization contacts.

SBM Simulations.

Initial structures were relaxed under the structure-based Hamiltonian, and the structures of different equilibrium ensembles were collected from Langevin dynamics at a low friction limit to improve sampling. Simulations were performed at 300 K. The equation of motion for Langevin dynamics used for integration is

$$m{\ddot{\overrightarrow{r}}}_i=-\zeta {\dot{\overrightarrow{r}}}_i-{\partial }_{\overrightarrow{r}}H\left(\left\{{\overrightarrow{r}}_i\right\}\right)+{\overrightarrow{\mathrm{\Gamma }}}_i\left(t\right),$$

where $\zeta$ is the friction coefficient, $-{\partial }_{\overrightarrow{r}}H\left(\left\{{\overrightarrow{r}}_i\right\}\right)$ is the conformational force, and ${\overrightarrow{\mathrm{\Gamma }}}_i\left(t\right)$ is random force, which satisfies $\langle {\overrightarrow{\mathrm{\Gamma }}}_i\left(t\right).{\overrightarrow{\mathrm{\Gamma }}}_j\left(t\right)\rangle =\left(6\zeta K_{B}T/h\right){\delta }_{ij}\left(t-t^{\text{'}}\right)$, where integration time h is discretized. In a natural time ${\tau }_L={\left(m{\sigma }^2/{\epsilon }_h\right)}^{1/2}$, we used $\zeta =0.05{\tau }_L^{-1}$ and $h=0.0025{\tau }_L$.