Ab initio structure determination from experimental fluctuation X-ray scattering data

Significance

Fluctuation X-ray scattering is a biophysical structural characterization technique that overcomes low data-to-parameter ratios encountered in traditional X-ray methods used for studying noncrystalline samples. By collecting a series of ultrashort X-ray exposures on an ensemble of particles at a free-electron laser, information-dense experimental data can be extracted that ultimately result in structures with a greater level of detail than can be obtained using traditional X-ray scattering methods. In this article we demonstrate the practical feasibility of this technique by introducing data-processing techniques and advanced noise-filtering methods that reduce the required data collection time to less than a few minutes. This will ultimately allow one to visualize details of structural dynamics that may be inaccessible through traditional methods.

Abstract

Fluctuation X-ray scattering (FXS) is an emerging experimental technique in which X-ray solution scattering data are collected from particles in solution using ultrashort X-ray exposures generated by a free-electron laser (FEL). FXS experiments overcome the low data-to-parameter ratios associated with traditional solution scattering measurements by providing several orders of magnitude more information in the final processed data. Here we demonstrate the practical feasibility of FEL-based FXS on a biological multiple-particle system and describe data-processing techniques required to extract robust FXS data and significantly reduce the required number of snapshots needed by introducing an iterative noise-filtering technique. We showcase a successful ab initio electron density reconstruction from such an experiment, studying the Paramecium bursaria Chlorella virus (PBCV-1).

X-ray solution scattering is often the technique of choice when studying the structure and dynamics of macromolecules in near-native conditions, providing unique insights into their function and regulation. However, traditional solution scattering methods, such as small- and wide-angle X-ray scattering (SAXS/WAXS), conducted at synchrotron light sources, suffer from a very low data-to-parameter ratio due to the fact that the X-ray exposure time is longer than the time it takes for the particles to undergo full rotation, resulting in an angularly isotropic scattering signal.

To overcome this information loss, it has been suggested to perform the solution scattering experiment at timescales below rotational diffusion times of the particles, resulting in angular fluctuations in the signal from which several orders of magnitude more information can be extracted by calculating angular correlations of the data (1). Although this experiment, named fluctuation X-ray scattering (FXS) (2), was originally proposed half a century ago, it has only recently become a practical reality due to advances in X-ray sources (3), sample delivery (4), and data analysis. In particular, X-ray free-electron lasers (XFELs) provide fully coherent, high-intensity X-ray pulses of femtosecond duration, allowing one to perform scattering experiments at the required timescales at room temperature, without the detrimental effects of radiation damage (5)

Whereas earlier work has demonstrated the experimental feasibility of FXS on single-particle X-ray scattering data (6–8) and on multiple-particle data from crystalline materials (9), as well as feasibility studies on partially oriented multiple-particle metallic nanoparticles (10), no low-contrast, noncrystalline, 3D FXS experiment with multiple particles per shot has been demonstrated to be feasible. Here we present an analysis of such an FXS experiment conducted at the Linac Coherent Light Source (LCLS) (3), providing updated insights into the general feasibility of multiple-particle FXS (11), and highlight challenges to be addressed to make this a mainstream technique for the study of structure and dynamics of particles in solution, at physiologically relevant temperatures.

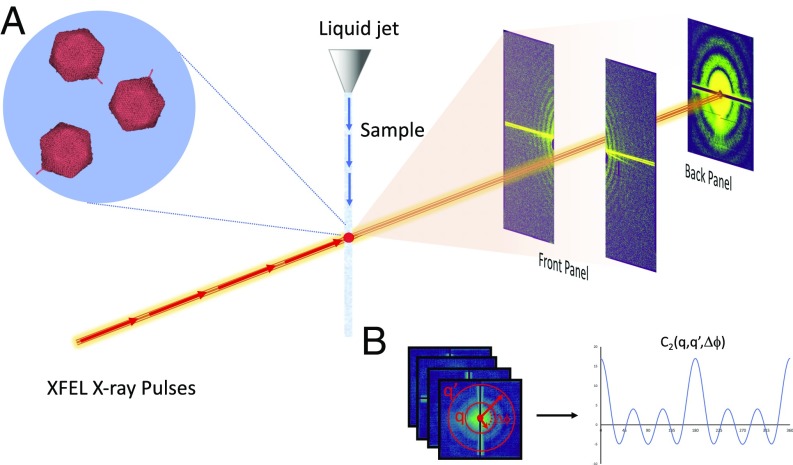
An FEL-based fluctuation scattering experiment can be performed by using a liquid jet to inject a continuous stream of particles in solution into the pulsed X-ray beam (4, 12), Fig. 1A. Unless the sample concentration is very low, each shot will contain multiple copies of the sample of interest and can thus be considered a hit, in sharp contrast to single-particle diffraction methods performed in the gas phase, where the hit rate is typically far below 1% (13). Several thousand of these femtosecond timescale diffraction snapshots are collected in this fashion and are used to compute angular intensity correlations, averaged over many independent snapshots, as

$$C_2\left(q,q\prime ,\mathrm{\Delta }\varphi \right)=\frac{1}{2\pi N}\sum _{k=1}^N{\int }_0^{2\pi }{J}_k\left(q,\varphi \right)J_k\left(q\prime ,\varphi +\mathrm{\Delta }\varphi \right)d\varphi ,$$ [1]

where $J_k$ is the $k$th diffraction snapshot, $N$ is the number of images, $q$ and $q\prime$ are a pair of radial coordinates in inverse resolution, and $\varphi$ is an angular coordinate for the detector pixels around the direct beam (Fig. 1B). It can be shown that the molecular structure of the scattering species is directly related to the intensity correlation function $C_2\left(q,q\prime ,\mathrm{\Delta }\varphi \right)$ through its Legendre series expansion

$$C_2\left(q,q\prime ,\mathrm{\Delta }\varphi \right)=\sum _{l\ge 0}{B}_l\left(q,q\prime \right)F_l\left(q,q\prime ,\mathrm{\Delta }\varphi \right)$$ [2]

with

$$F_l\left(q,q\prime ,\mathrm{\Delta }\varphi \right)=P_l\left({\cos \theta }_q{\cos \theta }_{q\prime }+{\sin \theta }_q{\sin \theta }_{q\prime }\cos \mathrm{\Delta }\varphi \right)$$ [3]

and $P_l$ is the $l$th-order Legendre polynomial, ${\theta }_q=\arccos \left(q\lambda /\left(4\pi \right)\right)$, and $\lambda$ is the incident wavelength. The Legendre coefficients $B_l\left(q,q\prime \right)$ are, up to a scaling factor, related to the spherical harmonic expansion coefficients $I_{lm}\left(q\right)$ of the 3D intensity function $I\left(\mathbf{q}\right)$ of the single particle, via (1)

$$B_l\left(q,q\prime \right)=k_l\sum _{m=-l}^l{I}_{lm}\left(q\right)I_{lm}^{*}\left(q\prime \right),$$ [4]

where the scale factor $k_l$ is proportional to the square number of particles per snapshot for $l=0$ and proportional to the number of particles for $l>0$. The 3D intensity is related to the electron density $\rho \left(\mathbf{r}\right)$ of the molecular structure via $I\left(\mathbf{q}\right)=|\widehat{\rho }\left(\mathbf{q}\right){|}^2$, where $\widehat{\rho }\left(\mathbf{q}\right)$ is the Fourier transform of $\rho \left(\mathbf{r}\right)$, and $\mathbf{r}$ and $\mathbf{q}$ are the real- and Fourier-space coordinates, respectively.

Fig. 1.

(A and B) An FXS experiment is performed by taking femtosecond X-ray diffraction snapshots of particles in solution (A) and computing angular intensity correlations over many images (B). The diffraction patterns consist of data collected on two detector pairs, the so-called back and front detectors, named after their location relative to the sample, capturing both the low and higher angular sections of the data. Artifacts, such as high-intensity streaks originating from the interface between the liquid jet and vacuum of the experimental chamber (depicted as yellow overloaded pixels), are present on both pairs and need to be identified and masked out before computing correlations.

Eq. 2 provides an orientation-invariant relation between the measured correlations and the underlying molecular structure which does not require determination of the particle orientations, as is needed for single-particle methods (14–16). Instead, reconstruction of the electron density from the correlations can be formulated as a hyperphase problem for recovering the 3D intensity from the $B_l$ coefficients in addition to the classical phase problem for recovering the electron density from the intensity (1). It has been shown that the 3D molecular structure can be reconstructed, without the need of symmetry constraints, by solving both these phase problems simultaneously using the multitiered iterative phasing (M-TIP) algorithm (17).

Results and Discussion

Here we present experimental intensity correlations, the data analyses, and the associated ab initio derived 3D structure of the Paramecium bursaria Chlorella virus [PBCV-1; diameter of 190 nm (18)] obtained from a solution scattering experiment at the atomic, molecular, and optical (AMO) instrument (19) of the LCLS, using an X-ray energy of 514 eV and with an estimated 50–200 virus particles per snapshot (20). The experiment was performed in the so-called water window, to maximize the scattering contrast of the virus with respect to the buffer. The data consist of close to $1\times 10^5$ diffraction images, collected in less than 15 min using a pulse rate of 120 Hz.

Several data-processing steps are required to obtain a high-quality correlation dataset. The data processing includes image selection, dark-current and background corrections, and beam center refinement, as well as streak and pixel masking. An initial selection of images is made on the basis of the total photon count, allowing one to easily reject anomalous diffraction events and shots containing little or no diffraction signal from the sample (20). The presence of high-intensity diffraction streaks, originating from the vacuum–liquid column interface, dominate the intensity correlation function in absolute terms and have to be masked out. The location of these streaks varies from shot to shot and is determined for each image individually. Due to general instrument instabilities, the beam center is not stationary and is reestimated for each individual diffraction pattern by maximizing centrosymmetry on each diffraction pattern. Images with an excessive beam center shift are rejected to avoid introduction of systematic errors.

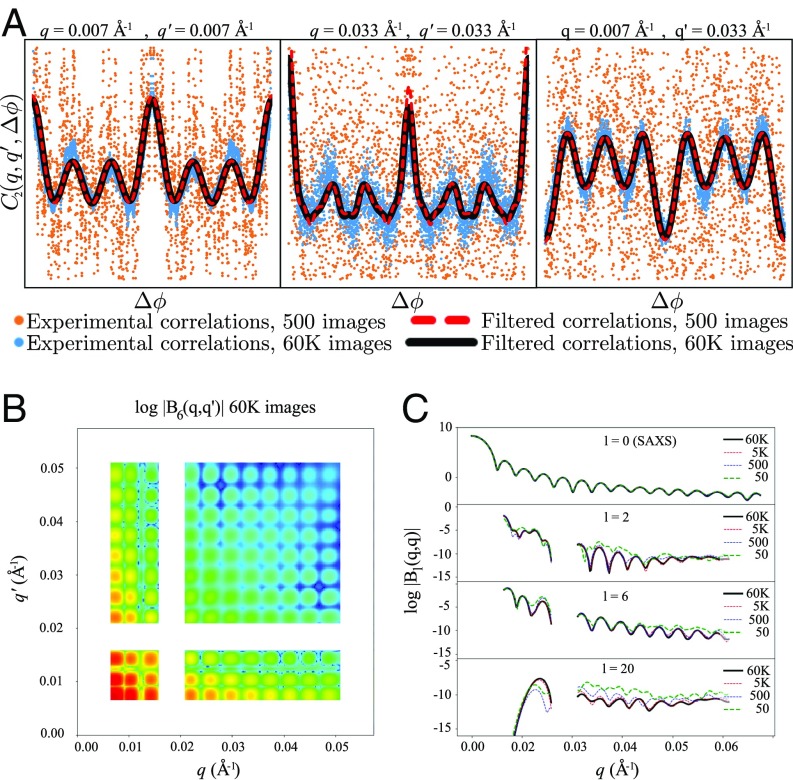
After the above corrections have been performed, the 1D SAXS curve and the average correlation function in Eq. 1 are computed using standard interpolation and fast Fourier transform (FFT) methods. To correct for the effect of angular anisotropy in the background caused by the experimental setup, the correlation of the mean diffraction image is subtracted (21). Although this last step removes the 0th-order term of the Legendre expansion in Eq. 2, it can be recovered directly from the SAXS curve. Data processing is carried out on both scattering patterns of the sample–buffer mixture, as well as on the buffer alone, ultimately resulting in two correlation and two SAXS datasets. Because of noise and interparticle interference effects due to the fully coherent X-ray beam, systematic peaks appear in the correlations when $q\approx q\prime$ and $\mathrm{\Delta }\varphi \approx 0$, and also when $\mathrm{\Delta }\varphi \approx \pi$ in regions where the Ewald sphere is sufficiently flat, and are masked out of the analysis. The buffer datasets are then scaled, offset corrected, and subtracted from the sample datasets, where the scale and offset parameters are chosen to maximize the consistency between the buffer-corrected correlations and the Legendre decomposition in Eq. 1 and yield a proper power-law decay in the SAXS curve. A multitiered iterative noise-filtering (M-TIF) algorithm (Materials and Methods) is then applied, enforcing consistency with the theory of band-limited functions to simultaneously remove noise from the correlation and SAXS datasets (Fig. 2A) and extract the $B_l$ coefficients (Fig. 2 B and C).

Fig. 2.

The correlations computed from the experimental PBCV-1 correlation data are subjected to the filtering procedure as outlined in detail in Materials and Methods. As can be seen in A, correlations obtained using 60,000 images (blue dots) or those obtained using 5,000 images (orange dots) result in very comparable correlations after the M-TIF technique (red and black lines). (B and C) The $B_l\left(q,q\prime \right)$ surface for $l=6$ obtained from the filtering procedure is shown B, as are the diagonal terms $B_l\left(q,q\right)$ for l equal to 0, 2, 6, and 20 from correlation data derived from various image counts (C). The gaps in the q range of the data (B and C) are regions deemed unreliable due to limited spatial coverage of the detectors in the diffraction setup.

The procedure described above was used to obtain correlation and SAXS datasets from the PBCV-1 solution scattering data, using 60,000 diffraction patterns; two subsets of 30,000; and subsets of 5,000, 500, and 50 diffraction patterns. The buffer dataset was at a fixed size of 30,000 shots. Images for which the refined beam center did not fall within 2 pixels of the mean beam center were excluded from the analysis. The results of the M-TIF noise filtering on the 60,000- and 500-image correlation sets are shown for autocorrelation (Fig. 2 A and B) and cross-resolution terms (Fig. 2C). Selected $B_l\left(q,q\prime \right)$ surfaces are shown as well for the correlations from the 60,000-image dataset. The $B_l\left(q,q\right)$ curves in Fig. 2C show the gradual decline in quality of the data as the number of images used is decreased.

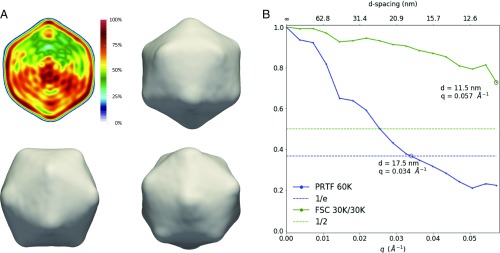
The M-TIP algorithm was applied to the Legendre expansion coefficients $B_l\left(q,q\prime \right)$ from the 60,000-image dataset to reconstruct the electron density of the virus. In particular, 96 independent M-TIP reconstructions, each initialized with different random starting densities, were aligned and combined to form an average model (Fig. 3A) and calculate reconstruction statistics (Fig. 3B). The resolution of the reconstruction was estimated using a phase-retrieval transfer function (PRTF) and a Fourier shell correlation (FSC) function (see SI Appendix for more details), using the two 30,000-image subsets, with established cutoffs of $1/e$ (22) and 0.5 (23), respectively (Fig. 2C). The PRTF indicates a resolution of 17.5 nm, while the FSC indicates 11.5 nm. The discrepancy between these two metrics reflects subtle differences in what they measure, as well as the arbitrariness in the established cutoff values. In this case, the resolution of the reconstruction was likely limited by the absence of a large region of correlation data near the gap between the back and front panels and toward the corners of the front panel (Fig. 2B and SI Appendix, Fig. S4), which were masked out due to the presence of large systematic detector issues. More details on the reconstruction and resolution estimates are provided in Materials and Methods and SI Appendix. Additional reconstructions were performed using the 5,000-, 500-, and 50-image subsets. The FSC between the 5,000- and 60,000-image datasets is almost identical to the FSC between the two 30,000-image datasets, which indicates that only 5,000 images are needed to reconstruct structural details to 11.5 nm resolution (SI Appendix, Fig. S5).

Fig. 3.

(A and B) Using the $B_l\left(q,q\prime \right)$ coefficients obtained from the filtering procedure from the 60,000-image PBCV-1 dataset, multiple independent M-TIP–based structure determinations were performed, and the resulting structures were aligned and subsequently averaged. (A) The resulting density has an approximately icosahedral outer capsid, with an asymmetric distribution of scattering mass inside the capsid. (B) The resolution of the reconstruction is approximately 11.5 nm on the basis of a FSC of two independent data halves (30,000 each) or 17.5 nm on the basis of the PRTF.

The reconstructed density has an approximately icosahedral capsid and a largely disordered interior, biased toward the lower half of the capsid. Near the fivefold vertex where less material seems present, there is evidence of a small quantity of more dense material. This type of asymmetry in the capsid has been seen in other reconstructions of large viruses as well, both from FEL data and in electron microscopy (24, 25). The dense region close to the fivefold axis may be related to the spike complex of PBCV-1 that facilitates cell-wall attachment and penetration; see SI Appendix text and SI Appendix, Fig. S6 for more details. No symmetry was enforced in the reconstruction algorithm or data-processing steps.

Conclusions

The results presented here provide confirmation of the feasibility of fluctuation X-ray scattering on biological solution scattering data with many particles per shot, originally proposed by Kam in the last century (1, 2). The synergy between developments in ultrabright X-ray lasers, sample delivery technologies, modern area detectors, and algorithms has resulted in providing an experimental method for the investigation of molecular structure in near-native conditions. Here we have shown that angular correlations can be accurately extracted from multiple-particle fluctuation X-ray scattering experiments and can be used to reconstruct ab initio macromolecular structure with more detail than typical SAXS reconstructions (SI Appendix, Fig. S7). Furthermore, we have demonstrated that redundancies in the correlation data can be exploited to drastically reduce the number of snapshots required to obtain a robust dataset compared with previous proposed estimates (11).

The upcoming availability of even brighter and faster FEL facilities, such as the European XFEL and LCLS-II, offers the possibility of collecting much larger volumes of higher-quality correlation data outside the water window, extending the resolution of the data, and thereby allowing high-throughput studies on smaller biomolecules at subnanometer resolution. However, several challenges still need to be overcome to extend the resolution of the data, understand signal requirements at higher X-ray energies, reduce systematic error in the data, and optimize sample delivery. Further advances in detectors, algorithms, and sample delivery offer the potential to transform fluctuation X-ray scattering into a routine imaging technique poised to study the structure and dynamics of macromolecules that are not optimally accessible via traditional methods.

Materials and Methods

Sample Preparation and Data Collection.

PBCV-1 samples were prepared using standard protocols, outlined in detail elsewhere (20, 26). Diffraction data were collected at the AMO instrument (19, 27) at the LCLS (3), using the Center for Free Electron Laser Science-Advanced Study Group (CFEL-ASG) multipurpose instrument (28) on a solution of PBCV-1 at a concentration of 5 $\times {\mathrm{10}}^{11}$ particles/mL, delivered at the interaction region via a diameter gas dynamic virtual nozzle (GDVN) (4, 12) at a flow rate of 20 $\mathrm{\mu }$L/min, with an approximate jet diameter of 5 $\mathrm{\mu }$m. The FEL was tuned to 512 eV (24.2 Å) with an electron bunch length of 100 fs and a repetition rate of 120 Hz and was focused to a spot size of 20–25 $\mathrm{\mu }{\mathrm{m}}^2$. The scattered X-rays were collected on two pairs of p-n junction charge-coupled device (pnCCD) detectors (28–30). Further details on experimental geometry are described elsewhere (20).

Data Analysis.

Data reduction and corrections.

Images were preprocessed using the CFEL-ASG Software Suite (CASS) (31). Electronic background due to offsets in the multiple-readout channels of the pnCCD was removed by subtraction of the mean intensity per pixel from a set of dark frames. Pixels that measured a high signal due to nonlinear detector response were corrected using an empirical formula as described in ref. 30. Consistently defective and hot pixels were masked out in every frame. This included areas of the detector that experienced stray scattering from the liquid jet, pixels along the outer edges of the detector containing shadows from the beamline apparatus, and unresponsive pixels.

There were variations in gain and dark current between the four quadrants of the CCD. Fluctuations in gain are normally corrected for by flat-field measurements, but were unfortunately not available for this experiment and could not be applied in this case. Variations in dark current are corrected by using a common-mode–like correction on a shot-by-shot basis by first subtracting the median of intensities in a region of interest (ROI) at the edge of each quadrant from pixels in the respective quadrant and then adding the mean of the four median intensities to all pixels in the frame. The center of each diffraction pattern is obtained by assuming centrosymmetry for the low-$q$ region and maximizing the Pearson correlation coefficient of unmasked centrosymmetric pixels. Each frame is then interpolated to a polar grid by using nearest-neighbor interpolation.

Image selection.

In an FXS experiment on samples of moderate dilution there is no need for traditional hit finding as required in single-particle imaging methods (32, 33) and serial femtosecond crystallography (SFX) (34) since almost every shot is a hit. However, datasets do contain some blank frames when no diffraction pattern was collected and/or there were buffer-only snapshots, aggregated particles, overload-dominated images, and other nonideal hits. Removal of such data frames is essential to obtain the highest possible overall data quality in the final processed dataset. A selection of images to be used for further processing was performed using the following criteria:

• i)Only frames with beam centers that have an offset of 2 pixels from the average center are selected.
• ii)The total intensity of each snapshot is calculated by summing intensities of unmasked pixels. Frames with intensity below a minimum or above a maximum threshold are rejected to remove blank and high-intensity frames, respectively.
• iii)The integrated intensities over a ring of 50 pixels at the first and second radial maxima and their median values are calculated. Frames where the integrated intensities are above or below the calculated median values by a certain threshold are rejected. This helps in removing frames from buffer and aggregated particles.

Image selection based on the above steps was done on frames from the back detector, and the corresponding frames from the front detector were selected. Whereas conditions i and ii are sample independent, the last criterion critically depends on the sample used. This sample-specific selection criterion can be replaced by a more general level of similarity to the expected SAXS curve in future experiments.

Dynamic masking.

One of the drawbacks of experiments in solution using a liquid jet as opposed to those using an aerosol injector (35, 36) is the stray scattering from the jet itself, which appears as high-intensity streaks radiating from the center of the diffraction pattern. Due to the stochastic nature of the liquid jet, the streak varies from shot to shot, requiring one to redetermine the streak mask for every individual shot.

Diffraction streaks are identified in polar-angle–resolved integrated intensity plots $P\left(\varphi \right)$:

$$P\left(\varphi \right)=\sum _{j=1}^{N_q}{I}_i\left(q_j,\varphi \right).$$ [5]

Polar angles are classified as containing a streak, if the associated Z score of the polar-angle–resolved integrated intensity is above a certain threshold $t$:

$$\frac{P\left(\varphi \right)-{⟨P\left(\varphi \right)⟩}_{\varphi }}{{⟨{\left(P\left(\varphi \right)-{⟨P\left(\varphi \right)⟩}_{\varphi }\right)}^2⟩}_{\varphi }^{1/2}}>t.$$ [6]

The bracketed terms ${⟨f\left(x\right)⟩}_x$ in Eq. 6 signify the mean value, but could be replaced with a more outlier-robust estimator like a median operator. The threshold $t$ is typically set to 3.

Correlations.

The calculation of the correlations of the diffraction patterns largely follows the procedure outlined in ref. 21, with the addition of including correction terms for masked angular ranges. The total scattered intensity $I_t^i\left(q,\varphi \right)$ on the $i$th diffraction pattern can be modeled by the sum of the isotropic signal $I_{\text{SAXS}}^i\left(q\right)$, the fluctuations from the sample $I_{\text{FXS}}^i\left(q,\varphi \right)$, and a nonisotropic signal from the background $I_b^i\left(q,\varphi \right)$,

$$I_t^i\left(q,\varphi \right)=I_{\text{SAXS}}^i\left(q\right)+I_{\text{FXS}}^i\left(q,\varphi \right)+I_b^i\left(q,\varphi \right),$$ [7]

where

$$I_{\text{SAXS}}^i\left(q\right)={⟨I_t^i\left(q,\varphi \right)⟩}_{\varphi }.$$ [8]

Since the background signal is instrument related, it can be approximated as being the same for every shot; i.e., $I_b^i\left(q,\varphi \right)\to I_b\left(q,\varphi \right)$. It can also be assumed that the intensity fluctuations when averaged over a large number of frames converge to zero. Hence, after subtracting the isotropic part of the signal and averaging over a large number of frames $N$, we get

$$I_b\left(q,\varphi \right)=\frac{1}{N}\sum _{i=0}^N\left[I_t^i\left(q,\varphi \right)-I_{\text{SAXS}}^i\left(q\right)\right],$$ [9]

and

$$I_{\text{FXS}}^i\left(q,\varphi \right)=I_t^i\left(q,\varphi \right)-I_{\text{SAXS}}^i\left(q\right)-\frac{1}{N}\sum _{i=0}^N\left[I_t^i\left(q,\varphi \right)-I_{\text{SAXS}}^i\left(q\right)\right].$$ [10]

This approach, originally proposed in ref. 21, is, under very general assumptions, equivalent to the approach outlined by ref. 8, but does not require the costly calculation of all cross-image correlation functions. In the following steps, the masked portions of $I_{\text{FXS}}^i\left(q,\varphi \right)$ are set to 0.

Following refs. 1 and 2 the correlation function for intensity fluctuations and the binary mask $I_{mask}^i\left(q,\varphi \right)$ and the normalized correlation function are computed as

$$C_2^i\left(q,q\prime ,\mathrm{\Delta }\varphi \right)={⟨I_{\text{FXS}}^i\left(q,\varphi \right)I_{\text{FXS}}^i\left(q\prime ,\varphi +\mathrm{\Delta }\varphi \right)⟩}_{\varphi }$$ [11]

$$C_{2,\text{mask}}^i\left(q,q\prime ,\mathrm{\Delta }\varphi \right)={⟨I_{\text{mask}}^i\left(q,\varphi \right)I_{\text{mask}}^i\left(q\prime ,\varphi +\mathrm{\Delta }\varphi \right)⟩}_{\varphi }$$ [12]

$$C_{2,\text{norm}}\left(q,q\prime ,\mathrm{\Delta }\varphi \right)=\frac{{⟨C_2^i\left(q,q\prime ,\mathrm{\Delta }\varphi \right)⟩}_i}{{⟨C_{2,\text{mask}}^i\left(q,q\prime ,\mathrm{\Delta }\varphi \right)⟩}_i}.$$ [13]

Similarly the SAXS signal is computed as

$$I_{\text{SAXS}}\left(q\right)={⟨I_{\text{SAXS}}^i\left(q\right)⟩}_i.$$ [14]

Since the scattering signal from the PBCV-1 solution is a result of scattering from the PBCV-1 particles and the buffer, it is important to account for the buffer contribution to the correlation function and SAXS. The background subtraction and additional masking procedure used is described in SI Appendix.

Data Quality.

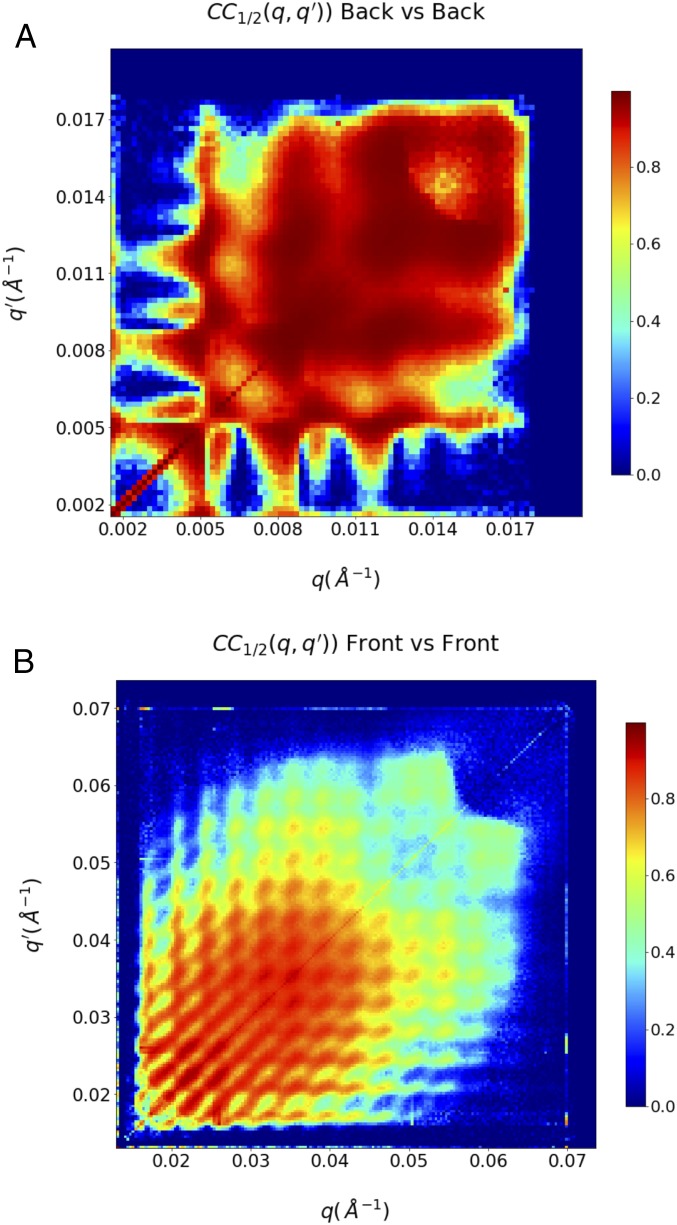
The quality of the processed data can be gauged by computing correlation coefficients between $C_2\left(q,q\prime ,\mathrm{\Delta }\varphi \right)$ curves obtained from two separately processed data halves (37). These correlation coefficients, denoted as ${\text{CC}}_{\frac{1}{2}}\left(q,q\prime \right)$, can then be classified as originating from $q,q\prime$ pairs from either the back or front detectors alone (Fig. 4) or coming from both (SI Appendix, Fig. S3). The correlations indicate the correlation data extend to ∼0.056 ${\AA }^{-1}$ (112 Å), where the consistency of the autocorrelation between the two data halves rapidly drops below 50% (SI Appendix, Fig. S3). Additional data quality analyses are presented in SI Appendix and in SI Appendix, Figs. S2–S4.

Fig. 4.

Correlation coefficients between two independent data halves collected on the back (A) and the front detector (B) indicate that there are usable data to approximately 0.056 ${\AA }^{-1}$. Data landing between the front and the back panel have not been recorded and have been masked out during the final reconstructions. The very low resolution data have been excluded from the analyses as well, due to the presence of systematic errors in the data. The correlation of the data halves for ($q,q\prime$) pairs falling on different detectors is show in SI Appendix, Fig. S3.

M-TIF.

We filter both the SAXS and correlation data using the theory of bandlimited functions (38). In particular, given a particle with a minimal bounding sphere of diameter $D$, one can express the spherical harmonic coefficients of the intensity function in an infinite series

$$I_{lm}\left(q\right)=\sum _{k=1}^{\infty }{I}_{lm}\left(q_{l,k}\right)S_{l,k}\left(q\right),$$ [15]

where the kernel functions are defined as

$$S_{l,k}\left(q\right)=\frac{2u_{l,k}{j}_l\left(qD\right)}{\left(u_{l,k}^2-{\left(qD\right)}^2\right)j_{l+1}\left(u_{l,k}\right)},$$ [16]

where $j_l\left(\cdot \right)$ is the $l$th-order spherical Bessel function, $u_{l,k}$ is the $k$th nontrivial zero of $j_l$, and $q_{l,k}=\frac{u_{l,k}}{D}$. The kernel function $S_{l,k}\left(q\right)$ has the property that the majority of its mass is concentrated around $q_{l,k}$, allowing truncation of the series to a small number $K_l$ of terms, which can be approximated as the smallest value of $k$ such that $u_{l,k}>qD$. As explained in the following subsections, enforcing Eq. 15 using a small number of terms can be used to reduce the noise in both the SAXS and the correlation data. An integral part of the filtering is the masking of correlations that are impacted by systematic effects as outlined in SI Appendix text and SI Appendix, Fig. S1.

SAXS filtering.

Since the SAXS data give $I_{\mathrm{S}\mathrm{A}\mathrm{X}\mathrm{S}}\left(q\right)=\frac{1}{2\sqrt{\pi }}{I}_{00}\left(q\right)$, they can be expressed using a small number of kernel functions via Eq. 15 with $l=m=0$. The filtered SAXS data are then obtained by applying Tikhonov regularization on Eq. 15, weighted down by the angular variances of the average image, with $l=m=0$ to determine the expansion coefficients, and then evaluating the resulting series expansion. The Tikhonov parameter was chosen based on the methods in ref. 39.

Correlation filtering.

The correlation function can be expressed as the Legendre decomposition (due to the subtraction of the isotropic component in Eq. 10, the $l=0$ term is absent from the Legendre expansions of the calculated correlations)

$$C_2\left(q,q\prime ,\mathrm{\Delta }\varphi \right)=\sum _{l=2}^{l_{max}}{B}_l\left(q,q\prime \right)P_l\left({\cos \theta }_q{\cos \theta }_{q\prime }+{\sin \theta }_q{\cos \theta }_{q\prime }\cos \mathrm{\Delta }\varphi \right),$$ [17]

where, up to a scaling factor,

$$B_l\left(q,q\prime \right)=\sum _{m=-l}^l{I}_{lm}\left(q\right)I_{lm}*\left(q\prime \right).$$ [18]

By combining Eqs. 15 and 18, it follows that

$$B_l\left(q,q\prime \right)=\sum _{k_1=1}^{K_l}\sum _{k_2=1}^{K_l}{G}_{l{k}_1{k}_2}{S}_{l,k_1}\left(q\right)S_{l,k_2}\left(q\prime \right),$$ [19]

where $G_l$ is a Kronecker product of the expansion coefficients in Eq. 15. This implies that $G_l$ has rank of at most $2l+1$ and nonnegative eigenvalues; i.e.,

$$G_{lkk\prime }=\sum _{i=1}^{2l+1}{\lambda }_{li}{v}_{li{k}_1}{v}_{lik\prime }^T,\hspace{1em}{\lambda }_{l\hspace{0.17em}1},\dots ,{\lambda }_{l\hspace{0.17em}2l+1}\ge 0.$$ [20]

By enforcing these three sets of decompositions in Eqs. 17, 19, and 20, we can greatly reduce the amount of noise in the system. This is accomplished by iterating over several steps of Tikhonov regularization to enforce Eq. 17, pseudoinversion to enforce Eq. 19, and principal component analysis to enforce [20]. For the Tikhonov regularization step, Eq. 17 was weighted down for each pair $\left(q,q\prime \right)$ by the number of available $\mathrm{\Delta }\varphi$ measurements multiplied by estimates of the error in the correlation curve. Both the error estimates and the Tikhonov parameter were computed based on the methods used in ref. 39. This process yields a set of expansion coefficients $G_{l{k}_1{k}_2}$ which are then evaluated using Eqs. 17, 19, and 20 to determine filtered correlations and $B_l$ coefficients, which are used in subsequent reconstructions.

Structure Determination via M-TIP.

A reconstruction of the electron density of the virus was obtained via the M-TIP algorithm, as described in ref. 17, without using any symmetry assumptions. Specific settings of the algorithm are detailed in SI Appendix. The quality of the reconstructions is gauged via PRTF and FSC plots as defined in SI Appendix. The results of the reconstruction on datasets with decreasing number of images are shown in SI Appendix, Fig. S4. As can be seen from the associated PRTFs and FSC between the reconstructions, the quality of the model derived from 60,000 images is nearly identical to that obtained from the 5,000-image dataset. Both the 500- and 50-image count correlation data-derived models retain an icosahedral character, but lose detail.