Machine learning material properties from the periodic table using convolutional neural networks

Convolutional neural networks directly learned chemical information from the periodic table to predict the enthalpy of formation and compound stability.

Abstract

In recent years, convolutional neural networks (CNNs) have achieved great success in image recognition and shown powerful feature extraction ability. Here we show that CNNs can learn the inner structure and chemical information in the periodic table. Using the periodic table as representation, and full-Heusler compounds in the Open Quantum Materials Database (OQMD) as training and test samples, a multi-task CNN was trained to output the lattice parameter and enthalpy of formation simultaneously. The mean prediction errors were within DFT precision, and the results were much better than those obtained using only Mendeleev numbers or a random-element-positioning table, indicating that the two-dimensional inner structure of the periodic table was learned by the CNN as useful chemical information. Transfer learning was then utilized by fine-tuning the weights previously initialized on the OQMD training set. Using compounds with formula X₂YZ in the Inorganic Crystal Structure Database (ICSD) as a second training set, the stability of full-Heusler compounds was predicted by using the fine-tuned CNN, and tungsten containing compounds were identified as rarely reported but potentially stable compounds.

Introduction

Machine learning is concerned with the automatic discovery of patterns in data through the use of computer algorithms.1 Then these patterns can be used to do data classification or value prediction. With growing experimental and simulated dataset size for materials science research,2–5 the ability of algorithms to automatically learn and improve from data becomes increasingly useful. Various types of machine learning algorithms, such as regression,6 support vector machines,7 random forest,8,9 least absolute shrinkage and selection operator (LASSO),10 kernel ridge regression,11 and neural networks,12–15 have recently been applied to materials research.

Among these machine learning algorithms, convolutional neural networks (CNNs)16 have been very attractive in recent years due to their great success in image recognition, such as ImageNet competition17 and AlphaGo.18 A CNN consists of multilayer neural networks, of which at least one layer employs a mathematical operation called “convolution” to enable the CNN to extract high-level features from data directly. Compared to many other algorithms which require artificial features based on domain knowledge, a CNN needs relatively little pre-processing as the features can be learned from the data. This is particularly useful when the features are difficult to be exactly defined.19 Unlike their long-used basic forms such as perceptron and fully connected neural networks,12,13 CNNs have been used for solving solid state problems very recently. The applications include, for instance, molecular fingerprint learning,20 property prediction of small molecules (ChemNet),21 inorganic crystal structure classification,22 and phase transition identification in condensed-matter.23 They clearly demonstrate the learning ability of CNNs. Another advantage of neural networks is that they are easy to utilize in transfer learning,24 which means that a neural network first learns from a large database with inexpensive labels (e.g., first principles calculation results), and then it is fine-tuned on a small dataset where much fewer labeled samples are available (e.g., experimental data). This technique can be used to overcome the data scarcity problem in materials research, and it has been applied to property prediction of small molecules21 and crystalline compounds25 very recently.

In this work, the powerful feature extraction ability of CNNs was used to directly ‘read’ the periodic table. This was done by using the periodic table as an input feature, which we referred to as ‘periodic table representation (PTR)’. Such a representation is different from others in the literature.26 In other machine learning models, the artificial sub-angstrom-level descriptors are usually atomic properties such as the atomic number, valence electronic states, and atomic mass/radius. These properties of one element closely relate to its position in the periodic table. Therefore, the two-dimensional layout of the periodic table can represent these individual atomic properties as a whole, and the mapping from element positions to material properties can be learned by CNNs. Full-Heusler compounds were chosen to demonstrate our approach of CNNs and PTR. Heusler compounds are important materials in sustainable technologies such as thermoelectric conversion.28 Stability prediction of Heusler compounds has been done in the literature using machine learning methods,8,29 chemical models30 and density functional theory calculations.31,32

Methods

Training datasets

Two training datasets were used. The first one was a density functional theory (DFT) calculated training dataset, taken from the Open Quantum Materials Database4 (OQMD) v1.1. The OQMD is a freely downloadable database containing nearly all the chemical-feasible L2₁ structure (Cu₂MnAl-type, shown in Fig. 1a) full-Heusler compounds. Compositions with lanthanides were excluded from our training set because the highly localized 4f electrons are difficult to treat with established DFT methods. Rare earth elements were also deliberately excluded in previous studies responding to the global need to reduced rare earth content.31 The training dataset had 65 710 entries, and each entry had a X₂YZ type chemical formula, a lattice parameter and enthalpy of formation. There were in total 52 elements in this dataset.

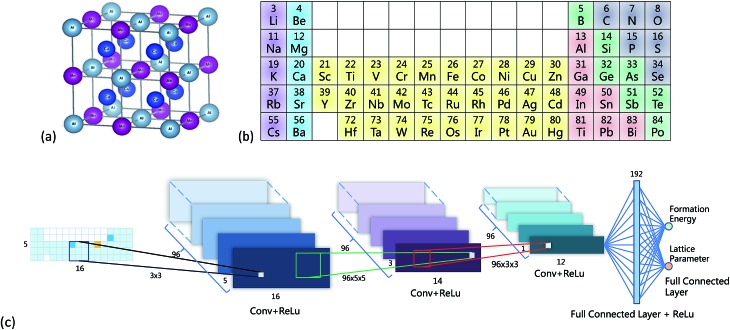
Fig. 1. (a) Crystal structure of an L2₁ full-Heusler compound, created by using VESTA.27 (b) Illustration of the periodic table representation. Colors were only guide for the eye, not used by the CNN. (c) Structure of the CNN.

Two data preprocessing methods, whitening and bound, were used to normalize the target values, i.e. the lattice parameter and enthalpy of formation. The distributions of the target values were generally consistent with Gaussian distribution, as shown in Fig. s1.† Therefore, whitening could be used to normalize the targets to a standard Gaussian distribution with a mean of 0 and a variance of 1. Whitening was performed using y* = (y – m)/σ, where m and σ were the mean and standard deviation of the training data, respectively, calculated from the Gaussian distributions shown in Fig. s1.† As a comparison to whitening, the target values were also linearly normalized into a bound of [–1, 1] by mapping the maximum to 1 and the minimum to –1.

The second training dataset was extracted from the Inorganic Crystal Structure Database (ICSD). All compounds with a formula of X₂YZ, where X, Y or Z is one element in the 52 elements, were extracted. In this training set the target value was the type of crystal structure, i.e. compounds with the L2₁ full-Heusler structure were labeled “1”, and compounds with other competitive structures were labeled “0”. From ICSD, 555 compounds were extracted, of which 216 had target values of “1” and 339 had target values of “0”.

Periodic table representation (PTR)

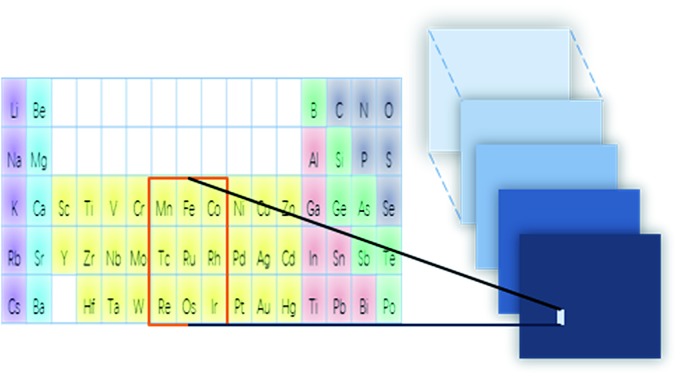
Fig. 1b shows the PTR with 5 rows and 16 columns, and the representation of Cu₂AlMn is shown in the leftmost part of Fig. 1c as an example. For simplification, only rows or columns containing the 52 elements were included. This representation was denoted by a matrix A and was initialized by –1, and the blank squares were set to 0 (Fig. 1b). Two tricks were used to make the CNN work smoothly: (1) the value of the corresponding X element position in matrix A was set to 28 and the values for Y and Z were set to 14. This made the mean of A equal to zero. (2) Matrix A was multiplied by 20 to mimic a digital image to ease the training process of the CNN.

Other representations were also used as comparisons. PTR contained chemical information in the two-dimensional arrangement of elements. So the representations without a two-dimensional layout or elemental order (Mendeleev numbers) or both were considered, as shown in Fig. s2.† (1) The element positions were totally randomized in a two-dimensional table (Figs. s2a and b†), so the elemental order was lost. (2) The elements were aligned in one line in a descending order according to Mendeleev numbers (Fig. s2c†), so the two-dimensional layout was lost. (3) The elements were totally randomized in one line (Figs. s2d and e†), so both were lost. For each randomized representation, two tables were given to make the comparison more reliable.

Convolutional neural networks (CNNs)

Fig. 1c gives the neural network structure. The CNN model had two parts, one was the feature extractor including the first three pairs of convolutional layers and ReLU (Rectified Linear Unit) layers33 which have a nonlinear activation function f(x) = max(0, x). The other part was the data predictor with two full connection layers. Pooling layers were not included in this model. As the PTR mimicked a digital image, the hyperparameters used for the CNN were chosen empirically following those used for typical image recognition CNNs in the machine learning literature.19 To be more specific, the size of convolutional filters was 3 × 3, 5 × 5 and 3 × 3 for the three convolutional layers, respectively, and the stride was set at 1. The number of convolutional maps in each convolutional layer was set to 96, and correspondingly there were 192 neurons in each full connection layer. Padding was used for the input of the first two convolutional layers by adding zeros around the border, i.e. a zero padding of one, to preserve as much information as possible in the early layers. Therefore, the input volumes were 18 × 7, 18 × 7 and 14 × 3 for the three convolutional layers, respectively, and the size of generated convolution maps after convolution was 16 × 5, 14 × 3 and 12 × 1, respectively. The most common type of convolution with a linear filter was used, and the value of each filter was learned during the training process. In the training phase, the output of the CNN fitted the ground truth, and the smooth L₁ loss was used to evaluate the fitness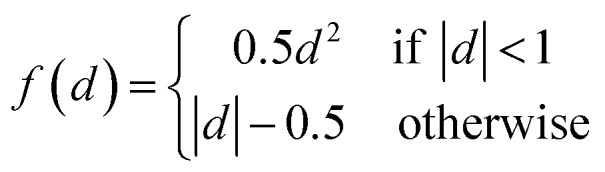where d is the difference between the ground truth and the prediction of the CNN. Then the learned neural network was applied to predict material properties in the test phase. The networks in all experiments were trained for 100 000 iterations using Nesterov's accelerated gradient34 with a starting learning of 0.01, step rate decay with a step size of 10 000, a weight decay of 0.005 and a momentum of 0.85. The OQMD training samples were randomly divided into eight groups, which were training sets with 1000 (1k), 5000 (5k), 10 000 (10k), 20 000 (20k), 30 000 (30k), 40 000 (40k), 50 000 (50k) and 60 000 (60k) samples, respectively, and the remaining samples were used as test sets to evaluate the finally trained network. Parameters including m and σ in the whitening procedure were estimated for each training set, respectively, and they were applied to the corresponding test set during the test phase.

When training on datasets from the OQMD, multi-task CNNs were trained to output the lattice parameter and enthalpy of formation simultaneously. CNNs with only one output neuron in the output layer were also trained separately on the lattice parameter or enthalpy of formation as comparisons. These three CNNs were independently carried out with stochastic weights as the initialization of the CNNs.

Transfer learning

Transfer learning was used to predict the stability of all the full-Heusler compounds in the OQMD. The CNN trained on the OQMD cannot be directly used to predict stability. From the point of view of the energy landscape, the free energy of all the competitive phases must be considered, while the CNN only had energy information about full-Heusler compounds. On the other hand, the ICSD dataset contains experimentally stable compounds, from which the CNN can learn stability information.35 Therefore, a second CNN was trained on the ICSD dataset for stability prediction, and its weights were initialized from those obtained for the previous CNN trained on the OQMD. This transfer learning technique can prevent overfitting, as the ICSD dataset was too small (555 entries) compared to the number of weights in the CNN. This CNN gave values in the range [0, 1], where “1” meant a stable full-Heusler phase.

Results and discussion

Prediction accuracy

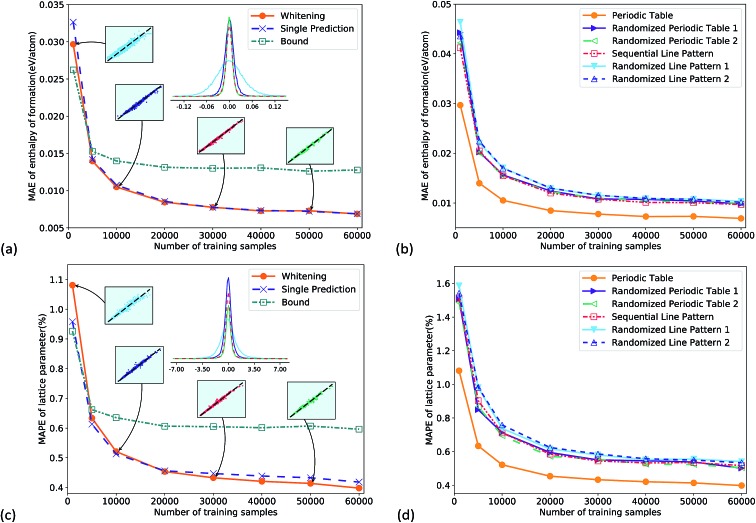
Fig. 2a gives the total performance of different CNNs as a function of training set size. All the CNNs were well trained as their training loss and test loss both converged with increasing iterations (Fig. s3†). For the two data pre-processing methods, the whitening normalization (orange circles) obviously outperformed the bound method (green square), and there was a considerable margin. The reason is that the whitening method statistically eliminated the bias of training data, by normalizing the data into a standard Gaussian distribution, while the bound method could not eliminate the bias. The multi-task CNN predicting both properties together had similar accuracy to the single output CNN. The prediction errors converged to a small value with increasing the number of training samples. The mean absolute error (MAE) reached 7 meV per atom for the enthalpy of formation in Fig. 2a, and the mean absolute percentage error (MAPE) reached 0.40% for the lattice parameter in Fig. 2c, which was comparable to the DFT error bar in a recent study.36 Such precision of the CNN demonstrated its good learning ability. It is worth noting that even for a much smaller training set of 5k samples, the prediction errors were 14 meV per atom (Fig. 2a) and 0.63% (Fig. 2c), respectively, only slightly lower than the best values. The probability distribution of prediction errors with 1k, 10k, 30k and 50k training samples is shown in the inset figures where the x and y axes are the ground truth and the predicted value, respectively. For display clarity 4000 test samples were randomly picked and plotted. They again indicated a systematic improvement of the predictive accuracy with increasing training set size. To make a comparison of accuracy vs. required training set size, a kernel ridge regression model was trained on the same dataset, using a vector representation like Fig. s2c.† The results show that at the same training dataset size, the accuracy of the CNN was twice that of kernel ridge regression (Fig. s4†).

Fig. 2. (a) Comparison of performance using two different target value normalization methods (i.e. whitening and bound methods) for the enthalpy of formation prediction using the multi-task CNN, while “single prediction” has only one output. Inset figures give prediction errors at different training sample sizes. (b) Comparison of prediction accuracy using six different representations for the enthalpy of formation prediction. (c) and (d) are for lattice parameter prediction.

Fig. 2b and d compare prediction errors using six different representations. The PTR outperformed all the other representations in the whole range; in other words, PTR was the best feature for the enthalpy of formation and lattice parameter predictions. Compared to the other five representations, the information carried by PTR was the two-dimensional layout and the Mendeleev numbers. The fact that PTR performed better not only means that the information was useful in the predictions, but also means that such information could be learned by CNNs. These statements are supported by physical chemistry and other machine learning investigations using atomic quantum numbers11 or Mendeleev numbers.13 Here we also show that the two-dimensional layout and Mendeleev numbers were both important, as shown in Fig. 2b and d.

For the line representations, the sequential line representation gave lower test errors than the randomized ones, which means that the CNN extracted some chemical information from the sequential line pattern. However, the difference between the test errors was quite small, especially for larger training sets. One reason can be that the CNN has been the most successful on a two-dimensional image topology,19 and it is less effective on line representations. In addition, the extraction of some important chemical information, e.g. the number of valence electrons, became more difficult on line representations compared with PTR.

Compared to previously reported handcrafted features,37 which should be optimized for specific machine learning problems, PTR directly learned features from the data and hence was more robust. PTR also had the potential to be incorporated with other features that cannot be captured at the element level, such as structural factors. It has recently been reported that CNNs can directly learn material properties from the connection of atoms in various types of crystal structures,38 and highly accurate prediction can be achieved. By integrating the CNNs39 using PTR and crystal structure based representation, structural features can also be included, which need further investigation.

Stability prediction

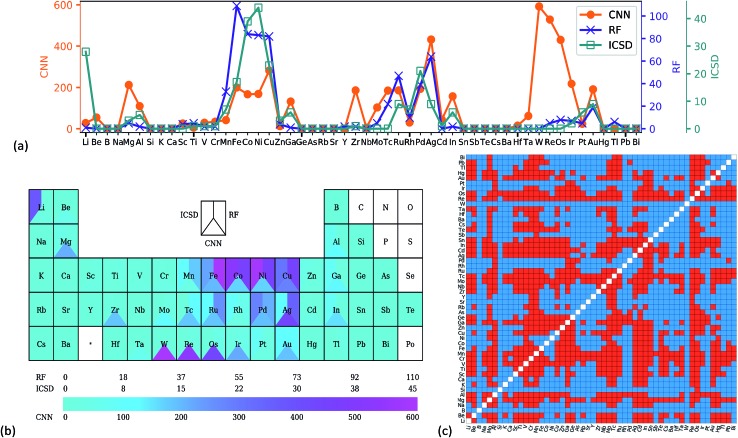
Transfer learning was utilized to predict the stability of all the full-Heusler compounds in the OQMD dataset, starting from the weights of the CNN trained on the 60k OQMD training set. Compounds with probability > 0.99 were considered as stable. Such a strict criterion was used to eliminate the 'false positive' results as much as possible. 5088 compounds were predicted to be stable and are listed in the ESI.† Fig. 3a shows the frequency of occurrence for each element on the X site in these X₂YZ compounds. Analysis of YZ sites is given in Fig. s5.† Two datasets were also considered as comparisons: 216 stable full-Heusler compounds from the ICSD and 667 compounds predicted by Oliynyk et al. using random forest (RF),8 for which the original dataset was modified to exclude rare earth metal containing compounds. In Fig. 3a, the ICSD and RF show very similar patterns, for example, a high frequency for Co/Ni/Cu and a low frequency for Na/K/Rb. This is not surprising as RF was trained on experimental datasets. For the CNN, while the general pattern was similar, there were some differences, especially the peak at tungsten. Contrast color can also be found for tungsten in Fig. 3b. The predicted stable full-Heusler W₂YZ compounds are shown in red colour in Fig. 3c, while blue colour means the formation of competitive phases. As Y and Z are equivalent in the full-Heusler structure, the heatmap is symmetrical.

Fig. 3. Number of stable X₂YZ full-Heusler compounds which have corresponding elements on the X site, shown in (a) a line chart and (b) the periodic table. The experiential data from ICSD and random forest (RF) results from ref. 8 are also shown. (c) Heatmap of stable W₂YZ compounds predicted by CNN transfer learning, and red means the compound is stable in the L2₁ full-Heusler form.

A comparison of stability prediction results using different OQMD training set sizes is shown in Fig. s6.† Generally, the stability prediction results were insensitive to the training set size. All the patterns are similar with some small deviations, and the patterns for 50k and 60k were nearly the same. To further demonstrate the similarity of the results for 50k and 60k training samples, and the heatmaps for the predicted stable full-Heusler W₂YZ are compared in Fig. s7.† The two heatmaps showed nearly the same pattern, indicating that the CNN had learned chemical information from the PTR, and transfer learning was effective to prevent overfitting.

The scarcity of tungsten containing full-Heusler compounds in the ICSD is probably due to synthesizability resulting from the good stability of tungsten. This is supported by the relatively higher enthalpy of formation for tungsten containing full-Heusler compounds shown in Fig. s8.† It is worth noting that high enthalpy of formation does not necessarily mean unstable,40 and probably high temperature and high pressure synthesis can help to synthesise these compounds. The CNN can find different patterns from the ICSD training set because that its weights were initialized on the OQMD training set, by utilizing transfer learning. And the PTR may enable the CNN to find latent features beyond atomic properties using the powerful feature extraction ability of the CNN. In other words, the combined information from the ICSD, OQMD and periodic table enabled the CNN to make such a stability prediction.

Conclusions

Periodic table representation (PTR) was used to train convolutional neural networks (CNNs), which can predict lattice parameters, enthalpy of formation and compound stability. By utilizing the powerful feature extraction ability of the CNN, information was directly learned from the periodic table, which was supported by comparison with the representation of randomized element positions. The CNN had the following characteristics. (1) Precise. The average prediction errors were comparable to DFT calculation error bars. (2) Multi-tasking. Two responses, i.e. lattice parameter and enthalpy of formation, can be simultaneously outputted by one CNN. (3) Transferable. When the training dataset is small, the CNN can be trained to start from the weight previously initialized on a much large training set, and hence information from both datasets can be used and the predictive accuracy can be improved. Our results suggest that the combination of PTR and CNNs has great potential for material property predictions.

Conflicts of interest

There are no conflicts to declare.