Stimulus-dependent hemodynamic response timing across the human subcortical-cortical visual pathway identified through high spatiotemporal resolution 7T fMRI

Abstract

Recent developments in fMRI acquisition techniques now enable fast sampling with whole-brain coverage, suggesting fMRI can be used to track changes in neural activity at increasingly rapid timescales. When images are acquired at fast rates, the limiting factor for fMRI temporal resolution is the speed of the hemodynamic response. Given that HRFs may vary substantially in subcortical structures, characterizing the speed of subcortical hemodynamic responses, and how the hemodynamic response shape changes with stimulus duration (i.e. the hemodynamic nonlinearity), is needed for designing and interpreting fast fMRI studies of these regions. We studied the temporal properties and nonlinearities of the hemodynamic response function (HRF) across the human subcortical visual system, imaging superior colliculus (SC), lateral geniculate nucleus of the thalamus (LGN) and primary visual cortex (V1) with high spatiotemporal resolution 7 Tesla fMRI. By presenting stimuli of varying durations, we mapped the timing and nonlinearity of hemodynamic responses in these structures at high spatiotemporal resolution. We found that the hemodynamic response is consistently faster and narrower in subcortical structures than in cortex. However, the nonlinearity in LGN is similar to that in cortex, with shorter duration stimuli eliciting larger and faster responses than would have been predicted by a linear model. Using oscillatory visual stimuli, we tested the frequency response in LGN and found that its BOLD response tracked high-frequency (0.5 Hz) oscillations. The LGN response magnitudes were comparable to V1, allowing oscillatory BOLD signals to be detected in LGN despite the small size of this structure. These results suggest that the increase in the speed and amplitude of the hemodynamic response when neural activity is brief may be the key physiological driver of fast fMRI signals, enabling detection of high-frequency oscillations with fMRI. We conclude that subcortical visual structures exhibit fast and nonlinear hemodynamic responses, and that these dynamics enable detection of fast BOLD signals even within small deep brain structures when imaging is performed at ultra-high field.

1. Introduction:

Functional magnetic resonance imaging (fMRI) is the highest spatial resolution method available for noninvasively measuring activity throughout the brain. A key advantage of fMRI is its ability to image activity in subcortical structures such as brainstem and thalamus in humans, as these areas are largely inaccessible through other noninvasive techniques such as EEG, and are rarely recorded from even in invasive intracranial studies. Imaging subcortical structures is more challenging than cortex, due to their small size and the reduced signal-to-noise ratio (SNR) of the receiver arrays in deeper regions of the brain. However, as the availability of ultra-high field (7 Tesla and above) MRI scanners increases, many sites now have improved sensitivity that can benefit subcortical imaging, leading to an increasing number of studies successfully using fMRI to track activity in small individual nuclei of the thalamus and brainstem (Bianciardi et al., 2015; Faull et al., 2015; Loureiro et al., 2016; Moerel et al., 2015; Satpute et al., 2013; Sclocco et al., 2017).

Since fMRI is an indirect technique, inferring neural activity through measurements of vascular and blood oxygenation signals, understanding the hemodynamic response properties of subcortical structures will be of increasing importance when studying their functional role within whole-brain circuits and in human cognition. The waveform of the hemodynamic response function (HRF) varies in shape and timing across cortical regions (Aguirre et al., 1998; Handwerker et al., 2004; Miezin et al., 2000) and across voxels within cortical regions (de Zwart et al., 2005; Saad et al., 2001), potentially reflecting different local distributions of vascular anatomy and morphology. HRF timing may also be different in thalamus and brainstem nuclei, as has been suggested by studies of the subcortical visual system. Studies in animal models (Lau et al., 2011; Yen et al., 2011) have shown that hemodynamic responses in the lateral geniculate nucleus (LGN) of the thalamus peak hundreds of milliseconds earlier than visual cortex, as measured in response to visual stimuli lasting several seconds. The superior colliculus (SC), a visual nucleus of the brainstem, is particularly challenging to image due to its small size of just a few millimeters, and its position immediately adjacent to the ventricles making it vulnerable to physiological noise, but several studies have nevertheless shown that its responses to visual stimuli can be detected in human fMRI (DuBois and Cohen, 2000; Loureiro et al., 2016; Savjani et al., 2018; Wall et al., 2009; Zhang et al., 2015). These studies have typically reported very small magnitude BOLD responses in SC, but with a time-to-peak that is faster than in visual cortex (Wall et al., 2009). The waveform shape of an assumed hemodynamic response function (HRF) is often used in fMRI analysis, and incorrect assumptions can lead to substantial inference errors (Gonzalez-Castillo et al., 2012; Greve et al., 2013; Lindquist et al., 2009; Uludağ, 2008), suggesting that different models will be needed for subcortical regions.

In addition to variation in the speed and amplitude of the hemodynamic response across regions, the hemodynamic response exhibits nonlinearities that are known to vary spatially across cortex. Nonlinearities in this context are changes in the hemodynamic response function shape that occur with changes in the stimulus, and can manifest as a difference in the apparent timing or amplitude of the hemodynamic response function. A major nonlinearity is seen when varying stimulus duration: brief stimuli elicit proportionally larger BOLD responses than would have been predicted from the response to slow stimuli (Glover, 1999; Miller et al., 2001; Vazquez and Noll, 1998; Yeşilyurt et al., 2008). While these observed response nonlinearities may be partially attributable to nonlinear neural responses, electrophysiological recordings demonstrate that the magnitude of the neural nonlinearity is not sufficient to explain the enhancement of fMRI responses (Janz et al., 2001; Li and Freeman, 2007), meaning that a hemodynamic nonlinearity must contribute. This nonlinearity varies across voxels (Birn et al., 2001; Pfeuffer et al., 2003), across cortical regions (Soltysik et al., 2004), and across individuals (Handwerker et al., 2004), and can lead to significant statistical errors if not characterized (Handwerker et al., 2004; Wager et al., 2005). Studies in the rat suggest that the nonlinearity of the hemodynamic response may be altered in subcortical structures (Devonshire et al., 2012). Characterizing this nonlinearity in thalamic and brainstem nuclei, particularly in the human brain, will be essential for applying ultra-high field fMRI to studying whole-brain circuits.

Understanding the temporal properties of the HRF is also needed to take advantage of recently developed methods for fast acquisition of fMRI data using simultaneous multi-slice (SMS) imaging (Breuer et al., 2005; Feinberg et al., 2010; Larkman et al., 2001; Moeller et al., 2010; Setsompop et al., 2012). These acquisition techniques allow fast (TR<400 ms) imaging of brain activity, and could potentially enable inference of faster neural dynamics. We have recently shown that surprisingly fast BOLD dynamics of up to 0.75 Hz can be detected in the human visual cortex using 7T fMRI, and that nonlinearities in the hemodynamic response support detection of high-frequency oscillatory signals (Lewis et al., 2016). The temporal properties and nonlinearities of the HRF in subcortical structures will therefore determine whether they also exhibit high-frequency signals. Characterizing spatial variation in hemodynamic response speed and nonlinearity will inform whether fast fMRI may be able to detect fast neuronal activity not just in cortex, but throughout the brain.

In addition to the importance of HRF properties for task-based fMRI, the temporal properties of local hemodynamic responses have major influences on resting state signals used to infer functional connectivity. A region with a faster HRF will appear to have signals that occur earlier in time, so temporal delays in the resting fMRI signal can originate from vascular rather than neuronal delays (Chang et al., 2008; David et al., 2008), and accounting for these delays in the analysis is needed. Furthermore, the local temporal properties of the hemodynamic response may influence the frequency content of the resting state BOLD signal, as narrower HRFs will produce more high-frequency power (Chen and Glover, 2015). Interpreting resting-state signals thus requires an understanding of the local hemodynamic properties of the brain regions being studied.

To examine the temporal characteristics and nonlinearities of the hemodynamic response within human subcortical structures, we focused on the visual system, measuring responses in SC, LGN, and V1 to visual stimuli of varying duration. We additionally tested whether high-frequency responses could be detected in LGN, by presenting oscillatory visual stimuli. We used deconvolution to estimate responses in each region, which relies on some assumptions of linearity. In particular, it assumes shift-invariant linearity, which has been demonstrated in cortex at long interstimulus intervals (ISIs), but different vascular anatomical properties could lead to different nonlinearities in subcortical structures. We therefore studied responses using both short ISIs (2–5 s), to analyze responses typical of event-related studies, and long ISIs (17–21 s) to allow sufficient time for responses to subside and reduce concerns about shift-invariant nonlinearity (as this property has not been examined in detail in subcortical structures).

Using this approach, we found that SC and LGN exhibit robust and fast responses at each stimulus duration, and that their temporal properties were not within the distribution of responses measured in visual cortex, suggesting fundamentally different response characteristics in these regions that should be taken into account in fMRI analysis. Each structure also exhibited a hemodynamic nonlinearity: responses to brief stimuli were faster and larger than would have been predicted by the responses to long stimuli. Despite differences in baseline hemodynamic timing, the nonlinearity in LGN was similar to that in cortex. Furthermore, LGN exhibited fast oscillations with a similar frequency response as in cortex, suggesting that hemodynamic nonlinearities result in relatively rapid BOLD signals even in small subcortical structures, due to the enhanced speed and amplitude of responses to brief neural activity. These results highlight fast response properties within subcortical structures that should be accounted for in analysis of fMRI data, and that could also be taken advantage of in future studies, as they may enable fast experimental designs that exploit the rapid nature of human subcortical hemodynamics.

2. Methods:

2.1. Subject population

All subjects provided informed written consent, and all procedures were approved by Massachusetts General Hospital’s Institutional Review Board. A total of 30 subjects were scanned and 28 subjects were analyzed. Two subjects were excluded, one for severe motion and one with poor behavioral performance who reported falling asleep during the experiment. The analyzed subjects were between the ages of 19–36 years (mean=24.8 years), with 17 female and 11 male.

2.2. MRI data acquisition

Experiment 1 (aimed at characterizing nonlinearity) analyzed 23 subjects, who were scanned on a 7T Siemens whole-body scanner with a custom-built 32-channel head coil array and birdcage head coil for transmit. Each session began with a 0.75 mm isotropic multi-echo MPRAGE (van der Kouwe et al., 2008) and ended with a whole-brain reference scan. The reference scan acquired a volume using the same fMRI acquisition parameters as the functional runs, except that it acquired additional slices to cover the whole brain in each subject, to aid with registration by providing whole-brain information with the same distortion patterns as the functional scans. Functional runs acquired 38 oblique slices, positioned to capture the superior colliculus (SC), lateral geniculate nucleus (LGN), and calcarine sulcus (primary visual cortex, V1). Functional scans consisted of a single-shot gradient echo SMS-EPI at 1.1 mm isotropic resolution (R=4 acceleration, MultiBand factor=2, matrix=174×174 full-Fourier, blipped CAIPI shift=FOV/2, TR=1.11 s, TE=26 ms, nominal echo spacing=0.79 ms, flip angle=70°, 4 dummy images). For seven of these subjects, no FLEET-ACS data were used, and occasional runs exhibited reconstruction artifact due to subject motion during acquisition of the pre-scan calibration in each run: a total of 7 runs (across all 7 subjects) were excluded manually due to this artifact. Runs lasted 260 seconds in these subjects. For the remaining 17 subjects, FLEET-ACS data were used (Polimeni et al., 2016), and no runs were excluded, with each run lasting 268 seconds. The FLEET-ACS technology was added to the functional sequence when it became available and reduced the effect of subject motion during pre-scan calibrations, enabling us to avoid the need to exclude runs in these subjects.

Experiment 2 (aimed at characterizing frequency responses) analyzed 5 subjects, with the same anatomical image acquisition as above. Functional runs were acquired as single-shot gradient-echo blipped-CAIPI SMS-EPI (Setsompop et al., 2012) with 15 oblique slices with 2 mm isotropic resolution (R=2 acceleration, MultiBand factor=3, 120×120 full-Fourier, blipped CAIPI shift=FOV/3, TR=227 ms, TE=24 ms, nominal echo-spacing=0.59 ms, flip angle=30°, 2 dummy images). Each run lasted 254 seconds.

2.3. Visual stimulus

Visual stimuli were presented using a DLP projector (Psychology Software Tools), with timing synchronized to the 60 Hz refresh rate of the stimulus delivery computer, onto a screen placed within the scanner bore near the top of the head. Subjects viewed the stimulus through an angled mirror placed above the eyes. Stimulus presentation code was written using Psychtoolbox (Kleiner et al., 2007).

Throughout all visual stimulation runs, subjects performed a simple visual fixation task. A red dot at the center of the screen alternated between light and dark red with switch times drawn from a uniform distribution between 0.8 and 3 seconds. Subjects were instructed to press a button on an MR-compatible USB button box every time the dot changed colour. Dot size was adjusted in a practice run prior to the beginning of the functional scans, targeting an 80–90% detection rate, and if performance dropped noticeably during the session, verbal feedback was provided to the subject.

In Experiment 1 (nonlinearity), the visual stimulus in either two or three runs (depending on total session length; see discussion at end of paragraph) consisted of a functional localizer in which a radial checkerboard counterphase flickering at 12 Hz was presented for 16 seconds, alternating with a blank gray screen for 13 seconds. Subsequent runs presented checkerboard stimuli lasting either 0.167, 0.5, 1, 2, or 4 seconds. In 12 subjects, stimuli lasting 8 seconds were also presented. Interstimulus interval (ISI) was manipulated across and within subjects, with 10 subjects viewing stimuli with 17–21 s ISIs; 9 subjects viewing stimuli with 2–5 s ISIs; and 4 subjects participating in both short and long ISI conditions: half of runs used ISIs between 17–19 s and half used ISIs between 2–3 s. The exact ISIs were generated pseudorandomly in Matlab for each subject, drawing from a uniform distribution across these time ranges, to provide temporal jittering. The total number of runs varied per subject, as we aimed to acquire as many runs as possible due to the small size of the investigated signals; we typically aimed to collect 12 runs (including localizers), but ended earlier if visual inspection suggested motion had increased, or if verbal checks with the subject suggested they were tired or uncomfortable, resulting in a median of 11 runs per subject (interquartile-range (IQR):10–12 runs).

In Experiment 2 (frequency response), stimuli consisted of counterphase flickering radial checkerboards presented continuously, beginning 14 seconds after the start of the scan. The luminance contrast of the checkerboards oscillated at a frequency of interest throughout the run as previously described (Lewis et al., 2016). A functional localizer run in each subject consisted of a checkerboard with luminance contrast oscillating as a sinusoid at 0.1 Hz. The remaining runs used a luminance waveform shaped as the square of a sinusoid, oscillating at either 0.2 Hz or 0.5 Hz. Subjects performed a median of 11 runs (IQR:11–12 runs).

2.4. ROI data analysis

Anatomical images were bias corrected to improve gray-white contrast at 7T (Polimeni et al., 2017). Surface reconstructions were then automatically generated using FreeSurfer (Fischl, 2012). ROIs were then defined using a combination of anatomical and functional information; the stereotyped anatomical locations of V1, LGN, and SC, were identified using the MEMPRAGE, and then further constrained to the subregions that were visually driven by our stimulus, using the functional localizer runs. None of the test data used for the HRF analysis were used for the ROI definition analysis to avoid circular inferences. This ROI definition aimed to identify voxels that were strongly visually driven by our stimulus within anatomically defined regions and therefore did not apply the same statistical thresholding across regions, as LGN and SC have lower SNR and this would lead to excessively small ROIs that discard visually driven areas due to the higher variance; however, all hypothesis testing is performed on the independent data and therefore verifies the significant visual drive to our identified ROIs.

Functional images were slice timing corrected using FSL slicetimer, adapted to handle SMS-EPI acquisitions, and motion corrected to the middle frame using AFNI 3dvolreg. No spatial smoothing was applied. To identify ROIs, the functional localizer runs were analyzed in FSL and combined with anatomical information. The localizer analysis in Experiment 1 was performed in FSL feat, high-passed with a 50 s cutoff, applied pre-whitening, and activation was modeled using the 16 s on/off stimulus waveform convolved with a canonical HRF (gamma function with mean lag 6 s, st. dev. 3 s, in FSL). The mean of the resulting contrast across all localizer runs was taken after transforming the statistical maps to the spatial reference frame of the MPRAGE (see below for details on registration procedures). The ROIs for the LGN and SC were then hand-drawn using the functional localizer contrast overlaid on the anatomical images as a guide. The ROI for visual cortex was computed by thresholding the z-statistic for the localizer runs with a value of 4.0 (analogous to cluster-corrected p<0.00007) and masking the contrast with the automatically generated V1 labels derived from Freesurfer. A deep ROI and a superficial ROI within V1 were generated by spanning the cortical depth between the gray-white boundary and the pial surface, and segmenting the 0–20% portion (deep-cortex surface) vs. 80–100% portion (superficial-cortex surface). The deep and superficial ROIs were then created by identifying voxels that were 80% filled by the deep-cortex or superficial-cortex surfaces. (Freesurfer command: mri_label2vol, using parameters: -fillthresh 0.8 and -proj frac 0 0.2 0.1 (deep) or 0.8 1 0.1 (superficial)). Any voxels appearing in both ROIs were excluded from the mask. The localizer analysis in Experiment 2 was performed in FSL feat, discarded the first 106 volumes to restrict the analysis to the steady-state oscillation, temporally high-passed with a 50 s cutoff, and prewhitened. A sine and cosine at the stimulus frequency were then used as covariates, and an F-statistic across the two contrasts was calculated. The LGN ROI was hand-drawn using the z-transform functional localizer map as a guide, and the V1 ROI was calculated automatically by thresholding the z-score at a value of 7.0 (analogous to cluster-corrected p<1×10⁻¹²); note that this higher threshold for these data is because of the higher SNR of the 2mm acquisition) and masking with the automatic V1 labels from FreeSurfer.

All analysis of functional data within the ROIs was performed by registering the ROI mask to the functional run, and preserving the timeseries information within its original spatial frame. Each functional run was aligned to the anatomical image using boundary-based registration (Greve and Fischl, 2009) using a rigid transformation with the reference scan as an intermediate volume (i.e., the partial-brain functional runs were first aligned to the whole-brain fMRI reference scan, and subsequently aligned to the anatomical scan). The ROI masks described above were transformed back into the spatial coordinates of each functional run by inverting the registration matrices. The mean timeseries across the ROI was then computed across these normalized timeseries within each voxel. The mean ROI timeseries was then spline detrended using piecewise knots every 50 seconds and normalized to percent signal change, using the mean value in the second half of the run as the baseline value. No prewhitening was performed on the functional data used for the HRF analysis to avoid altering the temporal properties of the test data.

2.5. Trial response estimation

Trial responses were calculated from the mean timeseries of the ROI using an FIR analysis, by modeling a series of non-overlapping delta functions lasting 0.25 s each, spanning a time window of varying duration following each stimulus presentation (windows: [16 20 22 24 28 30] seconds, corresponding to the [0.167 0.5 1 2 4 8] second stimuli). The ROI timeseries was upsampled to have a matching timescale to the delta function series. Additional covariates were included for each run consisting of a column of ones and a column linearly increasing from 0 to 1 to account for mean and linear drifts across runs. The parameter estimate for each delta function was then computed in Matlab by inverting the resulting matrix, yielding an estimated deconvolved trial response for each stimulus duration in each subject. The mean value between 0 and 1 seconds was subtracted from each trial response for display (Fig. 1b). Variance explained for individual subjects was calculated as the variance of the summed trial responses, divided by the variance of the mean data timeseries, in each ROI. An approximate measure of temporal SNR (tSNR) for each region was obtained by dividing the mean of the ROI timeseries by its standard deviation and averaging this value across runs (this calculation underestimates the true tSNR as variance is inflated by the stimulus-driven responses), reported in Supp. Table 1.

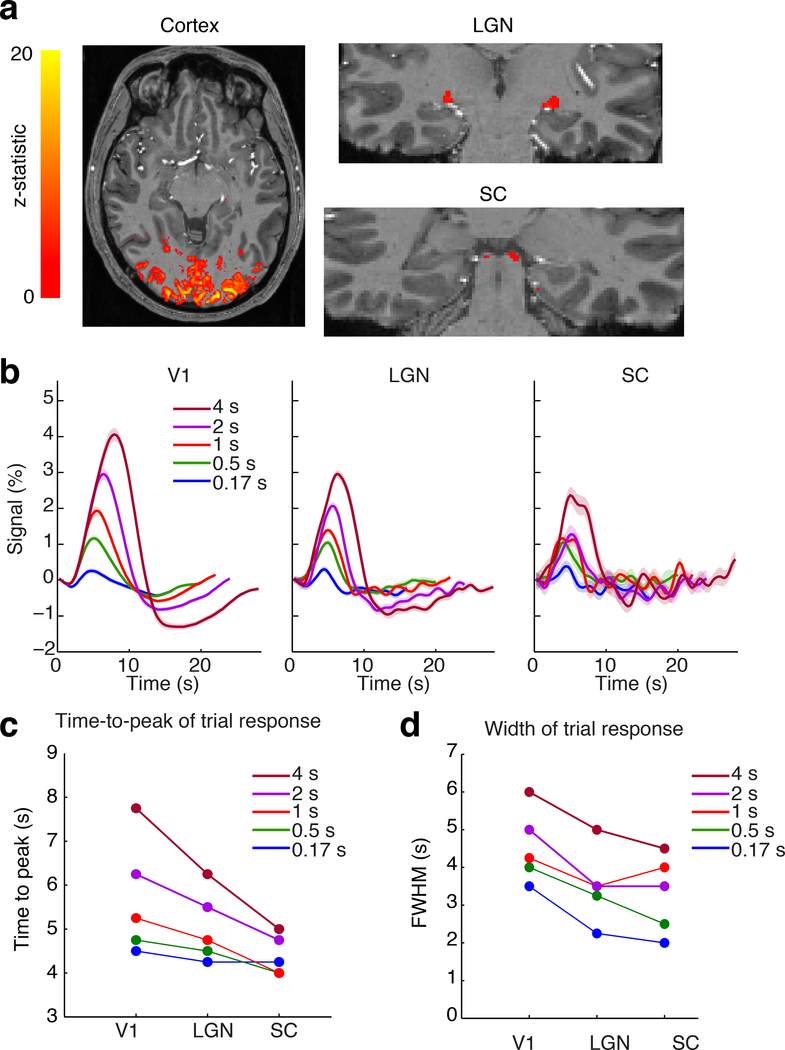
Figure 1: Visual-evoked activity in cortex, thalamus, and brainstem.

A) Activation map from a representative subject in the localizer runs (16 s block stimulus) shows activity across visual cortex, LGN, and SC. B) Mean trial responses to stimuli of varying durations in each ROI. Shaded regions reflect standard error across subjects (n=23). C) Peak time of the trial response in each region for each stimulus duration, shows consistently increased response speed in subcortical structures. D) Full-width-half-maximum of the trial response shows narrower responses in subcortical structures, across stimulus durations.

2.6. Impulse response estimation

Impulse responses were deconvolved using FSL’s linear optimal basis set (FLOBS), calculated over the entire fMRI volume. The deconvolution operated on the signal timeseries using a separate waveform for each stimulus duration, yielding a “deconvolved impulse response” representing the hemodynamic response for a specific stimulus duration condition. This method takes into account the stimulus duration in order to estimate a deconvolved impulse response for each stimulus type, and the basis set imposes temporal smoothness priors to help regularize the estimation. When no neural nonlinearity was included, the input stimulus waveforms were flat. In the neural nonlinearity case (Supp. Fig. 1), the stimulus waveform was calculated as stim(t)=1+0.25exp(−t/12), where t is time since stimulus onset, to approximate a ~20% decay in neural activity in response to longer stimuli based on prior studies (Janz et al., 2001; Li and Freeman, 2007); this form is similar to that used in previous models (Buxton et al., 2004). The resulting parameter estimates for each basis function were then averaged over the ROI, and the final impulse response was computed by taking the sum of these basis functions weighted by the parameter estimate values. Since the deconvolution is sensitive to noise, this analysis was restricted to runs with long (>16 s) ISIs, as deconvolutions in subjects with only short ISIs sometimes yielded physiologically implausible results due to the overlap in BOLD responses across closely spaced trials (total analyzed for impulse responses: n=14 subjects). To obtain confidence intervals and perform statistical testing, we conducted a bootstrap resampling 1000 times over subjects, as described below.

2.7. Waveform parameter and nonlinearity estimation

Shape parameters for the trial response waveforms across the group were calculated by first taking the mean waveform across all subjects, and then computing the time-to-peak (TTP), full-width-at-half-maximum (FWHM), and area values. Trial responses were baseline corrected by subtracting the mean value between t=0 and t=2 s from each response. For area and peak computation across conditions, in which we aimed to compute magnitude of the response relative to its most negative value, the trial response value at the timepoint 2 seconds post-stimulus was subtracted from each estimated trial response prior to calculating area and amplitude, as illustrated in Fig. 2a. The timepoint t=2 s was selected because it typically reflected the most negative value within the baseline period, enabling us to assess peak-to-peak magnitude and area, but overall conclusions were similar when selecting t=0 or t=1 s. The peak was then selected as the maximal timepoint in the trial response. The TTP was estimated as the time of the peak relative to stimulus onset; FWHM was estimated as the times at which the response reached and fell below half the value of TTP; and the area was computed numerically as the integral of the response waveform between 2 seconds post-stimulus until the first timepoint after the peak at which the waveform fell below its baseline value. Onset times were defined as the first time at which the trial response was larger than 0.1% and remained above this threshold until reaching the peak response value.

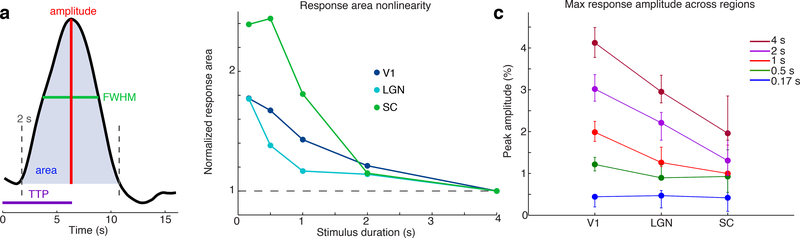
Figure 2: Nonlinear amplitude modulation of the trial response across stimulus durations in each ROI.

A) Schematic of parameter estimation from the trial response. B) Area of the trial response for each ROI and stimulus duration shows a nonlinearity in which shorter stimuli elicit proportionally larger responses. Area is normalized to the value of the 4 s stimulus. C) The peak amplitude of the trial response declines with shorter stimulus duration in each region. For the longest stimulus, V1 has larger responses than SC, but for the shortest stimulus there is no significant difference across regions. Error bars indicate 95% confidence intervals drawn from bootstrap across subjects (n=23 subjects).

Confidence intervals for the trial response waveform parameters were computed by resampling across subjects with replacement, drawing 1000 bootstrap samples. In each bootstrap sample, parameters were randomly drawn to create a resampled group with the same size as the original dataset (same number of subjects). The waveform parameters were recomputed on the mean of this new sample, and the reported 95% CI reflects the 2.5th and 97.5th percentiles of these resampled parameter values. A small proportion of such bootstraps (<1.5%) yielded a waveform for which TTP could not be defined; these were discarded. Statistical testing for a progressive change in waveform parameters across regions was performed by taking the difference of the mean value across stimulus durations for each bootstrap sample, and then testing for significant differences across each region, using Bonferroni correction for multiple comparisons across regions. Statistical comparisons of the nonlinearity between regions were performed by analyzing the magnitude of each response normalized by the stimulus duration. If responses are linear, these normalized magnitudes will fall on the line y=1, whereas nonlinear responses will deviate from that line (Fig. 3d). Magnitude of nonlinearity was thus calculated as the best-fit straight line to the normalized magnitudes, and then statistics between regions were calculated as the difference in the slope of this line (i.e. steep negative slope=highly nonlinear, with large responses to brief stimuli; slope of 0 = linear).

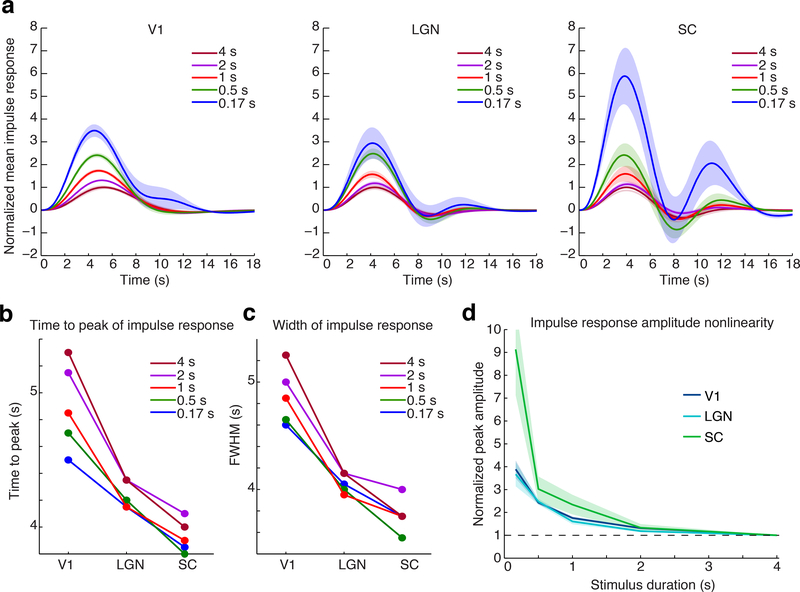
Figure 3: Deconvolved impulse response shows nonlinearity in timing and amplitude.

A) Mean impulse response across subjects for each ROI and stimulus duration, normalized to the peak amplitude of the response to the 4 second stimulus. Shaded region is standard error across subjects (n=14). B) Mean time-to-peak of the impulse response: each structure exhibits temporal nonlinearities, with faster responses to shorter stimuli. C) Mean full-width-half-maximum of the impulse response. D) Nonlinearity of the impulse response amplitude across ROIs shows similar amplitude nonlinearity in LGN and V1, and stronger nonlinearity in SC. Amplitudes are normalized to the value for the 4 s stimulus. Black dashed line indicates the linear response as a reference, shaded region is standard error across subjects (n=14).

The same shape parameters were also estimated from the impulse response waveform. The estimated impulse responses were smooth and originated at zero due to the nature of the FSL basis functions; the waveform parameters were therefore estimated without any baseline correction procedures. The reported waveform shape parameters (Fig. 3b,c) were computed on the mean impulse response across subjects to improve accuracy. Statistics for the waveform parameters were computed with the bootstrap as above. The amplitude nonlinearity was estimated as the slope of the change in peak amplitude of the impulse response across stimulus durations within each subject, and statistical differences in slope were calculated by comparing the subject-level nonlinearity estimates across regions.

2.8. Voxelwise temporal lag estimation

The response lag time for each individual voxel was estimated in the localizer run after the preprocessing described above. In Experiment 1, where the localizer consisted of a 16 s on/off checkerboard stimulus, a standard response prediction model for the mean response timecourse was constructed by convolving the square wave of the stimulus presentation with the SPM canonical HRF. Each voxel timeseries was then upsampled to 0.05 s time resolution, the first 50 interpolated timepoints were discarded, and the results were cross-correlated with the response prediction model with lags ranging from −3 to 3 seconds. The lag value with maximal cross-correlation was taken as the local lag estimate for that voxel. For Experiment 2, where the localizer was a 0.1 Hz sinusoidal oscillation, the local lag was estimated as the phase of the best-fit sine and cosine basis functions.

2.9. Simulations

The predicted response to an oscillatory stimulus was modeled numerically by convolving a sinusoidal input with an HRF. The HRF was taken as the deconvolved impulse response in either V1 or LGN, in the 0.167 s (‘fast HRF’) or 2 s (‘reference HRF’) trial condition. In the linear models (Fig. 4a), the HRF was convolved with stimuli ranging from 0.05 Hz to 0.5 Hz, and the magnitude of the resulting oscillation was plotted. To quantify the frequency response (FR), the percentage ratio of responses at 0.5 Hz relative to responses at 0.2 Hz was reported. In the linear case, a single HRF was used for both stimulus frequencies. In the nonlinear case, the fast HRF was convolved with a 0.5 Hz stimulus input and the reference HRF was convolved with a 0.2 Hz stimulus input.

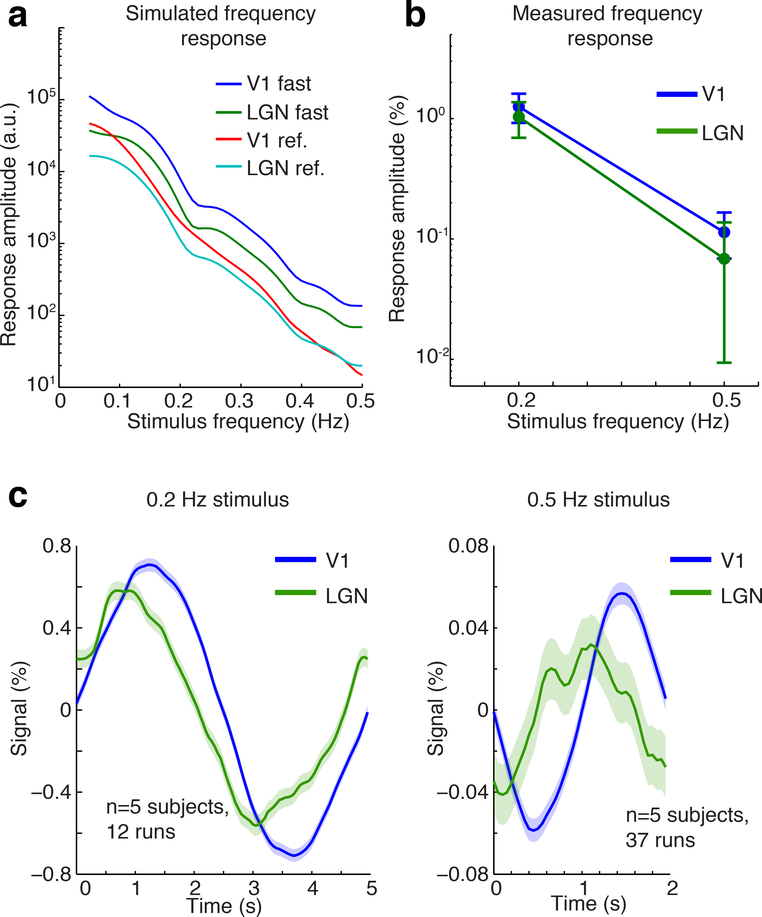
Figure 4: Detection of high-frequency oscillations within V1 and LGN.

A) Simulated frequency response with different HRFs, drawn from the impulse responses in V1 and LGN to 0.167 s (the ‘fast’ HRF) and 2 s stimuli (the ‘reference’ (ref.) HRF). The linear model predicts sharp drops for each HRF, but with less attenuation for the fast HRFs. B) Measured frequency response in V1 and LGN in response to oscillatory visual stimuli. Error bars are 95% confidence intervals - error bars for a small value can appear large when plotted on log scale, but oscillations were significant in each region. C) Mean fMRI response in V1 and LGN, locked to the oscillatory stimulus cycle. Oscillations are clearly detected in both structures, with a consistent phase offset such that LGN peaks earlier in time, consistent with its more rapid hemodynamic response.

2.10. Frequency response calculation

Analysis of the oscillatory responses was performed on the mean timeseries from the ROIs defined in the functional localizer, processed as described above. The timeseries for each region was upsampled to 10 Hz and the mean response across stimulus cycles was computed, discarding cycles within 14 seconds of stimulus onset to focus on oscillations around the plateau rather initial transients. The amplitude of the oscillation was calculated as the magnitude of the best-fit sine wave, fit using least-squares linear regression with a sine, cosine, and constant regressor. Confidence intervals for the amplitude were calculated by drawing a new sample of subjects, followed by a new sample of cycles, and recalculating the mean amplitude of a sine wave with the same phase as in the original dataset, resampling 1000 times. 95% CIs were drawn from the 2.5^th and 97.5^th percentile of these resampled magnitude values.

3. Results:

3.1. Nonlinear responses to brief stimulation across brainstem, thalamus, and primary visual cortex

We presented flickering checkerboards, inverting at 12 Hz, in order to induce sustained neural activity throughout the stimulus duration period (Janz et al., 2001; Liu et al., 2010). The functional localizer runs presented long-duration (16 s) visual stimulation to generate strong BOLD responses used to identify the stimulus-driven regions within V1, LGN and SC (Fig. 1a; mean ROI size=6516 voxels in V1; 92 in LGN; 20 in SC). We then calculated the trial responses of these ROIs in the runs using stimuli of varying durations, and found reliable activation of each region in response to brief stimuli as well (Fig. 1b). While individual subject variance was higher in subcortical regions due to their lower SNR (Supp. Fig. 1, Supp. Table 1), mean responses were nevertheless clearly detected across the group in each region (Fig. 1b). Comparing overall response characteristics demonstrated that BOLD responses were faster and narrower in LGN and SC than in V1 (Fig. 1c,d), consistent with previous studies using long stimulus durations (Wall et al., 2009). For a stimulus lasting 4 s, the mean BOLD response peaked at 5 s in SC, 6.25 s in LGN and 7.75 s in V1. We further observed that these earlier peak times were seen consistently at most stimulus durations (Fig. 1c), with peak timing in response to a 0.5 s stimulus of 4 s in SC, 4.5 s in LGN, and 4.75 s in V1. Across all conditions, responses had a significantly shorter time-to-peak (TTP) in SC than in LGN, and significantly shorter in LGN than in V1 (Fig. 1c, each p<0.0083 (corrected alpha), bootstrap). These responses were significantly faster across all conditions in the subset of subjects viewing stimuli with only short ISIs, as compared to those viewing only long ISIs (mean difference=0.8 s, Supp. Fig. 2, p=0.005, Wilcoxon signed-rank test), although the overlapping responses in the short ISI condition could potentially alter the observed response (see Discussion). Responses were also significantly narrower (Fig. 1d, smaller full-width-at-half-maximum (FWHM)) in V1 than in either subcortical structure (p<0.001, bootstrap) but did not differ between LGN and SC (p=0.29, bootstrap). These fMRI signal delays were far longer than the neural transmission delays between these structures, which are in the tens of milliseconds (Rockland et al., 1997; Schmolesky et al., 1998). These findings indicated a consistent progression in the timing of hemodynamic responses from brainstem to cortex, with the fastest responses in SC, later responses in LGN and latest in V1.

To assess the nonlinearity of the hemodynamic response across stimulus durations, we first calculated the area of the BOLD trial response (Fig. 2a), normalized by the response to a 4 second stimulus, in order to test whether the magnitude of the response area scaled proportionally with stimulus duration. Significant nonlinear responses were observed in each region (Fig. 2b, bootstrap 95% confidence interval (CI) of slope=[−0.30 −0.12] in V1; [−0.47 −0.01] in LGN; [−1.36 −0.03] in SC; where zero is linear). No significant difference in nonlinearity was observed between subjects in short ISI vs. long ISI conditions (Supp. Fig. 2, CI of slope difference=[−0.31 0.07] in V1, [−0.89 0.04] in LGN; [−1.82 3.01] in SC, bootstrap), although it is possible differences could be found with larger sample sizes. The nonlinearity in response area observed in V1 was consistent with previous studies (Pfeuffer et al., 2003; Soltysik et al., 2004), with subsecond stimuli yielding responses approximately twice as large as would be expected from the response to a 4 second stimulus, and the nonlinearity within LGN was of similar magnitude (Fig. 2b). The area nonlinearity in SC trended larger, with all subsecond stimuli eliciting increased amplitudes relative to the other ROIs, but the difference in area nonlinearity was not statistically significant due to high variance in area estimation in the SC trial responses (difference in slope between V1 and SC: CI=[−1.15 0.24]). Remarkably, the peak amplitude of the SC response to brief stimuli was as large as the response across the V1 ROI (peak response to 0.167 s stimulus: 0.44%, CI=[0.20 0.47]; LGN: 0.47%, CI=[0.18 0.60]; SC: 0.42%, CI=[0.10 0.95]), despite a twofold difference in response amplitude to longer duration stimuli (Fig. 2c, median diff. in 4 s response=1.67 percentage points, CI=[0.97 2.30], bootstrap).

The mean trial response varies due to stimulus duration, whereas the HRF is an idealized impulse response function that would be identical across stimuli if the responses were linear. To characterize the shape of the HRF, we next used smooth basis functions to deconvolve an impulse response for each stimulus duration and each ROI (Fig. 3a). While the trial responses were obtained using FIR analysis (minimizing assumptions about the response shape and avoiding temporal smoothing), the impulse response analysis used basis functions to constrain the deconvolved response to smooth, physiologically plausible waveforms. This analysis included only subjects that viewed stimuli with long (>17 s) inter-stimulus intervals (ISIs), to minimize errors in deconvolution due to overlapping response timecourses (n=14 subjects). The low SNR of the 0.167 ms stimulus introduced some noise in deconvolution, reflected in late timescale (>10 s) signals in SC that were not significant, but otherwise the mean impulse responses were consistent with our trial-based observations. The deconvolved impulse responses confirmed that the HRF was increasingly fast and narrow in deeper structures, with a shorter TTP (Fig. 3b, Table 2, Supp. Fig. 3; corrected p=0.006 (V1-LGN); 0.036 (LGN-SC); 0.018 (V1-SC); bootstrap) and smaller FWHM of the HRF in LGN and SC as compared to V1 (Fig. 3c, Table 2, corrected p=0.012 (V1-LGN); 0.13 (LGN-SC); <0.001 (V1-SC); bootstrap). In addition, the speed of the HRF depended on stimulus duration across brain regions, as it became increasingly rapid and narrow for shorter duration stimuli (Fig. 3b,c; Table 2; p=0.0197 for 0.5 s vs. 4 s stimulus, Wilcoxon signed-rank test). These results indicated relatively consistent nonlinearities in the temporal properties of the HRF across brain structures, as each region exhibited increased speed in response to shorter stimuli.

Table 2: Mean parameters and 95% confidence intervals (CI) for the impulse response across cortical depths.

Time-to-peak (TTP) and full-width-at-half-maximum (FWHM) are reported in seconds.

	0.167 s		0.5 s		1s		2s		4s
TTP:	Mean	CI	Mean	CI	Mean	CI	Mean	CI	Mean	CI
Deep	4.4	(4.15–4.75)	4.6	(4.33–4.90)	4.8	(4.45–5.15)	5.05	(4.75–5.38)	5.25	(4.90–5.60)
Superficial	4.55	(4.30–4.90)	4.75	(4.45–5.05)	4.9	(4.58–5.20)	5.1	(4.85–5.40)	5.3	(5.00–5.70)
FWHM:
Deep	4.5	(4.10–5.45)	4.55	(4.20–4.90)	4.75	(4.35–5.20)	4.9	(4.60–5.25)	5.15	(4.78–5.55)
Superficial	4.6	(4.20–5.60)	4.6	(4.30–4.90)	4.85	(4.55–5.25)	5.05	(4.70–5.40)	5.4	(5.05–5.85)

The magnitude of the HRF also increased with each decreasing stimulus duration, consistent with the nonlinearity observed in the trial responses where shorter stimuli elicited proportionally larger responses. The slope of the normalized impulse response magnitude was significantly less than zero for each brain region, indicating a nonlinearity in response magnitude with shorter stimuli inducing larger responses (Fig. 3d, Supp. Fig. 4, p<0.001 in each region, bootstrap). In addition, the nonlinearity was significantly different across regions (p=0.001, Kruskal-Wallis test): SC was significantly more nonlinear than cortex (p=0.003, Wilcoxon signed-rank test) and than LGN (p=0.004, Wilcoxon signed-rank test). Taken together, these results demonstrated that subcortical visual structures (LGN and SC) exhibit similar or larger nonlinearities than those previously reported in cortex, as brief stimuli elicit BOLD responses that are faster, narrower, and larger than would have been predicted by a linear model.

This deconvolution of the impulse response assumes that the neural response behaves linearly – i.e., that the impulse response function for the neural activity is identical across response durations, and that the neural activity can therefore be approximated by the stimulus timing waveform. Our flickering checkerboard stimulus is expected to induce sustained neural activity throughout the stimulus duration period, as a contrast inversion occurs every 167 ms, but nevertheless an approximate ~20% neural nonlinearity can be expected in V1 and LGN due to stronger neural responses at stimulus onset (Janz et al., 2001; Li and Freeman, 2007; Liu et al., 2010). These previous studies have also shown that this neural nonlinearity is not sufficient to explain the fMRI nonlinearity. To determine whether the neural nonlinearity could explain the fMRI response nonlinearity we observed, we repeated the impulse response deconvolution using a physiologically plausible nonlinear neural response, comprised of a 20% decrease in neural activity at longer stimulus durations. Even after incorporating this neural nonlinearity, we still found similar increases in the amplitude and speed of the hemodynamic impulse response to brief stimuli (Supp. Fig. 5), suggesting that changes in hemodynamic timing and amplitude with shorter stimulus durations occur across all three structures.

3.2. Frequency response of LGN and V1 measured at high temporal resolution

The nonlinear increase in the speed and amplitude of hemodynamic responses to brief neural activity can potentially enable detection of relatively fast oscillations in the BOLD signal, as the faster and larger hemodynamic response would enhance high-frequency content in the BOLD fMRI signal. These nonlinear properties are thought to contribute to fast (>0.2 Hz) oscillations measured in visual cortex (Lewis et al., 2016). Since LGN appeared to exhibit similar nonlinearity as in V1, we hypothesized that it might also be possible to detect >0.2 Hz oscillations in LGN despite the small size and lower SNR in this region. In addition, rapid and narrow HRFs can preserve highfrequency content even in a linear regime, if the temporal properties of the HRF are sufficiently fast. We modeled the predicted frequency response of V1 and LGN using the deconvolved impulse response from either the 2 s trials (the ‘reference’ HRF) or the 0.167 s trials (the ‘fast’ HRF), and simulated the response to oscillatory input ranging from 0.05 Hz to 0.5 Hz (Fig. 4a). Assuming linearity in the simulations (by using the same HRF for every stimulus frequency), each HRF predicted a steep drop in response amplitude, but with slightly greater preservation of high-frequency content for the fast HRF (Fig. 4a). We quantified the predicted frequency response (FR) as the response amplitude to a 0.5 Hz stimulus divided by the response to a 0.2 Hz stimulus, multiplied by 100 (i.e. percent scaling). We found stronger frequency responses were predicted for the fast HRF (2.1 FR in LGN; 1.7 FR in V1), as compared to the reference HRF (1.8 FR in LGN; 0.7 FR in V1). However, if we instead modeled the frequency response nonlinearly, using the fast HRF to model the response to a 0.5 Hz stimulus and the reference HRF to model the response to a 0.2 Hz stimulus, the predicted frequency response was stronger: 6.8 FR in V1 and 6.1 FR in LGN. We thus concluded that while the HRF waveform properties in V1 and LGN seen in response to long-duration stimuli are not sufficient to produce strong high-frequency responses, the nonlinearity in the shape of the impulse response leads to larger and faster HRFs in response to short stimuli, predicting stronger high-frequency signals both in visual cortex and thalamus.

To empirically test the predictions of these models, and determine whether it is possible to detect fast oscillatory signals within LGN, we measured the frequency response using oscillating visual stimuli, as done previously for V1 (Lewis et al., 2016). We presented stimuli with oscillating luminance contrast to induce oscillatory variation in neural activity at either 0.2 Hz or 0.5 Hz, imaging with lower spatial resolution (2 mm isotropic) to increase temporal resolution, and therefore focused on LGN and V1 (excluding SC). We found that significant oscillations were detected both in V1 and in LGN for both frequencies (Fig. 4b; V1: 0.2 Hz: 1.26%, CI=[0.95 1.61]; 0.5 Hz: 0.11%, CI=[0.07 0.16]; LGN: 0.2 Hz: 1.04%, CI=[0.71 1.38]; 0.5 Hz: 0.07%, CI=[0.01 0.13]). The phase of the oscillation in LGN preceded that in V1 (Fig. 4c), consistent with the faster time-to-peak of the HRF observed in LGN (Fig. 1b). The relative amplitude of the frequency response was similar across both regions, with 0.5 Hz oscillations that exhibited a 6.6 FR in LGN and 9.0 FR in V1 (Fig. 4b,c). These oscillations were several times larger than predicted by canonical HRF models (i.e. 5–7 times larger than the predicted 1.3 FR), consistent with previous reports (Lewis et al., 2016). These oscillations were also larger than predicted by our linear simulations (0.7–2.1 FR), and were instead near the simulated values when the hemodynamic response was modeled as faster and larger to brief stimuli (i.e. nonlinear). Since the reference HRF was faster and narrower in LGN, but the nonlinearity to brief stimuli was similar, these results suggested that a major determinant of the magnitude of high-frequency oscillations is the nonlinearity of the HRF when stimuli are brief. In contrast, the phase of the oscillations followed the same pattern as time-to-peak of the HRF, with oscillations in LGN exhibiting earlier phases.

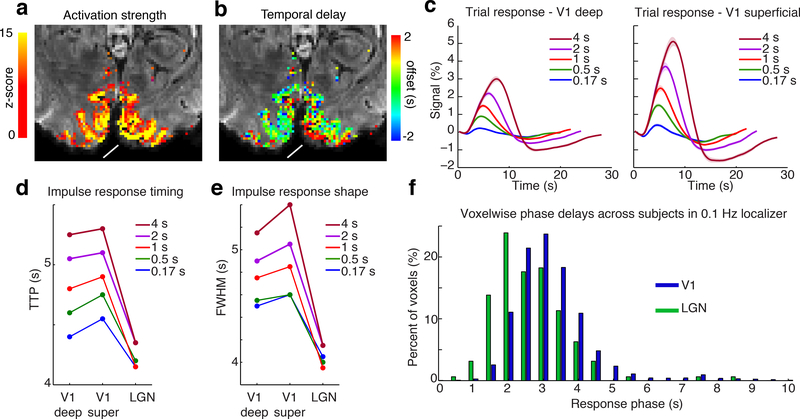
3.3. Thalamic responses precede cortical parenchymal responses

The local speed and amplitude of fMRI signals are influenced by the presence of large surface veins within individual voxels, which lead to larger, slower responses compared to those in the parenchyma, and could contribute to the observed differences between cortex and thalamus. To more finely separate out the effects of local vascular anatomy on nonlinear hemodynamic responses and frequency responses, we sorted voxels within V1 based on the relative delay of their responses measured in the Experiment 1 localizer run. We observed clear spatial structure in the temporal delays of individual voxels within V1, with later responses appearing to be near the cortical surface (Fig. 5a,b). To quantify the nonlinearity shift across this depth profile, we segmented two ROIs within V1, one spanning the 0−20% deepest portion of the cortical depth, and one spanning the 80−100% portion (i.e. superficial). Trial responses were 79% larger in the superficial ROI (Fig. 5c), consistent with previous findings showing that BOLD response amplitude increases from the white matter boundary to the pial surface (Polimeni et al., 2010; Ress et al., 2007; Siero et al., 2015). In addition, we found that the BOLD trial responses peaked earlier in the deep V1 voxels than in the superficial voxels (mean difference across durations=0.25 s), consistent with prior studies (Siero et al., 2011) and likely corresponding to faster responses within cortical gray matter parenchyma and slower responses in larger draining vessels on the cortical surface (Chen et al., 2011; Yu et al., 2012). Deconvolving the impulse response within deep and superficial V1 indicated that parenchymal responses were not simply shifted earlier in time (Fig. 5d), but also had a narrower shape (Fig. 5e), indicating more temporally precise and high-frequency signals might be expected in deeper layers (mean FWHM: 4.68 s deep V1; 4.83 s superficial V1, p=0.048, Wilcoxon signed-rank test). In addition, the superficial V1 amplitude response exhibited greater nonlinearity than the deep V1 amplitude response (p<0.001, Wilcoxon signed-rank test). However, impulse responses were still faster within the LGN than in the deep V1 voxels (mean TTP difference between deep V1 and LGN=0.58s, p=0.0003; mean FWHM difference=0.71 s, p=0.0004, Wilcoxon signed-rank test), suggesting that presence of surface vessels on the cortex is not sufficient to explain the different temporal properties across these tissues. To further test whether the distribution of voxel phase offsets in the LGN differed substantially from V1, we computed mean temporal delay values for each individual voxel in the 0.1 Hz oscillatory stimulus experiment. The distribution of temporal lags was consistently shifted earlier in LGN (Fig. 5f, Supp. Fig. 6, p<0.001 in 4/5 subjects, p=0.5 in 1/5 subjects, Kolmogorov-Smirnov test), again suggesting that the subcortical structures exhibit faster responses than even the fastest-responding segment of V1.

Figure 5: Distribution of temporal properties within cortex and LGN.

A) Example activation map within visual cortex in the localizer run (16 s block) in one subject shows stronger activation towards the pial surface. White arrow highlights a region of the surface with large and slow responses. B) Example temporal delay map within the same subject shows spatially structured delays, with larger delays towards the pial surface. C) Mean trial response in a V1 ROI defined to include deep (gray-white boundary) voxels and superficial (pial surface) voxels shows consistently larger and later responses in the deep ROI (n=23 subjects, shaded region is standard error). D and E) Time to peak (TTP) and full-width-half-maximum (FWHM) of the impulse response across deep and superficial V1 and LGN shows a gradient of peak timing (n=14 subjects). F) Distribution of temporal lags across structures in the 0.1 Hz oscillatory stimulus experiment shows heterogeneous properties across structures (n=5 subjects).

4. Discussion:

We identified a heterogeneous distribution of hemodynamic response timing and nonlinearity in subcortical and cortical visual structures, with consequences for imaging fast BOLD signals in these structures. The responses in subcortical structures were strikingly faster and narrower than in cortex. The bulk of these differences is likely due to hemodynamic effects, as the differences were hundreds of milliseconds, much larger than the expected delay in neuronal onset timing, which is on the order of tens of milliseconds (Rockland et al., 1997; Schmolesky et al., 1998). We also observed nonlinearities both in amplitude (with shorter stimuli eliciting proportionally larger responses) and in timing (with shorter stimuli eliciting faster and narrower responses) in both subcortical structures. These amplitude and timing nonlinearities supported detection of high-frequency fMRI signals within the LGN.

The responses we observed in SC were larger than reported in previous studies that carefully characterized SC responses (Anderson and Rees, 2011; Furlan et al., 2015; Katyal et al., 2010; Schneider and Kastner, 2005; Wall et al., 2009; Zhang et al., 2015), and did not require cardiac triggering or physiological noise reduction techniques, highlighting the benefits of ultra-high field for imaging these small subcortical structures (Loureiro et al., 2016). A large increase in sensitivity is provided at 7T, but even more beneficial may have been the reduction in partial volume effects provided by the small voxel size used here (Polimeni et al., 2017; Sclocco et al., 2017). The location of SC, at the upper boundary of the brainstem and adjacent to ventricles, makes it particularly vulnerable to physiological noise, and the spatially precise ROI defined here may thus have contributed to the large signals we observed by minimizing contamination from CSF signals. However, while the mean response amplitude in SC was large, stimulus-evoked responses within individual subjects were often still quite noisy and explained a lower proportion of the variance, due to the SC’s low SNR compared to other regions. This low SNR was expected, as physiological noise is high in these deep, small brainstem regions, but meant that averaging across subjects was needed in order to obtain reliable results, as the large stimulus-locked response was embedded in substantial noise. Our results demonstrate that the BOLD response in small subcortical nuclei can be nearly as large as that in cortex, and that higher spatial resolution acquisition can enhance these signals substantially.

Our results suggest there may be a progression of hemodynamic response speed within deeper brain structures, with brainstem and thalamus responses occurring faster. The LGN is a highly vascularized structure with a dense capillary bed (Duvernoy, 1999), and its responses occurred with faster timing than the V1 parenchyma. It is possible that higher spatial resolution fMRI data could identify a subregion of V1 with responses as rapid as thalamus. However, the large size of visual cortex meant that our analysis included a large number of voxels, and a broad distribution of anatomic properties, as reflected by the large timing differences across V1 voxels (Fig. 5). Our analysis therefore likely included many cortical voxels with little contamination from large surface vessels, and nonetheless responses were clearly faster within the LGN and SC. We hypothesize that different vascular anatomy within subcortical structures, such as increased density of capillaries or altered venous drainage patterns within the parenchyma, could contribute to these fast responses. In particular, venous drainage could potentially be slower in these structures due to the curved trajectory of the parenchymal venules compared to those in the cortex (Duvernoy, 1999), or physiological mechanisms of blood flow regulation could operate at different timescales. Biophysical models of the BOLD response also suggest some mechanistic possibilities: in the ‘balloon model’ fast dynamics can be generated through viscoelastic effects within veins, perhaps suggesting regional differences in venous elasticity, size, and density could lead to the differences in BOLD dynamics (Buxton et al., 2004; 1998); the ‘bagpipe’ model (Drew et al., 2011) suggests a potential influence of different ratios of arterioles to venules across regions; and the ‘arterial impulse response model’ (Kim and Ress, 2016) could suggest a role for related differences in oxygen delivery in subcortex following brief stimuli. Ultimately, animal studies directly imaging vessels could help identify what physiological mechanisms underlie these fast subcortical responses. While our experiments focused on the visual system, future studies could examine other thalamic and brainstem nuclei to whether this pattern of faster responses is a consistent feature of deep brain structures.

Our study focused on the positive peak of the BOLD response, but our results clearly also contain a post-stimulus undershoot, consistent with many previous studies (Buxton et al., 1998; Chen and Pike, 2009). Due to the smaller magnitude of this signal, we did not analyze it in detail here, and therefore how this post-stimulus undershoot varies across subcortical regions remains an open question. Future studies using fewer stimulus conditions (and thus higher trial numbers) could characterize how these other aspects of the BOLD response vary across regions.

In contrast to the large differences in response timing across structures, LGN and V1 exhibited very similar nonlinearity profiles. While nonlinearities in SC were larger than in cortex, this could be partially due to neural differences within this structure. Based on previous studies (Janz et al., 2001; Li and Freeman, 2007; Liu et al., 2010), we estimated an approximate 20% decrease in neural activity within LGN and V1 to longer stimuli, which is not sufficient to explain the observed hemodynamic nonlinearities. In contrast, brief visual stimuli could potentially elicit neural activity with nearly the same magnitude as longer stimuli within SC, as many SC neurons respond selectively to stimulus onset and to saccades (Furlan et al., 2015; Mohler and Wurtz, 1976; Shires et al., 2010). While some degree of neuronal response nonlinearity is expected across all three structures, the neural contribution to the observed nonlinearity may thus have been larger in SC than it was in LGN and V1. Invasive studies in animals may ultimately be needed to determine the exact contributions of neural and hemodynamic nonlinearities, but the large (>1 s) changes in time-to-peak in our data suggest a substantial hemodynamic contribution even in SC.

The robust and fast responses in LGN further suggest that fast imaging approaches could potentially be used to capture high-frequency dynamics even in small brain structures. We successfully detected oscillations at 0.5 Hz in the LGN, and these oscillations appeared with similar amplitude scaling to those seen in V1, which are an order of magnitude larger than predicted by the canonical HRF (Lewis et al., 2016). Two potential factors could have theoretically contributed to these large oscillations: 1) an HRF that is narrower than previously thought, yielding a stronger response at high frequencies; and 2) a nonlinearity such that briefer neural activity elicits faster and larger hemodynamic responses. Our current results suggest that the latter may play a more important role, as the LGN has a faster and narrower HRF across all stimulus durations but did not exhibit a stronger response at high frequencies. Instead, the similar nonlinearity properties in these two structures appears to be consistent with the similar frequency responses that they exhibit to oscillatory neural activity. The SNR was lower in LGN due to its small size and deep location, but the magnitude of the detected oscillation was nonetheless similar, suggesting that fMRI may be a useful approach for tracking >0.1 Hz dynamics in local thalamic nuclei.

Finally, cortical imaging could also benefit from these observations, by taking advantage of surface-based approaches to selectively analyze the rapidly-responding regions within the parenchyma. Functional signals dominated by surface vessels exhibit not just poorer spatial specificity (Polimeni et al., 2010), but are also temporally delayed relative to signals from the parenchyma (Chen et al., 2011; Yu et al., 2012), and may cause cortical ROIs to have greater temporal variability due to the same downstream signal pooling effects that reduce their spatial specificity (de Zwart et al., 2005; Siero et al., 2011). These features may obscure fast responses in cortex when low spatial resolution imaging or spatial smoothing preprocessing is used. Alternative functional contrasts such as those based on T2-weighted BOLD (e.g. spin-echo EPI) or cerebral blood volume (e.g. VASO) have demonstrated the improvements in spatial specificity that accompanies higher microvascular specificity (Huber et al., 2017; Yacoub et al., 2007), and spin-echo data exhibit HRFs with the same fast dynamics as observed in deep cortical ROIs (Siero et al., 2013), supporting this link between vascular anatomy and temporal dynamics. Similarly, masking out anatomically identified surface vessels could have an analogous effect, increasing temporal specificity. In addition to these methods, our results suggest that cortical depth-based analysis of gradient-echo EPI also provides a useful way to modulate and potentially remove the effects of downstream vessels on response timing, and could be used to enhance the high-temporal-frequency content of fMRI data.

Several limitations of our study could benefit from more detailed future investigations of subcortical response properties. Firstly, each region we studied is composed of functionally heterogeneous substructures (e.g. layered structure in SC and LGN), with potentially distinct vascular anatomy, rather than the single ROIs we defined here. Adding individual-level functional characterization of response properties across these regions and defining multiple ROIs through more complex functional localizers, could reveal heterogeneous dynamics within the regions we studied. Second, the neural drive to these regions is not known, and both its magnitude and timecourse is likely to differ. Future animal studies could quantify the relative response timescales across structures through invasive electrophysiology, to link with the observed hemodynamics. Third, our spatial resolution was limited by the need for rapid acquisition, and increasing resolution further could potentially greatly benefit imaging both SC and the laminar cortical differences we studied. In particular, improving the spatial resolution for the fast oscillations experiment could enable a direct analysis of whether deep vs. superficial cortex exhibits distinct frequency response properties. Fourth, we quantify the speed of the hemodynamic response through its time-to-peak and width. However, we were not able to precisely measure response onset times in these data due to the high noise levels in SC, and the difficulty of accurately estimating the time of onset of a small signal change. It is possible that the properties of onset times in these structures may differ from peak and width, as factors such as blood pooling and dynamics large surface vessels, and areas with faster time-to-peak do not necessarily have faster onsets. Future studies using fewer stimuli and acquiring more data per subject could investigate this other aspect of hemodynamic speed.

A final and important limitation is that our results use deconvolution to infer hemodynamic responses. Deconvolution can be a noisy process and its results depend on the assumptions of the analysis, for instance the smooth basis functions used to obtain the impulse response in this study. These basis functions impose temporal smoothness upon the deconvolved impulse responses (Woolrich et al., 2004); we therefore also analyzed trial responses using a non-smoothed FIR analysis to confirm the same dynamics are present with minimal temporal smoothing and when avoiding assumptions about the shape of the hemodynamic response. In addition, if responses are overlapping in time, deconvolution depends on time-shift invariance, which is unlikely to hold perfectly in the case of rapid event-related fMRI. Our analyses of our long ISI condition data (17–21 s) showed robust results, and this long temporal separation is likely to be sufficient for the brief stimuli used in this study, but this issue could potentially influence results in short ISI conditions. Through these alterations in acquisition and design, future studies could further resolve the dynamics and physiological mechanisms of subcortical fMRI signals.

We conclude that subcortical and cortical elements of the human visual system exhibit distinct hemodynamic temporal properties that should be accounted for in fMRI analyses, with a progression from fast to slow responses across brainstem, thalamus, cortical parenchyma, and pial surface. Our identification of local temporal characteristics associated with differences in frequency content suggest that an improved understanding of vascular anatomy, physiology, and neurovascular coupling could inform analysis of local and rapid fMRI responses. Furthermore, we find that nonlinearities in response timing and amplitude are a key driver of fast fMRI signals, suggesting that fMRI signals may preserve more high-frequency content when neural activity varies rapidly, which occurs in a broad range of natural contexts. fMRI experiments and analyses could potentially be designed to take advantage of the rapid response features in these structures, whether through closely-spaced trials or through naturalistic experimental designs with fast time-varying components. In doing so, future studies may be able exploit these faster dynamics within deep brain structures to enable both high spatial and temporal resolution imaging of activity in thalamic and brainstem nuclei.

Table 1: Mean parameters and 95% confidence intervals (CI) for the impulse response across regions and stimulus durations.

Time-to-peak (TTP) and full-width-at-half-maximum (FWHM) are reported in seconds.

	0.167 s		0.5 s		1s		2s		4s
TTP:	Mean	CI	Mean	CI	Mean	CI	Mean	CI	Mean	CI
V1	4.5	(4.25–4.80)	4.7	(4.45–5.05)	4.85	(4.55–5.20)	5.15	(4.85–5.45)	5.3	(5.00–5.65)
LGN	4.15	(3.80–4.85)	4.2	(4.05–4.30)	4.15	(4.00–4.30)	4.35	(4.20–4.50)	4.35	(4.20–4.50)
SC	3.85	(3.45–4.30)	3.8	(3.40–4.20)	3.9	(3.50–4.25)	4.1	(3.95–4.25)	4	(3.85–4.20)
FWHM:
V1	4.6	(4.15–6.88)	4.65	(4.35–5.00)	4.85	(4.50–5.35)	5	(4.70–5.35)	5.25	(4.90–5.70)
LGN	4.05	(3.60–4.95)	4	(3.90–4.15)	3.95	(3.80–4.15)	4.15	(4.00–4.33)	4.15	(4.00–4.35)
SC	3.75	(3.25–4.40)	3.55	(3.10–4.05)	3.75	(3.25–4.10)	4	(3.80–4.15)	3.75	(3.60–3.95)