Abstract
Propensity score methods are common for estimating a binary treatment effect when treatment assignment is not randomized. When exposure is measured on an ordinal scale (i.e. low–medium–high), however, propensity score inference requires extensions which have received limited attention. Estimands of possible interest with an ordinal exposure are the average treatment effects between each pair of exposure levels. Using these estimands, it is possible to determine an optimal exposure level. Traditional methods, including dichotomization of the exposure or a series of binary propensity score comparisons across exposure pairs, are generally inadequate for identification of optimal levels. We combine subclassification with regression adjustment to estimate transitive, unbiased average causal effects across an ordered exposure, and apply our method on the 2005–2006 National Health and Nutrition Examination Survey to estimate the effects of nutritional label use on body mass index.
Keywords: causal inference, propensity scores, potential outcomes, ordinal exposures, National Health and Nutrition Examination Survey
1. Introduction
Disclosure of ingredients and inclusion of a standardized label has been required on all US food and beverage since 1994 as a result of the National Labeling Education Act (NLEA1). The US Food and Drug Administration2 initially estimated, among other benefits, roughly 725,000 avoided cases of cancer and chronic heart disease over a 20-year period and a health care savings between $4.4 and $26.5 billion through expected dietary changes resulting from the NLEA.
Twenty years later, however, the effect of the NLEA on health outcomes remains largely unknown, as literature exploring the effect of label use has yielded mixed conclusions. While Variyam and Cawley3 and Loureiro et al.4 found a significant reduction in body mass index (BMI) among women label users, Drichoutis et al.5 found evidence that increased label use actually caused higher BMIs. However, both Variyam and Cawley and Loureiro et al. dichotomized label use, initially measured on a five-point scale, into “sometimes” frequency or above, making inference at a specific label use level impossible. Further, in dichotomizing an ordered exposure, both studies were more likely to suffer from bias due to confounded assignment mechanism.6
Estimating the effects of an exposure on an ordinal scale is useful for many public health interventions. For example, extensive clinical trials have contrasted the duration, length, and intensity levels of physical activity.7,8 Such research has aided in proposing recommendations for physical activity, including those touted by the US Surgeon General.9 Obviously, these guidelines cannot be enforced; however, they were written in order to motivate people to live healthier lifestyles, and to identify the average effects that are expected due to different activity levels.
Similar guidelines on how often one should read nutritional labels have not been issued, despite label use being a priority for several US organizations. The US Food and Drug Administration,10 the American Heart Association,11 and the American Diabetes Association,12 for example, all include label use directions on their websites. The Mayo Clinic13 goes as far as urging patients to “practice” label use when food shopping. However, none of these organizations supply any specific guidelines of how often individuals should be reading nutritional labels.
Observational data that use a simple comparison of health outcomes across those at different label use levels have limitations, because subjects in these label use groups differ with regard to personal, socio-economic, and demographic characteristics. For example, readers of nutrition labels are, on average, more active and health-conscious.14,15 With two treatment groups, a common statistical tool used to adjust for differences in the covariates’ distribution in estimation of the treatment effect is the propensity score, defined by Rosenbaum and Rubin16 as the probability of receiving treatment conditional on a set of observed covariates. Most propensity score methods and applications deal with binary treatments, while exposure to label use is often measured using an ordinal scale. In the 2005–2006 National Health and Nutrition Examination Survey (NHANES) data, label use is measured on a five-point scale, never, rarely, sometimes, most of the time (often), or always. Drichoutis et al.5 employed binary propensity score methods across the 10 possible pairs of label levels in their analysis of the NHANES, which yielded pairwise causal effect estimates that were not transitive. Specifically, estimates suggest that while sometimes label use level yields lower BMI than rare level and that rare level causes lower BMI than never level, sometimes level frequency actually results in a significantly higher BMI (p < 0.05) than never level.
We extend the data set used by Drichoutis et al.5 and reanalyze it with a generalized propensity score (GPS) method that will result in transitive estimates of the causal effects of increased label use on BMI between all pairs of label use levels. In doing so, this manuscript provides three important extensions to approaches which have been previously designed for ordinal exposures.17,18 Following the separation of the design and analysis paradigm in observational studies proposed by Rubin,19 we propose and implement novel graphical methods as well as introduce new metrics for assessing and depicting covariates’ similarity between individuals at different exposure levels. Second, we couple the subclassification-based strategies of Imai and Van Dyk18 and Zanutto et al.20 with regression adjustments to estimate causal effects and to obtain more precise and accurate point estimates. Last, we use simulations to demonstrate the benefits of combining subclassification with regression adjustment, relative to either method alone and to other previously proposed methods for ordinal exposures. Although previous statistical literature has touched on some of the analysis phase methods, the combination of the design, simulation, and analysis phases presented here provide other investigators a complete case study for estimating causal effects from observational studies with ordinal treatments. Our method is implemented on the 2005–2006 NHANES, and causal effect estimates suggest that reduction in BMI only occurs when reading labels often or always.
The outline of this paper is as follows. Section 2 introduces our notation, and Section 3 details our use of subclassification with regression adjustment to estimate the set of causal effects across levels of an ordinal exposure. Section 4 implements the proposed method on the NHANES data, Section 5 summarizes our results, Section 6 details a simulation study, and Section 7 concludes.
2. Causal inference and the Rubin causal model
2.1. Notation for binary treatment
Splawa-Neyman21 first described treatment effects in the context of potential outcomes for a randomized experiment. This concept was expanded to observational studies in what was eventually termed the “Rubin causal model” (RCM).22,23
Let Yi, Xi, and Ti be the observed outcome, set of p covariate values, and binary treatment indicator, respectively, for each subject i = 1,…n, n < N, where n is the sample size and N is the population size which is possibly infinite, with treatment , .
A commonly made assumption in the RCM is the stable unit treatment value assumption (SUTVA).24 SUTVA specifies both that the set of potential outcomes for a subject depends only on the treatment that subject was assigned to, and not on the treatment assignment of others, and that within each treatment condition, there are not multiple versions of the treatment. Assuming SUTVA, the potential outcome for unit i can be written as Yi(Ti = t)= Yi(t), which represents subjecti’s outcome if he or she would have received treatment t.
One common estimand of interest is the population average treatment effect (PATE), which is often approximated by using the sample average treatment effect (SATE).
| (1) |
| (2) |
In practice, however, each individual receives either the treatment or the control at the same point in time, but not both, and only Yi(1) or Yi(0) is observed for each unit, also known as the fundamental problem of causal inference.22 As a result, the RCM commonly relies on the assumption S1 to estimate 1 and 2.
S1: Strongly ignorable treatment assignment: (i) Pr({Y(0), Y(1)}|T, X) = Pr({Y(0), Y(1)}|X); and (ii) 0 < Pr(T = t|X) for t ∊ {0,1}.16 Under strongly ignorable treatment assignment, the set of potential outcomes and treatment assignment are conditionally independent given X. Implicit in this assumption is that differences in outcomes between those with the same X are unbiased estimates of the treatment’s causal effect to units with that X.
To estimate causal effects from observational data, matching subjects with the same X who received different treatments is an effective way of reducing bias, but as the dimension of X increases, this is nearly impossible.25 Propensity scores enable inference under the RCM even in a high dimensional setting. Let e(X) = Pr(T = 1|X) be the propensity score. If treatment assignment is strongly ignorable given X, then it is also strongly ignorable given e(X), Pr({Y(0), Y(1)}|T, e(X)) = Pr({Y(0), Y(1)}|e(X)). Thus, the comparison of units with equal e(X)s is unbiased for estimating unit level effects, and averaging over the distribution of e(X) in the population results in an unbiased estimate of the PATE.16
2.2. Expansions for more than two exposure levels
Assuming SUTVA, for Z exposures or exposure levels, with , let , where is the set of potential outcomes for unit i. With an ordinal exposure, possible estimands of interest are the PATEs between exposure levels t and s, PATEt,s, for all pairs {t, s}, where , which are commonly approximated by the sample average treatment effects, SATEt,s.
| (3) |
| (4) |
As with binary treatment, we cannot observe each SATEt,s because each unit only receives one treatment, and therefore SATEt,s is a random quantity due to the assignment mechanism being random. Assuming that the sample is randomly chosen from the population, then SATEt,s is an approximation for the PATEt,s. Because most applications are usually trying to estimate effects generalizing to the population, from this point forward, we will define PATEt,s as our estimand of interest and assume that the observed data were sampled at random from the population.
To estimate the PATE across exposure pairs, S1 is expanded such that a strongly ignorable treatment assignment mechanism (also called strong unconfoundedness) for multiple exposures states that (i) ; and (ii) 0 < Pr[T = t|X] > ∀ < 1 ∀ t. As in the binary treatment setting, SUTVA and a strongly ignorable treatment assignment mechanism enable us to estimate E[Y(t)], for all t, by conditioning on the observed covariates.
The propensity score has been expanded to multiple exposures through the GPS, r(t, X) = Pr(T = t|X = x).18,26,27 While propensity scores for binary treatment enable us to condition on a scalar in order to estimate treatment effects, the GPS with a discrete exposure may consists of multiple dimensions, thus requiring to condition on an entire vector of treatment assignment probabilities, r(X) = (r(1, X),…, r(Z, X)). As a result, two individuals with the same r(t, X) for one specific treatment level may not be equivalent with regard to their entire r(X). Thus, differences in outcomes between subjects with different exposure levels and similar r(t, X), but differing r(X), are not generally unbiased causal effect estimates.26
Joffe and Rosenbaum17 and Imai and van Dyk18 noted that modeling an ordinal exposure using an ordered logit model, also referred to as the proportional odds model,28 can provide a shortcut to conditioning on a multidimensional r(X). The ordered logit model is appropriate for exposures measured in doses (e.g. low, medium, high). For example, with Z total treatments (exposure levels), assuming
| (5) |
and defining the balancing score, b(X), as a function of the covariates such that Pr(T = t|b(X)) = Pr(T = t|b(X), X), the proportional odds model provides a scalar b(X). Specifically, for βT = (β1,… βp)T, βT X is a balancing score, such that
| (6) |
The combination of equation (6) with the assumption of a strongly ignorable treatment assignment mechanism allows us to establish that and the treatment assignment are conditionally independent given βT X (for a proof, see Imai and van Dyk18)
| (7) |
Under the expanded versions of SUTVA and S1, differences in observed Ys between subjects with different exposure levels but equal βT X are unbiased estimates of causal effects at that βT X. To estimate the PATEt,s for all treatment pairs {t, s}, we want to average E[Y(t) − Y(s)|βT X] over the distribution of βT X. Formally, we would estimate E[Y(t) − Y(s)] using the following
| (8) |
Direct computation of equation (8), however, is difficult because it requires integrating over the probability distribution of βT X.
One approach for approximating the PATEt,s is to partition subjects with similar values of βT X into subclasses, estimating the effect within each subclass, and combining these effects using a weighted average. A second alternative could be the use of radius matching29 to pair subjects with roughly equivalent βT Xs and average across pairs. However, individual matching techniques are not as well suited for multiple treatments.26 A third approach, which is discussed in Section 3.3, uses inverse probability weighting.
3. Subclass-weighted causal effects for an ordinal exposure
3.1. Design phase
Estimation of causal effects using observational data is composed of two phases: the design phase and the analysis phase.30 The design phase is done without the outcome in sight, and with the intent of obtaining the same treatment effects which would have been obtained in a completely randomized design.19 As suggested by Joffe and Rosenbaum17 and implemented by Lu et al.,31 we first use equation (5) to fit Pr(T|X) and generate an estimated for each individual, where is the maximum likelihood estimate of β. The goal in the design phase is to group subjects that are similar with respect to the observed covariates.19 Thus, we are not concerned with assessing the fit of treatment assignment (e.g. testing the proportional odds assumption), but whether balance on all covariates is obtained across treatment groups.
3.1.1. Covariate choice
The choice of which covariates to include in the GPS model should be made with the intent of satisfying the assumption of strong ignorability. Primarily, previous scientific research should be used to instruct choice of X,30 with all measured pre-treatment variables associated with both the treatment assignment and the outcome included.32 In addition, when in doubt, Stuart25 recommends a “liberal” inclusion variables associated with either the treatment assignment or the outcome, because exclusion of variables which are associated with the treatment assignment mechanism can increase bias.
While it cannot be verified that the chosen X satisfies the assumption of strong ignorability, Stuart25 argues that strong ignorability is often more valid than it appears because controlling for observed covariates also controls for correlated but unobserved ones. As part of the covariate selection, we propose to examine if any covariates that were not included in the treatment assignment model are also balanced across subclasses. Exact implementation will be described in Section 5.
3.1.2. Common support
As with propensity score analysis for binary treatment, it is important to eliminate subjects outside the range of common support.33 With binary treatment, a common support is often considered to be the range of propensity scores of those receiving both treatments. For an ordinal exposure, an extension is to use a common support region of the linear predictor, which eliminates subjects with beyond the range of values among those on other treatments. It is recommended that the propensity score model be re-fit after subjects are dropped to ensure that the estimated propensity scores are not disproportionately impacted by those outside the common support.34 Dropping units also changes the estimand of interest to include only units with a large enough probability of receiving any of the treatments. This is a different estimand than the PATEt,s, which cannot be estimated without making unassailable assumptions. Thus, it is good practice to describe the population which the estimand is generalizable to using the observed covariates.
The remaining subjects that are not discarded are partitioned into K subclasses, where each subclass contains subjects with similar . This partitioning is aimed at generating similar covariates’ distributions for all treatment levels in each subclass. The choice of K is flexible, and it has been suggested to examine the covariate balance for multiple values of K.30 Higher K will yield better within-subclass homogeneity of the covariates, resulting in smaller within-subclass bias. Too large of a K will result in low numbers of subjects within each subclass, which could restrict our ability to estimate causal effects when there are no units at a specific treatment level to compare to. For simplicity, we partition units into subclasses such that an equal number of units are within each subclass. Cochran and Rubin35 found little improvement when comparing the bias reduction of optimal subclassification to equally spaced subclassification with a single covariate and a binary treatment, and Rosenbaum and Rubin36 provided similar recommendations when estimating the treatment effect with multiple covariates and binary treatment. Our recommendation is to use equally spaced subclasses with ordinal treatments and multiple covariates, but this is an area of further research.
Let nk be the number of subjects in subclass k, k = 1,…, K. With binary treatment and p covariates in the propensity score model, it has been recommended to keep (i) at least three subjects at each combination of the subclass and treatment; and (ii) nk > p + 2.34 Our related recommendation is to generate the largest K possible with both (i) at least 3 + Z subjects at each exposure level in each subclass; and (ii) nk > p + Z.
3.1.3. Balance checks
To ensure that subclassification reduced the covariates’ bias across the different treatment groups, it is important to check the within-subclass distributions of each covariate before looking at within-subclass outcomes.19,30 This process examines how closely each subclass mimics a randomized experiment in which the distributions of covariates at each exposure level are similar in expectation.
The following two-step procedure was used to examine the covariate distributions within each subclass. First, tabular and graphical approaches assess the distributions of both and the continuous covariates in X by exposure level within each subclass.37 These checks include side-by-side boxplots of the balancing scores and continuous variables at each exposure level in each subclass.
Second, the dependencies between exposure level and covariate within each subclass, for all covariates, will be compared to both the dependencies in the original data and the hypothetical distribution of the statistics which would have occurred in a randomized experiment. Here, we use Kendall’s τb, abbreviated as τ from this point forward, which is a rank correlation coefficient, where positive τ values indicate that higher ranks of one covariate are positively associated with higher ranks of the exposure. Under the null distribution that the covariate and exposure are independent, τ = 0, and sample τ statistics are approximately distributed as standard Normal, making τ useful for examining non-linear correlations. We plot histograms of sample τ test statistics for each covariate at each subclass to check for normality, as well as to identify the proportion of τ statistics which remain significant after subclassification, relative to nominal level α.
Examining all of the τ values for each covariate in each subclass may be extensive with a large number of covariates. One way to summarize the benefits of subclassification is to average the within-subclass τ estimates for each variable over the number of subclasses, and compare these results to the values found in the original data. Formally, let τpk be the estimated τ between exposure level and covariate p in subclass k, and let be the proportion of subjects in subclass k. We define , the weighted subclass-averaged τ, as
Contrasting the values with the τ statistics from the original data can indicate if covariate imbalances still exist.
Section 4.2 details these checks through real data analysis. If these checks display covariate imbalances which deviate from a randomized experiment, one option would be to re-fit the ordered logistic model, possibly including interaction terms. Noticeable variations in the distributions of or significant τ dependencies within each subclass, for example, would suggest that the covariates are not properly balanced. If balance on X cannot be obtained, causal effects should not be calculated.
3.2. Analysis phase
Under strong ignorability, if the empirical distribution of the covariates is equal in expectation between those at different exposure levels within each subclass, estimated mean outcomes for each treatment level can be computed as weighted averages of the within-subclass sample means, with weights equal to the relative subclass size. Let and be the observed sample means in subclass k among those receiving treatments t and s, respectively. To test for a global difference in subclass-weighted mean outcomes between the exposure levels, Zanutto et al.20 use a randomized block analysis of variance model of outcome on subclass and exposure, treating subclass as the blocking variable. If the global difference in means hypothesis is rejected, pairwise PATEt,ss can be estimated using subclass-weighted mean differences, as in equation (9).
| (9) |
Without regression adjustment, however, subclass-weighted means may not eliminate the entire bias caused from differences in the covariates’ distribution, jeopardizing the accuracy of treatment effects estimated using equation (9). The intuition behind this is that while differences in outcomes are unbiased estimates of causal effects at exact values of the linear predictor, differences in covariates by exposure level could still exist when different linear predictors are pooled together. Several authors38–40 have noted that combining regression adjustment with matching for a binary treatment reduces bias relative to either method alone. An additional benefit of regression adjustment is that even in the case that the theoretical covariate balance of a completely randomized design is achieved within each subclass, regression adjustment can improve the precision of the causal estimates.34
We start the analysis by testing for a global effect of exposure using a randomized block analysis of covariance (ANCOVA) model of outcome on subclass, exposure, and X, treating subclass as the blocking variable. If the null hypothesis of no difference in means by exposure is rejected, we calculate pairwise causal effects.
Let Yik be the observed outcome of subject i in subclass k and let Yik(t) be the potential outcome of that subject at exposure level t. Next, letting Xik be the observed covariates of subject i in subclass k and I(Ti = t) be an indicator function for individual i receiving treatment t, we use the following steps to estimate PATE(t,s) for all pairs {t, s}.
Step 1: Assuming Yik(t)|Xik ~ N(E(Yik|Xik, T),σ2), model Yik|{Xik, T} within each subclass using the following regression model
| (10) |
Step 2: Estimate PATEk(t,s), the PATE(t,s) within-subclass k, using and , the maximum likelihood estimates of αkt and αks, respectively, from model (10)
| (11) |
Step 3: Estimate the variance of , , within each subclass, from regression model (10)
Let with . Based on equation (10), , and letting c = (0, I(T = t), 0, − I(T = s), 0), where I(T = t) and I(T = s) are indicators for treatments t and s, respectively, with 0 =(0,… ,0), we have
| (12) |
Step 4: Using , estimate PATEt,s by averaging over K:
| (13) |
| (14) |
Using our framework, , the estimated average treatment effect between level t and s in subclass k, is an unbiased estimate for PATEk(t,s) (For proof, see Appendix 1). It is important to note that because nk and the linear predictors are both based on the GPS model estimated from the data, responses within and between subclasses are dependent.41 As a result, the above aggregation of subclass-weighted standard errors can underestimate the true sampling variances, although regression adjustment usually helps in this regard.41,42
3.3. Alternative approaches
In addition to subclassification-based methods, other inference procedures exist for estimating causal effects from an ordinal exposure. Lu et al.31 used non-bipartite matching to pair subjects at lower exposure levels with ones at higher levels. However, the causal effect estimand generated using non-bipartite matching is not clearly defined, and a significant effect using this method would not specify an optimal exposure level.
The approach used by Drichoutis et al.,5 initially described by Lechner,43 is also common for estimating treatment effects from multiple exposures. Letting nt be the number of subjects receiving treatment t, this method implements a set of binary comparisons (SBC) attempting to estimate the PATE on the treated, PATTt|(t,s) = E[Y(t) − Y(s)|T = t], for all exposure pairs {t,s}, using propensity score matching for binary treatment on the population of subjects receiving either t or s. Because SBC yields causal effects conditional on a subject receiving one of two treatments, the resulting set of causal effects are usually not transitive. Specifically, the population receiving t which PATTt|(t,s) generalizes to likely differs from the population receiving s which PATTs|(s,r) generalizes to, and, as a result, it would be erroneous to use PATTt|(t,s) and PATTs|(s,r) to contrast treatments r and t.
Another approach for approximating the PATE between each exposure pair uses the inverse of the estimated probabilities from a statistical model of treatment assignment (e.g. multinomial logistic, proportional odds) as weights.26,44 Feng et al.45 used this procedure to estimate PATEt,s by weighting subjects by the reciprocal of their GPS.
| (15) |
One issue with this approach is that extreme weights can result in erratic causal estimates,46,47 an issue that becomes more likely as the number of treatments increases and treatment assignment probabilities decrease. While trimming has been shown to decrease the influence of extreme weights on causal estimates,48 trimming the extreme weights estimated from a GPS model can yield covariate bias’ in unknown directions.49
Nonetheless, our subclassification estimators can be viewed as weighted estimators, with weights coarsened by averaging them through subclasses. For binary treatment, this smoothing of the weights results in estimates which, compared to weighted methods, are more precise and less likely to be influenced by a misspecification of the propensity score model.34,50
4. Nutritional label use and BMI
4.1. Data description
The NHANES is a nationally representative research program of 15 US counties that measure demographic, health, nutritional, and behavioral variables, including nutritional label use and BMI. The 2005–2006 NHANES version measured label use via a questionnaire and BMI through a physical examination. Subjects were presented with an example of a food label and asked the question “How often do you use the Nutrition Facts panel when deciding to buy a food product? Would you say always, most of the time, sometimes, rarely, or never?” (See http://www.cdc.gov/nchs/data/nhanes/nhanes_05_06/sp_dbq_d.pdfhttp://www.cdc.gov/nchs/data/nhanes/nhanes_05_06/sp_dbq_d.pdf for more information.)
In a separate physical examination, trained medical personnel measured the height and weight of these subjects.
Thirty pre-treatment covariates that are possibly associated with label use exposure and BMI, including demographic, lifestyle, nutritional awareness, and health status information, were chosen after careful examination of the NHANES and a vast literature review.14,51 All of the variables recommended by Drichoutis et al.5 were included. We added squared terms for Metabolic equivalence and Meals away from home to account for the skewed nature of the original variables.30 The covariate Weight thoughts, which measures an individual’s categorized opinion of their weight (underweight, about the right weight, or overweight), was also included. Last, we included the variable Prior BMI, which is calculated using a self-reported estimate of a subject’s weight from a year prior to the survey and the subject’s current measured height.
The data set included a total of 4644 subjects with recorded label use and a measured BMI. As in Drichoutis et al.,5 we excluded the 298 subjects with missing covariates values. Including Prior BMI as a covariate eliminated an additional 74 subjects, yielding a sample size of 4272. Because dealing with missing covariates is not the focus of this paper, we made the naive assumption that data for these subjects were missing completely at random.52 Other options include introducing missing indicators for categorical covariates,53 using weighting methods based on the probability for missingness (as in Wooldridge54), or using multiple imputations to create complete data sets, where causal effect estimates are calculated across each of the data sets and combined using Rubin’s rules for multiple imputation.55 Because these techniques have not yet been used with GPS methods under multiple exposure levels, it is an important area for further research. Selected demographic variables of subjects dropped using these criteria and those remaining in the study population are shown in Appendix A2.1.
Table 1 lists our covariates, their τ statistics with label use, and a p-value testing the null hypothesis of no dependency between label use and each covariate. (There are 33 rows in Table 1, as we separated the variable for race into four categories. For a more complete description of these covariates, see Appendix A2.3.) Using these covariates, the ordered logistic model was used to estimate the probability of label use (the treatment).
Table 1.
Covariates and Kendall’s τ with nutritional label use.
| Variable | Type | Kendall’s τ | p |
|---|---|---|---|
| Gender, male | Binary | −0.19 | <0.001 |
| Race, Hispanic | Binary | −0.14 | <0.001 |
| Household size | Numeric | −0.13 | <0.001 |
| Born to be fat? | Ordinal | −0.07 | <0.001 |
| Drug user | Binary | −0.05 | <0.001 |
| Smoker | Binary | −0.04 | 0.003 |
| Safe sex | Binary | −0.01 | 0.338 |
| Race, black | Binary | 0.00 | 0.867 |
| Heart disease | Binary | 0.00 | 0.816 |
| Drinks per day | Numeric | 0.00 | 0.699 |
| Race, other | Binary | 0.01 | 0.292 |
| Pregnant | Binary | 0.01 | 0.430 |
| (Meals away from home)2 | Numeric | 0.02 | 0.060 |
| Meals away from home | Numeric | 0.02 | 0.048 |
| Prior BMI | Numeric | 0.04 | 0.001 |
| Age | Numeric | 0.06 | <0.001 |
| Diabetic medicine | Binary | 0.07 | <0.001 |
| Diabetic | Binary | 0.10 | <0.001 |
| Race, white | Binary | 0.11 | <0.001 |
| Doct. advice 2 (reduce weight for chol.) | Binary | 0.11 | <0.001 |
| Doct. advice 3 (less fat for disease risk) | Binary | 0.11 | <0.001 |
| Income | Ordinal | 0.12 | <0.001 |
| Weight thoughts | Ordinal | 0.12 | <0.001 |
| Food security | Ordinal | 0.13 | <0.001 |
| Doct. advice 1 (less fat for chol.) | Binary | 0.13 | <0.001 |
| Doct. advice 4 (reduce weight for disease risk) | Binary | 0.13 | <0.001 |
| Healthy diet | Binary | 0.16 | <0.001 |
| (Metabolic equivalence)2 | Numeric | 0.16 | <0.001 |
| Metabolic equivalence | Numeric | 0.18 | <0.001 |
| Heard of diet guidelines | Binary | 0.24 | <0.001 |
| Heard of 5-a-day program | Binary | 0.24 | <0.001 |
| Education | Ordinal | 0.25 | <0.001 |
| Heard of food pyramid | Binary | 0.28 | <0.001 |
BMI: body mass index.
4.2. Balance assessment
Subjects were partitioned into K equal size subclasses, with subclass boundaries defined by equally spaced quantiles of . There were 33 covariates in the propensity score model. To meet the restrictions of (i) at least 3 + Z subjects at each label use level within each subclass; and (ii) nk > p + Z, up to K = 15 subclasses were examined. Balance checks are presented for K = 5, 10, and 15.
4.2.1. Distributions of and balance checks for continuous covariates
Boxplots of by label use within each subclass show that while the linear predictors are distributed similarly among those at different label use levels for K = 10 and K = 15, those with higher label use levels have higher within each subclass for K = 5. For example, in subclass 4 with K = 5, the boxplots indicate a pattern of increasing by label use level (Figure 1). However, when these subjects are further split on , as in subclasses 7 and 8 with K = 10, the linear predictor appears more evenly distributed across label use levels (Figure 1).
Figure 1.
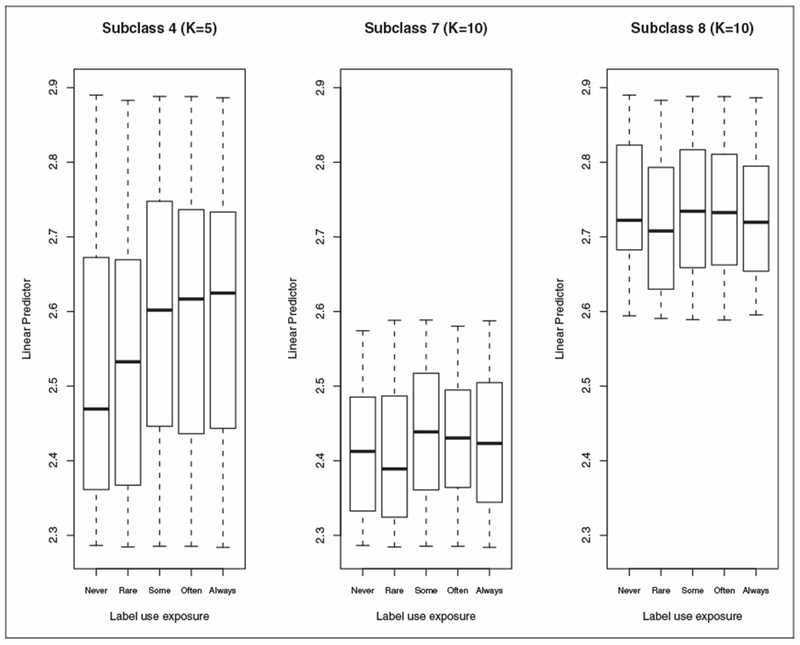
Boxplots of (the linear predictor) by label use in subclass 4 (K = 5) and subclasses 7 and 8 (K = 10).
Overlap and similarities in the distributions of continuous covariates by label use were also compared via side-by-side boxplots, both overall and within each subclass. Extreme continuous covariates’ values may have large influence on the causal estimates, particularly if the overlap of continuous variables is not roughly equal across label use levels. One option is to perform the analysis on a common support of continuous variables, by eliminating subjects whose covariates are beyond the range of those at other label use levels. For example, sample cutoff lines used with these inclusion criteria for the variable Prior BMI are shown in Figure 2, which eliminated, along other subjects, a subject with a Prior BMI of 87.5. This elimination was done before the propensity score model was estimated and would be done prior to any elimination of extreme linear predictors. Another option was to exclude subjects with extreme continuous variables within each subclass, but in the NHANES data set, this would eliminate more than 30% of the participants, and thus this strategy was not attempted. Elimination changes the population for whom the results can be generalized to, but it reduces the need for extrapolation and making assumptions which cannot be defended.
Figure 2.
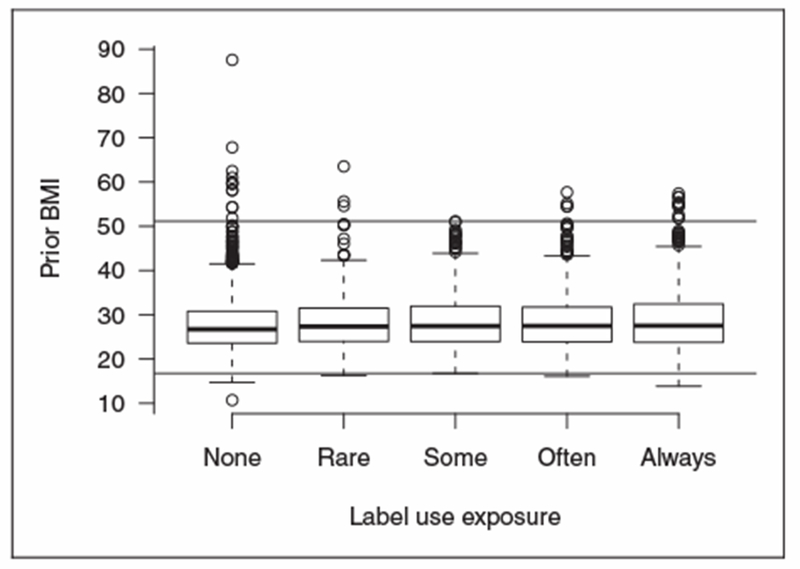
Boxplots of Prior BMI by label use, with cutoffs for “extreme” values.
4.2.2. Within-subclass associations between X and T using Kendall’s τ
As an example of balance assessment using τ, let Drug user be a binary variable for whether or not a subject indicated using hashish, marijuana, cocaine, heroin, or methamphetamine in the past 12 months. One significant sample τ statistic occurred with Drug user in subclass 2, for K = 10 (Table 2). In this example, τ = 0.09, suggesting an increase in label use is associated with an increase in the likelihood of using drugs, as the z-statistic for this association is 2.00.
Table 2.
Label use by drug user, subclass 2, K = 10.
| Drug user | Never | Rare | Some | Often | Always |
|---|---|---|---|---|---|
| Yes | 11 | 7 | 15 | 7 | 7 |
| No | 148 | 48 | 85 | 54 | 36 |
With several hundred such tests, however, we expected to find these associations by chance, as well. Figure 3 depicts the distributions of the test statistics plotted against a normal curve, and Table 3 shows the proportion of significant tests observed after subclassification at level α, α ∊ {0.01, 0.05}. In Figure 3, we look for normality in the histograms, and in Table 3, because the distribution of p-values is uniform under the null, we check that the proportion of significant tests is near α. Results are presented across three choices of K for the following three mechanisms of subject elimination, E1–E3:
E1: No subject elimination, n = 4272
E2: Eliminate subjects with extreme linear predictors, n = 4142
E3: Eliminate subjects with extreme continuous X or extreme linear predictors, n = 4076
Figure 3.
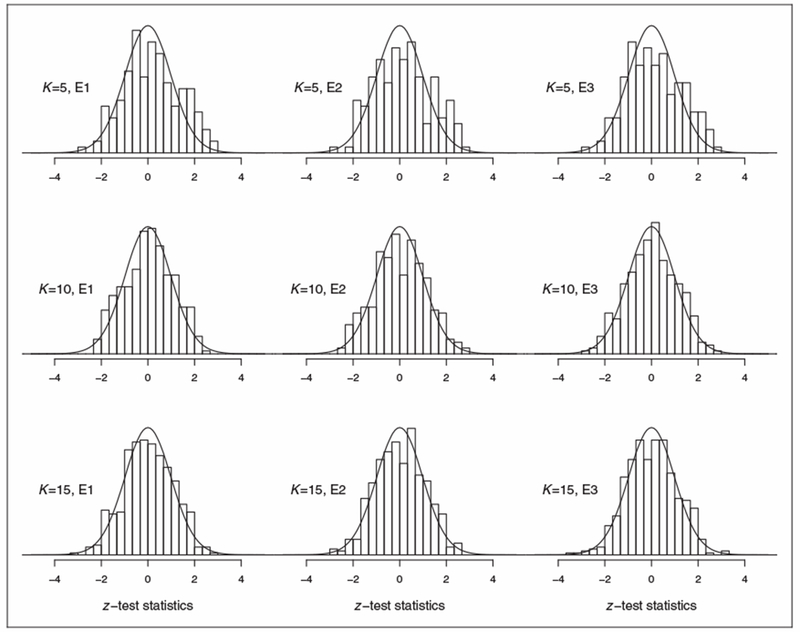
Histograms of z-test statistics of statistical dependency between covariates and label use using Kendall’s τ, for K subclasses and subject elimination E1–E3.
E1: no subject elimination, n = 4272; E2: eliminate subjects with extreme linear predictors, n = 4142; E3: eliminate subjects with extreme continuous X or extreme linear predictors, n = 4076.
Table 3.
Proportion of significant (p < α) within-subclass balance tests.
| Elimination | K (# subclasses) | α = 0.01 | α = 0.05 |
|---|---|---|---|
| E1 | 5 | 0.018 | 0.103 |
| 10 | 0 | 0.052 | |
| 15 | 0.004 | 0.042 | |
| E2 | 5 | 0.012 | 0.115 |
| 10 | 0.009 | 0.079 | |
| 15 | 0.006 | 0.053 | |
| E3 | 5 | 0.018 | 0.097 |
| 10 | 0.006 | 0.064 | |
| 15 | 0.014 | 0.048 |
These checks show that while there were significant within-subclass covariate imbalances beyond that which would have occurred in a randomized design when K = 5, the proportion of significant tests of dependency dropped for K = 10 and K = 15. The variables Age, Drug user, Healthy diet, Heard of food guide pyramid, Pregnant, Prior BMI, Weight thoughts, and Doct. advice 3: eat less fat for disease risk displayed the strongest (p < 0.05) tests of within-subclass dependency for K = 10 and 15.
Last, we compare τ statistics before any subclassification with subclass-weighted statistics, for K = 5 and 15, under elimination mechanism E3 (Figure 4). This figure is an extension of the “Love” plot proposed for binary treatment, which is popular for showing post-matching decrease in each covariates’ bias.56 Twenty six of 33 |τ| statistics using the original data are greater than 0.02, and 19 of these correlations are greater than 0.10. For K = 15, no is of magnitude greater than 0.016, and 29 of the 33 are less than 0.01. Dependencies appear to still exist within-subclasses for K = 5, where 10 are greater than 0.02. For K = 10 (not shown), the largest is 0.019 (Metabolic Equivalence).
Figure 4.
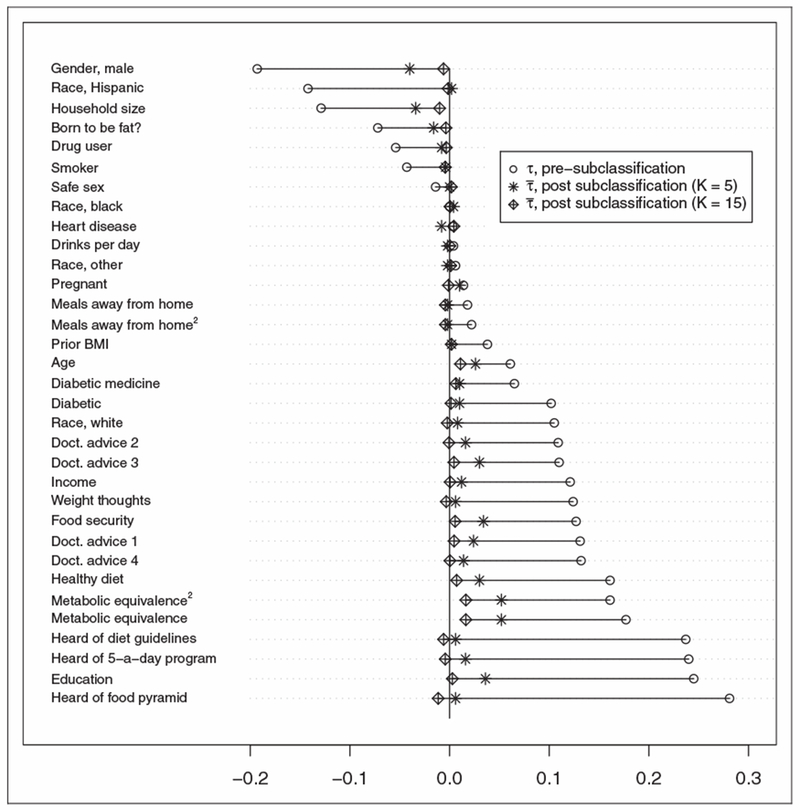
Kendall’s τ between covariates and label use, before and after stratification (using K = {5, 15}).
These results suggest that subclassifying with K = 10 and K = 15 eliminated most of the differences in observed covariate distributions across label use categories which were found in the original data. Because our checks deem covariates to be plausibly balanced for these Ks only, we do not estimate within-subclass causal effects for K = 5.
4.3. Subclass-weighted causal effect estimates of label use on BMI with regression adjustment
Let BMIik(t) be the potential outcome BMI of subject i in subclass k at label use t, for i = 1, …, n, k = 1, …, K, K ∊ {10, 15}, and t ∊ {1 = never, 2 = rare, 3 = some, 4 = most of the time (often), 5 = always}. With Z = 5 and Yik(t) = BMIik(t), equations (10) to (14) were used to estimate the PATE(t,s) and their variances for all pairs {t, s}.
Estimates for three forms of subject elimination (E1–E3) and two regression model adjustments (A1,A2) are shown in Table 4. The regression adjustment models were used to adjust for lingering bias that was not eliminated using subclassification. Model A1 included the set of covariates with questionable balance as judged by within-subclass τ statistics, as described in Section 4.2, and model A2 included all covariates in Table 1.
A1: X = Age, Drug user, Healthy diet, Heard of food guide pyramid, Pregnant, Prior BMI, Weight thoughts, and Doct. advice 3: eat less fat for disease risk (See Appendix A2.3 for variable definitions)
A2: X = All covariates in Table 1
Table 4.
PATE estimates (standard errors in parenthesis) of BMI due to increased nutritional label use.
| Elimination | K | Adjust. | Rare vs. never | Some vs. never | Often vs. never | Always vs. never | Some vs. rare | Often vs. rare | Always vs. rare | Often vs. some | Always vs. some | Always vs. often |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E1 | 10 | A1 | 0.30 (0.18) | 0.13 (0.14) | −0.09 (0.16) | −0.09 (0.17) | −0.17 (0.17) | −0.39 (0.19)** | −0.39 (0.20) | −0.22 (0.16) | −0.22 (0.16) | 0.00 (0.18) |
| A2 | 0.26 (0.18) | 0.19 (0.15) | −0.07 (0.17) | −0.08 (0.17) | −0.07 (0.18) | −0.33 (0.20) | −0.35 (0.20) | −0.26 (0.16) | −0.27 (0.17) | −0.01 (0.19) | ||
| 15 | A1 | 0.29 (0.18) | 0.17 (0.14) | −0.08 (0.17) | 0.01 (0.17) | −0.12 (0.17) | −0.36 (0.19) | −0.28 (0.20) | −0.24 (0.16) | −0.16 (0.17) | 0.08 (0.19) | |
| A2 | 0.25 (0.19) | 0.17 (0.15) | −0.09 (0.17) | −0.03 (0.18) | −0.07 (0.18) | −0.34 (0.20) | −0.27 (0.21) | −0.26 (0.17) | −0.20 (0.17) | 0.06 (0.19) | ||
| E2 | 10 | Al | 0.33 (0.18) | 0.14 (0.14) | −0.10 (0.16) | −0.08 (0.17) | −0.20 (0.17) | −0.43 (0.19)** | −0.41 (0.19)** | −0.23 (0.15) | −0.21 (0.16) | 0.02 (0.18) |
| A2 | 0.30 (0.18) | 0.17 (0.15) | −0.10 (0.17) | −0.10 (0.17) | −0.13 (0.17) | −0.40 (0.19)** | −0.39 (0.20) | −0.27 (0.16) | −0.26 (0.17) | 0.00 (0.18) | ||
| 15 | A1 | 0.32 (0.18) | 0.12 (0.14) | −0.08 (0.17) | −0.05 (0.17) | −0.20 (0.17) | −0.41 (0.19)** | −0.37 (0.20) | −0.20 (0.16) | −0.17 (0.17) | 0.04 (0.19) | |
| A2 | 0.28 (0.19) | 0.14 (0.15) | −0.09 (0.17) | −0.08 (0.18) | −0.14 (0.18) | −0.37 (0.20) | −0.36 (0.21) | −0.22 (0.16) | −0.22 (0.17) | 0.01 (0.19) | ||
| E3 | 10 | A1 | 0.39 (0.17)** | 0.15 (0.14) | −0.08 (0.16) | 0.00 (0.16) | −0.24 (0.16) | −0.47 (0.18)** | −0.40 (0.19)** | −0.23 (0.15) | −0.15 (0.16) | 0.08 (0.17) |
| A2 | 0.36 (0.18)** | 0.19 (0.14) | −0.04 (0.16) | −0.02 (0.17) | −0.17 (0.17) | −0.40 (0.18)** | −0.38 (0.19)** | −0.23 (0.15) | −0.22 (0.16) | 0.01 (0.17) | ||
| 15 | A1 | 0.33 (0.18) | 0.15 (0.14) | −0.08 (0.16) | 0.01 (0.17) | −0.18 (0.17) | −0.40 (0.18)** | −0.32 (0.19) | −0.22 (0.15) | −0.14 (0.16) | 0.09 (0.17) | |
| A2 | 0.25 (0.18) | 0.21 (0.14) | −0.10 (0.16) | −0.03 (0.17) | −0.04 (0.17) | −0.35 (0.19) | −0.28 (0.20) | −0.31 (0.15)** | −0.24 (0.16) | 0.06 (0.18) | ||
| SBC (as in Drichoutis et al.5) | −0.04 (0.69) | 0.95 (0.43)** | 0.60 (0.54) | 0.13 (0.65) | −0.45 (0.55) | 0.79 (0.67) | 0.54 (0.69) | 0.34 (0.41) | −0.63 (0.51) | −0.07 (0.48) | ||
| IPTW (as in Feng et al.45, E1) | 0.49 (0.42) | 0.39 (0.31) | −0.10 (0.35) | 0.53 (0.42) | −0.08 (0.41) | −0.58 (0.42) | 0.05 (0.47) | −0.50 (0.29) | 0.14 (0.45) | 0.63 (0.43) | ||
| IPTW (as in Feng et al.45, E2) | 0.52 (0.46) | 0.29 (0.31) | −0.24 (0.36) | 0.53 (0.43) | −0.23 (0.46) | −0.76 (0.43) | 0.01 (0.49) | −0.53 (0.34) | 0.24 (0.44) | 0.77 (0.41) | ||
| IPTW (as in Feng et al.45, E3) | 0.59 (0.41) | 0.61 (0.31) | −0.01 (0.31) | 0.54 (0.38) | 0.02 (0.46) | −0.61 (0.36) | −0.06 (0.42) | −0.62 (0.29)** | −0.08 (0.40) | 0.55 (0.38) |
E1: No subject elimination; E2: Eliminate subjects with extreme linear predictors; E3: Eliminate subjects with extreme continuous X or extreme linear predictors; A1: X = selected covariates (see Section 4.2); A2: X = all covariates; IPTW: Inverse Probability of Treatment Weighted; SBC: set of binary comparison.
Significant at 0.05 level
Two other sets of causal effects are presented in Table 4. First, estimates calculated using SBC, as detailed in Section 3.3 and calculated by Drichoutis et al.5 with this same data set, are displayed. (Drichoutis et al.5 used several matching algorithms in their analysis. The estimates shown in Table 4 reflect those using one-to-one nearest-neighbor matching.) Second, we calculated Inverse Probability of Treatment Weighted (IPTW) estimates of the PATEs, as in Feng et al.45 and equation (15). (As in Feng et al.,45 we used bootstrap sampling to estimate the variance of the IPTW causal effects.)
5. Results
Using a randomized block ANCOVA model with K = 10 and K = 15 subclasses as blocks, at the 0.05 nominal level, we rejected the global null hypothesis of no differences between the mean BMIs at each label use (p < 0.01 for both K, using each combination of unit discarding rule (E1–E3) and regression adjustment method (A1,A2)). Examining the estimated PATEs between the 10 pairs of label levels suggest that often or always label use may yield lower BMI than rare or sometimes usage. However, the majority of comparisons is not significant at the 0.05 level; the one comparison that was significant across most models examined suggests that an often usage yields a lower BMI than a rare one. Effect estimates are similar for different unit discarding rules (E1–E3), choice of K, and regression adjustment method (A1,A2). IPTW estimates are mostly inconclusive, save for limited evidence that often levels cause lower BMI than rare and sometimes levels.
The marginal increase in BMI with low levels of label use, relative to no label use, is a bit of a surprise; one possibility is that subjects who read labels at a minimum level falsely believe that they are acting sufficiently healthy, and respond with behaviors or eating habits which increase BMI. Another possibility is that the strong ignobility assumption is violated, which implies that subjects reading at the rare levels are unique in a dimension not captured by the observed covariates. However, this violation is less plausible when a large number of covariates are being balanced.
The causal estimates provided are only unbiased under the assumptions specified in Section 2. SUTVA seems reasonable for the NHANES. However, we caution that merging label use categories into two levels (as in Variyam and Cawley3 and Loureiro et al.4) may violate the multiple version of treatment assignment assumption. The NHANES data also included other covariates that were not included in the GPS model because we felt that other variables served as sufficient proxies. As a sensitivity analysis, we examined six of these covariates: cocaine use, marijuana use, marital status, an indicator for excessive alcohol consumption, blood pressure problems, and desires for weight control (listed in Appendix A 2.2, along with their pre-subclassification Kendall’s τ with label use). Using our split of subjects into 15 subclasses, we tested for within-subclass dependency between label use and these covariates using Kendall’s τ. Of the 90 tests, 1 (1.1%) and 4 (4.4%) were significant at α = 0.01 and α = 0.05, respectively, roughly what would have occurred in a randomized design. Thus, it appears that we were able to balance observed covariates even when they were not explicitly included in the GPS model.
Our decision to eliminate subjects with extreme linear predictors or continuous variables (E2, E3) results in estimands that are different than PATEs, and the estimates provided in Table 4 each generalize to different populations. However, under both E2 and E3, fewer than 5% of subjects were eliminated. Two variables, education level and familiarity with the food guide pyramid, offered the strongest insight into why subjects were not retained. Of the 130 subjects eliminated under E2 and the 196 subjects dropped under E3, 61 had the lowest education level and had no knowledge of the food guide pyramid. An additional 46 eliminated subjects had the highest education level and were familiar with the food guide pyramid. These types of subjects were less likely to be observed at all label use levels and would require extrapolation.
Compared to other methods for ordinal exposures applied to this data set, subclassification with regression adjustment provides important advantages. In the IPTW analysis, 309, 313, and 307 subjects were given a weight greater than 10 under E1, E2, and E3, respectively, yielding causal effects with larger variances in comparison to our proposed method. The maximum weights under the three elimination mechanisms were 129 (E1), 108 (E2), and 57 (E3). Subclassification-based estimates are also transitive and generalizable to the entire study population that is not discarded, whereas estimates using a SBC generalize to separate subsets of the population and are not transitive. Here, transitivity refers to the additive effects of causal estimates across different exposure levels. For example, using our method, but not that of a SBC, the additive effects of often to some and some to rare label use frequency is equivalent to comparing often to rare usage.
6. Simulation
In real data, true causal effects are not known because each subject receives only one treatment or exposure dose at a specific time point. If complete sets of potential outcomes were known for all subjects, however, it would be straightforward to compare competing methods to see which most accurately and precisely estimates the true PATE. Thus, we created two full data sets that include the full set of potential outcomes which could have occurred if we had observed the subjects at all label use levels. The two sets of full data, Set 1 and Set 2, used the 2005–2006 NHANES with label use as exposure and BMI as outcome. Letting BMIi(t) be the potential outcome BMI under treatment t for subject i, we imputed two fixed sets of potential outcomes as follows:
SET 1: PATE(t,s) = 0 for all {t, s}. Here, BMIi(t) = BMIi for all , where BMIi is the observed BMI for unit i in the data set.
-
SET 2: PATE(t,s) ≠ 0 for all pairs {t, s}. Imputation of these potential outcomes were obtained using the following algorithm.
-
(1)
The principal components of X, the matrix of covariates listed in Table 1, were calculated. (Here, we excluded the squared terms for Metabolic equivalence and Meals away from home, as the inclusion of these variables led to erratic principal components. For more information on the principal components procedure, see Jolliffe57.)
-
(2)
All subjects were projected to the eigenvector (V1) that corresponded to the largest eigenvalues of X, .
-
(3)
BMIi(Ti), the potential outcome at subject is observed treatment assignment, was set as the observed outcome, BMIi.
-
(4)
For t ≠ Ti, the potential outcomes were imputed using the observed BMI outcomes of the subjects receiving other treatment levels whose PC1s were closest to that of subject i. Specifically, BMIi(t) = BMIj(t) = BMIj, ∀ t = Tj = Tj′ ≠ Ti, where |PC1i − PC1j| ≤ |PC1i − PC1j′| ∀ j′.
-
(1)
For Set 2, the resulting population average causal effects for the different usage level comparisons were: −0.14 (rare vs. never), −0.18 (some vs. never), −1.20 (often vs. never), and 0.32 (always vs. never).
At each simulation step, we applied the following algorithm:
-
(1)
Randomly select 15 of the covariates listed in Table 1 without replacement, and let Xsim be the matrix with these covariates
-
(2)
Estimate , the maximum likelihood estimate of γ from the multinomial logistic regression model based on the observed T and Xsim.
-
(3)
Let be the estimated probability that unit i received treatment t, based on the model in the previous step with , and sample Tsim,i based on .
-
(4)
Set the observed outcome BMIsim,i = BMI(Tsim,i).
It is important to note that both the treatment assignment mechanism and the outcome model are different than the GPS model and the linear regression model, respectively. We used BMIsim, Tsim, and Xsim to compare seven methods of estimating the PATE across pairs of label use dosages. The seven methods included four variations of subclassification and three commonly used comparison approaches. Subclassification techniques were generated by combining two factors, the number of subclasses used (K = 5, 15) and whether or not regression adjustment for all covariates in X was used within each subclass (yes, no). The three commonly used estimation methods included the naive differences in the sample means of BMIsim between those at different treatment levels, . The second method used standard regression adjustment of BMIsim on Tsim and X, with the causal effects estimated using the coefficients on Tsim. The last method relied on IPTW with normalized weights (equation 15). In this calculation, subjects receiving level t were weighted by 1/(Pr(Tsim = t)), where Pr(Tsim = t) was calculated using the proportional odds model.
At each simulation m, m = 1,…,2000, we estimated and its standard error, , for each of the seven estimating procedures and dose comparisons. This yielded simulated bias (biasm) and coverage indicators (coveragem, all coveragem) for each procedure at each m:
The mean bias, , was calculated for each of the 10 pairs of dose comparisons, as well as the standard deviation of bias. We present results for the four dose comparisons with never label use, as results for other mean bias calculations are similar. Two summary statistics for coverage rates, Average and Complete coverage, are also shown for each method, where
Because we did not adjust for multiple interval estimations, Complete coverage is expected to be lower than both Average coverage and the nominal level.
Results of the simulations are depicted in Table 5. Regression alone and subclassification with regression adjustment yielded the lowest for Set 1, PATEt,s = 0. All of the subclassification approaches showed lower and higher coverage rates for Set 2, PATEt,s ≠ 0, compared to the other methods. Among the subclassification methods implemented, a higher number of subclasses and the inclusion of regression adjustment tended to yield higher coverage rates and lower . IPTW estimates showed higher bias and lower coverage, possibly due to the misspecified treatment assignment model or the sensitivity of this procedure to large weights. With a binary treatment assignment, misspecified treatment assignment models and extreme weights can yield causal effects with larger bias and higher mean squared error (MSE).47,50,58
Table 5.
Simulated coverage, bias, and standard deviation of bias of seven PATE estimators using two hypothetical full data sets.
| PATE | Estimator | Averagea | Completeb | Rare | Some | Often | Always |
|---|---|---|---|---|---|---|---|
| Set 1 PATEt,s=0 | Subclass only, K = 5 | 0.91 | 0.60 | 0.18 (0.41) | 0.12 (0.34) | −0.07 (0.35) | 0.14 (0.34) |
| Subclass w/Regression, K = 5 | 0.91 | 0.72 | 0.01 (0.17) | −0.01 (0.13) | 0.01 (0.13) | −0.01 (0.15) | |
| Subclass only, K = 15 | 0.95 | 0.59 | 0.15 (0.43) | 0.08 (0.35) | −0.12 (0.35) | 0.08 (0.34) | |
| Subclass w/Regression, K = 15 | 0.96 | 0.74 | 0.00 (0.17) | −0.00 (0.14) | 0.00 (0.14) | 0.02 (0.16) | |
| Naive difference in means | 0.77 | 0.22 | 0.45 (0.40) | 0.50 (0.38) | 0.44 (0.45) | 0.66 (0.48) | |
| Standard regression | 0.94 | 0.70 | 0.01 (0.16) | 0.00 (0.14) | 0.00 (0.14) | −0.00 (0.14) | |
| IPTW | 0.88 | 0.57 | 0.67 (0.36) | 0.46 (0.4l) | 0.06 (0.49) | 0.58 (0.62) | |
| Set 2 PATEt,s≠0 | Subclass only, K= 5 | 0.97 | 0.80 | 0.08 (0.39) | 0.05 (0.28) | 0.06 (0.3l) | 0.06 (0.35) |
| Subclass w/Regression, K= 5 | 0.96 | 0.80 | 0.03 (0.38) | −0.02 (0.27) | 0.03 (0.31) | 0.03 (0.34) | |
| Subclass only, K = 15 | 0.96 | 0.80 | 0.06 (0.41) | 0.02 (0.30) | 0.00 (0.32) | 0.04 (0.37) | |
| Subclass w/Regression, K = 15 | 0.97 | 0.78 | 0.03 (0.43) | −0.01 (0.30) | 0.02 (0.34) | 0.04 (0.37) | |
| Naive difference in means | 0.83 | 0.26 | 0.29 (0.36) | 0.41 (0.28) | 0.73 (0.31) | 0.24 (0.34) | |
| Standard regression | 0.90 | 0.52 | −0.01 (0.36) | 0.05 (0.25) | 0.21 (0.27) | −0.31 (0.3l) | |
| IPTW | 0.76 | 0.30 | 0.64 (0.37) | 0.81 (0.33) | 1.93 (0.36) | 1.03 (0.40) |
Fraction of all intervals containing the true PATE.
Fraction of simulations with all 10 pairwise intervals containing the true PATE.
IPTW: Inverse Probability of Treatment Weighted; PATE: population average treatment effect
The results of our simulations suggest that when the estimated treatment assignment mechanism, in this case the proportional odds model, does not reflect the true assignment mechanism, a method involving subclassification with regression adjustment can outperform competing estimators of PATE for ordinal exposures. Further, combining subclassification with regression adjustment yields lower bias and higher coverage rates when compared to either method alone.
7. Discussion
The analysis presented here adds to that of Variyam and Cawley3 and Loureiro et al.,4 who dichotomized label use as sometimes or higher and found significant health benefits of increased label use. We showed that a significant benefit of reading nutritional labels comes only with an often or always frequency, relative to reading at a rare frequency. Such a conclusion could not be reached after dichotomizing the exposure or by other previously proposed methods. In fact, we estimated the treatment effect in our data set after dichotomizing label use into sometimes or higher and rare or never levels. Under E1 elimination mechanism, and using subclassification on the propensity score with K = 15 subclasses followed by regression adjustment, the estimated effect was not significant at the 0.05 nominal level (−0.05, 95% CI, −0.29, 0.19). Although the direction of this effect was similar to our findings, this analysis did not capture the potential benefits of reading labels frequently. We recommend that policies and instructions for label use be updated to specify the extent with which one needs to read labels to reap the health benefits of a lower BMI.
Subclassification on a GPS requires two assumptions, SUTVA and strong unconfoundedness. In our study, both assumptions seem reasonable given the design of the NHANES and the large number of observed covariates that were sufficiently balanced within each subclass; however, the true validity of both of assumptions is unknown. Sensitivity approaches have been developed for binary treatment effects,59–62 and a useful area for further research would examine the validity of these assumptions with an ordinal treatment. Further, because the NHANES is not a random sample, but a stratified random sample, our treatment effects generalize specifically to the population created by the sample; see Hernán et al.63 and Pearl and Bareinboim64 for related discussions on the generalizability of observational data.
Inference using propensity scores is a preferred method of answering causal questions for comparative effectiveness research, but generalizations of propensity scores to the multiple treatment setting are limited.65,66 The balance and estimation procedures provided here are important extensions of propensity score analysis to causal effects estimation for observational studies when the exposure is ordinal. These procedures yield, under proper assumptions, unbiased and transitive estimates of average treatment effects.
Acknowledgements
The authors would like to thank the anonymous reviewers for their comments and suggestions.
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: MJ Lopez was supported by the National Institute of Health (grant number R25GM083270).
Appendix 1. Proof of unbiasedness
Here, we show that is unbiased for PATEk(t,s). With as in equation (10), we model Yik|{Xik, T} within each subclass, where
Using and , the maximum likelihood estimates of αkt and αks, we have .67
Next, we show E[αkt − αks] = PATEk(t,s). As in Section 3.1, we assume the covariate distribution within each subclass is equal in expectation between those at different doses, that
| (16) |
By properties of the Normal distribution, E[Yik|Xik, T = t] = αkt + γkXik and E[Yik|Xik, T = s] = αks + γkXik, thus
Appendix 2
A2.1. Study population and those excluded
The below table gives study characteristics of subjects included and excluded from our study for having missing covariate values (% shown unless otherwise indicated).
| In study |
Eliminated |
||
|---|---|---|---|
| Covariate | Description | n = 4272 | n = 372 |
| Age | Mean (SE) | 47.3 (18.5) | 53.2 (20.8) |
| BMI | Mean (SE) | 28.8 (6.8) | 28.7 (6.4) |
| Metabolic equivalence | Mean (SE) | 8.6 (12.1) | 7.9 (4.5) |
| Diabetic | 74 | 74 | |
| Drug user | 8 | 5 | |
| Heard of diet guidelines | 43 | 29 | |
| Gender | Males | 48 | 48 |
| Nutritional label use | Never | 32 | 45 |
| Rare | 10 | 10 | |
| Some | 22 | 20 | |
| Most of the time | 19 | 12 | |
| Always | 17 | 14 | |
| Race | Hispanic | 22 | 39 |
| White | 51 | 39 | |
| Black | 23 | 19 | |
| Other | 4 | 3 |
A2.2. Covariates not included in propensity score model
The below table shows variables not included in our propensity score model (which were eventually balanced on through subclassification), and their original Kendall’s τb correlation with label use
| Variable | Description | Kendall’s τb | p |
|---|---|---|---|
| Blood pressure problems | Binary | 0.07 | <0.001 |
| Cocaine use | Binary | −0.01 | 0.60 |
| Marijuana use | Binary | −0.05 | <0.001 |
| Marital status (Yes vs. No) | Binary | 0.03 | 0.03 |
| Ever drink 5+ drinks per day | Numeric | -0.06 | <0.001 |
| Weight control | Binary | 0.11 | <0.001 |
A2.3. Covariates used and a brief description
| Type | Variable name | Description/levels |
|---|---|---|
| Numeric | Age | Years of respondent |
| Drinks per day | # of alcoholic drinks consumed per day over the past 12 months | |
| Household size | # of people in household | |
| Meals away from home | # weekly meals prepared outside of home | |
| Metabolic equivalence | Total metabolic activity rate | |
| Prior BMI | Calculated using respondent’s estimate of their weight from one-year ago and their current height | |
| Ordinal | Born to be fat? | Are people born to be fat? Respondent answers: strongly disagree, somewhat disagree, neither agree nor disagree, somewhat agree, or strongly agree |
| Education | HS/GED, some college or associate’s degree, or college graduate | |
| Food security | Household food security: low, marginal, or full | |
| Income | Household income: Less than $24,999/year, between $25,000 and $54,999/year, or greater than $55,000/year | |
| Weight thoughts | Respondent’s thoughts on his or her own weight: underweight, about the right weight, or overweight | |
| Nominal | Race | Hispanic, non-Hispanic white (white), non-Hispanic black (black), Other |
| Diabetic | Respondent has been told by a doctor of diabetes or pre-diabetic conditions | |
| Diabetic medicine | Respondent takes insulin or pills for diabetes | |
| Doct. advice 1 | Doctor’s advice to respondent: eat less fat for cholesterol | |
| Doct. advice 2 | Doctor’s advice to respondent: reduce weight for cholesterol | |
| Doct. advice 3 | Doctor’s advice to respondent: eat less fat for disease risk | |
| Doct. advice 4 | Doctor’s advice to respondent: reduce weight for disease risk | |
| Drug user | Respondent has used hashish, marijuana, cocaine, heroin, or methamphetamine in the past month | |
| Gender | Male, female | |
| Healthy diet | Respondent rates diet as good or better | |
| Heard of 5-a-day program | Respondent has heard of 5-a-day program | |
| Heard of diet guidelines | Respondent has heard of diet guidelines | |
| Heard of food guide pyramid | Respondent has heard of food guide pyramid | |
| Heart disease | Respondent suffers from coronary heart disease, stroke, or liver condition | |
| Pregnant | Respondent is pregnant | |
| Safe sex | Respondent has not had sex without a condom in the past year | |
| Smoker | Respondent smokes cigarettes |
Footnotes
Declaration of conflicting interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
References
- 1.Food and Drug Administration. Education Act of 1990. Public law 1990; 101: 104. [Google Scholar]
- 2.Food and Drug Administration. Regulatory Impact Analysis of the Final Rules to Amend the Food Labeling Regulations. Federal Register. 1993. [Google Scholar]
- 3.Variyam JN and Cawley J. Nutrition labels and obesity. Cambridge, MA: National Bureau of Economic Research, 2006. [Google Scholar]
- 4.Loureiro ML, Yen ST and Nayga RM Jr. The effects of nutritional labels on obesity. Agric Econ 2012; 43: 333–342. [Google Scholar]
- 5.Drichoutis AC, Nayga RM Jr and Lazaridis P. Can nutritional label use influence body weight outcomes? Kyklos 2009; 62: 500–525. [Google Scholar]
- 6.Royston P, Altman DG and Sauerbrei W. Dichotomizing continuous predictors in multiple regression: a bad idea. Stat Med 2006; 25: 127–141. [DOI] [PubMed] [Google Scholar]
- 7.Chambliss HO. Exercise duration and intensity in a weight-loss program. Clin J Sport Med 2005; 15: 113–115. [DOI] [PubMed] [Google Scholar]
- 8.Puetz TW, Flowers SS and OConnor PJ. A randomized controlled trial of the effect of aerobic exercise training on feelings of energy and fatigue in sedentary young adults with persistent fatigue. Psychother Psychosom 2008; 77: 167–174. [DOI] [PubMed] [Google Scholar]
- 9.United States Public Health Service Office of the Surgeon General et al. Physical activity and health: a report of the surgeon. Darby, PA: DIANE Publishing, 1996. [Google Scholar]
- 10.U.S. Food and Drug Administration. How to understand and use the nutrition facts label. http://www.fda.gov/Food (2013, accessed 19 September 2013).
- 11.American Heart Association. Reading food nutrition labels. http://www.heart.org/HEARTORG/GettingHealthy/NutritionCenter (2013, accessed: 19 September 2013).
- 12.American Diabetes Association. Taking a closer look at labels. http://www.diabetes.org/food-and-fitness/what-can-i-eat (2013, accessed: 19 September 2013).
- 13.Mayo Clinic. Nutrition and healthy eating. http://www.mayoclinic.com/health/nutrition-facts/NU00293 (2013, accessed: 19 September 2013).
- 14.Neuhouser ML, Kristal AR and Patterson RE. Use of food nutrition labels is associated with lower fat intake. J Am Diet Assoc 1999; 99: 45–53. [DOI] [PubMed] [Google Scholar]
- 15.Satia JA, Galanko JA and Neuhouser ML. Food nutrition label use is associated with demographic, behavioral, and psychosocial factors and dietary intake among African Americans in North Carolina. J Am Diet Assoc 2005; 105: 392–402. [DOI] [PubMed] [Google Scholar]
- 16.Rosenbaum PR and Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika 1983; 70: 41–55. [Google Scholar]
- 17.Joffe MM and Rosenbaum PR. Invited commentary: propensity scores. Am J Epidemiol 1999; 150: 327–333. [DOI] [PubMed] [Google Scholar]
- 18.Imai K and Van Dyk DA. Causal inference with general treatment regimes. J Am Stat Assoc 2004; 99: 854–866. [Google Scholar]
- 19.Rubin DB. For objective causal inference, design trumps analysis. Ann Appl Stat 2008; 2: 808–840. [Google Scholar]
- 20.Zanutto E, Lu B and Hornik R. Using propensity score subclassification for multiple treatment doses to evaluate a national antidrug media campaign. J Educ Behav Stat 2005; 30: 59–73. [Google Scholar]
- 21.Splawa-Neyman J, Dabrowska D, Speed T, et al. On the application of probability theory to agricultural experiments. Essay on principles. Section 9. Stat Sci 1990; 5: 465–472. [Google Scholar]
- 22.Holland PW. Statistics and causal inference. J Am Stat Assoc 1986; 81: 945–960. [Google Scholar]
- 23.Rubin DB. Estimating causal effects of treatments in randomized and nonrandomized studies. J Educ Psychol 1974; 66: 688. [Google Scholar]
- 24.Rubin DB. Randomization analysis of experimental data: the Fisher randomization test comment. J Am Stat Assoc 1980; 75: 591–593. [Google Scholar]
- 25.Stuart EA. Matching methods for causal inference: a review and a look forward. Stat Sci 2010; 25: 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Imbens GW. The role of the propensity score in estimating dose-response functions. Biometrika 2000; 87: 706–710. [Google Scholar]
- 27.Lechner M Identification and estimation of causal effects of multiple treatments under the conditional independence assumption. Heidelberg: Springer, 2001. [Google Scholar]
- 28.McCullagh P Regression models for ordinal data. J R Stat Soc B 1980; 42: 109–142. [Google Scholar]
- 29.Caliendo M and Kopeinig S. Some practical guidance for the implementation of propensity score matching. J Econ Surv 2008; 22: 31–72. [Google Scholar]
- 30.Rubin DB. Using propensity scores to help design observational studies: application to the tobacco litigation. Health Serv Outcomes Res Methodol 2001; 2: 169–188. [Google Scholar]
- 31.Lu B, Zanutto E, Hornik R, et al. Matching with doses in an observational study of a media campaign against drug abuse. J Am Stat Assoc 2001; 96: 1245–1253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Rubin D and Thomas N. Matching using estimated propensity scores: relating theory to practice. Biometrics 1996; 52: 249–264. [PubMed] [Google Scholar]
- 33.Dehejia RH and Wahba S. Causal effects in non-experimental studies: re-evaluating the evaluation of training programs. Cambridge, MA: NBER, 1998. [Google Scholar]
- 34.Imbens G and Rubin DB. Causal inference in statistics and the social sciences. Cambridge, UK: University Press, 2013. [Google Scholar]
- 35.Cochran WG and Rubin DB. Controlling bias in observational studies: a review. Sankhya 1973; Series A: 417–446. [Google Scholar]
- 36.Rosenbaum PR and Rubin DB. Reducing bias in observational studies using subclassification on the propensity score. J Am Stat Assoc 1984; 79: 516–524. [Google Scholar]
- 37.Austin PC. Balance diagnostics for comparing the distribution of baseline covariates between treatment groups in propensity-score matched samples. Stat Med 2009; 28: 3083–3107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Rubin DB. Using multivariate matched sampling and regression adjustment to control bias in observational studies. J Am Stat Assoc 1979; 74: 318–328. [Google Scholar]
- 39.Lunceford JK and Davidian M. Stratification and weighting via the propensity score in estimation of causal treatment effects: a comparative study. Stat Med 2004; 23: 2937–2960. [DOI] [PubMed] [Google Scholar]
- 40.Abadie A and Imbens GW. Large sample properties of matching estimators for average treatment effects. Econometrica 2006; 74: 235–267. [Google Scholar]
- 41.Du J Valid inferences after propensity score subclassification using maximum number of subclasses as building blocks. Cambridge, MA: Department of Statistics, Harvard University, 1998. [Google Scholar]
- 42.Benjamin DJ. Does 401 (k) eligibility increase saving?: evidence from propensity score subclassification. J Public Econ 2003; 87: 1259–1290. [Google Scholar]
- 43.Lechner M Program heterogeneity and propensity score matching: an application to the evaluation of active labor market policies. Rev Econ Stat 2002; 84: 205–220. [Google Scholar]
- 44.McCaffrey DF, Griffin BA, Almirall D, et al. A tutorial on propensity score estimation for multiple treatments using generalized boosted models. Stat Med 2013; 32: 3388–3414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Feng P, Zhou XH, Zou QM, et al. Generalized propensity score for estimating the average treatment effect of multiple treatments. Stat Med 2012; 31: 681–697. [DOI] [PubMed] [Google Scholar]
- 46.Little RJ. Missing-data adjustments in large surveys. J Bus Econ Stat 1988; 6: 287–296. [Google Scholar]
- 47.Kang JDY and Schafer JL. Demystifying double robustness: a comparison of alternative strategies for estimating a population mean from incomplete data. Stat Sci 2007; 22: 523–539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Huber M, Lechner M and Wunsch C. The performance of estimators based on the propensity score. J Econ 2013; 175: 1–21. [Google Scholar]
- 49.Kilpatrick RD, Gilbertson D, Brookhart MA, et al. Exploring large weight deletion and the ability to balance confounders when using inverse probability of treatment weighting in the presence of rare treatment decisions. Pharmacoepidemiol Drug Saf 2013; 22: 111–121. [DOI] [PubMed] [Google Scholar]
- 50.Stuart EA and Rubin DB. Best practices in quasiexperimental designs. Best Pract Quant Methods 2008; 155–176. [Google Scholar]
- 51.Lewis JE, Arheart KL, LeBlanc WG, et al. Food label use and awareness of nutritional information and recommendations among persons with chronic disease. Am J Clin Nutr 2009; 90: 1351–1357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Rubin DB. Bayesian inference for causal effects: the role of randomization. Ann Stat 1978; 6: 34–58. [Google Scholar]
- 53.D’Agostino RB. Tutorial in biostatistics: propensity score methods for bias reduction in the comparison of a treatment to a non-randomized control group. Stat Med 1998; 17: 2265–2281. [DOI] [PubMed] [Google Scholar]
- 54.Wooldridge JM. Inverse probability weighted estimation for general missing data problems. J Econ 2007; 141: 1281–1301. [Google Scholar]
- 55.Rubin DB. Multiple imputation after 18+ years. J Am Stat Assoc 1996; 91: 473–489. [Google Scholar]
- 56.Ahmed A, Husain A, Love TE, et al. Heart failure, chronic diuretic use, and increase in mortality and hospitalization: an observational study using propensity score methods. Euro Heart J 2006; 27: 1431–1439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Jolliffe I Principal component analysis. New York: Wiley Online Library, 2005. [Google Scholar]
- 58.Waernbaum I Model misspecification and robustness in causal inference: comparing matching with doubly robust estimation. Stat Med 2012; 31: 1572–1581. [DOI] [PubMed] [Google Scholar]
- 59.Rosenbaum PR. Design sensitivity in observational studies. Biometrika 2004; 91: 153–164. [Google Scholar]
- 60.Daniels MJ and Hogan JW. Missing data in longitudinal studies: strategies for Bayesian modeling and sensitivity analysis. Vol. 109, Boca Raton, FL: Chapman and Hall/CRC, 2008. [Google Scholar]
- 61.Hosman CA, Hansen BB, Holland PW, et al. The sensitivity of linear regression coefficients confidence limits to the omission of a confounder. Ann Appl Stat 2010; 4: 849–870. [Google Scholar]
- 62.Liu T and Hogan JW. Inference about ATE from observational studies with continuous outcome and unmeasured confounding. arXiv preprint arXiv:13036165 2013.
- 63.Hernán MA, Alonso A, Logan R, et al. Observational studies analyzed like randomized experiments: an application to postmenopausal hormone therapy and coronary heart disease. Epidemiology 2008; 19: 766–779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Pearl J and Bareinboim E. External validity: from do-calculus to transportability across populations. UCLA Department of Computer Science: DTIC Document, 2012. [Google Scholar]
- 65.Johnson ML, Crown W, Martin BC, et al. Good research practices for comparative effectiveness research: analytic methods to improve causal inference from nonrandomized studies of treatment effects using secondary data sources: the ISPOR Good Research Practices for Retrospective Database Analysis Task Force ReportPart III. Value Health 2009; 12: 1062–1073. [DOI] [PubMed] [Google Scholar]
- 66.Rubin DB. On the limitations of comparative effectiveness research. Stat Med 2010; 29: 1991–1995. [DOI] [PubMed] [Google Scholar]
- 67.Myers RH. Classical and modern regression with applications. Vol. 2, Belmont, CA: Duxbury Press, 1990 [Google Scholar]


