Technical Note: Assessment of sampling technique from feeders for copper, zinc, calcium, and phosphorous analysis

Abstract

Diet treatments were arranged in a split-plot design with the whole-plot consisting of 1 of 6 concentrations of dietary Cu (22 to 134 mg/kg total Cu) and the subplot using 1 of 2 sampling techniques (probe vs. hand grab). A total of 6 feeders per treatment were sampled using a brass open handle probe. The probe was inserted into the feeder 4 times to obtain a 900 g of sample. The hand-collected samples were obtained by inserting a bare hand into the feeder approximately 8 times to obtain a 900 g of sample. Within a feeder and sampling technique, subsamples (200 g) were created by using a sample splitting device. In addition to the 6 individual feeder samples, a subsample (33 g) from each individual feeder was pooled within dietary treatment and sampling technique to form a single composite sample (200 g). This process was repeated until 4 individual composite samples were created for each diet and sampling technique. Next, all samples were ground through a centrifugal mill and submitted for mineral analysis in duplicate for Cu, Zn, Ca, and P analysis. Results indicated variability when sampling feeders with a probe were reduced (P = 0.013) for Cu and marginally reduced (P = 0.058) for Ca when compared with hand-sampling. However, no evidence for differences was detected among sampling techniques for Zn and P for the individual feeder analysis. When samples were pooled from 6 feeders to form a single composite sample, there was no evidence for differences detected among sampling techniques for Cu, Zn, Ca, and P analysis. From these results, sampling frequency calculations were determined to assess sampling accuracy within a 95% confidence interval. Results indicated that the number of feeders or composite samples required to analyze was less for Cu, Zn, Ca, and P analysis when using a probe compared with a hand sampling. In summary, sampling with a probe is associated with less variability on an individual sample basis, but when individual samples are pooled to form a composite sample, there was no evidence for difference among sampling techniques. Our results suggest samples collected for these analyses with a probe and composited would be the best option to minimize variation and analytical costs.

INTRODUCTION

The implementation and monitoring of quality control and quality assurance systems and their standard operating procedures in feed mill operations are integral in assessing the overall success and profitability of livestock operations (Richardson, 1996). The proper sampling of finished feed and its subsequent analysis is a common standard operating procedure that is used for most swine nutrition studies to ensure that adequate diet manufacturing and delivery has been met, thus serving as a control measure for both nutritionists and feed mill managers. Interestingly, extension bulletins have been published on how to collect a representative sample as well as other publications describing analytical variation (Reese and Miller, 2006; AAFCO, 2015; Herrman 2011a, 2011b).

Researchers have reported laboratory to laboratory analytic variation (Cromwell et al., 1999; Cromwell et al., 2000) but did not provide information about the variation from the sampling procedure itself. Additionally, minerals have been reported as one of the most variable nutrients evaluated in feed stuffs (Berger, 1996). We are unaware of any published information comparing diet collection methods or indicating how many samples to collect and if they should be pooled or not to minimize variation. Therefore, this study was designed to evaluate different sampling procedures and methods to achieve an accurate swine diet mineral concentration assessment.

MATERIALS AND METHODS

General

For this study, feed was manufactured at a commercial feed mill in southwestern Minnesota. Ingredients were added to a ribbon mixer (Scott Model 6013, New Prague, MN) in 2,722-kg batches and mixed for 60 s. These mash diets were then transported and delivered to a commercial growing-finishing swine barn. The barn contained 42 pens that were each equipped with 1 cup waterer and a 4-hole stainless-steel, dry self-feeder (0.97 m tall and 1.52 m long; Thorp Equipment, Thorp, WI) with approximately 130 kg of feed capacity. Feed additions to each individual pen were made and recorded by a robotic feeding system (FeedPro; Feedlogic Corp., Wilmar, MN).

EXPERIMENTAL DESIGN AND DIETS

A total of 36 feeders were used with 6 feeders per dietary treatment. This study was carried out as a split-plot design with the whole plot using 1 of 6 dietary Cu concentrations ranging from 22 to 132 mg/kg total Cu included in the diet, and the subplot using 1 of 2 sampling techniques from each feeder (probe vs. hand grab). The base diets (A and D) did not contain any added Cu from CuSO₄ beside that provided from the trace mineral premix (16.5 mg/kg; Table 1). An additional 57 mg/kg copper sulfate (Prince Agri Products Inc., Quincy, IL) was added to the basal diets to for diets B and E and additional 114 mg was added to diets C and F. The 6 dietary treatments consisted of 3 corn-soybean meal-based diets with 20% corn DDGS formulated to contain 0.91% SID Lys or a second set of corn-soybean meal-based diets with 10% corn DDGS and formulated to contain 0.65% SID Lys. Nutrient profiles of the ingredients used in this study were based on NRC (2012) values to calculate expected dietary concentrations for Cu, Zn, Ca, and P.

Table 1.

Diet composition (as-fed basis)

Item, %	Diets1
	A, B, and C	D, E, and F
Corn	61.33	79.48
Soybean meal, 46.0% CP	16.52	8.39
Corn DDGS2	20.00	10.00
Calcium carbonate	1.20	1.13
Monocalcium P, 21.5% P	—	0.09
Salt	0.35	0.35
L-Lys HCl	0.37	0.32
L-Thr	0.04	0.07
L-Trp	0.01	0.02
Phytase3	0.01	0.01
Trace mineral premix4	0.10	0.10
Vitamin premix5	0.08	0.05
Copper sulfate6	—	—
Total	100	100
Calculated analysis
Standardized ileal digestible (SID) amino acids, %
Standardized ileal digestible Lys %	0.91	0.65
NE, kcal/kg	2,462	2284
Ca, %	0.55	0.50
P, %	0.40	0.34
Standardized digestible P, %	0.296	0.252
Cu, ppm	22	21
Zn, ppm	139	132

¹Diets A, B, and C were formulated for pigs ranging from 50 to 75 kg, whereas diets D, E, and F were for pigs ranging from 100 to 130 kg.

²Corn distillers dried grains with solubles.

³Optiphos 2000 (Huvepharma, Sofia, Bulgaria) provided 626 phytase units (FTU/kg) of diet with a release of 0.11% available P.

⁴Provided per kg of premix: Zinc 110,000 mg, Iron 110,000 mg, Manganese 33,000 mg, Copper 16,500 mg, Iodine 330 mg, and Selenium 300 mg.

⁵Provided per kg of premix: Vitamin A 7,040,000 IU, Vitamin D3 1,100,000 IU, Vitamin E 35,200 IU, Vitamin B12 26.4 mg, Riboflavin (B2) 6,160 mg, Niacin 35,200 mg, d-Pantothenic acid 22,000 mg, and Menidione 3,520 mg per kg.

⁶The base diets (A and D) did not contain any added Cu from CuSO₄ beside that provided from the trace mineral premix (16.5 ppm). An additional 57 ppm Copper Sulfate (Prince Agri Products Inc., Quincy, IL) was added to the basal diets B and E and additional 114 ppm was added to diets C and F.

Sampling and Chemical Analysis

Two sampling techniques (hand vs. probe) were tested on a total of 6 feeders per dietary treatment. A 1.6-m brass open handle probe (Seedburo Equipment Company, Des Plaines, IL), which contained 10 openings spaced approximately 5 cm apart, was used to collect probe samples. The probe was inserted at a 45° angle in relation to the bottom of the feeder, with slots facing upward and closed. After the probe was fully inserted, the slots were opened, and the probe was moved up-and-down (~15 cm) in several short motions. The slots were then closed, and the probe was removed from the feeder. Each sample obtained with a probe was approximately 250 g. Samples taken by hand were collected by inserting one’s arm into the feeder at a depth of about 30 cm. Next, the individuals hand, wrist, and forearm were rotated so that their palm was facing upward toward the top of the feeder with their fingers placed together and slightly bent. The individual then lifted their arm out of the feeder. Each sample collected by hand was approximately 125 g. Each sampling technique was repeated within a feeder until approximately a 900 g of sample was collected, approximately 4 times with the probe and 8 times by hand. To prevent cross contamination, the probe and individuals arm were wiped clean between feeders with a towel (Scott Shop Towel, Kimberly-Clark Worldwide, Inc., Dallas, TX). All samples were collected by the same individual. Samples were then transported back to the Kansas State University Swine Nutrition Lab (Manhattan, KS) and stored at −20 °C until analyzed.

Samples were split using a riffle splitter (Humboldt Mfg. Co., Norridge, IL) and ground using a 0.5-mm screen (Retsch Ultra Centrifugal Mill ZM 200; Haan, Germany) prior to compositing and analysis. A 200-g subsample from each individual feeder and sampling technique was collected for analysis. In addition, a subsample (33 g) from each individual feeder and sampling technique was collected and pooled within dietary treatment and sampling technique to form a 200-g composite sample. This process was repeated until 4 individual composite samples were created for each diet and sampling technique. All samples were submitted to Cumberland Valley Analytical Services (Hagerstown, MD) for Cu, Zn, Ca, and P analysis (method 985.01; AOAC International, 2000) using a Perkin Elmer 5300 DV ICP (Perkin Elmer, Shelton, CT).

Statistical Analysis

Data were analyzed as a split-plot design, where the levels of the whole-plot treatment factor (diet) were assigned to feeders (i.e., the whole-plot experimental units) in a completely randomized design. The subplot treatment factor was sampling technique, and the feed sample collected via a given sampling technique was considered the subplot experimental unit. The duplicate assays on each feed sample were assumed to be subsamples. The concentrations of each analyte were fit to a linear mixed model using the PROC MIXED procedure in SAS (SAS Institute, Inc., Cary, NC) with the default estimation method REML. The Kenward–Roger method was used to adjust the denominator degrees of freedom and correct the standard errors for bias (Littell, et al., 2006). Diet, sampling technique, and diet × sampling technique interaction were modeled as fixed effects. Feeder nested within diet and the feeder × sampling technique interaction nested within diet were modeled as random effects. Mean concentrations of the various treatment combinations were computed using the LSMEANS statement.

A graphical analysis of the estimated random effects associated with the sampling techniques (results not shown here) indicated possible heterogeneous variances for the two sampling techniques. Additionally, heterogeneous variance was assessed via a likelihood ratio test conducted by comparing the difference of the −2log likelihood statistics of the reduced model (with common variance for sampling technique) and the full model (with a separate variance for each sampling technique) to a chi-square distribution with 1 degree of freedom (Stroup, 2013). Heterogeneity was considered significant at P ≤ 0.05 and marginally significant between P > 0.05 and P ≤ 0.10.

Next, variance estimates from the appropriate model were used to calculate the number of samples needed to determine sampling accuracy with a given margin of error using a 95% confidence interval. To assess this, a margin of analysis was utilized where σ² = feeder variance + sampling technique variance + assay variance/2. It is important to note that the variance for the residual from the covariance estimate was divided by 2 because each sample was analyzed in duplicate at the lab. We then calculated the margin of error from ± 2 to ± 30 mg/kg using the observed variances for the hand and probe samples for the individual and composite feeder analysis.

RESULTS AND DISCUSSION

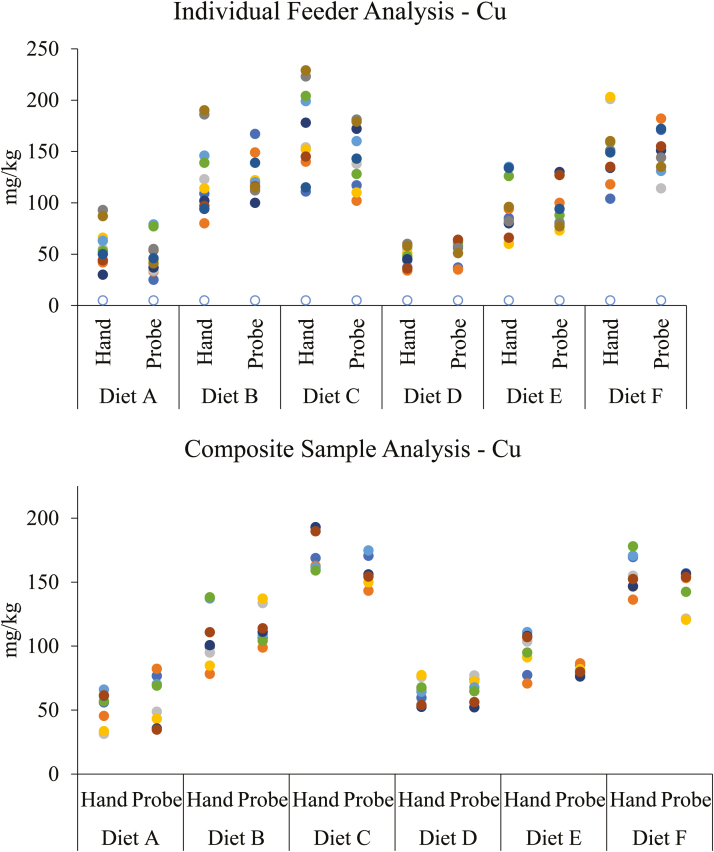
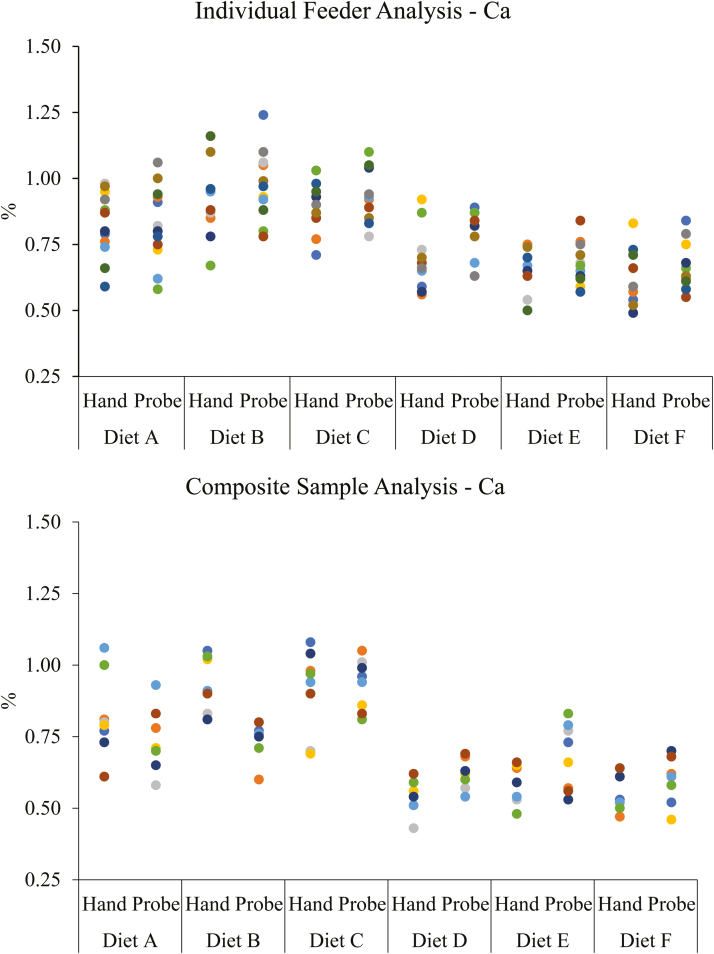
Results from chemical analysis of experimental diets can be found in Table 2. The observed variability when sampling feeders with an open handle probe was significantly reduced (P =0.013) for Cu (Figure 1) and marginally reduced (P = 0.058) for Ca (Figure 2) on the individual feeder analysis. There was no evidence for differences detected between sampling technique for Zn and P for the individual feeder analysis (P >0.527). Interestingly, when samples were pooled within sampling technique and dietary treatment to form a composite, there was no evidence for differences detected between sampling techniques for Cu, Zn, Ca, and P (P >0.221). Thus, these results would suggest that pooling samples to form a homogenized composite sample reduced total variability. Intuitively, this would be expected due to a homogenized sample being theoretically more uniform in composition throughout.

Table 2.

Chemical analysis of dietary treatments for Cu, Zn, Ca, and P

Item	Dietary Treatment
	A	B	C	D	E	F
Cu, mg/kg
Individual1	53	124	155	51	96	150
Composite2	55	110	163	66	88	151
Expected	22	79	136	21	78	134
Zn, mg/kg
Individual	159	154	162	139	165	141
Composite	151	154	145	153	145	139
Expected	139	139	139	132	132	132
Ca, %
Individual	0.83	0.98	0.91	0.73	0.67	0.64
Composite	0.78	0.83	0.92	0.58	0.63	0.56
Expected	0.55	0.55	0.55	0.50	0.50	0.50
P, %
Individual	0.51	0.51	0.50	0.39	0.39	0.40
Composite	0.51	0.50	0.51	0.42	0.41	0.41
Expected	0.40	0.40	0.40	0.34	0.34	0.34

All dietary samples were submitted to Cumberland Valley Analytical Services (Hagerstown, MD) for analysis. Expected values are based on NRC 2012 ingredient values.

¹Values reported are the mean of 24 values (duplicates from hand and probe samples across 6 feeders).

²Values reported are the mean of 16 values (duplicates from hand and probe samples across 4 composite samples).

Figure 1.

Distribution of analyzed mean Cu concentrations in diets (Hand: samples obtained by hand; Probe: samples obtained using a 1.6-m open handle probe).

Figure 2.

Distribution of analyzed mean Ca concentrations (Hand: samples obtained by hand; Probe: samples obtained using a 1.6-m open handle probe).

From these results, sampling frequency calculations were determined to assess sampling accuracy within a 95% confidence interval. To facilitate this, a margin of error analysis was utilized such that we wanted to estimate the mean concentration of a given diet with n samples and a margin of error (±) from the expected mean. Covariance parameter estimates generated from the heterogenous variances (full model) for Cu, Zn, Ca, and P were utilized in the calculation. Examples using the sampling frequency calculations are reported in Tables 3 and 4. For instance, if we wanted to estimate the mean concentration of 100 mg/kg Cu with a margin of error no larger or smaller than 15 mg/kg of Cu using a 95% confidence interval, we would need to sample 17 feeders by hand or 7 feeders by probe when analyzing on an individual feeder basis. Based on our pooling of samples from 6 feeders, we would need to submit 4 composite samples if sampling by hand and 2 composite samples if collected with a probe. It is also interesting to note that fewer samples at any given margin of error are needed for P analysis compared with Ca analysis. This is consistent with reported laboratory analytic variation ranges, which is less for P compared with Ca (AFCO, 2015) This is because sample size is a function of variability and the magnitude of the margin of error. Thus, analyses with less variability will result in less n required at a given margin of error.

Table 3.

Samples size calculations for a given margin of error and a 95% confidence interval

Margin of error, mg/kg	Cu				Zn
	Individual feeder analysis		Composite feeder analysis		Individual feeder analysis		Composite feeder analysis
	Hand	Probe	Hand	Probe	Hand	Probe	Hand	Probe
	No. of feeders1		No. of samples2		No. of feeders		No. of samples
±2	967	375	220	140	306	268	140	135
±4	242	94	55	35	77	67	35	34
±6	107	42	24	16	34	30	16	15
±8	60	23	14	9	19	17	9	8
±10	39	15	9	6	12	11	6	5
±15	17	7	4	2	5	5	2	2
±20	10	4	2	1	3	3	1	1
±25	6	2	1	1	2	2	1	1
±30	4	2	1	1	1	1	1	1

Values are calculated on the covariance parameter estimates obtained from the likelihood ratio test from the sampling and analysis of 6 individual feeders per dietary treatment or 4 composite samples across the individual feeders analyzed in duplicate.

¹No of feeders: refers to the number of feeders that would need to be sampled to be with (±) a given margin of error on an individual feeder analysis basis.

²No of samples: refers to the number of composite samples needed when pooling samples across 6 feeders to be within a given margin of error.

Table 4.

Samples size calculations for a given margin of error and a 95% confidence interval

Margin of error, %	Ca				P
	Individual feeder analysis		Composite feeder analysis		Individual feeder analysis		Composite feeder analysis
	Hand	Probe	Hand	Probe	Hand	Probe	Hand	Probe
	No. of feeders1		No. of samples2		No. of feeders		No. of samples
± 2	169	84	87	53	4	5	4	2
± 4	42	21	22	13	1	1	1	1
± 6	19	9	10	6	1	1	1	1
± 8	11	5	5	3	1	1	1	1
± 10	7	3	3	2	1	1	1	1
± 15	5	2	2	1	1	1	1	1
± 20	3	2	2	1	1	1	1	1
± 25	3	1	1	1	1	1	1	1
± 30	2	1	1	1	1	1	1	1

Values are calculated on the covariance parameter estimates obtained from the likelihood ratio test from the sampling and analysis of 6 individual feeders per dietary treatment or 4 composite samples across the individual feeders analyzed in duplicate.

¹No of feeders: refers to the number of feeders that would need to be sampled to be with (±) a given margin of error on an individual feeder analysis basis.

²No of samples: refers to the number of composite samples needed when pooling samples across 6 feeders to be within a given margin of error.

Based on these results, feed samples collected with a probe require fewer feeders sampled. These results are in agreement with Reese and Miller (2006), who indicated that sampling feed using a grain probe was the most accurate sampling technique due to its ability to deeply penetrate into feeders, bags, and other containers obtaining samples from different locations. We speculate that the probe sampling is potentially accounting for potential feed particle segregation within the hopper as finer and dense particles tend to push-away lighter particles and settle down toward the bottom, whereas larger and less dense particles rise to the top (Tang et al. 2006). Based on our results, a probed and pooled sample would lead to a lower number of samples and thus lower analytic cost for a given margin of error. One caution with the composite analysis is that this applies to composites of 6 feeders. Further investigation is needed to determine the optimum number of feeders that would be needed to make the composite pools.

In conclusion, equations can be used to generate the sample size needed to accurately determine nutrient concentrations in a diet. Our results suggest that the best option to minimize variation and reduce analytical cost is to collect samples with a probe from 6 feeders and composite before analysis.