Influence of particle size and shape on their margination and wall-adhesion: Implications in drug delivery vehicle design across nano-to-micro scale

Abstract

Intravascular drug delivery technologies majorly utilize spherical nanoparticles as carrier vehicles. Their targets are often at the blood vessel wall or in the tissue beyond the wall, such that vehicle localization towards the wall (margination) becomes a pre-requisite for their function. To this end, some studies have indicated that under flow environment, micro-particles have a higher propensity than nano-particles to marginate to the wall. Also, non-spherical particles theoretically have a higher area of surface-adhesive interactions than spherical particles. However, detailed systematic studies that integrate various particle size and shape parameters across nano-to-micro scale to explore their wall-localization behavior in RBC-rich blood flow, have not been reported. We address this gap by carrying out computational and experimental studies utilizing particles of four distinct shapes (spherical, oblate, prolate, rod) spanning nano- to-micro scale sizes. Computational studies were performed using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) package, with Dissipative Particle Dynamics (DPD). For experimental studies, model particles were made from neutrally buoyant fluorescent polystyrene spheres, that were thermo-stretched into non-spherical shapes and all particles were surface-coated with biotin. Using microfluidic setup, the biotin-coated particles were flowed over avidin-coated surfaces in absence versus presence of RBCs, and particle adhesion and retention at the surface was assessed by inverted fluorescence microscopy. Our computational and experimental studies provide a simultaneous analysis of different particle sizes and shapes for their retention in blood flow and indicate that in presence of RBCs, micro-scale non- spherical particles undergo enhanced ‘margination + adhesion’ compared to nano-scale spherical particles, resulting in their higher binding. These results provide important insight regarding improved design of vascularly targeted drug delivery systems.

Graphical Abstract

1. Introduction

The field of ‘drug delivery particles’ has focused significantly on: (i) the development of biomaterials for particle fabrication, (ii) surface-engineering of particles to modulate their circulation lifetime and (iii) utilization of disease-specific mechanisms to engineer the particles for site-selective action. The targets for such particles (and their drug payload) are often at the blood vessel wall or in the tissue compartments beyond the wall, such that their transport through the blood cell volume (mostly RBC) towards the vascular wall (i.e. margination) becomes a pre- requisite for their function (schematic in Figure 1). The factors that can influence the distribution and margination of particles in blood flow have undergone limited exploration so far. Establishment of the enhanced permeation and retention (EPR) mechanisms for nanoscale particles to leak across the endothelial barrier into the tumor tissue^{1, 2}, as well as, the benefit of high surface-to-volume ratio of nanoparticles to enhance biointeractions and payload delivery^{3, 4}, have led to most particulate drug delivery systems being designed as spherical nanoparticles. The size of such nanoparticles is usually in the range of 20-200 nm, since particles smaller than that are rapidly cleared by the kidney while particles larger than that have lower circulation lifetime due to rapid macrophagic uptake.^5–9 Some drug delivery approaches have also looked into micro-scale particles. In this domain, particles > 3µm in diameter pose the risk of occluding microvascular capillary networks and also show higher macrophagic uptake (hence rapid clearance). ^9–11 In addition, this microscale range is too big for EPR-based extravasation and uptake into the tissue compartments (e.g. in tumors), since the endothelial junctions in disease- associated leaky vasculature are in the 50-500 nm range.^12–15 Thus, the manufacture of particulate drug delivery systems has been primarily guided by design requirements for evading rapid macrophagic uptake, avoiding microvascular occlusion, minimizing renal clearance and facilitating extravasation (especially for cancer-targeted drug delivery), and not necessarily considering the effect of particle geometry on their interactions with the components of the blood flow volume, especially RBCs. A limited number of computational studies in the past have examined the potential effect of particle size in their interaction with RBCs and resultant vascular distribution, and even fewer experimental studies have been reported especially involving the presence of RBCs in the experimental set-up. For example, experimental studies were done with polymeric microspheres 5–20 µm diameter, decorated with ligands to attach to P- selectin-coated surfaces under flow in phosphate buffered saline (i.e. PBS only) and these studies showed that larger particles in that size range had reduced retention on target surface.¹⁶ Similar studies were carried out to analyze the ‘non-specific’ adhesion of microspheres on endothelial monolayer in a flow chamber in RBC-free environment and similar trends were observed.¹⁷ Further studies in PBS with spherical particles having diameters of 50, 100, 200, 500, and 750 nm and 1, 6, and 10 µm, showed that particles >500 nm in diameter are influenced more by gravitational forces to localize towards the wall, whereas particles <500 nm in diameter are influenced more by Brownian motion.¹⁸ Several recent computational studies, considering RBCs in flow volume, have indicated that nano-scale particles require a contribution of external forces beyond just hydrodynamic forces for effective margination towards the wall and that under hemodynamic flow, micro-scale particles undergo higher margination.^19–21 A few recent experimental studies with polymeric spherical particles in nano-scale and micro-scale show that in the presence of RBCs in laminar and pulsatile flow, micro-scale particles marginate better than nano-scale particles^22–25, but similar size-range studies have not been reported across various shape parameters of particles and at different shear flow ranges.

Figure 1.

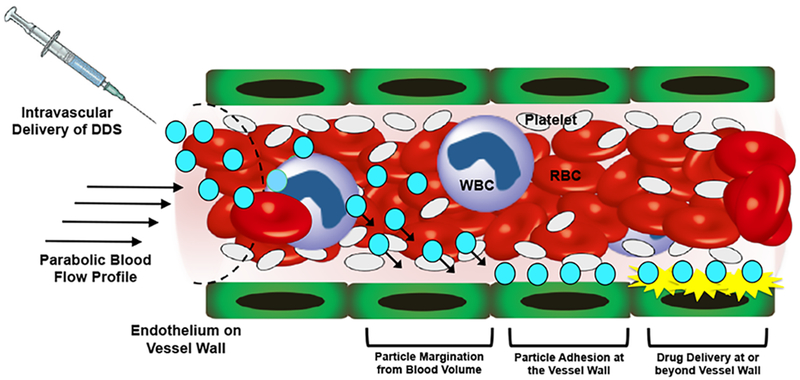
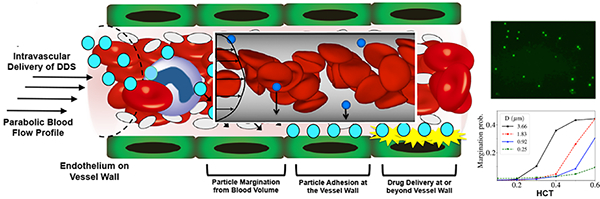
Schematic representation of the intended trajectory of particulate drug delivery systems (DDS) upon introduction into blood flow via intravascular administration; In parabolic flow profile, RBCs congregate towards the center of the flow volume while platelets are pushed towards the vessel wall --- a process termed as ‘margination’; Many DDS for their intended function would need to traverse through the RBC flow volume to marginate towards the vessel wall, undergo non-specific or ligand-mediated specific adhesion at the wall (e.g. to the endothelium or other targets) and render therapeutic delivery for action at or beyond the wall.

In the context of particle shape, most drug delivery approaches to date have looked into spherical particles since most particle fabrication processes (e.g. self-assembly, nano- and micro- precipitation, emulsion etc.) preferably produce spherical particles due to thermodynamic favorability. The seminal studies comparing worm-shaped micelles (filomicelles) versus spherical micelles and comparing spherical particles with ellipsoidal particles, demonstrated the influence of shape on circulation lifetime and macrophagic clearance.^26,27 Some computational studies in the past have indicated that spherical particles tend to follow flow streamlines with hydrodynamic forces correlative to their radius, such that lateral margination towards the wall can be rendered only by external forces such as gravity and electromagnetic fields.^19,20 In contrast, non-spherical particles (e.g. ellipsoids, rods etc.) can undergo significant lateral drift by virtue of their rotational motion (tumbling) under flow even in the absence of external forces.^19,20 Such computational models were further tested by experimental studies with silica particles of discoid, spherical and hemispherical geometries but these studies were done in an RBC-free set- up.^28,29 A recent computational study further reported that in presence of RBC flow, non- spherical particles are more likely to undergo large lateral drifts in blood flow to move into a cell-free layer away from the RBC volume and closer to the wall. ³⁰ Several computational studies have also indicated that anisotropic non-spherical shapes may have a higher extent of adhesion to target surfaces or cells due to higher surface area of interaction.^31–34 Interestingly, a recent study using ellipsoidal particles showed that the beneficial effects of anisotropic shape toward margination in the vascular compartment occur preferably more for microscale particles than nanoscale particles, suggesting a significant interplay between shape and size in determining ‘margination + stable adhesion’.³⁵ Therefore different computational and experimental studies have provided only in part evidence that both ‘particle size’ and ‘particle shape’ have distinct influences on particle behavior in blood flow, but the integration of both of these factors across a broad range of geometries in presence of RBC flow has not been reported. This emphasizes the need for detailed computational and experimental studies to systematically analyze the behavior of particles from nano- to micro-scale in size and with varying shapes in presence versus absence of RBC flow. To this end, we report on the computational and experimental analysis of the influence of particle geometry and size on their vascular margination and wall adhesion in presence of RBC flow volume, utilizing neutrally buoyant model polystyrene particles with size ranging from 100 nm-4.5 µm diameter and shapes varying as spherical, oblate (discoid), prolate and rod. Also, to impart the property of specific adhesion of marginated particles at the wall, we utilized biotin coating of the particles and avidin coating of the wall.

2. Materials and Methods

2.1. Materials

Fluoresbrite^® YG Carboxylate Polystyrene (PS) Microspheres (0.2, 0.5, 2 and 4.5µm diameter) were purchased from Polysciences, Inc. (Warrington, PA, USA). Polyvinyl alcohol (PVA, fully hydrolyzed), glycerol, mineral oil, and phosphate-buffered saline (PBS) tablets (pH 7.4) were purchased from Sigma Aldrich (St. Louis, MO, USA). EZ-Link^™ Amine-(PEG3)-Biotin, 1-ethyl-3-(3-dimethylaminopropyl) carbodiimide hydrochloride (EDC), 2-(N-morpholino) ethanesulfonic acid (MES, 0.5M, pH 5.5) buffer solution, Pierce™ Biotin Quantitation Kit and streptavidin coated plates (96 well, black) were purchased from Thermo Fisher Scientific (Waltham, MA, USA). Biotin and fluorescein isothiocyanate (FITC) labeled PS beads (50, 100, and 500 nm diameters) were purchased from Nanocs Inc. (Boston, MA, USA). Plain glass microscope slides (3” × 1” × 1 mm) were obtained from Fisher Scientific and a circular area 150 mm in diameter (templated using an O-ring) was coated with avidin to allow specific adhesion of biotin-coated particles. This circular area was maintained at least 50 mm from one edge of the slide so as to allow a fully developed flow interact with the coated area with respect to that edge placed at the entry point of a flow. For microfluidic studies, a Parallel Plate Flow Chamber (PPFC) with rectangular flow channel dimension (length: 750 mm, width: 10 mm, height: 254 µm) was obtained from GlycoTech (Gaithersburg, MD, USA). The glass slides mentioned above with the avidin-coated circular area were sealed inside the PPFC and fluid flow was maintained via silicone tubing and fixtures utilizing a programmable pump (Masterflex L/S model 7518-00 made by Cole-Parmer Instrument Company). For all experimental studies, human blood was obtained by venipuncture from healthy donors with informed consent, utilizing a phlebotomy protocol approved by the Institutional Review Board (IRB) at University Hospitals of Cleveland. RBCs (i.e. hematocrit or HCT) were separated by centrifugal fractionation (500×g for 10 minutes) and the RBCs were reconstituted in isotonic buffer at controlled volume fraction to provide fluids with various HCT conditions that was subsequently used for the microfluidic experiments.

2.2. Computational Models

For particle margination and adhesion modeling and analysis, mesoscopic simulations were performed using in-house highly parallel program based on the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) package.³⁶ The mesoscale fluid models were employed in the study for modeling hydrodynamic interactions. Dissipative particle dynamics (DPD)^37,38 and smoothed DPD (SDPD)^39,40 methods were used for 2D and 3D simulations of blood flow, respectively. Both methods model hydrodynamic effects and properly represent thermal fluctuations.⁴¹ While the fluid properties in SDPD can be set directly, in DPD they need to be calculated a priori for a specific set of parameters. Red blood cell (RBC) membranes in 3D are modeled by triangulated bead-spring networks, which conserve their area and volume and possess bending rigidity and shear elasticity.^42–44 The model and simulation parameters were adapted from previous reports.^43,45 The particles were modeled by the same bead resolution and kept rigid. In 2D, RBCs were modeled by closed polymer chains with bending rigidity and area conservation. The particles were modeled by rigid closed polymers with a similar resolution. For a detailed description of the membrane and particle models, see Supplementary Information Section S.1, and Tables S.1 and S.2.

To further assess the importance of other factors influencing particle adhesion and retention, we investigated via simulation the drag force exerted on particles by the fluid and quantify their adhesion strength defined by the total number of ligand interactions within the particle adhesion area. The drag force is obtained from simulations of a fixed particle at the wall subjected to shear flow, since the total drag force on an adhered particle consists of pressure and shear stress components. The pressure contribution is proportional to the cross-sectional area perpendicular to the flow direction, while the shear force is governed by the surface area of the particle. Both are proportional to the square of a characteristic size of the particle.⁵⁷ For our simulations, a pressure driven flow was induced by applying a constant force to fluid particles, which were confined in a slit together with RBCs and rigid micro/nano particles. The boundary conditions in the flow and vorticity directions were periodic. The walls were composed of frozen fluid particles with the same density and pair correlation function as those for the fluid. Furthermore, an adaptive shear force was applied to the fluid particles within a cutoff distance from the walls in order to have no-slip boundary conditions.^46,47 This cutoff distance is around tens of nanometers, an assumption motivated by the distance of common adhesive interactions.⁵⁸ Penetration of fluid particles into the walls was prohibited by bounce-back reflections. The fluid was coupled to the membranes by the DPD forces, excluding conservative part.⁴⁵ Additional details about the computational and simulation parameters are given in Supplementary Information Section S.1, Tables S.1-S.3, and Figure S.1.

2.3. Fabrication and characterization of particles

Non-spherical oblate, prolate and rod-shaped particles were fabricated using a previously reported one-dimensional and two-dimensional polymer film stretching method.⁴⁸ The process schematic is shown in Figure 4A. Briefly, ~10⁸ PS spheres were suspended in a 6.25% w/V aqueous PVA solution. 1.25% v/V glycerol was added as a plasticizer to lower the glass transition temperature of the films and facilitate stretching. The mixture was then cast into a film and dried for ~24 hours at room temperature to immobilize the PS particles. The dried films were mounted on a 1-D or a 2-D mechanical stretcher to obtain prolates/rods and disks, respectively. Further, the films were heated for 5 minutes at 120°C in mineral oil and stretched to obtain the desired geometry. The aspect ratio (AR) was controlled by limiting the extent of stretching. The stretched films were cooled to room temperature for 10 minutes to allow solidification of the particles in their new shape. Suitable sections were cut from the stretched films, dissolved in 70 ℃ MilliQ water overnight and centrifuged for particle recovery. The isolated particles were subsequently washed multiple times with MilliQ water via centrifugation and finally passed through a 100µm filter, for the removal of residual PVA. Concentration (w/V) of the respective particle suspensions was determined by lyophilization of a known sample volume. For characterization using scanning electron microscopy (SEM), sample preparation involved vacuum drying of 10µL particle suspension on an aluminum stub, followed by coating with palladium (Hummer 6.2 Sputtering System, Anatech Ltd., Union City, CA). The sputtered samples were imaged using the Sirion 400 SEM (FEI Company, Hillsboro, OR) at an acceleration voltage of 5 kV and a working distance of 5mm. Particle dimensions were measured from the SEM images using Metamorph image acquisition and analysis software (Universal Imaging Systems, Downingtown, PA). For particle surface-decoration with biotin, the spherical and non-spherical fluorescent carboxylate polystyrene particles were conjugated with EZ-Link™ Amine-(PEG3)-Biotin using carbodiimide coupling chemistry and stored at 4°C in PBS. Briefly, 12.5mg particles were washed twice with 50mM MES buffer and the carboxyl groups on their surface were activated with EDC for 15 minutes and further mixed with an excess of (900µg) the biotin reagent in a total volume of 500µL in a microcentrifuge tube. The reaction was allowed to run overnight at room temperature with gentle end-to-end mixing on a tube revolver. Particles were then washed twice with PBS to remove the unconjugated biotin and N-acyl urea by-product, before resuspending them at a concentration of 1mg/mL until ready to be used in the binding experiments. Figure 5A shows a schematic of this surface-modification strategy for the particles with biotin. The relative surface density for biotin modifications on the various particles were theoretically estimated. Total particle volume remains constant during stretching, governed entirely by the volume of initial sphere and thus, by the ESD. Dimensions and surface area of the stretched particles were estimated from their 2D SEM projections and mathematical volume equations for their respective geometries. Owing to the hydrophilic nature of the carboxylate functional groups on the polystyrene particles, it was assumed that majority of these ligands were conserved on the surface post stretching. However, their surface density decreases due to the generation of new surface area during the spherical to non-spherical shape transition. For a fixed number of ligands, the ligand surface density is inversely proportional to the surface area. Therefore, the relative carboxylate density can be calculated using the ratio of the non-spherical to spherical surface area. Supplementary Figure S.7 shows representative SEM images of biotin-coated particles. The conjugation with biotin was qualitatively validated using a binding assay through a 30- minute static incubation of the biotinylated and non-biotinylated (control) particles in streptavidin-coated well plates. The well plates were washed with PBS thrice and the fluorescence signal from bound particles was measured using Tecan M220 Infinite Pro plate reader. Furthermore, a standard 4’-hydroxyazobenzene-2-carboxylic acid (HABA) assay was used to quantify the amount of biotin conjugated onto the particle. Briefly, absorbance measurements were performed at 500 nm before and after addition of reaction supernatant to HABA solution, respectively. The decrease in absorbance is directly proportional to the amount of biotin present in the supernatant. Therefore, the amount of biotin attached to the particles was estimated as the difference between amount of biotin reagent added to reaction mixture and amount of biotin reagent in supernatant, determined from HABA assay. Supplementary Figure S.8 shows HABA-based biotin characterization for various particle geometries.

Figure 4.

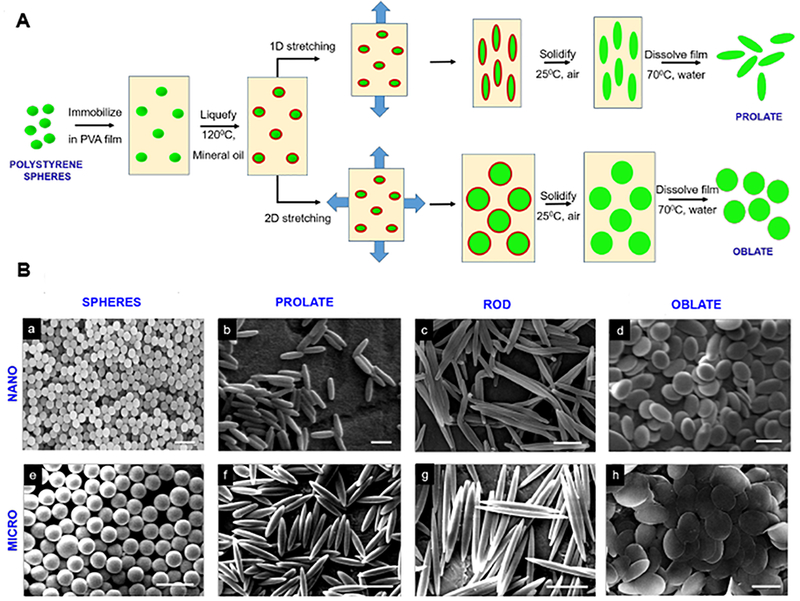
[A] Particle fabrication schematic where 1D and 2D heat-stretching techniques were employed on spherical polystyrene (PS) particles to yield non-spherical (prolate, oblate and rod shaped) particles; [B] Representative scanning electron microscopy (SEM) images of particles with various geometries, obtained by stretching nanoparticles (a-d, ESD 0.2 µm, scale bar: 0.5 µm) and microparticles (e-h, ESD 2 µm, scale bar: 5 µm).

Figure 5.

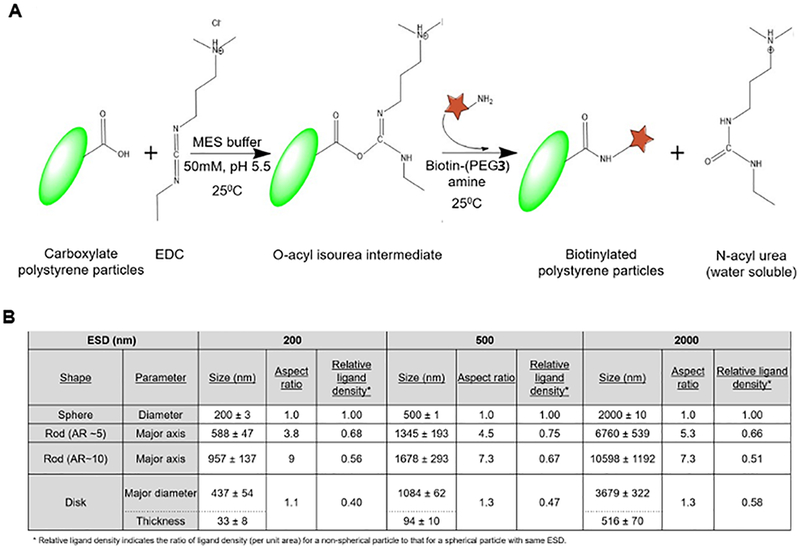
[A] Reaction scheme for the surface modification of the particles with biotin by carbodiimide-mediated conjugation with carboxylate motifs on particle surface; [B] Dimension calculations and relative surface ligand density estimation for particles with various geometries.

2.4. Flow chamber experiments

In the parallel plate flow chamber (PPFC) experimental set-up (schematic shown in Figure 5A) the flow was assumed to be Newtonian and accordingly, the wall shear stress (τW) was approximated to be proportional to the flow rate, assuming a constant viscosity value equivalent to plasma viscosity (0.015 cP). The flow rate was modulated to render low (5 dyn.cm⁻²), medium (30 dyn.cm⁻²) and high (60 dyn.cm⁻²) τW values that cover physiological vascular shear ranges. Varying suspensions of biotinylated fluorescent (FITC-tagged) particles in isotonic buffer (i.e. no HCT) or in isotonic buffer containing 20% or 40% v/v RBCs (i.e. controlled HCT) were flowed in a recirculating loop over the avidin-coated glass slides sealed within the PPFC. The avidin-coated region was ~ 5 cm from the flow inlet to allow particle margination in a fully developed flow. The rest of the slide was coated in 1% BSA. The particle concentration in the suspensions was kept constant at 1.0 × 10⁷ particles. The particles tested were: spheres (4.5 µm, 2 µm, 500 nm, 200nm, 100 nm), oblate ellipsoids (2 µm, 500 nm, 200 nm), prolate ellipsoids (2 um, 500 nm, 200 nm) and rods (2 µm, 500 nm, and 200 nm). The slides were imaged under a Zeiss Axio-Observer inverted fluorescence microscope, and images were acquired at 5 minute, 15 minute, and 30 minute time points after flow initiation. Images were analyzed to quantify ‘bound’ particle on the avidin-coated region. Twelve images were taken per experimental condition for analysis. To ensure that the image acquisition and analysis was representative of the whole avidin-coated area, each circular avidin-coated surface region was divided into quadrants with three images captured per quadrant. Images were analyzed using ImageJ (NIH) to quantify ‘bound’ particles per unit area. The overall ‘mode of action’ is that the ‘bound’ particle count over time is a cumulative equilibrium output of ‘margination + adhesion + retention’.

2.5. Statistical analysis

Statistical analysis was done using MiniTab to calculate the mean and standard deviation of each set of images. Images that contained a particle count outside of the standard deviation were not included. Outliers may have occurred due to the way the avidin dried or the particles could have aggregated in one location. The mean and standard deviation were divided by 0.07 mm², the area of each image, to represent the data in terms of the number of particles per unit area. The mean value from the control surface (no avidin) was then subtracted from the mean of the experimental surface. This was to account for differences in fluorescent intensity on imaging and any variations between ligand density on the particle surface between particles from different sources. Thus, the analysis measured specific binding of the particles to the avidin surface.

3. Results

3.1. Computational Analysis of Particle Margination

As described previously, RBCs play an important role in the process of particle margination towards the vessel wall. RBCs experience a hydrodynamic lift force from the vessel walls that arises from the pressure differences between the different sides of the cells. Such force also depends on cell (and particle) size, deformability, and dynamics, as investigated theoretically, in simulations, and in experiments.^49–51 Since RBCs are highly deformable with a non-spherical (biconcave discoid) shape, and since the lift force on such deformable particles is generally stronger than on rigid ones, therefore the lift force on RBCs is much stronger than that on rigid drug carriers. ^49–51 Due to this lift force, flowing RBCs migrate to the center of the vessel and push the other cells (and particles) toward the walls (Figure 2A). In addition, the migration of RBCs to the center of the flow creates a RBC free layer (RBC-FL), whose thickness (height) depends on several properties, such as hematocrit, shear rate, and channel size.^{52, 53} By virtue of RBCs moving towards the center flow volume, micro- and nano-particles are pushed into the RBC-FL (i.e. margination).^21,54 In order to quantify particle margination, ‘margination probability’ was defined as a probability of particles to be in a layer adjacent to the vessel walls of thickness 𝛿 (Figure 2B). It is important to note that this definition is sensitive to the way 𝛿 is selected. One of the most commonly used selections is to set 𝛿 as the thickness of RBC-FL.^21,55 For our studies, a different definition of 𝛿 was employed motivated by the thickness of a layer where particle adhesion can potentially occur, as 𝛿 = D_m + h , where D_m is the largest dimension of a particle, and h is the thickness of a layer which presents high probability of adhesion for particles in it. Thus, 𝛿 characterizes the probability of possible contact and particle adhesion with the wall.

Figure 2.

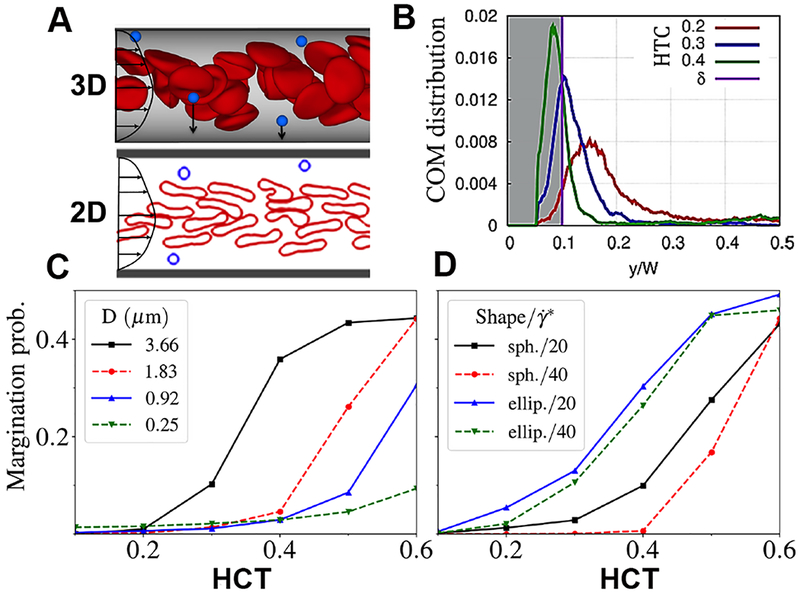
Computational results on particle margination trends; [A] Migration of RBCs in the pressure-driven flow toward the center of the vessel due to hydrodynamic lift force from the walls, leads to particle margination; 2D simulations reproduce qualitatively the margination trends in 3D; [B] Center-of-mass (COM) distribution of micro-particles in the vessel in blood flow with different hematocrits; [C] Margination probability of spherical particles of different sizes as a function of hematocrit (HCT) where margination probability is defined as the area under the COM distribution with a pre-defined distance δ away from the wall with δ = D_m + h, where D_m is the largest dimension of a particle, and h is the thickness of a layer which presents high probability of adhesion for particles in it (here, h = 100 nm); [D] Margination probability of micro-particles with spherical and ellipsoidal shapes for different shear rates as a function of HCT; Panels C and D show the 2D simulation results, indicating that microscale particles marginate more than nanoscale particles in presence of physiological HCT; furthermore, ellipsoidal microparticles possess a slightly higher margination probability compared to their spherical counterparts in presence of physiological HCT.

The most important factor in particle margination is the volume fraction of RBCs or hematocrit (HCT). As the hematocrit in blood vessels increases, RBCs fill more space in the vessel center and thereby force more particles toward the walls. This anticipated trend is illustrated in Figure 2C and 2D. The size of particles strongly affects this margination propensity. To that end, our simulations indicate that larger micro-particles marginate better in comparison to smaller nano-particles (Figure 2C). In fact, it has been demonstrated recently that nanoparticles because of their smaller size can easily occupy available space within RBC volume in the bulk flow (i.e. remain in the gaps between flowing RBCs), and therefore, their margination is not very efficient.²¹ This was also used to leverage nanoparticle attachment to RBCs for ‘hitchhiking’ technology in drug delivery.⁵⁶ Shape of the particles is also important in margination. Simulation results in Figure 2D show that the margination probability of ellipsoidal particles is larger than that of spherical particles for equivalent particle volumes. These findings are also consistent with previous investigation by 3D simulations.³⁰ Once in the RBC-FL, ellipsoidal particles can also make a more frequent contact with the wall in comparison to spherical particles, since the largest dimension of ellipsoids is larger than the radius of a sphere with the same volume. Furthermore, by tumbling in shear flow within the RBC-FL, ellipsoidal particles collide with RBCs more frequently than spherical particles so that they are more efficiently pushed toward the wall (i.e. higher margination).

3.2. Computational Analysis of Particle Adhesion

Since particle margination characterizes the frequency of particle contact with the wall, it therefore directly influences the adhesive interactions of particles to the wall. Also, retention of adhered particles on the wall is influenced by the drag force exerted on particles by the fluid and the resistance to lift-off imparted by the overall adhesion strength stemming from the total number of ligand interactions within the adhesion area. Figure 3 summarizes the results of these simulations for adhesion. The schematic of the different shapes of particles adhering to the wall is illustrated in Figure 3A, while Figure 3B shows how drag force can change depending on the shape as well as orientation (w.r.t. wall) of particles. The results indicate that the drag on particles of different shapes for a fixed particle volume is not extremely different from each other, and that the drag on prolate or rod-like particles placed perpendicular to the flow is the highest. It is also important to note here that in Stokes flow regime, the lift force is zero for symmetric rigid particles. Thus, spherical rigid particles will experience zero lift force; however, if these particles have a low probability of margination to the wall (e.g. spherical nanoparticles) or have a low adhesion strength at the wall, then their localization at the wall under blood flow conditions will be low. Adhesion strength of particles to the wall is directly associated with the surface area of the particle that participates in adhesion. Figure 3C shows a schematic of that for fixed particle volume, where non-spherical ellipsoidal shapes have a larger adhesion area in comparison to spherical particles. In case of specific molecular interactions, the adhesion strength also depends on the number of motifs (e.g. ligands) on the particle surface, which are able to interact with corresponding motifs (e.g. receptors) at the wall. For this reason, the adhesion area is calculated as the area of the particle that is located within a cutoff distance of approximately tens of nanometers, based the distance of common adhesive interactions.⁵⁸

Figure 3.

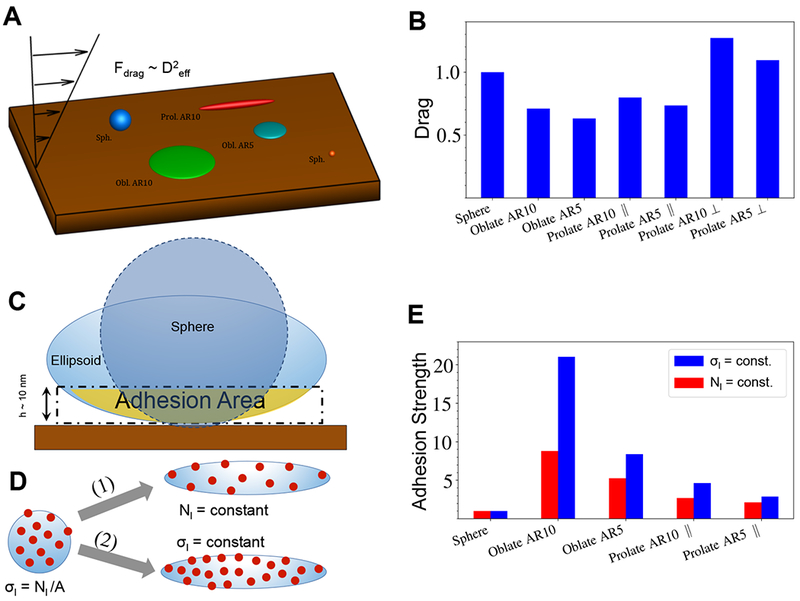
Adhesion of microparticles and nanoparticles; [A] Schematic of adhesion simulations where the drag force is proportional to the squared effective diameter (height) of the particle and this drag force is calculated for particles fixed at the wall; [B] Hydrodynamic drag force on particles with an equal volume normalized by the drag force on the spherical particle, showing that oblate ellipsoidal particles lying parallel to the surface will have the least extent of drag force on them; [C] Adhesion area is referred to the area on the particle (spherical or non- spherical) surface in a close distance of h ~ 10 nm from the wall where non-specific or specific interactions can prevail and adhesion strength is defined as the output of total ligand interactions within the adhesion area in a close distance h = 10 nm to the wall and is normalized by a value for the spherical particle; [D] Illustration of two different possibilities for ligand decoration on the DDS particle surface: (i) constant ligand density (σ_L=const) and (ii) constant total ligand number (N_L=const) at the particle surface; for experimental studies reported the particle manufacture process kept N_L constant; [E] Analytically calculated adhesion strength for different particle shapes shows that oblate shapes will have the highest strength of adhesion for both σ_L= constant and N_L= constant scenarios.

Furthermore, for ligand-decorated particles undergoing specific interactions with receptors on cells or proteins at the wall, there are two different ways for comparison of their adhesion between various particle geometries (Figure 3D): (i) setting a constant number of ligands 𝑁_L for all shapes (Figure 3D - path 1) or (ii) setting a constant ligand density 𝜎_L independent of shape (Figure 3D - path 2). Path 1 describes the situation when spherical particles are surface- functionalized with a certain number of ligand-anchoring motifs or ligands themselves, and then they are stretched into their final shape with ligands finally anchored, which corresponds to our experimental procedure for particle fabrication and surface modification (see Methods). Path 2 corresponds to the case when different geometry particles are first manufactured and then their surface saturated with a constant density of ligands. To this end, one should note that per Path 1, the overall surface density of ligands would be reduced in transitioning from spherical to non-spherical shapes. However, in such scenarios low surface density of ligands might be sufficient for overall firm adhesion (and retention) of the particles if the individual ligand-receptor molecular interaction is strong enough (high affinity, e.g. biotin-avidin interaction used in current studies) or when the overall interaction of multiple ligands with corresponding receptors occurs over a large surface area (high avidity, e.g. non-spherical particles compared to spherical particles of same volume). Figure 3E compares adhesion strength for different particle shapes for the two cases above. The simulation results clearly show that oblate ellipsoidal particles lead to the strongest adhesion in comparison to all other particles. In conclusion, the simulations suggest that the particles with non-spherical or flatter shapes such as oblate ellipsoids and discoids marginate and adhere better than symmetric spherical shapes, as they experience a lower drag force and expose a larger adhesion area in comparison to spherical particles. Furthermore, the simulations indicate that it is advantageous to have the size of particles in the micrometer range in comparison to nanometer-sized particles, as the larger particles seem to marginate much more efficiently. These trends were further tested experimentally using polystyrene (PS) particles of spherical, oblate, prolate and rod shapes, manufactured in nanometer and micrometer size ranges.

3.3. Manufacture and characterization of particles

Non-spherical oblate, prolate and rod-shaped polystyrene (PS) particles were fabricated from commercially obtained spherical PS particles using a previously reported one-dimensional and two-dimensional polymer film stretching method (process schematic shown in Figure 4A).⁴⁸ Total particle volume remained constant for each particle type during stretching, governed entirely by the volume of initial sphere and thus, by the equivalent spherical diameters (ESD). The aspect ratio (AR), defined as ratio of the major axis length to the minor axis length, was controlled by limiting the extent of stretching. The PS particles with various ESDs and geometries were characterized using scanning electron microscopy (SEM) as shown in Figure 4B. Dimensions and total surface area of the stretched particles were estimated from their 2D SEM projections and mathematical volume equations for their respective geometries. To this end, Figure 5B shows the dimensions (ESD-based calculations) for each of the geometries studied.

The commercially obtained spherical PS particles had carboxyl (-COOH) groups available primarily on the surface owing to the hydrophilic nature of the - COOH groups. These motifs stay conserved on the surface post stretching and remain available for biotin conjugation (process described in Methods section and in Figure 5A schematic). Resultant surface-modified spherical and non-spherical particles were characterized by SEM (Figure S.7) and a standard 4’- hydroxyazobenzene-2- carboxylic acid (HABA) dye assay for biotin quantification. The number of carboxyl (-COOH) groups on the particle surface depends on the amount of the acid monomer used for the original spherical particle synthesis (as per manufacturer description) and hence it is a function of total particle volume. Thus, particles with larger size have more number of -COOH ligands compared to smaller ones. Furthermore, since the total mass of particles was maintained constant for the conjugation reaction across various shapes and sizes, therefore the total number of -COOH ligands (primarily conserved on the particle surface) available for conjugation can be rationalized to be nearly equal for each of the particle type studied here. Therefore, the values for mg of Biotin-PEG3-Amine/mg of particles were found to be almost the same, as shown in Figure S.8. However, for each spherical particle type, the ligand surface density (i.e. ligand number per unit surface area) decreases when transformed into non-spherical particle, due to the generation of new surface area. The surface-modified particles were stored at 4°C in PBS until use.

3.4. Flow chamber experiments

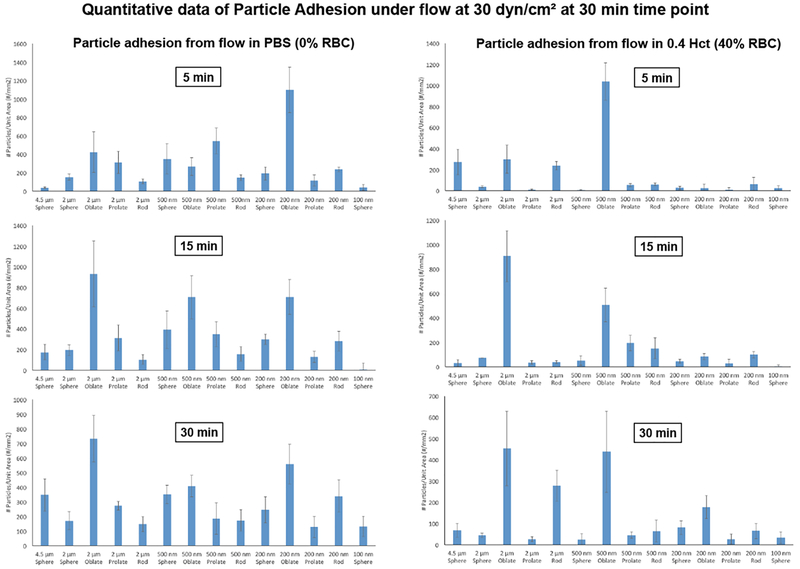
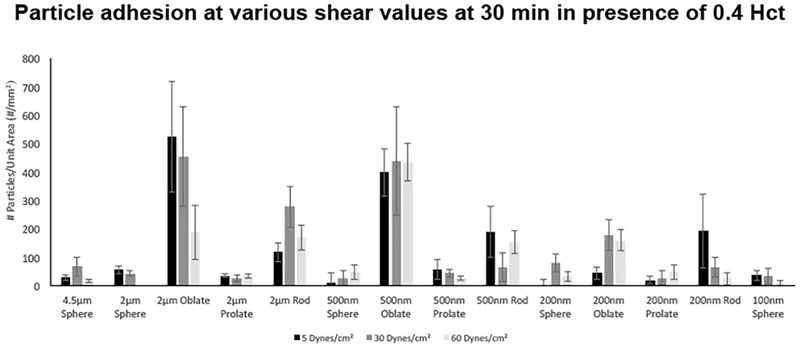
Figure 6B shows representative fluorescence microscopy images of particle adhesion at the wall in PBS flow only (no RBCs) and RBCs in flow at physiological volume (40% v/V i.e. 0.4 HCT) conditions, at τ_W of 30 dyn.cm⁻² at the 30 min time point. Additional representative microscopy images for the various particle sizes and shapes adhering at τ_W of 5 dyn.cm⁻² and 60 dyn.cm⁻² respectively in PBS (0 HCT) and 40% v/V RBC flow (0.4 HCT) conditions at 5, 15 and 30 min time-points are shown in Supplementary Figures S.2, S.3, S.4 and S.5. Figure 7 shows quantitative data for ‘number of adhered particles per unit surface area’ in absence (PBS) versus presence of RBCs (0.4 HCT) in flow, at 5, 15 min and 30 min time-points obtained from image analysis for experiments carried out at shear value of 30 dyn.cm⁻², while Figure 8 shows expanded quantitative data for ‘number of adhered particles per unit surface area’ for particles of various shapes and sizes, at 5, 30 and 60 dyn.cm⁻² shear flow conditions at 30 min in presence of 0.4 HCT. Additional data for similar experiments and analyses performed at mid-range RBC volume (20% HCT) for various time points and shear flow conditions are shown in Supplementary Figure S.6. From the qualitative images as well as quantitative analysis, it is apparent that in absence of RBCs (i.e. in PBS only) a lot more particles across all size and shape parameters become adhered at the wall while this is significantly reduced for all particle sizes and shapes once RBCs (20% or 40% HCT) are introduced in flow volume. Furthermore, in the presence of RBC flow volume, oblate particles and to some extent rod-shaped particles in the 500 nm or higher (e.g. 2 µm) diameter seem to undergo higher adhesion (and retention) at the wall compared to spherical particles and prolate particles, at all shear flow values. These experimental data appear to be in line with the simulation results that in the presence of RBC flow volume, the microscale particles have higher probability of margination compared to nanoscale particles into the RBC-FL, and once marginated, the particles of oblate ellipsoidal shape undergo lower drag force at the wall and higher adhesive interaction area at the wall compared to their spherical counterparts. It is also important to note here that these particles were made by a process that approximately kept a constant number of ligands (i.e. biotin), N_L, for all shapes and thus the surface density (per unit surface area) of ligands on the non-spherical particles is less than their spherical counterparts of equivalent volume. Therefore, the experimental data essentially indicate that even at a reduced overall surface density of ligands, oblate and rod-shaped particles of microscale size range manage to undergo higher extent of adhesion/retention compared to spherical particles of equivalent volume. This is potentially due to the fact that the total extent of adhesive interactions for such particles with the target surface may be higher than their spherical counterparts due to larger contact area of interaction at the wall.

Figure 6.

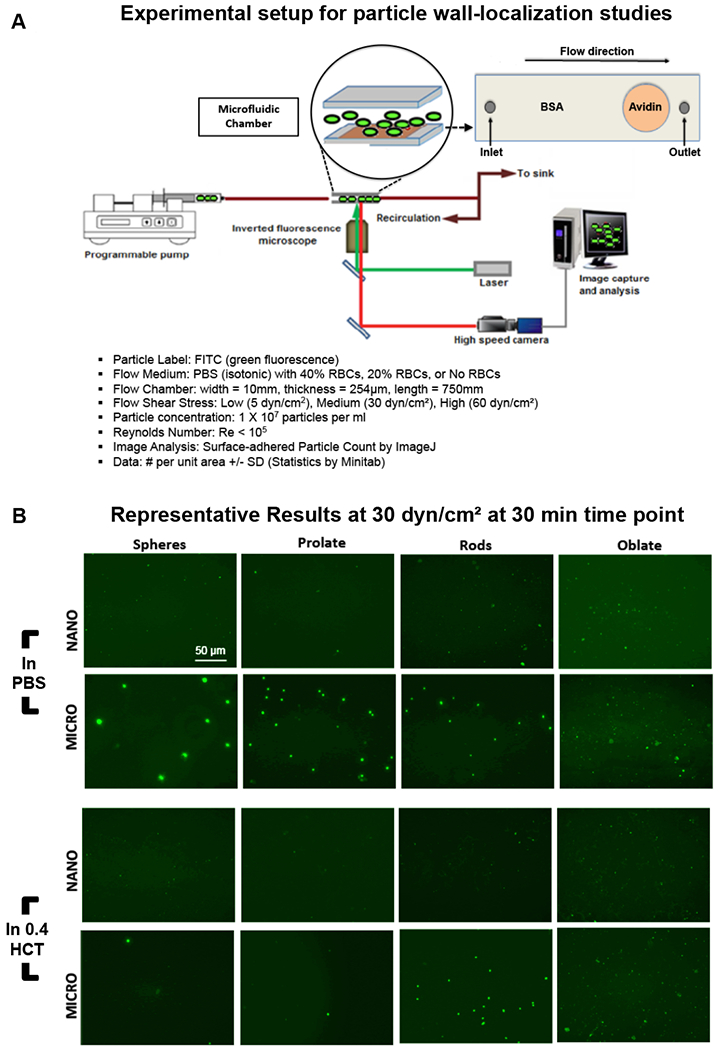
[A] Experimental setup and conditions for the study of particle margination and adhesion under flow of PBS only (no RBC) versus that of controlled percent (%) volume of RBCs (20% or 40% v/v) in a parallel plate flow chamber (PPFC) under an inverted fluorescence microscope; [B] Representative fluorescence images of nanoparticles and microparticles of various shapes adhered via biotin-avidin interaction at the wall at the 30 min time point under wall shear stress (τ_W) of 30 dynes cm⁻² in absence (PBS only) versus presence of 40% v/v RBCs (i.e. 0.4 HCT) in flow; In absence of RBCs in flow, nano-scale and micro-scale particles of all shapes show reasonable adhesion at the wall, while upon introduction of RBCs (0.4 HCT) in the flow the adhesion of nano-scale particles of spherical, prolate and rod shapes and micro-scale particles of spherical and prolate shapes were found to be reduced substantially.

Figure 7.

Quantitative analysis for ‘adhered particles per unit surface area’ at 5 min, 15 min and 30 min time point obtained from image analysis for experiments carried out at estimated wall shear stress (τ_W) value of 30 dyn.cm⁻²; In absence of RBCs in flow (i.e. flow in PBS with 0% RBC), nano-scale and micro-scale particles of all shapes show high levels of wall adhesion over time although there are some variabilities in-between the different particle shapes and sizes; In presence of RBCs (0.4 HCT) in flow, majority of nano-scale particles (except for 500 nm diameter oblate ellipsoids) show substantially reduced adhesion at the wall; For micro-scale particles, the 2 µm ESD oblate and rod shaped particles are found to still maintain high levels adhesion at the wall even in the presence of RBCs in flow.

Figure 8.

Expanded quantitative results for ‘adhered particles per unit surface area’ for estimated wall shear stress (τ_W) values of 5, 30 and 60 dyn.cm⁻² at 30 min in presence of 40% HCT; Oblate and rod-shaped particles in the 500 nm and 2 µm ESD range show the highest levels of wall adhesion and retention compared to micro- and nano-scale spherical particles.

4. Discussion

In the area of particle-based targeted drug delivery systems, a majority of the reported intravenously administered particles are in the nanoscale size range and have a spherical shape. The emergence of nanoparticles was (i) to facilitate their navigation through microvascular networks without causing occlusion, (ii) to allow their extravasation and permeation across leaky endothelial barriers into diseased tissue (e.g. tumors), and (iii) to achieve high surface-to-volume ratio for drug or ligand incorporation. However, many of these nanoparticle-associated mechanisms are expected to occur only if the particles can get to the vascular wall (and beyond the wall) via convective-diffusive trajectories in flow and margination. Several recent computational and experimental studies have indicated that compared to nanoscale particles, microscale particles have a higher propensity to marginate through the RBC flow volume towards the wall.^13,21,25,30 In addition, recent theoretical and computational studies have also indicated that non-spherical particles may have higher margination and adhesion probability at the wall due to a larger contact area.^30,32,34,59 These reports have led to our current studies of correlating computational and experimental assessment of particle margination and adhesion across a wide variety of size and shape ranges of particles tested in presence of RBC flow. Furthermore, to ensure that once marginated, the particles can interact with the wall via specific high affinity mechanism, we utilized the avidin-biotin interaction as a model, since it is one of the strongest known non-covalent interactions (K_D = 10⁻¹⁵M). To this end, the total number of ligands (N_L) was kept theoretically constant among all shapes of nanoscale particles and among all shapes of microscale particles, such that the relative surface density of ligands was changed (reduced) when spherical particles were deformed into non-spherical shapes.

Our computational study shows that microscale particles have a higher margination probability than nanoscale particles, and this probability increases with hematocrit (i.e. RBC fraction). Our microfluidic experimental studies indicate that in presence of RBCs, spherical nanoparticles and microparticles, as well as nanoparticles of prolate and rod shapes undergo significant reduction in localization at the wall. In contrast, non-spherical microparticles (and 500 nm particles) especially of oblate (ellipsoid or discoid) shape still show significant wall localization. This suggests significant promise of this size and shape range in designing drug delivery systems that can reach the wall with a higher probability and adhere (based on specific ligand-receptor interactions) to allow drug delivery at the wall or beyond. It is intuitive to point out here that circulating quiescent platelets, which are biconvex oblate (discoid) in geometry, are known to undergo enhanced margination in blood flow so as to be predominantly resident in a RBC-free zone near the vascular wall for continuous hemostatic surveillance and this can be considered a nature-inspired design cue for vascular drug delivery systems.^60–65 Also, it has been recently reported that even within the nanoscale domain, particle aspect ratios (i.e. shapes) can influence their permeation, diffusion and accumulation within tumors.⁶⁶ However, it is important to consider that such mechanisms for nanoparticles can only occur once the particles are able to first get to the vascular walls via margination and then extravasate. Given that our computational and experimental studies with model particles indicate a low margination probability of nanoscale particles, this can be a consistent challenge in tumor-targeted drug delivery. To this end, an interesting design concept is that of a multiscale drug delivery system where drug-loaded nanoscale particles can be embedded or aggregated within microparticles such that the microparticles first marginate efficiently to the vascular wall and then release the nanoparticles at the wall for further extravasation and diffusion into the target tissue. The promise of such strategies has been recently reported with discoid silica particles and micro-scale aggregates of polymeric nanparticles.^67,68

In the context of our computational study, it should be noted that the margination results correspond to a final state (i.e. fully developed probability distribution) of this process, excluding any transient margination states. At the inlet of the microfluidic system, the distribution of suspended particles can be considered uniform across the channel cross-section, and a certain channel flow length is required for the particles to fully marginate. A characteristic margination length has been predicted to be nearly independent of the flow rate, but is proportional to H³ with H being the channel height and inversely proportional to D_m², referring to the particle size.⁶⁹ Using this scaling, we estimate that complete particle margination in our microfluidic system may require several centimeters of channel length for some of the particle systems studied. In our experimental set-up, the avidin-coated region on the glass slide surface is about 5 cm away from the flow inlet and thus, it is likely that fully complete margination of suspended particles towards the avidin-coated region may not have been achieved for certain particle groups. This limitation should have a negligible effect on the adhesion of particles of different shapes with the same volume. However, the margination of large particles should proceed faster in comparison to small particles, since the margination length is inversely proportional to the particle size squared. Therefore, micrometer-sized particles exhibit not only more efficient margination, but also faster margination in comparison to their nanometer counterparts.

Our quantitative results based on image analysis also indicate that for some particles there is a certain level of variability in ‘number of adhered particle per unit area’ over the experiment time period. This may be attributed to the orientation in which the particles, especially non-spherical ones, might have interacted with the target surface over time. For spherical particles, the orientation and surface-area of interaction with the target surface is uniform over time. However for non-spherical particles, at any instant of time, the interaction may happen on their larger surface as well as their edge or smaller surface domains. Such orientation-based surface area of interaction may influence overall adhesion strength, so that weakly adhered particles may dislodge, flow away and re-bind relatively strongly due to the recirculating set-up of the experiments. These possibilities can influence overall quantity of particle adhesion over time for each particle type, to introduce some variabilities between results at 5 min, 15 min and 30 min. However, it becomes evident that over longer time periods (e.g. 30 min), the particles closer to microscale size range and of oblate (and rod) shaped geometry undergo significantly enhanced adhesion and retention on the target surface compared to their nanoscale and spherical (and prolate) counterparts.

An additional area of design parameter that is yet to be studied across multiple size and shape ranges is particle elasticity (i.e. stiffness vs. deformability). Computational studies have indicated that highly deformable particles are prone to undergo a larger lift force due to hydrodynamic interactions with the wall, resulting in their localization away from the wall.⁴⁹ This is evident for highly deformable healthy RBCs as they congregate in the center of the flow while rigid sickle RBCs show less propensity for such behavior.^70–73 At the same time, some recent studies have shown that softer (low modulus) gel microparticles could marginate and adhere to vessel wall at low shear rates, while more rigid (high modulus) particles showed favorable margination and adhesion at high shear rates.⁷⁴ In these studies, the softest particles had a Young’s modulus of 23 kPa and the most rigid particles had a Young’s modulus over 500 kPa. The reported Young’s modulus of normal healthy RBCs is 0.1-0.2 kPa⁷⁵ while that for normal circulating platelets is 20-30 kPa.⁷⁶ Thus the softest particles reported were essentially in the range of stiffness shown by circulating platelets that are known to have inherent property of higher margination. In another recent report, soft nanogel particles with modulus in the range of 48-71 kPa were shown to be capable of efficient targeting to lung microvasculature, while their rigid counterparts were incapable.⁷⁷ Therefore, such reports warrant continued computational and experimental efforts to elucidate the effect of particle elasticity integrated with particle size shape and surface-modifications, on margination probability and wall-adhesion efficacy. A persistent challenge in carrying out experimental studies across a wide range of sizes, shapes and elasticity parameters is the efficient manufacture of the corresponding particles at high yield with precisely controllable properties. In recent years, the emergence of unique particle fabrication approaches like ‘polymer replication in non-wetting template’ (PRINT®), nanoimprint lithography and template-induced thermo- stretching have opened the possibility to precisely modulate particle parameters and carry out detailed systematic studies to tailor specific drug delivery system design tailored to specific vascular profiles.^77–79 Furthermore, nanofabrication and microfabrication techniques have presented the possibility of carrying out experimental studies in complex channel networks that model microvasculature, where different particle geometries and moduli may provide unique functional outputs. Therefore, customizable drug delivery systems for enhanced performance in vascular applications can be envisioned.

5. Conclusions

Using computational approaches as well experimental microfluidic studies with model nanoscale and microscale particles of four different geometries, we demonstrate the interplay between the size and shape of particles regarding margination through RBC flow volume and adhesion (retention) at the wall in a hemodynamic environment. Our studies indicate that the presence of RBCs can significantly reduce the extent of particle localization at the vessel wall. Specifically, nanoparticles in the few hundred nm diameter range undergo substantially reduced localization and retention at the wall under a hemodynamically relevant RBC flow environment, compared to microparticles, irrespective of shape. Additionally, compared to isotropic spherical particles, anisotropic oblate and rod-shaped particles in the 500 nm-2 µm equivalent spherical diameter (ESD) range demonstrated the highest extent of wall-localization over time at low, medium and high shear flow conditions in presence of RBCs. While majority of particulate drug delivery systems are manufactured as spherical nanoparticles 50-200 nm in diameter, our results suggest that those size and shape parameters may be less favorable for in vivo vascular delivery applications that require particle margination through RBC volume and surface-interactive adhesion at the wall. These studies provide valuable design insight regarding the importance of tailoring and optimizing the size and shape of particles to enhance their margination and wall- adhesion capabilities in vascularly targeted drug delivery applications.