Ordered subset expectation maximization algorithm for positron emission tomographic image reconstruction using belief kernels

Abstract.

The aim of this study is to investigate the benefits of incorporating prior information in list mode, time-of-flight (TOF) positron emission tomography (PET) image reconstruction using the ordered subset expectation maximization (OSEM) algorithm. This investigation consists of an IEC phantom study and a patient study. For the image under reconstruction, the activity profile along a line of response is treated as a priori and is combined with the TOF measurement to define a belief kernel used for forward and backward projections during the OSEM image reconstruction. Activity profiles are smoothed and combined with the TOF kernels to control the adverse impact of noise, and different levels of smoothness are attempted. The standard TOF OSEM reconstruction is used as a baseline for comparison. Image quality is assessed using a combination of visual assessment and quantitative measurement including contrast recovery coefficients (CRC) and background variability. On the IEC phantom study, the reconstruction using belief kernels converges faster and the reconstructed images are more appealing. The CRCs for all sizes of regions of interest on images reconstructed with belief kernels are higher than those of the baseline. The background variability, measured as a coefficient of variation, is generally lower for the images reconstructed using belief kernels. Similar observations occur on the patient study. Particularly, the images reconstructed using belief kernels have better defined lesions, improved contrast, and reduced background noise. OSEM PET image reconstruction using belief kernels that combine the information from prior images and TOF measurements seems promising and worth further investigation.

1. Introduction

High image quality and quantitation accuracy are required in positron emission tomography (PET) imaging for accurate diagnosis, monitoring, and progression assessment. PET scanner vendors continue to invest in sophisticated instrumentation and advanced algorithms. The timing resolution in time-of-flight (TOF) PET scanners has been reduced to around or even less than $300\mathrm{ps}$, and PET scanners with digital detectors are commercially available.¹ As it becomes harder and more expensive to improve hardware performance, it is crucial to invest in advanced algorithms to improve system physics modeling, reconstruction methods, and postprocessing techniques.

Research on advanced PET reconstruction algorithms has a long history.^2–4 Maximum likelihood (ML) is a standard statistical estimation method, and expectation maximization (EM) is an efficient algorithm to find the ML estimate. MLEM is the foundation for many popular iterative methods for PET image reconstruction. To improve the convergence speed of MLEM, the ordered subset expectation maximization (OSEM) algorithm was proposed, the most popular flavor of which uses only part of the data (subset) at each iteration.^2,3 The OSEM algorithm has become a major workhorse in today’s scanner.

ML methods essentially assume a statistical model for the measured data. In addition to the ML criterion, one can pose desired image properties known as a priori knowledge on the reconstructed images, which leads to the formulation of maximum a posteriori (MAP) reconstruction. The priors are considered a penalty on solutions. MAP methods are thus called penalized or regularized ML methods. There are many kinds of priors that can be used in PET reconstruction. Commercial PET reconstruction software poses a smoothness constraint on the reconstructed images.⁵ Researchers also attempted to use anatomic information from CT or MR in PET image reconstruction.⁶ Yet, there are still other types of priors, e.g., the previous study can be treated as a priori for the current study, and images reconstructed by other algorithms or in a previous iteration, in the case of iterative algorithms, can be treated as a priori.

Before TOF became practical, the location of the detected coincidence event was assumed to be uniformly distributed along the line connecting two detector scintillators known as the line of response (LOR). With TOF, the location can be more accurately pinpointed and typically modeled by a Gaussian-shaped TOF kernel. In essence, the TOF kernel reflects one’s belief of where an annihilation event came from along the LOR. In fact, the TOF kernel has been called confidence weighting.⁷ We extended the notion of belief kernels to take into account prior knowledge, particularly the image contents under iterative reconstruction.⁸ The activity distribution along an LOR measured on a priori image can shape one’s belief of where the detected annihilation event came from. It is reasonable to assume, without any other information such as flight time difference, that the probability of where an annihilation event happens along a LOR is proportional to the activity along the LOR (prior). Once a coincidence event has happened, the TOF kernel represents one’s measurement uncertainty of where it happened (likelihood). By the Bayesian theorem, one can calculate the posterior probability (proportional to the product of the prior and likelihood) of the actual event location given the TOF measurement. Therefore, the TOF kernel and the trace activity along the LOR can be combined to improve one’s belief of the source of the annihilated event. A two-dimensional (2-D) phantom simulation and patient study using simple back-projection demonstrated the potential benefits of the belief kernel approach.⁸ Briefly, the simulation results suggest that the belief kernels generate images with a comparable mean absolute error relative to ground truth as those generated on a system with much poorer timing resolution, and the images have a better contrast if the belief kernel is the only difference. With the patient data, the lesion contrast as well as the overall image quality appears to be improved with the belief kernels.

In this paper, we implement the belief kernels based on the commercial OSEM reconstruction software in Philips Ingenuity PET/CT. Experimental results on an IEC phantom as well as patient data are reported to further demonstrate the potential benefits of the proposed belief kernel approach.

2. Methods

2.1. Belief Kernels in Ordered Subset Expectation Maximization

The main update equation for the OSEM algorithm is described by Ref. 9:

$${\hat{f}}_j^{(n,b)}=\frac{{\hat{f}}_j^{(n,b-1)}}{{\sum }_{i^{\prime }\in S_b}{H}_{i^{\prime }j}}\sum _{i\in S_b}{H}_{ij}\frac{p_i}{{\sum }_k{H}_{ik}{\hat{f}}_k^{(n,b-1)}+a_i},$$

where $f$ is the image under reconstruction, $j$ and $k$ are the voxel indices, $n$ is the iteration number, $b$ is the subset number, $i$ and $i^{\prime }$ are the LOR indices, $S_b$ is the subset $b$, $H$ is the system matrix, $p$ is the LOR measurement, and $a$ models the scatter and randoms corrections. For the list-mode reconstruction, the measurement $p$ takes into account the crystal efficiency and detector geometry corrections, as well as the count loss compensation. Attenuation correction and TOF modeling are part of the system matrix. Decay time and acquisition span time corrections are just constant factors thus not explicitly reflected in the above update.

From an implementation point of view, to put the belief kernel modeling in the OSEM algorithm, one can just replace the TOF modeling with the belief kernel in the forward and backward projections. We modified the OSEM algorithm based on the implementation in Philips Ingenuity TF PET/CT scanners. The prior image (image under iteration) was resampled along the LOR. Philips OSEM implementation uses blobs instead of voxels and blobs tend to have a strong noise. To reduce the level of noise, blobs were smoothed and the smoothed blobs were used for the belief kernel calculation only. The blobs have a body centered cubic structure. Thus, each blob has eight neighbors. The average blob value of the eight neighbors was calculated with equal weights. The value of the current blob was then smoothed as ${\overline{b}}_{\text{self}}=\lambda b_{\text{self}}+(1-\lambda ){\overline{b}}_{\text{neighbors}}$, where $\lambda$ is a weighting parameter and $b$ is the blob magnitude value. Three $\lambda$ values were tested, 0.95, 0.90, and 0.85, corresponding to belief kernels $A$, $B$, and $C$.

The smoothed activity distribution along the LOR was used as the prior, with a small added positive offset to avoid zero belief kernels along the LOR. The prior was multiplied by the TOF kernel, and the product was normalized properly to give it a posterior probability interpretation. The normalized distribution was used as the belief kernel. If the prior is invariably a constant, the belief kernels become the same as the TOF kernels. To put it mathematically, the TOF kernel is modeled with a Gaussian function:

$$g(x)\propto \exp (-\frac{{(x-x_0)}^2}{2{\sigma }^2}),$$

where $x$ is measured along the LOR, $x_0$ is the most likely position of the annihilation event on the LOR, and $\sigma$ is related to the TOF timing resolution. Here we have ignored the scaling constant. Assume $q(x)$ the activity measured along the LOR on the prior image. The belief kernel is simply written as

$$h(x)\propto g(x)q(x).$$

For each event, the belief kernel needs to be updated, which adversely slows down the reconstruction. The belief kernels also tend to increase the noise, although the noise could be controlled by carefully tuning the parameters, e.g., using the weighted average of the TOF kernel and so-calculated belief kernel. To avoid the adverse impacts, the belief kernels are only applied in the last grand iteration. We also attempted to apply the belief kernels to the latter subsets in the last iteration to trade-off speed and improvements, which is not discussed here due to space limitation. Applying the belief kernels in the last grand iteration also prevents a bad belief from being applied.

The standard OSEM and the modified OSEM algorithms with belief kernels were run on a laptop with 8 cores, using the MPI (message passing interface) parallel computing middleware.⁹ The laptop was an HP ZBook 17 G2, with Intel Core i74810MQ CPUs at 2.80 GHz and 8 GB RAM, running 64-bit Windows 7.

2.2. Phantom Evaluation

The body phantom of the National Electrical Manufacturers Association (NEMA) and International Electrotechnical Commission was used. The background of the phantom and the four smallest spheres were filled with ${}^{18}\mathrm{F}\text{-}\mathrm{FDG}$ mixed with pure water using a 4:1 sphere to background activity concentration ratio. The dose was 63.270 MBq of ${}^{18}\mathrm{F}\text{-}\mathrm{FDG}$. The data were acquired 46 min later on a Philips Vereos PET/CT scanner using the standard image quality protocol (the nominal timing resolution was 320 ps). Overall, 46.967 million events (36.772 prompts and 10.195 randoms) were acquired.

The images were reconstructed using the standard OSEM and modified OSEM algorithms using belief kernels. Standard reconstruction settings were applied, which includes sensitivity, crystal efficiency and geometry, attenuation, scatter, and randoms corrections. The reconstructed voxel size is $2\times 2\times 2{\mathrm{mm}}^3$. The number of iterations varied and the number of subsets was 17. Belief kernels $A$, $B$, or $C$ were used with the modified OSEM, and the belief kernels were applied only in the last iteration.

Evaluation of the region of interest (ROI) was performed with the open-source image analysis tool ImageJ with automated scripts to ensure a consistent analysis. ROIs with diameters equal to the physical inner diameters of the spheres were drawn on the spheres and background. The hot sphere contrast recovery coefficient (CRC) was calculated as

$${\mathrm{CRC}}_{\text{hot}}=\frac{\frac{C_{\text{hot}}}{C_{bkgd}}-1}{\frac{a_{\text{hot}}}{a_{bkgd}}-1},$$

while the cold sphere CRC was calculated as

$${\mathrm{CRC}}_{\text{cold}}=1-\frac{C_{\text{cold}}}{C_{bkgd}},$$

where $C$ is the average counts measured in ROIs enclosing hot spheres, background (bkgd), or cold spheres, and $a$ is the administrated activity in hot spheres or background.

The phantom background variability was simply calculated as the coefficient of variation: $\mathrm{CV}=\frac{\sigma }{\mu }·100\%$, where $\sigma$ and $\mu$ are the empirical standard deviation and mean within background ROIs, respectively.

2.3. Comparison with Postfiltering

To provide clinically meaningful images, preprocessing and/or postprocessing often times are used with image reconstruction. For PET images, the primary purpose of postprocessing is to reduce noise. In practice, partial volume effects can also be corrected as part of post-processing via the point spread function or modeled as part of reconstruction.¹⁰ Some popular linear filtering algorithms include Gaussian filtering and principal component analysis. Linear filtering tends to smoothen uniformly without preserving structures such as edges or boundaries. Some nonlinear filtering algorithms have been reported, such as bilateral filtering,¹¹ trilateral filtering,¹² guided filtering,¹³ nonlocal means,¹⁴ among others. Both linear and nonlinear filtering can be incorporated into the reconstruction iteration as well.

Belief kernel is different from image filtering, in terms of the concept and results. Belief kernel aims to improve the position estimation of annihilation events, while postfiltering smoothens the images and preserves image structures. To highlight that, OSEM reconstructions using belief kernels and OSEM reconstruction followed by postfiltering are compared. We chose the nonlocal means, given its recent popularity in PET imaging,¹⁵ and its accessibility as an open software tool.¹⁶ When using the nonlocal means as the ImageJ plugin, we chose the option “autoestimate sigma” and set smoothing factor to 2.

2.4. Patient Evaluation

The whole body patient data were acquired on an investigational Vereos PET/CT system (Philips) with a timing resolution of 320 ps. For patient privacy, patient demographics are not available except the patient weight (45.8 kg). The institutional review board approved this retrospective study and the requirement to obtain informed consent was waived. The injected dose was 505.8 MBq of ${}^{18}\mathrm{F}\text{-}\mathrm{FDG}$, acquisition started 59 min after injection. The step-and-shoot acquisition had nine frames (bed positions) at 39% frame overlap, with 90-s acquisition duration per frame, using Philips standard body protocol. However, we only reconstructed one bed frame so that other processing such as knitting will not impact the image quality. For the particular bed studied here, 21.4 million events (13.9 M prompts and 7.5 M randoms) were acquired.

Standard reconstruction settings were applied, which includes sensitivity, crystal efficiency and geometry, attenuation, scatter, and randoms corrections. The reconstructed voxel size is $2\times 2\times 2{\mathrm{mm}}^3$. In addition to the standard OSEM reconstruction, two belief kernels $B$ and $C$ were used with the modified OSEM. The belief kernel $A$ was not used due to noise. The number of iterations was 3 in all cases with 17 subsets. The belief kernels were applied only in the last iteration.

3. Results

3.1. Phantom Evaluation

Figure 1 shows the reconstructed phantom slice passing through the middle of all spheres. From left to right, the OSEM iteration numbers are 1, 3, 5, and 7, respectively. The first row shows the images reconstructed using the standard OSEM algorithm with TOF kernels (the same algorithm implemented in the Ingenuity TF PET/CT product line). Images on the latter three rows are reconstructed using the OSEM algorithm with belief kernels $A$, $B$, and $C$, respectively. The voxel values between 0 and 400 are mapped to gray values 255 and 0 for all images in this paper.

Fig. 1.

IEC phantom slices reconstructed using the OSEM algorithm with (a) TOF kernels and belief kernels (b) $A$, (c) $B$, and (d) (last row). From left to right, the numbers of iterations are 1, 3, 5, and 7, respectively.

As the number of iterations increases, the reconstructed images become noisier for both TOF kernels and belief kernels. The reconstructed images with belief kernels $B$ and $C$ appear to be more appealing than the images reconstructed with TOF kernels or belief kernel $A$. It is evident that the cold ROIs reconstructed with belief kernels are much cleaner. The quantitative characteristics revealed later in Figs. 2 and 3 are consistent with the visual appearance as shown in Fig. 1. Note that the belief kernels are used only in the last OSEM iterations and data points are connected in Figs. 2 and 3 to guide the eyes.

Fig. 2.

CRCs for four hot and two cold ROI. The diameters of four hot ROIs are 22 (red, square), 17 (green, circle), 13 (blue, triangle), and 10 (cyan, plus) mm, respectively, and of two cold ROIs are 33 (magenta, times) and 28 (black, diamond) mm, respectively. (a) The OSEM with TOF kernels and the others are for OSEM with belief kernels (b) $A$, (c) $B$, and (d) $C$.

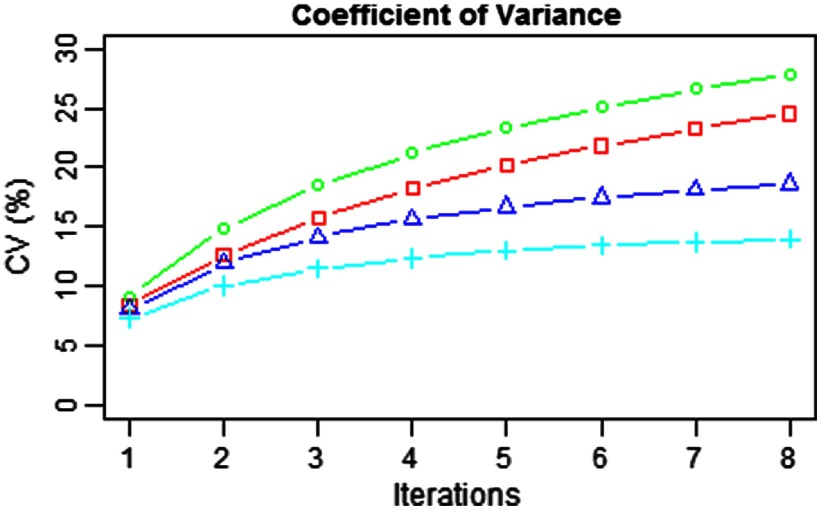
Fig. 3.

Coefficient of variation measured on the background of the reconstructed images with the TOF kernels (red, square) and the belief kernels $A$ (green, circle), $B$ (blue, triangle), and $C$ (cyan, plus).

The CRCs are measured for four hot and two cold ROIs at each iteration up to eight for the standard TOF kernels and belief kernels, and the results are shown in Fig. 2. In all four panels in Fig. 2, the red, green, blue, and cyan curves are for hot spheres with diameters of 22, 17, 13, and 10 mm, respectively, and the magenta and black curves are for cold spheres with diameters of 33 and 28 mm, respectively.

For the OSEM with the TOF kernels, the CRCs converge after three or four iterations, and they converge to different values, depending on the diameters of the spheres. For the OSEM with the belief kernels, however, the CRCs appear to converge faster, particularly for belief kernels $A$ and $B$. It is worth pointing out that, the convergence behavior of belief kernel $A$ is remarkable—they converge to more or less the same values, regardless of the size and heat (hot or cold) of the spheres. For all three belief kernels, the converged CRCs for the sphere with the same size are higher than those for the TOF kernels.

The background variability for each kernel is measured as a function of the iteration number, as shown in Fig. 3, where the red curve is for the TOF kernels and the green, blue, and cyan curves are for belief kernels $A$, $B$, and $C$, respectively. Compared with the baseline TOF kernels, the belief kernel $A$ increases the background variability slightly, while the belief kernels $B$ and $C$ both have a reduced background variability.

As for execution time, each OSEM iteration takes $51.2\pm 5.9\mathrm{s}$, and the overhead of the belief kernels on average is $19.3\pm 7.4\mathrm{s}$.

3.2. Comparison with Postfiltering

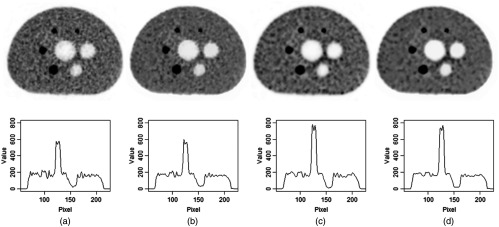
The results of OSEM reconstruction using belief kernels or using nonlocal means filtering as a postprocessing are compared and typical comparisons are shown in Fig. 4. The first image in the top row of Fig. 4 is reconstructed with the standard OSEM after three iterations (the same image as the second one in the top row of Fig. 1). The first image is filtered using the nonlocal means algorithm and the filtered image is shown as the second image in the top row of Fig. 4. Visually the nonlocal means filtered image is smoother than the unfiltered image and the structures are preserved, which is confirmed by the profile measurement. On the bottom row of Fig. 4 are the voxel values on the straight line passing through the centers of two circles on the lower part of the phantom (i.e., the hot sphere with a diameter of 22 mm and the cold one with a diameter of 28 mm). The respective profiles are shown below the images. Comparing the profiles before and after the nonlocal means filtering, one can see that the nonlocal means smoothens the images while keeps the structure almost intact (the voxel values from the background to the hot region have the similar transitions). The maximum voxel values in the hot region and the minimum values in the cold region change only slightly.

Fig. 4.

Images and respective line profiles passing through the centers of hot and cold regions on the lower part of the phantom. From left to right, (a) the images are OSEM reconstructed after three iterations, (b) the nonlocal mean filtered of the first image, (c) OSEM reconstructed using the belief kernels $B$ at the third iteration, and (d) the nonlocal means filtered version of the third.

It is constructive to compare the images reconstructed with the belief kernel and the images filtered with nonlocal means. The third image on the top row of Fig. 4 is reconstructed using the belief kernel $B$ after three iterations (the same as the second image in the third row of Fig. 1). The profile measurements indicate that the voxel values in the hot region are much higher than those in the nonlocal mean filtered image, and the voxel values in the cold region are lower than those in the nonlocal means filtered image. This comparison suggests that the postfiltering, nonlocal means in particular, is to smoothen the images, whereas the belief kernels proposed are to have a higher contrast recovery. As a matter of fact, the nonlocal means filtering and belief kernels can be combined to have the benefits of both, as shown on the image and profile in Fig. 4(d), where the image is the nonlocal means filtered version of the third image.

3.3. Patient Evaluation

The reconstructed patient transverse images are shown in Fig. 5, where three slices are 20 mm apart from left to right. The top row shows the images reconstructed using the OSEM algorithm with TOF kernels and the next two rows show the images reconstructed using OSEM with the belief kernels $B$ and $C$, respectively. The coronal slices of the same patient are shown in Fig. 6 (left: TOF kernels, middle: belief kernel $B$, and right: belief kernel $C$). Due to the decreasing sensitivity toward the top and bottom edges of the bed segment, the top and bottom portions of the coronal images exhibit noisier contents.

Fig. 5.

Transverse slices reconstructed using OSEM with (a) TOF kernels, (b) belief kernels $B$, and (c) belief kernels $C$. From left to right, the slices are 20 mm apart.

Fig. 6.

The coronal slices reconstructed using OSEM with (a) TOF kernels, (b) belief kernels $B$, and (c) belief kernels $C$.

The observed characteristics of the reconstruction on the IEC phantom are also seen on the patient study. In both Figs. 5 and 6, the inside of the heart is much cleaner in the images reconstructed with the belief kernels. Additionally, lesions appear to be better defined with higher contrast against their surroundings.

4. Concluding Remarks

Prior information on the image under reconstruction is abundant. This investigation combined the activity profile of the image under reconstruction and the TOF measurement, and formed a belief kernel that was used in forward and backward projections during the OSEM reconstruction. The experiments on IEC phantom and patient data both pointed to promising conclusions: OSEM reconstruction using belief kernels appears to converge faster than the standard OSEM version; the reconstructed images using the belief kernels have higher CRCs and lower background variability; and patient lesions appear to be better defined, with high contrast. We plan to further validate the potential benefits of belief kernels in future. While the empirical data seem to support a favorable conclusion on the use of belief kernels, a more rigorous or mathematical argument is still missing. We plan to investigate it as well.

Biography

Yang-Ming Zhu received his BS and MS degrees in biomedical engineering, his MS degree in computer science, and his PhD in physics. He is a software architect with Siemens Healthineers and was a principal scientist with Philips Healthcare before that. His research and development interests include image processing, software engineering, and applied machine learning.

Disclosures

The work was performed when the author was employed by Philips HealthTech. The author did not receive additional financial and material support. A patent application based on the same idea and preliminary simulation results was pending (assigned to Philips), for which the author was a coinventor. The author is not aware of any conflict of interests except as disclosed here.