On the Stability of BOLD fMRI Correlations

Abstract

Measurement of correlations between brain regions (functional connectivity) using blood oxygen level dependent (BOLD) fMRI has proven to be a powerful tool for studying the functional organization of the brain. Recently, dynamic functional connectivity has emerged as a major topic in the resting-state BOLD fMRI literature. Here, using simulations and multiple sets of empirical observations, we confirm that imposed task states can alter the correlation structure of BOLD activity. However, we find that observations of “dynamic” BOLD correlations during the resting state are largely explained by sampling variability. Beyond sampling variability, the largest part of observed “dynamics” during rest is attributable to head motion. An additional component of dynamic variability during rest is attributable to fluctuating sleep state. Thus, aside from the preceding explanatory factors, a single correlation structure—as opposed to a sequence of distinct correlation structures—may adequately describe the resting state as measured by BOLD fMRI. These results suggest that resting-state BOLD correlations do not primarily reflect moment-to-moment changes in cognitive content. Rather, resting-state BOLD correlations may predominantly reflect processes concerned with the maintenance of the long-term stability of the brain's functional organization.

Introduction

During the last two decades, the study of brain organization in humans has been greatly accelerated by the advent of resting-state fMRI, wherein blood oxygen level dependent (BOLD) signals are measured in quietly resting subjects. Using this paradigm, it has been shown that temporal correlations in ongoing fluctuations of the BOLD signal, that is, resting state functional connectivity (RSFC), correspond to known functional systems (Biswal et al. 1995; Smith et al. 2009; Power et al. 2011; Yeo et al. 2011). Thus, resting-state fMRI offers significant potential for understanding the brain's functional architecture. Much evidence supports the hypothesis that RSFC is, in part, explained by axonal connectivity (Honey et al. 2009), although it is also clear that many RSFC relationships must reflect multisynaptic pathways (Vincent et al. 2007; O'Reilly et al. 2013). Under this view, RSFC has been understood to reflect stable features of brain organization on a timescale of minutes to days and significant efforts have been made to describe the relatively high reliability of repeated RSFC estimates in the same individual from day to day (Shehzad et al. 2009; Zuo and Xing 2014; Chen et al. 2015; Laumann et al. 2015).

However, many recent reports have begun to explore “dynamic” RSFC, that is, dramatically fluctuating patterns of correlation over shorter timescales, on the order of seconds to minutes. These reports have suggested the presence of previously unrecognized intraindividual correlation variability (Chang and Glover 2010; Hutchison et al. 2013a). Several groups have extensively characterized these RSFC dynamics and have attempted to explain their physiological significance (Hutchison et al. 2013a; Calhoun et al. 2014; Kopell et al. 2014).

The most commonly used approach in studies of dynamic RSFC is the sliding window technique (Chang and Glover 2010; Hutchison et al. 2013b; Allen et al. 2014; Zalesky et al. 2014), in which the correlation structure of BOLD fMRI is estimated at successive time points over an interval of fixed duration on the order of 100s. Dynamic BOLD behavior has also been characterized in terms of transient patterns of coactivation over much shorter intervals (Tagliazucchi et al. 2012a; Liu and Duyn 2013; Karahanoglu and Van De Ville 2015). The multiple transient patterns of coactivation or correlation observed with these techniques often are clustered into sets of dynamically recurring patterns that have been interpreted as reflecting changes in brain state on a short timescale (Allen et al. 2014; Hutchison and Morton 2015). The hypothesized existence of such “dynamic” RSFC would suggest that the statistical properties of BOLD time series are nonstationary.

A process is said to be stationary if its statistics, for example, spectral content and moments (mean, variance, kurtosis, etc.) are constant over time. Critically, stationarity does not imply that a process is still. For example, a frictionless pendulum may remain indefinitely in oscillatory motion; nonetheless if the amplitude and frequency are constant, then the motion is stationary. If the pendulum frequency or amplitude were to change, say, in reaction to an applied force, then the motion would be nonstationary. The analogy to BOLD RSFC is not perfect because the motion of a pendulum is periodic whereas BOLD time series are aperiodic, that is, they exhibit approximately scale-free or 1/f-like the spectral content (He et al. 2010). Moreover, the pendulum moves in one dimension (angle relative to vertical), whereas BOLD time series are multidimensional. Nevertheless, the pendulum example illustrates a process that is constantly in motion but whose statistics are stationary. It is this property that is implicitly evaluated in studies that aim to characterize RSFC dynamics.

Several recent papers have pointed out that certain analytic techniques are prone to creating the false appearance of “dynamics” in RSFC that may be misinterpreted as nonstationarity (Lindquist et al. 2014; Zalesky et al. 2014; Hlinka and Hadrava 2015; Leonardi and Van De Ville 2015). We illustrate this principle in the present work by applying dynamic analyses to simulated data that are statistically stationary by design. Perhaps more importantly, it has become widely recognized that head motion is a prominent source of artifact in resting state fMRI (Power et al. 2012; Van Dijk et al. 2012; Zalesky and Breakspear 2015). Thus, head motion represents a significant potential source of artifactual nonstationarity. On the other hand, physiologically meaningful changes in brain state are also likely to change the correlation structure of the BOLD signal. In particular, it has been demonstrated that BOLD correlation structure changes according to sleep state (Horovitz et al. 2009; Tagliazucchi et al. 2012a; Tagliazucchi and Laufs, 2014). Similarly, it is known that the BOLD correlation structure varies in relation to the cognitive state imposed by external task demands (Cole et al. 2014; Krienen et al. 2014). Both of these processes are reasonably understood as sources of bona fide nonstationarity.

Here, we evaluate the above-enumerated potential sources of “dynamic” RSFC in terms of multivariate kurtosis (Henze, 2002; described in detail below). To obtain a heuristic understanding of the relevance of kurtosis, consider first a univariate time-dependent signal. The mean and the variance are statistics of orders 1 and 2, respectively. More generally, the sampling variability of a statistic of order m is proportional to the moment of order 2m (Weatherburn 1961). Thus, a statistic of order 4, that is, the kurtosis, is proportional to the sampling variability of an order 2 statistic. These statistical relations can be generalized to the multivariate case and applied to BOLD fMRI time series. The most direct measure of RSFC is the covariance matrix, which is a statistic of order 2. Thus, the multivariate fourth moment (kurtosis) of BOLD fMRI data can be used to assess the degree to which RSFC is stable. We compare the multivariate kurtosis of real data to that of a matched, stationary, synthetic surrogate. We use this strategy to assess the effects of head motion, sleep state, and imposed task states.

Materials and Methods

Several previously collected data sets were used for analyses (Figs 3, 4, and 6). These data sets are enumerated in Supplementary Table S1. Additional details of these data sets are reported in the Supplementary Materials. The primary data set is described below (Figs 1, 2, 5, and 6) with additional acquisition and processing details in the Supplementary Materials.

Figure 3.

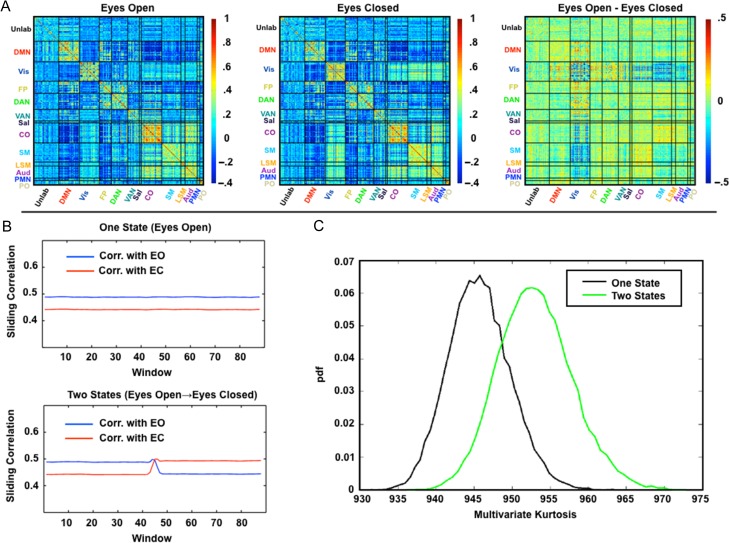
Multivariate kurtosis is sensitive to state changes in simulated multivariate data. (A) Average correlation matrices from real data acquired in eyes-open (EO; ten 10-min sessions) and eyes-closed (EC; ten 10-min sessions) conditions. The primary differences are in visual and somatomotor cortex. (B) Sliding window correlation results averaged over 10 000 simulations. The plotted values are the mean (over all simulations) Pearson correlation between the windowed correlation matrices and the “true” correlation matrices shown in panel A (blue = eyes-open, red = eyes-closed). The first simulation models the eyes-open condition throughout. The second simulation models the eyes closing halfway through the session. The plotted correlation values are substantially <1, even for windows matched to the reference state, because of sampling variability (Laumann et al. 2015). (C) Distribution of computed multivariate kurtosis values over the 10 000 simulations. pdf, probability density function. Multivariate kurtosis is systematically greater for the two-state simulation relative to the one-state simulation. Time series of finite duration yield kurtosis values that are systematically lower than expected in the limit of infinite sample size (see Supplementary Fig. S2). Thus, if d = 30, the expected kurtosis is d (d + 2) = 960 for data of infinite length, whereas the mean value in the perfectly stationary simulation here is 945.

Figure 4.

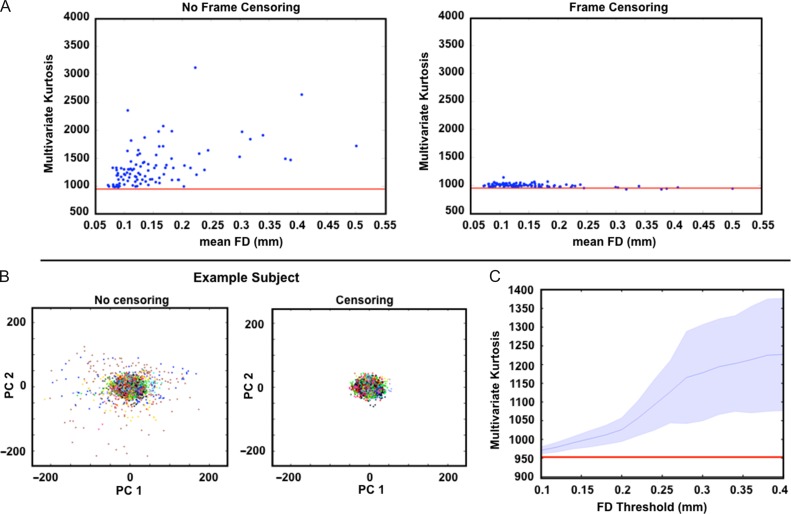
Multivariate kurtosis is related to head motion. (A) Multivariate kurtosis plotted against mean framewise displacement (FD). Each blue dot represents one session. All 10 sessions from each of 10 subjects are represented. Kurtosis is computed on the first 30 principal components derived from each session (see “Materials and Methods” section). The average kurtosis of simulated stationary data is indicated by the red line (~952). The top and bottom plots were generated without and with frame censoring, respectively. (B) BOLD fMRI data from all 10 sessions of one example subject projected onto the first two principal components. Each dot represents one frame. Colors correspond to session; note no systematic effect of session. Results obtained without and with frame censoring are shown on the left and right, respectively. Frame censoring (FD > 0.2 mm) markedly reduces outlier data. (C) Multivariate kurtosis as a function of frame censoring FD threshold across all sessions and subjects. Shading indicates the standard deviation. The red line indicates the average multivariate kurtosis of simulated data.

Figure 6.

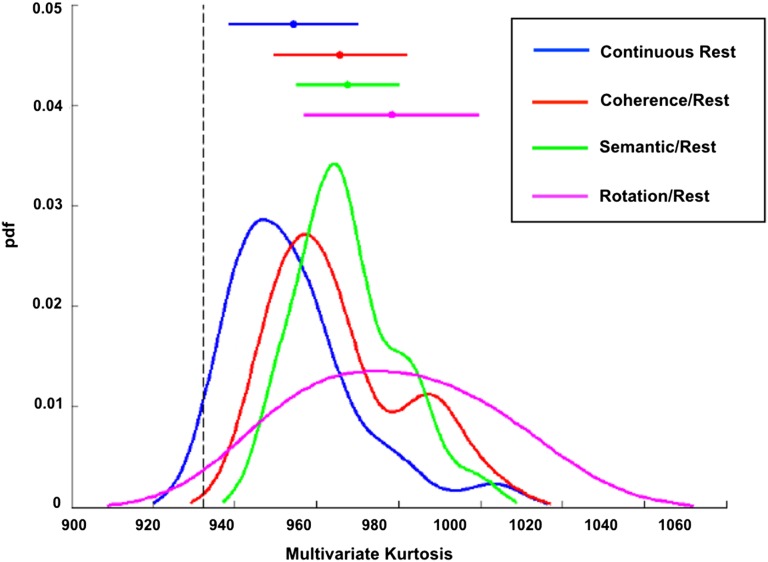
Alternating blocks of task/rest give rise to greater multivariate kurtosis than continuous resting state. Kurtosis values from task/rest runs (3 duplicate runs per paradigm) were averaged and compared with kurtosis values from continuous resting state runs of the same length (470 s) in the same subjects (N = 24). Three different task paradigms were used: Glass pattern coherence discrimination (red), noun versus verb semantic judgment (green), and mental rotation (purple). Plots represent smoothed histograms of the kurtosis values. Bars above indicate the mean and standard deviation for each condition. The dotted black line represents the mean kurtosis (932) of simulated stationary data of the same length as the task runs. Nonsmoothed histograms are reported in Supplementary Figure S5.

Figure 1.

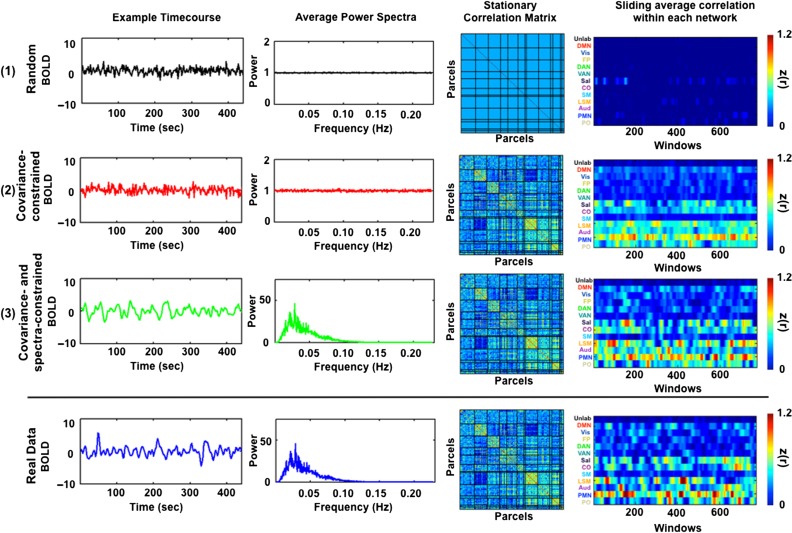
Generation of simulated data. (1) BOLD fMRI time series are simulated by first sampling random normal deviates. (2) These time series are projected onto the eigenvectors of the covariance matrix of real data averaged over ten 30-min sessions from each subject. (3) The projected time series then are matched to the average parcel-wise power spectrum of the real data by multiplication in the spectral domain. The final simulated data share the covariance and spectral features of real data (compare with bottom row) and are stationary by construction.

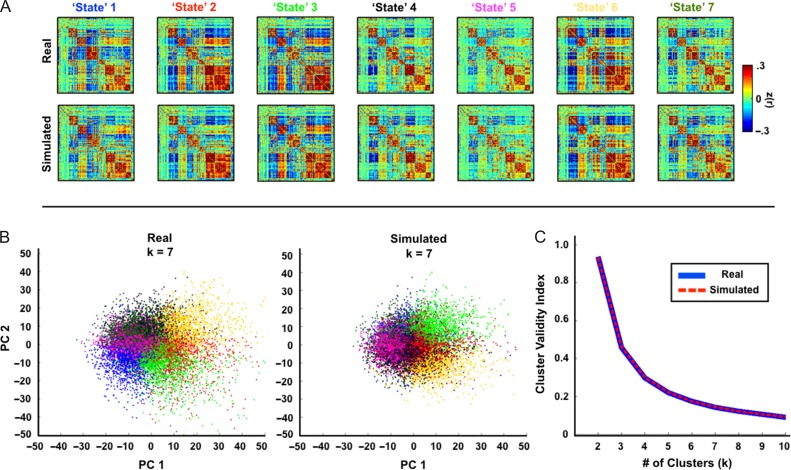
Figure 2.

Real and simulated data have the same “states.” (A) Average correlation matrices corresponding to clusters (k = 7) derived by analysis of correlation matrices over sliding windows. Real and simulated data produce very similar “state” patterns. (B) Sliding window correlation matrices projected onto the first two principal components. Colors correspond to “state” identity in (A). (C) Similarly, the cluster validity index by number of clusters is nearly identical in the real and simulated data. To specifically illustrate sampling variability masquerading as “nonstationarity,” the impact of artifactual nonstationarity was minimized by excluding data corrupted by head motion. Thus, sessions with fewer than 50% of frames retained by scrubbing criteria were excluded entirely.

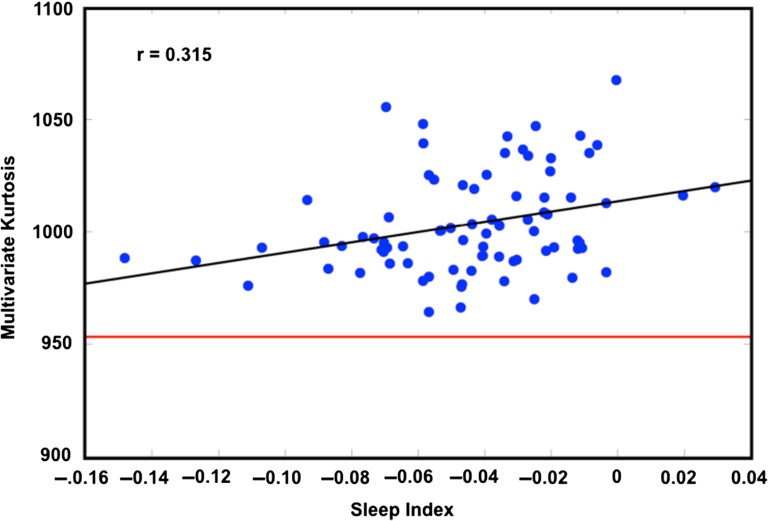
Figure 5.

Multivariate kurtosis correlates with SI. Kurtosis is computed on the first 30 principal components derived from each session. Sessions have been frame censored. Any session with fewer than 50% frames retained has been removed. One session with a kurtosis measure 4.7 SD from the mean was excluded. The average kurtosis corresponding to simulated stationary data is indicated by the red line (~952).

Subjects and Data Acquisition

Data contributing to the main analyses were collected in 10 healthy, right-handed, young adult subjects (5 females; age: 24–34). Two of the subjects are authors (N.U.F.D. and S.M.N.), and the remaining subjects were recruited from the Washington University community. Informed consent was obtained from all participants. Imaging was performed over 12 days on a Siemens TRIO 3 T MRI scanner. For each subject, 30 contiguous minutes of resting state BOLD fMRI data were collected on 10 separate days (total time = 300 min per subject).

RSFC Preprocessing

Artifacts were reduced using frame censoring, nuisance regression (excluding censored frames), interpolation, and bandpass filtering (0.009 < f < 0.08 Hz) following Power et al. (2014). Nuisance regressors included the whole-brain mean, white matter, and ventricular signals and their derivatives, in addition to 24 movement regressors derived by expansion (Friston et al. 1996; Satterthwaite et al. 2012; Yan et al. 2013). To assess the impact of motion, results are presented both with and without the frame censoring. Frames with framewise displacement (FD) > 0.2 mm were censored (Salek-Haddadi et al. 2006), as well as uncensored segments of data lasting fewer than 5 contiguous volumes (mean frames kept across sessions: 72.5% ± 25%). Censored frames were not counted in kurtosis estimations.

Region of Interest Definition

All analyses presented here are based on time series extracted using a group-level cortical parcellation described in Gordon et al. (2016). This 333-region parcellation covers most of the cortical surface, and has been divided into 12 networks based on the Infomap community detection technique (Rosvall and Bergstrom 2008; Power et al. 2011). The parcels and their network assignments are shown in Supplementary Figure S1.

BOLD fMRI Time Series Simulation

The objective of the simulation is to create surrogate multivariate time series matched in covariance and spectral properties to BOLD data acquired in individual subjects. A detailed formal account of the simulation algorithm is provided in the Appendix of Supplementary Materials. Figure 1 illustrates the principles of the procedure. In brief, we sampled random normal deviates of the same dimensionality as a real data set. These time series are multiplied in the spectral domain by the average power spectrum derived from the region of interests (ROIs) of a full-length real data set. It should be noted that the real data set has already undergone bandpass filtering (as described above). Therefore, the spectral matching of the simulated data reflects the spectral content of postfiltered real data. These time series are then projected onto the eigenvectors derived from the covariance matrix of real data computed from the full 30 min of a given run. As the eigenvectors derived from the decomposition are orthogonal, they provide a convenient means of reconstructing the covariance structure of the real data from random normal deviates. This procedure produces simulated data that are stationary by construction but matched to real data in the covariance structure and mean spectral content (compare last two rows of Fig. 1). These simulated time series can then act as a null against which to evaluate nonstationary features of real data. Matlab code used to create simulated time series is available at our lab website (http://www.nil.wustl.edu/petersenschlaggar/Resources.html).

Sliding Window Analysis

To estimate fluctuating connectivity over time, we adopt the commonly used sliding window strategy (Chang and Glover 2010; Hutchison et al. 2013b; Zalesky et al. 2014). Specifically, we extract time series from the cortical surface using the 333-area parcellation described in Gordon et al. (2016). Correlations are then computed at each time point between windowed samples of the time series tapered by a Gaussian function to center-weight the contribution of proximal time points. Window size is adjustable by changing the number of frames specified as the full width at half maximum. The time series are high-pass filtered at the frequency of the lowest frequency allowing a full cycle given the window length. Here, we use 100 s windows, according to the recommendation of Leonardi and Van De Ville, that the window length should exceed the slowest frequencies commonly assumed to comprise the BOLD signal (Leonardi and Van De Ville 2015; Zalesky and Breakspear 2015). Thus, the time series are high-pass filtered at 0.01 Hz. To illustrate sliding window fluctuations at the network level, we averaged all correlations between regions within each network at each window. Real and simulated time series of within-network connectivity can be seen in Fig. 1 in the far right column.

State Analysis

To group the correlation patterns generated by the sliding window procedure, we adopted the k-means clustering algorithm commonly used in the literature (Allen et al. 2014; Hutchison and Morton 2015). The correlation patterns were dimensionality reduced from 55 278 (333 parcels × 333 parcels) to 30 dimensions by principal component analysis (PCA) prior to clustering to stabilize the computations and reduce computational demand. The Mahalanobis distance function was used to compute the separation between each window's correlation pattern and the k-means algorithm was iterated 100 times with random centroid positions to avoid local minima. Windows from all sessions and all subjects were used in the clustering, excluding 19 sessions (8 from 1 subject) that had more than half of their frames discarded because of excessive head motion. The window length for this analysis was 100 s and the windows were overlapping with a separation of 11 s between window centers, generating 155 windows per session. The windowed correlation patterns were mean-centered by run to eliminate run-level or subject-level features from contributing to the clustering result. k-means clustering was applied in the same manner to 81 sessions of simulated data, where each subject's BOLD power spectrum and covariance were used to generate the same number of sessions as were used in the real data. The cluster validity index was used to evaluate the quality of clustering for a range of cluster numbers (k = 2–10). The cluster validity index was computed as the average ratio of within-cluster distance to between-cluster distance.

Kurtosis of Mardia

Nonstationarity in the context of electrophysiology is frequently evaluated using spectral descriptors (Wong et al. 2006; Halliday et al. 2009). Prior methods for evaluating nonstationarity in RSFC have relied on bivariate analyses, that is, analyzing multivariate data taken pairwise (Chang and Glover 2010; Hindriks et al. 2016). However, in these methods the number of free parameters grows in proportion to the square of the dimensionality of the data set, which limits computational tractability when the number of regions is large. Here, we take a different approach based on demonstrating that BOLD fMRI time series are consistent with a multivariate normal process. In greater detail, we evaluate the multivariate fourth moment (kurtosis) of BOLD fMRI data. Kurtosis values consistent with multivariate normality imply stationarity. On the other hand, kurtosis values inconsistent with multivariate normality may indicate either that (1) the data are multivariate normal but exhibit nonconstant covariance or (2) the data are stationary but not normally distributed. In addition, kurtosis is insensitive to nonstationarity of spectral content (see Discussion in Supplementary Materials). Thus, kurtosis estimation does not address stationarity in a strict sense. Nevertheless, kurtosis estimation is useful for investigating whether or not BOLD fMRI data exhibit nonconstant covariance, assuming multivariate normality.

We adopt a measure of multivariate kurtosis introduced by Mardia (1970) and Henze (2002). Let $Y_1,Y_2,\dots ,Y_n$ denote vectors $Y_j$ of dimension d, where $1\le j\le n$. Here, Y corresponds to preprocessed fMRI data of duration n frames and d corresponds either to number of ROIs or the dimensionality of the data following dimensionality reduction (see Supplementary Materials). Importantly, the data have been made zero-mean during preprocessing. Thus, $\stackrel{\circledR }{Y}$, the mean value over all frames, is a $\mathit{d}\times 1$ column of zeros. The sample covariance matrix is

$$C=\frac{1}{n}\sum _{j=1}^n\left(Y_j-\stackrel{\circledR }{Y}\right){\left(Y_j-\stackrel{\circledR }{Y}\right)}^{\mathrm{T}}=\left(1/n\right)\sum _{j=1}^n{Y}_j{Y}_j^{\mathrm{T}},$$ (1)

where the superscript, T, denotes matrix transpose and the equality holds because the data have been made zero-mean during preprocessing. The squared Mahalonobis distance between any two frames, indexed by j and k, is

$$D_{\mathit{jk}}=Y_j^{\mathrm{T}}{C}^{-1}{Y}_k,$$ (2)

where the superscript, $-1$, denotes the matrix inverse. Thus, $D_{\mathit{jk}}$ is a scalar that reflects the dissimilarity between frames j and k. These dissimilarity measures may be assembled into the symmetric $\mathit{n}\times \mathit{n}$ matrix, D. Multivariate kurtosis in the sense of Mardia may be evaluated by summing the squared diagonals of D. Thus,

$$b_{n,d}=\frac{1}{n}\sum _{i=1}^n{\left[D_{\mathit{ii}}\right]}^2.$$ (3)

Following the convention of Henze (2002), the subscripts in $b_{n,d}$ denote number of samples and dimensionality, respectively. One advantage of this statistic in this context is that it avoids arbitrary parameter choices (e.g., window size and window function—Hamming, Boxcar, etc.) that arise using sliding window statistics. Furthermore, sliding windows usually generate nonindependent successive estimates, which complicates the estimation of appropriate statistics for evaluating correlation variability. In the analyses presented here, multidimensional time series (both simulated and real) were extracted from the 333 cortical ROIs defined in the aforementioned cortical parcellation. This number of regions exceeds the dimensionality of BOLD fMRI data (Cordes and Nandy 2006). Thus, the 333 × 333 covariance matrix of the data would be rank deficient, and the inversion required by equation (2) would be unstable. Accordingly, the dimensionality of the “raw” data was reduced via principal components analysis from 333 to 30, thereby stabilizing the kurtosis calculation while still retaining a reasonable number of independent signals. In the limit of an infinite sample size ($\mathrm{n}\to \mathrm{\infty }$), the expected multivariate kurtosis of a normal stationary multivariate process of dimensionality d is d (d + 2). In practice, the obtained value depends on the sample size and the temporal autocorrelation of the simulated process. Thus, the multivariate kurtosis will be lower for simulations of finite length that are based on time series with filtered spectral content (Supplementary Fig. S2). Accordingly, in this work, the simulated data were always matched in size to the real data in comparisons of multivariate kurtosis.

Sleep Index

To assess the level of wakefulness in each session, we developed a sleep index (SI). This SI was based on a separate high-quality resting state fMRI data set (Data set 4, see Supplementary Materials) acquired on subjects in known states of wake and sleep as determined by EEG (Tagliazucchi and Laufs 2014). Using these data, we computed the difference between the light sleep (N1 and N2) and wake covariance matrices and applied spatial PCA to the difference matrix. The weights in the first PC highlight those voxels whose covariance structure is maximally altered in wake versus sleep (Mitra et al. 2015b). To select voxels exhibiting maximal change, we applied a Fisher z-transform to the weights in the first PC, and selected only voxels whose weights were in the 95th percentile. Voxels in the occipital cortex were manually excluded, to avoid confounds arising from the fact that the data in the main analysis were acquired in the eyes-open state, whereas the sleep data were acquired in the eyes-closed state (during both wake and sleep). Covariance matrices from these voxels were computed for each session of each subject in the main data set. These covariance matrices then were compared by Pearson correlation to the covariance matrices from the sleep (N1 and N2) and wake states of the sleep data set. The SI was computed as the similarity to the sleep state (averaged over N1 and N2) minus the similarity to the wake state. A higher value of the SI means the session had covariance relatively more similar to sleep than wake.

Results

Simulated Stationary Data Exhibit Apparently “Dynamic” RSFC

All present results were obtained by comparison of real data to a null model matched in covariance structure and spectral content to real BOLD fMRI data. The procedure used to generate time series with these properties are illustrated in Figure 1 for an exemplar subject. In the top row, we show the correlation structure and spectral content of random normal deviates of the same dimensionality as a particular real data set. As expected, on average, random normal deviates have identity correlation and flat spectral content. In the second row, we illustrate random normal deviates that have been projected onto the eigenvectors of the covariance structure of the real data. These time series have covariance structure matched to real data but lack the characteristic frequency content of BOLD data. In the third row, the time series have been spectrally filtered to duplicate the average power spectrum of real data and have been projected onto the eigenvectors of the covariance structure of the real data. This procedure produces simulated time series with the covariance (hence, network structure), spectral structure, and length of real data (compare last two rows of Fig. 1). These simulated data are stationary by construction.

The rightmost panel of Figure 1 shows within-network functional connectivity (averaged over within-network ROI pairs) computed over sliding windows of 100 s. The real and simulated data exhibit similarly patterned fluctuations in within-network RSFC.

To examine the dynamic properties of the simulated data in greater detail, we performed a k-means clustering analysis (k = 7) of sliding window correlation matrices as described in recent publications (Allen et al. 2014; Hutchison and Morton 2015). Figure 2A shows results obtained with both real data (excluding sessions with fewer than 50% frames retained) and a typical iteration of matched simulated data. The “state” correlation matrices obtained from real and simulated data are very similar—the average Pearson correlation between matched real and simulated “states” is r = 0.96 ± 0.01. Two additional analyses demonstrate the similarity between both types of data (Fig. 2B,C). First, correlation matrices computed at each sliding window were projected onto two dimensions and colored by their “state” assignments. Second, cluster validity indices were computed as described in Allen et al. (2014) (see “Materials and Methods” section). Inspection of these results reveals, first, that the distributions of windowed correlations exhibit no obvious evidence of separable “state” clusters and, second, that there are no discernable differences in the statistical properties of the real and simulated data. Since the simulated data are stationary, this result demonstrates that the appearance of discrete “states” can be generated by sampling variability. Furthermore, the appearance of nearly identical “states” in the real data suggests that these “states” likely may also be explained by sampling variability.

Excess Multivariate Kurtosis Is Detected in Multivariate Time Series That Include More Than One State

Variability of second-order statistics theoretically is reflected as elevated multivariate kurtosis (Martins 2007). Accordingly, we adopt a measure of multivariate kurtosis introduced by Mardia (1970). To illustrate the sensitivity of this measure to changes in covariance, we generated two simulations of multivariate processes based on the measured covariance structure of eyes-open and eyes-closed data. Data for this analysis were collected as part of the MyConnectome Project and have been previously reported (Laumann et al. 2015; Poldrack et al. 2015). Opening versus closing the eyes induces a well documented, albeit subtle, change in the covariance structure of BOLD fMRI data (Fig. 3A; McAvoy et al. 2008; Laumann et al. 2015). The first simulation assumes an “eyes-open” covariance structure over the entire run. In the second simulation, the covariance structure changed from “eyes-open” to “eyes-closed” halfway through the run. The multivariate kurtosis measures obtained from the two simulations are shown in Figure 3C. The two-state simulation yielded greater kurtosis relative to the one-state simulation. This observation demonstrates that multivariate kurtosis is sensitive to nonstationarity in the covariance structure of BOLD fMRI time series. It should be noted that the statistic should be sensitive to covariance changes regardless of their cause, for example, relative phase changes or changes in variance magnitude. Additional simulations in Supplementary Figure S3 illustrate this principle in a simple toy case of bivariate time series. However, they further show that multivariate kurtosis is not sensitive to disjoint spectral content across ROIs as long as the sum of the power across frequencies remains constant over time (Supplementary Fig. S3A).

Removal of High-Motion Frames Reduces Kurtosis

Head motion is known to cause transient whole-brain changes in BOLD fMRI data that substantially alter RSFC (Power et al. 2012; Satterthwaite et al. 2012; Van Dijk et al. 2012). Accordingly, head motion could be a cause of observed non-normality in resting state data. Here, we test this hypothesis by plotting measured kurtosis against FD, both measures being evaluated over whole runs (Fig. 4A). The relation across all runs between multivariate kurtosis and mean FD was evaluated by Pearson correlation. In the uncensored data, kurtosis was positively correlated with the mean FD of the run (r = 0.50, p = 10⁻⁷) and demonstrated values substantially above the baseline level observed in stationary simulated data (red line), especially in heavily motion-compromised runs. This relation was effectively eliminated following frame censoring (Power et al. 2014). Indeed, in several cases, frame censoring reduced multivariate kurtosis almost to the level computed in the corresponding simulated stationary data. Some runs with significant motion demonstrated measured multivariate kurtosis slightly below the expected mean value. This may be because, as shown in Supplementary Figure S2, multivariate kurtosis depends on run length and, for these runs, frame censoring substantially reduced the number of time points. We note, however, that random removal of frames (as opposed to frames selected for high motion) has a more modest effect on measured kurtosis (see Supplementary Fig. S4).

The underlying basis of this effect is illustrated in Figure 4B using all time points from all 10 sessions (818 frames per session) acquired in a single subject. Censoring high-motion (FD > 0.2 mm) frames removes time points inconsistent with a multivariate normal process. More generally, across all subjects and sessions, multivariate kurtosis systematically increases as a function of FD threshold (Fig. 4C). This result suggests that some data sets may be made to approach normality (red line) by application of a stringent frame censoring FD threshold. However, for many data sets such a maneuver would also eliminate much or all of the data.

Fluctuating Drowsiness Contributes to Nonconstant RSFC

Sleep changes the correlation structure of spontaneous BOLD fMRI (Picchioni et al. 2013). Moreover, Tagliazucchi and Laufs (2014) have demonstrated that many data sets acquired with the intention of studying the awake resting state are contaminated by sleep. Hence, drowsiness is a likely source of “bona fide” (i.e., of neural origin) nonstationarity in RSFC. Since our data were not acquired with simultaneous EEG recording, we used the Tagliazucchi/Laufs data set (Tagliazucchi et al. 2013), in which sleep stage is known, to define a set of regions by which it is possible to compute a “SI” for each fMRI run. The most discriminating regions for identifying sleep in eyes-closed data are in visual cortex, somatomotor cortex, and the thalamus (Tagliazucchi et al. 2012b). We omitted visual regions in formulating our SI as our data were collected with eyes-open, while Tagliazucchi/Laufs data set was collected with eyes-closed, as these regions are most affected by eye state (McAvoy et al. 2008; Bianciardi et al. 2009). Given that subjects tend to become drowsy over the course of a 30-min resting state fMRI run (even if they are instructed to stay awake and maintain visual fixation), we may expect that the SI should systematically increase with time in the scanner. Supplementary Figure S6 demonstrates that, on average, this effect was observed in our data.

We plotted kurtosis against the SI across sessions, restricting this analysis to frame-censored data. This analysis revealed a significant correlation between the two measures (r = 0.315, p = 0.0044; Fig. 5). Thus, fluctuating drowsiness over the course of a resting state session may contribute to observed non-normality in RSFC. However, in our data, this effect is quantitatively dwarfed by the effects of head motion (compare scales in Figs 4A vs. 5).

Induced Changes in Cognitive State are Detectable Using Multivariate Kurtosis

Accumulating evidence indicates that BOLD fMRI correlation relationships are altered during performance of various tasks (Fransson 2006; Al-Aidroos et al. 2012; Cole et al. 2014; Krienen et al. 2014). Hence, alternation between rest and task states should lead to nonconstant correlation structure detectable as elevated kurtosis. To test this hypothesis, we sampled time series from the same parcels used in prior analyses (see Supplementary Fig. S1), acquired while participants performed three different mixed block/event-related tasks (N = 24). Data used for this analysis have been previously described elsewhere (Dubis et al. 2016; see Supplementary Materials for acquisition details). Each task run began and ended with 50 s of resting-state fixation and included two 175-s task blocks separated by 50 s of resting fixation. Separate runs of rest data also were collected in the same subjects. The task data were processed in the same manner as the rest data, with the additional step of regressing out the mixed block/event task model, as in Al-Aidroos et al. (2012) to remove first-order time-locked responses from the time series. Processing included frame censoring to account for head motion for reasons discussed in the next section. We observed that relative to continuous resting-state runs multivariate kurtosis was increased in block-design in which tasks alternated with rest (Fig. 6). Paired t-tests indicated that all three tasks exhibited significant increases in multivariate kurtosis relative to resting runs (Coherence task: t(23) = 3.05, p = 0.006; Semantic task: t(23) = 3.51, p = 0.002; Mental Rotation task: t(23) = 5.19, p ≪ 0.001). The largest kurtosis increase was observed in the mental rotation runs. This task also induces the largest change in correlation structure relative to rest. These observations demonstrate that elevated kurtosis can be induced by alternating between task and rest blocks even after the removal of evoked responses.

Discussion

We evaluated the degree to which the correlation structure of BOLD fMRI is stable over time using multivariate kurtosis and comparing real data to statistically matched stationary simulations. In the resting state, we find that observed fluctuations in correlation structure are largely attributable to three major factors: 1) sampling variability intrinsic to measuring correlations in short windows; 2) signal changes related to head motion; and 3) correlation changes related to changes in sleep state. Of these, only the last is physiologically meaningful. Thus, the correlation structure of resting-state BOLD fMRI data appears to be very nearly constant, discounting the effects of sleep and head motion. On the other hand, changes in cognitive state induced by alternating task with rest blocks were associated with increased multivariate kurtosis (Fig. 6).

We should be clear that multivariate kurtosis assesses the degree to which a process is multivariate normal with constant covariance; it does not fully assess the stationarity of all aspects of a process. For example, nonconstant spectral content would not be detectable by kurtosis, provided that the covariance is constant (see Appendix of Supplementary Materials for further discussion of this point). Alternative measures that allow for testing of nonstationarity in higher-order statistics and in spectral content do exist (Last and Shumway 2008; Jentsch and Subba Rao 2015). We evaluated kurtosis because it offers the advantage of more straightforward applicability to multivariate data. Kurtosis is sensitive to nonstationarity of second-order statistics, which is the quantity of interest in RSFC studies. Moreover, multivariate kurtosis evaluates the FC of all pairs of regions at once. Alternative techniques are formulated in terms of single pairs of signals (Zalesky et al. 2014; Hindriks et al. 2016).

Sampling Error Can Lead to the Appearance of “Dynamic” Functional Connectivity

Using a stationary simulation incorporating the spectral content and covariance structure of real BOLD fMRI data, we demonstrate that sampling variability can contribute to the illusory appearance of discrete functional connectivity “states” (Fig. 2). Several recent papers have pointed out that much of the prior literature on “dynamic” functional connectivity is based on inappropriate analytic techniques (Lindquist et al. 2014; Zalesky et al. 2014; Leonardi and Van De Ville 2015). Our results reinforce this observation and further demonstrate that distinct correlation structures extracted from real data closely resemble the correlation structures in simulated stationary data. These results are consistent with work by Hindriks et al. (2016) that reported no evidence of nonstationarity in resting state BOLD correlations, and similar observations made in relation to EEG data (Hlinka and Hadrava 2015). We have also previously shown that day-to-day variability in the correlation structure of resting state BOLD fMRI data (acquired in a single individual) is almost entirely (>98%) attributable to sampling error, that is, is inversely proportional to the total quantity of analyzed data (Laumann et al. 2015). Thus, the model described in the prior work predicts that low reliability will be the dominant feature of RSFC estimation at very short timescales, purely as a result of sampling error. Indeed, the present findings confirm this expectation.

Head Motion is a Major Source of Artifactually Elevated Kurtosis

Head motion artifact accounts for much of the excess kurtosis observed in our data (Fig. 4). Head motion has already been identified as a major source of artifact in conventional resting state fMRI (Power et al. 2012; Van Dijk et al. 2012). Our analyses (Fig. 4) show that measured multivariate kurtosis is correlated with the quantity of head motion on a per-fMRI-run basis. Importantly, censoring of high-motion frames (FD > 0.2 mm), as previously described (Power et al. 2014) substantially reduced measured kurtosis, far more than randomly removing frames (Supplementary Fig. S4). In a minority of cases, kurtosis was reduced to levels obtained by analysis of matched simulated data (Fig. 4A). However, in most cases, this maneuver did not completely eliminate the effects of head motion. Figure 4C suggests that if even stricter movement criteria are used more sessions may approach this baseline. These results imply that a substantial portion of RSFC “dynamics” may be attributable to head motion and suggest that caution must be exercised when interpreting measurements of dynamic RSFC. Indeed, subject by subject and day by day differences in motion may lead to artifactual variability in dynamic RSFC measures (Lindquist et al. 2014), making reliable associations with behavioral measures a serious challenge.

Fluctuating Drowsiness Increases Multivariate Kurtosis of Resting State BOLD fMRI Data

Sleep unambiguously modifies intrinsic neural activity. Indeed, sleep stages are defined in terms of specific EEG signatures (Dement and Kleitman 1957). More recently, it has been shown that sleep staging also can be computed on the basis of RSFC data (Tagliazucchi et al. 2012a) and, moreover, that about one-third of publicly released RSFC data sets are affected by sleep within the first few minutes of scanning, although this finding was less prominent in data sets acquired with eyes-open fixation, as in the present case (Tagliazucchi and Laufs 2014). Nevertheless, we evaluated sleep as an explanatory factor in our results. Following aggressive frame censoring, measured kurtosis was still significantly correlated with the RSFC-derived SI (Fig. 5). Thus, at least some observed non-normality in RSFC is likely related to fluctuating drowsiness over the course of the scan.

Owing to limitations in the design of our SI (see “Materials and Methods” section), it is likely that the present results underestimate the extent to which sleep accounts for variability in RSFC. Our assessment may also be complicated by head motion in subjects who were struggling to keep their eyes-open and stay awake. Some periods of fluctuating drowsiness probably were discarded by frame censoring, thereby reducing our estimated prevalence of sleep.

Changes in Cognitive State Increase Multivariate Kurtosis of Resting State BOLD fMRI Data

We found that alternating task and rest blocks lead to a measurable, but modest, increment in kurtosis over the level observed in continuous resting state data (Fig. 6). Previous authors have emphasized that task performance does not greatly perturb the “core” architecture of functional connectivity (Cole et al. 2014; Krienen et al. 2014). Nevertheless, statistically reliable changes in correlation structure have been observed in a variety of task contexts (Cole et al. 2014; Krienen et al. 2014; Gonzalez-Castillo et al. 2015). These changes frequently localize to regions of the brain presumed to be involved in task-specific processing, for example, altered FC in visual regions during a visual attention task (Al-Aidroos et al. 2012). Additionally, it has been proposed that spontaneous activity itself is suppressed by task engagement (He 2013). Our results indicate that there are changes in correlation structure between resting state and goal-directed task states, although we cannot distinguish whether these effects reflect suppressed spontaneous activity or task-induced correlation changes. Moreover, as noted above, elevated kurtosis does not distinguish between nonconstant covariance in an otherwise stationary normal process versus other types of deviation from multivariate normality. However, it seems to us most likely that the effects of alternating task state as well as sleep are reflected primarily as changes in covariance.

Importantly, the resting state condition yielded mean kurtosis measures closer to the stationary null model than any of the task-alternation conditions. This observation suggests that the variability in correlation induced by the changes in cognitive state of the magnitude imposed by standard task paradigms does not occur during resting state BOLD runs.

BOLD Correlations Considered in Relation to Cognition

The present results suggest that the correlation structure of resting state fMRI is very nearly constant on a timescale of minutes, discounting the effects of drowsiness (Fig. 6). This result may not accord with the idea that changes in cognition might be reflected in ongoing BOLD activity. To be sure, cognitive processes must be reflected in the BOLD signal. Otherwise, task-fMRI would be impossible. Moreover, multiple studies have demonstrated that cognitive content can be “decoded” by analysis of BOLD fMRI data (Haxby et al. 2014; Yang et al. 2014). However, conventional task-evoked responses are distinct from the correlated patterns of BOLD activity under consideration here in important ways. Conventional fMRI assumes that cognitive content is reflected in the instantaneous activity profile (a first-order statistic) of the brain (appropriately corrected for hemodynamic delay). In contrast, functional connectivity is defined in terms of correlation (a second-order statistic) of BOLD signal pairs; the quantity of interest reflects how regions of the brain relate to each other rather than to cognitive content. Thus, intuitions regarding cognition derived from a rich history of functional neuroimaging may not apply in analyses of functional connectivity. Rather, changes in correlation structure that we do observe may relate to distinct underlying processes that broadly facilitate state-specific processing, for example, in the context of different task paradigms (Friston et al. 1997), as opposed to moment-to-moment item-level processing.

The present results also reinforce several previously articulated points concerning the robust character of spontaneous BOLD fMRI fluctuations as viewed from multiple perspectives (Raichle and Snyder 2007): 1) The topography of BOLD fMRI correlations remains largely intact during slow-wave sleep (Samann et al. 2011; Mitra et al. 2015b) and even anesthesia (Mhuircheartaigh et al. 2010; Palanca et al. 2015), conditions under which cognition is presumed to be either absent or greatly attenuated. The relative stability observed under these conditions is likely related to underlying constraints of anatomical connectivity (Honey et al. 2009; Lu et al. 2011; Barttfeld et al. 2015) and ongoing synaptic efficacies. 2) Task paradigms are capable of modifying the correlation structure of spontaneous BOLD signal fluctuations (Fig. 6), but only to a limited extent (Cole et al. 2014; Krienen et al. 2014). 3) Whereas unconstrained cognition might be expected to vary from subject to subject and from scan to scan, RSFC is consistent across subjects at the population level (Damoiseaux et al. 2006) and, within individuals, consistent across sessions (Laumann et al. 2015).

The preceding considerations raise two questions: 1) what physiological processes are predominantly represented in ongoing BOLD fluctuations? and 2) why do these processes exhibit a relatively stable correlation structure over time? To address these questions, we invoke the principle that the brain must allow for adaptive plasticity on the basis of new experiences while simultaneously maintaining its functional architecture over extended spans of time (Turrigiano 2012). Ongoing neural activity has been shown to contribute to the sculpting of functionally appropriate connectivity during development (Penn and Shatz 1999; Kirkby et al. 2013). It is likely that similar processes persist into adulthood (Nahmani and Turrigiano 2014). Hebbian-like mechanisms are believed to underlie experience-dependent synaptic plasticity (Lewis et al. 2009; Schacher and Hu 2014), These mechanisms, in turn, are balanced by homeostatic processes that adjust synaptic weights in the wake of experience-dependent perturbations (Marder and Goaillard 2006; Takesian and Hensch 2013; Vitureira and Goda 2013). Although the recent literature on this topic is largely focused on molecular mechanisms (e.g., receptor trafficking, regulatory proteins, and gene expression) (Malenka and Bear 2004; Kullmann et al. 2012), it is critical to keep in mind that plasticity generally is governed by neural activity and that this activity contributes to ongoing BOLD signal fluctuations. RSFC stability over timescales on the order of minutes follows naturally if ongoing neural activity is determined primarily by the long-term configuration of the brain rather than by recent experience. Thus, patterns of BOLD correlations may both reflect current synaptic relationships as well as serve to maintain them.

Stable RSFC is Compatible with “Dynamic” BOLD Features and the Possibility that Ongoing BOLD Activity Influences Behavior

It is important to note that a stable correlation structure in resting-state BOLD is compatible with a large repertoire of dynamic behavior and functional associations. For example, Liu and Duyn (2013) have described a “snapshot” phenomenon, that is, brief epochs in which the topography of particular RSNs emerges from the ongoing activity. In a univariate normal process, excursions exceeding ±2 SD may be expected to occur in 5% of samples. A similar principle applies to multivariate normal processes. Thus, the presence of single frame coactivation patterns is not precluded by the results of this work.

Stationarity of BOLD correlation structure also does not preclude the possibility that the instantaneous state of neural activity biases cognitive operations, perceptions, or motor behavior (Hutchison et al. 2013a). Several studies have reported that resting-state BOLD fMRI fluctuations bias perceptions as well as motor behavior (Bishop 1932; Fox et al. 2007; Hesselmann et al. 2008; Sadaghiani et al. 2010). It has been suggested that intrinsic variability (stochastic dynamics) is advantageous because it promotes exploration of the range of responses to a given circumstance (Deco et al. 2009). None of these considerations imply that the second-order statistics of ongoing neural activity necessarily are nonstationary. The aforementioned hypothetical frictionless pendulum again provides a useful analogy. Just as the pendulum might turn on a light at one end of its excursion, a similar process within the brain could influence behavior. Furthermore, just as an applied external force might cause the motion of the pendulum to be nonstationary, environmental events may generate neural responses. Such responses are, by definition, not “resting state.”

Propagation Analysis Provides a Means of Studying Time-Dependent Properties of Ongoing BOLD Activity

The present results suggest that the correlation structure of resting state BOLD activity is essentially stable over tens of seconds. However, the stability of BOLD signal correlations, which are computed by integrating over time, does not speak to the time-dependent properties of BOLD data as described by analyses of structured signal propagation at shorter timescales. Indeed, Mitra and colleagues have recently reported that resting state BOLD signals are characterized by propagating spatiotemporal sequences that play out on a timescale of ±1 s (Mitra et al. 2014, 2015a). Propagation is inferred on the basis of temporal lags in BOLD signals between pairs of regions across the whole-brain (Mitra et al. 2014). This temporal lag structure is highly reproducible over large groups of subjects studied in the awake resting state (Mitra et al. 2015a). Importantly, the lag structure is sensitive to changes in eye state (open or closed), recent history of task performance, time of day, and, most dramatically, to slow-wave sleep as compared with wake (Mitra et al. 2014, 2015b, 2015b). Furthermore, on comparing adults with autism spectrum disorder to age-matched controls, conventional RSFC measures showed no differences while clear abnormalities were observed in lag structure (Mitra et al. 2017). In the present context, it should be noted that propagating spatiotemporal processes are consistent with stationarity, so long as propagation patterns are stable within state.

Future Directions and Conclusion

The present analyses do not prove that resting state BOLD data are devoid of nonstationary features. Firstly, this is because the kurtosis assesses multivariate normality rather than stationarity per se. But beyond this limitation, there remains a small excess of kurtosis compared with simulated data evident in Figure 5 that is not readily attributable to head motion or fluctuating drowsiness. Potential sources of this excess kurtosis include the inability to completely eliminate the effects of head motion (Fig. 4C), underestimated sleep effects (Tagliazucchi et al. 2012c), fluctuating arousal (Chang et al. 2016), “unconstrained cognition,” or as yet unidentified factors. However, the unaccounted for excess of kurtosis is small relative to that accounted for by identified explanatory factors. Therefore, we suggest that any evaluation of these other possible explanatory factors of variability in RSFC over time should carefully account for sampling variability and known sources of nonstationarity (e.g., head motion and sleep state). Future investigations may identify physiologically meaningful contributors to correlation variability. However, the present observations suggest that correlations in infra-slow brain activity, at least as measured by resting-state BOLD, are relatively stable over short timescales, pointing to a role for these relationships that may be largely distinct from moment-to-moment cognitive processing.

Supplementary Material

Supplementary material can be found at: http://www.cercor.oxfordjournals.org/

Funding

F30MH100872 (T.O.L.), NS61144 (S.E.P.), NS26424 (S.E.P.), NS080675 (A.Z.S.), F30MH106253 (A.M.M.), K01MH104592 (D.J.G.), Hope Center for Neurological Disorders Pilot Award (B.L.S., S.E.P., N.U.F.D.), Intellectual and Developmental Disabilities Research Center at Washington University (P30 HD062171 and U54 HD087011), Mallinckrodt Institute of Radiology Pilot Grant (N.U.F.D.), Child Neurology Foundation Scientific Research Award (N.U.F.D.), NS088590 (N.U.F.D.), NSF GRFP DGE1143954 (A.W.G.), NSF-DMS1300280 (J.M.), Dart NeuroScience LLC (J.J.B.), the Bundesministerium für Bildung und Forschung (grant #: 01EV0703) and the LOEWE Neuronale Koordination Forschungsschwerpunkt Frankfurt (H.L., E.T.).