Ridesharing and Motor Vehicle Crashes in 4 US Cities: An Interrupted Time-Series Analysis

Abstract

Uber, the world’s largest ridesharing company, has reportedly provided over 2 billion journeys globally since operations began in 2010; however, the impact on motor vehicle crashes is unclear. Theoretically, ridesharing could reduce alcohol-involved crashes in locations where other modes of transportation are less attractive than driving one’s own vehicle while under the influence of alcohol. We conducted interrupted time-series analyses using weekly counts of injury crashes and the proportion that were alcohol-involved in 4 US cities (Las Vegas, Nevada; Reno, Nevada; Portland, Oregon; and San Antonio, Texas). We considered that a resumption of Uber operations after a temporary break would produce a more substantial change in ridership than an initial launch, so we selected cities where Uber launched, ceased, and then resumed operations (2013–2016). We hypothesized that Uber’s resumption would be associated with fewer alcohol-involved crashes. Results partially supported this hypothesis. For example, in Portland, Uber’s resumption was associated with a 61.8% reduction (95% confidence interval: 38.7, 86.4) in the alcohol-involved crash rate (an absolute decrease of 3.1 (95% confidence interval: 1.7, 4.4) alcohol-involved crashes per week); however, there was no concomitant change in all injury crashes. Relationships between ridesharing and motor vehicle crashes differ between cities over time and may depend on specific local characteristics.

Motor vehicle crashes are the leading cause of death for people aged 13–25 years (1). In 2015, 35,092 people of all ages were killed and a further 2.4 million were injured in an estimated 6.3 million police-reported crashes (2). In that context, innovative technologies that displace public and private transportation markets and alter the way populations use roadway networks will also affect public health. One such innovation is ridesharing, a technology that connects contracted owner-operator drivers with prospective passengers through a mobile application. Two ridesharing companies, Uber (Uber Technologies, Inc., San Francisco, California) and Lyft (Lyft, Inc., San Francisco, California), began operation in 2010 and 2012 and have achieved estimated market values of $62.5 billion and $5.5 billion, respectively (3, 4). In March 2016, Uber reportedly booked 50 million rides in the United States and Lyft 11 million rides (5). Uber has reportedly provided over 2 billion ridesharing journeys globally (6). Nevertheless, relationships between ridesharing and motor vehicle crashes are unclear.

The primary theoretical mechanism by which ridesharing may affect motor vehicle crashes is through alcohol-involved crashes. When deciding whether to drive after drinking, individuals weigh the prospective costs of drunk driving (i.e., due to crashing or being arrested for driving under the influence of alcohol) against the convenience and financial costs associated with alternative transportation (7–9). Ridesharing is advertised as a cheaper and more easily accessible alternative to taxis (10), and the lower perceived (or real) convenience and financial costs may lead to fewer instances of drunk driving and therefore fewer alcohol-involved crashes. Approximately one-third of all motor vehicle fatalities are alcohol-involved, and alcohol-involved crashes are associated with more serious injuries and more fatalities than are crashes that are not alcohol-involved (11, 12), so even a small relative reduction in alcohol-involved crashes might yield a substantial public health benefit (13).

Three empirical studies have examined relationships between ridesharing and crashes. All 3 used a differences-in-differences approach, comparing crash incidence over time for geographic areas in which ridesharing was introduced. Results are mixed. Dills and Mulholland (14) found that Uber operations in 155 US cities and counties were associated with fewer overall fatalities and arrests for driving under the influence of alcohol but not with alcohol-involved crash fatalities. Greenwood and Wattal (15) estimated that uberX (the cheapest variant of Uber) reduced the incidence of alcohol-involved crash fatalities by 3.6%–5.6% in California townships, but Brazil and Kirk (16) found that fatal crash incidence did not differ according to the presence or absence of Uber operations in 100 heavily populated US counties. Findings from these linear models are valuable because they reflect the average relationships between ridesharing and crashes for all included geographic regions, and are therefore useful for assessing the possible overall impact of this new technology. However, roadway network use and the spatial structure of cities can vary markedly (17), and ridesharing may affect crashes differently in different places. The inconsistent findings may be due to variation in the relationships across the geographic samples.

We conducted interrupted time-series analyses of motor vehicle crashes and ridesharing in 4 US cities. Focusing on the rideshare company with the largest market share, we took advantage of natural experiments in places where Uber launched, abruptly ceased operations, and then abruptly resumed. We took this approach because we considered that the workforce of contracted drivers and customer base of prospective passengers would build gradually over time after an Uber launch, and that an abrupt cessation followed by an abrupt resumption of services might produce a more acute disruption to the number of actual ridesharing journeys than the initial launch. We hypothesized that the resumption of Uber operations would be associated with a lower incidence of alcohol-involved crashes. We also tested relationships for other outcomes (all injury crashes, serious injury crashes) and other interruptions (Uber launch, Uber cessation).

METHODS

Data collection

Cities eligible for inclusion in this study were 1) located in the United States; 2) had populations greater than 200,000; 3) first had Uber operations between January 1, 2013, and December 31, 2015; 4) due to a ban or voluntary cessation, had no Uber operations for at least 3 months between January 1, 2013, and December 31, 2015; and, 5) had Uber operations continuously between January 1, 2016, and June 30, 2016. These criteria ensured that included cities had broadly comparable data sources, were sufficiently large to provide enough crashes for analysis, had sufficiently long periods when Uber was operating and when Uber was not operating, and had abrupt cessation and resumption of Uber’s services. Using Google searches for combinations of the terms Uber, ridesharing, ban, regulate, city, and operate, we identified 4 cities that met these criteria: Las Vegas, Nevada (2013 population: 603,488); Reno, Nevada (2013 population: 233,294); Portland, Oregon (2013 population: 609,456); and San Antonio, Texas (2013 population: 1.4 million).

The State departments of transportation in Nevada, Oregon, and Texas provided crash-level records for all crashes that occurred after January 1, 2013, and in which any person was killed or was injured and required medical treatment. Data from Reno were complete until February 23, 2016; data from Portland were complete until October 6, 2015; and data from San Antonio were complete until June 30, 2016. An alcohol-involvement field was incomplete for Las Vegas, but we retained this city in our study because data for all injury crashes were available until February 23, 2016.

Variables

Variables common to the data sets we accessed and relevant to our analysis were 1) crash date and time, 2) city and/or geographic coordinates (latitude and longitude) at which the crash occurred, and 3) police assessment of alcohol-involvement (dichotomous). Data for Portland and San Antonio contained an indicator that crashes were serious (defined as causing at least 1 incapacitating injury or death). Using either the city location or by mapping the crash coordinates in ArcGIS, version 10.3 (ESRI, Redlands, California) (18), we produced a binary indicator identifying crashes that occurred within the boundaries of the included cities.

We considered a weekly time series to be most appropriate for this analysis, because shorter partitions (e.g., days) produced a preponderance of temporal units with zero crashes, leading to non-normal distributions, but longer partitions (e.g., months) produced too few temporal units for analysis. We also considered weeks to be a plausible temporal scale over which changes to Uber operations might affect crashes. To construct time-series data sets for each city, we tabulated counts of all injury crashes, all alcohol-involved injury crashes, and all serious-injury crashes per week (12:00 am Wednesday to 11:59 pm Tuesday). Weekend nights are peak periods for alcohol-involved crashes (19). Selecting a time mid-week to delineate the temporal units ensured that crashes occurring on weekends were not arbitrarily separated into different weeks. Because changes in counts of alcohol-involved injury crashes and serious injury crashes may reflect changes in counts of all injury crashes (20), we denominated counts of alcohol-involved and serious crashes by the count of all injury crashes to calculate a proportion.

Our online searches identified the dates of changes, known in time-series analyses as “interruptions,” to Uber operations in the study cities. The main interruptions of interest were the dates that Uber operations resumed (restarted). However, we also identified and tested the dates that Uber operations launched (commenced) and ceased (temporarily ended). A summary of the interruptions for the 4 cities is presented in Table 1. For the weeks in which these changes occurred, we specified dichotomous independent variables in both step form (0 for weeks before the change and 1 in the week of the change and for subsequent weeks) and pulse form (1 for the weeks of the change and 0 otherwise).

Table 1.

Interruptions to Uber Operations in 4 Cities, United States, 2013–2016

City	Date	Type	Description
Las Vegas, Nevada	October 24, 2014	Launch	Uber operations launch in Las Vegas (33).
	November 25, 2014	Cease	The Washoe County District Court rules that Uber is an unacceptable safety risk. Uber operations are banned in Nevada (34).
	September 16, 2015	Resume	Uber operations resume following changes to state legislation (35).
Portland, Oregon	December 1, 2014	Launch	Uber operations launch in Portland (36).
	December 21, 2014	Cease	Uber voluntarily ceases operations 2 days prior to a scheduled US District Court hearing (36).
	April 21, 2015	Resume	Portland City Council votes to allow ride sharing for a 4-month trial period (37). This pilot is further extended in August 2015 (38) before permanent regulation is established in December 2015 (39).
Reno, Nevada	October 24, 2014	Launch	Uber operations launch in Reno (33).
	November 25, 2014	Cease	The Washoe County District Court rules that Uber is an unacceptable safety risk. Uber operations are banned in Nevada (34).
	September 16, 2015	Resume	Uber operations resume following changes to state legislation (40).
San Antonio, Texas	March 28, 2014	Launch	Uber operations launch in San Antonio (41).
	April 1, 2015	Cease	Uber voluntarily ceases operations during a dispute with the San Antonio City Council over driver fingerprinting and drug testing (42).
	October 1, 2015	Resume	Uber and the San Antonio City Council reach an agreement, and operations resume (26, 43).

Statistical analysis

To assess relationships between Uber operations and all injury crashes, alcohol-involved injury crashes, and serious injury crashes, we conducted interrupted time-series analyses using autoregressive integrated moving average (ARIMA) models (21), estimated using SCA Workbench, version 6.2.1 (Scientific Computing Associates Corp., River Forest, Illinois) (22). This statistical approach assumes the dependent variable is approximately normally distributed (20). The time series should be stationary (i.e., with constant mean and variance), to reduce the risk that seasonal trends are mistakenly attributed to the interruptions, and analyses should include more than 50 temporal units, because results from those using fewer units may be unreliable (20).

We began by visually inspecting line plots, calculating summary statistics, and applying the Augmented Dickey-Fuller unit root test for stationarity to each time series (23). In each case there was evidence of nonstationarity, so we detrended the dependent variables by subtracting the observed value for the previous week from each observation (i.e., the first-order difference; d). This approach accounts for measured and unmeasured temporal trends (20), so it was not necessary to adjust for factors that might be related to motor vehicle crashes over time (e.g., increased motor vehicle use) (24). To identify the ARIMA models that best fit each time series, we inspected plots of the autocorrelation function and partial autocorrelation function and calculated the Ljung-Box Q statistic at a lag of 24 units (21). We retained an autoregressive term (p), a moving average term (q), and the model constant where these parameters were significant at P < 0.05. Per convention, specification of the identified models is described by the notation ARIMA(p,d,q). Where there was evidence of 52-week seasonality (i.e., autocorrelation with values from the corresponding week of the previous year), model specification is described as ARIMA(p,d,q)(P,D,Q)₅₂.

To assess associations between ridesharing and motor vehicle crashes, we applied 3 different transfer functions in separate models (20). To test abrupt permanent associations, we applied a zero-order transfer function to the step variables; to test gradual permanent associations, we applied a first-order transfer function to the step variables; and to test abrupt temporary associations, we applied a first-order transfer function to the pulse variables. This procedure estimates the magnitude of the change in the outcome variable associated with each interruption. For the gradual permanent and abrupt temporary associations, the rate of decay (i.e., the denominator) was also estimated. To determine which transfer function, if any, best fit the data, we considered the P value of the interruption variables and compared the autocorrelation function, partial autocorrelation function, and Q statistic between each model’s residuals relative to the residuals of the null model (i.e., with no transfer function).

RESULTS

Summary statistics for each time series are presented in Table 2. Specification and results for the ARIMA models for all alcohol-involved injury crashes (the main time series of interest) are presented in Table 3.

Table 2.

Weekly Counts of All Injury Crashes, the Proportion of All Injury Crashes That Were Alcohol-Involved, and the Proportion of All Injury Crashes That Were Serious in 4 Cities, United States, 2013–2016

City and Proportion	No. of Weeks	Mean (SD)	Minimum	Maximum
Las Vegas, Nevada
All injury crashes	164	95.256 (12.474)	67.000	127.000
Portland, Oregon
All injury crashes	144	100.722 (16.569)	51.000	150.000
Proportion alcohol-involved	144	0.049 (0.026)	0.000	0.125
Proportion serious	144	0.041 (0.021)	0.000	0.090
Reno, Nevada
All injury crashes	164	31.573 (8.423)	12.000	60.000
Proportion alcohol-involved	164	0.082 (0.051)	0.000	0.320
San Antonio, Texas
All injury crashes	182	198.121 (28.616)	113.000	276.000
Proportion alcohol-involved	182	0.068 (0.021)	0.023	0.124
Proportion serious	182	0.070 (0.019)	0.032	0.123

Abbreviation: SD, standard deviation.

Table 3.

Autoregressive Integrated Moving Average Models for the Proportion of Weekly Counts of All Injury Crashes That Were Alcohol-Involved in 3 Cities, United States, 2013–2016

	Association Type
	Abrupt Permanent			Gradual Permanent					Abrupt Temporary
	Magnitude	95% CI	Q	Magnitude	95% CI	Growth Rate	95% CI	Q	Magnitude	95% CI	Decay Rate	95% CI	Q
Portland, Oregona
Launch	−0.01	−0.03, 0.01	19.3	−0.01	−0.05, 0.03	−0.25	−4.44, 3.94	19.3	−0.01	−0.05, 0.03	0.57	−1.70, 2.84	20.3
Cease	0.00	−0.02, 0.02	19.6	0.00	−0.04, 0.04	−0.91	−6.75, 4.93	−0.3	0.00	−0.02, 0.02	−0.95b	−1.32, −0.58	19.8
Resume	−0.03b	−0.05, −0.02	17.6	−0.04	−0.08, 0.00	−0.17	−1.37, 1.03	17.6	−0.03b	−0.05, −0.01	1.00b	0.96, 1.04	19.1
Reno, Nevadac
Launch	0.00	−0.04, 0.04	22.4	0.00	0.00, 0.00	1.13b	0.62, 1.64	22.9	0.09	−0.01, 0.19	0.67b	0.04, 1.30	25.0
Cease	0.03	−0.07, 0.13	23.3	−0.04	−0.14, 0.06	−0.14	−2.92, 2.64	22.5	−0.04	−0.08, 0.00	1.00b	0.98, 1.02	22.5
Resume	0.02	−0.02, 0.06	23.3	0.01	−0.05, 0.07	0.85	−0.76, 2.46	22.8	0.02	−0.04, 0.08	1.01	0.83, 1.19	23.1
San Antonio, Texasd
Launch	0.00	−0.02, 0.02	20.6	0.00	0.00, 0.00	0.94	−0.02, 1.90	21.3	0.00	−0.02, 0.02	0.98	−6.00, 7.96	20.6
Cease	−0.02b	−0.04, 0.00	18.2	−0.04b	−0.06, −0.02	−0.71b	−1.24, −0.18	19.9	−0.04b	−0.08, 0.00	0.79b	0.54, 1.04	16.6
Resume	−0.02b	−0.02, −0.02	22.5	0.00	0.00, 0.00	0.81b	0.40, 1.22	21.7	0.00	−0.02, 0.02	0.89	−0.38, 2.16	39.6

Abbreviations: ARIMA, autoregressive integrated moving average; CI: confidence interval.

^a Portland null model: ARIMA(0,1,1); Q(24 lags) = 20.0.

^b Estimate was significant at P < 0.05.

^c Reno null model: ARIMA(0,1,1); Q(24 lags) = 22.4.

^d San Antonio null model: ARIMA(0,1,1); Q(24 lags) = 20.6.

In Portland, Oregon, the resumption of Uber operations (the main interruption of interest) was significantly related to both an abrupt permanent and an abrupt temporary reduction in alcohol-involved crashes. The Q statistic at a lag of 24 units for the abrupt permanent association (Q = 17.6) was smaller than the Q statistic for the null model (Q = 20.0) and the abrupt temporary association (Q = 19.1). Assessed in terms of the autocorrelation function, partial autocorrelation function, and these Q statistics, the model containing the abrupt permanent association best fit the data. Compared with the mean proportion of alcohol-involved crashes of 0.06 prior to the interruption, the parameter estimate of −0.03 (95% confidence interval (CI): −0.05, −0.02) equates to a relative decrease of 61.8% (95% CI: 38.7, 86.4) and an absolute decrease of 3.1 (95% CI: 1.7, 4.4) alcohol-involved crashes per week.

In San Antonio, Texas, the resumption of Uber operations was associated with an abrupt permanent reduction in the proportion of crashes that were alcohol-involved of 0.02 (95% CI: 0.02, 0.02). Nevertheless, the model containing the interruption (Q = 22.5) was a slightly poorer fit than the null model (Q = 20.6). We also detected relationships between alcohol-involved crashes and Uber’s cessation in San Antonio. This interruption was associated with an abrupt permanent decrease, a gradual permanent decrease, and an abrupt temporary decrease in alcohol-involved injury crashes. The abrupt temporary transfer function was the best fit for this time series. The estimated magnitude of −0.04 (95% CI: 0.08, 0.00) and the decay rate of 0.79 (95% CI: 0.54, 1.04) can be interpreted as an initial decrease of 0.04 (i.e., a 58.9% reduction compared with a rate of 0.07 prior to the interruption), with 79% of the decrease retained each subsequent week.

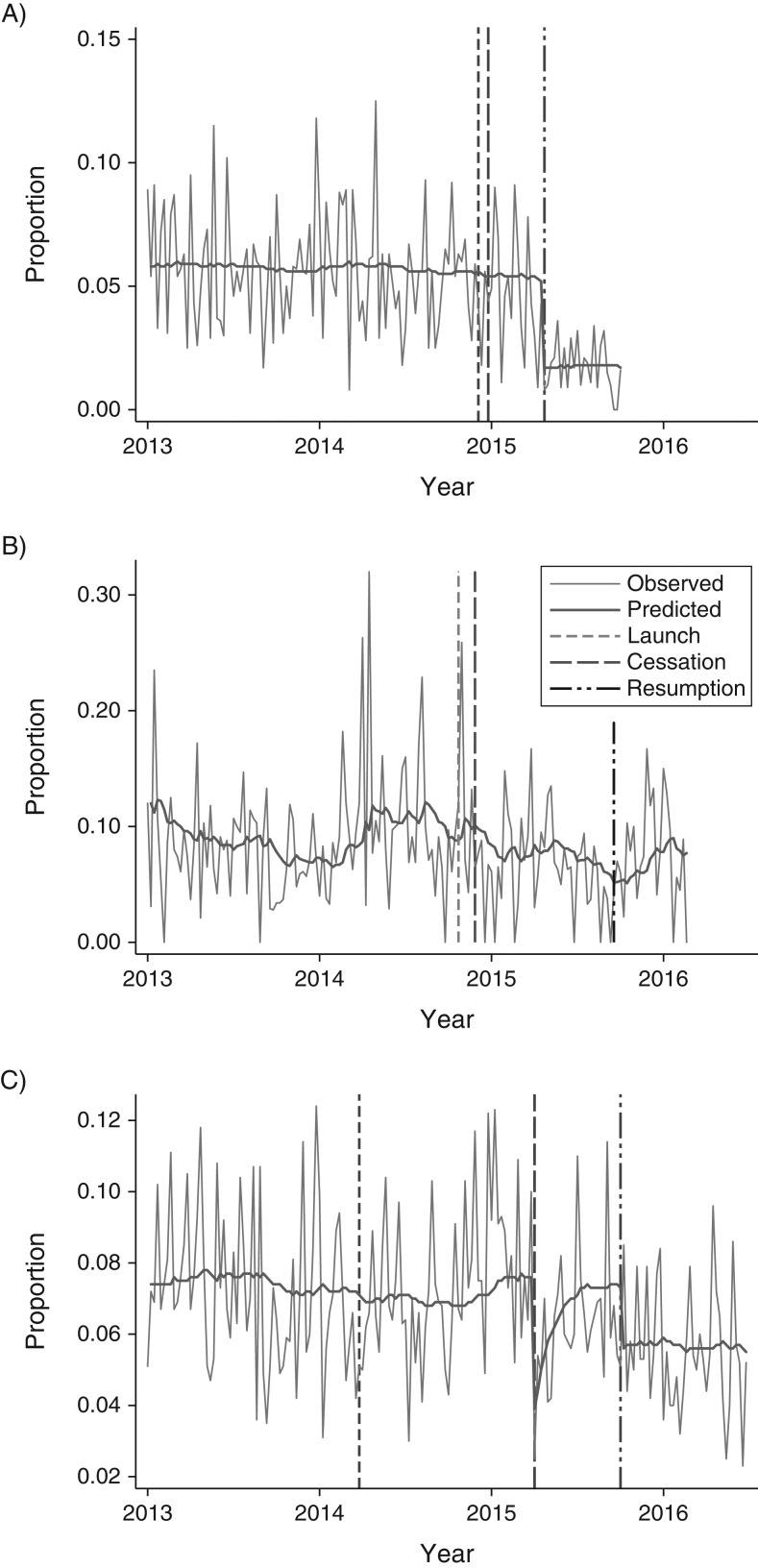
The observed values for alcohol-involved injury crashes are presented graphically in Figure 1. Overlaying these observations are the predicted values from the model that included any significant associations and that we selected as the best fit. Changes in predicted values due to the interruptions are clearly visible. In Portland, Oregon (Figure 1A), the fitted line for alcohol-involved crashes dropped substantially after Uber operations resumed. In San Antonio, Texas (Figure 1B), we included both an abrupt temporary association corresponding with Uber’s cessation and an abrupt permanent association corresponding with Uber’s resumption. Alcohol-involved crash rates dropped when Uber operations ceased, gradually returned to their previous level, and then permanently decreased when Uber operations resumed.

Figure 1.

Weekly time-series plots for the proportion of all injury crashes that were alcohol-involved in Portland, Oregon (A); San Antonio, Texas (B); and Reno, Nevada (C); January 1, 2013, to June 30, 2016. Standard notation is provided to describe (autoregressive integrated moving average (ARIMA)) model specification, ARIMA(p,d,q), where p describes the autoregressive term, d describes the difference term, and q describes the moving average term. We also provide a Q statistic at a lag of 24 units, where lower values indicate better model fit. The predicted values for Portland are obtained from an interrupted time-series model with an abrupt permanent association in the week of April 21, 2015 (ARIMA(0,1,1); Q(24 lags) = 17.6). The predicted values for San Antonio are from a model with an abrupt temporary association in the week of April 1, 2015, and an abrupt permanent association in the week of October 1, 2015 (ARIMA(0,1,1); Q(24 lags) = 17.3). The predicted values for Reno are from a null model (i.e., with no interruptions) (ARIMA(0,1,1); Q(24 lags) = 22.4).

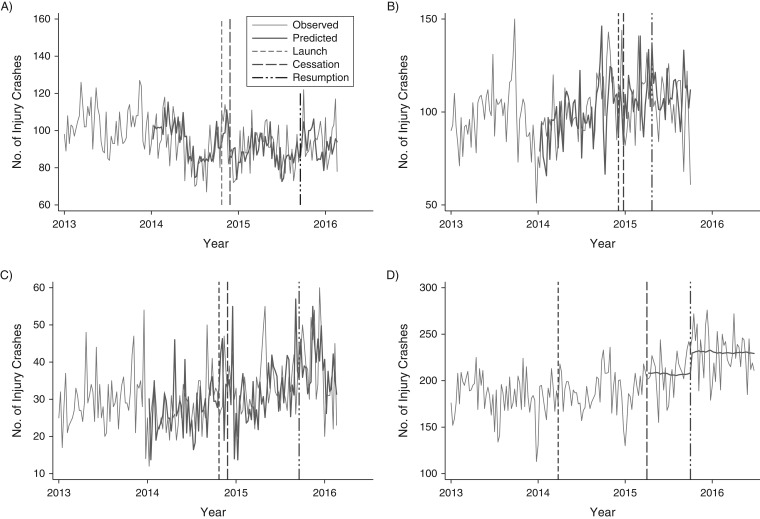
Figure 2 (and Web Table 1, available at https://academic.oup.com/aje) shows the results for all injury crashes. A single model provided a poor fit for San Antonio, so we separated this time series at the interruptions (Figure 2C). The resumption of Uber operations in this city was associated with an abrupt permanent increase of 20.8 injury crashes per week (95% CI: 5.6, 36.0). We retained the interruption for visual display, but we note that the model containing the interruption variable (Q = 31.2) was a slightly poorer fit than the null model (Q = 29.5), and that the sample size for this analysis was small (n = 65 weeks).

Figure 2.

Weekly time-series plots for counts of all injury crashes in Las Vegas, Nevada (A); Portland, Oregon (B); San Antonio, Texas (C); and Reno, Nevada (D); January 1, 2013, to June 30, 2016. Standard notation is provided to describe (autoregressive integrated moving average (ARIMA)) model specification, ARIMA(p,d,q), where p describes the autoregressive term, d describes the difference term, and q describes the moving average term. We also provide a Q statistic at a lag of 24 units, where lower values indicate better model fit. The predicted values for Las Vegas are from a time-series model with no interruptions (ARIMA(0,1,1)(0,1,1)52; Q(24 lags) = 19.3). The predicted values for Portland are from a null model (ARIMA(0,1,1)(0,1,0)52; Q(24 lags) = 14.5). The predicted values for San Antonio are from a model with an abrupt permanent association in the week of October 1, 2015 (ARIMA(0,1,1); Q(24 lags) = 31.2). The predicted values for Reno are from a null model (ARIMA(0,1,1)(0,1,0)52; Q(24 lags) = 31.1).

We also assessed the proportion of injury crashes that were serious in Portland, Oregon, and San Antonio, Texas (Web Figure 1). In neither city was Uber’s resumption associated with changes in this outcome; however, Uber’s launch in San Antonio (Web Figure 1B) was associated with an abrupt permanent decrease of 0.01 (95% CI: 0.02, 0.00), which equates to a 12.8% reduction in serious injury crashes relative to the mean rate prior to the interruption (mean = 0.076), and an absolute decrease of 1.9 serious injury crashes per week.

We conducted sensitivity analyses in which we replaced the proportions of alcohol-involved injury crashes and serious injury crashes with counts of these outcomes. Findings were substantively similar to the results for the main effects models reported here, but low absolute numbers in some cities led to non-normal distributions. Using alternative definitions for weeks (e.g., 12:00 am Sunday to 11:59 pm Saturday) also produced similar results.

DISCUSSION

Ridesharing is an innovative technology with demonstrated capacity to alter the way in which populations use motor vehicles and roadways (5). This time-series analysis, conducted in 4 cities where Uber, the dominant ridesharing company in the United States, launched, ceased, then resumed operations, demonstrates that the technology may also affect motor vehicle crashes, particularly alcohol-involved crashes, in some locations at some times.

We proposed that the lower perceived financial and convenience costs of ridesharing would reduce incidence of alcohol-involved motor vehicle crashes when Uber was present in a city (7–9). Because ridership is unlikely to peak immediately upon a ridesharing service’s launch in a city, we also proposed that a temporary break in operations followed by a resumption of services would produce a more acute disruption to patronage and would therefore have a greater effect on crashes. Thus, we hypothesized that the resumption of ridesharing operations would be associated with decreased incidence of alcohol-involved crashes. Findings partially supported our hypotheses. Decreases in alcohol-involved crashes coincided with Uber’s resumption in Portland, Oregon, and San Antonio, Texas, but not in Reno, Nevada, and in no case was Uber’s resumption related to fewer injury crashes overall or fewer serious crashes. In fact, in San Antonio, Uber’s resumption was associated with more injury crashes, although this model used a very small sample and was a poor fit to the data, so this estimate may be unstable.

To some extent, the observed variability in the estimated relationships between cities and between interruptions may be due to the differing circumstances in which ridesharing operations changed. For example, police in Las Vegas reportedly cited drivers and impounded vehicles immediately upon Uber’s launch, and the company was initially operational for only 1 month (25), whereas ridesharing was permitted in San Antonio throughout, but Uber temporarily suspended operations in response to new legislation requiring drivers to undergo fingerprint checks (26). Differing police activity, media attention, and public interest across geographic settings and across times may differentially affect both rideshare use and reported crash rates.

Alternatively, the observed variability may also be due to the spatial structure of the study cities and the willingness of local populations to use transportation other than private motor vehicles (17). For example, Las Vegas attracts over 40 million visitors per year, many of whom will not have access to private vehicles (27). The effect of ridesharing on motor vehicle use and drunk driving in this city is likely to differ compared with locations that attract fewer tourists. Similarly, the reduction in financial and convenience costs of ridesharing compared with drunk driving may not be uniform across cities. The perceived attractiveness of ridesharing will depend, among other things, on a city’s topology and the strength and enforcement of drunk-driving laws.

A further possible interpretation of our results is that ridesharing increases the incidence of all crashes. Because rideshare drivers must monitor a mobile device, and distraction in the form of glances away from the road increases crash risks (28–31), it is conceivable that rideshare drivers are at increased risks for crashing compared with non-rideshare drivers. Future research should examine whether such risks obtain for individual rideshare drivers, and whether any increase in distracted-driver crashes due to ridesharing is sufficient to wholly offset any reduction in alcohol-involved crashes.

Our findings may help explain the mixed results of 3 previously published studies (14–16). Applying a differences-in-differences approach to spatial panel data in a linear model framework enables researchers to compare motor vehicle crashes both within spatial units and across spatial units over time, thus reducing the likelihood that the estimated associations are confounded by universal linear trends or assessed characteristics of the included locations. This approach has clear utility. Understanding aggregate associations between ridesharing and crashes is critical for policy and planning at a state or national level. However, as we demonstrate, associations may differ greatly at smaller geographic scales. This finding suggests that the results of any aggregate analysis may be positive or negative depending on the characteristics of the included locations. It also suggests that analyses conducted within individual cities (or within groups of cities deliberately selected based on theoretically relevant characteristics) may be required in order to identify the specific mechanisms by which these differential associations arise.

Interrupted time-series analyses must be interpreted in the context of their limitations. Most importantly, although ARIMA models implicitly account for seasonal trends, results may be contaminated by events that co-occur with the interruptions (20). For example, the change in alcohol-involved crashes in Portland, Oregon, after April 21, 2015, may be due to Uber’s resumption at that time, but it may also be due to other coincidental changes to local conditions (e.g., data collection practices, transportation policies). Future research should confirm that the identified relationships are not unique to Portland, Oregon, and San Antonio, Texas, and that local residents use ridesharing as a substitute for drunk-driving and other private transportation in these locations.

The data available for this study gives rise to further limitations. We did not assess the possible effects of Uber’s main competitor, Lyft, although Uber is the dominant rideshare provider in the 4 study cities, and in many cases the regulatory changes affected both providers simultaneously. Police assessment of alcohol involvement may be unreliable (32), and any systematic error in coding crashes as alcohol-involved before or after the interruptions will bias results. Additionally, the very brief period (<5 weeks) between the dates of Uber’s launch and cessation in Las Vegas and Reno, Nevada, and in Portland, Oregon, may make estimates for these interruptions unreliable. The poor fit for the San Antonio models containing interruptions also suggests that results for this city should be replicated, including in analyses using longer time series. Finally, although selecting cities in which Uber operations ceased then resumed likely produced more substantial disruptions to ridesharing patronage than using Uber’s launch date alone, we were still limited by the use of a dichotomous variable to describe ridesharing’s presence or absence. Continuous measures of rideshare utilization (e.g., counts of Uber journeys) are essential if we are to better understand relationships between ridesharing and road crashes.

This study emphasizes that ridesharing may affect motor vehicle crashes, particularly alcohol-involved crashes, but that relationships are likely to differ across geographic settings and over time. This finding has important implications for policy and future research. Authorities should assess relationships within specific jurisdictions before establishing regulations based on perceived or aggregate public health impact. Future research should seek to identify the key drivers of these differential relationships and the characteristics of cities where the public health impacts of ridesharing are greatest. Rigorous scientific study will provide essential information to guide policies that maximize the potential road safety and public health benefits of this novel technology.

Abbreviations

ARIMA

autoregressive integrated moving average

CI

confidence interval