Linking Entropy at Rest with the Underlying Structural Connectivity in the Healthy and Lesioned Brain

Abstract

The brain is a network that mediates information processing through a wide range of states. The extent of state diversity is a reflection of the entropy of the network. Here we measured the entropy of brain regions (nodes) in empirical and modeled functional networks reconstructed from resting state fMRI to address the connection of entropy at rest with the underlying structure measured through diffusion spectrum imaging. Using 18 empirical and 18 modeled stroke networks, we also investigated the effect that focal lesions have on node entropy and information diffusion. Overall, positive correlations between node entropy and structure were observed, especially between node entropy and node strength in both empirical and modeled data. Although lesions were restricted to one hemisphere in all stroke patients, entropy reduction was not only present in nodes from the damaged hemisphere, but also in nodes from the contralesioned hemisphere, an effect replicated in modeled stroke networks. Globally, information diffusion was also affected in empirical and modeled strokes compared with healthy controls. This is the first study showing that artificial lesions affect local and global network aspects in very similar ways compared with empirical strokes, shedding new light into the functional nature of stroke.

Introduction

The brain is a system that facilitates information processing through a wide range of states. As diversity increases, the complexity of the system increases. Local measurements of information integration have been used to address the amount of information a specific region (node) can sustain both in health (Achard et al. 2006; Tomasi and Volkow 2010, 2011) and disease (Bassett et al. 2008; Achard et al. 2012; van den Heuvel and Fornito 2014). Traditionally speaking, these measurements convey information about topological features (Bullmore and Sporns 2012) that can be extracted from structural and functional networks. Likewise, graph-theory has served as a baseline for understanding the brain’s intrinsic topology (Rubinov and Sporns 2010). Structure and function are deeply related (Honey et al. 2007, 2009; Rubinov and Sporns 2010; Messe et al. 2014), while modeling of resting state fluctuations has improved our understanding of this relationship (Nakagawa et al. 2013, 2014; Deco et al. 2016). Modeling work also suggests that the resting brain operates at a point (Ghosh et al. 2008; Deco et al. 2011; Deco and Kringelbach 2016) where the system is maximally sensitive to external stimulations (Deco and Kringelbach 2016).

Although many studies have related structure and function at the scale of the whole brain (Greicius et al. 2009; Honey et al. 2010; Goñi et al. 2014), the study of possible functional roles of nodes is mostly done in structural networks (Rubinov and Sporns 2010), while nodes from functional networks usually remain overlooked. Entropy, which is the fundamental information theoretical metric (Shannon 1997) has recently been applied to the brain to measure repertoire diversity (Anderson et al. 2013) and state variability (Wang et al. 2014) with higher entropy indicating a larger repertoire of available states (Carhart-Harris et al. 2014). However, whether the entropy of a single node (diversity of its functional weights) relates to its topological attributes and whether higher diversity leads to functional benefits remain unclear. Indeed, local anatomical aspects of the brain have hierarchical and small-world features (Hagmann et al. 2008), while each region, represented as a node in a graph, is positioned at a certain level in the hierarchy transmitting signals to many other regions (Zamora-Lopez et al. 2010; van den Heuvel and Sporns 2013). The entropy of a particular node therefore must depend on its underlying structural backbone. Additionally, the integrity of this backbone should also have an effect on entropy given that structural lesions have a direct impact on function (Alstott et al. 2009; Carter et al. 2010; Corbetta et al. 2015).

To test this, we first uncovered basic mechanisms relating structure with function by investigating the relation between node entropy and the underlying structural topology using 3 well-known graph-theoretical metrics in healthy empirical data. This link was further clarified by addressing the same relations in simulated functional networks generated with a whole-brain computational model constrained by topology. Given that focal structural lesions affect inter- and intrahemispheric functional communication in brain networks (He et al. 2007; Carter et al. 2010; Corbetta et al. 2015; Siegel et al. 2015; Baldassarre et al. 2016), change network organization (Grefkes and Fink 2011) and correspond with loss of modularity (Desikan et al. 2006; Gratton et al. 2012; Arnemann et al. 2015), we also investigated the link between structural lesions and functional entropy in networks from patients who suffered a stroke.

Building on the idea that artificial lesioning creates a reduction of global communicability (Alstott et al. 2009), artificially lesioned structural networks were generated to model lesioned functional networks, thereby corroborating whether structural integrity could cause node entropy alterations while clarifying the link between structure and function. We also examined the relationship between node entropy and interhemispheric functional connectivity (FC), which is the most consistent functional alteration of connectivity in stroke (Siegel et al. 2016). Combining analysis of empirical data with large-scale modeling of healthy and stroke whole-brain activity should expand our understanding of how the underlying structural topology relates to its functional weight diversity (entropy).

Methods

Acquisition and Preprocessing of Structural Data

Structural data were collected from 10 healthy right-handed male subjects using diffusion spectrum imaging (DSI) on a Siemens 3.0 T TIM Trio Scanner after obtaining informed consent from all subjects in accordance with experimental protocols approved by the Ethics Committee of the Faculty of Biology and Medicine at the University of Lausanne, Switzerland. The MPRAGE acquisition had a 1 mm in-plane resolution and 1.2 mm slice thickness covering 240 × 257 × 160 voxels. Time repetition (TR),  time echo (TE), and T1 were set to 2300, 2.98 and 900 ms, respectively, which was later used for segmentation into gray and white matter volumes and for coregistration with diffusion images. The DSI sequence consisted of 128 diffusion-weighted images, each with a different diffusion encoding gradient direction and intensity. Maximum b-value was 8000 s/mm². We also collected one b0 reference image. The acquisition volume was set to 96 × 96 × 34 voxels with 2.2 × 2.2 × 3 mm resolution (TR: 6100 ms; TE: 144 ms). Importantly, DSI tractography accurately reconstructs interhemispheric tracts passing through crossing-fiber areas (Wedeen et al. 2008). DSI was reconstructed estimating an orientation distribution function on a tessellated sphere in each white matter voxel (Wedeen et al. 2008) and identified up to 3 fiber directions as the largest maxima in each voxel.

Structural Connectivity

The Desikan–Killiany anatomical atlas (Desikan et al. 2006) composed of 68 regions was used as template for network segmentation (see Table 1 for abbreviations). Surface registrations were generated using FreeSurfer (http://surfer.nmr.mgh.harvard.edu). Deterministic streamline tractography on reconstructed DSI was performed by initiating 32 streamline propagations per white matter voxel and per fiber direction. The anatomical connectivity weight between every pair of nodes was calculated by dividing the number of fibers crossing through every pair by the average spatial surface of both nodes (Hagmann et al. 2008), which allowed rendering the symmetric structural connectivity (SC) matrix. Finally, this subject-specific reconstruction was used to compute an average SC matrix.

Table 1.

Abbreviations for the 34 regions used per hemisphere

Region	Abbreviation
banks superior temporal sulcus	bksts
caudal enterior cingulate gyrus	caAC
caudal middle frontal gyrus	caMF
cuneus	cun
entorhinal gyrus	eR
fusiform gyrus	fus
inferior parietal gyrus	infP
inferior temporal gyrus	infT
isthmus cingulate	iCin
lateral occipital gyrus	latOc
lateral orbitofrontal gyrus	latOF
lingual gyrus	lin
medial orbitofrontal gyrus	medOF
middle temporal gyrus	midT
parahippocampal gyrus	paraH
parecentral gyrus	paraCe
pars opercularis	parsOp
pars orbitalis	parsOr
pars triangularis	parsTr
pericalcarine sulcus	peric
postcentral gyrus	postCe
posterior cingulate	postCi
precental gyrus	preCe
precuneus	precu
rostral anterior cingulate gyrus	rAC
rostral middle frontal gyrus	rMF
superior frontal gyrus	supF
superior parietal gyrus	supP
superior temporal gyrus	supT
supramarginal gyrus	supM
frontal pole	fronP
temporal pole	tempP
transverse temporal gyrus	transT
corpus callosum	cCal

Acquisition of Resting State Functional Data

A set of 18 unilateral stroke patients as well as 18 healthy age-matched control participants were extracted from an initial cohort as described in Corbetta and colleagues (Corbetta et al. 2015) and used to understand the impact of lesions in node entropy and on whole-brain communicability. Written informed consent was obtained from all participants in accordance with procedures established by the Institutional Review Board of Washington University in Saint Louis, USA. Scanning for both groups was performed using a Siemens 3 T Tim Trio scanner at the School of Medicine in Washington University, St. Louis. Patients underwent a scanning session within 2 weeks after suffering a stroke. Further details on scanning, preprocessing, quality control, demographics, and lesion segmentation procedures can be found in previous studies from the same group (Corbetta et al. 2015; Baldassarre et al. 2016; Adhikari et al. 2017) and in the Supplementary Material. In short, resting state scans were acquired with a gradient echo EPI sequence with a TR of 2000 ms, an TE of 27 ms and 32 contiguous 4-mm slices with a 4 × 4 mm in-plane resolution. During scanning, participants were instructed to fixate on a small cross. A total of 30 min of resting activity was acquired over 6 to 8 runs including 128 volumes each.

Functional Connectivity

For each recording session, the mean blood oxygen level-dependent (BOLD) time series was extracted from the same 68 brain regions used in the parcelation scheme of the structural matrix reconstruction (see previous section). Finally, the Pearson correlation coefficient was calculated between the mean BOLD time series from every pair of nodes resulting on an FC matrix for each participant in both groups. Further, the collection of 18 healthy FC matrices was then averaged to create an empirical average healthy FC matrix.

For most of our analysis we used networks with 68 nodes. To explore the impact of using a finer parcellation, a supplementary set of 29 healthy controls and 29 stroke patients from the same original cohort (Corbetta et al. 2015) was used to reconstruct FC matrices with 114 nodes using the same Desikan-Killiany (Desikan et al. 2006) scheme (see Supplementary Material for more information).

Modeled Networks

We first modeled a healthy FC matrix through a whole-brain dynamical mean-field model of the brain (Deco et al. 2014) using the averaged SC as a structural blueprint. The model is composed of N brain regions that are interconnected following the SC matrix. A detailed description of the model as well as the values of all parameters (Supplementary Table 1) are taken from Deco et al. (2014) and can be found in the Supplementary Material. To allow comparison between the modeled and the averaged (across all 18 healthy subjects) empirical functional data, the modeled synaptic activity was transformed to BOLD signals using the Balloon-Windkessel hemodynamic model (Friston et al. 2003), which further allowed the construction of a modeled FC. Because the network’s global coupling parameter G can be adjusted, a total of 60 modeled matrices were constructed, one per G value (from 0 to 6 with steps of 0.1). The optimal fitting is identified at the point in G space where the simulated FC is maximally similar to the empirical averaged FC given by a Pearson correlation between them (Deco et al. 2014). This method also allowed us to explore the changing relation between modeled entropy and static structural properties as a function of G.

Entropy

There are many metrics that can be applied to a structural or functional network in order to extract information about the topology of a node (Rubinov and Sporns 2010). To approach a node from simplified perspective, a normalized version of Shannon entropy (Zhao et al. 2010) was used to measure the entropy of every node in any given FC. Shannon entropy was computed from the distribution of the correlation values or functional weights (R_ij) in a node (e.g., complete column of a FC matrix) and it’s given by:

$$H=-\sum _{l=1}^m{p}_l\log p_l/\log m,$$ (1)

where m is the number of bins used to construct the distribution. The entropy is divided by log m, which is the Shannon entropy of a uniform distribution and used here as a factor to normalize entropy values between 0 and 1 (Zhao et al. 2010). The higher the diversity of correlation values, the higher the entropy of that node will be. As entropy requires distributions to be partitioned in bins, we fixed this value to 10 bins for all nodes in every network to avoid bias. This was based on the mean optimal number of bins (10.3; SD: 0.53) required to create a distribution (Scott 1979) computed from all nodes in every functional network analyzed.

To clarify if a higher diversity of functional weights (translating to larger entropy) eases communication efficiency, we created a semirandom walker algorithm and measure its ability to visit or diffuse over the network. In short, this algorithm allowed us to understand information diffusion in any given functional network. Although the biological role of this method is not clear, other studies have used a very similar approach to clarify the nature of brain topology and its role with signal propagation in large-scale brain networks (Misic et al. 2014, 2015). A finer description and exploration of this method can be found in the Supplementary Material.

Link Between Entropy and Structure

Next, we investigated the relation between node entropy and the underlying topological structure of the nodes. Three well-known node metrics were used and extracted from the averaged SC: (1) “Degree,” which is the binary sum of connections in a given node, (2) “Strength,” which is the sum of all connection weights per node, and (3) “Betweenness centrality” that relates to how centralized is the role of a node in terms of possible paths crossing through it (see Rubinov and Sporns 2010 for a detailed description). Note that “Degree” is the only metric that requires binarizing the network and also is sensitive to arbitrary thresholding (Wang et al. 2010). To reduce bias, we decided to binarize the SC after applying a minimal connectivity threshold (for degree only). We then measured the correlation between these 3 metrics and node entropy in each of the 18 empirical healthy control FCs. The P values of all correlations were corrected for multiple comparisons using Bonferroni correction yielding a significance level of P = 0.0027 (0.05/18). The mean node entropy was used to compute the mean correlation between entropy and structure.

Likewise, the correlation coefficient r and additionally mutual information MI were both calculated between these structural metrics and node entropy for each modeled FC matrix across the coupling strength parameter. To test for significance of mutual information (François et al. 2006), all node entropy values were shuffled 10 000 times creating 10 000 randomized vectors. A randomized mutual information MI_R was computed between each of these vectors and vectors corresponding to all structural metrics. Significance was inferred if only less than 5% of these MI_R estimations were larger than the original MI estimation. Further, MI values were normalized between 0 and 1. This process was repeated across G for each modeled FC.

Artificial Lesioning

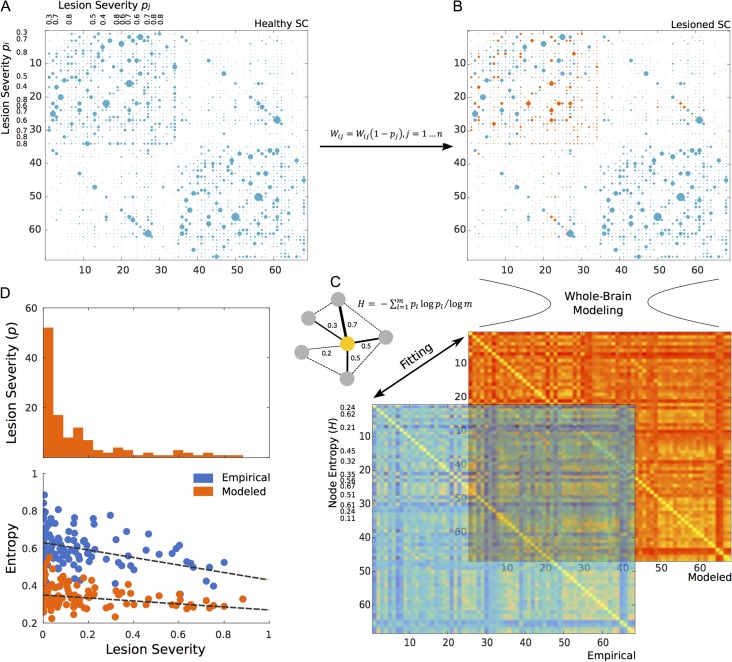
Similar to work done by Alstott et al. (2009), 18 individual lesioned structural matrices were generated by artificially lesioning the averaged SC (Fig. 1) according to the subject-specific cortical damage percentage (lesion severity) in a node for each stroke patient (Supplementary Table 2). To do this, the following weight reduction method was applied for each node in the averaged SC:

$$W_{ij}=W_{ij}(1-p_j),j=1\cdots n,$$ (2)

where all connection weights $W_{\mathit{ij}}$ in a given node i were reduced according to the percentage of lesioned voxels p running across all neighboring nodes j. Since this only covers connectivity from i to j, the procedure is also applied such that connectivity from j to i is also lesioned (Fig. 1). Then, the computational model used to generate the healthy modeled FC was applied on these lesioned SC matrices to construct modeled stroke FCs.

Figure 1.

Artificial lesioning procedure for one subject. The weights of nodes from the original mean healthy SC matrix (A) are reduced or lesioned based on the lesion severity of one sample subject (B). Once this subject-specific lesioned SC is generated, whole-brain modeling is performed and a modeled stroke FC is fitted to its corresponding empirical stroke FC (C). Then, node entropy is calculated in lesioned nodes (yellow node in toy network) both from the empirical and modeled FC to finally explore the relation of entropy and lesion severity (distribution represented as a histogram) across all subjects (D).

In short, based on the lesioned node information from each subject (Supplementary Table 2), the average healthy SC was “lesioned” 18 independent times (one per subject) creating 18 artificially lesioned structural networks. These networks were used to model 18 independent stroke FCs. Finally, empirical stroke FCs were used to identify all optimal modeled networks (Supplementary Fig. 1).

The Impact of Lesions on Entropy and Function

To understand the impact that lesion severity has on node entropy, H values were collected only from lesioned regions across all 18 empirical and 18 modeled stroke matrices leading to a total of 124 potentially affected nodes per group. A Pearson correlation coefficient between lesion severity from these 124 regions and modeled/empirical node entropy was finally computed. Since most stroke patients presented unilateral damage (Supplementary Table 2), the same procedure was applied to the contralateral hemisphere to explore if this effect was also present in contralesional nodes, as well as on the FC of homotopic regions. As a baseline control analysis, lesioned node location indexes were used to filter entropy values from the healthy control group to create a healthy surrogate sample. Note that in this case, entropy from healthy nodes and the lesion severity distribution do not present any statistical association. Finally, we applied the diffusion walker algorithm in both healthy and stroke functional networks to explore if the lesioned brain leads to loss in global communicability.

Results

Basic Mechanisms Linking Entropy and Structure

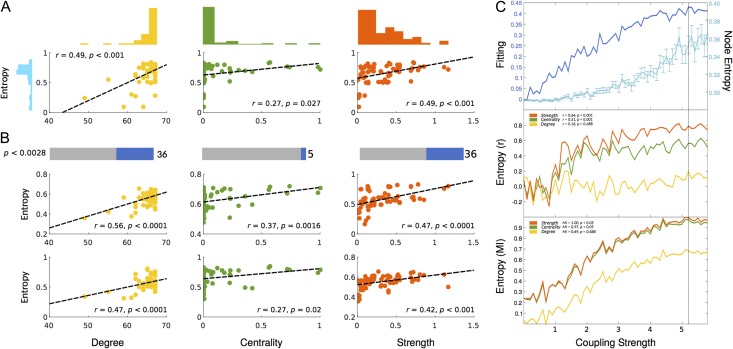
We first determined the relation between node entropy from a set of 18 healthy empirical FCs and its underlying structure using 3 graph-theoretical metrics computed from an average SC: betweenness centrality, strength and degree (see Methods). The mean node entropy of all healthy controls positively and significantly correlated with strength (r = 0.49, P < 0.001), degree (r = 0.49; P < 0.001) and marginally with betweenness centrality (r = 0.27; P = 0.027) (Fig. 2A). However, by exploring correlations within each subject and after correcting for multiple comparisons (see Methods), the proportion of significant correlations remained relatively high for both strength and degree (36%) but not for betweenness centrality (only 5%). These findings were also observed by using mutual information (Zhou et al. 2009) FCs (Supplementary Fig. 2) with an even higher proportion of corrected correlations for strength (57%) compared with degree (47%) and centrality (18%) suggesting that nonlinear interactions play an important role in this relation and that at the node level, the structural strength (sum of weights) might be the best predictor of functional variability (entropy).

Figure 2.

Correlation between node entropy and 3 widely used topological metrics in the empirical and modeled data. These metrics are: Degree (Yellow), Betweenness Centrality (Green) and Strength (Red). (A) Scatter plots for correlations in the empirical average healthy control group with their corresponding distributions. (B) Significant subject-by-subject correlations between node entropy and all 3 metrics. Bars represent the percentage of corrected significant correlations (Bonferroni correction). Scatter plots represent 2 sample subject-by-subject correlations. (C) Behavior of the fitting, node entropy and correlations between node entropy and all 3 topology metrics as a function of the coupling strength. Top plot represents the fitting between the modeled and empirical FC (dark blue) as well as node entropy (light blue). Middle plot represents the Pearson correlation between node entropy and degree, betweenness centrality, and strength. Insert values represent the correlation at maximum fitting (dashed vertical line). Bottom plot represents the normalized (see Methods) mutual information (MI) between node entropy and degree, betweenness centrality and strength as a function of the coupling strength. Insert values represent the MI at maximum fitting.

Modeled data were able to replicate these observations, where the correlation between node entropy and structural measurements reached a plateau around the optimal fitting. Specifically, the correlation between node entropy and the node strength (Fig. 2C, orange plot) is the highest (r = 0.84, P < 0.001). In contrast the correlation between node entropy and betweenness centrality is also high (r = 0.51, P < 0.001, green plot) at the optimal G (near straight black line). This relation was less noticeable and not significant with the degree of the node (r = 0.16, P = 0.48, yellow plot), which is different from what we observed and expected from the empirical analysis. A similar profile holds for mutual information (a measure that does not assume normality) between node entropy and these metrics (Fig. 2C, bottom panel). Mutual information between node entropy and strength presented the highest value and survived the permutation test (MI = 1, P < 0.05, orange curve). Mutual information between node entropy and betweenness centrality was also high and significant (MI = 0.97, P = 0.001, green curve), while mutual information between entropy and the degree of a node scored the lowest. (MI = 0.68, P = 0.18, yellow curve). By using a modeled mutual information FCs, the behavior was replicated, where node entropy and strength presented the largest correlation at optimal G (Supplementary Fig. 2) while with degree was the lowest.

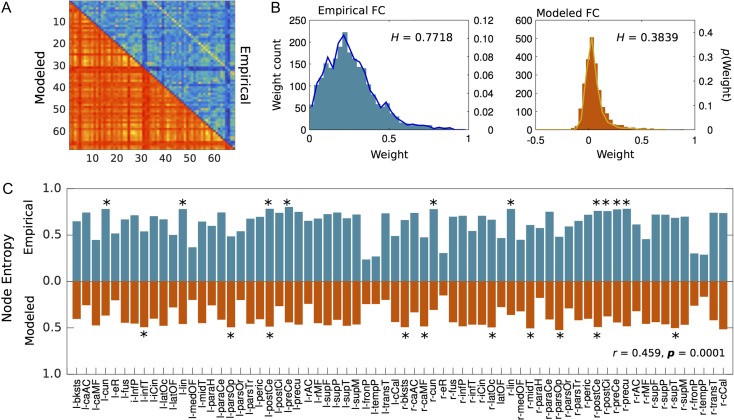
Generally speaking, node entropy from modeled data was lower than node entropy from empirical data (Fig. 3). This could be explained by the fact that the probability distribution of functional weights on the modeled FC has less variability compared with the empirical FC (Fig. 3B) also evidenced by lower whole-brain entropy values (0.38 and 0.77 respectively). This did not appear to be a problem in our analysis as local modeled entropy values significantly correlated (r = 0.49, P < 0.0001) with empirical values (Fig. 3), which crucially validates the local accuracy of modeled entropy. In addition, a finer exploration of entropy values across nodes showed that regions such as the cuneus, precuneus and posterior cingulate are among regions with the highest entropy values, especially in the empirical data (Fig. 3C).

Figure 3.

Node entropy in both empirical (blue) and modeled (red) control data and whole-brain functional weight distribution. (A) Empirical and modeled FC. (B) Whole-brain weight distribution histograms for both empirical and modeled data. H represents the normalized entropy value of the whole network. (C) Bar plots representing node entropy for both groups. The correlation value in the bottom right (r = 0.459, P = 0.0001) is the correlation between modeled and empirical node entropy and represents an indirect validation of the local accuracy of the model.

The Effect of Structural Lesions on Entropy

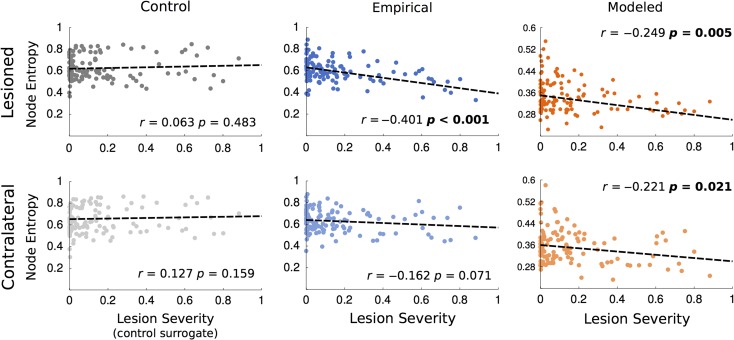
Once the basic mechanisms linking entropy and structure in the healthy brain were addressed, we tested the hypothesis that entropy is directly affected by the integrity of the structural backbone. In the present study, lesion severity (percentage of cortical damage) negatively correlated with node entropy from lesioned nodes both in the empirical (r = −0.401, P < 0.001) and modeled (r = −0.249, P < 0.001) stroke groups (Fig. 4), which means that overall, the larger the cortical damage is, the smaller the functional diversity of the system will be. This indirectly validates the uncovered link between the structural “strength” of a node (sum of weights) and its functional entropy (Fig. 2) as cortical damage is in fact a reduction of the weights of a node (see equation 2). Perhaps more surprising, is that a negative and significant (r = −0.221, P < 0.021) correlation was also observed between lesion severity and contralateral nodes in the modeled group while the empirical showed the same trend with a near significant (r = −0.162, P < 0.071) negative correlation suggesting that lesion severity, although constrained to one hemisphere, affects the functional weight diversity of both hemispheres. As expected, since healthy controls have no lesions, no significant correlation was observed between lesion severity and node entropy in the control surrogate group (see Methods) in either of the 2 hemispheres.

Figure 4.

Correlations between lesion severity (see Methods) and node entropy from healthy controls (gray) and from empirical (blue) and modeled stroke patients (red). Lesion severity in healthy controls represents the matched lesioned node index used as a baseline control. Left column (darker colors) represents data from lesioned nodes. Top row represents data from the lesioned hemisphere. Bottom row represents data from the contralateral hemisphere.

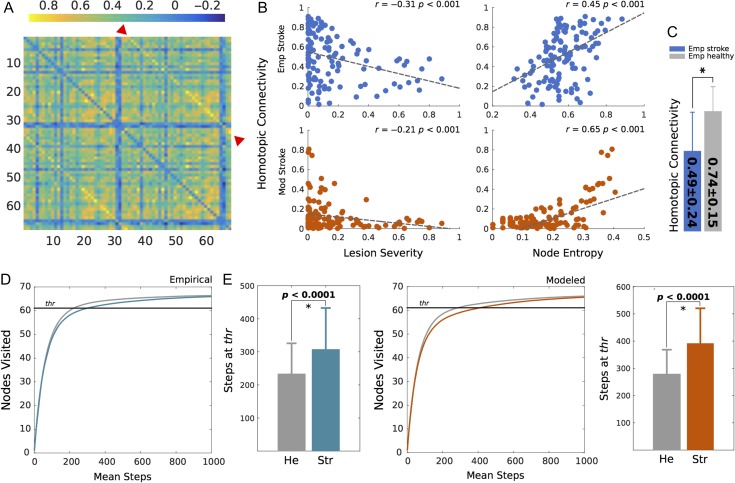
In line with previous findings suggesting a strong and robust link between stroke and decline in interhemispheric (homotopic) connectivity (Siegel et al. 2015; Thiel and Vahdat 2015; Baldassarre et al. 2016), we found that lesion severity negatively correlated with homotopic FC (Fig. 5B) for the empirical and modeled data. These results corroborate findings showing that a decrease in homotopic connectivity is a direct consequence of stroke (Siegel et al. 2016) that surprisingly can be artificially replicated. Also interesting is the fact that a strong positive correlation was found for both data sets between node entropy and homotopic connectivity (Fig. 5B), while the mean homotopic connectivity of healthy controls was significantly (unpaired t-test, P < 0.0001) higher than that of stroke patients (Fig. 5C). At a whole-brain scale, our diffusion walker showed that diffusion of information is more efficiently broadcasted throughout the network in healthy controls compared with stroke patients (Fig. 5D,E), which supports the idea that structural lesions caused by stroke lead to loss in global communicability. These findings were replicated in the supplementary set parcellated into 114 nodes (Supplementary Fig. 3)

Figure 5.

Exploring local and global effects of stroke. (A) A sample FC from one stroke patient. Color code indicates correlation values while homotopic (interhemispheric) connections are highlighted by red arrows. (B) Correlation between lesion severity and homotopic connectivity and node entropy with homotopic connectivity both for modeled (red) and empirical (blue) stroke data. (C) Mean homotopic connectivity of empirical stroke and healthy patients. The star represents a significant difference (P < 0.0001) computed with an unpaired t-test. (D) Diffusion of information by means of a walker in the empirical lesioned (blue) and healthy control (gray) brain. Curves represent the mean amount of nodes visited as a function of the walker steps while bars depict the mean steps and standard deviation for each condition. The straight black line represents the threshold (90%) at which steps were counted. (E) Diffusion of information in modeled stroke (red) and healthy control (gray) networks.

Discussion

This study clarifies the link between resting functional node entropy (which measures weight diversity) and node-wise topological features, especially the strength of a node. These results were replicated by whole-brain modeling, showing that nodal entropy is highly determined by the interplay of structural connections and neural dynamics. Once the basic mechanisms were exposed, results from stroke patients suggested that structural damage (which reduces the strength of a node) had a negative impact on functional weight diversity. Modeled data was able to replicate most of the findings, indicating that whole-brain models can be used to further explore and understand the nature of stroke and other diseases.

Linking Entropy with Structure

Although the vast majority of graph-theoretical metrics are applied to structure (Rubinov and Sporns 2010), some studies have previously used them in functional networks (Deuker et al. 2009) while local dynamical properties are starting to be uncovered (Deco et al. 2017). Some important limitations could appear. For example, calculating a simple metric such as degree (e.g., number of binary links of a node) on a functional matrix yields further restrictions such as thresholding and the need of binarizing the network (Wang et al. 2010). On the other hand, node entropy can be easily computed to explore the local diversity of functional networks without the need of applying arbitrary thresholds.

A clear difference in the first part of the analysis was the divergence between the empirical and modeled data with respect to the link between node entropy and betweenness centrality. Centrality seemed to marginally correlate with entropy in the empirical data, while in the modeled data degree and not centrality presented the least robust correlation. As described above, this might be caused by network thresholding (Wang et al. 2010). By definition, degree requires thresholded and binarized networks and therefore the correlation between degree and entropy highly depends on the threshold level. In contrast, the correlation between entropy with strength, betweenness centrality and other weighted metrics do not require the use of an arbitrary threshold. To clarify this, Supplementary Figure 4 shows the behavior of the correlation between degree and entropy as a function of the threshold for both modeled and empirical data using strength and centrality correlations as static points of reference. This showed that computing degree and using it to understand the relation between structure and function was troublesome as threshold intensity greatly changed this correlation. Interestingly, strength seemed to better correlate with entropy irrespective of threshold used for degree, while not the same could be said for centrality (Supplementary Fig. 4). Overall, this result suggests that strength is a better predictor of entropy and therefore of entropy reduction in stroke.

In line with findings addressing the role of information flow and integration throughout the brain, many regions that have been previously defined as central cores (Sporns et al. 2007) presented high entropy in both data sets. It is notable that entropy at the cuneus, precuneus and posterior cingulate ranked high especially in the empirical data (Fig. 3C). This comes as great interest as some of these regions are a part of a centralized core known as the rich-club (van den Heuvel and Sporns 2011) and are among the most prominent functional hubs in the brain (Tomasi and Volkow 2010, 2011). By using a similar random walker technique to quantify information flow, one study found that the rich-club plays a fundamental role in information trafficking (Misic et al. 2014). A caveat worth remarking is that some of these regions, for example, posterior cingulate in the default mode network, do not appear to be “hubs” if a different criterion based on modularity is used to compute centrality (Power et al. 2011). Another limitation is that although the model showed similar local entropy variability compared with the empirical data (Fig. 3C), the precise ranking was not preserved as only the postcentral gyrus from the top ten modeled nodes also ranked in the top 10 empirical nodes (starred regions in Fig. 3C).

Entropy in the Lesioned Brain

Both empirical and modeled lesioned groups showed that node entropy decayed as lesion severity increased. Notably, this decline was also present in the contralateral hemisphere (Fig. 4). Importantly, this decay reflected lower communication efficiency as evidenced by a longer diffusion time for both empirical and modeled stroke FCs. The higher correlation between node strength and entropy (Fig. 2) further suggests that a structural weight reduction should translate as functional diversity loss. The observed decrease in entropy on modeled FC matrices obtained from lesioned SC matrices indicated that it was indeed the reduction of structural weights a primary cause of entropy decay. The intricate interplay between structure and function has been started to be uncovered in stroke patients (Thiel and Vahdat 2015).

Original observations in stroke patients affected by neglect and motor deficits indicate a loss of interhemispheric correlation of spontaneous activity (i.e., measured in a no task condition) in appropriate networks that relates to the severity of impairment (He et al. 2007; Carter et al. 2010). These observations support our findings that the extent of a lesion correlated with interhemispheric connectivity in both empirical and modeled groups and that this connectivity in turn, presented a high correlation with node entropy. Future studies could build on the ideas brought up by a recently published study showing that the loss in interhemishperic connectivity correlates with behavioral impairment in multiple cognitive domains (Siegel et al. 2016). Notably, similar results have been found experimentally in animals (van Meer et al. 2012; Bauer et al. 2014) and human stroke subjects (Park et al. 2011; Golestani et al. 2013; Tang et al. 2016). Furthermore, abnormalities in task-free conditions can lead to abnormal recruitment and interactions between regions during active behavior (Grefkes and Fink 2011) possibly leading to entropy alterations. Accordingly and also confirming our findings in information diffusion, one study found that attributes of global network communication of stroke patients are affected in both the lesioned and contralesional hemisphere (Crofts et al. 2011), while another recent study reported decreased FC in homotopic regions (Tang et al. 2016) supporting results of the present study.

Limitations and Future Considerations

Because a direct biological interpretation of diffusion efficiency by the walker algorithm is difficult to make, it is also of great interest to understand the impact of weight diversity on the walker behavior. To test this, we shifted the weight distribution of the original healthy FC matrix to make it either more regular or random (more at the Supplementary Material) and ran the walker in each of these shifted networks to find the optimal functional weight distribution. Interestingly, we found that the observed configuration is the one that maximizes information diffusion (Supplementary Fig. 5), suggesting that the brain operates at an optimal working point by creating a trade-off (Bullmore and Sporns 2012) between randomness and regularity, a concept deeply linked to criticality (Deco et al. 2016).

It has already been mentioned that some of the regions that exhibited high entropy such as the posterior cingulate, do not appear to be centralized hubs if criteria based on modularity (Power et al. 2011) or in global integration (Deco et al. 2017) are considered. This adds further limitations as entropy was calculated for each node in the network, but not for subsystems in the brain. Hence, an interesting follow up study would be to analyze entropy of complete subnetworks (e.g., resting state networks) with different functions and examine if entropy values vary across networks with higher values in more centralized or cognitively relevant networks. Carhart-Harris et al. (2014) found that resting state networks exhibit varying entropic configurations pre and post infusion of psilocybin while another study used Shannon’s entropy to show that the functional repertoire of the brain can be use to fingerprint cognitive domains (Anderson et al. 2013). Additionally, novel and more refined parcellation schemes (Glasser et al. 2016) might provide important information about entropy and its relation with structure. Accordingly, we were able to corroborate the effect of stroke on entropy as well as on information diffusion and homotopic connectivity using a finer parcellation (Supplementary Fig. 3) validating the specificity and sensitivity of our method.

Another limitation of the present study worth remarking was the lack of directionality information in the data, as all analyzed networks were symmetric and therefore undirected. Effective connectivity analysis (Friston 2011; Gilson et al. 2016) could provide a better ground for understanding the causal impact of stroke (Grefkes and Fink 2011) as well as providing a better description of the functional significance of entropy. For example, it is expected that the reduction of entropy in the contralesional hemisphere is a direct consequence of stroke, but the precise causality and directionality of this observation still remains uncovered. Directed networks could help clarify how localized lesions translate into global effects.

Conclusion

The unique combination of basic and clinical computational approaches in the present study uncovered an important link between structure and functional entropy at rest while exposing the mechanisms of how lesions affect this relation. This link seems to be stronger for the structural weights of the connections as correlations between strength and node entropy were higher and more frequent. Moreover, lesion severity had a negative impact on node entropy both for modeled and empirical strokes, corroborating that lesion strength and therefore the integrity of the structural backbone impacts the functional diversity of the system. Remarkably, lesions affected entropy in both the lesioned and contralateral hemisphere as well as interhemispheric connectivity. Global diffusion of information was also affected in empirical and modeled stroke networks compared with healthy control networks. This is also the first study that showed that artificial lesions affect local and global network aspects in very similar ways compared with empirical data. This study might offer novel mechanistic interpretations on the nature and origin of stroke and its relation with function.

Supplementary Material

Supplementary data is available at Cerebral Cortex online.

Funding

In this work, G.D. was supported by the ERC Advanced Grant DYSTRUCTURE (n. 295129), by the Spanish Research Project PSI2016-75688-P (AEI/FEDER) and by the European Union’s Horizon 2020 research and innovation program under grant agreement n. 720270 (HBP SGA1). M.A. was supported by the ERC Advanced Grant DYSTRUCTURE (n. 295129). A.P.-A. was supported by a Juan de la Cierva fellowship (IJCI-2014–066) from the Spanish Ministry of Economy and Competitiveness. V.M.S. was supported by the Research Personnel Training program (PSI2013-42091-P) funded by the Spanish Ministry of Economy and Competitiveness.