Abstract
Synchrony between local field potential (LFP) rhythms is thought to boost the signal of attended sensory inputs. Other cognitive functions could benefit from such gain control. One is categorization where decisions can be difficult if categories differ in subtle ways. Monkeys were trained to flexibly categorize smoothly varying morphed stimuli, using orthogonal boundaries to carve up the same stimulus space in 2 different ways. We found evidence for category-specific patterns of low-beta (16–20 Hz) synchrony in the lateral prefrontal cortex (PFC). This synchrony was stronger when a given category scheme was relevant. We also observed an overall increase in low-beta LFP synchrony for stimuli that were near the category boundary and thus more difficult to categorize. Beta category selectivity was evident in partial field–field coherence measurements, which measure local synchrony, but the boundary enhancement was not. Thus, it seemed that category selectivity relied on local interactions while boundary enhancement was a more global effect. The results suggest that beta synchrony helps form category ensembles and may reflect recruitment of additional cortical resources for categorizing challenging stimuli, thus serving as a form of gain control.
Keywords: categorization, oscillations, prefrontal cortex, synchrony
Introduction
Categorization is the ability to carve the world into functional distinctions. It is closely related to the concept of invariance (Riesenhuber and Poggio 2000) and thus provides the fundamental grist for high-level cognition (Rosch 1973). Indeed, impaired visual category learning is common in various cognitive disorders, including autism (Hill 2004; Kobari-Wright and Miguel 2014) and schizophrenia (Kéri et al. 2000; Micoulaud-Franchi et al. 2011). Although categorization occurs even at basic levels of sensory analysis (e.g., contrast enhancement and color) and is even present in insects (Benard et al. 2006; Avargues-Weber et al. 2011), it is at the higher levels of processing where it has additional properties that we associate with cognition.
One is flexibility. Category membership can change depending on task demands. Sometimes an airplane is transportation; other times it is a flying thing. Thus, category representations need to be supported by a neural infrastructure that allows the flexibility to favor different category representations at different times. Also, not all categorical decisions are created equal. Some are quite easy because members of different categories look very different; the distinction can rely largely on bottom-up information. But sometimes members of different categories look similar, at least superficially, or may rely on less obvious criteria (e.g., “tools”). This places extra demands on top-down processing. In visual attention, some sort of gain control is thought to favor processing of some stimuli over others (Buschman and Miller 2007; Saalmann et al. 2007; Lee et al. 2013). Presumably similar mechanisms can be in play for categorization, to favor different aspects of the same stimuli.
Rhythmic synchrony could play that role. Increases in local field potential (LFP) synchrony and spike-LFP synchrony are common during cognitively demanding tasks (Buschman and Miller 2007; Gregoriou et al. 2009; Siegel et al. 2009; Buschman et al. 2012; Nacher et al. 2013; Antzoulatos and Miller 2014). This is consistent with reports of increased synchrony when attention is focused (Buschman and Miller 2007; Fries et al. 2008). Different visual categories and behavioral rules result in different patterns of beta synchrony between recording sites, suggesting the dynamic formation of distinct computational ensembles (Buschman et al. 2012; Antzoulatos and Miller 2014). If so, gain control might be implemented through changes in synchrony.
To test this, we used neurophysiological data from monkeys trained on a category task (Roy et al. 2010). A morphing system (Shelton 2000) generated stimuli that varied smoothly between prototypes (e.g., cat and dog). Thus, stimuli close to the category boundary looked like stimuli from the other category and were therefore more difficult to categorize. Flexibility was tested by randomly cueing monkeys to switch between using 2 orthogonal category boundaries to categorize the stimuli (Fig. 1). We previously reported that the spiking activity of prefrontal cortex (PFC) neurons showed a sharp distinction between, and generalization within, categories: both hallmarks of categorization (Freedman et al. 2001, 2002, 2003; Cromer et al. 2010; Roy et al. 2010). Here, we report category-specific patterns of low-beta (16–20 Hz) oscillatory synchrony that had many properties in common with the previously reported single-neuron spiking activity. Superimposed on this category-dependent beta synchrony was evidence for a role of beta in gain control. It was stronger when categories were relevant and when the assigning category membership was more difficult.
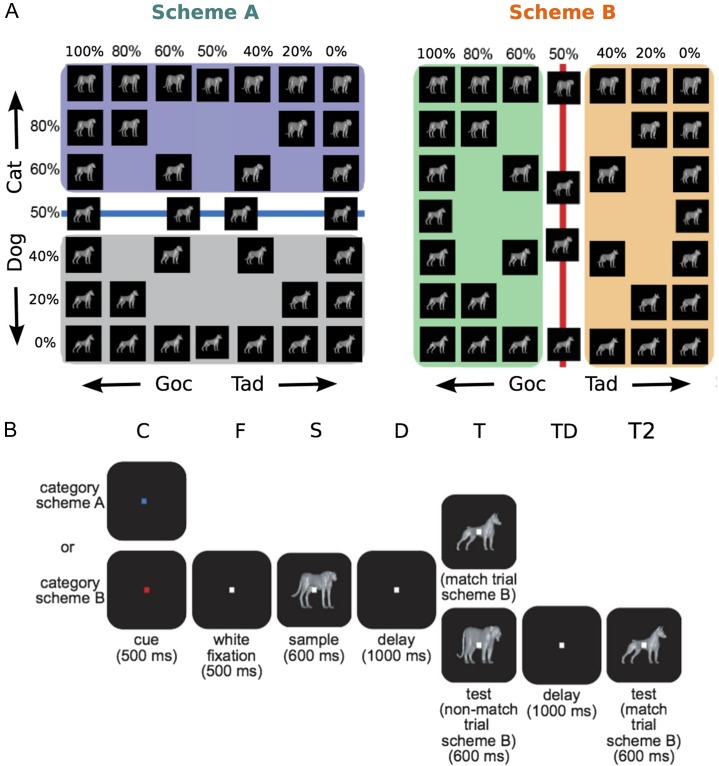
Figure 1.
Flexible categorization task overview. (A) A morphing system was used to generate stimulus images that varied smoothly between 4 original prototypes (located in the corners). Monkeys grouped images using 2 different categorization schemes. Stimuli lying on the category boundary were ambiguous and were assigned category labels randomly. We use the arbitrary terms Goc and Tad to describe the pairs of Cat and Dog prototypes that are on the left and right side of Scheme B, respectively. (B) The flexible categorization task followed a delayed match-to-category paradigm. The trial began with monkeys pressing a lever and fixating on a dot. The dot changed color, which served as the context cue instructing which categorization scheme to apply. After a period of fixation, monkeys were shown a stimulus image. After a delay stage, monkeys were then shown a test image and they had to assess whether it was a match or nonmatch based on the relevant categorization scheme. If the images were a match, the monkey released a lever. Otherwise, the monkeys held onto the lever through a second delay stage, at which point the correct matching image was shown. The letters above each stage indicate stage symbols used throughout the paper.
Materials and Methods
This paper uses LFP data that were collected during an earlier study (Roy et al. 2010) that focused exclusively on neuron spiking activity. We briefly report data collection methods here.
Two adult monkeys (8–10 kg) used in this study were handled conforming to National Institutes of Health (NIH) guidelines and the Massachusetts Institute of Technology Committee on Animal Care. Recording electrodes were implanted using previously described hardware (Roy et al. 2010). Eye movement was tracked using an infrared eye tracker (Iscan), sampled at 240 Hz.
Flexible Categorization Task
Monkeys were trained to perform a delayed match-to-category task. During this task, they were required to categorize stimuli that could vary smoothly between 4 different prototype images. Stimuli, or “morphs,” were generated by a morphing system that used the vector differences between the corresponding points in 2 different prototype images to generate linear combinations of the original images (Shelton 2000). This yielded a 2-dimensional space of stimulus images (Fig. 1A), with the prototype morphs located at the 4 corners of this space.
Two orthogonal categorization schemes, referred to as Scheme A and Scheme B, were defined using 2 orthogonal boundary lines in the stimulus state space (Fig. 1A). These boundary lines separated morphs with more than 50% contribution from a prototype from those with less. This effectively split the stimulus space into cat-like and dog-like morphs for Scheme A (Fig. 1A, left), and Scheme B grouped together different pairs of cat and dog prototypes (Fig. 1A, right).
During training, animals were exposed to a wide range of possible morphs that could vary from the original prototypes, to morphs within several percentage points of the category boundary, and to the 50% morphs themselves. During testing and recording, 34 images were generated from 7 morph mixtures (100%, 80%, 60%, 50%, 40%, 20%, 0%). The pair of images at the center of the stimulus space represent 50% morphs between the 2 diagonally opposed prototypes (i.e., between (100%,100%) and (0%,0%) and between (0%,100%) and (100%,0%)); they are offset from the center (50%,50%) for visualization purposes. Monkey behavioral performance for this data set is reported in our earlier paper (Roy et al. 2010), which used the same data. Briefly, both monkeys classified stimuli at >80% correct, even for stimuli close to the category boundary. There were no significant differences in their performance for categorization Scheme A or B at each morph level (Roy et al. 2010).
The task began with the monkeys pressing and holding a lever and maintaining fixation on a target for 1000 ms (Fig. 1B). For the first 500 ms (cue), this target was either red or blue and served as a context cue. This cue instructed the animal which categorization scheme to implement; blue denoted Scheme A and red denoted Scheme B. For the next 500 ms (fixation), the fixation dot reverted to white and remained white for the rest of the trial. Monkeys were then shown a sample image for 600 ms (sample). This was followed by a 1000-ms delay, after which a test image was presented. If the category of the test image matched the category of the sample (based on the context cue), then the trial was considered a match and the monkey released the lever for a juice reward. If the categories did not match, then the monkey continued holding the lever. After a second 1000-ms delay, a second test image was shown that matched the category of the sample image, and the monkey released the lever for a juice reward. Monkeys were randomly rewarded for trials containing ambiguous stimuli (50% morphs). Match/nonmatch trials and category Scheme A/B context cues were randomly interspersed with similar frequencies.
Recording
Full details of recording procedures are supplied in Roy et al. (2010). Briefly, placement of recording chambers over lateral PFC was stereotaxically guided using magnetic resonance imaging images and an anatomical atlas (Paxinos et al. 2000). The chamber targeted the principal sulcus and anterior arcuate sulcus (areas 45, 46, and 12). On each day of recording, between 8 and 16 epoxy-coated tungsten electrodes (FHC Inc.) were inserted into the brain using customized microdrives. Each microdrive lowered 2 electrodes through a 1-mm plastic grid (Freedman et al. 2001, 2002, 2003; Cromer et al. 2010; Roy et al. 2010). LFP waveforms were digitized and stored. Firing activity was recorded from well-isolated neurons (in general 0–2 per electrode) and digitized waveforms were saved for offline sorting using principal component analysis (Offline Sorter, Plexon Inc.). Over 40 recording sessions, 209 neurons and 300 electrodes were recorded from monkey L. Over 39 recording sessions, 340 neurons and 573 electrodes were recorded from monkey O. Recording locations included both ventrolateral and dorsolateral PFC.
Data Analysis
Preprocessing
All analysis was performed in Matlab (Mathworks). First, LFP recordings were filtered to remove 60 Hz line noise using an ideal notch filter between 59.5 and 60.5 Hz. Bad electrodes were identified and excluded from the study.
Coherence Estimates
Field-to-Field Coherence (FFC) was estimated using Matlab (Mathworks) and Chronux (chronux.org) (Mitra and Bokil 2007). Coherence Cxy(f) between LFP signals from 2 different electrodes, x(y) and y(t), was estimated as
where Gxy(f) is the multitapered cross-spectrum and Gxx(f) and Gyy(f) are the multitapered autospectra, with * denoting complex conjugate. Coherence, Cxy(f), ranges between 0 and 1, with values close to 1 indicating that y(t) can be well represented by linear system acting on x(t) at frequency f. Different tapers settings were used depending on the situation. When analyzing FFC spectra and spectrograms (time vs. frequency plots), tapers were set with time-bandwidth product (TW) equal to 3 and number of tapers (K) equal to 5 unless otherwise specified. Partial FFC estimates were noisier due to the removal of shared components of the signal, and therefore it was necessary to use additional bandwidth smoothing. Hence, for partial FFC, we used TW = 5 and K = 9. In estimating FFC we only considered correct trials, with the exception of 50% morphs. For 50% morphs, all trials were included regardless of the animal's response.
Z-Score Statistics
We quantified evidence for FFC modulation by experimental conditions nonparametrically using a bootstrap normalized sensitivity statistic. This statistic was calculated by, first, estimating the absolute difference in FFC (|ΔFFC|) for the 2 groups of trials corresponding to 2 conditions of interest (e.g., cat stimuli vs. dog stimuli). Then, a null distribution of |ΔFFC| was generated by randomly shuffling the trials between these 2 groups. Lastly, we divided the original |ΔFFC| by the mean of the shuffled distribution. Because the shuffling destroys any special influence of trial conditions, this quantity has an expectation value of 1 under the null hypothesis of no FFC modulation. Values greater than 1 indicate greater differences in FFC than expected by chance and, therefore, increasing evidence for FFC modulation. Values less than 1 may arise in special situations but are not prominent in our data and indicate smaller differences in FFC than expected by chance. This quantity is similar to a z-score in that it is normalized by the spread of the data. Throughout the paper, we will use the term z-score to refer to data that have been bootstrap normalized in this manner. Evidence for modulation of neuron firing activity by experimental conditions was assessed in the same manner.
Significance Testing
In addition to examining the average behavior of the network, we also identified specific electrodes of interest via significance testing. The same permuted null distributions that were used to calculate z-scores were used here. Specifically, an electrode pair was considered significant if its |ΔFFC| (as defined above) was greater than the 1-α percentile of the permuted null distribution of |ΔFFC|, where α is the desired Type 1 error. Unless otherwise stated, false discovery rate (FDR) was controlled by using the Benjamini–Hochberg (BH) step up procedure to determine α so as to give an FDR of 20%. The FDR rate of 20% was used to achieve a balance between Type I and Type II error rates. In other words, while we wanted to limit false discoveries, we did not want to have so many false negatives that it would decimate our pool of electrode pairs available for subsequent analysis.
Identification of significant electrode pairs was generally an intermediate step in our analysis and, as discussed below, subsequent statistical tests were conducted at α = 0.05. However, we repeated our analysis with an FDR of 5% and arrived at similar findings, although in some cases spectra appeared more noisy due to fewer trials.
Significant differences in coherence between groups of electrode pairs were tested using the Wilcoxon signed-rank test for paired data and Wilcoxon rank-sum test for unpaired data, with a Holm–Bonferroni correction applied for multiple comparisons (α = 0.05). The time windows of analysis were slightly delayed to allow for propagation delays from sensory regions. For the sample and delay stages, the analysis windows were 100–600 and 900–1700 ms, respectively, after sample onset. For FFC analysis, spectral broadening resulted from the multitaper method (Thomson 2007). Thus, statistical tests for differences in FFC centered at a specific frequency (e.g., 18 Hz) actually incorporated a range of frequencies approximately 18 ± W, where W = x/T, T is the time window and x is the time-bandwidth product in use. We denote this central frequency of analysis using the “@” symbol (e.g., @18 Hz).
Category Index
To evaluate the strength of category representation, we used a category index (CI), introduced in previous works (Freedman et al. 2001, 2002, 2003). This statistic depends on both the between category difference (BCD) and the within category difference (WCD). We considered both adjacent stimuli (“one-step” differences, WCD1 and BCD1) and also pairs of stimuli that differed by 2 steps (WCD2 and BCD2), calculated as follows:
Here, Fx refers to the estimated FFC (at a particular frequency) for morph percentages x. We took the final WCD as the average of WCD1 and WCD2, and likewise for BCD. This ensured that the average morph distance was identical for WCDs and BCDs. Ci was defined as a standard contrast index of these 2 quantities, yielding CI = (BCD − WCD)/(BCD + WCD). CI ranges from −1 to +1, with a value close to +1 denoting a large difference between categories and a value close to −1 denoting a large difference within categories.
Normalized Analysis of Boundary Trials
In our analysis of the monkeys’ responses to boundary trials, we implemented 2 procedures to ensure our results were unbiased. First, estimates of coherence are biased by sample size (number of trials), increasing when few trials are available (Bokil et al. 2007). We found this affected our estimates of coherence in certain situations. In particular, in order to keep monkeys engaged in the task, it was necessary to use somewhat fewer boundary trials than nonboundary trials. This paucity of boundary trials meant coherence bias could be an issue when comparing boundary with nonboundary trials. Hence, for comparisons between 2 experimental conditions C1 and C2 with N1 and N2 trials respectively, assuming for example N1 < N2, we repeatedly estimated FFCC2 ⌊N2/N1⌋ times, using N1 randomly selected trials each time, until all trials were consumed. Here ⌊x⌋ is the largest integer ≤x. These estimates of FFCC2 were averaged together for a final value. In this manner, estimates of both FFCC1 and FFCC2 were always calculated using N1 trials and were therefore comparable. When comparing more than 2 experimental conditions, the minimum number of trials across all conditions was used.
Second, from Figure 1A, it is clear that there were fewer choices of boundary morphs than nonboundary morphs. For example, along the Cat/Dog boundary, possible morphs were (100%,50%), (50%,50%) and (0%,50%). In contrast, nonboundary morphs consisted of the set of (X,Y) with Y = 100% or 0% and X = 100%, 80%, 60%, 50%, 40%, 20%, or 0%. To ensure a balanced comparison between boundary versus nonboundary conditions, only nonboundary morphs with X = 100%, 50%, or 0% were included in our analysis of the Cat/Dog boundary (likewise for Goc/Tad). We repeated our boundary response analysis using instead the full set of nonboundary morphs and arrived at similar results (not shown).
Time-Frequency Visualizations
Changes in coherence were visualized over time using spectrogram plots. This involved calculating coherences (or z-score statistics) with 90% overlapping 300 ms windows. For visualization of firing rates (FRs) over time, average FRs (or z-score statistics) were smoothed with a third order Savitsky-Golay filter of duration 301 ms.
Effect of Ensemble Membership on Neuron Firing Activity
Upon identifying LFP ensembles that modulated their coherence in response to experimental conditions, we sought to characterize the behavior of neurons that were part of these ensembles. This allowed assessment of the effects of LFP ensemble membership on neural activity. Our method for classifying membership of a neuron in an ensemble is as follows. First, we identified all pairs of electrodes that exhibited significant responses to the experimental conditions of interest using the permutation test (described above). For each neuron, we then identified all possible electrode pairs involving that neuron's recording electrode. If at least x% of these electrode pairs were significant (e.g., for Cat vs. Dog trials), we considered it as being part of the LFP ensemble. We refer to x as the “ensemble inclusion threshold” and its default value was 10%, although a range of values from 1% to 50% were explored. Setting x to a very small value (close to zero) corresponds to the very liberal requirement of selecting neurons on “any” electrode in the LFP ensemble, while setting x to a high value corresponds to the conservative requirement of only selecting neurons on electrodes that modulate their coherence with a large number of other electrodes.
Rejection of Bad Data
It was necessary to reject data from certain electrodes. This was due to a technical issue whereby high amplitude LFP signals caused the amplifier to saturate. We identified electrodes where this was the case and rejected all electrode pairings involving those channels. Generally, LFP amplitudes were higher during the delay stage than during the sample stage, so there were typically fewer pairings during the delay stage.
Results
Monkeys were required to categorize stimuli using 2 category schemes. One boundary divided “Cat versus Dog” (Scheme A) while the other divided the same stimuli along an orthogonal dimension (“Goc vs. Tad,” Scheme B) (Fig. 1A). Visual cues instructed animals which categorization scheme was currently relevant (see Materials and Methods).
Several previous studies (Buschman et al. 2012; Antzoulatos and Miller 2014; Bastos et al. 2015) found coherence effects across both long and short distances. Since it was not clear a priori which electrodes were relevant, we used a data-driven approach. We initially considered all electrode pairs and tested for changes in their coherence in response to task conditions; subsequently, we used statistical testing to identify specific electrode pairs of interest.
We began by examining the average population FFC across all correct trials and all electrodes. We found that FFC synchronization was primarily confined to low-beta (peak centered at 18 Hz) with also some alpha (peak centered at 11 Hz, Supplementary Fig. 1). This occurred during presentation of the to-be-categorized sample and subsequent memory delay.
Category Selectivity of Low-Beta Coherence
Previous studies have shown category and rule-specific increases in beta FFC between electrode pairs within the PFC and between the PFC and striatum (Buschman et al. 2012; Antzoulatos and Miller 2014). We tested for such category selectivity in FFC using the entire population of electrode pairs. We computed the z-score of the absolute difference in FFC to Cat versus Dog stimuli and to Goc versus Tad stimuli. This analysis included all trials (whether the category distinction was currently relevant or not; below we test the effects of relevance) and covered a wide range of frequencies (1–100 Hz). This statistic has a mean value of 1 under the null hypothesis (no modulation). Values greater than 1 indicate FFC modulation by category over that expected by chance. This z-score statistic is roughly proportional to the fraction of electrodes exhibiting significant responses (see Materials and Methods and Supplementary Fig. 2).
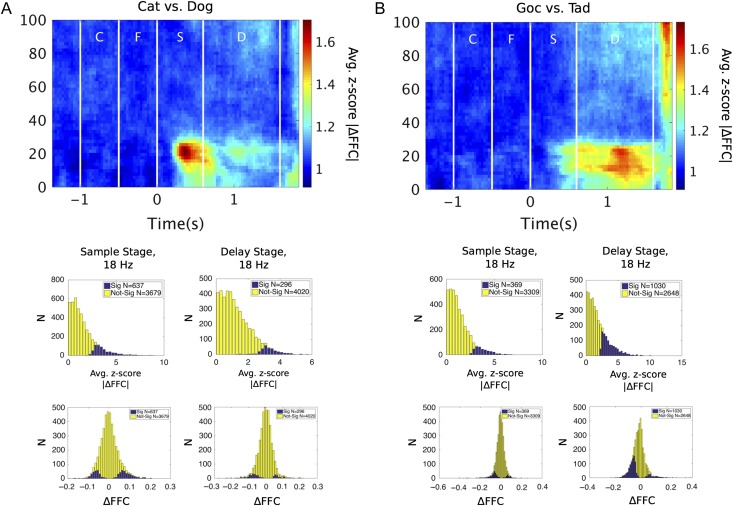
Figure 2A shows the z-score statistic for FFC category selectivity for Cat versus Dog (Scheme A) and Figure 2B shows it for Goc versus Tad (Scheme B). Mirroring the peaks in the raw FFC spectrum (described above), category-dependent modulation of FFC could be seen in low beta during the sample presentation and memory delay. FFC category selectivity was stronger for Cat versus Dog during sample presentation and stronger for Goc versus Tad during the delay (Fig. 2). Cat/Dog and Goc/Tad coherent ensembles overlapped in terms of their spatial distributions and spanned a range of electrode distances, suggesting that volume conduction was not the source of these effects (Supplementary Fig. 3).
Figure 2.
Low-beta coherence is modulated by stimulus category. Modulation of FFC was assessed for (A) Cat versus Dog categories and (B) Goc versus Tad categories. Evidence for FFC modulation was quantified by measuring the absolute difference in coherence (|ΔFFC|) and normalizing this quantity by its trial-shuffled null distribution. The resulting z-score has an expected value of 1 under the null hypothesis (no sensitivity). Spectrograms show average z-scores of |ΔFFC| for all electrode pairs across time and frequency. Histograms show distributions of these z-scored |ΔFFC| values, and also of raw coherence differences (ΔFFC), at 18 Hz for both sample and delay stages. Electrode pairs with significant category selectivity (Sig.) were identified by permutation test. C, cue; F, fixation; S, sample; D, delay.
Low-Beta Category Selectivity Is Enhanced When Categories Are Relevant
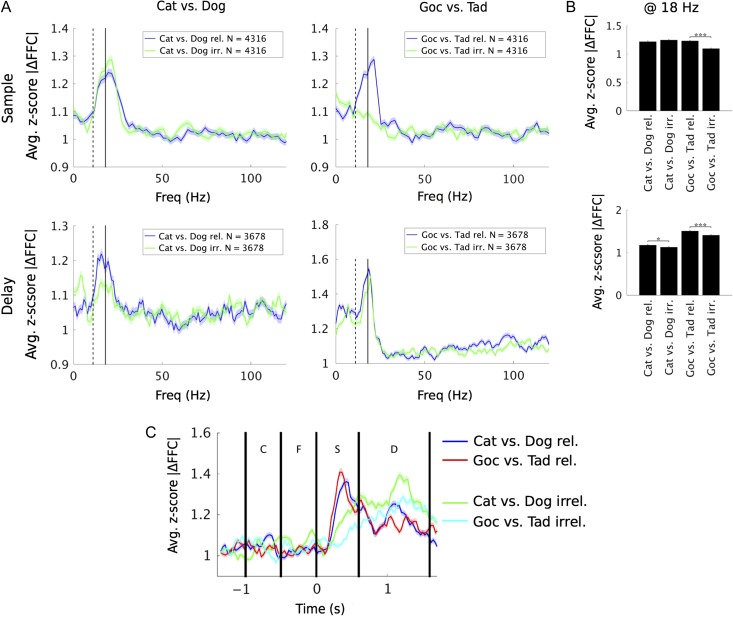
The behavioral task required animals to switch between the 2 category schemes from trial to trial. When one scheme was relevant, the other was irrelevant. We found that FFC category selectivity was stronger when the given category scheme was relevant. This is shown in Figure 3, which collapses the z-score for category selectivity across time (separately for sample and delay epochs) and plots it separately for the 2 category schemes when they were relevant versus irrelevant.
Figure 3.
Low-beta (16–20 Hz) category response is flexibly modulated by the context cue. (A) To assess flexibility of FFC modulation, we compared the z-score statistic in response to Cat/Dog categories when Cat/Dog was both relevant and irrelevant. Likewise was done for Goc versus Tad. (B) Examining the differences in z-score metric at low-beta (centered at 18 Hz) for relevant and irrelevant conditions, we found evidence for flexible modulation of Goc/Tad responses in the sample stage, and both Cat/Dog and Goc/Tad responses in the delay stage. (C) Time courses showing progression of low-beta FFC selectivity under relevant and irrelevant conditions (sampled at 18 Hz from spectrograms in Supplementary Fig. 4). Solid and dotted vertical lines in (A) denote locations of peaks centered at 11 and 18 Hz in raw FFC (Supplementary Fig. 1). Significance in (B) was tested by Wilcoxon signed-rank test with a Holm–Bonferroni correction for multiple comparisons. *P < 0.05; ***P < 0.001.
The effects of category scheme relevance were mixed when the sample was in view but when the memory delay ensued, FFC category selectivity was higher for both schemes when they were relevant. During the sample presentation (Fig. 3A, top-left), FFC category selectivity for Cat versus Dog (Scheme A) was equally high whether relevant (blue line) or irrelevant (green line). For Goc versus Tad (Scheme B), though, FFC category selectivity was much higher when that scheme was relevant versus irrelevant (Fig. 3A, top-right). During the memory delay, however, FFC category selectivity for both schemes was significantly higher when relevant versus irrelevant (Fig. 3A, bottom). These results are summarized in Figure 3B, which shows the average category selective FFC z-score centered at low beta (18 Hz, but results do not depend on the exact beta peak used). There was also some FFC category selectivity in the alpha band, especially in the delay, but there is a clear and higher peak in beta (Fig. 3A). Time courses of this activity at 18 Hz are presented in Figure 3C, which shows that Goc/Tad selectivity was attenuated when it was irrelevant, particularly during the sample stage. Attenuation of Cat/Dog selectivity when irrelevant did not emerge until the delay stage and, then, only weakly. These time courses are extracted from spectrograms, which are presented in Supplemenatry Figure 4.
Category-Selective Coherence as a Function of Morph Level
Next, we examined FFC category selectivity as a function of morph level. The morphs allowed us to test for a hallmark of categorization: a sharp transition across the category boundary. The prototypes of each category were the most physically distinct from one another. In Figure 1, the prototypes are arbitrarily designated at the 0% and 100% morphs. At intermediate levels (80% and 60%, 20%, and 40%), there is progressively more of the other category blended in. The boundary is at the 50% morph level. Thus, the 60% and 40% category morphs belonged to different categories, but nonetheless physically look alike. Spiking activity in the PFC is known to show a sharp change at the category boundary (i.e., between 60% and 40%) and relatively little distinction within a category (i.e., from 100% to 60% or from 0% to 40%) (Freedman et al. 2001, 2002, 2003; Roy et al. 2010). We tested for the same effect in FFC category selectivity and found it.
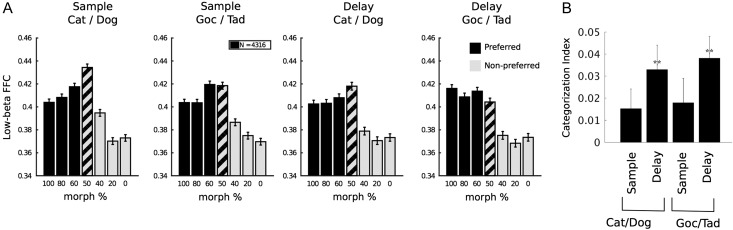
Figure 4A plots the average beta-band FFC for all electrode pairs as a function of morph level. For each pair, the prototypes of the preferred category (the one that elicited higher average FFC) were defined as the 100% prototypes. Note the marked difference between the average FFC for the 60% morphs of one category relative to the 40% morphs of the other (i.e., across the category boundary) with relatively less difference for morphs within each category. Thus, low-beta FFC, like spiking activity, showed hallmarks of categorization: sharp transitions across the category boundary and generalization within categories.
Figure 4.
Morph-response profiles of low-beta FFC. (A) Average low-beta (18 Hz) FFC responses are plotted as a function of stimulus morph percentage. Responses were sorted prior to averaging, so that the preferred category of each electrode pair always corresponded to morph percentages >50% (black). This provides a visualization of the morph-response profiles. These profiles indicate that low-beta FFC responded not only to category, but also to morphs near the boundary. (B) CI was significantly positive during the delay stages, but not the sample stage. Significance in (B) was tested by Wilcoxon signed-rank test with a Holm–Bonferroni correction for multiple comparisons against CI = 0 and against adjacent columns. **P < 0.01.
To quantify these effects, we calculated a CI (Freedman et al. 2003) using the 0–40% and 60–100% morph levels (the 50% morphs will be considered below). This statistic ranges from −1 to +1. Positive values indicate a sharper difference to equally spaced pairs of morphs that straddle the category bound compared with those that do not. Negative values indicate greater differences to morph pairs within the same category (see Materials and Methods). During the memory delay, the CI values were significantly positive (Fig. 4B), showing that the delay low-beta response exhibits the sharp transition across the boundary that we would expect from a category representation. During the sample stages, the CI values, although positive, were not significant (Fig. 4B).
Note in Figure 4A the high level of FFC to the 50% morphs, particularly during the sample stage. It is curious that the FFC response to them was even higher than to the preferred category. These morphs do not belong to either category. Thus, we would have expected their FFC to be halfway between the 2 categories. It occurred to us that there could be 2 effects at play here: higher low-beta FFC for preferred categories (i.e., category selectivity) and, added on top, increased FFC for more difficult category decisions. The 50% morphs, being unclassifiable, were the most difficult to classify. We examine this next.
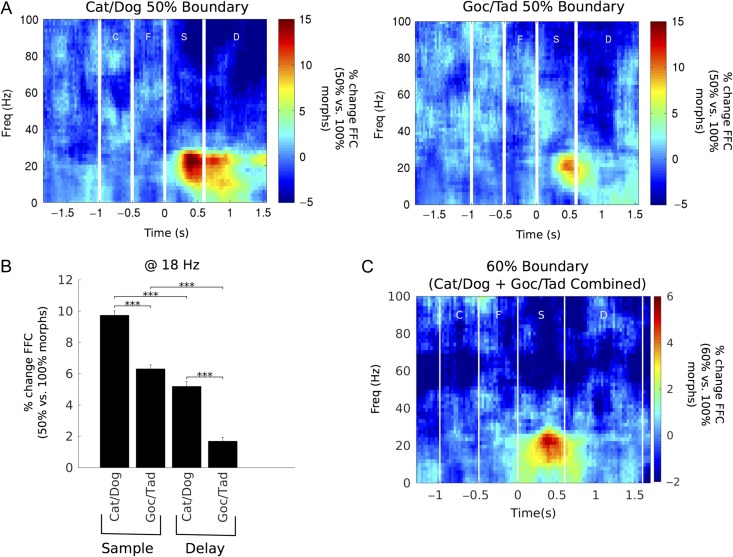
Increased Low-Beta Coherence Near the Category Boundary
The patterns of results described in the previous section raised the possibility that 2 effects were contributing to higher beta FFC: higher FFC for a given category (i.e., category selectivity) and a boost in FFC when the category decision was difficult. To investigate this, we examined 2 sets of trials: boundary trials, in which the sample stimuli were situated directly on the category boundary (i.e., 50% morphs), and near-boundary trials, in which morphs from the preferred category were adjacent to the category boundary (60% morphs). The 50% morphs were the most difficult to categorize because they had no category membership (the animals were randomly rewarded). The 60% morphs were next most difficult because they were physically similar to the 40% stimuli from the nonpreferred category. We compared the beta FFC for these morphs with that for the 100% morphs (which were the easiest to categorize).
We found increased low-beta FFC to boundary and near-boundary morphs during sample presentation and similar but weaker effects during the memory delay. Figure 5A plots the % change in FFC for boundary (50%) morphs versus the 100% morphs. As above, there was a peak of increased FFC for the 50% morphs (relative to the 100% morphs) in the low-beta band. This peak was largest late into the sample presentation and the first part of the memory delay. The FFC increase was significantly higher for Cat/Dog boundary (50% morphs) than for Goc/Tad boundary (Fig. 5B).
Figure 5.
Low-beta LFP coherence is augmented for stimuli close to the category boundary. (A) Percent increase in FFC for Cat/Dog and Goc/Tad boundary trials versus their nonboundary counterparts. Boundary effect was strongest during the sample stage. (B) On average, the boundary effect was significantly greater for Cat/Dog than for Goc/Tad. Additionally, the boundary effect was significantly greater during the sample stage than during the delay stage for both category boundaries. (C) Response for 60% near-boundary trials versus 100% nonboundary trials (Cat/Dog and Goc/Tad data pooled together). Bar plots ***P < 0.001 by Wilcoxon signed-rank test for Cat/Dog versus Goc/Tad and Wilcoxon rank-sum test for Sample versus Delay; all statistical tests were Holm–Bonferroni corrected for multiple comparisons.
This analysis was repeated for near-boundary (60%) morphs versus the 100% morphs (Fig. 5C). Unlike the 50% morphs, 60% morphs had clear category membership and only correct responses were considered. Nonetheless, the low-beta augmentation also appeared for 60% morphs and was concentrated in the sample stage, where the effect was significantly stronger than during the delay stage (P < 0.001, Wilcoxon rank-sum test). The boundary effect was even evident when the morphs were on or near the currently irrelevant boundary (Supplementary Fig. 5), although this effect was weaker than that for the relevant boundary. We also examined in isolation morphs at the center of the morph space (see Fig. 1), which were ambiguous under both category schemes. However, we did not find any evidence that these “doubly ambiguous” morphs had any greater FFC than those ambiguous only under Cat/Dog (at least when Cat/Dog was relevant; Supplementary Fig. 6).
Finally, we examined spiking activity to boundary morphs to determine whether there was a single neuron correlate to the boundary effect. Like previous studies (Freedman et al. 2001, 2002, 2003; Cromer et al. 2010; Roy et al. 2010), our analysis detected no significant boundary effects on the level of PFC single-neuron activity (Supplementary Fig. 7). The contrast between single-neuron and FFC activity near the boundary is perhaps most readily apparent by comparing morph-response profiles (compare Supplementary Fig. 7C and Fig. 4A). This difference is quantified in Supplementary Figure 8 and is shown to be significant for all cases, with the exception of the Goc/Tad boundary during the delay stage.
There is Greater Category Selectivity for Neurons That Are Part of the Corresponding Low-Beta Category Ensemble
The pattern of FFC results described above suggests that low-beta synchrony helps form the functional networks (“ensembles”) that contribute to the category decisions. PFC neurons are known to show category selectivity in spiking activity (e.g., Roy et al. 2010 using these same data). Here, we test whether these neurons had any relation to the category-selective beta ensembles.
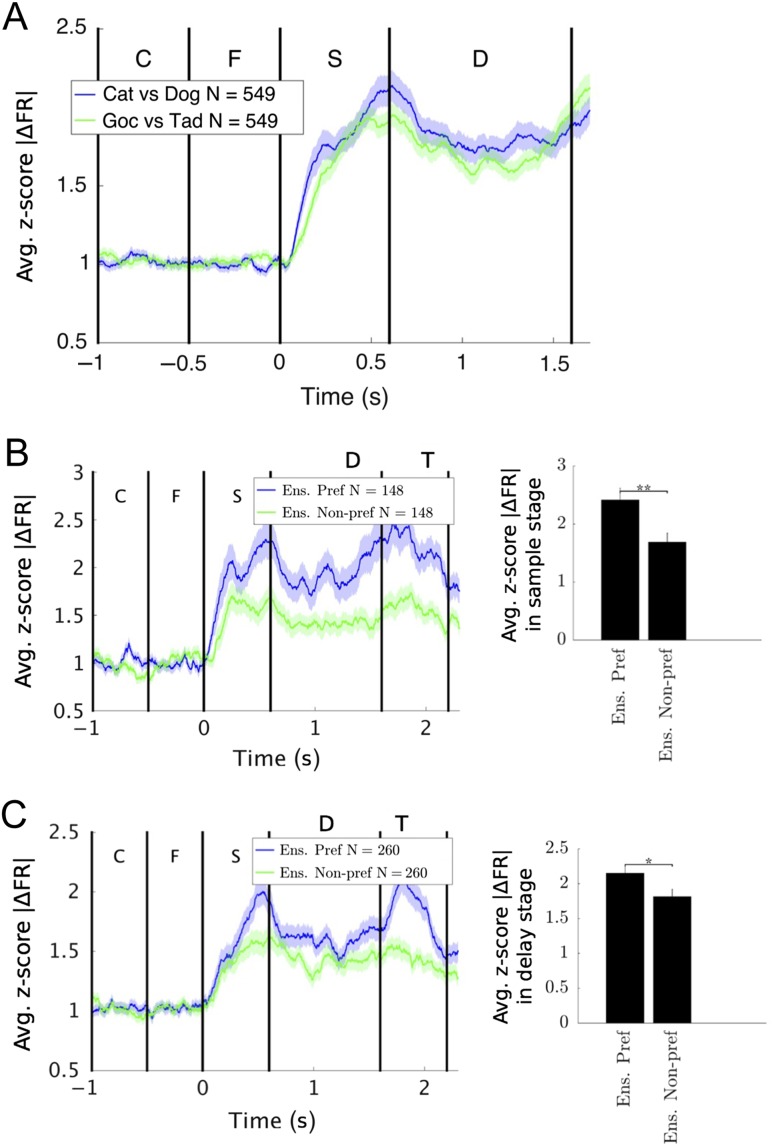
The category selectivity of individual neurons was quantified by the z-score of the absolute differences in spike rate. As in Roy et al. (2010), we found individual neurons with category selectivity. Across all recorded neurons, category selectivity under the 2 schemes was roughly equal, so we pooled their results for subsequent analyses. Figure 6A plots the average difference in spike rate (across all 549 recorded neurons). Note that across the population, there is significant selectivity in spikes rates for both category distinctions.
Figure 6.
Single-neuron category selectivity is enhanced for the preferred category of the corresponding low-beta ensemble. (A) The z-score statistic for category selectivity of single-neuron FR was evaluated for Cat versus Dog and Goc versus Tad. As in Roy et al. (2010), neurons responded to Cat/Dog and Goc/Tad; these responses were similar and were pooled together for subsequent analysis. (B,C) We identified ensembles of electrodes preferring either Cat/Dog or Goc/Tad category schemes (see text). We plotted the category selectivity of neurons within these ensembles in response to the ensemble's preferred (blue) and nonpreferred (green) category schemes. We found that the neural response was significantly stronger for the ensemble's preferred category scheme than for the nonpreferred scheme. This was true for ensembles identified in both the sample (B) and delay (C) stages. Significance was tested by Wilcoxon signed-rank test with a Holm–Bonferroni correction for multiple comparisons. *P < 0.05; **P < 0.01.
We then asked whether category selectivity was stronger for neurons belonging to (i.e., colocalized with) the “ensemble” of electrodes preferring Cat/Dog or Goc/Tad. For each neuron, we examined all possible pairings between its electrode and other electrodes. If at least 10% of the neuron's electrode pairs had low-beta FFC that was significantly sensitive to Cat versus Dog (by permutation test, see Fig. 2 and Materials and Methods), we considered this neuron as part of the Cat/Dog ensemble. Likewise for Goc/Tad, neurons part of both ensembles (i.e., with at least 10% of pairings significant for Cat vs. Dog and for Goc vs. Tad) were not considered; thus all neurons had a preference (in terms of their LFP pairings) for one category scheme over the other. We refer to the percentage (10% in this case) as the “ensemble inclusion threshold.” Below, we will show that results were impervious to the exact percentage used. See Materials and Methods for details of ensemble calculations.
We found that average neuron category selectivity was significantly stronger for the preferred category distinction of its corresponding low-beta FFC ensemble. Figure 6B,C illustrates this for the sample and delay epochs, respectively. In both cases, the blue line shows the average z-score statistic of neural spiking selectivity for the ensemble's preferred FFC category. The green line is the average z-score of the selectivity of those same neurons for the ensemble's nonpreferred category distinction. As can be seen, average neuron category selectivity is significantly higher for the category distinction that matches its electrode's FFC ensemble's category preference. This effect was impervious to how we define electrode membership in an ensemble. Different ensemble inclusion thresholds from 1% to 20% produced similar results to those presented in Figure 6. Above 20%, the same trend was apparent (higher z-scores for the preferred category), but results were not significant due to the low number of neurons in the ensemble group (see Materials and Methods).
Low-Beta Category Selectivity Is Local While Boundary Enhancement Is Global
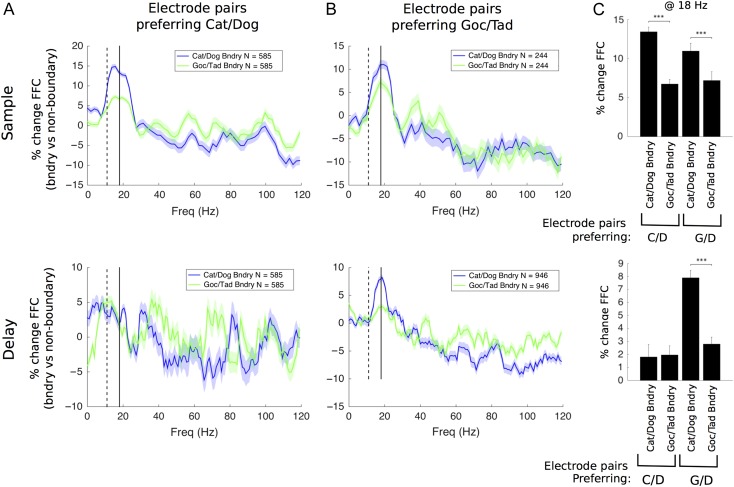
Above, we showed that 2 different factors influenced low-beta FFC. There was increased FFC for one category over the other (i.e., category selectivity) and increased FFC for morphs near the category boundary (i.e., a boundary effect). This led us to wonder whether these effects were the result of a common mechanism. In other words, is the boundary enhancement simply a “turning up the volume” of the same mechanisms that produce the category selectivity? Alternatively, the boundary effect could result from an independent mechanism. We found evidence for the latter.
If the FFC boundary effect was an enhancement of category selectivity, we would expect a correspondence between them. For example, if a given electrode pair prefers (shows FFC selectivity for) Cat/Dog over Goc/Tad, we would expect to see a boundary effect for the former and not the latter. Instead, we found something different. The boundary effect tended to be stronger for the Cat/Dog boundary, regardless of whether the electrode pair in question showed FFC selectivity for Cat/Dog or Goc/Tad. This is shown in Figure 7. For the Cat/Dog preferring electrodes (Fig. 7A), FFC % difference for the Cat/Dog boundary (blue line) was higher than that for the Goc/Tad boundary (green). But note that this is also true for the Goc/Tad preferring electrodes. Their FFC for the Cat/Dog boundary (blue) was higher than for the boundary for the Goc/Tad distinction that the electrode pair preferred (Fig. 7B, green). This was significant for both the sample and delay epochs (Fig. 7C). Thus, the boundary enhancement of FFC is not simply an amplification of the FFC category selectivity of a given electrode pair. Rather, the fact that both Cat/Dog and Goc/Tad electrodes responded more strongly to the Cat/Dog boundary is likely a result of the fact that the Cat/Dog boundary effect was much stronger overall (Fig. 5) and was the first category distinction learned by the animals. This suggests that the boundary enhancement is governed by a broader and less electrode-specific mechanism.
Figure 7.
The boundary response of an electrode pair was always stronger for Cat/Dog than for Goc/Tad, regardless of the electrode pair's preferred category selectivity scheme. For Cat/Dog preferring electrodes (A), we compared their boundary responses along preferred (Cat/Dog) and nonpreferred (Goc/Tad) category boundaries. Likewise for Goc/Tad preferring electrodes (B), despite the difference in category preference, both groups exhibited stronger boundary responses along the Cat/Dog boundary (C). This was mainly the case during the sample stage, when the boundary response was strongest. However, it also appeared weakly during the delay stage. Stimulus-sensitive electrode pairs were identified by estimating P values relative to the trial-shuffled null distribution (alpha = 0.05). C/D = Cat/Dog; G/D = Goc/Tad. Significance tested by Wilcoxon rank-sum test with a Holm–Bonferroni correction for multiple comparisons. ***P < 0.001.
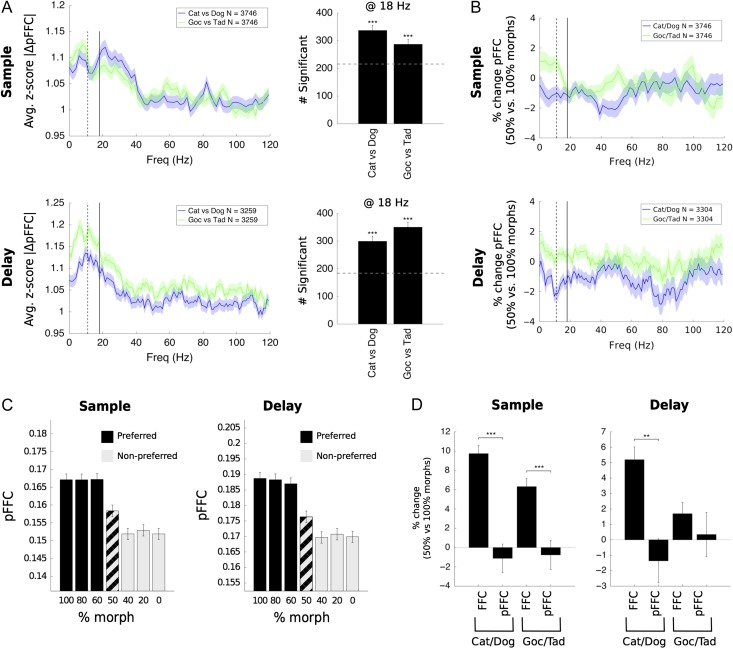
Other evidence for the broader nature of the boundary effect came from a repeat of our FFC analyses using partial field–field coherence (pFFC). Partial coherence measures the coherence between pairs of electrodes only considering activity that is temporally uncorrelated with the rest of the network. In other words, any coherence that is common across all electrodes is subtracted. Thus, pFFC captures local synchrony and removes highly correlated system-wide effects, such as those locked to the stimulus or to input activity from another brain region (DeGutis and D'Esposito 2009).
Figure 8 shows a re-analysis of our results of category selectivity and boundary effects using pFFC. The average pFFC of all electrode pairs showed significant category selectivity (Fig. 8A). However, the boundary enhancement was almost completely abolished (Fig. 8B). Note that the plot of pFFC by morph level no longer shows enhancement to the 50% boundary morphs (Fig. 8C) like we found using FFC (contrast this with Fig. 4A). Direct comparison to the FFC boundary effect showed that the reduction for pFFC was significant in all cases (Fig. 8D). Thus, it seems that FFC category selectivity is a locally generated effect while the boundary effect is more global.
Figure 8.
Partial coherence showed low-beta response to categories but not to boundaries. (A) Z-score statistic showing sensitivity of partial coherence (pFFC) to stimulus category (left). Significantly more electrode pairs responded to Cat/Dog and Goc/Tad categories than expected by chance (right). (B) Percent change in FFC in response to boundary versus nonboundary trials for Cat/Dog and Goc/Tad boundaries. Responses were not significant. (C) Morph-response profiles for low-beta partial coherence, showing a sharp category response and the absence of any boundary effect. Cat/Dog and Goc/Tad responses were similar and were merged. (D) Direct comparison of the boundary effect for pFFC to that for FFC, previously measured, shows that the pFFC boundary effect was significantly weaker in all cases. Significance in (A, right) was tested by binomial test against those values expected by chance at alpha = 0.05 (dotted line; no false discovery control). Significance in (D) was tested by Wilcoxon rank-sum test. In all cases, a Holm–Bonferroni correction was used for multiple comparisons. **P < 0.01; ***P < 0.001.
Discussion
We found low-beta (16–20 Hz) LFP oscillatory coherence in lateral PFC that was influenced by 2 factors. First, coherence was category selective. Different pairs of recording sites showed increased coherence for one or the other category. In other words, across the PFC, there were different patterns of low-beta coherence for the different categories, as if low-beta coherence was helping to form the neural ensembles that represented the categories. Second, we found that low-beta coherence was augmented for exemplars close to the category boundary, as if the brain was turning up the gain for the more difficult category decisions. By contrast, there was no boundary effect on the single-neuron level.
Category and rule-selective beta coherence has been seen within the PFC as well as between the PFC and striatum (Buschman et al. 2012; Antzoulatos and Miller 2014). The hypothesis that it helps form ensembles is supported by our observation that category selectivity of spiking of single neurons was better if that neuron's recording site showed category-selective coherence for that category distinction. Similarly, Buschman et al. (2012) showed that individual PFC neurons that were selective for the color or orientation of a visual stimulus synchronized to the corresponding beta rule ensemble (pay attention to color vs. orientation). We do not yet conclusively know the directionality of the relationship between spiking and LFP synchrony. Does local spiking generate beta coherence on the LFP level or do local neurons entrain to beta oscillatory LFP afferents? Local spiking activity could synchronize at beta frequencies via inhibition from local interneurons (such as low-threshold spiking cells), and thus give rise to local beta LFP oscillations (Roopun et al. 2010; Lee et al. 2013). Afferent sources of low-beta input could include the inferior temporal cortex (ITC), which is associated with processing high-level visual features (Miller et al. 1996; Freedman et al. 2003; De Baene et al. 2008) and which also synchronizes at low beta (15–20 Hz) (Tallon-Baudry et al. 2004). Additionally, the category-selective low-beta observed during the delay stage may be associated with input from posterior parietal cortex (PPC). PPC and PFC have been previously shown to synchronize at low beta (15–25 Hz) during the delay stages of a visual working memory task, with PPC being more influential in driving this process (Salazar et al. 2012).
It is important to note that, although we found category selectivity of single-neuron firing activity and FFC to be related (Fig. 6B,C), the relationship is not one-to-one. For example, Cat/Dog and Goc/Tad selectivity peaked at roughly the same times near the end of the sample stage for neuron activity; however, for FFC, Goc/Tad selectivity emerged much later (compare time courses in Fig. 6A with Figs. 2 and 3C). This could be due to an initial lack of synchrony among neurons underlying the Goc/Tad ensemble, or synchrony at shorter length scales (higher frequencies) than the electrode grid could accommodate (1 mm spacing).
Additionally, both the raw FFC peaks (Supplementary Fig. 1) and strongest category selectivity were observed at low beta (~16–20 Hz), whereas other studies have reported LFP activity at a higher frequency range (25–35 Hz) (Siegel et al. 2009; Buschman et al. 2012; Antzoulatos and Miller 2014). There are a number of possible reasons for this difference. It may be due to differences in recording location, as Buschman et al. recorded in dorsolateral PFC, while the majority of our electrodes were in ventrolateral PFC. It may also be due to differences in the stimuli or task structure, which were different across all 4 studies. Future work will be required in order to build a clear picture of which frequencies correspond to which tasks and brain regions.
Low-beta category selectivity and boundary enhancement at low-beta seemed to have different mechanisms of genesis. We drew this conclusion because, first, their temporal patterns did not always match. For example, category selectivity appeared during both sample and delay stages, whereas the boundary effect was concentrated primarily during the sample stage. Second, in terms of spatial patterns, the boundary effect was stronger for the Cat/Dog boundary, even for the recording sites preferring Goc/Tad in terms of their low-beta category selectivity (Fig. 7). This could be a consequence of the Goc/Tad categorization scheme being innately less challenging or because it was the second scheme learned. In any case, it is clear that the boundary enhancement did not just “turn up of the volume” of local category selectivity; instead, it seemed to blanket the entire network, regardless of local selectivity. Indeed, the boundary effect was largely eliminated when we used partial coherence, a measure that eliminates global and stimulus-locked effects, whereas category-selective coherence remained.
The lack of boundary effect on the neuron level suggests that the observed boundary responses on the LFP level might be generated by neurons located outside the recording site (i.e., extrinsic inputs). Alternatively, it is also possible the LFP boundary responses might be mediated entirely by interneurons that we failed to record due to their small size or number. These neurons could nonetheless have wide-ranging effects on synchronization in the lateral PFC.
Low-Beta Boundary Effect as a Source of Top-Down Attentional Control
What might be the function of the enhancement of low beta at category boundaries? One possibility is that it provides additional attentional control for processing “difficult” stimuli that are close to the category boundary. It could be a top-down signal to devote more cortical resources to processing these difficult stimuli. Beta oscillations have been implicated in top-down feedback processing in the cortex (Buschman and Miller 2007; Engel and Fries 2010; Bastos et al. 2015). It can be thought of as a form of gain control: the physical differences between morphs near the boundary are subtle and must be amplified to achieve reliable categorization. This is consistent with our observation that low-beta boundary enhancement was evident when the category exemplars were being viewed and presumably their category being determined. It was not evident in the memory delay, presumably after the exemplar had already been categorized. Indeed, our analysis of PFC neurons showed that category distinctions were maximally resolved by the beginning of the delay epoch (Supplementary Fig. 9). Also, we previously tested PFC neuron activity with purely ambiguous stimuli (50% morphs) (Roy et al. 2014). Because these stimuli had no correct categorizations, monkeys guessed about their category membership. Neural information corresponding to the monkeys’ guess appeared during viewing of the category exemplar and well before the beginning of the delay epoch. Thus, evidence suggests that categorical decisions were made when exemplars were viewed, in other words, before the memory delay and abatement of the low-beta boundary enhancement effect.
It is also possible that the increased low-beta coherence for boundary trials reflects uncertainty. This could certainly be the case for 50% morph trials, for which there were no correct answers. However, the boundary effect was also observed for near-boundary trials (60% morphs, Fig. 5C) and animal behavioral performance on these trials was almost as good as for 100% morphs (Roy et al. 2010). Thus, while signatures of categorization uncertainty have been observed in PFC (Grinband et al. 2006), it is unlikely that they are the cause of the boundary effect observed here.
The neural circuit underlying the low-beta boundary enhancement is not clear. A previous fMRI study on face categorization found that a number of brain regions exhibited elevated responses to boundary stimuli, including face-selective ITC, lateral PFC, and dorsal striatum (DeGutis and D'Esposito 2007, 2009). In contrast, the authors found that hippocampus and left superior frontal sulcus responded most to faces farthest from the category boundary (i.e., to stimuli more similar to the category prototypes). Several other studies have found that ITC neurons show greater activity for boundary stimuli, in particular emphasizing critical stimuli and features useful for performing categorization (Baker et al. 2002; Sigala and Logothetis 2002; Freedman et al. 2003; DeGutis and D'Esposito 2007; Seger and Miller 2010). Parietal cortex, known for its role in processing spatial categories, may also play a role in boundary processing. Studies using visual motion categorization tasks showed that neuron firing activity in lateral intraparietal area (LIP) reflected monkey decisions about the category membership of ambiguous stimuli (Williams et al. 2003; Swaminathan and Freedman 2012). This selectivity during ambiguous stimuli was in fact stronger for LIP neurons than for PFC neurons (Swaminathan and Freedman 2012), although this could be particular to LIP and the spatial nature of these tasks (Goodwin et al. 2012; Crowe et al. 2013) and may be correlative rather than causal (Katz et al. 2016). Another study, using magnetoencephalography to investigate processing of bistable images, reported increases in beta synchronization (14–30 Hz) in occipital and parietal brain regions following a perceptual shift in the perception of the bistable image (Okazaki et al. 2008). Previous studies have reported top-down beta-frequency (22–34 Hz) interactions between prefrontal and parietal cortices (Buschman and Miller 2007).
Implications for System Architecture
The findings in this paper are indicative of the underlying PFC architecture. One possibility is that the animals automatically computed Cat/Dog categorization as a default strategy immediately after sample onset during each trial, because it was the first scheme trained, and then overrode this with Goc/Tad later on in the trial. This is supported by Figure 2, which shows that Goc/Tad FFC selectivity emerged later in the trial than did Cat/Dog selectivity. Additionally, selectivity for Cat/Dog was not significantly modulated by the rule cue in the sample stage, suggesting that Cat/Dog categories were initially calculated regardless of the rule, whereas Goc/Tad was significantly suppressed on Scheme A trials (Fig. 3).
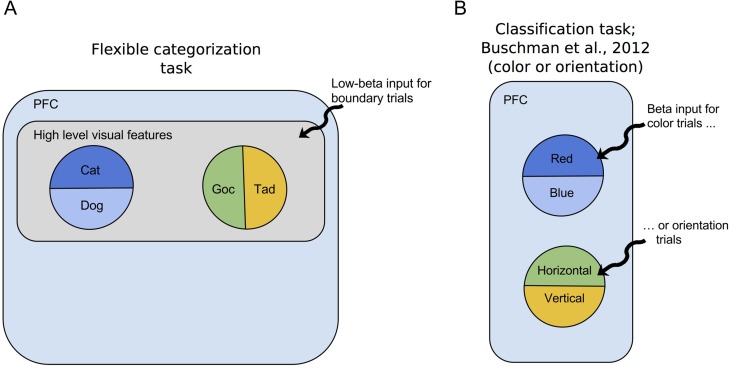
Another possibility is that, during the sample stage, the Cat/Dog circuit was still useful in some way for processing the Goc/Tad categorizations, and this is why it was not attenuated during Scheme B trials. During training, animals originally learned the Cat/Dog categorization. When they later learned the Goc/Tad categorization scheme, perhaps they did not begin from scratch, but rather built on their familiarity with the stimulus shapes. Thus, underlying circuitry originally established for processing the Cat/Dog categorization may have been co-opted in learning the Goc/Tad categorization, which would explain why some Cat/Dog selectivity was still present during Scheme B trials (Fig. 3). Similarly, although Goc/Tad selectivity was significantly reduced when irrelevant, it was still present for Scheme A trials, particularly during the delay stage (Fig. 3C), and thus this circuit might have been employed by the Cat/Dog ensemble. In other words, rather than conceptualizing the system in terms of Cat/Dog and Goc/Tad ensembles, it might be more appropriate to think of an overall task-relevant ensemble with interdependent subspecializations in Cat/Dog and Goc/Tad (Fig. 9A).
Figure 9.
Proposed organization of beta inputs to PFC in our task versus that of Buschman et al. (2012). (A) In our flexible categorization task, Cat/Dog and Goc/Tad category-sensitive ensembles might be built upon a larger ensemble. This larger ensemble processes high-level visual features of the stimulus morphs (i.e., a “task relevant” ensemble) and provides this information to the category-sensitive neurons. Low-beta input for boundary trials activates the task relevant ensemble as a whole. (B) The task by Buschman et al. (2012) involved classification of much simpler objects (i.e., bars). Bars were classified based on orientation (horizontal/vertical) or color (red/blue), depending on a rule. They observed beta-frequency synchronization in 1 of 2 distinct ensembles in response to the current rule cue.
The concept of an overall task-relevant ensemble is supported by previous studies on a similar categorization task, which identified neurons responding to high-level visual features in ITC and, to a lesser extent, in PFC (Freedman et al. 2003). These neurons might, for example, specialize in responding to specific subregions of the morph space in Figure 1, and thus be useful inputs to both Cat/Dog and Goc/Tad ensembles. It is also likely that the PFC neurons are not so rigid in their function, but rather exhibit mixed selectivity (Rigotti et al. 2013). For example, a neuron selective for Cat/Dog may also carry information about high-level visual features, which would make it a useful input to Goc/Tad-selective neurons. In fact, it is entirely possible that the majority of PFC neurons multiplex their categorization duties with more specialized roles.
Such architecture could also help explain the global nature of the boundary effect. Specifically, the boundary effect appears not to follow specific local patterns of Cat/Dog or Goc/Tad selectivity (Fig. 7). Thus, the boundary effect might be more associated with the processing of high-level visual features of the boundary morphs, rather than calculating the categories themselves. Like the boundary effect, neurons processing high-level visual features in PFC and ITC were generally most active during sample presentation (Miller et al. 1996; Freedman et al. 2003).
This invites comparison with an earlier study on decision making in PFC, which used much simpler stimuli and lacking categorical ambiguity (Buschman et al. 2012). This study reported 2 distinct beta-synchronized ensembles in PFC, each one associated with a different task rule (Fig. 9B). In contrast, in our study, we did not observe substantial modulation of low-beta activity in response to the rule cue. Thus, it appears the PFC arrived at 2 very different “optimal” solutions for processing these tasks. In Buschman et al.’s case, beta is synchronizing the rule-relevant ensemble; in our case it is synchronizing the entire task-relevant ensemble depending on difficulty. In both cases, however, it is essentially performing the same function of top-down control. The differences between these 2 cases are likely driven by differences in complexity of the stimuli, with the shapes in Bushman et al.’s task being simple horizontal and vertical bars and therefore not requiring high-level feature processing or consideration of boundaries.
This idea of a common underlying architecture yields an experimentally falsifiable hypothesis. Specifically, this study used a flexible categorization task in which 2 categorization schemes were applied orthogonally to the same set of stimulus morphs. In contrast, an earlier study required monkeys to learn 2 distinct sets of morphs (Cat vs. Dog and Sport Cars vs. Sedans), for which we would not expect a shared architecture to be necessary (Cromer et al. 2010). In the latter study, we would predict that boundary enhancement would depend on local, not global, circuitry.
We identified category-sensitive low-beta oscillations in PFC that appear to be locally generated and associated with category-sensitive PFC neurons, previously characterized (Freedman et al. 2001, 2003; Miller et al. 2002; Cromer et al. 2010; Roy et al. 2010). We also found that low-beta oscillations are augmented for boundary trials, an effect that cannot be decoded from single-neuron FR alone. We suggest that low-beta oscillations provide a mechanism for increasing the gain of PFC neurons, thereby allowing them to accurately respond to stimuli close to the category boundary. While beta oscillations have previously been associated with visual categories and rules in PFC, this is the first demonstration of their response to category boundaries.
Supplementary Material
Funding
This work was supported by NSF DMS-1042134 to N.J.K. and NIMH R01 MH065252 to E.K.M.
Supplementary Material
Notes
We thank U.T. Eden, K.Q. LePage, and S. Ardid for useful comments about the manuscript. Conflict of Interest: None declared.
References
- Antzoulatos EG, Miller EK. 2014. Increases in functional connectivity between prefrontal cortex and striatum during category learning. Neuron. 83:216–225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avargues-Weber A, Deisig N, Giurfa M. 2011. Visual cognition in social insects. Annu Rev Entomol. 56:423–443. [DOI] [PubMed] [Google Scholar]
- Baker CI, Behrmann M, Olson CR. 2002. Impact of learning on representation of parts and wholes in monkey inferotemporal cortex. Nat Neurosci. 5:1210–1216. [DOI] [PubMed] [Google Scholar]
- Bastos AM, Vezoli J, Bosman CA, Schoffelen J-M, Oostenveld R, Dowdall JR, DeWeerd P, Kennedy H, Fries P. 2015. Visual areas exert feedforward and feedback influences through distinct frequency channels. Neuron. 85:390–401. [DOI] [PubMed] [Google Scholar]
- Benard J, Stach S, Giurfa M. 2006. Categorization of visual stimuli in the honeybee Apis mellifera. Anim Cogn. 9:257–270. [DOI] [PubMed] [Google Scholar]
- Bokil H, Purpura K, Schoffelen JM, Thomson D, Mitra P. 2007. Comparing spectra and coherences for groups of unequal size. J Neurosci Methods. 159:337–345. [DOI] [PubMed] [Google Scholar]
- Buschman TJ, Denovellis EL, Diogo C, Bullock D, Miller EK. 2012. Synchronous oscillatory neural ensembles for rules in the prefrontal cortex. Neuron. 76:838–846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buschman TJ, Miller EK. 2007. Top-down versus bottom-up control of attention in the prefrontal and posterior parietal cortices. Science. 315:1860–1862. [DOI] [PubMed] [Google Scholar]
- Cromer JA, Roy JE, Miller EK. 2010. Representation of multiple, independent categories in the primate prefrontal cortex. Neuron. 66:796–807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crowe DA, Goodwin SJ, Blackman RK, Sakellaridi S, Sponheim SR, MacDonald AW, Chafee MV. 2013. Prefrontal neurons transmit signals to parietal neurons that reflect executive control of cognition. Nat Neurosci. 16:1484–1491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Baene W, Ons B, Wagemans J, Vogels R. 2008. Effects of category learning on the stimulus selectivity of macaque inferior temporal neurons. Learn Mem. 15:717–727. [DOI] [PubMed] [Google Scholar]
- DeGutis J, D'Esposito M. 2007. Distinct mechanisms in visual category learning. Behav Neurosci. 7:251–259. [DOI] [PubMed] [Google Scholar]
- DeGutis J, D'Esposito M. 2009. Network changes in the transition from initial learning to well-practiced visual categorization. Front Hum Neurosci. 3:44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engel AK, Fries P. 2010. Beta-band oscillations—signalling the status quo? Curr Opin Neurobiol. 20:156–165. [DOI] [PubMed] [Google Scholar]
- Freedman DJ, Riesenhuber M, Poggio T, Miller EK. 2001. Categorical representation of visual stimuli in the primate prefrontal cortex. Science. 291:312–316. [DOI] [PubMed] [Google Scholar]
- Freedman DJ, Riesenhuber M, Poggio T, Miller EK. 2002. Visual categorization and the primate prefrontal cortex: neurophysiology and behavior. J Neurophysiol. 88:929–941. [DOI] [PubMed] [Google Scholar]
- Freedman DJ, Riesenhuber M, Poggio T, Miller EK. 2003. A comparison of primate prefrontal and inferior temporal cortices during visual categorization. J Neurosci. 23:5235–5246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fries P, Womelsdorf T, Oostenveld R, Desimone R. 2008. The effects of visual stimulation and selective visual attention on rhythmic neuronal synchronization in macaque area V4. J Neurosci. 28:4823–4835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodwin SJ, Blackman RK, Sakellaridi S, Chafee MV. 2012. Executive control over cognition: stronger and earlier rule-based modulation of spatial category signals in prefrontal cortex relative to parietal cortex. J Neurosci. 32:3499–3515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gregoriou GG, Gotts SJ, Zhou H, Desimone R. 2009. High-frequency, long-range coupling between prefrontal and visual cortex during attention. Science. 324:1207–1210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grinband J, Hirsch J, Ferrera VP. 2006. A neural representation of categorization uncertainty in the human brain. Neuron. 49:757–763. [DOI] [PubMed] [Google Scholar]
- Hill EL. 2004. Executive dysfunction in autism. Trends Cogn Sci. 8:26–32. [DOI] [PubMed] [Google Scholar]
- Katz LN, Yates JL, Pillow JW, Huk AC. 2016. Dissociated functional significance of decision-related activity in the primate dorsal stream. Nature. 535:285–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kéri S, Kelemen O, Szekeres G, Bagóczky N, Erdélyi R, Antal A, Benedek G, Janka Z. 2000. Schizophrenics know more than they can tell: probabilistic classification learning in schizophrenia. Psychol Med. 30:149–155. [DOI] [PubMed] [Google Scholar]
- Kobari-Wright VV, Miguel CF. 2014. The effects of listener training on the emergence of categorization and speaker behavior in children with autism. J Appl Behav Anal. 47:431–436. [DOI] [PubMed] [Google Scholar]
- Lee JH, Whittington MA, Kopell NJ. 2013. Top-down beta rhythms support selective attention via interlaminar interaction: a model. PLoS Comput Biol. 9:e1003164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Micoulaud-Franchi J-A, Aramaki M, Merer A, Cermolacce M, Ystad S, Kronland-Martinet R, Vion-Dury J. 2011. Categorization and timbre perception of environmental sounds in schizophrenia. Psychiatry Res. 189:149–152. [DOI] [PubMed] [Google Scholar]
- Miller EK, Erickson CA, Desimone R. 1996. Neural mechanisms of visual working memory in prefrontal cortex of the macaque. J Neurosci. 16:5154–5167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller EK, Freedman DJ, Wallis JD. 2002. The prefrontal cortex: categories, concepts and cognition. Philos Trans R Soc Lond B Biol Sci. 357:1123–1136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitra P, Bokil H. 2007. Observed brain dynamics. Oxford University Press. [Google Scholar]
- Nacher V, Ledberg A, Deco G, Romo R. 2013. Coherent delta-band oscillations between cortical areas correlate with decision making. Proc Natl Acad Sci. 110:15085–15090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okazaki M, Kaneko Y, Yumoto M, Arima K. 2008. Perceptual change in response to a bistable picture increases neuromagnetic beta-band activities. Neurosci Res. 61:319–328. [DOI] [PubMed] [Google Scholar]
- Paxinos G, Huang X-F, Toga AW. 2000. The rhesus monkey brain in stereotaxic coordinates. 1st ed Academic Press. [Google Scholar]
- Riesenhuber M, Poggio TA. 2000. Models of object recognition. Nat Neurosci. 3 (Suppl):1199–1204. [DOI] [PubMed] [Google Scholar]
- Rigotti M, Barak O, Warden MR, Wang X-J, Daw ND, Miller EK, Fusi S. 2013. The importance of mixed selectivity in complex cognitive tasks. Nature. 497:1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roopun AK, Lebeau FEN, Ramell J, Cunningham MO, Traub RD, Whittington MA. 2010. Cholinergic neuromodulation controls directed temporal communication in neocortex in vitro. Front Neural Circuits. 4:8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosch EH. 1973. Natural categories. Cogn Psychol. 4:328–350. [Google Scholar]
- Roy JE, Buschman TJ, Miller EK. 2014. Prefrontal cortex neurons reflect categorical decisions about ambiguous stimuli. J Cogn Neurosci. 26:1283–1291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy JE, Riesenhuber M, Poggio T, Miller EK. 2010. Prefrontal cortex activity during flexible categorization. J Neurosci. 30:8519–8528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saalmann YB, Pigarev IN, Vidyasagar TR. 2007. Neural mechanisms of visual attention: how top-down feedback highlights relevant locations. Science. 316:1612–1615. [DOI] [PubMed] [Google Scholar]
- Salazar RF, Dotson NM, Bressler SL, Gray CM. 2012. Content-specific fronto-parietal synchronization during visual working memory. Science. 338:1097–1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seger CA, Miller EK. 2010. Category learning in the brain. Annu Rev Neurosci. 33:203–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shelton CR. 2000. Morphable surface models. Int J Comput Vis. 38:75–91. [Google Scholar]
- Siegel M, Warden MR, Miller EK. 2009. Phase-dependent neuronal coding of objects in short-term memory. Proc Natl Acad Sci U S A. 106:21341–21346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigala N, Logothetis NK. 2002. Visual categorization shapes feature selectivity in the primate temporal cortex. Nature. 415:318–320. [DOI] [PubMed] [Google Scholar]
- Swaminathan SK, Freedman DJ. 2012. Preferential encoding of visual categories in parietal cortex compared with prefrontal cortex. Nat Neurosci. 15:315–320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tallon-Baudry C, Mandon S, Freiwald WA, Kreiter AK. 2004. Oscillatory synchrony in the monkey temporal lobe correlates with performance in a visual short-term memory task. Cereb Cortex. 14:713–720. [DOI] [PubMed] [Google Scholar]
- Thomson DJ. 2007. Jackknifing multitaper spectrum estimates. IEEE Signal Process Mag. 24:20–30. [Google Scholar]
- Williams ZM, Elfar JC, Eskandar EN, Toth LJ, Assad JA. 2003. Parietal activity and the perceived direction of ambiguous apparent motion. Nat Neurosci. 6:616–623. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.