Abstract
The effect of dose-delivery time with flattening filter (FF) and flattening filter-free (FFF) photon beams based on microdosimetric kinetic model (MKM) was investigated in this study. Monte Carlo simulation with the particle and heavy ion transport code system (PHITS) was performed to calculate the dose-mean lineal energy yD (keV/μm) of FF and FFF 6 MV photon beams using the IAEA phase-space files of Varian TrueBeam linear accelerator. Human non-small cell lung cancer NCI-H460 cells were used to determine the MKM parameters under the condition that dose-delivery times with continuous irradiation were 1, 5, 10, 30, and 60 min, and the adsorbed dose was 2, 4, and 8 Gy in this study. In addition, the relative biological effectiveness (RBE) of FF and FFF photon beams were calculated for evaluating the effect of dose delivery time. The RBE of FF decreased to 99.8% and 97.5% with 5 and 60 min for 2 Gy in comparison to 99.6% and 95.1% for 8 Gy, respectively. Meanwhile, that of FFF decreased to 99.5% and 94.9% with 5 and 60 min for 2 Gy in comparison to 99.5% and 94.9% for 8 Gy, respectively. Dose-delivery time has an effect on the RBE with photon beams. In other words, the dose-delivery time should be considered during radiation therapy. Furthermore, FFF photon beams were an effective irradiation method compared to FF in dose-delivery time on account of improving clinic throughput.
Introduction
Flattening filter-free (FFF) photon beams provide an increased instantaneous dose of X-ray pulses compared with a conventional flattening filter (FF) photon beams by removing the flattening filter. The high dose rate provided by the FFF photon beams decreases the beam-on-time and improves clinical throughput [1–3]. These features can be effectively used for minimization of intrafraction motion of lung tumors [4].
Sublethal damage repair (SLDR) is induced over times ranging from several minutes to hours after irradiation of DNA by photon beams. The effect of cell death decreases with increased dose-delivery time [5, 6]. For the treatment of tumors, such as lung cancers that exhibit intrafraction motion, it takes approximately 10 min or longer to deliver the dose per fraction, depending on the irradiation technique of dose-delivery. Several techniques can be employed, such as stereotactic body radiation therapy (SBRT) [7, 8], real-time tumor tracking radiation therapy [9], and respiratory-gated radiation therapy [10]. Therefore, it is necessary to evaluate the effect of dose-delivery time on the radiation therapy techniques.
Hawkins proposed the microdosimetric kinetic model (MKM) in 1994 [11]. The MKM was developed by considering repair-misrepair [12], and lethal and potentially lethal [13] models. The model was developed to reveal the relationship between the surviving fraction (SF) and absorbed dose (D) by calculating the total energy deposition and analyzing the dose-rate effect [14]. Matsuya et al. reported MKMs which include various irradiation methods with photon beams [15, 16]. In addition, they evaluated DNA damage using the MKM and modified MKM; changes in the amount of DNA per nucleus during irradiation was analyzed [17]. The modified MKM provided a better SF estimate, which is used in the high dose range, compared with the previous MKM. Therefore, the dependence of the SF as a function of dose-delivery time was evaluated in the high dose range using the modified MKM.
Previous studies suggested that the RBE of the FF beams can be explained using the MKM [18, 19]. On the other hand, to the best of our knowledge, several studies investigated the dependence of RBE of FF beams with increased dose-delivery time. The dependence of the RBE of the FFF beams as a function of dose-delivery time has not been reported.
In this study, using the MKM, we investigated the effect of dose-delivery time for both the FF and FFF beams.
Materials and methods
MKM
The nucleus of the considered cell is divided into several hundred independent areas, which are called domains. Potentially lethal lesions (PLLs) emerge after irradiation of the domains in the MKM [12]. The PLLs are classified into four categories according to their transformations: (I) irreparable lethal lesion (LL) that emerges through a first-order process (a is the transformation rate constant); (II) converted to LLs through a second-order process (rate constant of the transformation; (III) repaired through first-order process (c is the transformation rate constant); (IV) lesions that resist becoming LLs for a period of time tr, after which they do become LLs and are not repairable. In the MKM, the PLLs are supposed to be DNA double-strand breaks. The average number of LLs per cell nucleus (Ln) was defined as:
| (1) |
| (2) |
| (3) |
| (4) |
where z is the specific energy deposited in the domain [Gy], N is the number of domains, A and B are coefficients, rd is the radius of the domain (0.5 μm), ρ is the density of the domain (1.0 g/cm3), D is the absorbed dose [Gy], and yD is the dose-mean lineal energy [keV/μm]. The parameters α0 and β0 were obtained by single instantaneous irradiation using a linear-quadratic (LQ) model. Matsuya et al. have modified the MKM while considering various irradiation schemes with photon beams. They considered changes in the amount of DNA per nucleus during irradiation (modified MKM). The equation that defines the modified MKM is defined as:
| (5) |
Therefore, we have
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
where is the dose rate [Gy/min], T is the dose-delivery time [min], and F was obtained using the Lea–Catcheside time-factor G [20]. One can see that the value of α is affected by the dose-mean lineal energy yD (Eq 7).
Monte Carlo simulations performed using the particle and heavy ion transport code system (PHITS)
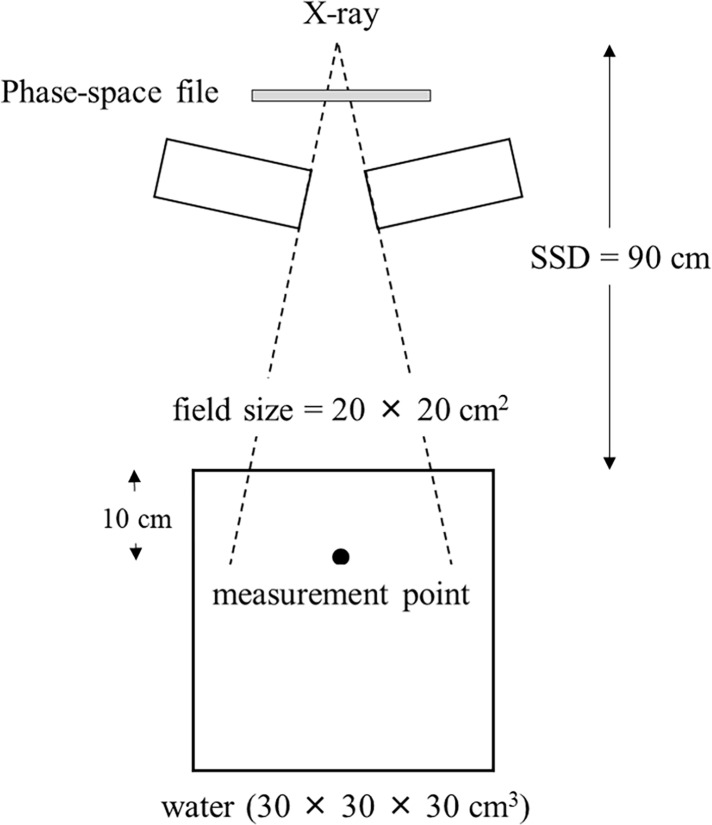
The BEAMnrc code is based on the EGSnrc platform and is optimized for modeling the treatment head of radiotherapy linear accelerators [21]. This code includes several geometry and source subroutines, along with variance reduction techniques to enhance simulation efficiency [22]. PHITS can address photons, electrons, positrons, neutrons, and heavy ions [23]. In this study, International Atomic Energy Agency (IAEA) phase-space files for the Varian TrueBeam linear accelerator (Varian Medical Systems, Palo Alto, USA) were used to simulate the 6 MV FF and FFF beams. Fig 1 shows the irradiation geometry for the 6 MV FF and FFF beams, which is employed in the PHITS simulations. The measurement point was located at a 10 cm depth in the water-equivalent phantom material. The dose-mean lineal energy yD [24–26] was calculated as:
| (11) |
| (12) |
where ε, l, f(y), and d(y) are the energy deposited in a domain, mean chord length, probability density of the lineal energy, and dose distribution of the lineal energy, respectively.
Fig 1. Irradiation geometry for the Monte Carlo calculations for both 6 MV FF and FFF beams.
Determination of biological parameters for the MKM by analyzing NCI-H460 lung cancer
Human non-small-cell lung cancer NCI-H460 cells were used to determine the MKM parameters. The parameters α0 and β0 were obtained using the LQ model [27], while the values of α and β were determined using Eqs (9) and (10), respectively. The PLL repair rate (a + c) was equated with the first-order rate constant λ, which was calculated using the DNA repair half-time T1/2. The value of the DNA repair half-time T1/2 for H460 was already reported [28, 29]. The characteristic damage repair rate λ [20, 30] was defined as:
| (13) |
Although each of the DNA repairs occurred with a different rate constant, the DNA repair rate was simply calculated as λ in the MKM. Table 1 shows the calculated parameters for the NCI-H460 cells used in the MKM simulations.
Table 1. MKM simulation parameters obtained using NCI-H460 cells.
| Parameters | Values |
|---|---|
| α0 (Gy−1) (FF) | 0.24 ± 0.19 |
| α0 (Gy−1) (FFF) | 0.21 ± 0.11 |
| β0 (Gy−1) (FF) | 0.06 ± 0.03 |
| β0 (Gy−1) (FFF) | 0.07 ± 0.02 |
| a + c (h−1) | 0.46 |
| γFF | 2.96 |
| γFFF | 2.98 |
| ρ (g/cm3) | 1.00 |
| rd (μm) | 0.50 |
SF and RBE calculations for both FF and FFF beams using the MKM
The absorbed dose on the NCI-H460 cells was varied from 0 Gy to 8 Gy by applying single instantaneous irradiation, and the dose-delivery time was varied from 0 to 60 min. Moreover, the RBEs for both the FF and FFF beams were calculated in order to evaluate the effect of the dose-delivery time. For the FF and FFF beams, the RBE was defined using instantaneous irradiation (T = 0) as a reference [31] (Eq 14):
| (14) |
Results
Microdosimetric energy distribution calculations yD
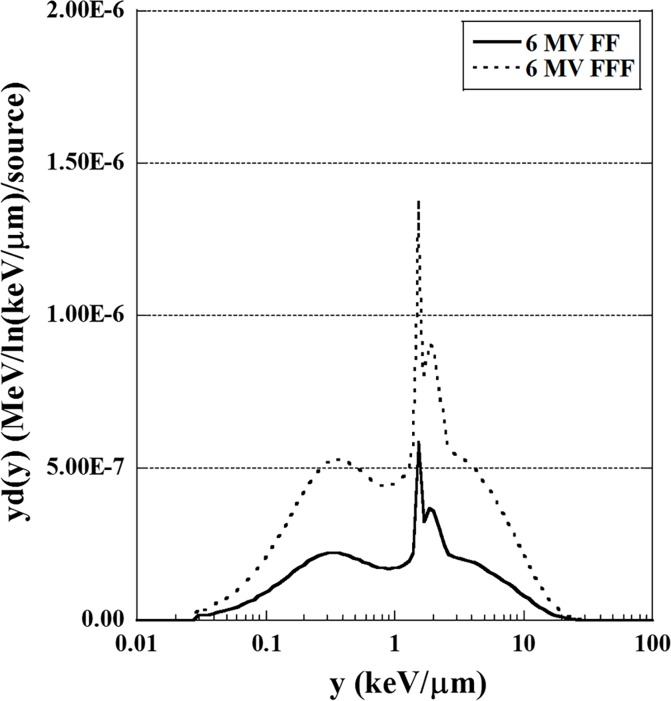
The energy distributions of the FF and FFF photon beams in a domain were calculated using PHITS. The yD(y) distributions for the FF and FFF photon beams are shown in Fig 2. One can notice that the yD(y) distributions of the FF and FFF beams show similar behavior. The yD(y) distributions were used to calculate the dose-mean lineal energy yD using Eq (12).
Fig 2. Microdosimetric energy distributions yD as a function of y for 6 MV FF and FFF beams at a depth of 10 cm in a water-equivalent phantom material.
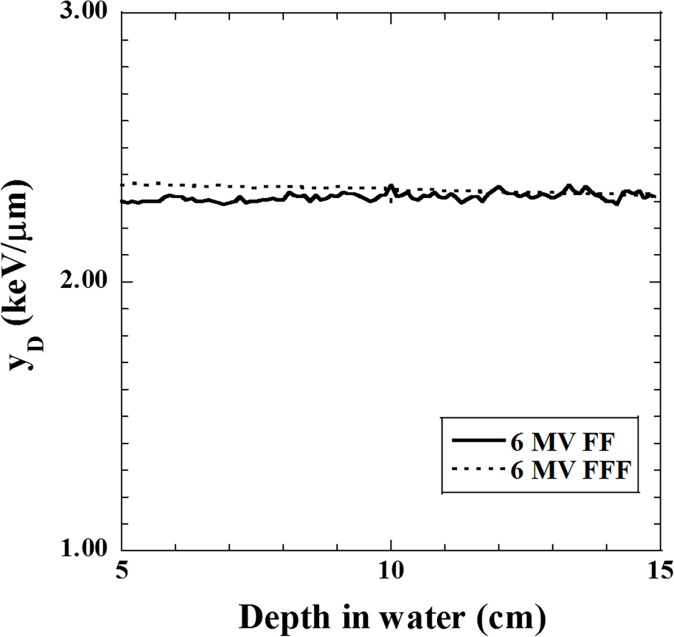
Fig 3 shows the relationships between the measured depth in water and dose-mean lineal energy yD for both FF and FFF beams. One can see that the value of yD was affected by the depth. Therefore, yD was averaged over depths ranging from 10 cm to 13 cm. Table 2 shows the average yD value for the FF and FFF beams. The average yD value was used for to calculate the SF and RBE using the MKM.
Fig 3. Relationships between the depth in water and dose-mean lineal energy yD for the 6 MV FF and FFF beams.
Table 2. Average value of the dose-mean lineal energy yD for FF and FFF beams.
| Dose-mean lineal energy | Value (mean ± standard deviation) |
|---|---|
| 2.32 ± 0.01 | |
| 2.34 ± 0.01 |
Effect of the dose-delivery time on the SF for the FF and FFF beams using the MKM
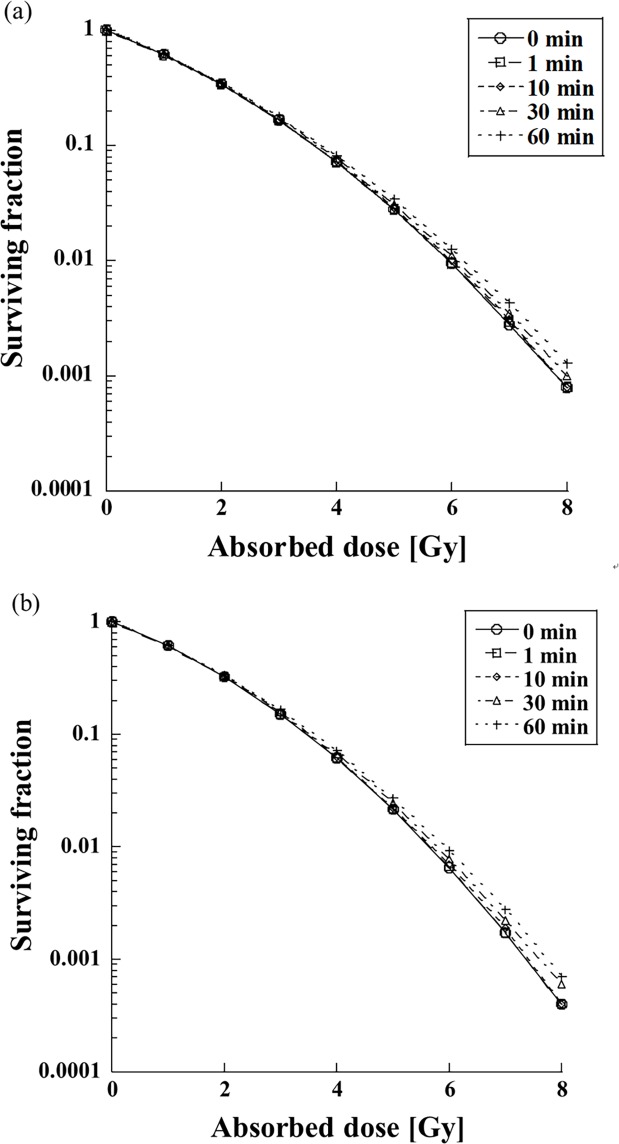
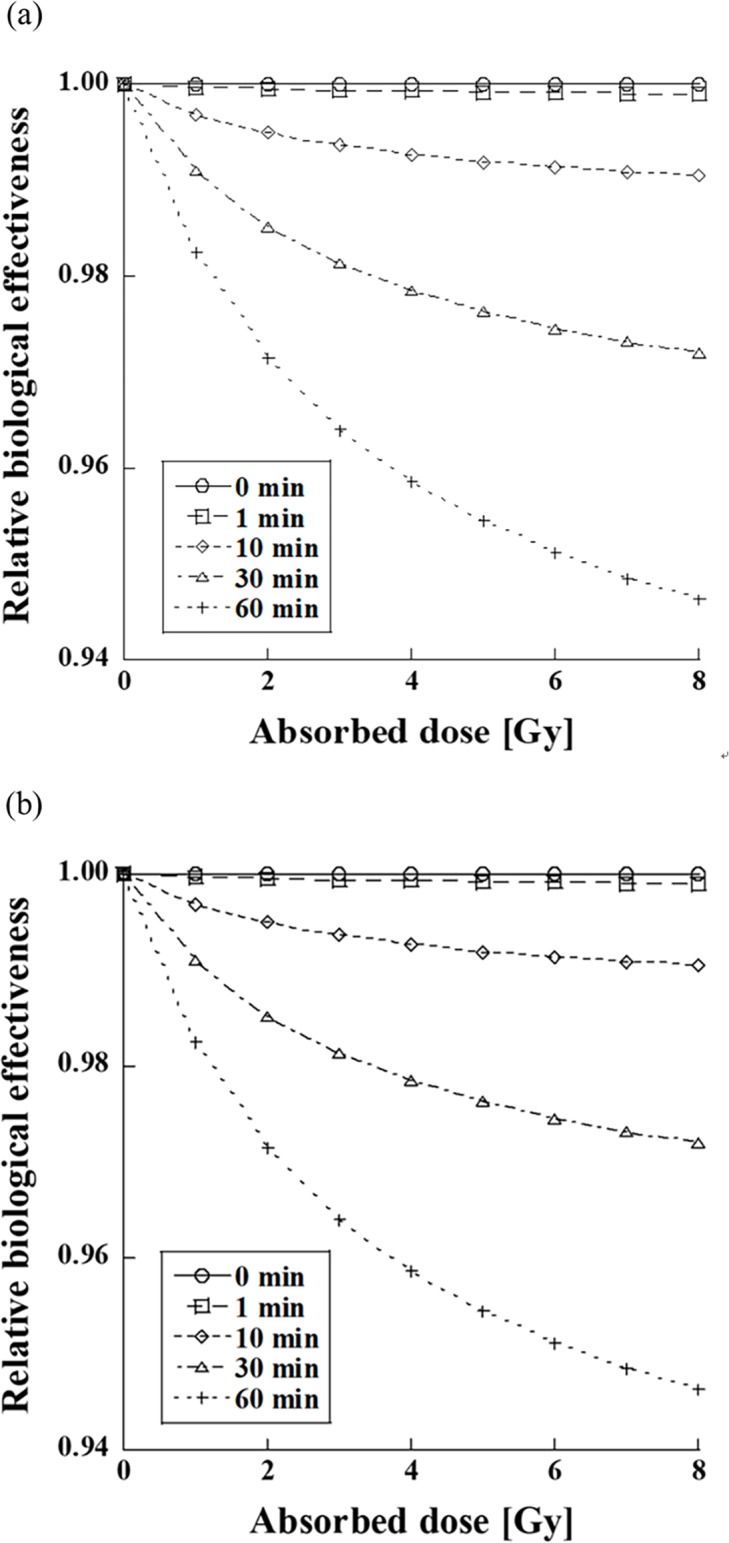
Fig 4 shows the dependence of SFs for the FF and FFF beams. Although there was no difference between the FF and FFF beams, the SF decreased with increased dose-delivery time. The difference between SFs for the FF and FFF beams was emphasized when the dose-delivery time was 30 min or longer.
Fig 4. Effect of the dose-delivery time on the SF for FF (upper plots) and FFF (lower plots) beams for various dose-delivery times.
Fig 5 shows the RBE of the FF and FFF beams for different dose-delivery times. The RBE of the FF beam decreased to 0.998 and 0.974 after 5 min and 60 min, for a dose of 2.0 Gy, respectively. For a dose of 8.0 Gy, it decreased to 0.996 and 0.951 after 5 min and 60 min, respectively. The RBE of the FFF beam decreased to 0.997 and 0.972 after 5 min and 60 min for a dose of 2.0 Gy, respectively. For a dose of 8.0 Gy, it decreased to 0.995 and 0.949 after 5 and 60 min, respectively. The RBEs of the FF and FFF beams decreased by ~5% when the dose-delivery time was 60 min.
Fig 5. Effect of the dose-delivery time on the RBEs of the FF (upper plots) and FFF (lower plots) beams.
Discussion
The RBEs of the FF and FFF beams for various dose-delivery time values obtained from the SF using the modified MKM were calculated in this study. No significant differences between the RBEs of FF and FFF beams were found, and both RBEs decreased with increased dose-delivery time. Both RBEs were affected when the dose-delivery time was 30 min or larger, where they decreased by more than 2% as a function of the absorbed dose. The dose-delivery time for photon irradiation in clinical applications depends on the irradiation techniques, which include SBRT, tumor tracking, and respiratory-gated radiation therapy. If the dose-delivery time is prolonged in order to apply a large dose of about 8 Gy, it is possible that the treatment effects with photon irradiation are reduced due to SLDR. Therefore, the dose-delivery time should be considered as an additional factor for achieving successful photon treatment. The FFF beams could provide better clinical throughput since the FFF beams have high dose rate compared to the FF beams.
There was no significant diferrence in the effect of dose-delivery time from FF and FFF since the dose-mean lineal energy yD values of the FF and FFF were nearly equivalent in this study. However, the comparison between the FF and FFF beams shows that FFF beams provide better clinical throughput. In other words, the FFF beams could decrease the required dose-delivery time [31, 32]. Therefore, the FFF beams could be employed for effective irradiation in radiation therapy due to their smaller dose-delivery time.
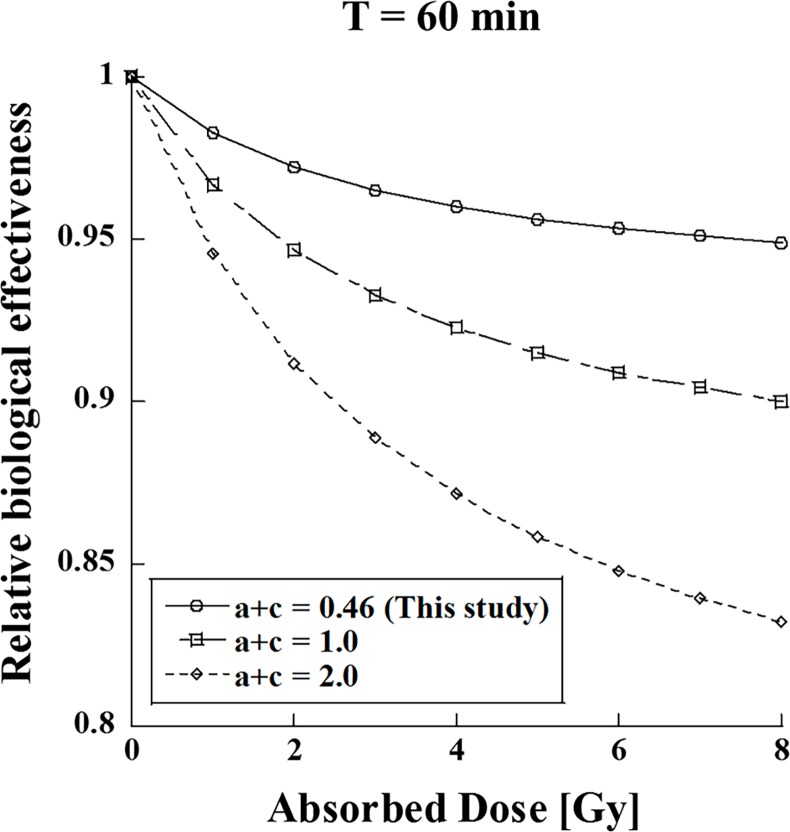
Fig 6 shows the dependence of the RBEs for various cell specific values (a + c) (T = 60 min). One can see that the RBE is affected by the value of (a + c). The effect of the dose-delivery time was significantly different by more than 10% (Fig 6). As the cell specific value (a + c) depends on the type of tumor cell [33, 34], it is necessary to evaluate how the dose-delivery time affects each type of tumor cell.
Fig 6. Effect of relative biological effectiveness as a function of the cell-specific repair rate (a + c) (T = 60 min).
However, only in-vitro studies on NCI-H460 cells were performed in this study in order to evaluate the effect of the dose-delivery time. It is necessary to examine the effect of the dose-delivery time by performing in-vivo studies on various tumor cells. In addition, the effect of the dose-delivery time for clinical irradiation applications, including multiple-field therapy, intensity-modulated radiation therapy, and volumetric-modulated arc therapy should be investigated.
Conclusions
In this study, it was shown that the dose-delivery time affects the RBE during photon irradiation. The effects of the dose-delivery time are important and should be considered in radiation therapy.
Acknowledgments
We thank our colleagues who provided insight and expertise that significantly assisted our research.
Data Availability
All relevant data are within the paper.
Funding Statement
The authors received no specific funding for this work.
References
- 1.Prendergast Brenden M., Fiveash John B. et al. Flattening filter-free linacs improves treatment delivery efficiency in stereotactic body radiation therapy. Med Phys 2013;14:64–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kragl Gabriele, Wetterstedt Sacha af, et al. Dosimetric characteristics of 6 and 10 MV unflattened photon beams. Radiat Oncol 2009;93:141–146. [DOI] [PubMed] [Google Scholar]
- 3.Tsimas P, Sajo E, Cifter F, et al. Beam quality and dose perturbation of 6MV flattening-filter -free linac. Phys Med 2014;30:47–56 10.1016/j.ejmp.2013.02.004 [DOI] [PubMed] [Google Scholar]
- 4.Purdie Thomas G., Jean-Pierre Bissonnette, et al. Cone-Beam Computed Tomography for On-Line Image Guidance of Lung Stereotactic Radiotherapy: Localization, Verification, and Intrafraction Tumor Position. Radiat Oncol 2007;68:243–252. [DOI] [PubMed] [Google Scholar]
- 5.Elkind MM, Sutton H, et al. Radiation response of mammalian cells grown in culture. Repair of X-ray damage in surviving Chinese hamster cells. Radiat Res 1960;13:556–93 [PubMed] [Google Scholar]
- 6.Elkind MM. Repair processes in radiation biology. Radiat Res 1984;100:425–49 [PubMed] [Google Scholar]
- 7.Palma David A., John Van Sorenson, et al. Lung density changes after stereotactic radiotherapy: a quantitative analysis in 50 patients. Int.J Radiat Oncol Biol Phys 2010;81:974–78. 10.1016/j.ijrobp.2010.07.025 [DOI] [PubMed] [Google Scholar]
- 8.Allibhai Zishan, Taremi Mojgan, et al. The Impact of tumor size on outcomes after streotactic body radiation therapy for medically inoperable early-stage non-small cell lung cancer. Int J Radiat Oncol Biol Phys 2013;87:1064–70. 10.1016/j.ijrobp.2013.08.020 [DOI] [PubMed] [Google Scholar]
- 9.Shiinoki T, Kawamura S, Uehara T, et al. Evaluation of a combined respiratory-gating system comprising the TrueBeam linear accelerator and a new real-time tumor -tracking radiotherapy system: a preliminary study. J Appl Clin Med Phys 2016;17:202–13. 10.1120/jacmp.v17i4.6114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Saito T, Matsuyama T, Toya R, et al. Respiratory Gating during Stereotactic Body Radiotherapy for Lung Cancer Reduces Tumor Position Variability. Plos One 2014;9:e112824 10.1371/journal.pone.0112824 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hawkins RB. A statistical theory of cell killing by radiation of varying linear energy transfer. Radiat Res 1994;140:366–74. [PubMed] [Google Scholar]
- 12.Tobias CA, Blakely EA, Ngo FQH et al. The repair–misrepairmodel of cell survival In: Meyn RE, Withers HR (eds). Radiation Biology in Cancer Research. New York: Raven; 1980, 195–230. [Google Scholar]
- 13.Curtis SB. Lethal and potentially lethal lesions induced by irradiation a unifed repair model. Radiat Res 1986;106:252–70. [PubMed] [Google Scholar]
- 14.Hawkins RB. A microdosimetric-kinetic model of cell death from exposure to ionizing radiation of any LET, with experimental and clinical applications. Int J Radiat Biol 1996;69:739–55. [DOI] [PubMed] [Google Scholar]
- 15.Matsuya Y, Ohtsubo Y, Tsutsumi K, et al. Quantitative estimation of DNA damage by photon irradiation based on the microdosimetric-kinetic model. J Radiat Res 2014;55:484–93 10.1093/jrr/rrt222 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Matsuya Y, Tsutsumi K, Sasaki K, et al. Evaluation of the cell survival curve under radiation exposure based on the kinetics of lesions in radiation to dose-delivery time. J Radiat Res 2015;56:90–9. 10.1093/jrr/rru090 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Matsuya Y, Tsutsumi K, Sasaki K, et al. Modeling cell survival and change in amount of DNA during protracted irradiation. J Radiat Res 2017;58:302–12. 10.1093/jrr/rrw110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Okamoto H, Kanai T, Kase Y, et al. Relation between Lineal Energy Distribution and Relative Biological Effectiveness for Photon Beams according to the Microdosimetric Kinetic Model. J Radiat Res 2011;52:75–81 [DOI] [PubMed] [Google Scholar]
- 19.Okamoto H, Kohno T, Kanai T, et al. Microdosimetric study on influence of low energy photons on relative effectiveness under therapeutic conditions using 6 MV linac. Med Phys 2011;38:4714–22. 10.1118/1.3613152 [DOI] [PubMed] [Google Scholar]
- 20.Brenner D. J. The Linear-Quadratic Model Is an Appropriate Methodology for Determining Isoeffective Doses at Large Doses per Fraction. Semin Radiat Oncol 2008;18:234–9 10.1016/j.semradonc.2008.04.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Rogers DW, Walters B, Kawrakow I. BEAMnrc users manual National Research Council of Canada Report PIRS-0509(A) revL. Ottawa, Canada: NRCC; 2016. [Google Scholar]
- 22.Rogers DW, Faddegon BA, Ding GX, Ma CM, We J, Mackie TR. BEAM: a Monte Carlo code to simulate radiotherapy treatment units. Med Phys. 1995;22:503–24 10.1118/1.597552 [DOI] [PubMed] [Google Scholar]
- 23.Puchalska M, Sihver L, et al. PHITS simulations of absorbed dose out-of-field and neutron energy spectra for ELEKTA SL25 medical linear accelerator. Phys Med Biol 2015;60:261–70 [DOI] [PubMed] [Google Scholar]
- 24.Sato T, Kase Y, Watanabe R, et al. Biological Dose Estimation for Charged-Particle Therapy Using an Improved PHITS Code Coupled with a Microdosimetric Kinetic Model. Radiat Res 2009;171:107–17 10.1667/RR1510.1 [DOI] [PubMed] [Google Scholar]
- 25.Sato T, Furusawa Y. Cell Survival Fraction Estimation Based on the Probability Densities of Domain and Cell Nucleus specific energies Using Improved Micorodosimetric Kinetic Models. Radiat Res 2012;178:341–56 [DOI] [PubMed] [Google Scholar]
- 26.Sato T, Hamada N. Model Assembly for Estimating Cell Surviving Fraction for Both Targeted and Nontargeted Effects Based on Microdosimetric Probability Densities. Plos One 2014;9:e114056 10.1371/journal.pone.0114056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.King RB, Hyland WB, Cole AJ, et al. An in vitro study of the radiobiological effects of flattening filter free radiotherapy treatments. Phys Med Biol 2013;58:83–94 [DOI] [PubMed] [Google Scholar]
- 28.Hyland WB, Mcmahon SJ, Butterworth KT, et al. Investigation into the radiobiological consequences of pre-treatment verification imaging with megavoltage X-rays in radiotherapy. Br J Radiol 2014;87:20130781 10.1259/bjr.20130781 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bewes JM, Suchpwerska N, Cartwright L, et al. Optimization of temporal dose modulation: Comparison of theory and experiment. Med Phys 2012;39:3181–88. 10.1118/1.4712223 [DOI] [PubMed] [Google Scholar]
- 30.Brenner DJ, Hlatky LR, Hahnfeldt PJ, et al. The Linear-Quadratic Model and Most Other Common Radiobiological Models Result in Similar Predictions of Time-Dose Relationships. Radiat Res 1998;150:83–91. [PubMed] [Google Scholar]
- 31.Inaniwa T, Kanematsu N, Suzuki M, et al. Effects of beam interruption time on tumor control probability in single-fractionated carbon-ion radiotherapy for non-small cell lung cancer. Phys Med Biol 2015;60:4105–4121 10.1088/0031-9155/60/10/4105 [DOI] [PubMed] [Google Scholar]
- 32.Kawai D, Takahashi R, Kamima T, et al. Variation of the prescription dose using the analytical anisotropic algorithm in lung stereotactic body radiation therapy. Phys Med 2017;38:98–104. 10.1016/j.ejmp.2017.05.058 [DOI] [PubMed] [Google Scholar]
- 33.Dang Thu M, Peters Mitchell J, Brigid Hickey, et al. Efficacy of flattening -filter-free beam in stereotactic body radiation therapy planning and treatment: A systematic review with meta-analysis. J Med Imaging Radiat Oncol 2017;61:379–87 10.1111/1754-9485.12583 [DOI] [PubMed] [Google Scholar]
- 34.High-dose-rate and pulsed-dose-rate brachytherapy for oral cavity cancer and oropharynx cancer. J Contemp Brachytherapy 2009;1:216–23 [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All relevant data are within the paper.