Computational Studies of Intrinsically Disordered Proteins

Abstract

Frequently elusive to experimental characterizations, intrinsically disordered proteins (IDPs) can be probed using molecular dynamics to provide detailed insight into their complex structure, dynamics, and function. However, previous computational studies were often found to disagree with experiment due to either force field biases or insufficient sampling. In this study, nine unstructured short peptides and the HIV-1 Rev protein were simulated and extended to microseconds to assess these limitations in IDP simulations. In short peptide simulations, a tested IDP-specific force field ff14IDPSFF outperforms its generic counterpart ff14SB as agreement of simulated NMR observables with experiment improves, though its advantages are not clear-cut in apo Rev simulations. It is worth noting that sampling is probably still not sufficient in the ff14SB simulations of apo Rev even if ten microseconds have been collected. This indicates that enhanced sampling techniques would greatly benefit IDP simulations. Finally, detailed structural analyses of apo Rev conformations demonstrate different secondary structural preferences between ff14SB (helical) and ff14IDPSFF (random coil). A natural next step is to ask a more quantitative question: whether ff14SB is too ordered or ff14IDPSFF is too disordered in simulations of more complex IDPs such as Rev. This requires further quantitative analyses both experimentally and computationally.

Graphical Abstract

1. INTRODUCTION

As structural data accumulates at an ever increasingly fast pace, intrinsically disordered proteins (IDPs) have garnered widespread acknowledgment for their ubiquitous presence in biochemical pathways vital to eukaryotic systems. Although the exact correlation between disordered protein regions and function remains elusive, IDPs or proteins containing both structured and intrinsically disordered regions (IDRs) have been experimentally shown to participate in DNA binding, transcription, translation, cell signaling, and the overall regulation of the cell cycle.^1–6 Mutations in IDPs/IDRs or expression pathways of IDPs/IDRs have been implicated in various neurological disorders, cancers, and other disease-related conditions.^7–9 These proteins also vary considerably in behavior, occupying a fully disordered state, exhibiting folding only upon binding (known as coupled folding and binding),⁶ or existing in mixed states of structured/unstructured regions. Experimental methods to characterize IDPs and elucidate structure-function associations can therefore be arduous and challenging. To explore the dynamic structures of IDPs, computational methods can provide the expansive sampling to complement experimental measurements.

Widely used to simulate globular proteins, generic protein force fields (e.g. ff14SB¹⁰ and CHARMM36¹¹) have been shown to disagree with experimental observables due to biases towards structured motifs.¹² Improvements to address this bias have resulted in multiple IDP-specific force fields (CHARMM36m,¹³ ff99IDPs,¹⁴ ff14IDPs,¹⁵ CHARMM36IDPSFF¹⁶) to replicate the disordered characteristics of IDPs. The ff14IDPs force field developed by Song et al.¹⁵ included dihedral energy corrections for only eight disorder-promoting residues (A, Q, G, P, R, K, S, E).^17–19 Although this resulted in improved IDP sampling, several inconsistencies with experimental observables arose due to the limited number of residues corrected.¹⁵ In 2017, Song et al.²⁰ extended their optimization of dihedral energy terms using grid-based energy correction maps^21–23 to all 20 amino acids resulting in the ff14IDPSFF force field. This new force field simulated chemical shift values in closer agreement with experimental values.²⁰

Thus, our first goal of this computational study of disordered proteins is to assess the quality of both the generic protein force field (ff14SB¹⁰) and its IDP-specific counterpart (ff14IDPSFF²⁰), However, it is notoriously difficult to obtain adequate conformational sampling for IDPs/IDRs due to the lack of one or few dominant conformations. Since microsecond timescales and multiple independent trajectories may be required, our second goal of this study is to assess the extent of sampling that is needed for quantitative structural annotation of IDPs/IDRs and to explore how to assess the sampling convergence. Here, nine short IDP peptides of the motif EGAAXAASS (X = D, E, Q, W, Y, P, L, H, K)^{24, 25} and the RNA-binding protein, HIV-1 Rev (Rev)^26–31 were chosen as test cases to assess the quality of MD simulations with the two Amber protein force fields. The EGAAXAASS short peptides were thoroughly characterized experimentally and were found to exhibit a combination of disordered behavior and local interactions between the 5X substituted residues and adjacent neutral alanine residues.^{24, 25} The longer and more complex Rev protein is a more challenging and realistic system for assessment of sampling techniques and accuracy of the tested force fields. Composed of highly charged residues (10 arginines out of 23 residues), the Rev protein is a vital component in the regulation of the HIV-1 replication cycle.^26–28 Despite its short sequence the Rev protein has been shown to adopt a diverse array of conformations (α-helices, disordered, beta) and simultaneously bind to target proteins or RNA-substrates with high affinity.^{27, 28, 32, 33} Once bound to its target, it was found to adopt a very stable conformation, providing a very interesting system to probe the binding-induced folding process.

By tackling issues of force field accuracy and sampling convergence, force field advancements in the realm of IDPs can be highly informative, revealing behaviors otherwise experimentally inaccessible or providing details potentially useful in guiding experimental studies. After careful analysis of the simulation sampling convergence and force field accuracy, we further analyzed the diverse conformational preferences of the Rev protein in both the apo and bound state to complete the computational analysis of this important protein.

2. METHODS

2.1. Force Fields Tested.

In this study, two Amber protein force fields (ff14SB and ff14IDPSFF) were tested to assess their quality in reproducing IDP structural properties. In the generic protein force field ff14SB,¹⁰ dihedral modifications and validation relied primarily on comparison to crystal structures exhibiting ordered secondary structures. To address the limitations of increased structured propensity propagated by the ff14SB force field, the IDP-specific force field ff14IDPSFF was developed to address the deficiency of generic protein force fields by modification of the main-chain dihedral terms.²⁰ The ff14IDPSFF force field is the most recently developed AMBER IDP-specific force field, improved upon from older versions.^{14, 15} Song et al.²⁰ provided the CMAP (grid-based energy correction map) parameters for ff14IDPSFF and a utility perl script to revise ff14SB-parameterized topology files into ff14IDPSFF topology files.

2.2. Molecular Dynamics Simulations.

The molecular dynamics package, Amber version 16, was used to generate all trajectories.^34–37 Nine short peptides with the sequence motif of EGAAXAASS (X = D, E, Q, W, Y, P, L, H, K) were tested in this study. All 9 peptides were built in the all-trans initial conformation using the Amber LEaP module, followed by minimization with the steepest descent and conjugate gradient methods, each 500 steps. Short peptides were then simulated in the GB implicit solvent for 10 ns (time steps of 1 fs) at 450K to generate 10 random conformations per peptide per force field (Table 1). The randomized initial structures were solvated with explicit TIP3P waters in a truncated octahedron box, with a buffer of 10 Å (Table 1). Neutralization was accomplished with the addition of either Na+ or Cl− ions depending on the total charge of a peptide. All solvated structures were minimized for 20,000 steps steepest descent, heated up for 20 ps in the NVT ensemble from 0K to 298K, and were equilibrated for 20 ps in the NPT ensemble at 298K. The CUDA-accelerated PMEMD^{36, 37} in Amber16 was then used to generate production trajectories in the NVT ensemble at 298K. The Langevin thermostat was used for all temperature regulation.

Table 1.

Summary of Simulation Setups

Short peptide	Citations BMRB, PDB	Force fields	Simulation number	Length per simulation	Ions	Waters
EGAADAAS	24	ff14SB	10	1 μs	1 Na+	1532-2178
S		ff14IDPSFF	10	1 μs	1 Na+	1465-2569
EGAAEAAS	24	ff14SB	10	1 μs	1 Na+	1628-2622
S		ff14IDPSFF	10	1 μs	1 Na+	1464-3151
EGAAQAAS	24	ff14SB	10	1 μs	1 Na+	1299-2752
S		ff14IDPSFF	10	1 μs	1 Na+	1520-3668
EGAAWAAS	24, 25	ff14SB	10	1 μs	0	1574-2637
S		ff14IDPSFF	10	1 μs	0	1876-3092
EGAAYAAS	24	ff14SB	10	1 μs	0	1804-2867
S		ff14IDPSFF	10	1 μs	0	1888-3141
EGAALAAS	24	ff14SB	10	1 μs	0	1373-3224
S		ff14IDPSFF	10	1 μs	0	1606-3131
EGAAPAAS	24	ff14SB	10	1 μs	0	1751-2713
S		ff14IDPSFF	10	1 μs	0	1693-2885
EGAAHAAS	24	ff14SB	10	1 μs	0	1498-2675
S		ff14IDPSFF	10	1 μs	0	1430-3159
EGAAKAAS	24	ff14SB	10	1 μs	1 Cl−	1733-2434
S		ff14IDPSFF	10	1 μs	1 Cl−	1633-2399
apo Rev (23 amino acids)	(ΔδCα),31	ff14SB	10/50	1 μs / 200 ns	9 Cl−	3727-11638
	(3JHNHα),31 BRMB:1885131	ff14IDPSFF	10/50	1 μs / 200 ns	9 Cl−	4424-13224
RRE - Rev complex	(ΔδCα),30, 38	ff14SB	5	200 ns	53 Na+ 29 Cl−	10928
	(3JHNHα),38 PDB:1ETF30	ff14IDPSFF	5	200 ns	53 Na+ 29 Cl−	10928

Force fields were also tested via simulation of a larger IDP, the HIV-1 apo Rev protein (apo Rev), by extracting the protein from its bound conformation in the crystal structure (PDB ID: 1ETF) as the initial conformation. MD preparation protocols (minimization, heating, etc.) were mostly identical to those for the nine peptides mentioned above, except that 60 random conformations per force field were generated in the GB implicit solvent. These conformations were used as the initial starting structures for two sampling strategies also outlined in Table 1: fifty 200ns simulations (short) and ten 1 μs simulations (long). Here we chose to simulate a total of 10 μs in the form of both short and long protocols to assess which strategy leads to faster convergence of tested NMR observables.

In addition to the apo Rev simulations, we also simulated the HIV-1 Rev protein bound to its RNA-binding partner Rev responsive element (RRE). Beginning with the full NMR solution structure (PDB: 1ETF), we repeated MD simulation protocol as mentioned previously, except that only five production trajectories of 200 ns each were collected.

2.3. Analyses of Simulations.

Post-simulation analysis incorporated a variety of software to extract observables for comparison with experiment. NMR observables – chemical shift and ³J_HNHα-coupling values – were calculated to validate the performance of both tested force fields and assess the quality of MD sampling. The Amber module, cpptraj,³⁹ was used to remove solvent for subsequent frame-by-frame processing and analysis. All chemical shift values were calculated using the SPARTA+ package.^{40 3}J_HNHα-coupling constants were calculated using the Karplus equation that was programmed with the MDTraj python library⁴¹ and coefficients from literature.⁴² Experimental values (Figures 10C-D, 11B) were extracted from published figures in respective papers if raw data were not available from the authors (Table 1).

Figure 10.

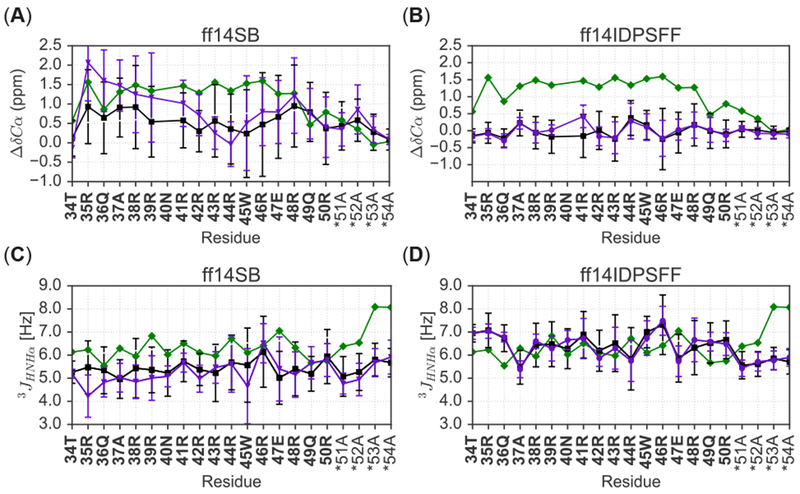
Comparison of force field and simulation types of apo Rev to experimental results. Colors are labeled according to experiment (green), short simulations (black), and long simulations (purple) and an asterisk (*) denotes non-native residues. (A) Comparison of short and long ff14SB-derived secondary chemical shifts with experiment.³¹ (B) Comparison of short and long ff14IDPSFF-derived secondary chemical shifts to experiment.³¹ (C) Comparison of short and long ff14SB-derived J-coupling constants with experiment.³¹ (D) Comparison of short and long ff14IDPSFF-derived J-coupling constants with experiment.³¹

Figure 11.

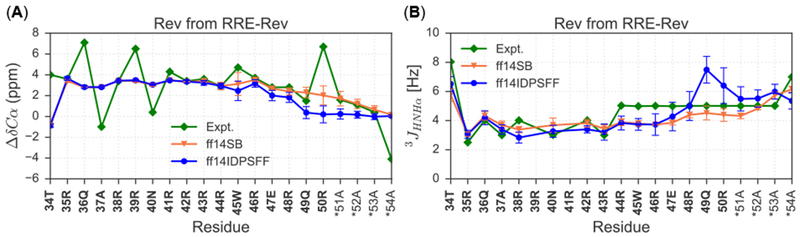
Simulated NMR observables are superimposed with experimental NMR values of Rev bound to the Stem IIB of RNA-binding partner, Rev-response element. Bold residues indicate native residues and asterisk (*) denotes non-native residues. (A) Comparison of experimental^{30, 38} and average simulated ΔδC^αvalues. (B) Comparison of experimental³⁸ and average simulated ³J_HNHα-coupling constants.

Time-dependent cumulative averages of both NMR observables were calculated for convergence assessment. From these cumulative average calculations, the rate of change per NMR observable (ΔNMR Observable) was calculated to assess its rate of convergence. Rate of change datasets were fitted to a biphasic exponential-decay model:

$$\Delta NMRObservable=A_1{e}^{-\frac{x}{{\tau }_1}}+A_2{e}^{-\frac{x}{{\tau }_2}}+c$$

Of the fitted parameters, the slower τ₂ values were calculated and utilized to assess the rate of convergence of the observable. Kernel density estimations (KDEs) were used to analyze the detailed distribution of each predicted observable per frame. KDE’s were calculated using the python packages Scikit-Learn and Seaborn.^{43, 44} Epanechnikov kernels were adopted with appropriate bandwidths (h=0.5) in KDEs.⁴⁵ Initial bandwidths were determined using Scikit-Learn’s grid search and cross validation function (GridSearchCV) (h=0.1) and further rescaled to h=0.5 as it yields comparable distributions with less noise.

Secondary structure propensity estimates were calculated using the DSSP program.⁴⁶ Prior to clustering, frames were pre-sorted using DSSP secondary structure assignments. Since DSSP default settings assign residues with three basic secondary structure assignments – H (α-helix, 3₁₀-helix, π-helix), E (beta ladder, isolated beta-bridge residues), C (hydrogen bond turn, bend, loops, irregular residues) – frames were first grouped into the following categories if they contained at least one of the 3 assignments: H only, E only, C only, EH only, CH only, CE only, CEH only. Frames for all simulations fell into only four of the categories: C only, CH only, CE only, and CEH only. Clustering was then restricted to a single secondary structure category (e.g. C only). This pre-clustering assortment permits filtering based on secondary structure and increases accuracy in the clustering step.

After pre-clustering, ϕ and φ torsion angles were extracted from trajectories with the MDTraj⁴¹ module as input in our clustering methodology. Torsional data was then subjected to PCA dimensionality reduction with settings specified to retain 99% of variation in torsion angle data. Clustering was performed by generating gaussian mixture models (GMM)⁴⁷ for each secondary structure category (e.g. C only), in which each frame was clustered depending on its likelihood of occupying a specific component/cluster. GMMs consist of a mixture of multidimensional gaussian probability distributions from which the number of components/mixtures (number of “clusters”) can be estimated using cross-validation techniques such as Bayesian information criterion (BIC).⁴⁸ The lowest BIC value was used to estimate the appropriate number of mixtures for each GMM model (Figure S14). GMMs were created using the Scikit-Learn⁴⁴ python module and implemented using the expectation-maximization algorithm⁴⁹ to fit and achieve converged mixtures/clusters.

In RRE-bound Rev (RRE-Rev) simulations, the snapshot closest to the average was used as a representative of the average structure and implemented using cpptraj.³⁹ Hydrogen bond occupancies were calculated using the Baker-Hubbard⁵⁰ criteria from the MDTraj⁴¹ python module and ionic salt bridge interactions were determined with a strict distance criterion⁵¹ (4Å) between centers of charged groups (positively charged atoms from residues Arg and Lys: NH*, NZ*; negatively charged atoms: OP* phosphate backbone atoms in the RNA-binding partner RRE). Pymol was used to generate the representative structural image and TOC image.

3. RESULTS AND DISCUSSION

Nine short peptides, EGAAXAASS (X = D, E, H, K, L, P, Q, W, Y) and the structurally dynamic apo Rev protein from type-1 HIV were simulated to illustrate the issues that must be addressed in computational studies of IDPs, namely both the accuracy of force fields and convergence of sampling. In the following, the convergence issue of the sampling is addressed before studying the quality of the two selected force fields in reproducing NMR observables. Finally, the structural characteristics of both disordered and ordered apo Rev protein are discussed based on the expansive MD simulations in explicit solvent.

3.1. Convergence Analysis.

Previous studies of IDPs relied on backbone RMSD analysis and/or clustering of MD trajectories within hundred nanosecond timescales to confirm proper sampling and convergence of IDPs.^{20, 31} In this study, we relied on direct analysis of time-dependent cumulative averages of specific NMR observables, a reasonable technique to investigate the convergence of simulated observables.

We analyzed time-dependent cumulative averages (Figure S1–S5) of simulated secondary chemical shifts and ³J_HNHα-coupling constants to estimate the time scales at which the rates of change of the observables go to zero, an indication that convergence is achieved. A convergence decay was fitted to a biphasic exponential decay model ($\Delta NMRObservable=A_1{e}^{-\frac{x}{{\tau }_1}}+A_2{e}^{-\frac{x}{{\tau }_2}}+c$) thereby allowing for the determination of τ₂. Here, the parameter generated from the first rapid decay phase, τ₁ is discarded. The implementation of this technique allows us to quantitatively assess and compare the convergence rates of tested systems and sampling protocols.

Short Peptides.

Table 2 summarizes the average τ₂ values – derived from simulated ΔδC^α – of the 9 short peptides. These values are further represented in boxplots detailing their ranges, medians, and lower/upper quartiles (Figure 1). Detailed fitting plots for all residues and simulation types are shown in the SI file (Figure S6–S7). Calculated average τ₂ values of EGAAXAASS simulations reveal a stark contrast between ff14SB- and ff14IDPSFF-generated simulated ΔδC^α values, with ff14IDPSFF exhibiting lower values than the generic ff14SB force field, except the Q-substituted simulations, whose τ₂ values are quite similar between the two. The analysis suggests ff14IDPSFF simulations converge mostly faster than the ff14SB simulations for the chemical shifts monitored (Figure 1).

Table 2.

Average τ₂ Values ΔδC^α and ³J_HNHα-coupling constants) of 9-Residue EGAAXAASS with Standard Deviations (SDs)

Protein	Avg. τ2 ± SD from ΔδCα (ns)		Avg. τ2 ± SD from 3JHNHα (ns)
	ff14SB	ff14IDPSFF	ff14SB	ff14IDPSFF
EGAADAASS	705 ± 134	221 ± 22	679 ± 242	761 ± 187
EGAAEAASS	389 ± 63	195 ± 25	639 ± 179	715 ± 179
EGAAHAASS	561 ± 104	508 ± 107	686 ± 193	786 ± 279
EGAAKAASS	412 ± 68	163 ± 21	570 ± 130	685 ± 183
EGAALAASS	307 ± 50	239 ± 36	692 ± 163	710 ± 185
EGAAPAASS	247 ± 31	270 ± 40	716 ± 205	581 ± 181
EGAAQAASS	435 ± 68	437 ± 74	747 ± 225	689 ± 154
EGAAWAASS	423 ± 60	343 ± 40	631 ± 113	525 ± 136
EGAAYAASS	511 ± 93	480 ± 77	641 ± 173	687 ± 250

Figure 1.

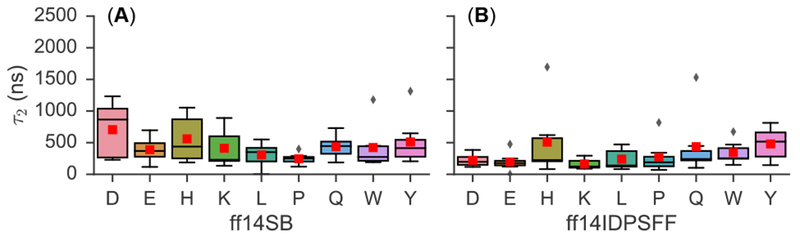
Summary of τ₂ values (medians, ranges, quartiles, outliers) for peptides of EGAAXAASS (X=D, E, H, K, L, P, Q, W, Y), derived from ΔΔδC^α calculations. Simulations are labeled by peptide and force field: (A) ff14SB and (B) ff14IDPSFF. Diamonds indicate outliers and a red box denotes the average τ₂ value. Fitted plots from which boxplots were derived can be found in the SI (Figure S6–S7).

Next, we repeated the above biphasic exponential fitting to cumulative averages of a second simulated NMR observable – ³J_HNHα-coupling constants (Figure S10–S11). Overall, the range of calculated τ₂ values is narrow and comparable between both force fields (Figure 2). Upon closer inspection, the average τ₂ (indicated by red boxes) is generally higher in ff14IDPSFF simulations than those in ff14IDPSFF simulations, different from the chemical shift analysis. Interestingly, the final ³J_HNHα-coupling constants are comparable between the two force fields, as the average values are within standard deviations. Peptides substituted with P, Q, or W in ff14IDPSFF simulations, exhibit lower τ₂ values in comparison to other substituted short peptides, suggesting possible conformational preferences leading to increased convergence rate. Comparison of the τ₂ values for the two NMR observables suggests that J-coupling constants in general converge slower than secondary chemical shifts in our simulations, as shown in Figures 1–2 and Table 2. Nevertheless, both sets of simulations are believed to be converged as far as both NMR observables are concerned, as the τ₂ values are much shorter than the cumulative simulation time scales sampled.

Figure 2.

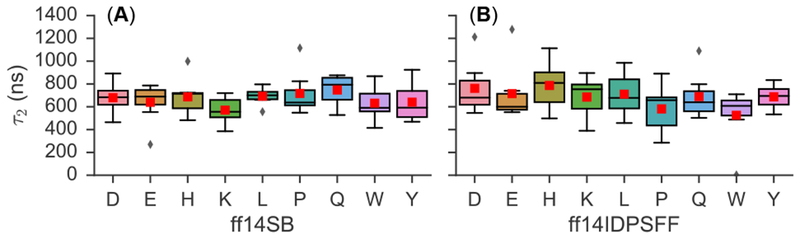
Summarization of τ₂ values (median, range, quartiles, outliers) for peptides of EGAAXAASS (X=DEHKLPQWY), derived from ³J_HNHα-coupling constants. Diamonds indicate outliers and a red box denotes the average τ₂ value. Fitted plots from which boxplots were derived can be found in the SI (Figure S10–S11).

Apo Rev and RRE-Rev.

We extended the convergence analysis of the two tested force fields for the simulations of both apo and bound Rev. Biphasic exponential decay models were fitted (Figure S8–S9, S12–S13) as outlined in the Short Peptides subsection, using cumulative averages (Figure S3–S5) of simulated secondary Cα chemical shifts and ³J_HNHα-coupling constants. A summary of τ₂ values for apo Rev in Table 3 reveals a consistent pattern in comparison to the short peptides: the τ₂ values for ΔδC^α in ff14IDPSFF simulations are lower than those in ff14SB simulations and the τ₂ values of ³J_HNHα-coupling constants in ff14IDPSFF simulations are higher than those in ff14SB simulations.

Table 3.

Average τ₂ Values (ΔδC^α and ³J_HNHα-coupling constants) of apo Rev and RRE-Rev with SDs

Protein	Avg. τ2 ± SD from ΔδCα (ns)		Avg. τ2 ± SD from 3JHNHα (ns)
	ff14SB	ff14IDPSFF	ff14SB	ff14IDPSFF
Apo Rev (1 μs × 10)	445 ± 75	396 ± 70	642 ± 166	710 ± 209
Apo Rev (200 ns × 50)	119 ± 73	115 ± 58	422 ± 71	451 ± 67
RRE-Rev (200 ns × 5)	21.8 ± 1.6	24.0 ± 2.3	3.4 ± 0.3	3.6 ± 0.3

We also explored the convergence behavior of different simulation protocols in the simulations of apo Rev. Since the duration of MD simulations can significantly impact the conformational sampling, a total of 10 microseconds of MD simulation with both short (200 ns × 50) and long (1 μs × 10) protocols was generated for comparative analysis. Initial, qualitative inspection of cumulative averages (Figure S3–S4) of simulated NMR observables reveals higher fluctuations in the long protocol. Different observations in the short and long protocols suggest the two probably converged to different conformational minima, though it is clear via inspection of cumulative averages (Figure S3–S4) that the short protocol transitioned to their minima faster.

Cumulative averages were then fitted as biphasic exponential decay models (Figure S8, S12, summary of fitted τ₂ in Table 3 and Figure 3). Table 3 and Figure 3 clearly show that both NMR observables converge faster in the short protocol. This is consistent with the initial qualitative inspection of apo Rev cumulative averages (Figure S3–S4), where it appears that the short protocol produces overall better convergence trends in all cases. The τ₂ values are also consistently distributed within narrower ranges (aka smaller SDs) in the short protocol, indicating consistent convergence of simulated NMR observables. In contrast the distributions of τ₂ values from the long protocol strongly depend on force fields and observables analyzed.

Figure 3.

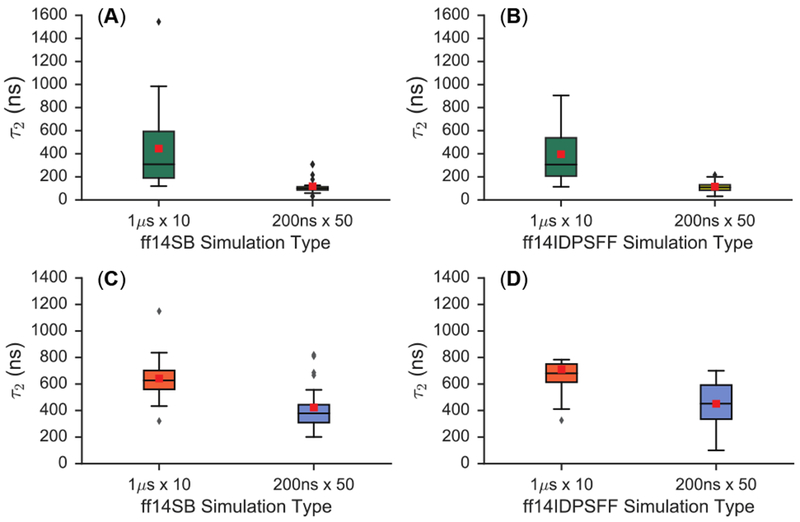
Summarization of τ₂ values derived from cumulative averages of ΔδC^α and ³J_HNHα-coupling constants for apo Rev. Boxplots depict median, range, quartiles, outliers, and averages (red box). (A) Details only ff14SB-parameterized simulations of ΔδC^α-derived τ₂ values. (B) Details only ff14IDPSFF-parameterized simulations of ΔδC^α-derived τ₂ values. (C) Only ff14SB-parameterized simulations of ³J_HNHα-coupling-derived τ₂ values are shown. (D) Details only ff14IDPSFF-parameterized simulations of ³J_HNHα-coupling-derived τ₂ values.

Finally, convergence rates for RRE-Rev simulations in Table 3 also indicate comparable convergence between ff14SB and ff14IDPSFF simulations, although ³J_HNHα-coupling-derived τ₂ values are much smaller than ΔδC^α-derived τ₂, apparently due to the much more stable Rev in the bound state. Overall the convergence rate analysis shows that it is important to monitor individual observables for their convergence trends.

3.2. Distributions of Simulated Observables.

We implemented the kernel density estimation (KDE) method to determine the probability density distributions of simulated NMR observables. There are two purposes in conducting this analysis. First, it provides a more detailed view of simulated observables. Second, it provides a means to cross-validate, in more detail, the different simulation protocols used in the simulations of the more challenging apo Rev.

Short Peptides.

Figure 4 shows KDE analyses for Cα secondary chemical shifts. The distribution in Figure 4 shows that ff14SB conformations (first/third columns) are concentrated into multiple peaks in regions characteristic of helices (3 α 1 ppm) and random coil (~0 ppm).⁵² As an example, peptide EGAADAASS (ff14SB) exhibits multiple peaks, and a higher concentration of positive secondary Cα chemical shifts. In contrast, the ff14IDPSFF distributions (second/fourth columns) are overall narrower, more symmetrical, and more Gaussian-like centered around 0 ppm, suggesting more uniform disordered structures in the ensemble (Figure 4).

Figure 4.

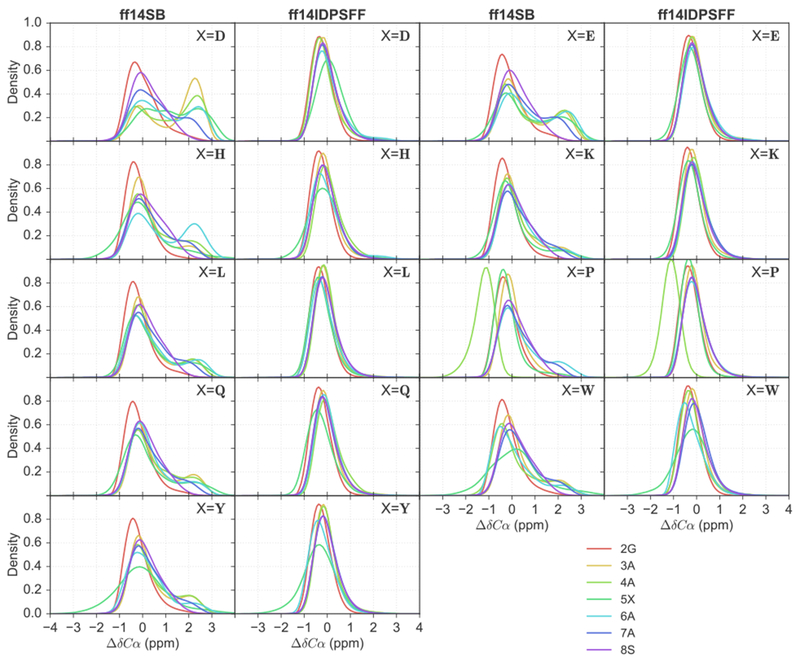
Kernel density estimations (KDEs) of secondary Cα chemical shift values for 9 short peptides of EGAAXAASS (X = D, E, H, K, L, P, Q, W, Y) and residues 2-8. Residues are colored as indicated in the legend.

KDEs of ³J_HNHα-coupling scalar coupling constants are shown in Figure 5. Scalar ³J_HNHα-coupling constants for helical structures typically average 4.2–5.6 Hz, beta sheet conformations average 8.5–10 Hz, and random coil average 5.9–7.7 Hz.⁵³ In Figure 5, a significant proportion of residues display peaks within the helical region, from both force fields. However, distributions in ff14SB simulations display higher densities characteristic of helices than those in the ff14IDSPFF simulations for most peptides. A high concentration of peaks can also be observed in the 8.5–10 Hz range typical of beta conformations in the ff14IDPSFF simulations. However only a small fraction of conformations are within values characteristic of beta conformations in the ff14SB simulations. We supplemented the NMR observables with a more detailed secondary structure analysis based on the DSSP⁴⁶ program. The DSSP data shows, however, that beta secondary structure is nonexistent in both simulations (Figure S17). The discrepancy is not a surprise given that the ³J_HNHα-coupling constant calculation only considers the main-chain torsion angles while DSSP considers a range of different structural and energetic properties.

Figure 5.

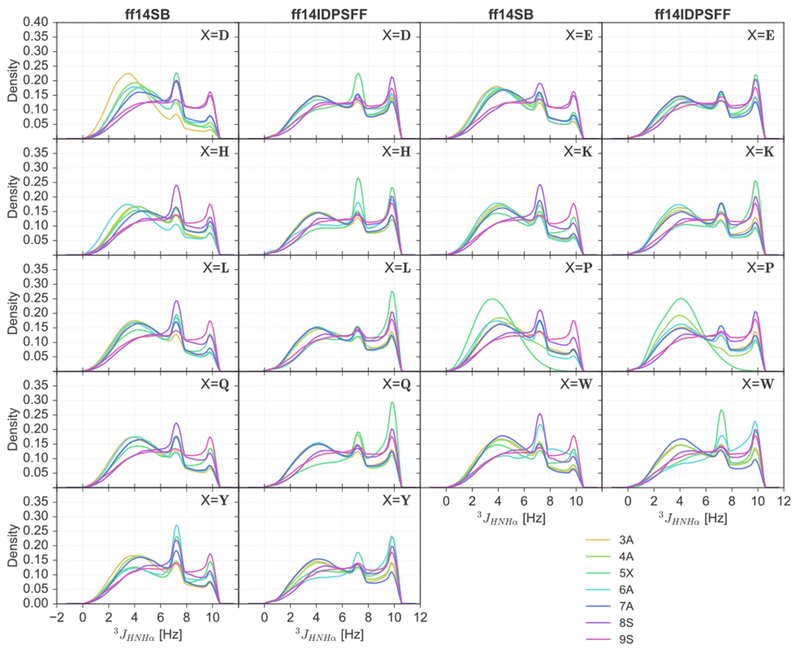
KDEs of ³J_HNHα-coupling constants for 9 short peptides of EGAAXAASS (X = D, E, H, K, L, P, Q, W, Y) and residues 3-9.

Apo Rev.

Apo Rev simulations also display similar distributions described above – increased peak densities in the helical region in the ff14SB simulations compared to the ff14IDPSFF simulations. Juxtaposition of the two distributions displays an overall heterogeneous distribution in the ff14SB force field, with peaks in ranges typical of helical character (3 α 1 ppm) (Figure 6A-B). The long-protocol simulations contain higher density peaks in the 3 ± 1 ppm range, indicating that more conformations contain helical content compared to the short-protocol simulations (Figure 6B). This increased helicity observed in long ff14SB simulations suggests the impact of timescales (short vs. long) is more apparent in ff14SB simulations than ff14IDPSFF simulations. In the ff14IDPSFF simulations, both timescale types produce almost identical homogenous distributions centered ~0 ppm (Figure 6C-D).

Figure 6.

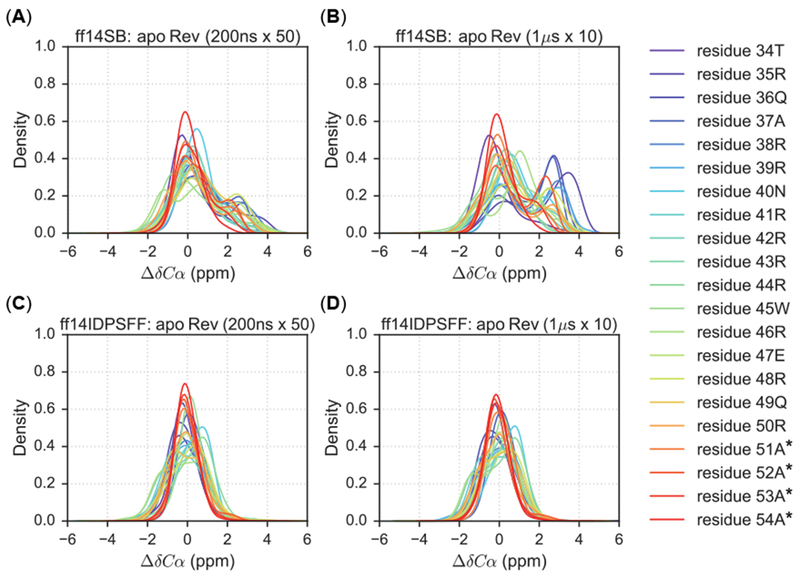
KDEs of secondary Cα chemical shift values for 1 μs × 10 (long) simulations and 200ns × 50 (short) simulations. Residues are colored according to the legend and simulations are plotted according to the following combination of force field and timescale types: (A) Short simulations using the ff14SB force field. (B) Long simulations using the ff14SB force field. (C) Short simulations using the ff14IDPSFF force field. (D) Long simulations using the ff14IDPSFF force field. Asterisks (*) indicate non-native residues.

The KDE analysis was also conducted for simulated ³J_HNHα-coupling constants. In all simulations, we observed three general regions in the KDE distributions: helical region (average 4.2–5.6 Hz), beta region (average 8.5–10 Hz), and disordered/coiled region (average values 5.9-7.7 Hz).⁵³ Similar observation was also noted in experimental findings.³¹ Both force fields and simulation protocols exhibit similar peaks in the helical region (broad with densities less than 0.2), but differ in the following: 1) ff14SB simulations peaks contain higher densities, indicating more helical content than both ff14IDPSFF simulations; and 2) the long-protocol ff14SB simulations peaks are more left-shifted indicating increased helicity than its short protocol counterpart (Figure 7A–7B). In the disordered region: 1) the ff14SB simulations exhibit less disordered secondary structures as density peaks are lower than the ff14IDPSFF simulations; and 2) the peaks are similar between short and long-protocol simulations when apo Rev is modeled with ff14IDPSFF, In the beta region, density peaks in the ff14SB simulations are in general lower than those in the ff14IDPSFF simulations.

Figure 7.

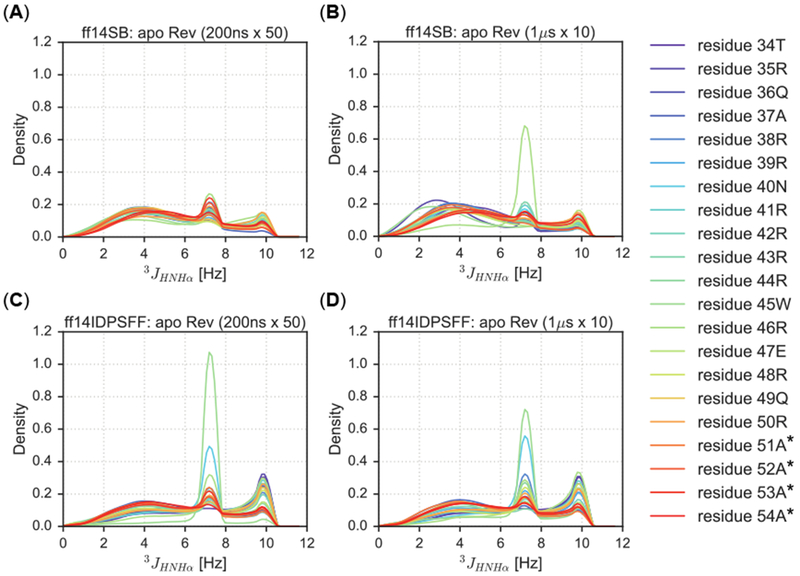
KDEs of ³J_HNHα-coupling constants of short (200 ns × 50) and long (1μs × 10) simulations types. Residues are colored according to the legend and simulations are plotted according to the following combination of force field and timescale types: (A) Short simulations using the ff14SB force field. (B) Long simulations using the ff14SB force field. (C) Short simulations using the ff14IDPSFF force field. (D) Long simulations using the ff14IDPSFF force field. Asterisks (*) indicate non-native residues.

Several observations, however, are contradictory to those in the chemical-shift KDE analysis. A single peak representing residue 46R is the only density peak > 0.6 in the ff14SB simulations (long protocol), while all other peaks are ~0.2 density within Figure 7B. The beta region is also more readily populated with high densities in the ³J_HNHα-coupling, distributions for all simulations whereas minimal densities were observed in the beta region (−1.48 ± 1.23 ppm)⁵² in the ΔδC^α distributions for the ff14IDPSFF simulations (Figure 6 and 7). This discrepancy might result from our uses of the ³J_HNHα-coupling constants to infer secondary structures as discussed in the Short Peptide analysis.

KDE distribution analysis of simulated NMR observables is also a useful assessment of convergence quality, supplementing the convergence rate analysis in section 3.1. The distribution data show that the ff14SB force field is more sensitive to simulation protocols than ff14IDPSFF. Consistently converged distributions in the ff14IDPSFF simulations allow us to use the convergence rates obtained in section 3.1 to compare which protocol is better. However, the rate estimations (Table 3 and Figure 3A–3B) show that the convergence rates between the two are quite similar, within 200 ns in general, though it is clear that the short protocol converges faster than the long protocol. For ff14SB simulations, the different distributions presented here give us pause to claim that the sampling of the apo Rev is sufficient in either protocol even if 10 microseconds worth of sampling has been collected (Figure 6). This indicates that enhanced sampling techniques would greatly benefit IDP simulations for systems as small as 23 amino acids such as apo Rev.

3.3. Comparison of Simulated and Measured NMR Observables.

Short Peptides.

We next calculated the final averages of secondary Cα chemical shifts for both sets of simulations and compared with experimental values (Figures 8). Figure 8 shows that experimental chemical shifts^{24, 25} of the 5X-substituted residues often result in a more negative ppm shift. This suggests that the 5X-substituted residues are more disordered/extended than their adjacent residues.⁵² This trend can be reproduced by both force fields, with the exception of the 5W-substituted simulations (Figure 8). In 5P-substituted simulation simulations, the proline residue is expected to rigidify and increase overall order in the peptide.^{24, 54} Both sets of simulations agree well with experiment, replicating the expected −2 ppm shift observed for residue 4A, with ff14DIPSFF generating a slightly more negative shift (Figure 8). In simulations of aromatic-substituted residues (5X = W, Y), both force fields also replicate a similar observation by Dames et. al,²⁴ a negative −0.3 ppm shift in residue 6A. Overall, the agreement between simulation and experiment is summarized in Table 4, which shows improved performance of ff14IDPSFF over its generic counterpart ff14SB in modeling the tested peptides (Table 4, Figure 8).

Figure 8.

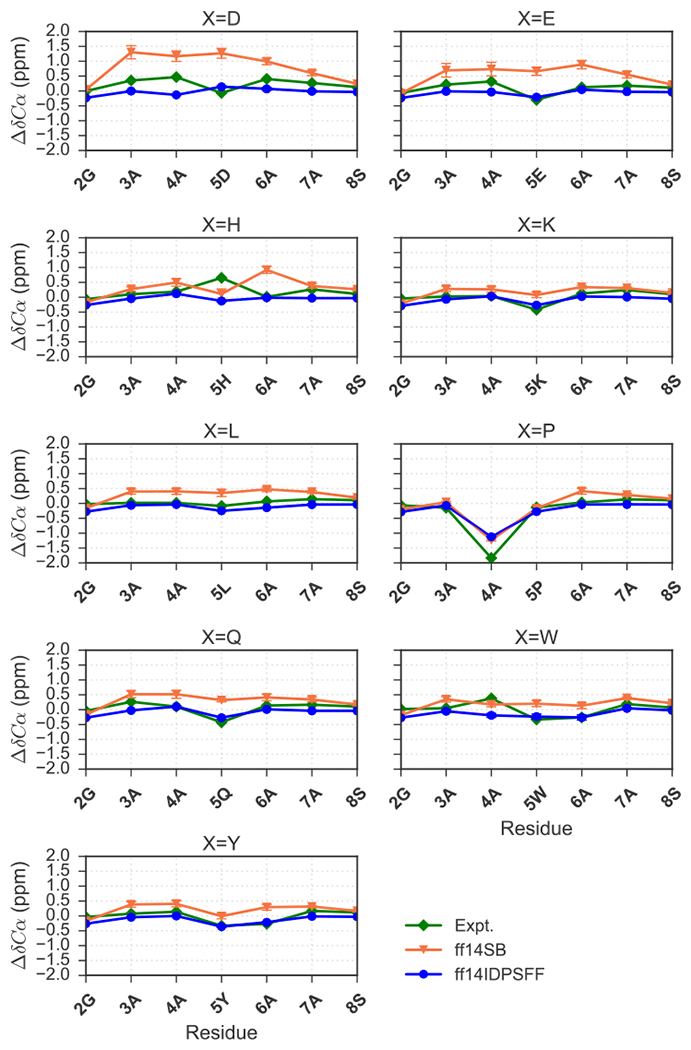
Comparison of experimental^{24, 25} secondary Cα chemical shift values and simulated chemical shifts for the 9 short peptides (EGAAXAASS, X = D, E, H, K, L, P, Q, W, Y). Experimental and simulated values are colored as indicated in the legend. Standard deviation error bars are also visible for simulated values.

Table 4.

RMSE of Calculated Cα Chemical Shifts and ³J_HNHα-coupling Constants with Respect to Experimental Values

Protein	ΔδCα RMSE (ppm)		3JHNHα-coupling RMSE (Hz)
	ff14SB	ff14IDPSFF	ff14SB	ff14IDPSFF
EGAADAASS	0.72	0.34	0.95	0.42
EGAAEAASS	0.54	0.20	1.01	0.61
EGAAHAASS	0.43	0.33	1.01	0.56
EGAAKAASS	0.25	0.16	0.53	0.36
EGAALAASS	0.32	0.17	0.61	0.50
EGAAPAASS	0.29	0.30	0.79	0.67
EGAAQAASS	0.36	0.18	0.88	0.57
EGAAWAASS	0.31	0.26	0.65	0.44
EGAAYAASS	0.30	0.14	0.76	0.66
Apo Rev (1 μs × 10)	0.64	1.16	1.34	1.03
Apo Rev (200 ns × 50)	0.68	1.19	1.17	1.02
RRE-Rev (200 ns × 5)	2.35	2.62	0.90	1.08

We also compared simulated ³J_HNHα-coupling, constants to experimental values for these disordered peptides in Figure 9. Table 4 presents corresponding root mean square errors (RMSEs) with respect to experiment, indicating overall better agreement between experimental and ff14IDPSFF-simulated values (Table 4, Figure 9). In summary, both simulated chemical shifts and J-coupling constants demonstrates that the ff14IDPSFF simulations can better reproduce the two tested NMR observables than the ff14SB simulations in these short peptides.

Figure 9.

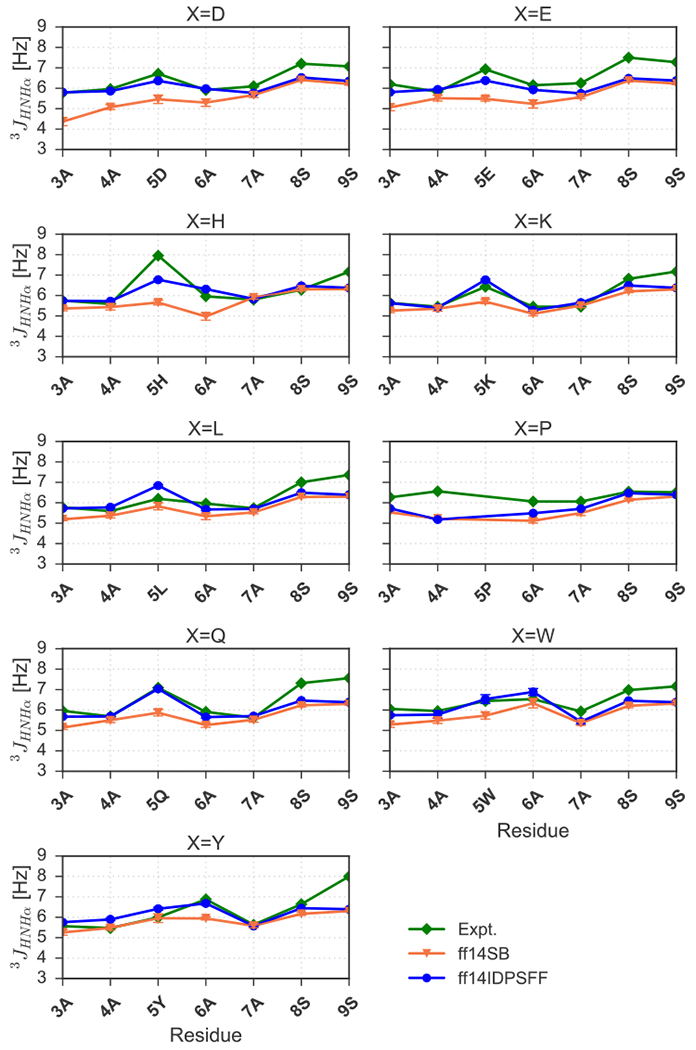
Calculated ff14IDSPFF- and ff14SB-parameterized ³J_HNHα-coupling constants compared to experimentally-derived^{24, 25} constants. Experimental and simulated values are colored as indicated in the legend. Standard deviation error bars are also visible for simulated values.

Apo Rev.

In simulations of the more complex apo Rev, simulated secondary chemical shifts do not agree with experiment as well as those in the tested short peptides. For ff14SB simulations, short (200 ns × 50) and long (1 μs × 10) protocols overall agree with each other but not in the N-terminal portion (residues 35 to 41) (Figure 10A). Overall the long protocol agrees a bit better with experiment (Table 4). Experimental values occupy mostly positive secondary chemical shifts, indicating possible residual helical secondary structure in apo Rev and this is reproduced well in the ff14SB simulations. It is also worth noting experimental secondary chemical shifts are still within reasonable values typical of random coil, < 2 ppm. For ff14IDPSFF simulations, both short and long protocols produce nearly identical secondary chemical shift values (Figure 10B), lending support that the simulated observables converged very well. However, the agreement with experiment is not as good as the ff14SB simulations (Figure 10B and Table 4). Specifically, the ff14IDPSFF simulations may overestimate disordered structures in apo Rev.

Interestingly worse agreement is apparent between ff14SB-simulated ³J_HNHα-coupling constants and experimental values (Figure 10C). Overall higher helical propensity is visible in the ff14SB simulations (average 4.2–5.6 Hz) versus higher disordered propensity (average 5.9–7.7 Hz) in the experiment (Figure 10C). Notably, ff14IDPSFF simulations agree closer to experiment in this regard with ³J_HNHα-coupling constants in the similar range as in the experiment. Nevertheless, both experimental and simulated ³J_HNHα-coupling constants are still within reasonable range of disordered secondary structure. These ambiguous, sometimes overlapping secondary structure boundaries used in NMR experiments highlight the difficulty in definitively assigning secondary structures based on either chemical shifts and ³J_HNHα-coupling constants. Multiple, independent CD experiments, however, suggest the conformational landscape of apo Rev is more populated as disordered than helical.^{26, 30, 31, 55} In summary, the ff14IDPSFF simulations agree surprisingly well with both NMR and CD experiments with disordered structures dominant in its simulations of apo Rev. These observations will be highly useful in further refining IDP-specific force fields to improve simulation of complex, dynamic IDPs such as apo Rev.

RRE-Rev.

Since the Rev protein is known to sustain a helical structure upon binding to its RNA-binding partner, Stem IIB of Rev response element (RRE), we also simulated the RRE-Rev complex (PDB: IETF) and compared to the apo Rev simulations. Experimental ΔδC^α and ³J_HNHα-coupling constant datasets were extracted from two separate literature sources and each source used different non-native residues in the N-terminal portion of otherwise identical Rev peptides.^{30, 31, 38} The ³J_HNHα-coupling dataset³¹ was generated from a Rev peptide containing a 4-residue non-native extension (GAMA) at the N-terminus, while the ΔδC^α dataset³⁸ resulted from a Rev peptide containing a non-native, N-terminal residue Asp. The GAMA sequence was a byproduct leftover from His6-GB1 tag, and the Asp non-native sequence was used as an alternative to a synthetic N-terminal sequence from earlier experiments. Although we chose to simulate Rev bound to RRE with the N-terminal Asp from the literature,³⁸ the remaining 22 residues are identical between Rev peptides used in both experiments. Nevertheless experimental data show that both sequences from literature^{30, 31, 38} exhibited RNA-binding specificity/activity in addition to disordered secondary structure in the apo state.

Although experimental chemical shifts fluctuate significantly, simulated values are stable and almost identical between the two force fields except terminal residues 49–52 (Figure 11). Both C-terminal experimental and simulated values seem to be decreasing to ranges characteristic of random coil (Figure 11). In analyses of ³J_HNHα-coupling constants, experimental values and ff14SB-simulated values occupy typically helical ranges (< 5.6 Hz), whereas ff14IDPSFF-simulated values are almost identical to both ff14SB and experimental values until residue 49Q (Figure 11). The comparison shows that the beta-forming tendency is too strong for 49Q in the ff14IDPSFF simulations of the bound Rev (Figure 11B). Similar tendency is also noticeable in the ff14IDPSFF simulations of the apo Rev (Figure 10D) where the ³J_HNHα-coupling constant is also overestimated for 49Q. This suggests further refinement is clearly required in the development of IDP force fields. RMSE differences between simulated NMR observables and experimental values are also rather close (Table 4), though the chemical shift agreement is not as good as those for the apo Rev simulations. This is probably because RRE was not considered in the conversion from MD conformations to chemical shifts by the SPARTA+ package.⁴⁰ Overall both ff14SB and ff14IDPSFF are adequate in the RRE-Rev simulations, with accuracy in predicted NMR observables comparable to that obtained for the NMR structure (RMSE of 2.50 ppm for ΔδC^α and RMSE of 1.86 Hz for ³J_HNHα-coupling constants).

3.4. Structural Signatures of Apo Rev Disordered State.

Despite the extensive investigation of the Rev protein, as evidenced by 1647 hits from a general Pubmed search, this highly dynamic protein only occupies a monomeric state at submicromolar concentrations,⁵⁶ thus remaining elusive to structural characterization. Previous pursuits to structurally characterize the apo form of Rev encountered difficulties ranging from protein solubility to oligomerization, preventing characterization of apo Rev in physiological conditions.⁵⁷ Early circular dichroism (CD) and mutagenesis experiments suggest that apo Rev is disordered, forming helical structure depending on terminal amino acids (e.g. amidated C-terminus, C-terminal extension AAAR).²⁹ Overall, attempts to characterize monomeric apo Rev have required techniques to induce ordered structure propensity, such as specific helix-inducing solution buffers (e.g. 2,2,2-trifluoroethanol), residue mutations to prevent oligomerization, or the introduction of structure-inducing binding partners.^29,58 MD simulations thus provide a useful tool to probe the highly mobile conformations of Rev in its physiological disordered state. In previous structural modeling studies and MD simulations from Song et. al²⁰ and Casu et. al³¹, researchers observed primarily coiled secondary structure of apo Rev. These simulations however simulate apo Rev in nanosecond timescales. Herein we generated tens of microseconds trajectories to ensure proper sampling of disordered apo Rev conformations.

Clustering and secondary structure propensity calculations are discussed hereafter, highlighting the differences between the ff14SB and ff14IDPSFF simulations (in the long protocol). Although both ff14SB and ff14IDPSFF simulations exhibit ordered and disordered characteristics, the two force fields differ in secondary structure preferences: increased helical content observations in the generic ff14SB simulations (Figure 12), disordered structural preferences in the ff14IDPSFF simulations (Figure 13). The top ten clusters between both force fields occupy similar percentages: ff14SB at 17.87% versus ff14IDPSFF at 17.41%. Further evidence from DSSP⁴⁶ (hydrogen bond estimation algorithm) calculations also suggests the majority of ff14IDPSFF conformations exhibit coiled secondary structure, in Figure S18. All residues in ff14IDPSFF simulations exhibit roughly equal probabilities of coiled secondary structure (average > 80%) in addition to some beta contents (Figure S18B-C, S19B-C). DSSP (Figures S18–S19) and clustering results (Figures S15–S16) of the short protocol simulations are also provided in the supplementary information although simulations from the long protocol are the primary focus in this section. Experimental findings ranging from secondary chemical shift, ³J_HNHα-coupling, and CD suggests apo Rev is mainly disordered when unbound.³¹ Despite the observation that both force fields replicate the average coiled secondary structure as in experiment, these clustering analyses show that each force field exhibits either disordered or ordered structural bias – observations that will be useful in future refinement of IDP-specific force fields.

Figure 12.

Top 10 clusters of ff14SB-parameterized simulations encompass 17.87% of all frames. Clusters are labeled C1-C10 and colored according to N- to C-termini sequence (red to blue).

Figure 13.

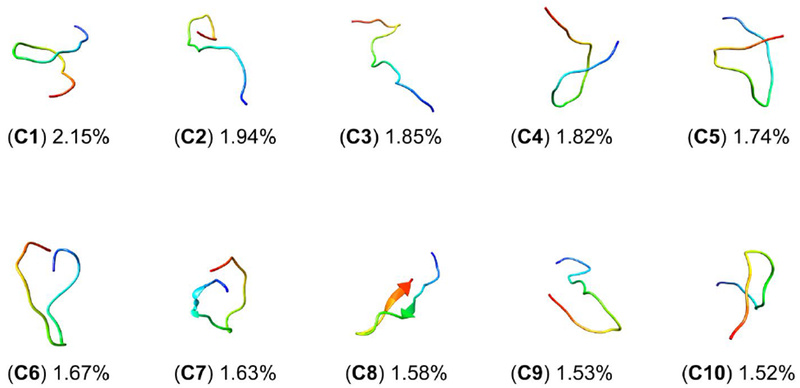
Top 10 clusters of ff14IDPSFF-parameterized simulations encompass 17.41% of all frames. Clusters are labeled C1-C10 and colored according to N- to C-termini sequence (red to blue).

3.5. Conformational Analysis of Bound Rev Ordered State.

To supplement our apo Rev simulations above, we also simulated Rev bound to its RNA binding partner, RRE Stem IIB, to assess how our simulations perform in replicating experimentally-observed behaviors such as induced fit.^{56, 59} Previous studies emphasize induced fit and proper RRE binding requires the presence of a single Rev monomer, from which more Rev monomers are recruited and oligomerize.⁵⁶ The NMR solution structure depicts an α-helical Rev situated in the major groove of RRE-Stem IIB.³⁸ After simulating this complex, we proceeded to align the Rev peptide from the NMR solution structure (PDB: IETF) to the average Rev structure extracted from RRE-Rev simulations (Figure 14). Simulations of Rev bound to RRE yield significantly more stabilized conformations compared to apo simulations. In the ff14SB simulations, we observed almost entirely helical content (Figure 14). In ff14IDPSFF force field simulations, helical secondary structure was observed in N-terminal residues, whereas coiled, disordered structure was observed in C-terminal residues (Figure 14). We also estimated the average secondary structure propensities of each residue for all simulations using the DSSP algorithm (Figure S20). Despite some fluctuation in the last 4–5 C-terminal residues, most residues remain fairly stable, retaining the characteristic helical conformation found in the NMR solution structure (Figure S20).³¹

Figure 14.

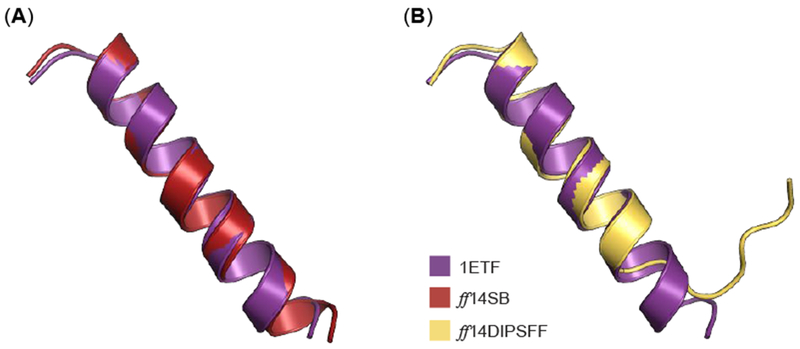
Alignment of average Rev structure from ff14SB and ff14IDPSFF RRE-Rev simulations to chain B in the NMR solution structure (PDB: 1ETF). (A) The average structure from ff14SB simulations is superimposed to Rev protein from IETF, with an RMSD of 0.57 Å (Cα atoms). (B) The average structure from ff14IDPSFF simulations is superimposed to Rev protein from IETF, with an RMSD of 1.14 Å (Cα atoms).

Unsurprisingly, ff14SB simulations yield a lower RMSD than ff14IDPSFF simulations from alignments to the experimental structure (Figure 14). This induced helical content is most likely attributed to inherent native-structure-biases of the generic ff14SB protein force field.^60–63 Although the RMSD of the experimental and ff14IDPSFF-derived structure is larger, it is notable that the helical component is quite stable (first 16 residues), with the remaining 7 residues exhibiting multiple helix-to-coil transitions (Figure 14, S20). Chemical shift and CD data of the wild-type Rev and various mutants (oligomerization-deficient mutant V16D/I55N Rev, and L60R mutant Rev bound to Stem IIB RRE), also suggests disordered content in the C-terminus.^{26, 30, 31, 55} The stable N-terminal fragment found in ff14SB- and ff14IDPSFF-simulated residues contrasts sharply with the high structural fluctuation observed in apo Rev simulations, and is consistent with experimental RRE-Rev results.³¹ Alignment of average simulated complexes also generated structures similar to the experimental NMR solution structure (Figure 15).

Figure 15.

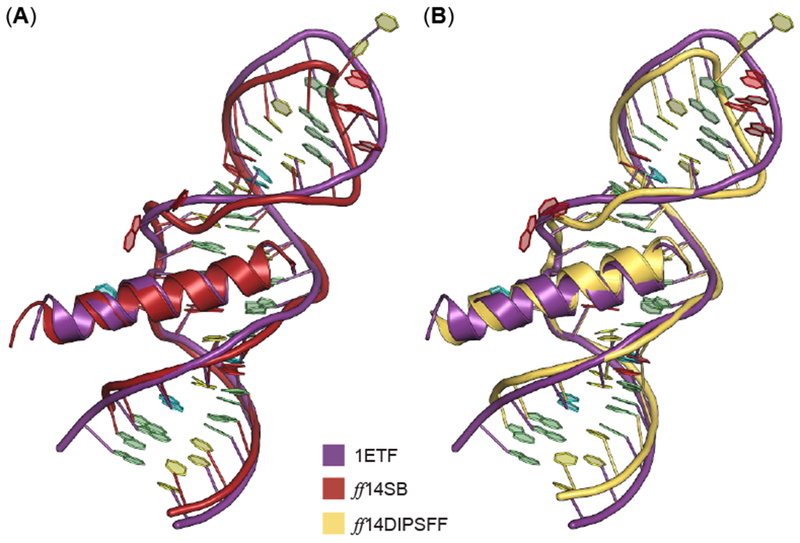
Alignment of average complex structure from ff14SB and ff14IDPSFF RRE-Rev simulations to the full NMR solution structure (PDB: 1ETF). Nitrogenous bases are colored according to Nucleic Acid Database convention: A – red, U – cyan, C – yellow, and G – green. (A) The average structure from ff14SB simulations (red) is superimposed to RRE-Rev from 1ETF, with an RMSD of 1.48 Å (backbone atoms: CA, P, O5′, O3′, C3′, C4′, C5′). (B) The average structure from ff14IDPSFF simulations is superimposed to RRE-Rev from 1ETF, with an RMSD of 1.9 Å (backbone atoms: CA, P, O5′, O3′, C3′, C4′, C5′).

Fluctuation of Rev backbone atoms are further explored via root-mean squared fluctuation (RMSF) analyses for apo and bound Rev simulations. In all Rev simulations, backbone atoms (Cα) fluctuate more in ff14IDPSFF simulations than the ff14SB simulations (Figure 16). Comparison of apo and bound simulations shows the bound Rev fluctuates less, due to the stabilization from binding with RRE (Figure 16C, S21). Unsurprisingly terminal residues display the highest fluctuation in all simulations, except the relatively stable N-terminal region in the bound Rev simulations. This is corroborated by hydrogen bonding populations of residues 34–36 (Figure 16, S21, Table 5), which stabilizes the N-terminal region. The observed different fluctuation trends can also be explained by the different secondary structure propensities. For instance in Figure 16B, residues 36–38 in the ff14SB apo Rev simulations exhibit lower RMSF values and also exhibit higher helical propensity (Figure S18A).

Figure 16.

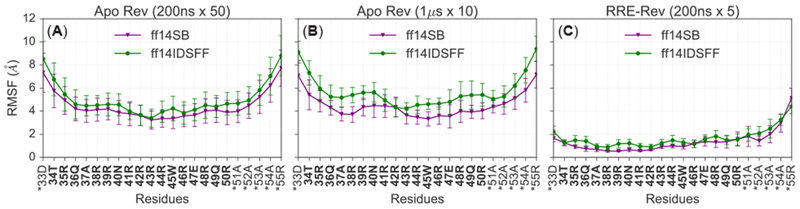
RMSF analyses of backbone Cα atoms per force field and simulation type. (A) Average RMSF of backbone atoms between fifty, 200ns apo Rev simulations. Asterisks (*) indicate non-native residues. (B) Average RMSF of backbone atoms between ten, 1 μs apo Rev simulations. (C) Average RMSF of backbone atoms between five, 200ns RRE-Rev simulations.

Table 5.

Intermolecular Hydrogen Bond Occupancy (criteria: θ > 120°, distance < 2.5Å)⁵⁰

Row Number	Donor Residue	Acceptor Residue	Freq. (ff14SB)	Freq. (ff14IDPSFF)
0	THR34	G47	0.5926	0.6576
1	ARG35	C65	0.753	0.5848
2	ARG35	U66	0.8388	0.7287
3	GLN36	G48	0.7831	0.6025
4	ARG38	U66	0.9777	0.9303
5	ARG38	G67	0.7867	0.7301
6	ARG39	G70	0.9918	0.9702
7	ASN40	G47	0.8201	0.9814
8	ASN40	G46	0.6765	0.8927
9	ARG41	G46	0.6674	0.7484
10	ARG42	G67	0.8515	0.8345
11	ARG42	A68	0.764	0.8502
12	ARG44	U45	0.7013	0.728
13	ARG46	U72	0.6373	0.4805
14	ARG48	U43	0.8294	0.7139
15	ARG48	C44	0.6949	0.6611
16	GLN36	G47	0.3891	0.5076
17	ARG41	U45	0.4667	0.5766

Inspection of intermolecular hydrogen bond and ionic salt bridge occupancies (only frequencies > 0.5 is shown) in Table 5 and 6 reveals similar interactions between simulations of both force fields, but with slight differences (Table 5). Since ionic salt bridge formations are almost identical between the two force fields (Table 6), we chose to focus primarily on differences in hydrogen bond formation. In ff14SB complex simulations, the hydrogen bond pair ARG46-U72 dominates compared to ff14IDPSFF complexes due to the increased stability and helical propensity of the C-terminal end (Table 5). While retaining mostly helical character between residues 33–46, Rev contains two hydrogen bonds (GLN36-G47, ARG41-U45) in the N-terminal region in the ff14IDPSFF simulations, which are less frequent in the ff14SB simulations, an unexpected outcome considering the stability of the ff14SB simulations over that of the ff14IDPSFF simulations (Table 5). Co-existence of stabilized N-terminal helices and coiled C-terminal components in the ff14IDPSFF simulations of bound Rev suggests this new force field is able to simulate disordered region in an otherwise ordered protein, while the ff14SB simulation retains more helical characteristics.

Table 6.

Intermolecular Ionic Salt Bridge Occupancy (criterion: distance < 4Å)⁵¹

Row Number	Acidic Residue	Basic Residue	Freq. (ff14SB)	Freq. (ff14IDPSFF)
0	U43	ARG48	0.8611	0.7314
1	C44	ARG48	0.7535	0.8062
2	U45	ARG44	0.5244	0.5146
3	G46	ARG41	0.7136	0.8019
4	C65	ARG35	0.7934	0.6226
5	U66	ARG35	0.8821	0.7189
6	U66	ARG38	0.9821	0.9527
7	G67	ARG38	0.7981	0.7406
8	G67	ARG42	0.9152	0.9513
9	A68	ARG42	0.7722	0.8712
10	U72	ARG46	0.6879	0.6017
11	U45	ARG41	0.4922	0.5960

4. CONCLUSIONS

IDPs remain elusive by standard experimental methods due to their conformational flexibility. Molecular dynamics simulations can thus provide detailed insight into their complex structures, dynamics, and functions, if they can reproduce the available experimental observables. However, there are several issues in computational studies. First the generic force fields were found to be biased towards ordered structures in many prior simulation studies. Second the expansive conformations occupied by IDPs is often beyond typical simulation amount needed for ordered proteins.

Thus, our first goal of this computational study is to assess the quality of both a generic protein force field (ff14SB) and its IDP-specific counterpart (ff14IDPSFF) that was intended to address the biases in the generic force field. Overall simulated average observables from ff14IDPSFF replicate experimental chemical shifts and ³J_HNHα-coupling constants more accurately than those derived from ff14SB simulations for the tested EGAAXAASS peptides. DSSP analyses also suggest different secondary structural biases between the two force fields, increased helical content from ff14SB and coiled content from ff14IDPSFF, with the latter in higher agreement with experiment. When used to simulate more complex proteins such as Rev in apo and bound forms, computational models gravitate toward either ordered secondary structure (ff14SB) or disordered secondary structure (ff14IDPSFF) as the clustering analyses revealed. However simulated observables between the two force fields are roughly comparable to experiment, ff14IDPSFF simulations agree with both NMR and CD measurements slightly better.

Our second goal of this study is to assess the extent of sampling that is needed for quantitative structural annotation of IDPs and to explore how to assess the sampling convergence. This was first conducted by analyses of convergence rates of individual observables in the form of bi-phasic decays. Convergence analyses of both NMR observables show that ff14IDPSFF simulations converge slightly faster than ff14SB simulations in the chemical shift calculations for all tested systems, though they converge slightly slower for ³J_HNHα-coupling constants for all tested systems. This is consistent with the observations that conformations in ff14IDPSFF simulations are more diversified, sampling a larger range of main-chain torsion angles, leading to slower convergence in ³J_HNHα-coupling constants that solely depends on these torsion angles. The decay half times also show that the total sampling amount (in term of nanoseconds simulated) is adequate as they are much less the total amount collected.

In addition, simulation protocols were also tested by simulating apo Rev as either many short (50 × 200ns) trajectories or a few long (10 × 1 μs) trajectories. Consistently converged distributions in the ff14IDPSFF simulations allows us to use the convergence rates to compare which protocol is better. However, the rate estimations show that differences in the convergence rates between the two are small, within 200ns in general, though it can be said the short protocol is slightly faster than the long protocol. For ff14SB simulations, the different distributions give us pause to claim that the sampling of the apo Rev is sufficient in either protocol even if 10 microseconds worth of sampling has been collected. This indicates that enhanced sampling techniques would greatly benefit IDP simulations for systems as small as 23 amino acids such as apo Rev.

Despite the short sequence length of apo Rev, no monomeric disordered Rev protein has been structurally characterized as demonstrated by its absence in the Protein Data Bank (PDB). To compensate for this lack of structural characterization, we utilized a combination of NMR and CD data for comparison to our clustering and secondary structural analyses. Chemical shift and CD studies from various different sources of oligomerization-deficient mutants and wildtype Rev conclude that monomeric Rev is mostly disordered.^{26, 30, 31, 55} These experimental findings are comparable to random coil clusters and DSSP calculations from the ff14DIPSFF simulations of and differ from the ff14SB simulations where increased helical content was found. Both force fields also generate stabilized helical structure and induced fit in RRE-REV simulations, exhibiting a coiled C-terminus as shown by the chemical shift data.^{30, 31, 38} These structural computational studies of apo and bound Rev stress the importance to assign the correct secondary structural biases in both force fields.

Interesting observations were also found when Rev was simulated with its RNA-binding partner RRE, ff14DIPSFF was able to replicate the structured regions in the bound form, despite over-representation of coiled secondary structure in the apo Rev simulations. Detailed analysis of the average conformation and secondary structures of the ff14IDPSFF simulations shows that both the helical N-terminal region and coiled C-terminal region are readily observed, in agreement with experimental findings, despite coiled secondary structural preferences in the apo Rev simulations. In comparison, a more stable helical structure was observed throughout the ff14SB simulations. A natural next step is to ask a more quantitative question: whether ff14SB is too stable or ff14IDPSFF is too unstable in the simulations of more complex IDPs such as Rev. This requires further quantitative stability analysis both experimentally and computationally.

This study articulates the difficulties of obtaining converged and expansive sampling of IDPs, though our exploration of different simulation protocols demonstrates consistent observations with the ff14IDPSFF force field regardless of the protocols used. Although successful in simulating short peptides and bound Rev, the advantages offf14IDPSFF are not as clear-cut for the more complex apo Rev. These findings also suggest future refinements of IDP-specific force fields and reduction of force field biases are still necessary for consistent performance in modeling IDPs.