On the Significance of Systolic Flow Waveform on Aortic Valve Energy Loss

Abstract

This study aims to quantitatively and qualitatively assess energy dissipation in the aortic valve as a function of systolic aortic flow waveform representing pathologies where flow time-to-peak is delayed.

A bioprosthetic valve was tested in the aortic position of a left-heart simulator under physiological pressure and flow conditions. The flow loop piston pump was programmed to generate three different flow waveforms each with a different peak time annotated as Early Peak(EP) with a rapid acceleration, Mid Peak(MP) and Late Peak(LP) with a rapid deceleration. Energy dissipation was calculated from flow and pressure measurements while sinus vorticity dynamics were evaluated using time-resolved planar particle image velocimetry.

Average pressure gradients during systole are found 30.2±0.19mmHg, 30.7±0.25mmHg and 32.9±0.29mmHg and average dissipation over systole is found 0.95±0.026W, 1.05±0.034W and 1.25±0.043W for EP, MP and LP respectively. As systole’s acceleration phase is slower, sinus vortices are more likely to form, necessitating more energy exchange from shear layers inducing more viscous dissipation. EP found in healthy individuals is superior in terms of reducing energy dissipation and increasing aortic valve efficiency. In the context of possible left ventricular dysfunction and aortic stenosis, this means that delayed time-to-peak in the aortic flow waveform seen is not compensatory.

Introduction

The aortic valve opens at the beginning of systole as the left ventricle contracts and closes before the start of diastole as the ventricle relaxes ²⁷. For the ventricle to operate with a maximal efficiency, the aortic valve needs to offer minimal resistance during systole for the ventricle to overcome²⁶. Should this fail to happen, the heart ultimately becomes unable to cope with the flow demands and congestive heart failure ensues²⁶. Thus inefficiency and energy loss fall under the main constituents of aortic valve and left ventricle pathologies.

In healthy individuals, blood flows through the aortic valve at the onset of systole quickly accelerating to its peak value such as the peak flow occurs before mid-systole. This characteristic can be impaired for several reasons, either high valve resistance due to aortic stenosis or left ventricular muscle inability to quickly generate sufficient force, thus compromising its systolic performance ^{3, 13}. These slow progressing pathologies are often associated with changes in flow characteristics, notably compromising the shape of the flow waveform causing it to shift peak further during systole, even after mid-systole^{13, 14}.

Integrative physiological analysis of the heart as a pump provides insight on the overall mechanism required to ensure efficient pumping and to understand the effects of diseases in terms of compensatory and de-compensatory mechanisms to cope with the flow demands^{12, 15, 16, 24, 25}. From a fundamental fluid dynamics standpoint, the systolic aortic valve flow waveform shape must significantly control the energy efficiency of the valve itself because the rate of flow acceleration can determine the sinus vortex strength, while the rate of flow deceleration can determine the magnitude of adverse pressure gradients during the latter half of systole. High pressure gradients cause instabilities and turbulence and lead to significant system energy losses⁶. Although axial pressure gradients were demonstrated to be sufficient factors to close the aortic valve²², it has been hypothesized that sinus vortices play a role in the mechanism energy efficiency²⁷.

The objective of this study is to quantitatively and qualitatively assess the energy dissipation in the aortic valve. This is achieved by examining hemodynamic valve energy dissipation and sinus velocity and vorticity fields in 3 different cases of disease progression starting from an early flow peak (EP) to a mid-flow peak (MP) and finally a late flow peak (LP). Knowledge about the aortic flow waveform significance on the energy loss characteristics of the aortic valve can help better appreciate normal hemodynamics through the lens of mechanical efficiency. This can potentially offer new parameters to improve accuracy of assessing the severity of a pathological ventricle-valve system as a whole.

Methodology

To evaluate the flow waveform influence on pumping efficiency and valve performance, flow visualization, particle image velocimetry (PIV), hemodynamic testing calculations including pressure gradients and energy dissipation were performed.

Hemodynamic Assessment

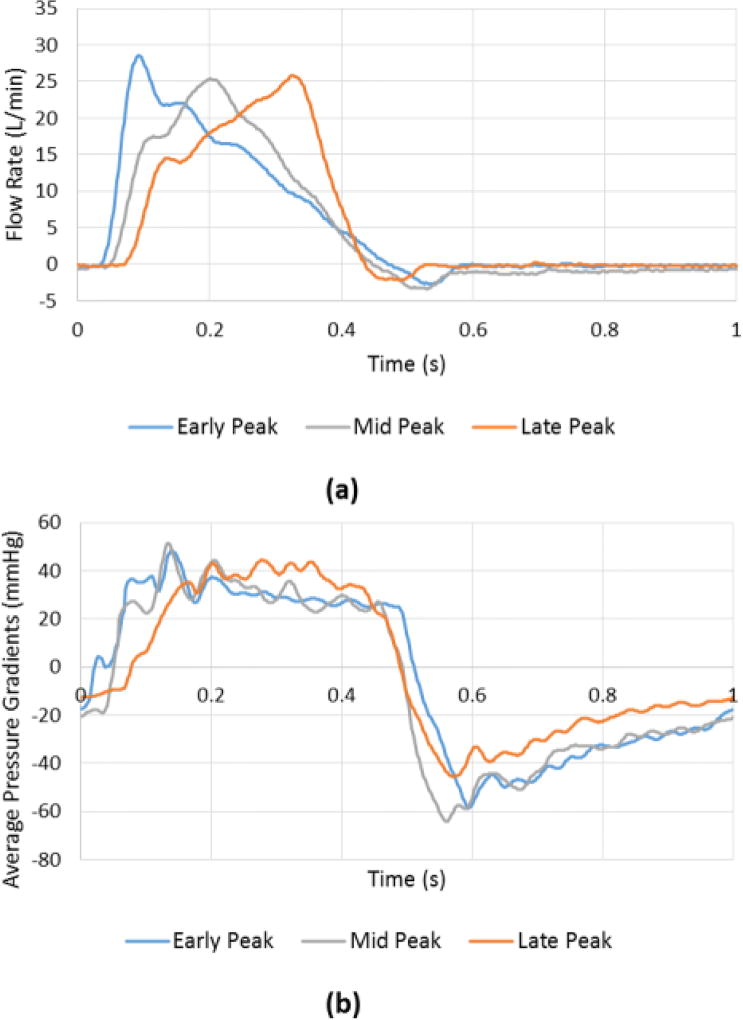
A Hancock II 21 bioprosthetic valve (Medtronic Inc, Minneapolis, MN) was mounted inside an aortic valve chamber placed in the aortic position of a left-heart simulator flow loop as shown in Fig.1 under physiological pressure and flow conditions. The flow loop piston pump (LinMot, Elkhorn, WI) was controlled by an in-house LabVIEW (National Instruments, Austin, TX) program generating three different flow waveforms each with a different peak time annotated as EP, MP and LP. An EP flow time was created by imposing a rapid acceleration of the piston pump along with a gradual deceleration. Contrariwise, a gradual piston acceleration and abrupt deceleration created an LP in the aortic flow waveform. Then equal rates of piston acceleration and deceleration formed the MP case. The resulting flow curves for the three cases are shown in Fig.2a. The desired outputs can be summarized as establishing a systolic to diastolic pressure of 120/80mmHg with a mean aortic pressure of 100mmHg, a 1 beat per second heart rate and a cardiac output of 5L/min. The working fluid is a water-glycerine (99% pure glycerine) mixture yielding a density of 1080 Kg/m³ and a kinematic viscosity of 3.5cSt similar to blood (volume fractions of water/glycerin used are 60/40). Twenty consecutive cardiac cycles of aortic pressure, ventricular pressure and flow rate data were recorded. Flow data were acquired using ultrasonic flow probes (Transonic Inc., Ithaca, NY), and pressures upstream and downstream of the valve were measured with Validyne pressure transducers (Validyne Engineering Corp., Northridge, CA). More details of the methodology conditions can be found in previous publications^6–11.

Figure 1.

Piston pump flow loop schematic.

Figure 2.

(a) Flow and (b) Pressure gradient waveforms over the cardiac cycle for EP, LP and MP cases.

The mean transvalvular pressure difference – that we will refer to as pressure gradient (PG) as adopted clinically - is defined as the average of positive pressure difference between ventricular and aortic pressure curves during forward flow. Instantaneous pressure gradients curves are shown in Fig.2b.

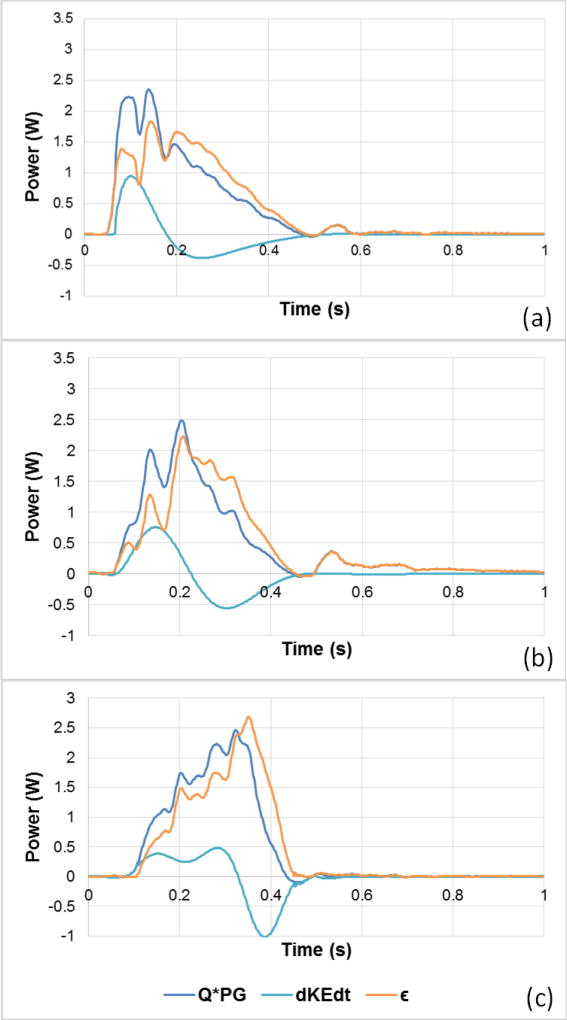
Instantaneous energy dissipation rate is calculated following the methodology in Yap et al²⁶ based on control volume analysis. It is calculated using the energy balance equation, then solving for the instantaneous energy dissipation over systole with the other terms experimentally measured.

$$\frac{\partial (\mathit{\text{KE}})}{\partial t}=∆\mathit{\text{PQ}}-\in$$ (Equation 1)

Where: $\frac{\partial (\mathit{\text{KE}})}{\partial t}$ is the rate of change in kinetic energy (KE) of the fluid mass enclosed in the control volume between the ventricular and aortic pressure taps calculated by volume integrating the velocity as described in Yap et al.; ∈ is the energy dissipation rate and ΔPQ the instantaneous pressure-flow work supplied per unit time; and ΔP is the pressure difference between the instantaneous ventricular and aortic pressure measurements.

Also, energy dissipation rate per unit volume over the experimentally measured flow domain is calculated following the methodology of Okafor et al²¹. The equation used is as follows integrated over the flow domain:

$$\mathit{\text{EDR}}=\mu [{(\frac{\partial V_x}{\partial x})}^2+{(\frac{\partial V_y}{\partial y})}^2+0.5{((\frac{\partial V_x}{\partial y})+(\frac{\partial V_y}{\partial x}))}^2]$$ (Equation 2)

PIV

The flow was seeded with fluorescent PMMA-Rhodamine B fluorescent particles with diameters ranging from 1 to 20 µm. The sinus flow domain was assessed using time-resolved PIV that involves illuminating the centre plane through the sinus region using a laser sheet created by Nd:YLF single cavity diode pumped solid state, high repetition rate laser coupled with external spherical and cylindrical lenses. The laser was generated using the Photonics Industries DM40-527 diode-pump Q-switched laser (Photonics, Bohemia, NY) with optics to covert the output beam into an expanded laser sheet. PIV measurement was repeated 2 times and recorded roughly 1.5 cardiac cycles at a 1kHz sampling rate. A Photron Fastcam SA3 CCD high-speed-video camera (Photron, San Diego, CA) synchronized to the laser system via a high-speed controller (HSC) (LaVision, Ypsilanti, MI) captured focused images of the illuminated polyamide particles within the laser sheet in the measurement plane. Vectors were calculated using adaptive cross-correlation algorithms described in our previous studies^{10, 20}. The resulting velocity field spatial resolution was 237.11 µm and temporal resolution was 5000Hz.

Vorticity dynamics were evaluated in this study to analyze coherent structures evolution in the sinus region to appreciate flow instabilities for the three cases. Vorticity is the curl of the velocity field and therefore captures rotational components of the blood flow shearing ^{2, 20, 27}. Regions of high vorticity along the axis perpendicular to the plane indicate both in-plane shear and rotation of the fluid particles. Out of plane vorticity in the z-direction was computed using the following equation:

$${\omega }_z=-(\frac{d{V}_x}{\mathit{\text{dy}}}-\frac{d{V}_y}{\mathit{\text{dx}}})$$ (Equation 3)

Where ω_z is the vorticity component with units of s⁻¹; V_x and V_y are the x and y components of the velocity vector with units of m/s. The x and y directions are defined in Fig. 4 with the z-direction being out of measurement plane. More information on the methodology can be found in previous publications^{7, 8, 11}.

Figure 4.

Energy dissipation waveform over the cardiac cycle for EP, LP and MP cases. The dots correspond to the time point of maximum flow corresponding to each case.

Results

Pressure and flow data

Following the flow and pressure profiles from Fig.2, average PG during EP decreases slowly before the sharp decrease when leaflets start closing in systole decelerating part, while it shows a quicker decrease in MP then LP. During the deceleration part, PG in LP has the sharpest slope compared with that during MP and EP. The average PGs during systole are found to be 30.2±0.19mmHg, 30.7±0.25mmHg and 32.9±0.29mmHg for EP, MP and LP respectively. These average pressure gradients exceeding 10mmHg were achieved as simulating aortic stenosis was intended. The peak pressure gradients are found to be 48.08±0.36, 51.47±0.51 and 44.40±0.55 mmHg for EP, MP and LP respectively.

Energy dissipation

The positive energy dissipation profile calculated over systole using Equation 1 is shown in Figs.3a, b and c along with the pressure work supplied per unit time and the rate of change of kinetic energy. The pressure work supplied per unit time QΔP is highest in magnitude and slope at the beginning for EP, followed by MP. In EP, the beginning is gradual however, and due to the abrupt deceleration, $\frac{\mathit{\text{dKE}}}{\mathit{\text{dt}}}$ is more negative (−1.0W) and steeper compared to EP (−0.38W) and MP (−0.55W). For EP, $\frac{\mathit{\text{dKE}}}{\mathit{\text{dt}}}$ shows a slower and smoother change from beginning to end while MP shows a faster change and a more negative value as deceleration starts. In Fig.4, energy dissipation over systole is compared between the 3 cases. Consistently with the flow profiles, the peaks of the plots occur successively starting with EP then MP then LP. The lowest peak value is 1.82W found in EP, followed by 2.23W in MP and the highest 2.69W found in LP. The EP dissipation is characterized by a sharp slope before the peak is reached versus a sharp decrease in the case of LP after the peak is reached consistently with the flow waveform profile. The average dissipation over systole is found to be 0.95±0.026W, 1.05±0.034W and 1.25±0.043W for EP, MP and LP respectively and the total work over the whole cardiac cycle is found to be 0.433±0.010W, 0.470±0.012W and 0.467±0.016W for EP, MP and LP respectively.

Figure 3.

Pressure work supplied per unit time, rate of change in kinetic energy, and energy dissipation waveforms over the cardiac cycle for (a) EP, (b) MP and (c) LP cases.

The error sources in computing instantaneous dissipation rate stem from ignoring the KE flux as well as experimental measurement errors in the PG, flow, and the total KE estimation in the control volume assuming the Womersley profile. Based on instantaneous KE dissipation rate error propagation the corresponding error is given by the equation:

$$\frac{\delta \epsilon }{\epsilon }={[\frac{\delta ∆P}{∆P}+\frac{\delta Q}{Q}+2\frac{\delta K.E}{K.E}]}^{0.5}$$ (Equation 4)

Where the error estimates for PG $\frac{\delta ∆P}{∆P}\sim 0.003$ (estimated as an error of 0.1mmHg over a PG of 30mmHg); and the error in flow is estimated as $\frac{\delta Q}{Q}\sim 0.004$ (estimated as an error of 0.1l/min over a peak flow of 25l/min). The error estimate for $\frac{\delta K.E}{K.E}$ is about 0.043 based on experimentally estimating actual KE averaged over full volume compared to KE estimated based on flat Womersley profile. Therefore $\frac{\delta \epsilon }{\epsilon }$ is about 6% and reasonable.

Similarly, from Figs.5a, b and c, EDR patterns follow those of the dissipation for the different cases. LP shows the highest EDR value 0.079W/m³ compared with 0.063W/m3 for EP and 0.064W/m³ for MP. The average values throughout systole are 0.2065W/m³ for EP, 0.2154W/m³ for MP and 0.223W/m³ for LP.

Figure 5.

Energy dissipation rate (EDR) waveforms over for (a) EP, (b) MP and (c) LP cases.

Flow Velocity Fields

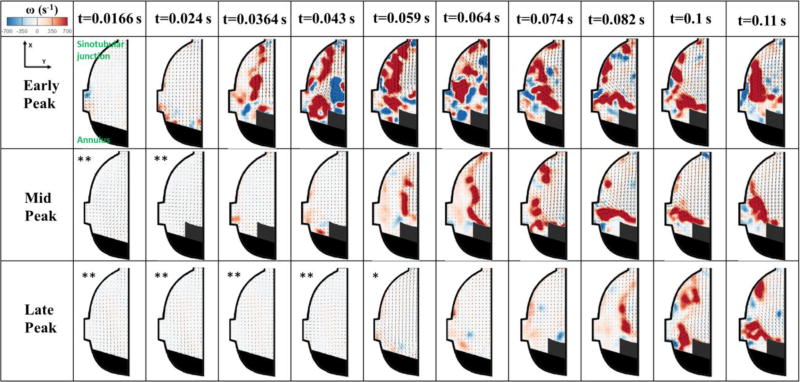
Sinus flow is shown in Video 1 and still frames are in Fig.6a and 6b. Fig.6a and 6b show comprehensively at certain time increments the velocity and vorticity fields throughout systole and a part of diastole. Only the differences between the 3 different cases will be highlighted. The later the peak the slower the onset of fluid motion is inside the sinus and the more small vortices form. This can be clearly seen at certain time points when comparing the 3 different cases. In EP, at 0.024s, the velocity starts increasing to reach 0.36±0.03 m/s while even though systole has started for MP and LP, the velocity is almost near 0 m/s for both latter cases (0.025±0.001m/s for LP and 0.052±0.001 for MP). The main vortex in EP starts forming at 0.059s where the velocity reaches 0.72±0.02m/s and ω = 1176±8 s⁻¹ and the vortex becomes clear at 0.064s where velocity reaches 1.06±0.02m/s and ω = 2244±5s⁻¹. For MP, the main vortex starts forming at 0.082s (0.023 s from the onset of the vortex in EP) where velocity and vorticity reach 0.82±0.02m/s and 1385±9s⁻¹ respectively. And for LP, the vortex starts forming at 0.1s (0.041s from the formation of EP vortex and 0.018s from the formation of MP vortex) where velocity and vorticity reach 0.76±0.03m/s and 1495±9s⁻¹ respectively.

Figure 6.

a and 6b Velocity vectors and vorticity contours within the sinus for EP, MP and LP throughout the cardiac cycle.

* Vector length increased by 6 times.

** Vector length increased by 12 times.

As peak systole is crossed for the 3 different cases, velocity and vorticity start decreasing. In EP, as peak systole is crossed at t=0.082s, flow towards the sinotubular junction with V=1.1±0.05 m/s is the main feature in the sinus with recirculating flow near the leaflet with ω = 1240±6s⁻¹. In the decelerating part when t>0.092s, vorticity starts fading away from ω=1460±8s⁻¹ to 1076±5s⁻¹ at 0.204s. Small vortices start forming throughout deceleration until the beginning of diastole with ω = 537±5s⁻¹. The velocity is the sinus decreases gradually to reach 0.25m/s at the end of deceleration.

For MP, in the decelerating part when t>0.2s, vorticity starts fading away gradually going from 1285±7 s⁻¹ and reaching 258±5 s⁻¹ by the end of deceleration, with small vortices forming in the zone adjacent to the leaflet. The velocity in the sinus drops from 1.1±0.02m/s to 0.2±0.015m/s by the end of systole.

For LP, when t>0.242s, vorticity decreases and fades away from 1853±10s⁻¹ to reach 961±6s⁻¹ at 0.349s. Velocity also decreases from 1.04±0.03 to 0.69±0.02 m/s. By end of systole, velocity reaches 0.16±0.03m/s.

In EP, longer times of sinus flow movement exist specifically from 0.043s to 0.4s (0.357s duration), while in MP these phases are only obvious from 0.059s to 0.349s (0.29s duration) and for LP from 0.082s to 0.349s (0.267s). Also the decelerating changes happen continuously without drastic variations in velocity and vorticity in EP (as shown in the results above) from 0.349s to 0.475s while the changes happen faster in MP and even faster in LP for the same time interval.

Discussion

In this manuscript, to evaluate the flow waveform influence on pumping efficiency and valve performance, several parameters evaluated in this study are used: (a) pressure gradient data, (b) energy dissipation data and (c) sinus flow velocity fields for the 3 different regimes to track flow instabilities that can further shed insight into the pressure fluctuations and energy dissipation characteristics.

Pressure and flow data

A pressure drop is a measure of flow potential energy losses that occur when viscous blood flows through the heart valve²⁷. However, it is only a gross measure of heart valve efficiency¹ as the magnitude also depends on flow rate of change, and the magnitude of flow rate itself. Nevertheless, a large pressure drop across the aortic valve necessitates a larger systolic pressure in the left ventricle to drive the flow²⁷. The lower PGs are favorable and a gradual change ensures smoothness of valve closure. Sudden closure brings the fluid velocity to zero at the face of the valve in a short time creating significant wave speeds at which disturbances and instabilities propagate. As illustrated in the results, EP presents an optimum case of achieving lower and gradual PGs during systole and before valve closure (systole deceleration phase) respectively. Because the pressure gradient is dependent on the velocity, and acceleration, energy dissipation characteristics need to be examined to ascertain if and why EP is optimal.

Energy dissipation

Energy dissipation in the aortic valve is the result of mixing, fluid instabilities and transfer of momentum and kinetic energy to the smaller scales where it is ultimately converted to heat through viscosity¹¹. In systole’s acceleration, the valve leaflets start opening with the blood flow rapidly accelerating. This leads to a buildup of KE (within the control volume) that reaches its maximum when the flow reaches its maximum. This KE buildup is characterized by a positive rate of change with a comparable order of magnitude to the work done by pressure-flow per unit time thus leading to a small or negligible energy dissipation rate during early systole. The inference is that nearly all the pressure-flow work done during early systole is converted to kinetic energy.

As highlighted in the results and in agreement with previous publications²⁶, more dissipation occurs in the later part of systole than the early part. Further, both the systolic average and peak dissipation rates increases significantly (by over 50%) with the peak shifting from before to after the middle of systole. This may be attributed to the stronger adverse pressure gradients as well as higher magnitude of negative $\frac{\mathit{\text{dKE}}}{\mathit{\text{dt}}}$ that starts developing in the deceleration phase leading to exponentially more fluid instabilities, enhancing mixing, and turbulence.

During EP, dissipation waveforms exhibit 3 local peaks that coincide with the fluctuations in the corresponding PG waveform despite having the flow decrease. This observation highlights the importance of the disturbances and instabilities in the flow and velocity field almost independently of the flow magnitude. During MP and similar to EP, dissipation profile follows PG profile such as the most notable fluctuations occur at the time fluctuations in PG occur. The only difference is that the maximum dissipation peak in this case though not exactly occurring at the time the corresponding flow peaks (at t = 0.202s), seems to be dependent on both magnitude of flow and PG fluctuations. This observation leads to a key point that the flow KE rate reached zero at this point and loss of energy due to viscous dissipation fully accounts for the pressure-flow work per unit time. During LP, the sharp decrease in pressure gradient along with the abrupt decrease in flow lead to the fast and almost linear decrease in dissipation through the remainder of systole. Thus, fluctuations due to pressure gradients dictate the dissipation pattern more prevalently when abrupt change of flow rate takes place as is in the case of EP and LP. However, in LP, dissipation magnitude is higher than in EP. This is a direct result of having a high resistance aortic valve necessitating more pressure gradients to achieve the necessary flow, thus leading to higher dissipation. In addition, in the deceleration part, $\frac{\mathit{\text{dKE}}}{\mathit{\text{dt}}}$ is strongly negative, the pressure gradient starts dropping and becomes sharply negative too consequently, forcing the flow regime to become highly dissipative to generate the braking force needed to being the flow to an abrupt stop.

EP presents an optimal case where energy dissipation is lowest and its rate of change with time is most gradual. EDR measures presented in Fig. 5 reflect the same arguments as above.

Flow Velocity Fields Impacts on Energy Dissipation

Given the importance of sinuses in blood flow and control of the aortic valve²⁷, sinus flow velocity fields for the 3 different regimes are examined to track flow instabilities that can further shed insight into the pressure fluctuations and energy dissipation characteristics discussed above. Vorticity dynamics were evaluated in this study to analyze coherent structures evolution in the sinus region to appreciate flow instabilities for the three cases. Vorticity is the curl of the velocity field and therefore captures rotational components of the blood flow shearing ^{2, 20, 27}. Regions of high vorticity along the axis perpendicular to the plane indicate both in-plane shear and rotation of the fluid particles. Investigating vorticity is important as it provides one of the main characteristics of the flow in terms of assessing energy dissipation: the more the vorticity fluctuations (in space and time) the more the turbulence thus the higher the energy dissipation. Vorticity constitutes one of the component of flow deformation and characterizes turbulent eddies investigating the swirling features as they appear, progress and dissipate in the flow.

Contrary to EP, MP and LP are characterized by the formation of multiple vortices (as explained in the results) throughout systole as shown in Video 1 and Fig.6a at t=0.082s till 0.11s. The existence of multiple vortices divides the main vorticity flux⁴. As acceleration is slower, more vortices form as is the case comparing EP (till t=0.043s) with MP (till t=0.074s) and LP (till t=0.1s) on one hand and MP with LP on the other. In the neighborhood of the valve orifice, the high speed of the jet causes a shear layer to develop. The shear layer grows very rapidly engendering instabilities in the flow expressed by vortex rings. This enhances the mixing between the existing sinus fluid and the fluid ejected from the valve¹⁷. During the beginning of this vortex formation process, the ejected fluid carrying a specific amount of KE, impulse and circulation is fed into the vortex and continues to add more perturbations⁵ as obvious in EP starting from t=0.043s, in MP at t=0.139s and in LP at t=0.204s. At the early stage, the vortex ring grows in size and translates downstream due to its self-induced velocity¹⁹. Its volume also increases as it propagates downstream because of the entrainment of the surrounding fluid in order to conserve momentum²³. Because of viscosity, the total energy and circulation of the flow will be diffused with time as is the case in all of the 3 regimes EP, MP and LP¹⁸. This clearly explains why vorticity field gradually disconnects from the trailing jet that comes with the vortex as progression in systole continues ⁵ as shown in EP from t=0.064s, in MP from t=0.074s and in LP from t=0.082s. In addition, because the vortex pushes the shear layer, vorticity destruction takes place. The vortex takes its energy from the shear layer and thus stops growing as the fluid decelerates¹⁹.

The higher the number of vortices generated the higher the energy requirement to create them and maintain their rotation and strength. However, due to viscous dissipation energy losses increase. Thus, more energy dissipation occurs as acceleration is gradual which explains the higher energy dissipation in MP compared to EP and LP over the cardiac cycle and the higher energy dissipation in LP over systole. The abrupt start in EP allows for more entrainment into the main jet minimizing energy requirements. Due to the sudden deceleration in LP, the main vortex splits into smaller vortices with high vorticity exceeding those formed in MP and EP in number and magnitudes creating more instabilities and causing more energy dissipation.

As described in the results, abrupt changes in vorticity going from low to high then high to low are prevalent in MP and LP compared with EP with more emphasis on LP compared with MP. These abrupt vorticity changes are related to disturbances in the flow field.

Thus an abrupt acceleration followed by a gradual deceleration tends to minimize the energy dissipation for an optimized aortic valve system.

Conclusion

An in-vitro study was performed for 3 different cases of aortic flow waveforms characterized by an early peak, a mid-peak and a late peak in order to evaluate the energy dissipation and efficiency of opening and closing mechanisms of the aortic valve. This study highlighted the superiority of early peak flow found in healthy individuals in terms of energy dissipation and efficiency of the aortic valve based on hemodynamic parameters and sinus flow fields in the context of possible left ventricular dysfunction and aortic stenosis.

Limitations

A few limitations were present in this study. The use of a rigid sinus chamber is not completely physiological. However, this simplification is not expected to significantly skew results because we have built into the setup the effects of compliance through a controlled aortic pressure condition by adjusting the compliance section of the loop. The piston pump setup that despite achieving physiological aortic pressure, did not achieve an entirely physiological diastolic ventricular pressure. However, given the systolic portion was physiological this did not cause a problem for the investigation. Despite having a 3.5cSt mixture of water-glycerin, it does not reflect the complete non-Newtonian properties of blood. The higher energy losses observed in the mid-peak and late-peak cases could also be partially due to reduced systolic duration as having less time for the same stroke volume usually means higher energy losses. Finally, 2D fluid mechanics analysis may not be sufficient to comprehensively evaluate the flow feature in the sinus and further studies are required to investigate these flow features in more details.

Supplementary Material

10439_2018_2102_MOESM1_ESM

Main sinus flow streak visualization for Early Peak, Mid Peak and Late Peak cases.