Relational concurrency, stages of infection, and the evolution of HIV set point viral load

Abstract

HIV viral load (VL) predicts both transmission potential and rate of disease progression. For reasons that are still not fully understood, the set point viral load (SPVL) established after acute infection varies across individuals and populations. Previous studies have suggested that population mean SPVL (MSPVL) has evolved near an optimum that reflects a trade-off between transmissibility and host survival. Sexual network structures affect rates of potential exposure during different within-host phases of infection marked by different transmission probabilities, and thus affect the number and timing of transmission events. These structures include relational concurrency, which has been argued to explain key differences in HIV burden across populations. We hypothesize that concurrency will alter the fitness landscape for SPVL in ways that differ from other network features whose impacts accrue at other times during infection. To quantitatively test this hypothesis, we developed a dynamic, stochastic, data-driven network model of HIV transmission, and evolution to assess the impact of key sexual network phenomena on MSPVL evolution. Experiments were repeated in sensitivity runs that made different assumptions about transmissibility during acute infection, SPVL heritability, and the functional form of the relationship between VL and transmissibility. For our main transmission model, scenarios yielded MSPVLs ranging from 4.4 to 4.75 log₁₀ copies/ml, covering much of the observed empirical range. MSPVL evolved to be higher in populations with high concurrency and shorter relational durations, with values varying over a clinically significant range. In linear regression analyses on these and other predictors, main effects were significant (P < 0.05), as were interaction terms, indicating that effects are interdependent. We also noted a strong correlation between two key emergent properties measured at the end of the simulations—MSPVL and HIV prevalence—most clearly for phenomena that affect transmission networks early in infection. Controlling for prevalence, high concurrency yielded higher MSPVL than other network phenomena. Interestingly, we observed lower prevalence in runs in which SPVL heritability was zero, indicating the potential for viral evolution to exacerbate disease burden over time. Future efforts to understand empirical variation in MSPVL should consider local HIV burden and basic sexual behavioral and network structure.

1. Introduction

HIV set point viral load (SPVL)—generally defined as the average viral load (VL) an individual achieves during the period immediately following acute infection—varies among individuals and across populations, and impacts both clinical outcomes and onward transmission. Among individuals, SPVLs can vary over orders of magnitude (Mellors et al. 1996; Bonhoeffer et al. 2003; Bonhoeffer, Fraser, and Leventhal 2015). Predictors for higher SPVL include CCR5, HLA, and other host genotypes (Blanpain et al. 2002; van Manen et al. 2011; McLaren et al. 2015), sex (Gandhi et al. 2002), genital inflammation (Roberts et al. 2012), age (Hollingsworth, Anderson, and Fraser 2010) and possibly viral subtype (Robb et al. 2016, but see subsequent correspondence), although the causal mechanisms for these predictors are not all clear. Recent mathematical modeling work suggests that intra-host meta-population dynamics may also be responsible for some of this variation (Lythgoe et al. 2016).

The distribution of individual SPVL values does not occur randomly across populations. For instance, one recent meta-analysis (Herbeck et al. 2012) found that mean SPVL (MSPVL) observed in different populations ranged from 4.2 to 5.1 log₁₀ copies/ml (nearly an order of magnitude), with the majority between 4.30 and 4.55 (Müller et al. 2006; Dorrucci et al. 2007; Herbeck et al. 2008; Gras et al. 2009; Müller et al. 2009; Potard et al. 2009; Troude et al. 2009; Crum-Cianflone et al. 2010). These differences, while far narrower than those occurring among individuals, are still clinically significant (Modjarrad, Chamod, and Vermund 2008). Efforts to explain the correlates of this population variation, and the causal mechanisms for them, have met limited success. For example, while transmission risk group was associated with different MSPVL and different temporal trends in an analysis of the Italian HIV epidemic (Müller et al. 2009), the aforementioned meta-analysis (Herbeck et al. 2012) considered multiple predictors for population variation in SPVL trends, and found only seroconversion lag time to be significant; other potential predictors, such as transmission risk group composition, were not. Sampling variation and sampling bias undoubtedly contribute to SPVL variation, although we are unaware of any efforts to quantify these effects.

By being partially heritable from donor to recipient (Alizon et al. 2010; Fraser et al. 2014), SPVL contains the necessary conditions for evolution by natural selection as a viral phenotype. It entails an evolutionary trade-off, with higher SPVL leading to conditions for the virus that are both positive (higher transmissibility, e.g. Quinn et al. 2000; Fideli et al. 2001) and negative (higher host mortality, e.g. Coombs et al. 1996; Welles et al. 1996). Because it affects host morbidity and mortality, it is considered a measure of virulence, and a long theoretical literature hypothesizes that virulence will often evolve to some intermediate, optimum level under this type of trade-off (for a review, see Alizon et al. 2009). Modeling of some specific virological features of HIV has suggested that the MSPVL observed in some populations appears to be close to a hypothesized evolutionary optimum of 4.52 log₁₀ copies/ml (Fraser et al. 2007). A later model predicted a higher optimum (4.75, Herbeck et al. 2014), whereas other models suggest that SPVL may still be evolving in some settings (Blanquart et al. 2016), as do some empirical analyses (Müller et al. 2009; Herbeck et al. 2012; Pantazis et al. 2014). Interventions can further complicate HIV dynamics; e.g. treatment scale-up (Herbeck et al. 2016) has been predicted to affect expected MSPVL. Given the rapid levels of intra-host viral evolution in the face of short-term selection pressures, this between-host heritability and the evolutionary dynamics that depend on it might seem surprising and to require an argument for group selection; however, Fraser et al. (2014) hypothesize multiple mechanisms by which this apparent puzzle may be explained.

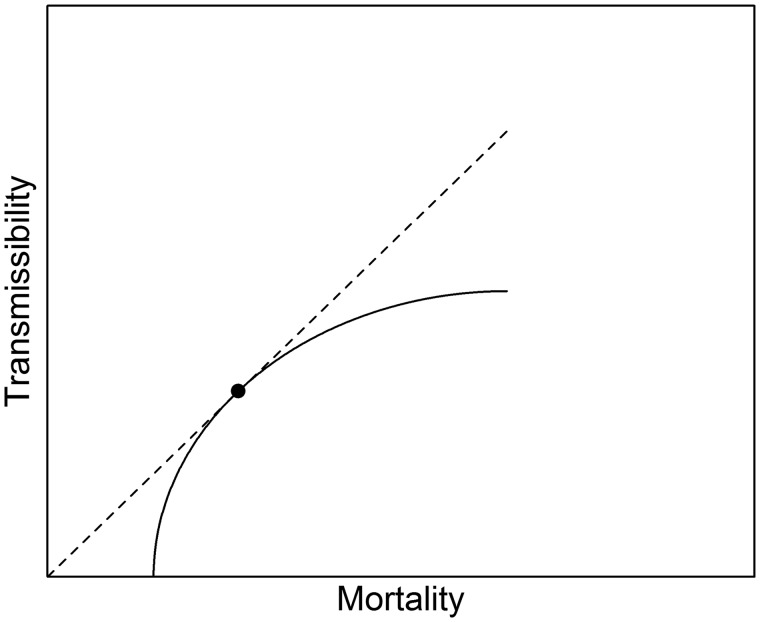
The theoretical literature on virulence evolution emphasizes that the nature of the trade-off curve between transmission and duration of infection (a function of both recovery and mortality) should change the level of virulence that evolves. For example, in models with random mixing and other key simplifying assumptions, pathogen virulence is expected to evolve to the value represented by the intersection of the tangent to the trade-off curve that passes through the origin (van Baalen and Sabelis 1995; Bull and Lauring 2014). This is the point representing the highest R₀—or reproductive ratio—achievable by the virus given its evolutionary constraints. For HIV—where there is obviously no recovery—duration is determined by mortality (Fig. 1; note that the curve does not hit the origin since the x-axis includes background mortality). These basic insights derive from purposefully simple models; the literature has also generated various hypotheses about ways that relaxing different assumptions may alter the expected pattern of virulence, both over time and at equilibrium. For example, one line of work predicts that, under modeled conditions, more virulent strains may be selected for early in an unfolding epidemic, even when at equilibrium less virulent strains are favored (Andre and Hochberg 2005).

Figure 1.

Schematic diagram of a potential trade-off function between virulence (as measured by mortality) and transmissibility, for a pathogen like HIV that has no recovery. Under a host of simplifying assumptions, virulence is expected to evolve to the level marked by the dot, located at the point of intersection for the tangent line that contains the origin, and representing the conditions under which R₀ is maximized. Adapted from Bull and Lauring (2014).

Extensions to this literature have explored how non-random mixing affects virulence. Many of these focus on spatial models (e.g. Boots and Sasaki 1999; Haraguchi and Sasaki 2000; Kamo, Sasaki, and Boots 2007; Berngruber, Lion, and Gandon 2015), although at least two considered additional forms of contact heterogeneity in the form of networks (van Baalen 2002; Read and Keeling 2003). The former compares purely random networks to two structures: a “small worlds” model common in the networks literature that draws on the statistical physics tradition, and a network model with high transitivity (one’s partners’ partner is one’s partner). They find that the transmission/survival trade-off leans more heavily towards high transmission in high-transitivity networks than elsewhere, since strains are in more competition with closely related virus. Evolutionary dynamics in both types of structured networks are much slower than in the random network. The latter paper also compares networks with different levels of transitivity (there called ‘regularity’). The author finds that the effects of transitivity on virulence evolution matter most in sparse networks (those in which individuals have few contacts), and that in these cases, the higher the regularity, the more that less virulent strains are able to dominate. While both papers provide novel theoretical insights, they are limited in their ability to elucidate evolutionary dynamics in real-world sexual networks, as the authors themselves acknowledge. For instance, both assume a static network (relationships do not form or break); one assumes people average eight simultaneous partners (roughly an order of magnitude higher than seen in empirical sexual networks) while the other assumes no variance in partner number; and one assumes no births and deaths.

Real sexual networks are, of course, dynamic, and vary in the number of persons having multiple relationships at any time point. One analysis that incorporated a more complex dynamic network model in the context of HIV SPVL is Herbeck et al. (2016). Their model included multiple risk groups, each displaying different relational durations and numbers of cumulative partners over time. However, the analysis focused on evolution of HIV virulence in response to different approaches to scaling up of antiretroviral therapy, not in terms of variation in network structure per se. The authors explored sensitivity analyses in which network features were changed, but did not report on the direct impacts of those changes on SPVL; rather, the focus was on demonstrating that the primary conclusion comparing different treatment allocation strategies in terms of evolutionary impact was insensitive to assumptions of network structure. Moreover, the included network structure was selected primarily to replicate existing ART models, with some parameters tuned to calibrate the model to observed HIV prevalence, rather than derived from data.

There has been much debate about how realistic models with so-called core-group dynamics like these are; one common critique is that, in order to generate generalized heterosexual epidemics in this framework, the proportion of the population having very high cumulative partner numbers needs to far exceed that seen in any empirical data set (Deuchert and Brody 2007; Goodreau 2013). Heterogeneity in cumulative partner numbers surely exists, with important implications for the epidemiology of HIV and other STIs, but researchers have sought additional network features that could generate observed epidemics in ways that match empirical data. The most prominent topic in this literature is concurrency—the practice of having multiple relationships that overlap in time (e.g. Watts and May 1992; Morris and Kretzschmar 1995; Eaton, Hallet, and Garnett 2011; Goodreau et al. 2012a; Mah and Halperin 2010; Morris, Epstein, and Wawer 2010; Epstein and Morris 2011; Maughan-Brown, Kenyon, and Lurie 2014; Kenyon et al. 2016). Concurrency has been argued to play a central role in creating the connectivity needed to sustain heterosexual HIV epidemics, where high mean lifetime partner numbers are not commonly reported. More recent work has considered the prevalence and consequences of relational concurrency among men who have sex with men (MSM; Beyrer et al. 2010; Solomon et al. 2010; Rosenberg, Khosropour, and Sullivan 2012; Rosenberg et al. 2013; Rosenberg 2014; Steele et al. 2013; Pines et al. 2016; Pines, Karris, and Little 2017). In any population where persistent relationships are common, concurrency plays a unique role in determining whether an individual can expose an HIV-negative partner shortly after becoming infected, i.e. while still in the acute phase. Although it plays a major role in the behavioral epidemiology of HIV literature, the topic of concurrency and relational timing is largely absent from the theoretical literature on virulence evolution. One exception is a sensitivity analysis presented in the supplement to Fraser et al. (2007), which modeled different relational durations under the case of strict serial monogamy (no concurrency), and found shorter relationships leading to slightly higher SPVL. However, they did not consider more realistic models involving different levels of ongoing concurrent relationships.

Because concurrency’s impacts on epidemic dynamics are especially strong during early infection, it might be expected to impact evolutionary trade-offs differently than, say, a behavior whose main impacts occur later in infection or which are spread evenly throughout. These include multiple behavioral parameters that appear in the epidemiological literature and in dynamic models of HIV transmission, and which vary among populations. For example, overall coital frequency within relationships should affect epidemic potential fairly consistently throughout most of the course of infection. The timing of coital cessation in AIDS obviously impacts transmission potential late in infection (Wawer et al. 2005), reflecting the fact that morbidity as well as mortality impacts HIV’s epidemiology and evolution, an important consideration in virulence modeling (Alizon et al. 2009). Relational durations represent a more complex example. When comparing populations or individuals with the same number of partnerships at any point in time, shorter relational durations means higher cumulative partner numbers. Shorter relational durations provide more opportunity for transmission overall, but they also play a particular role, like concurrency, in making it possible for an individual to both become infected from one partner and expose another in quick succession, maximizing HIV’s ability to make use of hyperviremia during acute infection. Thus, comparing concurrency’s impacts on SPVL evolution to these other phenomena provides additional insight into the role of infection stages in the overall evolution of virulence for multi-stage pathogens like HIV.

One might expect that disease burden, e.g. as measured by prevalence, would play a prominent role in the literature on HIV virulence evolution. Higher epidemic potential, whether due to higher coital frequencies, higher partner change rates, or other factors, might be expected to lead to both higher virulence and higher disease burden under many circumstances. This is in contrast to transmissibility and mortality, which would each increase with higher virulence but have countervailing effects on prevalence, presumably generating a more complex relationship between prevalence and virulence. Notably, however, key works in both the modeling (Fraser et al. 2007) and empirical (Herbeck et al. 2012) realms provide no information on the prevalence of HIV infection found in either their simulated or observed populations. This precludes considerations of how overall disease burden and MPSVL might co-vary, and how prevalence might mediate the relationships between various network factors and the resulting MSPVL.

In this modeling study, we assess how variation in sexual behaviors and networks across populations might explain variation in HIV-1 MSPVL. We focus on relational concurrency given its prominence in the behavioral epidemiology literature, but we compare this to other behaviors whose greatest impacts are expected to be felt at different times during the course of infection or equally across the board. These include overall coital frequency, mean relational duration, and the timing of coital cessation during AIDS. For each, we set a default drawn from data and compare with values above and below this. We measure the impact each parameter has on an epidemiological outcome (HIV prevalence) and an evolutionary one (MSPVL), and consider the nature of the relationship between these two outcomes across different levels of predictors. We choose prevalence over incidence since the latter is much more widely and easily measured among populations. We focus on endemic measures, following much of the theoretical literature reviewed above. Given the challenges of measuring epidemiological quantities imposed by relational concurrency and other sexual network features, we focus this analysis on simulation-based outcomes rather than analytical solutions.

Our aims in this work are two-fold: to gain insight about how these types of behavioral phenomena can impact virulence and infectious burden and the relationship between the two; and to identify whether the range of variation in MSPVL observed among empirical populations is similar to that obtainable by considering different types of behavioral variation. Given the latter goal, we build off a pre-existing, relatively complex model containing many features specific to HIV, mindful of the assertion that detailed pathogen-specific models like this are best suited to make predictions unique to that pathogen (Alizon et al. 2009; Bull and Lauring 2014; Ebert and Bull 2003). We run this model using parameters derived from behavioral data; then vary key behavioral parameters alone and in combination. We also conduct sensitivity analyses, varying three aspects of virology around which considerable uncertainty remains: the level of heightened infectivity during acute phase (Wawer et al. 2005), the level of SPVL heritability, and the relationship between VL and transmission probability. We conclude with a discussion of the relevance for population MSPVL variation.

2. Methods

We adapted a stochastic, dynamic, agent-, and network-based model that builds on model components, code and parametrizations previously described (see MSM model in Herbeck et al. 2018). Code was written in R and C++ and constructed using the EpiModel package API (Jenness, Goodreau, and Morris 2016b); it is available at github/EvoNetHIV. A full description of the methods and all parameters used is in the Supplementary data. Since MSM are the most prominent risk group in longitudinal SPVL studies (Herbeck et al. 2012), we developed our model for one sex, with transmission probabilities associated with anal sex. Behavioral parameters were derived from existing MSM models (Jenness et al. 2016a; Goodreau et al. 2017), which were in turn based on two empirical studies of MSM sexual networks from Atlanta (Hernández-Romieu et al. 2015; Sullivan et al. 2015). We begin our analyses with a scenario that reflects all of our behavioral parameters as measured in the Atlanta cohort, and then follow with a series of analyses in which we systematically vary one or two features at a time away from those observed values.

Agents were defined by a variety of attributes (e.g. age; CD4+ count); key attributes for this model included SPVL (fixed per individual) and current VL (time-varying). Sexual networks were governed by a separable-temporal exponential random graph model (STERGM, Krivitsky and Handcock 2014). This is a general statistical framework for networks that allows relationships to form and break stochastically, while matching an arbitrary set of target network statistics (e.g. mean concurrency prevalence), thus making it increasingly common in network-based epidemic modeling (e.g. Ezenwa et al. 2016; Jenness et al. 2016a; Webber et al. 2016; Goldstein et al. 2017; Herbeck et al. 2018; Robinson et al. 2018; Vandormael et al. 2018). STERGM terms were implemented in such a way that the mean degree (i.e. average number of partners) was held constant across scenarios despite some individuals having more than one partner at a time, in order to isolate the effects of network structure from simple network density. Within relationships, coital acts occurred stochastically with a constant rate per day, equal across all relationships; the only exception was for relationships in which either partner had reached the point of coital cessation within AIDS stage. This implies no coital dilution (i.e. that those with multiple concurrent partners do not have less sex with each than those with one partner), consistent with some recent findings (Delva et al. 2013; Jenness et al. 2015). Condom use per coital act was also stochastic.

Given a serodiscordant coital act, transmission was a function of donor’s current VL, type of sex (insertive or receptive), recipient’s circumcision status (if insertive), and condom use. We used a modified version of one published transmission function (Hughes et al. 2012), simplified to reduce the number of covariates, and adjusted from penile-vaginal to penile-anal rates (Patel et al. 2014). We chose this for its ability to incorporate the most covariates in a jointly estimated unified model, and because it expresses transmission probabilities as per-act, as required by our behavioral scenarios. This transmission function assumes an exponentially rising transmission probability with VL; however, one of our sensitivity analyses considered a function with transmission rates that plateau with VL (Fraser et al. 2014).

Each individual’s SPVL included viral and environmental contributions. The former came from the donor, with a random mutational parameter. The latter (a combination of undefined host and environmental factors) followed a normal distribution with mean 0 and SD that was a function of heritability. The viral contribution in the initial population followed a normal distribution with mean 4.5 log₁₀ SPVL copies/ml. All subsequent references to SPVL are expressed as log₁₀ copies/ml, unless otherwise noted.

All newly infected individuals’ VL began at 10⁻⁴ (a proxy for zero VL) and rose exponentially to 7.7 × 10⁶ (log₁₀ VL = 6.89) over 21 days. It then declined biphasically, to an intermediate value after 11 days, and then to SPVL after another 58 days; collectively, these three phases imply a total duration of 90 days for acute infection. VL increased by 0.14 per year across the period of chronic infection. At AIDS onset (defined by CD4 count; see below), VL increased at a rate corresponding to a 400-fold increase on the linear scale over 4 years, until it reached the VL maximum in AIDS, set at 6.38. Although VL affected transmission, CD4 count affected progression and mortality. CD4 count was measured in four categories, split at 500, 350, and 200, with progression to AIDS defined as entering Category 4 (Cori et al. 2015). SPVL influenced both initial CD4 category placement and subsequent progression rates.

The modeled population included 5,000 individuals between 18 and 55 years of age, seeded with 10% HIV prevalence, a value within the range estimated for MSM populations in different US metropolitan areas (Centers for Disease Control and Prevention 2016). Simulations were run for 50 years with 1-day time steps. The rate of new arrivals reflected a Poisson distribution, and departures occurred through AIDS mortality, background mortality, or aging out. We excluded antiretroviral treatment and opportunistic infection prophylaxis in our model, in order to focus on the variation in SPVL independent of treatment dynamics.

Our main outcome measures were final HIV prevalence and MSPVL among incident infections during the last 10 years of the simulation (years 40–50). We select prevalence over incidence for our epidemiological outcome because it is easier to measure in a wider range of populations, but we note that results for incidence were qualitatively similar (data not shown). We used incident MSPVL in the final 10 years to ensure sufficient data to make comparisons meaningful. We also tracked the percentage of transmissions occurring during the donor’s acute infection stage. We conduct statistical tests on outcomes (Kruskal-Wallis test, multiple linear regression), but note that the use of statistical tests in the context of simulation is debated. Any difference can become significant with large enough sample size, and conducting more simulations is typically easier than generating larger samples in empirical research. Thus, for modeling research significance tests are best conducted when number of simulations is pre-determined, and is within a typical range, as is the case here (100 replicates). Although such tests should not be over-interpreted, they can still provide a useful roadmap for distinguishing the most salient patterns within the data.

Table 1 lists the set of parameters that were systematically varied across at least one set of simulations to isolate the impact on SPVL evolution. We include default and explored values for each varied parameter; default values reflect those derived from our Atlanta data, in some cases rounded to make the subsequent sensitivity analysis more interpretable. Default values were used for each experiment in which that parameter was not experimentally varied. All other model parameters were fixed across all runs, and are listed and derived in the Supplementary data.

Table 1.

Parameters and model forms varied across scenarios (in order of exploration).

Model parameter	Measured value	Values / forms explored
Coital frequency (mean sex acts per day per extant relationship)	0.23 (Goodreau et al. 2017)	0.10, 0.15, 0.20 (default), 0.25
Proportion of population with concurrent partners	0.142 (Goodreau et al. 2017)	0.00, 0.05, 0.10, 0.15 (default), 0.20
Mean relational duration	212 days (Goodreau et al. 2017)	50, 100, 200 (default), 300, 400, 500, 750, 1,000 days
Acute-phase relative risk	N/A	1 (default), 3, 5, 10
Proportion of time through AIDS before coital cessation	0.47 (Hollingsworth et al. 2008)	0, 0.5 (default)
Heritability of SPVL	0.36 (Hollingsworth et al. 2010)	0, 0.36 (default), 0.5
Relationship between VL and transmission probability	N/A	Increasing (default, Hughes et al. 2012); plateauing (Fraser et al. 2007)

A full list of parameters held constant across scenarios, as well as further information on the derivation of these values, can be found in the Supplementary data. References to Goodreau et al. (2017) entail re-analyses of the data included in that article, calculating single overall means instead of separate values by race and relationship type, in some cases rounded to make the subsequent sensitivity analysis more interpretable. Mean relational duration presented includes those relationships for which duration is defined (i.e. that involved more than a single contact). Including one-time contacts as duration of 1 day yields a mean duration of 54 days, similar to the 50 days explored in the sensitivity analysis. Actual relational durations in the model follow a geometric distribution. Concurrency prevalence reflects the mean proportion of actors with at least two ongoing relationships at a given time point. The acute relative risk reflects the added transmissibility of acute-stage viruses beyond elevated VL, following evidence that recently transmitted viruses might be preferentially transmitted (Gnanakaran et al. 2011; Redd et al. 2012; Parrish et al. 2013).

We present one set of runs as a time series, to identify the time frame and pattern over which evolution is predicted. We then analyze results in two forms. In the first, the relationship between predictors and evolved MSPVL is considered; in the second, predictors are described in relation to both prevalence and evolved MSPVL. We conduct a Kruskal-Wallis test to determine if scenarios are significantly different from each other given within-scenario variability across runs when considering one predictor, and multiple linear regression with interactions when considering multiple predictors. All analyses were conducted in R.

3. Results

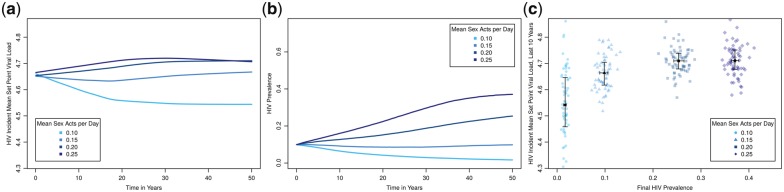
We first consider the run that reflects our best estimate for every behavioral parameter (scenario in Fig. 2a with mean sex acts per day=0.20). This model predicts that incident MSPVL should evolve to ∼4.7, which is consistent with two different papers by Herbeck et al. (2014, 2016) that each share some similarities to this model and some differences. HIV prevalence for this run (panel b) increases to a mean of 25.3% (95% range: 22.6–27.9%) over the course of the simulation; the actual race-reweighted prevalence in the source study was 27%, providing one measure of our model’s overall validity.

Figure 2.

Scenarios with all default parameters but varying coital frequency within extant relationships. (a) Time series of incident MSPVL evolution; (b) time series of HIV prevalence; (c) final HIV prevalence plotted against MSPVL. Blue dots represent outcomes from individual runs; black squares represent the mean of these and bars represent the inner 50% of the data for each scenario. HIV prevalence is measured at the end of the simulation. MSPVL is measured across all incident infections from the last 10 years of the simulation. Selection of prevalence for the x-axis and MSPVL for the y-axis is arbitrary, as the two epidemic outcomes are linked together in a feedback loop and are mutually dependent.

We next explore variation in overall coital frequency (Fig. 2), since it represents a behavioral change occurring all across the duration of infection, and thus provides a convenient baseline against which to compare features like concurrency whose effects are more concentrated at specific time points. Considering the time series (Fig. 2a and b), MSPVL evolutionary divergence among scenarios has become clear within a decade, and shows minimal additional evolution (reduced slope) after about 20 years. Prevalence, however, is still diverging after 40 years. Panel c plots the same scenarios, with final HIV prevalence (x-axis) against incident MSPVL (y-axis). The choice of axes is arbitrary, since these quantities exist in a feedback loop with no simple direction of causality; our primary interest is to understand the emergent functional relationship between the two. Despite large variation within each scenario, MSPVL varies significantly across scenarios (Kruskal-Wallis, P < 2.2e-16) covering nearly 0.2 log₁₀ units, with evidence for a plateau at higher levels. Scenarios yield a range of MSPVL values (4.54–4.71) that lies entirely between the 4.52 in one modeling work (Fraser et al. 2014) and the 4.75 in another (4.75, Herbeck et al. 2014), although some scenarios contain one or the other previous value within their simulation range. Coital frequency has a strong, non-linear effect on prevalence, as one might expect. Over the modeled range, higher prevalence was associated with higher MSPVL.

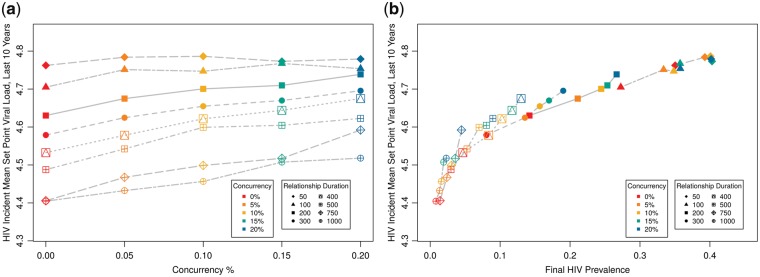
We next vary two behavioral determinants jointly: level of concurrency and relational duration. Both of these might be expected to provide disproportionate impact on the opportunity for an individual to expose a partner during acute infection, since they impact the probability that someone might contact two individuals in quick succession—one transmitting to them, and one who they can then transmit to. As noted in Section 2, all of these runs preserved the same total expected relationship time and mean number of relationships per person at any time. Given the complexity of the scenario combinations, we present both the results with one input (concurrency) plotted against MSPVL (Fig. 3a) and with the two outcomes (prevalence and MSPVL) plotted against one another (Fig. 3b). For simplicity, we suppress the individual runs and plot only means, noting that variation for these and subsequent runs followed similar patterns as for coital frequency. We analyze the results in Fig. 3a using linear regression (Table 2), which indicated that greater concurrency has a significant positive effect on incident MSPVL, relational duration has a significant negative effect, and the interaction is also significant and positive. Prevalence is strongly (but again non-linearly) associated with MSPVL across these runs (Fig. 3b). We see larger variations in MSPVL across scenarios here (∼0.4 log₁₀ units) than for coital frequency, concentrated in the low-prevalence scenarios. Runs with ∼5% prevalence or lower yielded MSPVL numbers near Fraser’s evolutionary optimum (4.52) and similar to some observed populations not captured by earlier scenarios. Although prevalence was strongly associated with MSPVL, it did not explain the entire effect of network factors on MSPVL; otherwise the lines in Fig. 3b would be superimposed, not stacked.

Figure 3.

Incident MSPVL and final HIV prevalence, varying mean relational duration and level of relational concurrency. (a) MSPVL; (b) prevalence plotted against MSPVL.

Table 2.

Multiple linear regression results for impact of predictors on MSPVL.

	Estimate	SE	P-value
(A) Concurrency and relational duration
Intercept	4.734	0.007	<0.0001
Relational durationa	−0.039	0.001	<0.0001
Concurrency	0.282	0.061	<0.0001
Rel. duration x concurrencya	0.057	0.012	<0.0001
Adjusted R2: 0.920
(B) Concurrency and acute relative risk of transmission
Intercept	4.643	0.008	<0.0001
Acute relative risk	0.003	0.001	0.0312
Concurrency	0.537	0.065	<0.0001
Acute rel. risk x concurrency	0.032	0.011	0.0056
Adjusted R2: 0.837
(C) Concurrency and coital cessation
Intercept	4.550	0.015	<0.0001
Coital cessation	0.193	0.046	0.0001
Concurrency	0.767	0.124	<0.0001
Coital cessation x concurrency	−0.562	0.372	0.1403
Adjusted R2: 0.670

^arelational duration coefficients are expressed per 100 days.

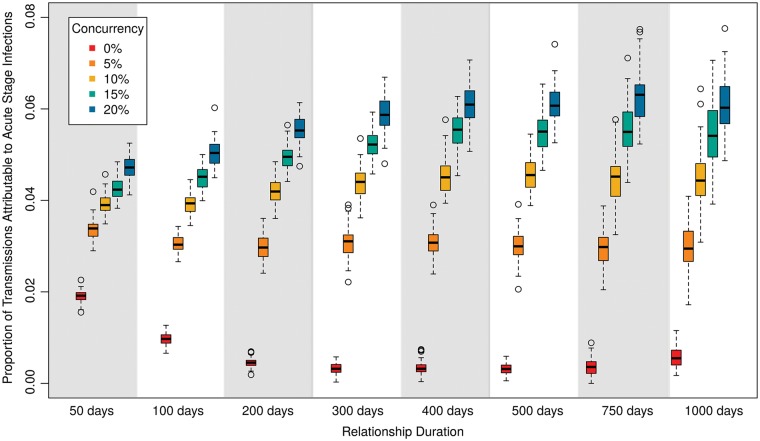
Figure 4 helps demonstrate why. Although both concurrency and relational duration impacted the percentage of transmissions occurring during the donor’s acute stage, concurrency had a much stronger influence. This is particularly dramatic at longer relational durations, where concurrency was the main mechanism allowing an individual to transmit to one partner shortly after acquisition from another. This disproportionate effect of concurrency during acute infection appears to shift the evolutionary trade-off in ways that are not fully captured by differences in prevalence among scenarios. Note that the proportion of transmissions attributable to acute infections is <7% for all of these scenarios; these numbers are in line with some estimates from the literature but lower than others, as described in one review (Goodreau et al. 2012b).

Figure 4.

Percent of transmissions that occur during the acute HIV infection phase, for the same scenarios as in Figure 3. Measure is taken for all transmissions during the final year of the simulation.

To consider how behavioral and virological determinants may compare or interact, we jointly considered one type of each phenomenon that impacts acute-phase transmission: concurrency, and the relative risk of transmission per acute-phase serodiscordant coital act, beyond elevated VL (Wawer et al. 2005). This latter measure is subject to debate, and indeed is the source for some of the variation previously mentioned among estimates for the proportion of transmissions attributable to acute infection. Here (and henceforth), we present only the multiple linear regression with MSPVL as outcome (Table 2[B]), and the figure panel with prevalence and MSPVL plotted against one another (Fig. 5). Boosting viral transmissibility during acute infection had effectively no impact when concurrency was absent, since there were few instances of serodiscordant contacts during acute infection. As concurrency increased, however, higher acute relative transmission rates increased both prevalence and MSPVL, but the latter faster than the former, relative to the scenarios in Fig. 3. This is reflected in Table 2, where the main effect of the acute transmission rate is only marginally significant, but the interaction effect with concurrency is highly so. Note that in these scenarios the proportion of incident infections attributable to acute infection rose as high as 13.4, 18.2, and 25.6% for the highest concurrency level for acute relative transmission rates of 3, 5, and 10, respectively.

Figure 5.

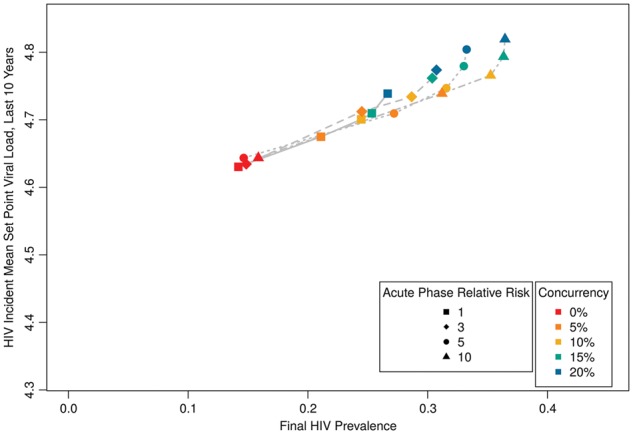
HIV prevalence by incident MSPVL, for different levels of heightened infectiousness during acute infection (above and beyond heightened VL) and varying concurrency.

We next shifted to the timing of coital cessation in AIDS (Table 2[C];Fig. 6); we again included different levels of concurrency for comparison. We see a dramatic reduction in HIV prevalence, but much less change in MSPVL than in previous scenarios across the same range of prevalence values. For instance, comparing across the two runs with 15% concurrency, we see large differences in prevalence (1.3 and 25% for earlier and later coital cessation, respectively), but relatively little difference in MSPVL (4.66, 4.71). This is the first model where we do not see a significant interaction between our two predictors (Table 2[C]); this makes sense, given that concurrency primarily impacts transmission during acute infection and coital cessation during late infection.

Figure 6.

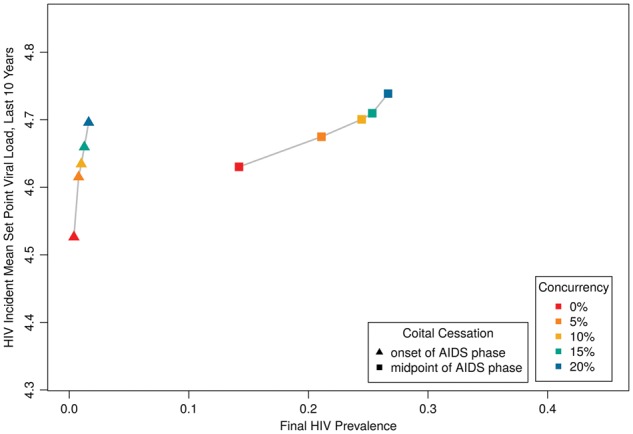
HIV prevalence by incident MSPVL, for scenarios varying timing of coital cessation during AIDS stage, and concurrency.

Figure 7 displays a sensitivity analysis using a plateauing VL transmission function (Fraser et al. 2007), rather than a continually increasing one. The plateauing scenario that used default parameters led to higher prevalence values than that for the continually increasing model, largely because the former assumed higher transmissibility than the latter at moderate VLs, where most HIV-infected persons are found. To facilitate comparisons across a similar range of prevalence values, we thus considered a broad range of coital frequencies. The plateauing function always led to lower incident MSPVL than the increasing function, whether comparing across identical coital frequency or identical prevalence. The plateauing function’s predicted MSPVL was most commonly ∼4.4–4.5, similar to the prediction of Fraser et al. (2007). At lower prevalence levels, incident MSPVL values dropped to 4.3, making this parametrization the first to generate MSPVL values consistent with certain empirical populations—e.g. Amsterdam MSM cohort (Fraser et al. 2007), US military cohort (Crum-Cianflone et al. 2010)—while no longer consistent with others, including a heterosexual cohort in Zambia (Fideli et al. 2001; Fraser et al. 2007), and a mixed predominantly European cohort (Dorrucci et al. 2007).

Figure 7.

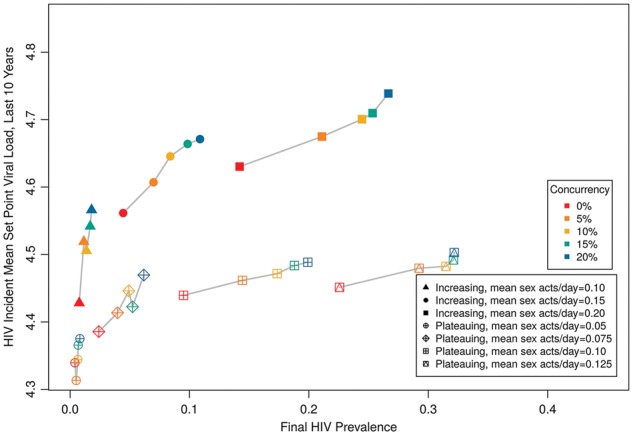
HIV prevalence by MSPVL, comparing two functional forms for the relationship between VL and transmission (continually increasing vs. plateauing), for a range of coital frequencies and concurrency levels. Here the filled symbols signify the increasing transmission function, open symbols signify the plateauing transmission function. Because the two models yielded different prevalence levels with default parameters, we vary coital frequency over different ranges for the two forms in order to compare across scenarios with similar prevalence.

Finally, we conducted a sensitivity analysis on the level of heritability, given differences on this metric in the literature and, likely, in real populations (Fig. 8). We included a higher level (0.5) that is more similar to estimates derived using phylogenetic methods (Alizon et al. 2010), and a lower level of 0% as an extreme case and as a means of confirming that no evolution should be enabled here. If SPVL heritability truly equaled 0.5, our model could explain MSPVLs in individual populations as high as 4.8. As expected, with 0% heritability the virus was unable to evolve away from initial MSPVL (4.5). Prevalence in the no-evolution runs was 8–16% lower than in comparable scenarios with default heritability; incidence (not shown) was 15–24% lower. The divergence in incidence tended to be higher with higher concurrency. This potential excess epidemic burden of behavioral phenomena like concurrency made possible by viral evolution would be missed by traditional epidemic models that do not account for this possibility.

Figure 8.

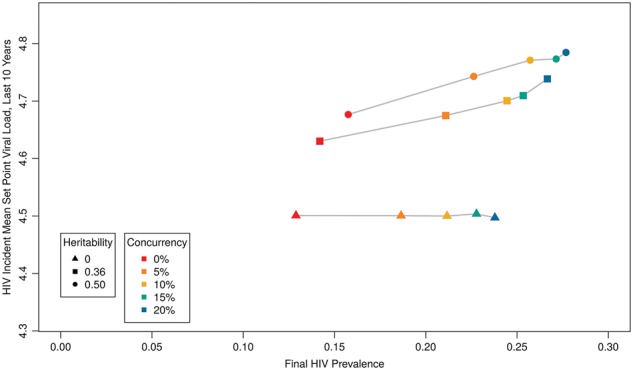
HIV prevalence by MSPVL, varying heritability and concurrency.

4. Discussion

For reasons that are not fully explained, the distribution of SPVL varies across populations. Beginning with a network model parameterized from published data and then varying key parameters, we identified multiple aspects of sexual networks that could influence the evolution of MSPVL in different populations. These include relational concurrency, which has received considerable attention in the literature on population disparities in HIV burden (Mah and Halperin 2010; Morris et al. 2010; Kenyon et al. 2016), along with behaviors that impact transmission potential at different stages, such as the timing of coital cessation during AIDS. Our base model, using only data-derived parameters, generated incident MSPVL of 4.7, consistent with previous models that share some similarities (Herbeck et al. 2018). By varying these features in models using our baseline transmission function (transmission probability continually increases with increasing VL), we were able to generate epidemics in which incident MSPVL varied systematically between scenarios from ∼4.4 to 4.8 log₁₀ copies/ml. This range in magnitude is greater than the traditional threshold for clinical significance (0.3 log10 copies/ml, Modjarrad et al. 2008), and is as wide as the variation among the majority of populations in a recent meta-analysis of SPVL evolution (Herbeck et al. 2012).

Much of this effect was mediated by impacts on overall HIV burden as measured by HIV prevalence. For prevalence values up to at least about 30–40%, ceteris paribus models with higher HIV prevalence had higher MSPVL. Presumably the increase in MSPVL with prevalence is because the greater overall transmission opportunity shifts the virus’s evolutionary landscape, with the shortened lifespans generated by increased virulence more than compensated for by higher transmission opportunities. At most prevalence levels, our models overall yielded higher MSPVL estimates than that predicted by Fraser et al. (4.52 log₁₀ copies/ml). Only for a handful of scenarios at low prevalence (∼5%) did we obtain expected MSPVL values that low. We also saw that the level of heritability of HIV, which may vary among populations or through time (Fraser et al. 2014), could shift these results up or down. Likewise, they were sensitive to the assumption we made about the nature of infectiousness at high VLs, with a plateauing relationship between VL and transmission probability such as that used in Fraser et al. yielding lower predicted MSPVLs.

The elements of sexual behaviors and networks considered had additional impacts on SPVL beyond those mediated by prevalence. Specifically, factors that disproportionately impacted transmission opportunities during early infection—especially the prevalence of relational concurrency—more strongly affected MSPVL evolution than did factors whose impacts were spread throughout the course of infection, and much more strongly than those whose effects appeared during AIDS. This makes sense from an evolutionary perspective—the earlier in an infected lifespan that a phenomenon increases transmission opportunities, the less crucial it is for a pathogen to delay host death. However, these effects were not straightforward, instead interacting in complex ways. For instance, concurrency’s impact on MSPVL varied depending on mean relational duration, since the two jointly determine infection opportunities during acute infection.

We saw large stochastic variation within scenarios; for example, individual simulations in a scenario with 0.1 coital acts/day in ongoing relationships varied over nearly 0.3 log₁₀ SPVL units, from ∼4.5 to 4.8. Some of the observed MSPVL variation seen among real populations is undoubtedly due to stochasticity; however, we caution against interpreting the level of stochasticity in our runs as a measure of the expected stochastic variation among real populations, which vary in size and interconnectedness. We reiterate that our analyses demonstrated significant systematic differences for most comparisons between scenarios despite this stochasticity.

We parametrized our model using MSM transmission probabilities and related parameters. Notably, this model generated HIV prevalence consistent with that in the source population for the behavioral parameters, and an expected log₁₀ MSPVL of 4.7, consistent with two previous papers using variations on this model (Herbeck et al. 2014, 2016). We anticipate that a model focused on heterosexuals and penile-vaginal sex would yield qualitatively similar phenomena across scenarios. Such an analysis would allow for comparisons between MSM and heterosexual epidemics, and is underway. Notably, however, one large meta-analysis (Herbeck et al. 2012) did not find transmission group to be a significant predictor of VL. Moreover, cohorts that contained MSM exclusively or predominantly, and MSM subsamples of larger studies, cover the full range of observed SPVL values (Müller et al. 2006; Troude et al. 2009).

That lack of difference in MSPVL between heterosexuals and MSM is surprising for multiple reasons, including the fact that one might expect these two groups to differ on some of the key factors found in this paper to influence SPVL, noticeably concurrency and mean degree. However, there remain many additional network effects that could further impact SPVL and its relationship to prevalence, and it may be that these roughly cancel out in the pooled populations in Herbeck et al. (2012). For example, one can imagine a highly heterogeneous population containing some people with high risk and many isolated from any meaningful HIV risk; this is similar to structures commonly modeled in HIV epidemiology in order to calibrate to observed HIV prevalence. This population should exhibit lower overall HIV prevalence relative to a population in which those without risk were simply absent, while having no impact on viral evolution, since this larger population is invisible to the virus. Many other features—anything from the functional form of new arrivals in the population to the rise of antiretroviral treatment and PrEP—may further complicate these relationships (Herbeck et al. 2016). We are exploring some of these additional effects in ongoing work, including risk heterogeneity in the form of both partner numbers and sexual role (insertive vs. receptive), in both MSM and heterosexual populations.

Our models considered HIV prevalence and SPVL in a mature epidemic, i.e. after the effects of initial spread had passed. Theoretical work shows that short-term virulence evolution can differ from longer-term dynamics (Day and Proulx 2004; Andre and Hochberg 2005). Considering HIV, e.g. one might expect that a larger proportion of the population is in acute infection during initial rapid spread than later, providing a different fitness landscape at that point. Our results did suggest that SPVL evolution within a stable behavioral regime is most concentrated in the first two decades of spread, even as prevalence continues to change beyond that. However, without deeper analysis of time trends, it is difficult for us to determine how much of observed heterogeneity on MSPVL among populations is due to the different times since epidemic initiation. Nonetheless, we have demonstrated that observed ranges are at least plausible from variation in sexual network structure alone. Analysis of time trends, and comparison to observed data, are part of the extensions we are currently conducting.

All models require decisions about the levels of forms of complexity and specificity to include. General models allow for basic insights, while more complex models allow for knowledge specific to a given case. We opted for a detailed model containing many features specific to HIV since one of our primary goals was to determine the extent to which observed variation in HIV MSPVL among populations could be captured by variation in a few key parameters. However, this limits our ability to extrapolate our findings to pathogens with features different than HIV, e.g. with recovery, or where transmission is density-dependent. We believe that such detailed models have an important place in understanding the dynamics of specific pathogens under different conditions, in line with previous calls in the virulence evolution literature (Ebert and Bull 2003; Alizon et al. 2009; Bull and Lauring 2014). Although we cannot prove it, our assumption is that a simpler model would find qualitatively similar findings as long as it contained a core set of features—i.e. heritability of SPVL, background births and deaths, dynamic partnerships, VL impacts on transmission and survival, acute infection with elevated VL, and rising VL and mortality with AIDS. Given our focus on relational concurrency, such a model would of course also need to be able to represent this phenomenon. Although explicit models of networks can do so, various methods have also been developed to consider relational concurrency within a compartmental modeling or analytical framework (Powers et al. 2011; Leung, Kretzschmar, and Diekmann 2012; Miller and Slim 2017). Key features that we believe any framework needs to include to model this phenomenon faithfully to empirical data and replicate our results include allowing for ongoing (not just one-time) concurrent relationships, allowing some but not all people to have concurrent partners, and somehow assessing epidemic potential along the reachable path of infection multiple steps out from currently infected individuals, as these paths can vary dramatically with small changes in concurrency prevalence (Morris et al. 2007). Determining for certain the ability for different model approximations to identify the impact of concurrency on SPVL evolution would require a full comparative investigation.

This study suggests that the observed range of variation in MSPVL across populations could in theory be explained by variation in underlying sexual behaviors and sexual network characteristics. Many, but not all, of those underlying behavioral factors also predict higher prevalence populations having higher MSPVL, suggesting a correlation across populations in prevalence and MSPVL. However, the relationships between these network factors, prevalence, and SPVL can be quite complex. Previous work to explain SPVL evolution and variation, whether empirical or model-based, has not fully considered these relationships (Fraser et al. 2007; Herbeck et al. 2012). Future efforts to understand the empirical variation in SPVL among populations should consider the magnitude of local HIV burden and features of network structure and sexual behavior.

Data availability

Data (in the form of parameter values derived from the literature) can be found in the Supplementary data. Model code can be found at https://github.com/EvoNetHIV/Goodreau_et_al_Behavior_-_SPVL.