Aiding the Digital Mammogram for Detecting the Breast Cancer Using Shearlet Transform and Neural Network

Abstract

Objective:

Breast Cancer is the most invasive disease and fatal disease next to lung cancer in human. Early detection of breast cancer is accomplished by X-ray mammography. Mammography is the most effective and efficient technique used for detection of breast cancer in women and also to improve the breast cancer prognosis. The numbers of images need to be examined by the radiologists, the resulting may be misdiagnosis due to human errors by visual Fatigue. In order to avoid human errors, Computer Aided Diagnosis is implemented. In Computer Aided Diagnosis system, number of processing and analysis of an image is done by the suitable algorithm.

Methods:

This paper proposed a technique to aid radiologist to diagnosis breast cancer using Shearlet transform image enhancement method. Similar to wavelet filter, Shearlet coefficients are more directional sensitive than wavelet filters which helps detecting the cancer cells particularly for small contours. After enhancement of an image, segmentation algorithm is applied to identify the suspicious region.

Result:

Many features are extracted and utilized to classify the mammographic images into harmful or harmless tissues using neural network classifier.

Conclusions:

Multi-scale Shearlet transform because more details on data phase, directionality and shift invariance than wavelet based transforms. The proposed Shearlet transform gives multi resolution result and generate malign and benign classification more accurate up to 93.45% utilizing DDSM database.

Introduction

The main cause of mortality for women is due to breast cancer which occurs mostly between the ages of 35 and 55 years. It has been shown that early detection and timely treatment of breast cancer can be the most effective method in reducing mortality rate. Currently mammography is the most efficient tool used by radiologists for the detection of breast cancers (Highnam et al., 1999). Digital mammography with its improved features has been successful in reducing negative biopsy ratio and cost to society. From the literature, it is found that digital mammography is a convenient and important tool used in the classification of tumors (Anuj Kumar et al., 2015). It has proved its effectiveness in the diagnosis of breast cancer.

Wavelet Transform

Wavelet transform makes an efficient representation for mammographic images. Recently, several methods were introduced for mammogram analysis using wavelet (Dheeba et al., 2014; Pereira et al., 2014; Meenakshi Pawara et al.,2016). In multi resolution analysis of mammograms proved that wavelet transform coefficient is more effective for diagnosis Liu et al. in (Liu et al., 2001). These studies of mammogram diagnosis, a list of statistical features are extracted using binary tree classifier. Ferreira and Borges (2003) have introduced that getting the wavelet coefficients are biggest at the lowest frequency of Wavelet transform and it could be used as a coefficient value the particular mammogram. It obtained results are the Wavelet coefficients and it produced the accuracy of classification is better. Rashed et al., (2007) in to extract a fraction of the biggest coefficients from the multi-resolution mammogram analysis in multilevel decomposition.

Space scale decomposition of images u can be done by wavelet transformation where u ϵ M²(S²).‘u’ can be mapped using the coefficient C_ψu(b,x) depending on xϵS² with b be a positive value. Moreover, the Wavelet transformation of u is relative to gradient of image u_b.

It indicates that highest magnitude for the smoothed image’s gradient ub relates exactly to the highest magnitude of Wavelet transformation C_ψu(b,x). It serves a framework for multi scale edge analysis mathematically (Mallat et al., 1992). Apart from this there is a number of efficient numerical wavelet transformation exists. But the most challenges task is to detect the image with sharp edges (Ziou et al., 1998) or changes.

This trouble is due to the occurrence of noise in image when more edges crosses each other or coupled with each other. During those situations, Wavelet approach plays a vital role.

• It is daunting to detect the close edges - The closed edges are made blurred in single curve using Gaussian filtering technique.

• Angular accuracy is meager - The Gaussian filtering causes edge orientation detection inaccurate with the availability of sharp changes in curvature. This lead to weaker detection of junctions and corners.

To avoid these difficulties one has to add the addition feature is anisotropic of edge lines and curves.

Materials and Methods

Shearlet Transform

As already mentioned digital mammography has been an indispensible method for diagnosis tumors and other applications found in the literature survey have declared its effectiveness in identification of breast cancers (Fu et al., 2005). The proposed algorithm enhances mammogram image quality using multi-resolution analysis based on the Shearlet transform. The proposed method is based on the new multi-scale and multi-resolution transforms (Labate et al., 2005). Instead of the traditional Wavelets which are not success to capture the geometric information regularity because it is only supports the isotropic. On the contrary, Shearlet transform produces a good performance in many applications that include medical image processing gave more information on data and directionality better than Wavelet transform (Nan-Chyuan et al., 2011). An application of Shearlet transform results in enhanced image quality is clearer for calcifications. This makes that very small contour more prominent and the radiologist can easily diagnosis a cluster of calcifications and getting features of the calcifications from the images are made more evident, it would be helpful to the radiologist can determine whether the calcifications are normal or abnormal.

Shearlet filters are more directional sensitive when compared to Wavelet filters like Gabor filters (Jayasree et al., 2015) so that it is more suitable for tiny cells of cancer. The Shearlet transform collects visual information from the edges found from various orientations and scales using multi scale decomposition (Guo et al., 2009; Rezaeilouyeh et al., 2013; Sheng et al., 2009). The images are classified into malign and benign by representing them as a histogram of Shearlet coefficients.

In Haralick et al., (1973) proposed a new multidimensional representation to replace the scalable collection of isotropic Gaussian filters into a family of steerable and scalable anisotropic Gaussian filters. But the wavelet transform do not support well in multi-dimensional data.

Wavelets are very well performed in point-wise singularities. But the Wavelet transform is not able to detect the directionality information about the image. Wavelet transform is basically associated with two parameters, one is the scaling parameter a and another one is the translation parameter t. To overcome these limitations, while retaining most of the aspects of the mathematical framework of wavelets is shearlet transform. The Shearlet transform shows an optimal behavior about the detection of directional information. The basic idea for the definition of continuous Shearlets transform is two dilation groups; it consists of products of parabolic scaling matrices and shear matrices. The reference (Easley G et al., 2008) provides more details about the comparison of Shearlets and other orientable multi-scale transforms. Compared to the ordinary Wavelets, Shearlet can capture directional features information like orientations in images, which is the most discriminating factor.

The singularities of the signal can be easily identified by continuous wavelet transformation. This transformation decomposes into b->0 until t is closer to x₀ when the function u is smooth (Holschneider M, 1995). This will be more useful when the points are irregular and for the ability to detect the edges.

The extra information regarding the set of singularities u is not generated by continuous wavelet transform. The gathering of geometric information like edge orientation will be more helpful in many situations. Continuous Shearlet transform can be used to achieve this task. The representation of this transform will be,

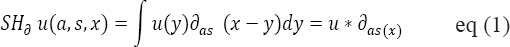
The Shearlet transform is similar to the Curvelet transform (Sami et al., 2015) it was introduced by Candès and Donoho. Shearlets and Curvelets are well known mathematical representation of images with edges but different spatial-frequency representations. Curvelet transform implementation is same tiling as that of the Shearlet transform. The Shearlet approach has similar that of other methods are contourlets (Do et al., 2005; Po et al., 2006) complex wavelets (Selesnick et al., 2005), ridgelets (Candès et al., 1999), and curvelets (Candès et al., 2004; Candès et al., 2005) used in applied various mathematical and engineering applications overcoming the limitations of the traditional Wavelets. Shearlet framework is different from the other method and it has a unique combination of mathematical rigidness, optimal efficiency and computational efficiency when it representing the edges.

When considering the recovering f as a function where f ϵ M²(S) from data y, where y can be derived as

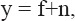
where n is the white noise with SD σ. The optimization of ~f reducing the estimator is the main action to be done which can be measured using the M² norm as

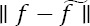
The risk of ~f can be defined by Mean Square Error

Here, the probability distribution function for noise ‘n’ is used to calculate the expectation. ‘f’ is the key factor to assess the risk. When working with multivariable functions, this wavelet transforms will be optimal which shows that the minimax value for MSE will not be provided by Wavelet threshold. For example Processing the cartoon like images when the function fϵε²(R²), define |c(f)ⁿ|_(N) to be the N-th highest value in the wavelet coefficient of f stated as (Easley, 2002):

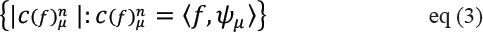
Where{ ψµ } is a 2D Wavelet basis. Since :

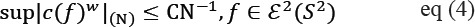
The wavelet estimator obeys:

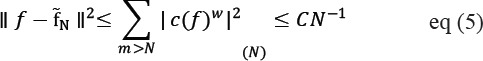
It shows that wavelet threshold estimator’s MSE obeys

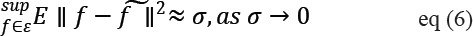
Here σ indicates the level of noise.

Say, |c(f)^S|_(N) is the N-th highest entry in the Shearlet coefficients sequence f which can be derived by,

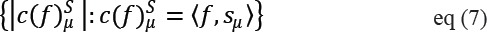
where s_μ is a Shearlet frame. The result will be:

When log factor is neglected, ~f_N fulfills:

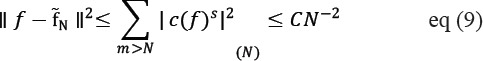
The threshold process of Shearlet coefficient’s is the key issue of denoising policy produce the estimator f as ~f MSE can be defined as

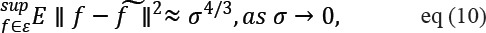
The observation of Shearlet threshold process is capable of attaining minimax mean square error for edges of the images. Finally, the Shearlet can work as a multi scale and directional operator with many useful features as follows.

• - Edge orientation can be detected more accurately.

• - The geometry of the edges can be captured by Shearlet transform with the help of multiple orientations and anisotropic dilations.

• - Shearlet transform maintains efficient and stable decomposition and reconstruction of images using algorithms.

Results

The proposed system is developed by Shearlet transform which is based on multi-resolution and multi-scale representation of the mammogram images. The largest coefficient value is extracted and that coefficient value is applied to the image.

Database Collections

DDSM is a resource for mammographic image. Data set in the proposed method is taken from DDSM and it is use to apply the proposed technique. These images were already analyzed and an expert radiologist can label for each images based on technical experience and biopsy. In DDSM database, depth of each pixel is 12 bits and size of each pixel is 0.043mm. The selected dataset includes varies cases. 300 mammograms is taken from the dataset which is left and right breast and it consists of 100 were detected as malignant and 100 as benign and 100 as normal.

Breast Region Segmentation

Each mammogram images size are 1,024 × 1,024 pixels. First Shearlet transform is applied to that image. Need to cut off the unwanted portion of an image, the cropping operations is applied on that image. Cropping operation is performed manually and it produces Region of Interest (ROI) for the given abnormality of images.

After identifying ROI, the next step is to detect edges of the enhanced image. Edges are detected by applying canny edge detection algorithm for segmenting the ROI image. To take the detailed description of the image, need to perform segmentation process. In segmentation process, an image is taken as input and some detailed description of the scene or object is found for output.

Figure 1.

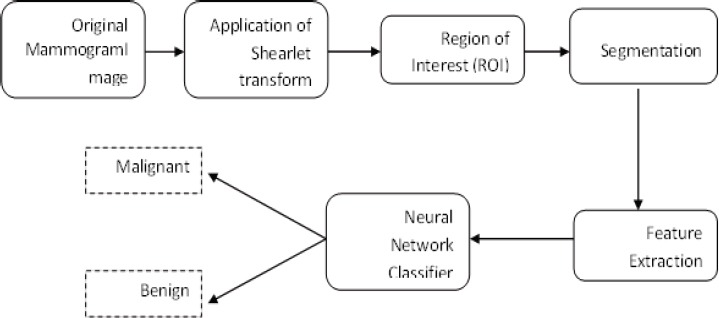
The Entire Workflow of the System

Figure 2.

(a) Original image (b) Enhanced image using Shearlet transform (c) ROI image (d) Segmented image

Figure 4.

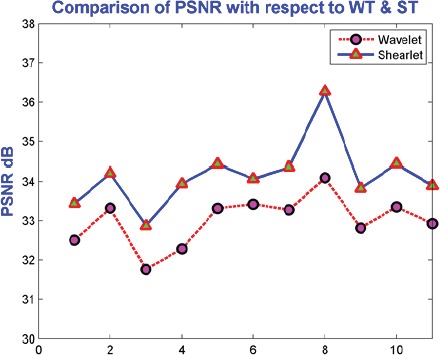
Comparison of PSNR with Respect to Wavelet and Shearlet Transform.

Mean Square Error (MSE)

Mean Square Error (MSE) is the simplest quality measurements in images. The performance of denoising is evaluated using Peak Signal to-Noise Ratio (PSNR) and Mean Square Error (MSE). PSNR is defined as the ratio of signal power to noise power. It basically obtains the gray value difference between resulting image and original image.

MSE is given by:

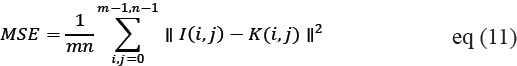
MSE value is get larger then it declares that poor image quality. Figure-3 shows MSE values for denoising images by Wavelet and Shearlet transform.

Figure 3.

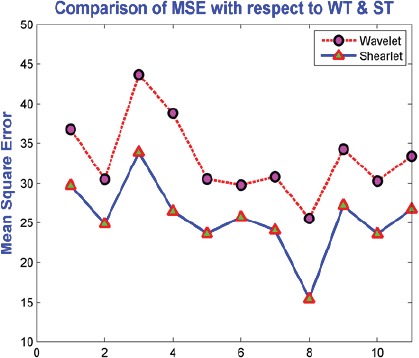
Comparison of Mean Square Error Values with Respect to Wavelet and ShearletTransform

Peak Signal to Noise Ratio (PSNR)

Experimental result of shearlet shows that it has improved value of PSNR and MSE when compared to the Wavelet transform. Demonstration of Shetarlet denoising experimental work has more effective than Wavelet as evaluated in terms of MSE.

Proposed method gave well performance of MSE and PSNR value for noise contaminated images. Higher value of Peak Signal to Noise Ratio is from the high quality image and The PSNR is defined as:

Figure 5.

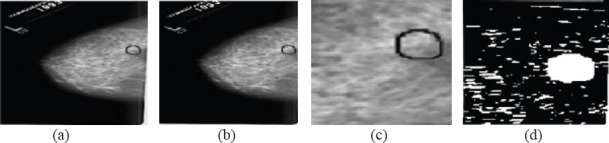
(a) Original image (b) Enhanced image by wavelet transform (c) Region of Interest (ROI) (d) detected region

Figure 6.

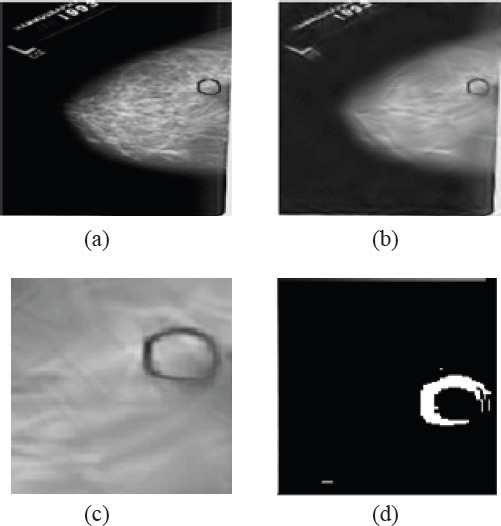
(a) Original image (b) Enhanced image by shearlet transform (c) Region of Interest (ROI) (d) detected region

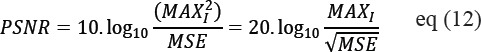
Here, the maximum value for the pixel is MAX. The above mentioned are the PSNR value of denoised is compared with Wavelet and Shearlet transform.

Features Extraction

Features extraction is the one of the important techniques for classifying the images. The features are extracted for classifying the image (Clausi DA, 2002). Features are array of gray level variation that is Gray Level Co-occurrence Matrix (GLCM) (Cheng HD et al., 2003). In GLCM mathematical measurements are correlation, energy, entropy, homogeneity and contrast. Table 3 shows GLCM features of normal and cancer. These features as input and it could be given to the neural network classifier (Shekar Singh et al., 2011) and these features are used to train the neural network until reaching the best classification.

Table 1.

GLCM Features value for Normal and Cancer Class

Image id	Image class	contrast	Correlation	Energy	homogeneity	Entropy
1.	Normal	0.7044	0.8447	0.3243	0.9206	3.6319
2.	Normal	0.6436	0.8908	0.6859	0.9472	1.7817
3.	Normal	0.6066	0.9612	0.3577	0.948	2.6953
4.	Normal	0.4013	0.9287	0.4871	0.9484	2.4014
5.	Cancer	1.1898	0.7602	0.7099	0.9523	0.8173
6.	Cancer	0.0533	0.9733	0.4851	0.9902	1.6779
7.	Cancer	0.1178	0.9727	0.4761	0.9844	1.2735
8.	Cancer	0.1851	0.8988	0.8729	0.9859	0.5689
9.	Benign	1.0129	0.7755	0.8258	0.9716	0.6722
10.	Benign	0.6446	0.8679	0.8215	0.9809	0.6659
11.	Benign	1.4076	0.787	0.7366	0.9592	0.8398
12.	Benign	0.828	0.9493	0.491	0.9736	1.2693

Table 2.

Confusion Matrix

Actual	Predicted
	Positive	Negative
Positive	TP	FN
Negative	FP	TN

Table 3.

Performance Metrics

Measures	Formula
Sensitivity	TP/(TP+FN)
Specificity	TN/(TN+FP)
Accuracy	(TP+TN)/(TP+FP+TN+FN)

Neural Networks

Neural network can be built using a set of input, activation functions and hidden unit amd output units. The first layer consist of 5 nodes and second one with 2 nodes.

The network’s overall output is dependent on functions like sigmoid. The training of experience is made by neural network. It can be done by providing the input to the neural network and using the past experience, it will generate the result. Totally 5 GLCM features were fed into the input layer of the neural network. The output of the neural network is binary i.e. Either 1 (normal) or 0 (cancer attacked).

• - Input Unit: initially raw data will be fed into the network using this layer.

• - Hidden Unit – The work is this unit is controlled by two factors. The input units and weights on connections in between input and hidden units.

• - Output unit – The performance of output unit depends on hidden units and weights of hidden and output units.

Back Propagation Neural Network (BPNN)

The BPNN connects the artificial neurons layer by layer by acting as a mathematical model. The error function’s local minima are calculated using this BPNN. It performs major functionalities like error propagation, calculation of errors, data presentation and adjustment of synapses. They perform this work continuously to evaluate the output, training arriving inputs and adapting weights. The dual layer neural network has input unit, output unit and hidden unit. In this, the input unit is not accounted as they are used to disperse the data inside the network.

On combining all the functions from training to learning through transfer function, the classification utilizes BPNN the most successful tool. All the nodes of the output units are connected to a node which evaluates ½(oij − tij)2 where both tij and oij represents the elements of the target ti and the output vector oi. The output sum Ei will be produced when summing up the m nodes collected at a node. This extension of network pattern should be followed for all the pattern ti. The errors are collected and summed by the computing sum,

The error function E will be the output of the extended network. The resulting output is multiplied using the value of left part of unit after the incoming information is summed up. Finally the result is returned to the unit’s left side. Totally 300 mammograms are used to extract 5 GLCM features and the neural network are fed with these inputs. Weight values are stored and updated after the training process. More than 200 mammogram images are used to make trained network tests. Saved weight values are used to calculate the output of the training process. Here in Figure 7, the working of the training process is defined.

Figure 7.

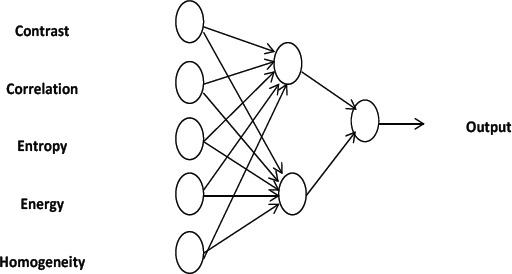
Working of Neural Networks

Discussion

Confusion matrix table is a 2*2 Table used to define the count of true positives, false positives, true negatives, false negatives. It produces more accurate and detailed analysis rather than guessing the values. The performance of the classifier not depends on the accuracy because if data set is unbalanced the result will be misleading. This matrix shows the difference between the actual and predicted information generated by the classification. The correct and incorrect patterns are examined to analyze the performance.

Neural network classifier used GLCM features for classification. The Classifier used some portion of data as training data and some portion as testing data. Proposed work considered the DDSM database for experiment. Training dataset contains 225 mammograms (each with 75 counts of normal, benign, cancer) and testing dataset with 75 mammograms (each with 25 counts of normal, benign and cancer).

Initially all the features from mammograms are extracted. Our proposed work has 5 units in input layers, 1 unit of output layer, 2 units in of hidden layers. The confusion matrix is defined in Table 2. The sensitivity and specificity values will be larger if the performance is higher.

The matrixes that we calculate from this experiment are as follows. Sensitivity of the data is derived as the ration between the count of true positive predictions and the total count of regions in the test set. It is defined as:

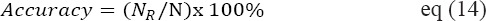
Here the count of exactly classified regions are denoted by NR and the count of test set are denoted by N. Count of FPs per case are denoted by False positive fraction (FPF) whereas true positive detection rate are denoted by true positive fraction (TPF).

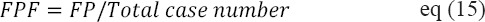
Formula for Measures

• TP-prediction of cancer as cancer

• FP-prediction of cancer as normal

• TN-prediction of normal as normal

• FN- prediction of normal as cancer

DDSM database is used for Mammograms data. The images have been taken to calculate the system performance.

Table 4 shows the Shearlet transform’s system performance indicating sensitivity of 91.66%, 95.45% specificity and 93.47% accuracy. FPF is 0.08 and TPF is 0.92.

Table 4.

Confusion Matrix of Classification

	Malignant (Cancer)	Benign (Normal)
Malignant (Cancer)	22	1
Benign (Normal)	2	21

In conclusion, it is proposed with a novel idea of digital mammogram image classification. Mammogram image processing is more efficient for Multi-scale Shearlet transform because more details on data phase, directionality and shift invariance than wavelet based transforms. The proposed Shearlet transform gives multi resolution result and generate malign and benign classification more accurate up to 93.45% utilizing DDSM database. The final result of the classification proved to be more hopeful and more accurate. In future the possibilities of considering the most optimal set of features are to be done in order to create more accurate classification.