Geometric partitioning of cohesin and condensin is a consequence of chromatin loops

Abstract

SMC (structural maintenance of chromosomes) complexes condensin and cohesin are crucial for proper chromosome organization. Condensin has been reported to be a mechanochemical motor capable of forming chromatin loops, while cohesin passively diffuses along chromatin to tether sister chromatids. In budding yeast, the pericentric region is enriched in both condensin and cohesin. As in higher-eukaryotic chromosomes, condensin is localized to the axial chromatin of the pericentric region, while cohesin is enriched in the radial chromatin. Thus, the pericentric region serves as an ideal model for deducing the role of SMC complexes in chromosome organization. We find condensin-mediated chromatin loops establish a robust chromatin organization, while cohesin limits the area that chromatin loops can explore. Upon biorientation, extensional force from the mitotic spindle aggregates condensin-bound chromatin from its equilibrium position to the axial core of pericentric chromatin, resulting in amplified axial tension. The axial localization of condensin depends on condensin’s ability to bind to chromatin to form loops, while the radial localization of cohesin depends on cohesin’s ability to diffuse along chromatin. The different chromatin-tethering modalities of condensin and cohesin result in their geometric partitioning in the presence of an extensional force on chromatin.

INTRODUCTION

Cohesin and condensin are both SMC (structural maintenance of chromosomes) complexes that form tripartite, ring-like molecular complexes that interact with chromatin and are localized throughout the genome (Nasmyth and Haering, 2009; Jeppsson et al., 2014; Hirano, 2016; Makrantoni and Marston, 2018). Cohesin is responsible for sister-chromatid cohesion and chromosome condensation (Guacci et al., 1997; Michaelis et al., 1997), while condensin is responsible for chromosome condensation (Hirano, 2012, 2016; Schalbetter et al., 2017). Both complexes are critical for proper genome organization yet have distinct geometric localizations within chromosomes (Hirota et al., 2004; Ono et al., 2017; Walther et al., 2018). A key characteristic of chromosome organization in higher eukaryotes, based on studies using HeLa cells and Xenopus egg extract (Ono et al., 2003) and DT40 cells (Green et al., 2012), is a condensin II rich axial core with more radial distribution of condensin I (Hirano, 2016). Addition of reconstituted condensin I to condensin-depleted Xenopus egg extracts resulted in the formation of chromosomes with condensin localizing to chromosome axes (Kinoshita et al., 2015). Even upon depletion of nucleosomes in Xenopus egg extracts, chromatid-like structures formed with condensin present along their axes (Shintomi et al., 2017). Loss of condensin in DT40 cells resulted in larger fluctuations in interkinetochore distance during metaphase of mitosis (Ribeiro et al., 2009). A recent study has demonstrated, using micromanipulation of single human mitotic chromosomes from HeLa cells, that the elastic stiffness of chromosomes is reduced upon condensin depletion and increased upon condensin enrichment (Sun et al., 2018). These studies demonstrate condensin alters chromatin organization to be more resistive to deformation. Studies using 5C and Hi-C techniques on human derived cell lines and DT40 (chicken) cells have concluded that mitotic chromosomes of higher eukaryotes are composed of a series of chromatin loops (Naumova et al., 2013; Gibcus et al., 2018). Unlike condensin I and II, cohesin, another SMC complex, is peripheral to the chromosome axis during early prophase of mitosis in chromosomes of higher eukaryotes (Losada et al., 2000; Hirano, 2012, 2016; Liang et al., 2015) based on studies with HeLa cells and Xenopus egg extract (Losada et al., 2000) as well as Muntjac cells (Liang et al., 2015). The molecular mechanism that localizes condensin but not cohesin to the chromosome axis is not currently understood.

In budding yeast both condensin and cohesin are enriched in the pericentric region (Megee et al., 1999; Tanaka et al., 1999; Glynn et al., 2004; Weber et al., 2004; D’Ambrosio et al., 2008; Hu et al., 2011). As in higher-eukaryotic chromosomes, condensin localizes to the axial core of the pericentric region of budding yeast (Stephens et al., 2011). Disruption of condensin in budding yeast increased fluctuations in spindle length during metaphase (Stephens et al., 2011), suggesting yeast condensin stiffens axial pericentric chromatin during mitosis. The observation that lacO/LacI-GFP arrays placed within the pericentric region of budding yeast were radial when they appeared as foci, but were axial when they appeared extended, led to the discovery that the pericentric region was highly looped (Stephens et al., 2011). The observation that pericentric chromatin can convert from a compact focus to an extended, filamentous signal and vice versa suggests that the increased fluctuations in spindle length is due to pericentric chromatin converting between these two conformations more frequently (Stephens et al., 2011). Cohesin is radially displaced from the axis to form a barrel-like distribution (Yeh et al., 2008), indicating that cohesin is in the periphery of chromatin loops in yeast. Both higher-eukaryotic chromosomes and the pericentric region have axial condensin, increased resistivity to chromatin deformation due to condensin, a high density of chromatin loops, and radial cohesin. We posit that the pericentric region of budding yeast serves as a model of chromosome organization in higher eukaryotes.

Recent studies have shown condensin binds to DNA (Piazza et al., 2014), and can both extrude DNA loops (Ganji et al., 2018) and translocate across taut DNA in a highly processive manner (Terakawa et al., 2017). Simulations of condensin that can translocate across DNA revealed that the mechanism that allows for translocation on a taut substrate can also result in loop extrusion on a slack substrate (Lawrimore et al., 2017). In contrast, cohesin has been shown to passively diffuse along taut DNA (Stigler et al., 2016). If these studies are representative of condensin and cohesin function in the pericentric region, only condensin should be able to form chromatin loops and disruption of cohesin should have different effects than disruption of condensin. Moreover, the changes in pericentric chromatin stiffness observed in cells with disrupted condensin should also occur in pericentric chromatin simulations lacking chromatin loops. In this study we use live-cell microscopy to determine whether the different DNA-binding modalities of cohesin and condensin affect the motion and organization pericentric chromatin differently, and we compare experimental data with polymer simulations of pericentric chromatin to determine whether condensin-mediated chromatin loops are capable of stiffening axial pericentric chromatin and geometrically partitioning pericentric condensin from cohesin.

RESULTS

Cohesin, not condensin, confines radial pericentric chromatin

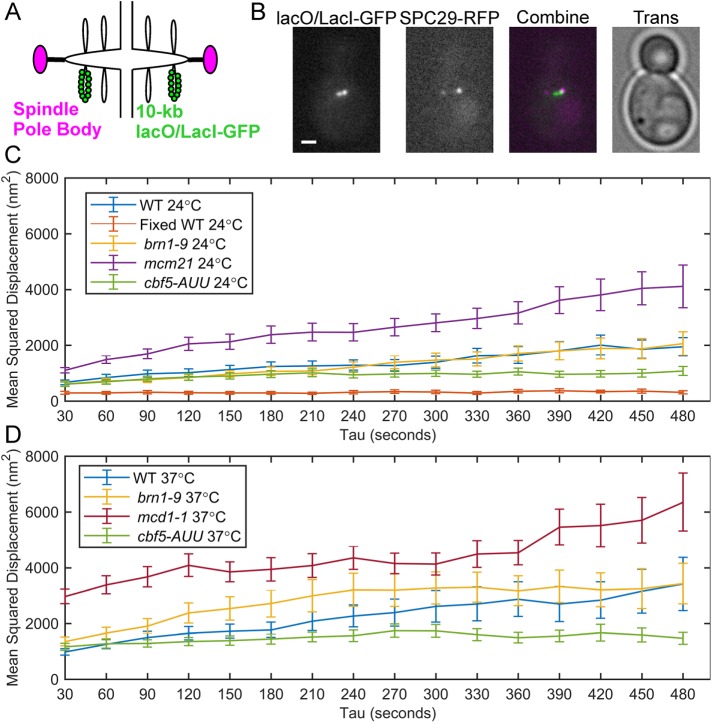
Pericentric chromatin labeled with a fluorescent reporter–operator system (FROS), such as lacO/LacI-GFP, can appear as a compact focus or as a stretched, anisotropic filament. The foci signals are radially displaced above or below the kinetochores, whereas the filamentous signals appear closer to the sister kinetochore axis (Stephens et al., 2011). We wanted to determine how the motion of radially displaced pericentric chromatin is affected by depletion and disruption of cohesin and condensin. We measured the dynamics of pericentric chromatin using a 10-kb lacO/LacI-GFP array placed 1.8 kb from CEN15 (Figure 1, A and B). To separate thermal from ATP-dependent chromatin motion, we depleted cells of ATP by treatment with sodium azide and deoxy-glucose. We imaged metaphase cells every 30 s for 10 min and tracked the motion of separated sister chromatids relative to each other (Chacon et al., 2014) using Gaussian fitting to determine the centroids of the LacO/LacI-GFP sister foci (Wan et al., 2009; Verdaasdonk et al., 2013; Lawrimore et al., 2015). The 10-kb lacO/LacI-GFP foci localize to the periphery of the pericentric region, colocalize with cohesin, and are radially displaced from condensin (Stephens et al., 2011). Only small-budded cells with bioriented sister-chromatid foci with both spindle pole bodies (SPC29-RFP) within the mother were measured (Figure 1B). We quantified the motion and confinement of the lacO/LacI-GFP foci by calculating mean-squared displacement (MSD) over time (Figure 1, C and D) and the mean radius of confinement for each strain (Figure 2A). The radius of confinement is based on the variance of the positions of the lacO/LacI-GFP foci over time, and, like MSD, represents the area over which the foci can freely diffuse (Verdaasdonk et al., 2013; Lawrimore et al., 2015). To determine our measurement accuracy, we fixed yeast cells with formaldehyde and tracked the motion of separated lacO/LacI-GFP foci. The MSD curve of the fixed cells exhibited a maximum MSD of 371 nm², well below the curves of the ATP-depleted cells (Figure 1C). Both the MSD curves and the radii of confinement show that lacO/LacI-GFP foci explore a greater area upon depletion of pericentric cohesin (mcm21Δ [Eckert et al., 2007; Ng et al., 2009; Stephens et al., 2011]) or disruption of cohesin (mcd1-1; Guacci et al., 1997; Michaelis et al., 1997). However, lacO/LacI-GFP foci do not explore a significantly greater area upon depletion of pericentric condensin (cbf5-AUU; Snider et al., 2014) or disruption of condensin (brn1-9 [Lavoie et al., 2000]; Figures 1, C and D, and 2A). Depletion of pericentric cohesin (mcm21Δ) does not affect the enrichment of pericentric condensin (Stephens et al., 2013), nor does disruption of condensin (brn1-9) affect enrichment of pericentric cohesin (Supplemental Figure S1). The increase in the radius of confinement in cohesin mutants but not condensin mutations demonstrates radial pericentric chromatin is confined by cohesin, but not condensin.

FIGURE 1:

Motion analysis of pericentric sister-chromatid foci in ATP-depleted metaphase cells. (A) Schematic of the 10-kb lacO/LacI-GFP array in the pericentric region during metaphase. (B) Representative images (in-focus planes) of ATP-depleted (sodium azide and deoxy-glucose treated) budding yeast cells in metaphase containing lacO/LacI-GFP (green) and SPC29-RFP (magenta). Scale bar is 1 µm. Mean-squared displacement curves of sister lacO/LacI-GFP foci in ATP-depleted, metaphase cells at 24°C (C) and at 37°C (D). Fixed WT 24° are WT cells that were grown at 24°C and fixed with formaldehyde. WT 24°C, n = 36; fixed WT 24°C, n = 42; brn1-9 24°C, n = 46; mcm21Δ 24°C, n = 40; cbf5-AUU 24°C, n = 36; WT 37°C, n = 49; and brn1-9 37°C, n = 42; mcd1-1 37°C, n = 39; and cbf5-AUU 37°C, n = 48 time lapses. Error bars are SEM.

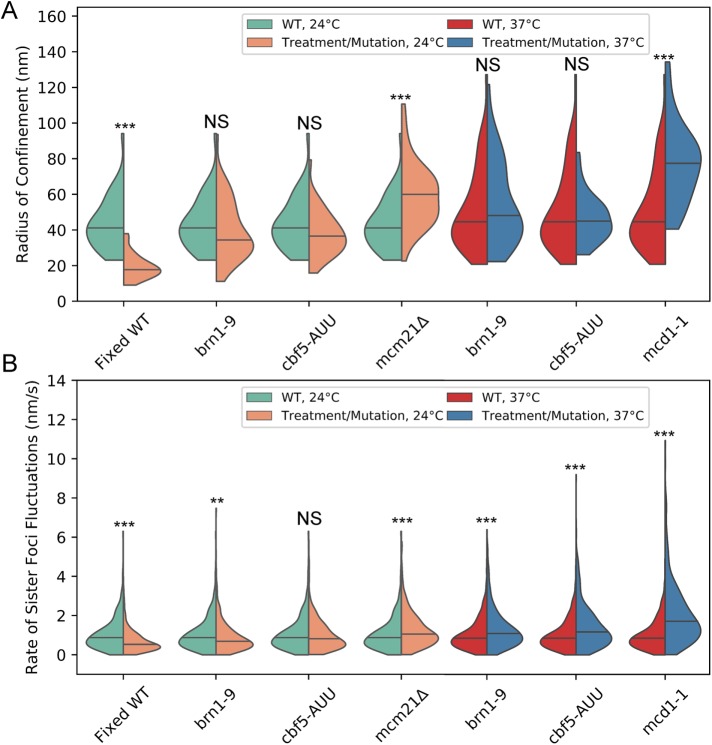
FIGURE 2:

Cohesin confines pericentric chromatin while both cohesin and condensin limit rate of sister foci fluctuations. (A) Violin plot of the radii of confinement of the 10-kb lacO/LacI-GFP array in the pericentric region during metaphase (generated from the same data as Figure 1, B and C). The black line represents the median and the colored shapes are a smoothed histogram of the distribution of each strain’s radii of confinement. Wilcoxon rank-sum test (two-sided) p values compared with WT at corresponding temperature: Fixed WT 24°C = 2 × 10⁻¹², brn1-9 24°C = 0.2, cbf5-AUU 24°C = 0.1, mcm21Δ 24°C = 2 × 10⁻⁵, brn1-9 37°C = 0.4, cbf5-AUU 37°C = 0.8, and mcd1-1 37°C = 7 × 10⁻⁷. (B) Violin plot of the rate of sister foci fluctuations. WT 24°C, n = 459; fixed WT 24°C, n = 538, brn1-9 24°C, n = 546; cbf5-AUU 24°C, n = 447; mcm21Δ 24°C, n = 459; WT 37°C, n = 605; and brn1-9 37°C n = 543, cbf5-AUU 37°C, n = 620; and mcd1-1, 37°C, n = 482; persistent motion events. Wilcoxon rank-sum test (two-sided) p values compared with WT at corresponding temperature: Fixed WT 24°C = 1 × 10⁻¹⁵, brn1-9 24°C = 0.002, cbf5-AUU 24°C = 0.4, mcm21Δ 24°C = 9 × 10⁻⁶, brn1-9 37°C = 2 × 10⁻⁸, cbf5-AUU 37°C = 6 × 10⁻¹², and mcd1-1 37°C = 8 × 10⁻⁴¹. Multiple comparisons of WT data (four for 24°C and three for 37°C) to mutants was corrected using the Bonferroni correction (see Materials and Methods) such that NS is p ≥ 0.05/number of comparisons, ** is p < 0.01/number of comparisons, and *** is p < 0.001/number of comparisons.

Considering disruption of condensin, using the brn1-9 allele, and depletion/disruption of cohesin (mcm21Δ and mcd1-1, respectively) resulted in increased fluctuations in metaphase spindle lengths in budding yeast (Stephens et al., 2011), the inability of condensin disruption/depletion (brn1-9 and cbf5-AUU, respectively) to alter the confinement of radial pericentric chromatin was unexpected. However, we reasoned that a confined yet more deformable pericentric region would result in more varied spindle lengths. We assumed deformation of the pericentric region would cause the lacO/LacI-GFP foci to fluctuate more persistently toward or away from each other, representing compression and extension of the pericentric region, respectively. We measured the mean rate of sister chromatin fluctuations by calculating how far the sister foci traveled either toward or away from each other without switching direction and divided that distance by the duration of the persistent motion. Cohesin depletion and disruption (mcm21Δ and mcd1-1, respectively) had significantly faster rates of sister foci fluctuations than WT strains (Figure 2B). For cells grown at 24°C, condensin depletion (cbf5-AUU) did not significantly alter the rate of sister foci fluctuations, while the temperature-sensitive allele, brn1-9, has significantly slower rates of sister foci fluctuations at permissive temperature (Figure 2B). We found that enrichment of pericentric condensin is disrupted at permissive temperature (24°C) in untreated cells (Supplemental Figure S2, A and B). Additionally, pericentric SMC4-GFP exhibited greater signal recovery in the brn1-9 cells than in WT cells at permissive temperature, 17 ± 3% versus 5% ± 1% (mean percent recovery ± SEM, Wilcoxon rank-sum test P value = 8 × 10⁻⁵), respectively (Supplemental Figure S2, C and D), with a half-life of 3.3 and 7.7 s for brn1-9 and WT cells, respectively. The loss of pericentric enrichment and increased turnover may be due to alterations in chromatin structure, altered condensin-binding kinetics, or changes in condensin’s ATPase activity. However, for cells grown at 37°C, both condensin disruption and depletion (brn1-9 and cbf5-AUU, respectively) resulted in significantly faster rates of sister foci fluctuations (Figure 2B), demonstrating cells with reduced pericentric condensin enrichment react differently to increased temperature than WT cells. These results recapitulate the observation that mcm21Δ, mcd1-1, and brn1-9 mutations all result in more varied spindle lengths (Stephens et al., 2011), demonstrating that a more deformable pericentric region correlates to greater spindle length variability. Although both cohesin and condensin enable pericentric chromatin to resist deformation, cohesin achieves this by confining the motion of chromatin, whereas condensin does not.

Condensin, not cohesin, stiffens centromere proximal chromatin in endogenous chromosomes

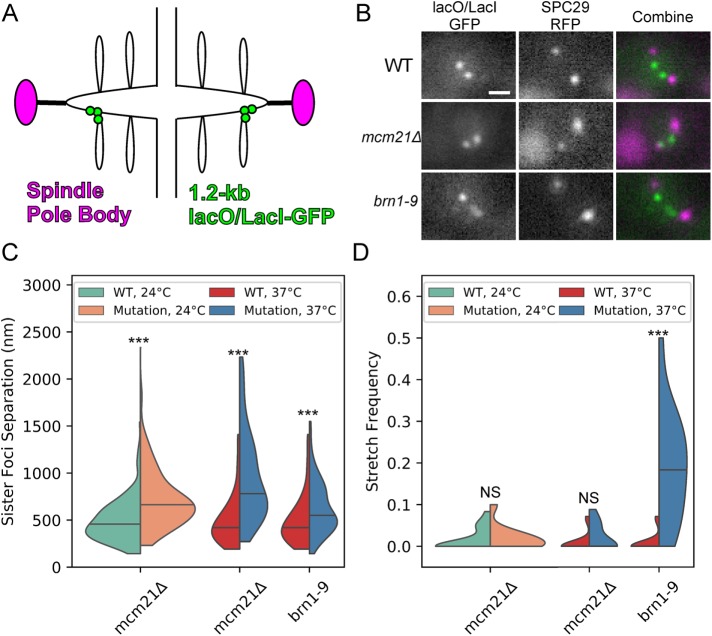
Depletion of radially enriched pericentric cohesin (Yeh et al., 2008) and disruption of axially enriched condensin (Stephens et al., 2011) both resulted in increased frequency of the extended, filamentous signals when pericentric chromatin was labeled with the same 10-kb lacO/LacI-GFP array used in Figures 1 and 2 (Stephens et al., 2011). The pericentric region is estimated to be 30–50 kb (Megee et al., 1999; Tanaka et al., 1999; Glynn et al., 2004; Weber et al., 2004; D’Ambrosio et al., 2008; Hu et al., 2011); given the lacO array is a large fraction of this region (the pericentric region extends 15–25 kb from each side of CEN) we reasoned this array will contain radial chromatin and may not be representative of the axial chromatin proximal to the centromere. To distinguish the roles of cohesin and condensin proximal to the centromere, we obtained population images of cells with a 1.2 kb lacO/LacI-GFP array centered 1.7 kb from CEN3 (Figure 3, A and B) in cells with depleted pericentric cohesin (mcm21Δ) and disrupted condensin (brn1-9). The 1.7-kb array (Figure 3A) is more proximal to the centromere, which defines the pericentric chromatin axis, than the 10-kb array (Figure 1A). Previously, this probe has been used to measure changes in chromatin tension (Pearson et al., 2003; Chacon et al., 2014). Both cohesin depletion (mcm21Δ) and condensin disruption (brn1-9) caused a significant increase in mean sister foci separation (Figure 3C). However, only condensin disruption (brn1-9) resulted in a significant increase in stretch frequency (Figure 3D). These results demonstrate that both cohesin and condensin enable pericentric chromatin to resist deformation, but condensin achieves this by preventing stretching of chromatin near the centromere, whereas cohesin does not.

FIGURE 3:

Condensin, not cohesin, stiffens endogenous pericentric chromatin. (A) Schematic of the 1.2-kb lacO/LacI-GFP array in pericentric region during metaphase. (B) Representative images of lacO/LacI-GFP array (green in Combine) and SPB protein SPC29-RFP (magenta in Combine). Scale bar is 1 µm. (C) Violin plot of mean sister foci separation. The black line is the median of the distribution and the colored shapes are smoothed histograms of the distribution of sister foci separation for each strain. WT 24°C, n = 164; mcm21Δ 24°C, n = 156; WT 37°C, n = 74; mcm21Δ 37°C, n = 84; and brn1-9 37°C, n = 97 cells. Wilcoxon rank-sum test (two-sided) p values compared with WT at corresponding temperature: mcm21Δ 24°C = 5 × 10⁻¹⁴, mcm21Δ 37°C = 5 × 10⁻¹³, and brn1-9 37°C = 3 × 10⁻⁴. (D) Violin plot of mean stretch frequency. The black line is the median of the distribution and the colored shapes are smoothed histograms of the distribution of signal stretch frequency for each strain. WT 24°C, n = 18; mcm21Δ 24°C, n = 11; WT 37°C, n = 16; mcm21Δ 37°C, n = 11; and brn1-9 37°C, n = 16 image sets. Wilcoxon rank-sum test (two-sided) p values compared with WT at corresponding temperature: mcm21Δ 24°C = 0.6, mcm21Δ 37°C = 0.2, and brn1-9 37°C = 1 × 10⁻⁵. Multiple comparisons of WT 37°C to mutants was corrected using Bonferroni correction.

Condensin compacts and stiffens axial chromatin in the pericentric region

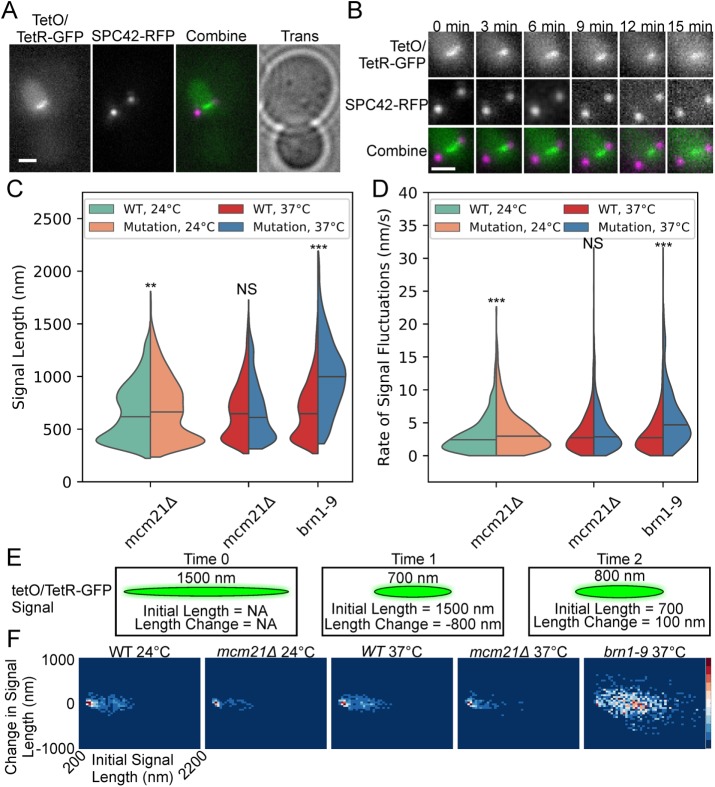
The dicentric plasmid pT431 can efficiently biorient during metaphase (Dewar et al., 2004). The 5.5-kb tetO/TetR-GFP array within pT431 can appear as a compact focus or a stretched, filamentous signal (Figure 4, A and B; Lawrimore et al., 2015). After excision of the ARS sequence (see Materials and Methods), the plasmid is a single, contiguous molecule of DNA with two active centromeres. Thus, the plasmid acts as a molecular tensometer allowing for direct observation of the dynamics of pericentric chromatin. The plasmid signal appears more compact in cells treated with low doses of the microtubule poison benomyl (Lawrimore et al., 2015), which has been shown to decrease tension at kinetochores in yeast (Suzuki et al., 2016), thus correlating tension with signal length. If condensin is capable of compacting pericentric chromatin into a state that is less deformable to spindle forces, the tetO/TetR-GFP array should be more extended upon condensin disruption or depletion. To observe the effects of cohesin and condensin on the plasmid, we imaged cells every 30 s for 20 min and measured the length of the tetO/TetR-GFP signals (Figure 4B). The length and aspect ratio of the tetO/TetR-GFP signals and the spindle length were measured using a custom MATLAB GUI (see Materials and Methods).

FIGURE 4:

Condensin condenses and stiffens pericentric chromatin via loop formation. Representative image (A) and montage (B) of a cell containing the fluorescently labeled, conditional dicentric plasmid pT431 and SPB protein SPC42-RFP. The tetO/TetR-GFP image (green in Combine) and the SPC42-RFP image (magenta in Combine) are maximum intensity projections. The Trans image (A) is the in-focus plane. Scale bars are 1 µm. (C) Violin plot of signal lengths of tetO/TetR-GFP array from time lapses. The black line is the median of the distribution and the colored shapes are smoothed histograms of the distribution of signal length for each strain. WT 24°C, n = 1732; mcm21Δ 24°C, n = 1455; mcm21Δ 37°C, n = 1171; WT 37°C, n = 1887; and brn1-9 37°C, n = 838 plasmid signals. Wilcoxon rank-sum test (two-sided) p values compared with WT at corresponding temperature: mcm21Δ 24°C = 0.01, mcm21Δ 24°C = 0.3, and brn1-9 37°C = 3 × 10⁻¹²¹. (D) Violin plot of the rates of signal fluctuations of tetO/TetR-GFP array from time lapses. The black line is the median of the distribution and the colored shapes are smoothed histograms of the distribution of the rates of signal fluctuations for each strain. WT 24°C, n = 1041; mcm21Δ 24°C, n = 881; mcm21Δ 37°C, n = 666; WT 37°C, n = 1101; and brn1-9 37°C, n = 495 extension/compaction events. Wilcoxon rank-sum test (two-sided) p values compared with WT at corresponding temperature: mcm21Δ 24°C = 1 × 10⁻⁵, mcm21Δ 37°C = 0.05, and brn1-9 37°C = 3 × 10⁻³¹. (E) Illustration of three frames of a time lapse of the tetO/TetR-GFP array on the dicentric plasmid pT431. The signal length at the current time point is displayed above the signal. The initial signal is the length of the signal of the previous time point (X axis in panel F). The length change is the difference between the signal length at the current time point and the previous time point (Y axis in panel F). (F) Probability density maps of change in signal length as a function of initial signal length. Red is most dense; blue is least dense.

We found that condensin-disrupted cells (brn1-9) had a large increase in signal length, while cohesin-depleted cells (mcm21Δ) had a small increase in the signal length when grown at 24°C but did not significantly alter the signal length when cells were grown at 37°C (Figure 4C). Additionally, we acquired population images of the dicentric plasmid in cells with the condensin temperature-sensitive allele ycg1-2 and the cbf5-AUU allele. The ycg1-2 allele resulted in a significantly larger signal, while the cbf5-AUU strain did not significantly alter the length of the plasmid signal (Supplemental Figure S3). Given Cbf5 is enriched 1.5- to 3.5-fold across tDNAs, which act as binding sites for condensin and Cbf5 (Snider et al., 2014), the lack of an effect of cbf5-AUU on the plasmid may be due to the plasmid lacking a transfer DNA (tDNA) site. We measured the mean rate of signal fluctuations in the same manner as the mean rate of sister foci fluctuations. The persistent increase/decrease in signal length was divided by the duration of the extension/compaction event. Condensin-disrupted cells (brn1-9) had an increased rate of signal fluctuations (Figure 4D), consistent with the increase in the mean rate of sister foci fluctuations (Figure 2B) upon depletion or disruption of pericentric condensin. However, depletion of pericentric condensin (mcm21Δ) only significantly increased the rate of plasmid signal fluctuations when cells were grown at 24°C, but not when the cells were grown at 37°C. Thus, condensin has a greater impact on the plasmid dynamics than cohesin, suggesting that condensin plays a crucial role in enabling axial chromatin to resist deformation.

To examine the relationship between chromatin compaction and chromatin dynamics, we created probability density maps of the change in signal length after a 30 s timestep versus initial signal length, which is the length of the signal at the previous timepoint (Figure 4, E and F). Condensin-disrupted (brn1-9) cells showed a radically altered plasmid dynamics profile compared with WT cells (Figure 4F). However, cohesin-depleted cells (mcm21Δ) showed a similar plasmid dynamics profile compared with WT cells (Figure 4F). WT and cohesin-depleted cells (mcm21Δ) exhibited a dense cluster of 300–400 nm signal lengths with ±50 nm changes in their signal lengths that the condensin-disrupted (brn1-9) cells lacked (Figure 4F). The density maps reveal that in cells with functional condensin, plasmids of all signal lengths exhibit smaller changes in signal length than cells with disrupted condensin. Thus, condensin compacts chromatin into an organization that effectively resists deformation.

Simulated condensin-mediated loops condense and stiffen underlying DNA

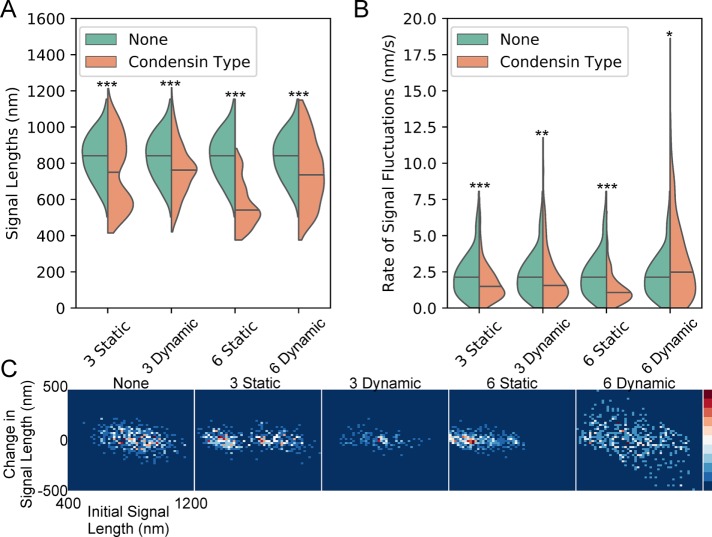
The dynamics of the dicentric plasmid signal provide a signature of condensin’s effect on pericentric chromatin motion on a contiguous piece of circular DNA. Thus, if condensin’s primary role is to form loops in the pericentric region, chromatin loops should result in the same dynamics profile of the WT probability density maps, while disruption of those loops should result in a dynamics profile similar to brn1-9 (Figure 4). To determine whether a stochiometric amount of condensin-mediated chromatin loops is sufficient to recapitulate the WT dynamics profile in a simulated version of the conditionally dicentric plasmid, we used the polymer dynamics simulator ChromoShake (Lawrimore et al., 2016) to run models of the plasmid with and without condensin complexes. The size of the dicentric plasmid pT431 after excision of the ARS is ∼11 kb. In our model, each bead has a diameter of 10 nm, representing ∼29 base pairs of DNA. We simulated the plasmid as a circle of 386 beads. We did not simulate histone compaction in our plasmid model. The typical distribution of condensin is one complex per 10 kb with threefold enrichment of condensin within the pericentric region (Megee et al., 1999; Wang et al., 2005; D’Ambrosio et al., 2008). Therefore, we added either three condensin complexes to our plasmid simulations to represent the typical pericentric density of condensin, or six condensin complexes because there are two centromeres on the plasmid. Each simulation type was run 10 times with different random seeds. The simulated tetO/TetR-GFP array (green beads, Figure 5) was convolved with an experimentally obtained point spread function to generate simulated time lapses of the array (Figure 5, D–F). Because condensin loop extrusion slows upon substrate tension (Ganji et al., 2018) and the dicentric plasmid is already under tension from biorientation of the two centromeres, we simulated condensin as randomly placed linear springs connecting nonconsecutive DNA beads to form static loops (Figure 5B). Additionally, we simulated condensin as a bead-spring complex capable of extruding loops dynamically on slack chromatin and translocating across taut chromatin using RotoStep (Lawrimore et al., 2017) to mimic the behavior of condensin observed in Terakawa et al. (2017) (Figure 5C). In the RotoStep algorithm, condensin translocation results in the loss of the previously extruded loop (see Materials and Methods). Both static and dynamic condensin simulations compacted the simulated tetO/TetR-GFP array (Figure 6A). Both three and six static condensin loops decreased the rate of signal fluctuation. The addition of three dynamic condensin loops reduced the rate of signal fluctuation, whereas six dynamic condensin loops significantly increased the rate of signal fluctuation.

FIGURE 5:

ChromoShake simulations and corresponding simulated fluorescent images of the dicentric plasmid pT431. Three-dimensional visualizations of simulated dicentric plasmids without condensin (A), with static condensin (white beads; B), and dynamic condensin (white beads; C). (D–F) Simulation visualizations overlaid with simulated fluorescent images of the tetO/TetR-GFP array generated by Microscope Simulator 2.

FIGURE 6:

Static and dynamic condensin-mediated loops compact and alter fluctuation rate of simulated dicentric plasmids. (A) Violin plot of simulated signal lengths. The black line is the median of the distribution and the colored shapes are smoothed histograms of the distribution of simulated signal length for each simulation type. Each simulation type was repeated 10 times using different random seeds. A simulated image stack was generated every 30 s from each simulation (assuming a nuclear viscosity of 141 P; see Materials and Methods) and the signal length was measured using the same analysis as for the experimental images. None, n = 470; three static condensins, n = 470; three dynamic condensins, n = 478; six static condensins, n = 470; and six dynamic condensins, n = 480 simulated plasmid signals. Wilcoxon rank-sum test (two-sided) p values compared with none: three static condensins = 1 × 10⁻¹³, three dynamic condensins = 1 × 10⁻¹⁷, six static condensins = 4 × 10⁻¹¹³, and six dynamic condensins = 2 × 10⁻¹⁶. (B) Violin plot of simulated rates of signal fluctuations. The black line is the median of the distribution and the colored shapes are smoothed histograms of the distribution of the rates of signal fluctuations for each simulation type. None, n = 261; three static condensins, n = 310; three dynamic condensins, n = 342; six static condensins, n = 337; and six dynamic condensins, n = 360 fluctuation rates. Wilcoxon rank-sum test (two-sided) p values compared with none: three static condensins = 1 × 10⁻⁶, three dynamic condensins = 0.001, six static condensins = 2 × 10⁻¹⁹, and six dynamic condensins = 0.005. Bonferroni correction applied to simulation comparisons. (C) Probability density maps of change in simulated signal length as a function of initial simulated signal length.

To determine whether compacted plasmid signals were less dynamic than extended signals, as the experimental data showed (Figure 4F), we generated probability density maps of initial signal length versus change in signal length (Figure 6C). Given the random placement of the static loops in each of the replicates of the simulations, three static condensing-mediated loops resulted in a more or less compact signal, resulting in a heterogeneous population (Figure 6C, 3 Static panel). Conversely, the six static condensin loop simulations resulted in a single cluster of compact array signals with small fluctuations observed experimentally (compare Figure 4F, WT panels and Figure 6C, 6 Static panel). The three dynamic condensin simulations lack the large population of compacted array signals with small fluctuations, whereas the six dynamic condensin simulations result in more dynamics tetO/TetR-GFP arrays (Figure 6C). Thus, static chromatin loops qualitatively recapitulate the dynamics of dicentric plasmids in cells with functional condensin, suggesting that condensin-mediated chromatin loops strongly affect the dynamics of pericentric chromatin.

Polymer simulations reveal condensin-mediated loops aggregate into condensin-rich, axial chromatin within pericentric region upon centromere biorientation

Previously, we developed a three-dimensional model of the budding yeast pericentric region (Lawrimore et al., 2016). The organization of the model was based on the pericentric distributions of cohesin, condensin, and the position of a 10-kb lacO/LacI-GFP array located 1.8 kb from CEN15 in metaphase cells. The simulation models DNA as a series of 10-nm masses, connected by springs, and stiffened by a hinge force to set the polymer chain to a persistence length of 50 nm (Lawrimore et al., 2016). By default, the masses in our simulations cannot pass through each other, preventing DNA strand passage. To recapitulate the radial localization of pericentric DNA and cohesin, the DNA was composed of 10-kb loops radially extending from a central axis of chromatin (Figure 7A, Initial; Lawrimore et al., 2016). The loops are formed by condensin, which is modeled as a linear spring connecting nonconsecutive DNA beads on the same DNA strand to form static loops of 73 beads (∼10 kb). Condensin is not directly shown in the model, but the sites to which condensin bind, mimicking the pericentric tDNA sites, are shown in white (Figure 7A). Cohesin (purple beads, Figure 7A) is modeled as a ring of 16 beads, encircling disparate DNA strands (pink, Figure 7A). Cohesin is free to diffuse along the DNA but cannot pass through DNA because masses in our simulations cannot pass through each other by default. We introduced thermal motion to the model using the ChromoShake simulator and found the distributions of cohesin and dynamics of the DNA approximated experimental observations (Lawrimore et al., 2016). Previously, we found that a pericentric simulation lacking condensin resulted in a simulated 10-kb array located 1.8 kb from the centromere becoming more radially displaced from the spindle axis. Removal of cohesin from the simulation did not alter the radial displacement of the array, but removal of both cohesin and condensin resulted in a larger radial displacement of the array than condensin removal alone (Lawrimore et al., 2016). These results suggested condensin-mediated loops were critical to the organization of pericentric chromatin. In our previous study, we attached the pericentric model to a static spindle, effectively pinning the model in space. This pinning allowed us to observe the pericentric chromatin as it would appear in vivo during metaphase but prevented the pericentric chromatin from reaching equilibrium. Here, we query how static, condensin-mediated loops affect the dynamics and organization of pericentric chromatin approaching equilibrium.

FIGURE 7:

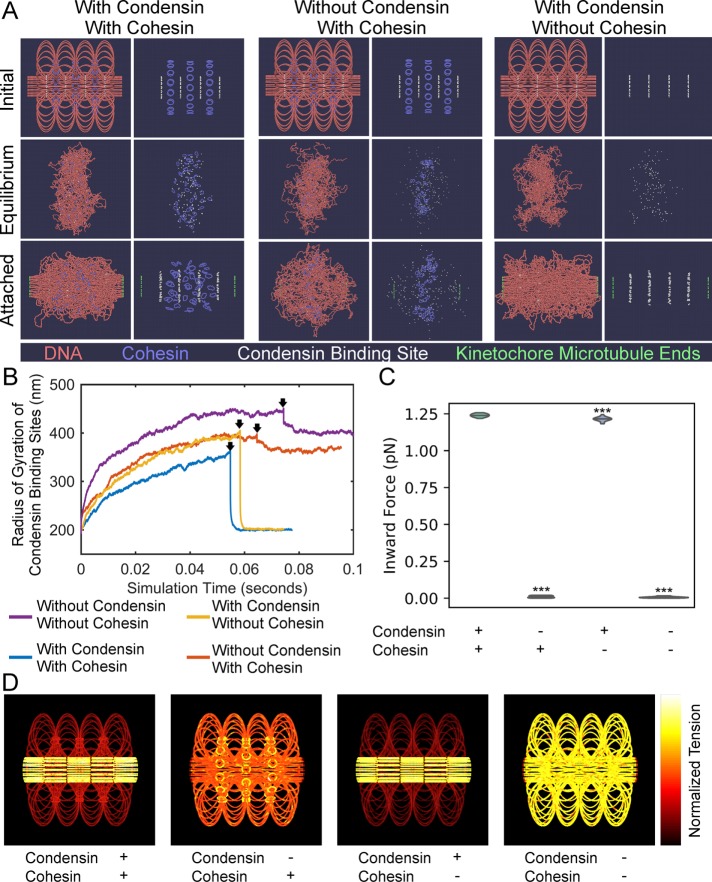
Condensin creates two force regimes in chromatin. (A) ChromoShake simulations of pericentromeres with or without cohesin and condensin. Initial configurations are in the top panel. Centromeres, the leftmost and rightmost beads, are separated by 800 nm. Middle panels correspond to timepoints indicated by black arrows in B. The bottom panels correspond to final timepoints in B. Each panel is also shown without DNA for clarity. Condensin-binding sites are in white and are shown in each panel. (B) Line plots of radius of gyration of condensin -binding sites over simulation time. Black arrows indicate timepoints before attachment to kinetochore microtubules is introduced. (C) Violin plot of inward force in pericentromere simulations with permanent attachment to kinetochore microtubules with or without cohesin and/or condensin. The black line is the median of the distribution and the colored shapes are smoothed histograms of the distribution of the inward forces for each simulation type. All simulations contained n = 16 sister centromere pairs. Wilcoxon rank-sum test (two-sided) p values as compared with simulation with condensin and with cohesin: without condensin and with cohesin = 2 × 10⁻⁶, with condensin and without cohesin = 5 × 10⁻⁵, and without condensin and without cohesin = 2 × 10⁻⁶. (D) Initial configurations of pericentromere simulations with permanent attachment to kinetochore microtubules where DNA beads are colored based on the mean tension on that bead after the simulation has run for 0.05 s of simulation time. The bead with the most tension in each simulation is white, whereas the bead with the lowest tension is black. The leftmost and rightmost beads are not shown.

Disruption and depletion of either cohesin or condensin resulted in faster sister foci fluctuations of radial pericentric chromatin (Figure 2B). These results suggest both condensin-mediated loops and cohesin-mediated cross-linking of those loops should affect the dynamics of pericentric chromatin. To measure the effect of chromatin loops and cross-linking of those loops on pericentric chromatin motion, we generated pericentromere models that lack cohesin and/or condensin that lack attachment to the mitotic spindle. We added thermal motion using the polymer simulator ChromoShake to drive each model to its equilibrium position (Lawrimore et al., 2016). Each simulation ran for over 0.05 s of simulation time. Assuming a nuclear viscosity of 141 P (Fisher et al., 2009), the simulations equilibrated without spindle attachment for at least 11.75 min of real time. To measure the motion of the pericentric DNA, we calculated the radius of gyration of the condensin-binding sites in the simulation at each timepoint. The radius of gyration is a measure of the volume of DNA in the simulations (see Materials and Methods). Simulations lacking either cohesin or condensin had a faster expansion of the pericentric region than the simulation with cohesin and condensin (Figure 7B). The simulation lacking both cohesin and condensin had the fastest expansion (Figure 7B), suggesting both loop formation and loop cross-linking each slow the motion of the pericentric region in separate ways.

During metaphase, pericentric cohesin and condensin are geometrically partitioned (Stephens et al., 2013), but the cause of this partitioning is unknown. After equilibration, the pericentric simulation with both cohesin and condensin had the condensin-binding sites (white beads) intermixed with the cohesin complexes (Figure 7A, Equilibrium row, With Condensin With Cohesin column). Simulations without cohesin or without condensin (Figure 7A) and the simulation with neither cohesin nor condensin (Supplemental Figure S3A) all had the condensin-binding sites (white), which label the normally axial pericentric chromatin, as radially displaced. To test whether sister centromere separation was required for the axial localization of condensin, the centromeres of the pericentromere simulations were attached to simulated kinetochore microtubules (green, Figure 7A, Attached row) forcing the sister centromeres apart by 800 nm, the mean kinetochore–kinetochore distance in metaphase budding yeast (Verdaasdonk et al., 2014). Upon spindle attachment, simulations with condensin, regardless of whether cohesin was present, quickly returned condensin-binding sites to an axial position (Figure 7A). However, in simulations lacking condensin, regardless of whether cohesin was present, failed to return the condensin-binding sites to an axial position (Figure 7A and Supplemental Figure S3A). These results indicate that the axial localization of condensin requires both an extensional force on the chromatin, provided by sister centromere separation through kinetochore attachment to spindle microtubules, and condensin-mediated chromatin loops. When simulations of the pericentric region lack spindle attachment the condensin-­mediated loops still exist, but do not aggregate until the chromatin undergoes an extensional force due to kinetochore microtubule attachment inducing centromere biorientation (Figure 7A). In the absence of chromatin loops, kinetochore microtubule attachment is not sufficient to aggregate the condensin-binding sites (Figure 7A). Therefore, the extensional force due to biorientation drives chromatin-bound condensin complexes to an axial position in pericentric chromatin. Given cohesin cannot form loops but can only diffuse along chromatin (Stigler et al., 2016) to the radial tips of condensin-mediated loops, the robust partitioning of cohesin and condensin is a direct consequence of their disparate DNA-binding modalities.

Both endogenous axial chromatin and the dicentric plasmid showed significantly more extension of fluorescent chromatin upon disruption of condensin (Figures 3D and 4C). Moreover, the simulated dicentric experiments illustrated that chromatin loops could both compact and stiffen chromatin (Figure 6), suggesting the pericentric loop formation is compromised in a brn1-9 mutant. The extension of the pericentric region upon spindle attachment (Figure 7A, Equilibrium panels vs. Attached panels), prompted us to determine whether condensin-mediated loops increased the inward force generated by the entropic fluctuations of DNA in pericentromere simulations with spindle attachment. We allowed the simulations to equilibrate for 0.05 s of simulated time before calculating the mean inward pulling force generated by each sister centromere pair (see Materials and Methods). We found the simulation with condensin and cohesin had a mean ± SD inward force of 1.24 ± 0.011 pN, the simulation without condensin but with cohesin had a mean inward force of 0.0097 ± 0.0072 pN, a 128-fold decrease (Figure 7C; Wilcoxon rank-sum test P value = 1.5 × 10⁻⁶). The simulation with condensin but without cohesin had a mean inward force of 1.21 ± 0.015, statistically lower than the simulation with condensin and cohesin (Figure 7C; Wilcoxon rank-sum test P value = 5.1 × 10⁻⁵). The simulation with neither condensin nor cohesin had a mean inward force of 0.0055 ± 0.0062, 225-fold less (Figure 7C; Wilcoxon rank-sum test P value = 1.5 × 10⁻⁶) than the simulation with condensin and cohesin. Thus, condensin-mediated loops greatly amplify the inward force on centromeres from the entropic fluctuations of the chromatin, whereas cohesin’s interstrand tethering minorly contributes to the inward force on centromeres, explaining why condensin disruption causes extension of axial pericentric chromatin.

One prediction of our looped pericentric model is that there should be more tension in the axial chromatin than the radial loops (Lawrimore et al., 2015). ChromoShake simulations of the pericentric chromatin contain a precise record of each bead’s location over time. This data set allows us to calculate the mean tension on each bead in the simulation, enabling us to visualize how tension is distributed across the entire pericentric region in simulations with spindle attachment. We measured the mean separation of each bead to its two adjacent beads (end beads were not measured) after the simulations reached equilibrium (0.05 s of simulated time). In simulations with condensin, tension was isolated to the axial DNA beads independent of the presence of cohesin (Figure 7D). In simulations without condensin, tension was amplified in the cohesin rings (Figure 7 D). In the simulation with neither condensin nor cohesin, tension was distributed evenly along the DNA (Figure 7D). We generated a centromere model with condensin and cohesin but allowed beads to exist in the same location simultaneously, eliminating crowding effects and cohesin function. Eliminating collisions resulted in a small but significant decrease in inward force, 1.19 ± 0.011 pN, compared with the simulation with condensin and cohesin (Supplemental Figure S4; Wilcoxon rank-sum test P value = 1.5 × 10⁻⁶) and compared with the simulation with condensin but without cohesin (Supplemental Figure S4B; Wilcoxon rank-sum P value = 3.7 × 10⁻⁴), but had no effect on the localization of tension to axial DNA (Supplemental Figure S4C). Therefore, a major consequence of condensin-mediated chromatin loops is the isolation of tension to axial chromatin. These simulations demonstrate that extensional force from biorientation act disproportionately on condensin-bound DNA, forcing it to the axial core of the pericentric region. This forced axial localization of condensin directly leads to the spatial partitioning of cohesin and condensin in the pericentric region of budding yeast.

DISCUSSION

In budding yeast, the two classes of SMC complexes, condensin and cohesin, occupy nonoverlapping domains within the pericentric region (Stephens et al., 2011). Because both cohesin and condensin are both loaded at centromeres (Uhlmann, 2016), what properties of these ring complexes cause their disparate geometric localizations? Our simulations illustrate that intrastrand tether points, that is, condensin, are driven to the axial core of DNA substrate in the presence of an extensional force mimicking chromosome biorientation (Figure 5A). During metaphase, chromosome biorientation leads to sister centromere separation of 800–1000 nm. That distance of sister centromere separation in mitosis is conserved across a range of eukaryotic organisms (Verdaasdonk et al., 2014), suggesting that the separation of sister centromeres is functionally important during mitosis. The reliance of pericentric condensin on the extensional force provided by biorientation would explain the extreme conservation of the distance of sister centromere separation. Slip-link tethers, that is, cohesin, diffuse to the radial periphery of the DNA substrate regardless of the presence of an extensional force on the DNA substrate (Figure 7A). In contrast, condensin, if forming a chromatin loop, is driven to the axial core of the pericentric region in the presence of an extensional force (Figure 7A).

Live-cell imaging and fluorescence recovery after photobleaching (FRAP) of condensin subunit SMC4-GFP showed that condensin’s pericentric enrichment is reduced and condensin turnover increases in cells with the brn1-9 allele (Supplemental Figure S2). The cause of the reduced enrichment and the increased SMC4-GFP turnover may be due to misregulation of condensin activity, increased complex dissociation from chromatin, loss of ATPase activity, or alteration in chromatin structure. However, the increased signal length of the tetO/TetR-GFP array in metaphase cells in the temperature-sensitive alleles brn1-9 (Figure 4) and ycg1-2 (Supplemental Figure S3) indicate pericentric condensin’s looping function is compromised in these mutants. Our data support two hypotheses of how condensin loop extrusion may be disrupted in a brn1-9 allele. The dynamics of the simulated tetO/TetR-GFP signal in dicentric plasmid simulation lacking condensin and with six dynamic condensin complexes are both qualitatively similar to the dynamics of the tetO/TetR-GFP in the brn1-9 strain (compare Figure 4F with Figure 6C). This is due to fact that a high enough density of loop-extruding condensin complexes that disassociate their loops when the substrate becomes too taut will make chromatin more dynamic. The observation that condensin slows its loop extrusion as the substrate becomes more taut (Ganji et al., 2018) means that the condensins on the plasmid would not be extruding loops as the plasmid is under tension from biorientation of the two centromeres. This would explain why the dynamics of the six static condensin plasmid simulation most resembles the dynamics of the plasmid in WT cells (compare Figure 4F with Figure 6C). The brn1-9 allele may be eliminating condensin’s throttle, resulting in cycles of loop extrusion and translocation and thus increased chromatin dynamics (Figure 6B). Alternatively, condensin complexes may simply unbind from chromatin more rapidly, resulting in fewer and/or shorter chromatin loops. In either case, a mutant condensin complex that cannot act as an intrastrand tether will prevent its localization to the axial core of the pericentric region, providing a mechanism for the reduced pericentric enrichment of SMC4-GFP in brn1-9 cells (Supplemental Figure S2, A and B). This result is supported by the pericentric simulations as condensin-binding sites remain dispersed even upon attachment of centromeres to the spindle in simulations without condensin (Figure 7A). In the pericentric simulations, the presence of either cohesin or condensin slowed the fluctuation DNA to its equilibrium position (Figure 7B), recapitulating our experimental results that both cohesin and condensin appear to slow changes in the distances between sister foci (Figure 2B) and dicentric plasmid signal length (Figure 4D). Condensin confers resistivity to deformation by forming chromatin loops, whereas cohesin makes chromatin functions by loosely tethering chromatin loops together (Figure 8). The presence of the tethers increases the apparent viscosity of the pericentric chromatin, making the entire pericentric region more resistive to deformation from outside forces. In other words, condensin and cohesin transform the pericentromere into a unified, gelatinous substrate. Extension of this substrate migrates condensin to an axial core (Figure 7A) and results in amplified tension in that axial chromatin (Figure 7C). Under tension, this substrate has a robust organization with condensin at its axial core and cohesin at its radial periphery due to the physical consequence of an extensional force on looped chromatin.

FIGURE 8:

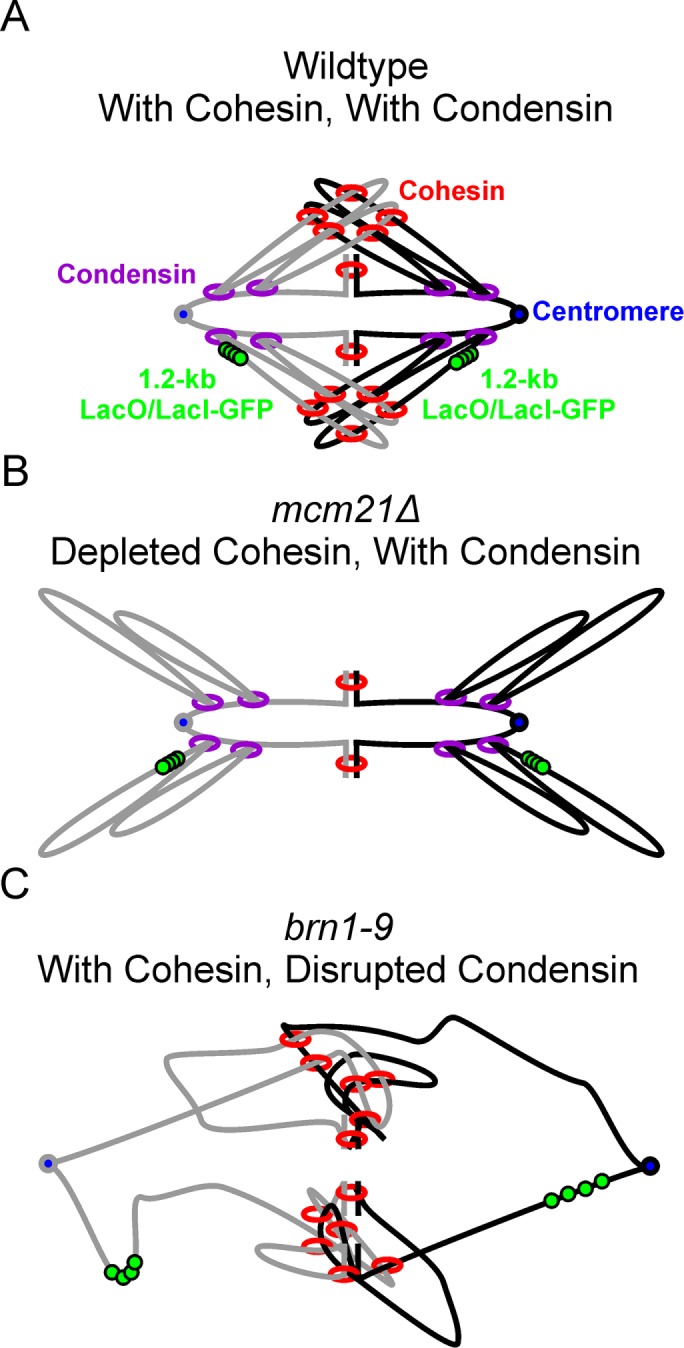
Models of WT, mcm21Δ, and brn1-9 pericentric regions. Models of the pericentric region during metaphase (sister strands are gray and black) labeled with the 1.2-kb lacO/LacI-GFP array (green) centered 1.7 kb from the centromere (blue) with either both cohesin (red) and condensin (purple; A), depleted cohesin (B), or disrupted condensin (C).

The geometric partitioning of cohesin and condensin in pericentric chromatin requires the presence of an extensional force (Figure 7A). In the pericentric region this force is provided by the mitotic spindle. However, in higher eukaryotes this extensional force can be provided by a sufficient density of chromatin loops. Bottle-brush polymers, a highly branched polymer with many sidechains emanating from a single polymer backbone, have high axial tension due to steric repulsion of the sidechains extending the polymer backbone. The magnitude of axial tension is dependent on the density and length of the sidechains (Rubinstein and Colby, 2003; Panyukov et al., 2009a,b; Lebedeva et al., 2012). In chromosomes, the condensin-rich chromosome axis acts as the polymer backbone and the loops act as the sidechains. Polymer simulations of a 30-Mb chromosome show that condensin-mediated chromatin loop extrusion can convert an isotropic sphere of chromatin into an anisotropic chromosome due to the extensional force from steric repulsion between loops (Goloborodko et al., 2016). Our work predicts that loop repulsion drives the axial localization of condensins in chromosomes of higher eukaryotes. Condensin’s persistent binding to chromatin loops entropically drives its axial localization if a sufficiently large extensional force is present in the chromatin. Therefore, the localization of condensin is influenced by condensin’s ability to form chromatin loops. The greater the concentration of condensin, the higher the chromatin loop density and the greater the extensional force that aggregates condensin to the central axis of chromosomes.

MATERIALS AND METHODS

Strain growth and imaging preparation

Detailed strain genotypes are listed in Supplemental Table S1. Strain JLY1043-1 had mcm21 removed using primers AAAG­AAAAGAGCTAAGCTGGAGAATGAGGAAATTTTACCAGAACAAGAATGGGTTTTAAAGACCCAGCCACAGCTGAAGCTTCGTACGC and TATCTATGATAAACAGAGAAAATTAGCTCTATCCT­CTTTCTATAAAGTATATTTTTGTTAACATGCATAGGCCACTAGTGGATCTG to PCR, a KAN marker from plasmid pFA6a-kanMX6. Bold portions of sequence have homology to pFA6a-kanMX6 plasmid. Transformants were screened by PCR fragment size with primers CAGTAATGGCCGACCAATTCTATGATAGATCTTC and GGCAA­TATATCCATTCTTGCTAGATAGTGGAAG. Strain JLY1071-1 had mcm21 removed using primers GAGAGCGCTAATCCTATAGTACA and TACGAGCTTGCCTTGCCATTGTT on a genomic DNA sample extracted from KBY9059. Transformants were screened by PCR fragment size with primers GAGAGCGCTAATCCTATAGTACA and TACGAGCTTGCCTTGCCATTGTT. Strains JLY1041-1 and JLY1074-1 were transformed with PCR fragments of cbf5-AUU from the genomic DNA of KBY9518-1 (Snider et al., 2014) using the primer pair ACCTTGTTGAGACTTAACCAACCTG and CGTAACATATGATC­TTCTGTTCTCA. Strains JLY1062-1 and JLY1072-1 were transformed with the plasmid pSOI digested with Pvu1 and Xho1 to introduce the brn1-9 mutation. The JLY1056 strain was transformed with the plasmid p290, kindly provided by Damien D’Amours (University of Ottawa), after digestion with XhoI and XbaI to introduce the ycg1-2 allele. Strains were screened for temperature sensitivity to 42°C. The dicentric plasmid was transformed into yeast and screened using the GFP signal. All strains were grown in liquid media 24°C. All biological experiments were performed using at least three different liquid yeast cultures grown on separate days. All strains were grown to midlogarithmic phase before imaging. Strains with temperature-sensitive mutations and their wild-type control strains were grown at 37°C for 3 h before imaging. Strains, excluding strains containing the dicentric plasmid, were grown in rich YPD media. Strains with an adenine mutation were grown with 0.5 mg/ml additional adenine. Strains with the dicentric plasmid pT431 were grown in YCAT-galactose media with 0.5 mg/ml additional adenine and methionine. Four hours before imaging, cells with the dicentric plasmid pT431 were washed and incubated in SG (synthetic-containing galactose) media lacking methionine with 0.5 mg/ml additional adenine to induce the recombinase to excise the ARS sequence of the plasmid. Cells were then resuspended in YPD for 20 min to repress transcription from the GAL1 promoter and activate the second, conditional centromere (Dewar et al., 2004). Cells were then washed and resuspended in YC-complete media with 2% filter sterile glucose. Before imaging, cells with Smc4-GFP were washed and resuspended with YC-complete media lacking sugar. Before imaging, cells with the 10-kb lacO/LacI-GFP array were washed and then incubated for 20 min with YC-complete media with 0.02% sodium azide and 1 µM deoxy-glucose. Before imaging, cells with the 1.2-kb lacO/LacI-GFP array were washed and then resuspended in YC-complete media with 2% filter sterile glucose. Strains containing the dicentric plasmid were imaged on slides with agar pads composed of 2% low melting temperature agarose and YC-complete media with 2% filter sterile glucose. All other strains were imaged on untreated glass coverslips.

Microscopy

Time lapses of strains containing the 10-kb lacO/LacI-GFP array or containing the dicentric plasmid were performed at room temperature (25°C) using an Eclipse Ti wide-field inverted microscope (Nikon) with a 100× Apo TIRF 1.49 NA objective (Nikon) and Clara charge-coupled device camera (Andor) using Nikon NIS Elements imaging software (Nikon). Time lapses of strains containing the 10-kb lacO/LacI-GFP array were 10 min in duration with 30 s intervals. At each interval a seven-step Z-stack of 300-nm step size was acquired in the GFP, RFP, and Trans channels. Time lapses of strains containing the dicentric plasmid were the same as above but with a duration of 20 min.

Population images of the dicentric plasmid strains and of strains containing the 1.2-kb lacO/LacI-GFP array were imaged at room temperature (25°C) using an Eclipse E600FN microscope (Nikon) with a 100× Plan Apo TIRF 1.45 NA objective (Nikon) and ImagEM EM-CCD digital camera (Hamamatsu) with a custom Lumencor LED illumination system (Lumencor) using MetaMorph 7.7 imaging software (Molecular Devices). Each acquisition was a seven-step Z-stack with a 300-nm step size in the GFP, RFP, and Trans channels.

FRAP

FRAP of strains containing SMC4-GFP was performed at room temperature (25°C) using the Eclipse Ti wide-field inverted microscope (Nikon) described above. For each experiment, a single seven-step Z-stack with 300-nm step size was acquired before bleaching in the GFP, RFP, and Trans channels, then the laser image, then a 30 s time lapse with 1 s intervals in the same z-plane as the laser bleaching in the GFP channel only. Image analysis was carried out using a custom MATLAB GUI, FRAP_gui.m. The GUI allows the user to generate and alter binary masks of the bleached nucleus, a reference nucleus, and the bleached region. The program then generates a bleach curve for the reference region, the unbleached portion of the nucleus, and the bleached region and saves all the relevant data to a MAT data file that is parsed by an analysis program, FRAP_summary_ind_t_half.m, to generate the average bleach curves shown in Supplemental Figure S2D and calculate the half-life and percent recovery of the curves.

Signal variance analysis

The prebleach image stacks of strains containing SMC4-GFP were cropped such that only nuclei remained in the image. The cropped stacks were converted into maximum intensity projections. The intensities of the projections were then normalized by dividing each intensity value by the maximum intensity value of the projection. The background was removed by using Otsu thresholding with the MATLAB function multithresh. The variance of the remaining signal was calculated for each image using the MATLAB program SMC4_GFP_variance_analysis.m.

ChromoShake simulation and analysis

The centromere models were generated using the ChromoShake_make_spindle C++ program to generate a configuration file. Unpinning of the models was performed by altering the drag coefficient term in the configuration file from 3.38889 × 10⁻¹⁵ to 3.38889 × 10⁻²⁰. Simulations were then run using the ChromoShake simulator. Radius of gyration calculations of condensin-bound DNA beads were performed using a custom MATLAB program (rog_specific_large_edit.m) that parses the ChromoShake outfiles, and a list of beads to use in the calculation. Radius of gyration is a measure of the volume of the distribution of points and is defined as 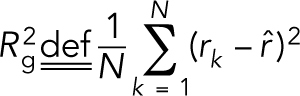, where 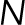is the number of beads, 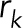is the position of an individual bead, and 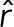is the mean position of all the beads.

Calculating the mean inward force from pinned centromere simulations was performed using custom MATLAB programs end_to_end.m and inward_force.m to determine the mean drag force of the end beads. In pericentromere simulations, the centromeres are composed of two beads. Each of these beads has 10⁵-fold greater drag force on each of them than all other beads in the simulation. The larger drag force effectively pins the centromeres in space to mimic attachment to the mitotic spindle. Each centromere bead has a corresponding sister centromere bead. To calculate the inward force on each centromere bead pair, the mean velocity of the sister centromere beads relative to each other was calculated after a 0.05 s equilibration time. The inward force is based on viscous drag and is calculated as 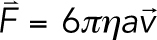, where viscosity (η) is 0.001 Pa⋅s, the drag radius (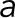) is 10 nm, and the velocity (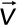) is the mean velocity of the sister centromere beads relative to each other. These calculations were performed with the inward_force.m program. The mean inward force per centromere (Figure 7C) was calculated by summing the inward force of each sister centromere bead and taking the mean of the resulting 16 centromere inward force measurements. The coloration of the pericentromere models based on normalized tension on each bead used a custom Python script, AvgTensionTotalNorm.py, run by Blender. This program colored each bead in the simulation based on the mean bead–bead separation of each bead with its two neighbors across time. The mean bead–bead separations were normalized by dividing each bead–bead separation by the maximum bead–bead separation of that simulation. The inward force and tension visualization analyses were applied to the centromere simulations from Lawrimore et al. (2016).

The initial dicentric plasmid model was created using the ChromoShake_make_chromatin_loop C++ program. The model is composed of 386 beads to mimic the size of the plasmid after the ARS sequence is looped out, ∼ 11 kb. The centromeres of the plasmid were physically pinned 800 nm apart by altering the positions of the centromere beads in the configuration file and running the model for 0.18 s at a timestep of 0.9 ns using the ChromoShake simulator. The color section was altered to match the size and position of the tetO array. Ten simulations of this dicentric plasmid model were run with different random seeds. Static condensin was added to the dicentric plasmid model by using Excel’s (Microsoft) RANDBETWEEN function to generate three random bead pairs within the plasmid and adding three springs pairing the beads to the dicentric plasmid outfile. The springs were given the default rest length (10 nm) and spring constant (∼0.23 N/m). Ten versions of the static dynamic simulations were created using different spring locations. Each static condensin simulation was run using the ChromoShake simulator. Three dynamic condensins were added to the dicentric plasmid model using the MATLAB program add_condensin.m. Ten versions of the dynamic simulations were created using different random seeds to generate different starting positions for the dynamic condensin complexes. Each dynamic condensin simulation was run using the ChromoShake-derived program RotoStep (Lawrimore et al., 2017). RotoStep edits the ChromoShake outfile to alter the masses to which condensin binds based on two rules. If the condensin complex is not extended past 30 nm, the two condensin beads that bind to DNA beads, representing Ycs4, rotate to step along the DNA while the condensin bead, representing Ycg1, stays bound to its DNA bead. If the condensin complex is extended past 30 nm, then the Ycg1 bead’s connection to the DNA bead weakens 1000-fold, causing condensin’s internal spring to bring the Ycg1 bead toward the Ycs4 beads, and then the Ycg1 bead rebinds to the most proximal DNA bead, mimicking condensin “stepping” along the DNA substrate. Condensin’s internal spring was set to 0.023 pN to allow condensin to processively step along a taut DNA substrate, not to reflect the stiffness of the condensin holocomplex. We simulated condensin to extrude loops at a rate of 60 base pairs per second, the same rate as condensin translocation reported in Terakawa et al (2017). Simulated images of the tetO array were created using Microscope Simulator 2 (Quammen et al., 2008). The simulated images were analyzed using a custom MATLAB program that automatically converted the simulated images into binary masks and used the REGIONPROPS function in MATLAB to measure the signal lengths. Simulated density maps of dicentric plasmids (Figure 6C) were generated using the data from the REGIONPROPS analysis using the MATLAB program sim_plasmid_heatmap_summary.m, which uses the same plasmid_heatmap function used to generate the experimental density maps (Figure 4F) using MATLAB’s HeatMap function. The mean simulated plasmid signal length and mean rate of change in signal length were calculated using the MATLAB programs sim_plasmid_rate_analysis.m and simulated_plasmid_barcharts.m.

Motion tracking and analysis

Timelapses of the 10-kb lacO/LacI-GFP arrays were analyzed using Speckle Tracker (Wan et al., 2009) and an automated version of Speckle Tracker called Auto Track. Both programs fit a 2D Gaussian to each GFP signal (5 × 5 pixel region) to generate a subpixel position in X and Y using the MATLAB function LSQCURVEFIT. The mean position of the sister GFP foci was calculated as a fiducial point for the motion of the GFP foci as described in Chacon et al. (2014). After subtracting the fiducial point from the foci, the foci positions over time are used to calculate the MSD curves and the radii of confinement using the MATLAB program midpoint_motion.m. The radius of confinement was calculated using the equation 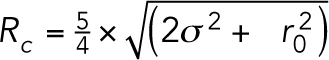, where 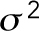is the mean of the variance of the foci position in X and Y and 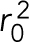is the mean-squared deviation from the mean position calculated by 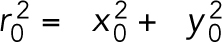. Each time lapse represents a biological replicate.

The mean rate of sister foci fluctuations was calculated using the MATLAB program sister_rate_analysis.m. The program identified persistent motion events, sister foci coming toward/away from each other, in the time lapses. The rate of the fluctuation was calculated by dividing the total displacement of the event by the duration of the event. Each event was treated as a random sample, and all the events for each treatment group or strain were pooled to determine the mean rate of sister foci fluctuation.

Dicentric plasmid image analysis

Both time lapse and population images of strains containing dicentric plasmids were analyzed using a custom MATLAB GUI, population_GUI_v1_2.m. The GUI allows users to select plasmid signals in the GFP channel, select a background region in the GFP channel for background subtraction, generate and alter a binary mask based on background subtraction of plasmid signal, and select spindle pole bodies in the RFP channel. Only cells containing a single plasmid signal were analyzed. The data for each plasmid signal were saved in a .MAT file for summary analysis of plasmid signal length, plasmid stretching (aspect ratio greater than or equal to 1.5), plasmid signal length changes over time, and spindle length by various MATLAB programs. Density maps of plasmid dynamics were constructed using the MATLAB program plasmid_heatmap.m that utilizes MATLAB’s HeatMap function.

Population image analysis of 1.2-kb lacO/LacI-GFP array

Population images of strains containing the 1.2-kb lacO/LacI-GFP array were analyzed using the MATLAB GUI heatmap_GUI.m, which allows the user to measure the positions (brightest pixel) and the stretched state (determined by user) of the array signals and the positions (brightest pixel) of the spindle pole bodies. Various summary MATLAB programs were used to measure the mean separation of the sister arrays and the mean stretch frequency of the arrays from the .MAT files generated by the heatmap_GUI.m program. For mean sister foci separation each cell was considered a biological replicate. For the mean stretch frequency each image session, containing multiple cells, was considered a technical replicate.

Statistical analysis

We use the Bonferroni correction for multiple comparisons. Unless otherwise noted in the figure legends markers of statistical significance in the figure legends are NS, p ≥ 0.05; *, p < 0.05; **, p < 0.01; ***, p < 0.001 divided by the number of comparisons. The nonparametric Wilcoxon rank-sum test, MATLAB function ranksum, was used for all statistical comparisons. We chose a minimum sample size of 34 assuming 0.9 power and a large effect size (Cohen, 1988).

Code availability

All programs, scripts, and data files are available upon request by contacting the corresponding author. ChromoShake simulations are written in C++. ChromoShake analysis codes are in MATLAB and Python. RotoStep is written in MATLAB. Image analysis programs are written in MATLAB.

Abbreviations used:

GFP

green fluorescent protein

lacO

lactose operon

MSD

mean-squared displacement

R_c

radius of confinement

R_g

radius of gyration

SMC

structural maintenance of chromosomes

SPB

spindle pole body

tetO

tetracyline operon.