Partitioning and Classification of RNA Secondary Structures into Pseudonotted and Pseudoknot-free Regions Using a Graph-Theoretical Approach

Abstract

Dual graphs have been applied to model RNA secondary structures with pseudoknots, or intertwined base pairs. In this paper we present a linear-time algorithm to partition dual graphs into maximal topological components called blocks and determine whether each block contains a pseudoknot or not. We show that a block contains a pseudoknot if and only if the block has a vertex of degree 3 or more; this characterization allows us to efficiently isolate smaller RNA fragments and classify them as pseudoknotted or pseudoknot-free regions, while keeping these sub-structures intact. Applications to RNA design can be envisioned since modular building blocks with intact pseudoknots can be combined to form new constructs.

I. Introduction

GRaph theory is a field of mathematics with applications to many research areas where the objects can be represented as discrete structures called graphs.

In mathematical terms, an undirected graph G = (V, E) is a discrete object described by a finite set of vertices V and a set E of unordered pair of vertices called edges, where each edge represents a connection between two vertices.

Waterman [19] was one of the first researchers to represent RNAs as graphs. The graph representations discussed in this paper, called dual graphs, were introduced in 2003 by Gan et. al [7], and were applied to model RNA secondary structures (2D). The 2D elements of RNA molecules consist of double-stranded (stem) regions defined by base pairing such as Adenine-Uracil, Guanine-Cytosine, Guanine-Uracil, and single stranded loops; stems and loops are mapped to the vertices and edges of the corresponding dual graph, respectively (later we present an alternative definition of dual graphs). Dual graphs are needed to represent pseudoknots (PKs), structures involving an intertwining of two-base-paired regions of the RNA. These are common elements in many biologically important RNAs.

Let the degree of a vertex u ∈ V be the number of edges incident at u in G. In this paper we introduce a partitioning algorithm for dual graph representations of RNA 2D structures to recognize PKs. Our algorithm partitions a dual graph into graph-theoretic components called blocks and then determines whether each block contains a pseudoknot; a block contains a pseudoknot if and only if the block has a vertex of degree 3 or more. Thus our procedure provides a systematic approach to partition an RNA 2D structure, modeled as a dual graph, into smaller RNA regions containing pseudoknots, while providing a new topological perspective for the analysis of RNAs.

Pseudoknots can be classified into two main groups: standard and recursive pseudoknots [5], [20]. The latter is distinguished from the former by having nested pseudoknots within a pseudoknot. While our partitioning algorithm can detect general pseudoknots, it cannot classify them. Extensions, however, may be possible to analyze and treat standard and the more complex recursive pseudoknots structures further, as needed for specific biological applications.

In the next section, we present background material relevant to this paper, as well as notation and mathematical definitions of RNA primary, secondary, and of pseudoknot structures. In Section III we describe our partitioning approach of a dual graph G into components G′ ⊆ G called blocks. In Section IV, we characterize these blocks, as either pseudoknotted or pseudoknot-free. In Section V and Section VI we illustrate algorithmic tests performed on different motifs. We summarize the findings and outline new directions in Section VI. An Appendix section includes definitions, mathematical proofs, and supporting material.

II. Background and Definitions

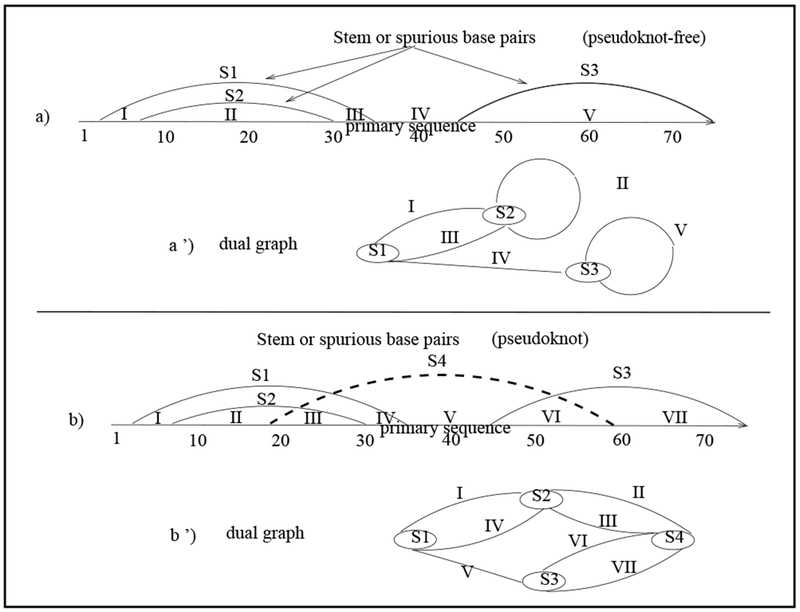
In 2003, Gan et. al introduced tree and dual graph-theoretic representations of RNA 2D motifs in a frame-work called RAG (RNA-As-Graphs) [6], [7], [8], [11]. Dual graphs can represent complex RNA secondary structures with pseudonots; a pseudoknot is an intertwining of two-based-paired regions (stems) of an RNA (see Figure 1).

Fig. 1.

Graphical and dual graph representations of an RNA 2D structure. (a) graphical representation of a pseudoknot-free RNA primary sequence and embedded stems or base pairs; (a′) corresponding dual graph representation. (b) graphical representation of a pseudoknotted RNA 2D structure; (b′) corresponding dual graph.

The structural configuration of pseudoknots does not lend itself well to computational detection due to its overlapping nature. The base pairing in PKs is not well-nested, making the presence of PKs in RNA sequences more difficult to predict by the dynamic programming [3], [4] and context-free grammars standard methods [2]. Our methodology, based on topological properties of dual graphs, suggest a new way to look at the problem of detection and classification of PKs and of general RNAs.

Following (Kravchenko, 2009 [12]), we define our biological variables as follows.

Definition 1:

General terms:

1. RNA primary structure: a sequence of linearly ordered bases x₁, x₂, … ,x_r, where x_i ∈ {A, U, C, G}.

2. canonical base pair: a base pair (x_i, x_j) ∈ {(A, U), (U, A), (C, G), (G, C), (G, U), (U, G)}.

3. RNA secondary structure without pseudoknot - or regular structure, encapsulated in the region (i₀, … , k₀): an RNA 2D structure in which no two base pairs (x_i, x_j), (x_l, x_m), satisfy i₀ ≤ i < l < j < m ≤ m₀ (i.e., no two base pairs intertwined).

4. a base pair stem: a tuple (x_i, x_i+1, … ,x_i+r, x_i+(r+1), … , x_j−1, x_j) in which (x_i, x_j), (x_i+1, x_j−1), … , (x_i+r, x_i+(r+1)) form base pairs.

5. loop region: a tuple (x₁, x₂, … , x_r) in which ∀_i≤j≤r (x_i, x_j) does not form a base pair.

6. a pseudoknot encapsulated in the region (i₀, … , k₀): if ∃l, m, (i₀ < l < m < k₀) such that (x_i0, x_m) and (x_l, x_k0) are base pairs.

A graphical representation is an intuitive and natural way to depict an RNA 2D structure (see Figure 1-(a),(b)), in which the x-axis is labeled according to the primary linearly ordered sequence of bases (Definition 1-a), and a stem (Definition 1-d) is represented by arcs connecting base pairs. A region on the x-axis between the end-points of the arcs representing stems is called a segment.

A dual graph can be equivalently defined from the graphical representation of an RNA 2D structure as follows (Figure 1).

Definition 2:

The dual graph is defined by mapping stems and the segments between stems (x-axis), of the graphical representation of an RNA 2D structure, to the vertices and edges of the dual graph, respectively.

In the next section we propose our partitioning approach of a dual graph G, into subgraphs G′ ⊆ G, called blocks.

III. Graph Partitioning Algorithm

Our graph-theoretic partitioning methodology is based on identifying articulation points in the dual graph representation of an RNA secondary structure. An articulation point partitions a graphs into connected components, that is, its deletion disconnects a graph.

We need to define the following.

Definition 3:

Connectivity

1. A vertex-set X ⊆ V is a vertex-disconnecting set if deletion of X from G, denoted by G − X, results in a disconnected graph.

2. A vertex v is an articulation point or cut-vertex if G − v results in a disconnected graph (i.e., at least two components remain).

3. The vertex-connectivity, κ(G), is the minimum number of vertices whose removal from G results in a disconnected graph or in a isolated vertex. If G is a single edge, then κ(G) = 1.

4. A connected component is non-separable if it does not have an articulation point (or cut-vertex). Please note that single edges or isolated points are non-separable.

5. A block is a maximal (edge-wise) non-separable graph.

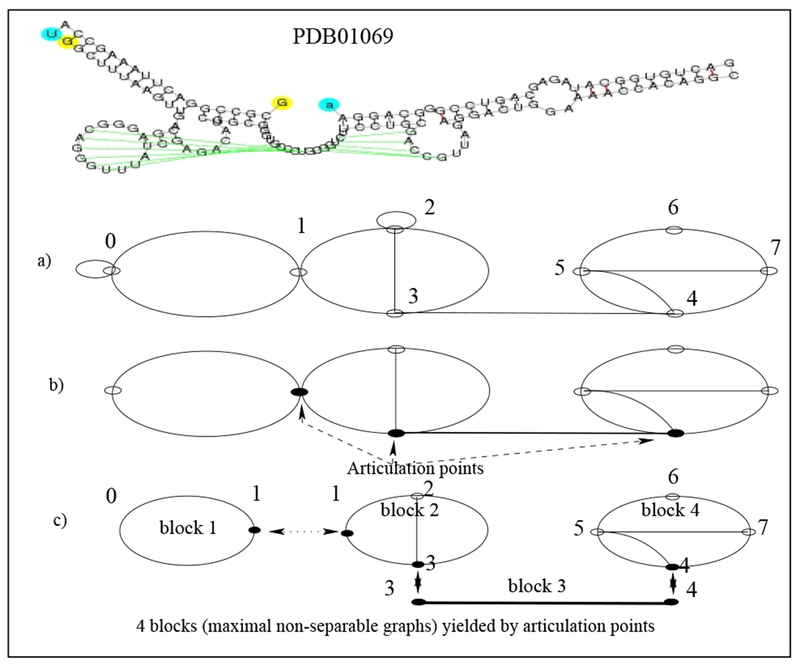
Indeed, identification of articulation points allow us to identify blocks (see Fig. 2). Since a block is a maximally non-separable component, a pseudoknot cannot be then contained in two different blocks. Thus identification of blocks allows us to isolate pseudoknots (as well as pseudoknot-free blocks), without breaking their structural properties.

Fig. 2.

Identification of articulation points and partitioning of the dual graph corresponding to PDB01069 RNA 2D (Catalytic Ribozyme RNA) into blocks.

Our partitioning algorithm is based on the classical result for identifying block components in a connected undirected graph introduced to John Hopcroft and Robert Tarjan (1973) [10]) that runs in linear computational time.

Classification of blocks as either pseudoknotted or pseudoknot-free are discussed in the next section.

IV. Classification of blocks and partitioning algorithm

The mathematical proofs of the lemmas stated in this section, are shown in Appendix B.

In preparation to the main results of this chapter, we first define the following.

Definition 4:

For any graph G, blocks can be partitioned into three classes,

1. Single edges.

2. Cycles.

3. Blocks containing a vertex v of degree at least 3.

From Definition 1-c, an RNA 2D structure is regular (pseudoknot-free) and encapsulated in a region (i₀, … ,k₀), if no two base pairs (x_i, x_j), (x_l, x_m), satisfy i < l < j < m, i₀ ≤ i, j, l, m ≤ m₀. Under the assumption that self-loops are deleted, this definition yields the following lemma.

Lemma 1:

Each block in the dual graph representation of a regular RNA 2D structure is either a bridge or a cycle of length l, l ≥ 2.

Conversely we show the following.

Lemma 2:

If an RNA 2D structure contains a pseudoknot, then its corresponding dual graph contains a block having a vertex of degree 3 or more.

Lemma 1 and Lemma 2 yield our main result as follows.

Corollary 3:

Given a dual graph representation of RNA 2D structure, a block represents a pseudoknot if and only if the block has a vertex of degree 3 or more.

To summarize our partitioning algorithm, we perform the following steps.

1. Partition the dual graph into blocks by application of Hopcroft and Tarjan’s algorithm.

2. Analyze each block to determine whether contains a vertex of degree at least 3. If that is the case then the block contains a pseudoknot, according to Corollary 3. If not then the block represents a pseudoknot-free structure.

V. Illustrative examples of the partitioning algorithm

We illustrate our partitioning algorithm on the dual graph representations of two RNA 2D structures, based on the New York University’s RAG database [11]. Our partitioning algorithm was implemented in C++ and runs on a Hewlett-Packard Pavilion Dv6 (2.4 GHz) notebook; the time taken for each partitioning is insignificant because of the linear computational complexity of Hopcroft and Tarjan’s algorithm.

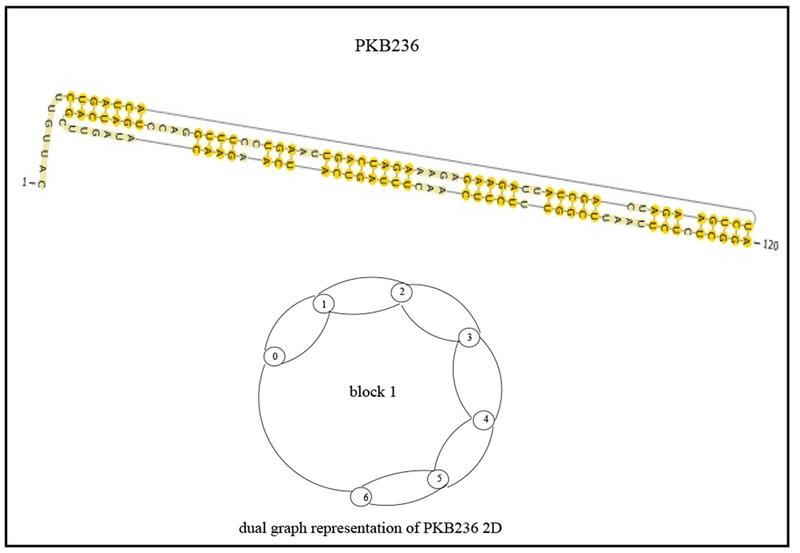
Consider the PDB01069 RNA 2D structure, Post-Cleavage State of the Thermoanaerobacter Tengcongenis GlmS Ribozyme, known to be the only catalytic RNA to require a small-molecule activator for catalysis (see Klein et al. [15]). Its dual graph is decomposed into 4 blocks as illustrated in Figure 2. According to Corollary 3, block 1 and block 3, a cycle and an edge, respectively, correspond to regular regions, while blocks 2 and 4, correspond to pseudoknots. We next consider the dual graph representation of PKB236 (see Fig. 3), Regulatory Pseudoknot of the Interferon-gamma Gene 5’-UTR, thought to be involved in regulatory translation (see Ben-Asouli et al. [1]); in this case the only block is the dual graph itself. As this block contains a vertex of degree 3 or more, this block is a pseudoknot.

Fig. 3.

Partition of the dual graph corresponding to motif PKB236 (Regulatory Pseudoknot of the Interferon-gamma gene 5′-UTR).

In the next section we depict the output generated by the partitioning algorithm when tests were performed on the aforementioned RNA structures.

VI. C++ algorithmic tests performed on RNA motifs

In this section (a, b) represents an edge of a dual graph with end-vertices a and b.

The following is the output yielded by our partitioning program when tests were performed on motifs PDB01069 and PKB236.

 ————— Motif :PDB01069 —————

========= New Block =========

(7,5) - (7,4) - (6,7) - (5,6) - (4,5) - (4,5) -

degree of 7 is 3

degree of 4 is 3

degree of 5 is 4

—- this block represents a pseudoknot —-

========= New Block =========

(3,4) -

—- this block represents a regular-region —-

 ========= New Block =========

(3,1) - (2,3) - (2,3) - (1,2) -

degree of 3 is 3

degree of 2 is 3

—- this block represents a pseudoknot —-

========= New Block =========

(0,1) - (0,1) -

—- this block represents a regular-region —-

 ——— Summary information for Motif :PDB01069 —

——— Total number of blocks: 4

——— number of PK blocks: 2

———— number of regular blocks : 2

——————————————————

————— Motif :PKB236 ————

======== New Block ==========

(6,0) - (5,6) - (5,6) - (4,5) - (4,5) - (3,4) - (3,4) - (2,3) -

(2,3) - (1,2) - (1,2) - (0,1) - (0,1) -

degree of 6 is 3

degree of 5 is 4

degree of 4 is 4

degree of 3 is 4

degree of 2 is 4

degree of 0 is 3

degree of 1 is 4

—- this block represents a pseudoknot —-

 ——— Summary information for Motif :PKB236 —-

——— Total number of blocks: 1

——— number of PK blocks: 1

——— number of regular blocks : 0

——————————————————

VII. Conclusions and Ongoing Work

We have presented a partitioning approach of the dual graph representation of RNA 2D structures into maximal non-separable components called blocks. Partitioning of a graph into blocks can be efficiently accomplished by application of Hopcroft and Tarjan’s algorithm. From mathematical definitions of RNA 2D structures and of pseudoknots, we proved that an RNA 2D structure contains a pseudoknot if and only if the dual graph representation has a block in which one of the vertices is of degree 3 or more, providing a systematic way to classify different RNAs regions.

Ongoing work involves applying the described dual-graph partitioning algorithm to the full library of dual graphs representing RNAs up to 9 vertices (98 different graph topologies for 1785 RNA secondary structures). All available RNA secondary structures are taken from the RNA Strand Database [18]. Using the Hopcroft and Tarjan algorithm for identifying non-separable graph components in a connected graph, our algorithm uses the adjacency matrix of the dual-graph as input and determines articulation points. That is, such a point (vertex v) is defined if G — v (where G is the dual graph of the RNA secondary structure) is a disconnected graph or a single vertex. Detection of the articulation points permit us to partition the graph into subgraphs, or building blocks, of the dual graph library that contain no such articulation points (non-separable units).

Applications to evolutionary analysis of organism complexity are also in progress through analysis of ribosome structures from different species, from archea to human. Ribosomal RNAs catalyze protein synthesis, and proteins are essential to life. Ribosomal RNA structures, both secondary and tertiary, are thus highly conserved, and a common structural/functional core has been identified. This core evolves in complexity as the organism’s complexity increases from archea to human. Current work on partitioning both small and large ribosomal RNA subunits for five organisms reveals core structural features as well as branching patterns with evolution. These subgraph patterns will be connected to other evolutionary techniques.

APPENDIX A

Graph Theory formulations and definitions

Let G = (V, E) be a graph with vertex-set V and edge-set E. We next present general graph-theoretic definitions following Harary [9].

Definition 5:

General graph-theoretic terms:

• a.Let H₁.x.H₂ represent the graph composed of two graphs, H₁, and H₂, sharing the same vertex x.
• b.A walk between two vertices u and v in graph G = (V, E), is an alternating sequence of vertices and edges < v_o = u, e₁, v₁, … , e_k, v_k = v > such that e_i = (v_i−1, v_i) is an edge of G.
• c.A trail between two vertices u and v in graph G = (V, E), is a walk between u and v with no repetition of edges.
• d.A path between two vertices u and v in graph G = (V, E), is a walk (or trail) between u and v with no repetition of vertices.
• f.A graph is Eulerian if there exist a trail from a vertex v₀ of G, ending at vertex v_k, covering all the edges of the topology, and if v₀ = v_k then the graph is an Eulerian cycle.

Dual graph representations of RNAs, and of PKs, can be easily shown to be Eulerian graphs from Definition 2. By starting from the origin on the x-axis of the graphical representation and traversing to the right, a unique trail in its dual graph can be described, where all edges are covered. Also it is easy to show the degree of any vertex in a dual graph is at most 4 as its corresponding stem in the graphical representation can be adjacent to at most 4 other stems.

Claim 4:

The dual graph representations of RNA 2D structures and of PKs are Eulerian. In addition the degree of a vertex v is at most 4.

APPENDIX B

Proof of Lemmas stated in Section III

From Definition 1-c, an RNA 2D structure is regular (pseudoknot-free) and encapsulated in a region (i₀, … , k₀), if no two base pairs (x_i, x_j), (x_l, x_m), satisfy i < l < j < m, i₀ < i, j, l, m ≤ m₀. Under the previous assumption that self-loops are deleted, this definition yields the following lemma,

Lemma 1:

Each block in the dual graph representation of a regular RNA 2D structure is either a bridge or a cycle of length l, l ≥ 2.

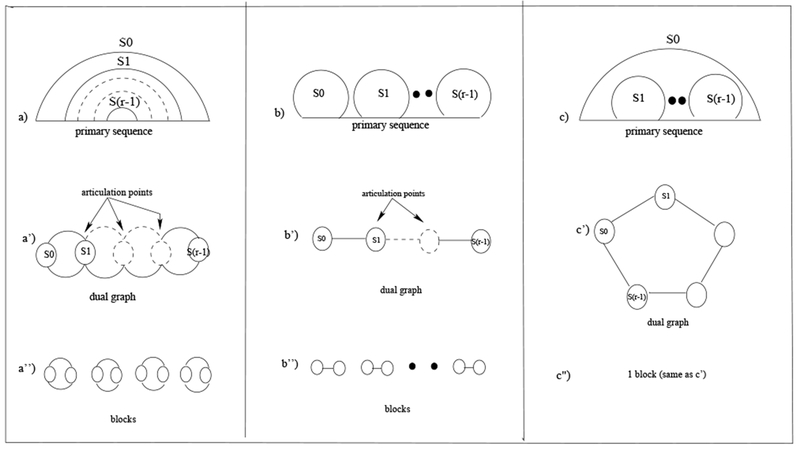
Proof. Consider the graphical representation of a regular RNA 2D structure; we will proceed by construction. A regular (pseudoknot-free) region can be recursively defined as follows (see Fig. 4): (a) a region composed of r nested-stems; (b) r adjacent stems, (c) a stem containing a sequence of r − 1 adjacent stems; (d) a single stem (represented as an isolated vertex in its dual graph, not illustrated in Fig. 4). In a transformation, a set of stems identified by properties a, b, and c in the graphical representation, are reduced (converted) into a single stem, while its corresponding dual graph is generated (see Definition 2). The blocks obtained from the dual graph representations of these properties, are either cycles of length 2, single edges, a cycle of length r, or an isolated vertex, respectively. Consider a sequence of transformations of dual graphs G₁ ⇒ G₂ ⇒ … ⇒ G_n, where the dual graph G_i+1 is obtained from dual graph G_i by following the precedence rules in which, first, internal stems of the ones identified by properties (a) through (c) of the graphical representation are reduced into a single stem, while the corresponding dual graph is generated; in the dual graph we distinguish the vertex corresponding to the outer-stem. Because only distinguished vertices could be later made adjacent to other vertices in a transformation, the blocks generated by the sequence of transformations from G₁ through G_n−1 will remain blocks in G_n, with the possible addition of blocks composed of single edges. □

Fig. 4.

Classification of PK-free regions and graphical/dual/block representations. (a) graphical, dual, and block representations of r nested-stems - (b) graphical, dual, and block representations of r adjacent stems - (c) graphical, dual, and block representations of a stem containing r − 1 adjacent stems.

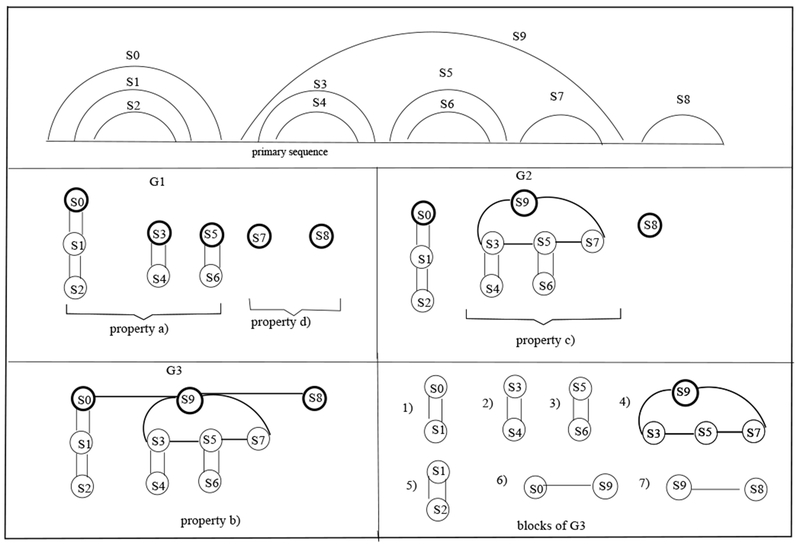
To illustrate Lemma 1, consider Figure 5 depicting the graphical representation of a pseudoknot-free region. The stems S₀, S₁ and S₂, identified by property (a), with corresponding dual graph with distinguished vertex S₀, are then reduced into a single stem in the graphical representation. Similarly, by property (a), we reduce the pairs of nested-stems S₃, S₄, and S₅, S₆, to two single stems with distinguished vertices S₃ and S₅, in the dual graph, respectively. As the stem S₉ contains a sequence of 3 (reduced) stems, by application of property (c), it can be reduced to a single stem with dual graph composed of a cycle on 4 vertices, and distinguished vertex S₉. Finally, by property (b), we connect the sequence of 3 (reduced) stems (i.e., S₀, S₉, and S₈) by single edges in the dual graph.

Fig. 5.

An example illustrating Lemma 1.

Conversely we show the following.

Lemma 2:

If an RNA 2D structure contains a pseudoknot, then its corresponding dual graph contains a block having a vertex of degree 3 or more.

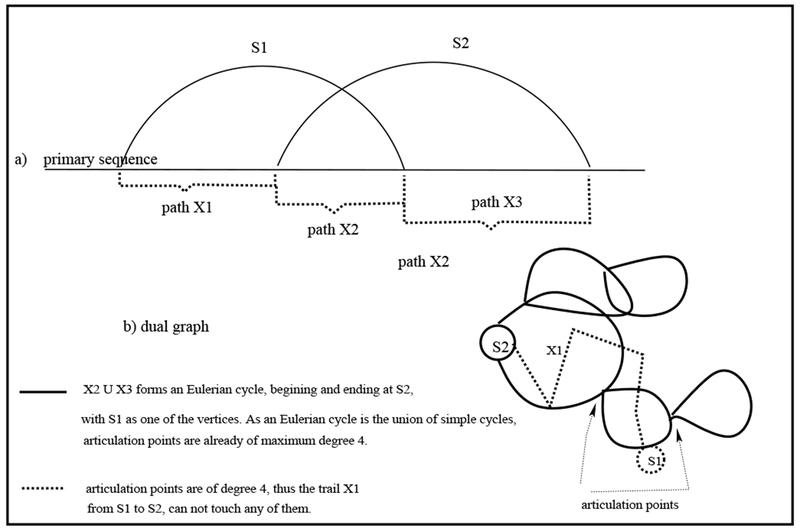
Proof. By Definition 1-f, if an RNA 2D structure contains a pseudoknot, there exist a stem crossing (interweaving) another stem. Let us denominate these interweaving stems, in the graphical representation, S₁ and S₂, respectively. There exist then three independent paths, X₁, X₂, and X₃, from S₁ to S₂ (see Figure 6-(a)), following the primary sequence of the graphical representation; these three paths correspond to trails in the dual graph representation (see Definition 5-c). We first note that X₂ ∪ X₃ forms an Eulerian cycle G₁ in the dual graph representation (see Definition 5-e, and Claim 4), beginning and ending at S₂, having S₁ as one of its vertices. Because an Eulerian cycle is the union of simple cycles ([9], pg. 64) (Figure 6-(b)), then the articulation points of G₁ have maximum possible degree 4 (Claim 4); when we add then the trail X₁, from S₁ to S₂ to G₁, X₁ cannot touch (include) any of the articulation points of G₁. Let G₂ = B₁.a.B₂.b.B₃.c.B₄ … B_r (see Definition 5-a) be a subgraph of G₁ describing a sequence of blocks B₁, B₂, … , B_r, S₁ is a vertex of B₁, and S₂ is a vertex of B_r, in which the set $\tilde{A}=\{a,b,c\dots ..\}$ is the set of articulation points connecting the blocks of G₂. Let G* be the graph obtained by adding the trail X₁ to G₂. Clearly κ(G*) (see Definition 3-c) is at least 2 as deleting a single articulation point in $\tilde{A}$ won’t disconnect G* as X₁ does not have a vertex in $\tilde{A}$, thus G* is a non-separable graph (Definition 3-d). As both S₁ and S₂ have degree at least 3 in G*, then there is a block containing G* (possibly itself) having a vertex of degree 3 or more. □

Fig. 6.

Supporting illustration for the proof of Lemma 2