Molecular Mechanics Parameterization of Anesthetic Molecules

Abstract

Anesthetic drug molecules are being increasingly studied through the use of computational methods such as molecular dynamics (MD). Molecular mechanics force fields require the investigator to supply parameters for the force field equation, which are not available for novel molecules. Careful selection of these parameters is critical for simulations to produce meaningful results. Therefore, this chapter presents a state-of-the-art method for determining these parameters by comparison to quantum mechanics calculations and experimental quantities. Ketamine is used as an example to demonstrate the process.

1. INTRODUCTION

1.1. Molecular Mechanics

Molecular dynamics (MD) simulations are often employed in the study of molecular systems relevant to anesthetic function. Essentially, an MD simulation considers atoms to be soft spheres with point charges and velocities, and propagates Newton’s second law of motion over time, generating a trajectory of atomic paths and energies. This simplification of reality is called molecular mechanics (MM)–as opposed to quantum mechanics (QM). MM is designed to produce a reasonable approximation to the experimental behavior of a system. Various thermodynamic properties of MM systems can be derived using statistical mechanics, which is a sub-field of physics that formalizes the relationship between the microscopic behavior of a collection of particles and macroscopic properties. Within the MM framework, the microscopic behavior of these particles is governed by a relatively simple potential energy function, an example of which is shown here:

$$\begin{gathered} V=\sum _{\text{bonds}}{k}_b{\left(b-b_0\right)}^2+\sum _{\text{angles}}{k}_{\theta }{\left(\theta -{\theta }_0\right)}^2+\sum _{\text{Urey-Bradley}}{k}_u{\left(u-u_0\right)}^2 \\ +\sum _{\text{dihedrals}}{k}_{\varphi }\left[1+\text{cos}\left(n\varphi -\delta \right)\right]+\sum _{\text{impropers}}{\left(k_{\omega }-{\omega }_0\right)}^2+\sum _{\text{residues}}{V}_{\text{CMAP}}\left(\Phi ,\psi \right) \\ +\sum _{\text{nonbonded}}\epsilon \left[{\left(\frac{R_{ij}^{\text{min}}}{r_{ij}}\right)}^{12}-{\left(\frac{R_{ij}^{\text{min}}}{r_{ij}}\right)}^6\right]+\frac{q_i{q}_j}{\epsilon r_{ij}} \end{gathered}$$

This is the CHARMM force field equation (Brooks et al., 2009). While this equation looks long and complicated, it is actually conceptually quite simple. Different types of interactions are deemed to be separable and additive, and are expressed with simple functional forms. Many excellent treatments of the theory behind MM exist which justify these approximations (Cramer, 2004; Leach, 2001); therefore, we will limit the scope of this chapter to practical aspects of preparing ligand parameters, with a special emphasis on anesthetics. We will also limit our scope to “all-atom” force fields, which represent each atom with one discrete particle. By contrast, “united-atom” or “coarse-grained” force fields may use a single coarse-grained particle to represent more than one atom, in the process sacrificing precision for computational efficiency.

Many parameters (k_b, k_u, etc.) which are specific to the particular atoms being considered, must be chosen. This has been done already for most atoms in biomacromolecular systems, and these parameters have been extensively validated. But it may not have been done for a particular molecule of interest. Here, we describe our methodology for choosing these parameters, a process called “parameterization.” What may be the optimal parameterization methodology is a matter of debate, but we hope to provide a good starting point. This chapter is written with the CHARMM all-atom force field (Brooks et al., 2009), NAMD molecular dynamics software (Phillips et al., 2005), and Gaussian QM software (Gaussian, Inc., Wallingford, CT, USA) in mind, but the concepts are applicable to others. Ketamine, a drug in common use as an anesthetic, is presented as an example.

1.2. Bonded vs Nonbonded Terms

Bonded terms restrict the motion of atoms that are connected by bonds and encompass bonds, angles, Urey–Bradley angles, dihedral angles (“dihedrals” for short), and improper dihedral angles (impropers). Bonded terms define bonds and angles between atoms as harmonic oscillators, with an equilibrium value and force constant. This represents the fact that stretching or squeezing a bond, or distorting an angle, is energetically unfavorable. An example of this would be the equilibrium O–H bond length of 0.9572 Å and H–O–H angle of 104.5 degrees in water, which are explicitly made part of the widely used TIP3P water model (Jorgensen, Chandrasekhar, Madura, Impey, & Klein, 1983). A crucial property of harmonic bonds is that they are nondissociative: energy grows rapidly as a function of bond length, so that the bond may not break. Thus, the bonded chemical structure remains fixed in such MM simulations, which may therefore not describe chemical reactions. Those require more complex and computationally expensive strategies, such as “reactive” force fields or QM simulations.

Dihedral terms allow for refining conformational preferences around rotatable bonds that are not accurately modeled by other parts of the MM equation. Improper dihedral terms are typically used to enforce the planarity of sets of four atoms.

Nonbonded terms in the equation describe van der Waals and Coulombic (electrostatic) interactions. Van der Waals interactions are usually modeled with the 6–12 Lennard-Jones potential (Jones, 1924), which includes an attractive term describing dispersion forces between atoms, and a very short-distance core repulsion, which combine to yield an equilibrium distance. The Lennard-Jones equation is computationally efficient: the dispersion energy behaves as the inverse 6th power of the distance and the repulsion term is defined as the inverse 12th power. These can be easily calculated as the products of second and third powers. So even though more accurate potentials exist, the Lennard-Jones potential is preferred in MM calculations.

As noted earlier, each atom is assigned a partial charge, which is related to the overall molecular charge distribution and does not need to be (and rarely is) an integer, as it represents a notional partitioning of the overall charge density among the particles in the simulation. Note that this approximation of a continuous, fluctuating charge density as a constellation of static point charges is a very real limitation of MM. These charges are used with the Coulomb equation to determine the electrostatic inter-action energy, and hence forces. In biomacromolecules at physiological temperature, electrostatic interactions normally contribute the bulk of the potential energy. Be sure to consider the pK_a of the ligand being parameterized, which normally is available experimentally. If it is likely to exist in a protonated form at physiological pH, you will need to study the protonated form. Finally, consider whether environment effects such as a hydrophobic or charged cavity might create enough of a pK_a shift to change the dominant species.

2. OVERVIEW OF PARAMETERIZATION METHOD

The overall workflow suggested here is a progressive refinement of an energy surface by fitting to a QM energy surface, along the way choosing force field parameters that optimize the fit. The resulting parameters can be used to compute experimental quantities such as partition coefficients, as well as solvation and binding energies, for validation. A detailed approach for CHARMM all-atom models is outlined in Mackerell et al. (1998).

The QM level of theory and basis set should be chosen to capture the behavior of the ligand in question, and normally should be in accordance with the development philosophy of the force field employed. In the case of CHARMM, this is something like B3LYP/6–31G^**. A treatment of QM methods is outside the scope of this chapter. Suggested introductory reading includes (Cramer, 2004; Leach, 2001).

It is imperative to start from an energy-minimized structure when generating any type of QM energy surface for fitting. Such a structure represents a stationary point on the potential energy surface and is easily obtained using the geometry optimization function of a QM software, such as with the Opt keyword in Gaussian. If this is not done, the derived parameters will erroneously stabilize what would be an experimentally unstable structure, and in particular the Hessian matrix (discussed later) will include spurious derivatives reflecting restorative forces to a stationary point.

A potential energy surface is generated by varying some parameter along a degree of freedom of interest and calculating a single-point energy at each of those points. Here, each of these points represents a new ligand configuration. For example, one might vary a particular dihedral angle involving a bulky group that would be expected to have high-energy interactions in some positions: this is depicted in Fig. 1.

Fig. 1.

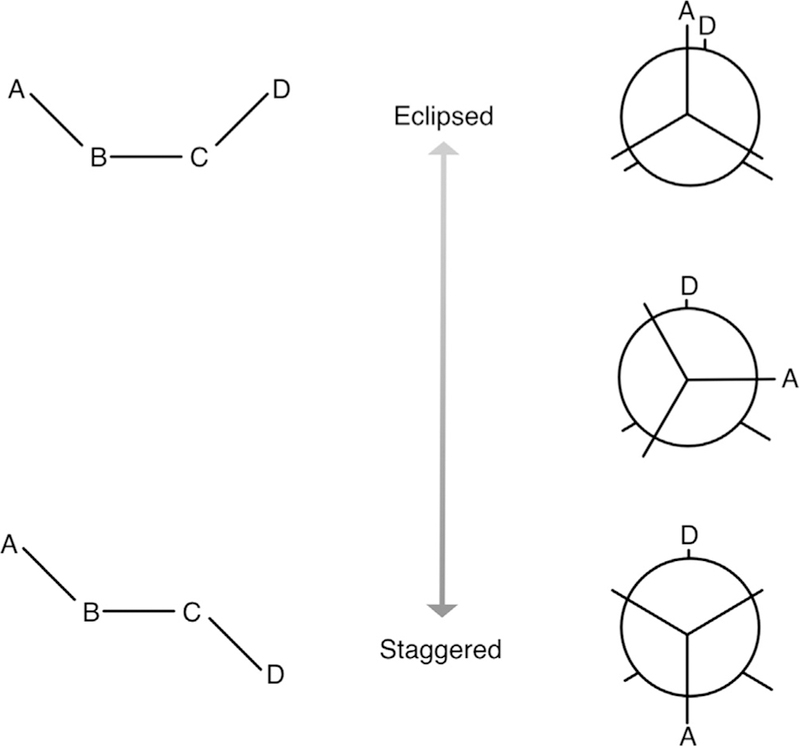
Notional diagram of butane. The four carbon atoms are labeled A, B, C, and D, and hydrogens are omitted for clarity. Again ignoring hydrogens, bond terms are A–B and C–D, which would be equivalent, and B–C. Angle terms are A–B–C and B–C–D, also equivalent, and the dihedral term is A–B–C–D. The eclipsed version of the dihedral is at the top and staggered at the bottom. Newman projections are at the right. The eclipsed conformation is higher energy than the staggered conformation, because carbons A and D are further apart in the staggered conformation.

At each point, a constrained QM geometry optimization (keeping the selected coordinate constant and optimizing the rest) and single-point energy calculation are done. At each of the same points, a short MM minimization of the structure is undertaken by analogy to the QM geometry optimization, for practical reasons, a strong harmonic restraint is often used instead of a geometric constraint. Then, a single-point MM energy is computed, in gas phase, without periodic boundary conditions. Because potentials do not have a physically significant energy reference, the energy zero points will not match, but the energy surfaces can be aligned with zero energy being defined as the original optimized molecular configuration.

It is most important to meticulously fit the low-energy regions, because the lowest energy states are the most probable states. In a Boltzmann distribution, the probability P(x) of a state x is related to its energy E(x) by

$$P\left(x\right)\sim \text{exp}\left[-E\left(x\right)/RT\right]$$

Here, R represents the molar gas constant and T represents the temperature (see Fig. 2 for a plot of this equation).

Fig. 2.

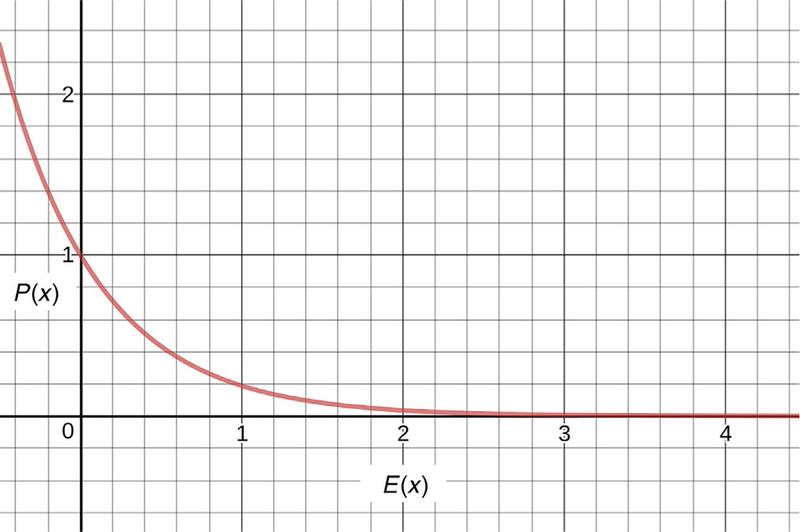
Probability of a state as a function of energy. Note that the probability drops as exp(−E), which means that the probability of high energy states is quite low.

A high-energy peak is extremely unlikely to be accessed in MD simulation because these simulations are normally done at near physiological temperatures. For example, if QM calculations identify a peak with height 50 kcal/mol, it is acceptable for the MM energy surface to peak at, say, 45 or 55 kcal/mol, because the probability of the states with those energies is incredibly small. On the other hand, if QM calculations identify a peak with height 1 kcal/mol, the MM energy surface should reproduce this to yield realistic transitions across that barrier.

Some of these steps can be automated with software such as Force Field Toolkit (FFTK) (Mayne, Saam, Schulten, Tajkhorshid, & Gumbart, 2013) which is included with recent versions of VMD (Humphrey, Dalke, & Schulten, 1996). Indeed, we describe its use as such below. Keep in mind though that while it is a time saver, it is imperative to double-check its output at every stage, e.g., by visualizing the results of QM geometry optimizations or conformational scans.

3. METHODS FOR CHOOSING PARAMETERS

3.1. Implementation Details

Here, we discuss briefly the implementation details of working with the CHARMM force field. The interested reader is advised to peruse the CHARMM force field website and documentation for more information (http://mackerell.umaryland.edu/charmm_ff.shtml), particularly including the details of the relevant file formats. These include the Residue Topology File (.rtf ) and parameter file (.prm). These are both text files that may be combined into a single “stream” (.str) file; this capability is an artifact of its original use with the CHARMM molecular dynamics software. The .rtf file describes how atoms are connected in each type of molecule. Amino acids, nucleic acids, and various lipids are defined, as well as water, ions, and others. Atom types, masses, and charges are specified. Atom charges are molecule-specific, and the same atom type may occur multiple times in a single residue with different charges. The specific MM force field parameters used in the simulation are then a function of the atom types and how they are connected. Those parameters—bond, angle, dihedral terms, as well as Lennard-Jones parameters—reside in the .prm file.

Each atom in an MM system has a type and a name. An atom type identifies the correct parameters to use for that atom. Chemically similar atoms may be assigned the same atom type if energetically appropriate. For example, the C2 and C3 atoms in phenol are both assigned the CG2R61 atom type, even though one is ortho and the other is meta from the hydroxyl group. On the other hand, an aliphatic carbon behaves differently from an aromatic carbon, and these require separate parameters: among other differences, a C–C aromatic bond has a different equilibrium length and force constant than a C–C alkane bond. The C2 and C3 atoms in cyclohexanone are assigned the CG321 atom type.

We assume that atom types and their force field terms can be reused across different molecules; this assumption is called transferability. Atom names, on the other hand, are just names used as identifiers, and are unique to atoms within the ligand or residue. When possible these follow common conventions for ease of reading.

Before constructing .rtf and .prm files of your own, it will be extremely helpful to peruse these files as included in the CHARMM force field in con-junction with the file format documentation to understand how parameters for a given molecule are retrieved and plugged into the force field equation. The suggested approach here involves starting with the CGenFF extension of CHARMM, which is contained in the top_all36_cgenff.rtf and par_all36_cgenff.prm files. For the example provided earlier, see the parameters including CG2R61 and CG321 atom types, respectively, as well as PHEN and CHON residues.

3.2. Automatic Parameterization Software

Some force fields include molecular fragments that have already been parameterized, and all that may be required is to stitch these fragments together to produce a complete molecule. This is an ideal starting point because these fragments have usually been extensively validated for use with the other parameters in the force field. Various software is available to automate this task, such as ParamChem and SwissParam for CHARMM-compatible parameters, and Antechamber for AMBER-compatible parameters. How-ever, these services may not always provide an adequate set of parameters. This can occur when:

• There is a potential energy term that cannot be varied independently (e.g., two dihedrals with interacting groups) and further correction terms are required (propofol hydroxyl group, see Section 3.5);

• Not all dihedral parameters are present or accurate (dexmedetomidine);

• A novel functional group is present (diazirines);

• Atoms joining functional groups are not yet parameterized (ketamine).

Some software, such as ParamChem, gives a penalty score that provides an idea how close the match is. If the software does not think it made a good match, you should validate and possibly tweak the parameters, by using the generated parameters as a starting point for the procedures described later. Even if the parameters themselves are completely wrong, this type of software automates the creation of skeletal .rtf and .prm files that can be subsequently modified.

3.3. Creating a Residue Topology With Atom Types and Partial Charges

The first step is to create the topology of the molecule by choosing atom types and charges and defining the bonds among them yourself, or using automatic parameterization software to provide a starting point. A reasonable starting point for assigning atom types and partial charges is an existing molecule in a given force field. For example, CHARMM includes CGenFF (Vanommeslaeghe & MacKerell, 2012; Vanommeslaeghe, Raman, MacKerell, 2012), which contains parameters for many common functional groups that can be assembled into a complete molecule.

In most cases, atom types may be taken from groups containing the same elements in similar chemical environments; the associated Lennard-Jones parameters can then be reasonably expected to transfer. If this process does not give good results and refinement of Lennard-Jones parameters is necessary, a higher level of care and expertise might be necessary, because Lennard-Jones parameters are generally underdetermined and reliable data (usually pure condensed phase properties) to fit them are not always available. Therefore, this falls outside the scope of this piece.

Once this is done, refinement of partial charges can begin. Many partial charges in the CHARMM force field were refined by fitting their interaction energy with water using the TIP3P model from MM calculations against those from QM calculations (Mackerell et al., 1998) and are therefore a useful approach for anesthetics (Henin, Brannigan, Dailey, Eckenhoff, & Klein, 2010).

Here is our suggested approach to assigning partial charges:

1. Find the most similar functional groups available in the force field to those comprising your molecule. For each atom, consider valence, bond order, and whether the atom is part of a ring. Using these as a guide, write the topology of your ligand. You must define all bonds between atoms. Or, use a parameterization server as described earlier to generate an initial guess, which will also generate a valid topology file. Some of the parameters chosen may be wrong, but you will refine them. In certain cases, for very similar molecules to compounds that are already parameterized, the parameters generated by such a server may be adequate as they are, and the rest of the steps can be avoided.

2. Ensure that the sum of the charges is correct. A neutral ligand should of course have a total charge of zero. In any event, the ligand cannot have a noninteger charge for an accurate simulation. NAMD will produce a warning but will not stop execution for a noninteger charge. Make an educated guess as to how to tweak the charges by examining other similar molecules if available.

3. Determine which atoms have the most questionable charges. This is to some extent a judgment call as you do not know a priori how reasonable the assigned partial charges are. Of note, charges with a magnitude greater than 1 are usually too large. Generally, functional groups appearing in your molecule should be similar to those already in the CHARMM or CGenFF residue library.

4. For each of these atoms, run a QM geometry optimization, with a water molecule in a hydrogen bonding configuration with that atom. Repeat with the water in multiple initial positions in an arc around the atom. In Gaussian, this type of “arc scan” can be automated by specifying the water part of the system as a Z-matrix and varying the appropriate angle using the Opt = ModRedundant keyword. The end-point interaction energy from each of these calculations is printed with units of hartrees in the output.

5. Evaluate the same ligand–water configurations as an MD single-point interaction energy calculation after a short minimization. Compare this energy profile with the QM energy profile and tweak charges as necessary to achieve a closer fit. Repeat as necessary.

While tools such as FFTK can automate the derivation of partial charges, unsupervised charge fitting calculations can produce bizarre values that are at odds with standard values in the force field. For example, in most six-membered aromatic rings with the CHARMM force field, the carbons have charge –0.115 and the hydrogens +0.115, but FFTK will not necessarily end up at these values.

Ketamine example.

For simplicity, we will discuss deprotonated ketamine, even though at physiologic pH the protonated form dominates. We consider here the S–(+) enantiomer because that is more clinically potent. Ketamine consists of cyclohexanone and chlorobenzene functional groups joined together, with a methylamine group bonded to the cyclohexanone (see Fig. 3). The former two functional groups are already available in CGenFF as the CHON and CHLB residues, respectively, and so they were copied directly. The methylamine was built by analogy with the dimethylamine (DMAM) residue. The charges did not add up to zero so the charges near the interfaces between the groups were adjusted by hand to produce a reasonable starting point. To refine the charges, arc QM water scans on the nitrogen and chlorine were done as described earlier.

Fig. 3.

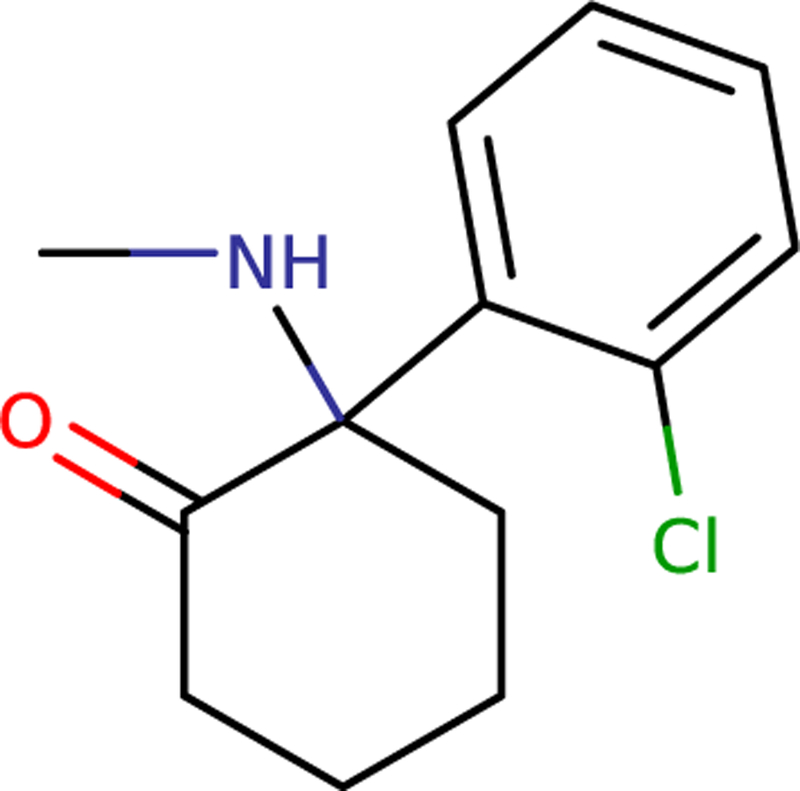
Diagram of ketamine. Note the constituent functional groups: cyclohexanone, chlorobenzene, and methylamine.

3.4. Bonds and Angles

Recall that in MM bonds are modeled as harmonic springs. Given sufficient force separating the two-bonded atoms, a real atomic bond will break, and the electron density will redistribute between the two pieces. As molecular dynamics is not intended to sample very high energy states, it does not attempt to model covalent bonds breaking, and so the bond potential equation can be kept simple for computational efficiency. Thus in the harmonic spring approximation, as the atoms are separated, the restoring force increases linearly and energy required increases quadratically. At great distances this is wildly inaccurate, but since we are only concerned with relatively low–energy configurations close to equilibrium, this is acceptable.

Nominally, bond and angle terms should reproduce vibrational spectra. However, these may not be readily available for comparison for your molecule of choice. Therefore, we adopt the approach taken by the FFTK (Mayne et al., 2013), which automates this calculation through the use of the Hessian matrix, which contains partial second derivatives of the energy with respect to each atom coordinate, and can be calculated ab initio from QM.

1. Make a list of the atom types in your ligand and make note of all bond or angle terms already present that include any of these atom types. Make note of any bonded atoms in your ligand that do not have bond or angle terms. These are the terms that will need to be predicted or refined.

2. Using as a starting point the geometry-optimized structure already determined using QM optimization, calculate the Hessian matrix at the same level of theory and with the same basis set used for the geometry optimization. In Gaussian this is done using the Freq keyword.

3. Using the Hessian matrix, you can approximate the local shape of the potential energy surface by small perturbations of bonds and angles, and use the Hessian force constants to calculate the resulting potential energy. The MM bond and angle force constants can then be fitted to reproduce these local energy surfaces. This step is automated by the FFTK.

Urey–Bradley terms allow modifications of the potential energy as a function of the distance between the first and third atoms in an angle: effectively, it adds a bond between these atoms. These are poorly transferable and are only useful for reproducing subtle aspects of vibrational spectra. Therefore, they are not required for pharmacological applications, and will not be further discussed here.

Ketamine example.

Many of the bond and angle terms exist in CGenFF, so these are used directly. However, bond and angle terms involving the atoms joining the three main functional groups in ketamine did not exist in CGenFF. Therefore, the Hessian was calculated and FFTK was used to automate the process of fitting these bond and angle terms.

3.5. Dihedrals

Dihedral terms give a potential energy as a function of dihedral angle. They are important when other terms are not sufficient to properly reproduce the potential energy surface.

Consider butane. The four carbon atoms—let’s call them A, B, C, and D—can be twisted, with the midpoint defined as a plane perpendicular to the B–C bond. Importantly, the potential energy surface of this rotation is periodic. This lends itself to the functional form of the dihedral potential energy expression. Dihedral terms are expressed with a force constant multiplied by a cosine which provides periodicity and phase. As with the other types of potential energy terms, dihedral terms are additive: it is often the case that multiple dihedral terms with different coefficients will be needed for the same four atoms in order to properly reproduce the potential energy surface as the atoms are rotated—but not always. When several cosine terms with different periods are added, the dihedral potential is effectively defined as a truncated Fourier series. One should strive to use the fewest possible dihedral terms to avoid adding spurious, underdetermined parameters.

1. Choose the dihedrals that are worth refining, or any that are required but not already included in the force field. Energetically important dihedrals describe those rotatable bonds that may produce transitions between low–energy conformers.

2. Run a dihedral torsion scan at the appropriate QM level. In Gaussian, this can be done with the Mod = OptRedundant keyword. We tend to use an angle increment of 15 degrees, for a total of 24 points.

3. Using your parameter set in progress, run an MM dihedral torsion scan at the same angles. To minimize the effect of small differences between MM and QM minima, at each step a short MM minimization is necessary prior to the single-point energy calculation.

4. Modify or add dihedral terms as necessary to improve the fit of the MM surface to the QM surface, and repeat the MM torsion scan. Remember that the QM and MM zero energies will be different, so they must be aligned by adding a constant.

In some cases, the energy profile of a given dihedral depends on another dihedral angle. This can happen when two bulky or charged groups, otherwise separated, can be brought near each other by torsional rotation. Such dihedrals must be optimized self-consistently by adjusting each of them in turn and iterating. In some cases, however, the nature of the coupling makes it impossible to capture using isolated dihedral potentials. An example is the hydroxyl group of propofol, where the hydrogen interacts with the isopropyl groups depending on their relative rotations (LeBard, Henin, Eckenhoff, Klein, & Brannigan, 2012). In such cases, the CHARMM force field allows an explicit correction to be applied in the form of a potential energy term that couples both dihedrals. Initially developed for protein backbone corrections (Best et al., 2012), such “CMAP” correction terms have proven useful in ligand parameterization as well.

“Impropers” are a form of dihedral term that is used to maintain either planarity or a given chirality in groups of four atoms. They are not necessary for most molecules, and so they will not be discussed further here.

Ketamine example.

Since N, O, and Cl atoms are in relatively close proximity, dihedrals involving the amine group as well as the atoms connecting the two rings were evaluated at 15–degree intervals by conducting QM geometry optimizations at each point. Dihedral terms were modified to closely reproduce the fit of MM to QM energy surface, with a particular focus on the low–energy regions. The amine methyl was thought likely to interact with the chlorobenzene, so torsions of these groups with respect to the central carbon were scanned together. Fitting MM to QM energies produced a table of CMAP correction terms.

3.6. Comparison With Experiment

There is no universally accepted method of validating new parameters. However, since the ultimate objective of molecular simulation is to predict real life, one reasonable approach is to use the parameters in an MD simulation to estimate some experimental result to show concordance of the simulation with reality. A dilemma may occur when a limited amount of precise experimental data must be divided between a training set and a test set for the model. It is then tempting to use most of the information in the training set to improve parameter quality, thus leaving little reference data for tests. Extensive use of QM calculations for parameterization brings the benefit of requiring little in the way of experimental observables, possibly paving the way for more extensive a posteriori tests.

A common and relatively simple experimental quantity is the octanol–water partition coefficient. Octanol and water are poorly miscible and will separate into layers when mixed. A third added chemical will partition itself between the two, reaching an equilibrium distribution. The ratio of the concentrations is an equilibrium constant, which can be related to a free energy change by the relation $\Delta G=-RT\ln K,$ , where R is the gas constant, T is the temperature, and K is the equilibrium constant. This describes the thermodynamic cost of transferring the chemical from one layer to another on a molar basis. In practice, the base-10 logarithm of the equilibrium constant is reported, and this is referred to as “log P” or “log K_ow.” Note that predicted log P values are often reported as “cLogP” values, which are merely the result of a proprietary computation based on an empirical model (BioByte Inc., Claremont, CA) rather than experiment.

To compute log P of a molecule, one could simulate the process of moving one molecule from octanol to water or vice versa and determine the free energy cost of the geometrical translation, e.g., using the adaptive biasing force method (Darve & Pohorille, 2001) as implemented in NAMD and LAMMPS molecular simulation software (Henin, Fiorin, Chipot, & Klein, 2010). Another method is to use free energy perturbation (FEP) to calculate the free energy of decoupling the molecule from octanol and recoupling it to water. Because free energy is a state function—free energy changes do not depend on the path—the sum is equal to the energy of moving the molecule from octanol to water. Our preferred approach is to simulate decoupling of the molecule from each solvent and subtracting the decoupling free energies to yield a value for ΔG. The log P can then be calculated according to

$$\text{log}P=\Delta G/2.303RT$$

The constant 2.303 is used for conversion between natural and base-10 logarithms.

Dissociation constants of the ligand with a known protein can be determined by experiment, and in some cases these can be compared in simulation. For example, many diazirine photoaffinity ligands bind to horse spleen apoferritin (HSAF) in a presumed binding site with known affinity (Oakley et al., 2012; Vedula et al., 2009). A standard free energy of binding can be computed using alchemical FEP. This is itself a substantial undertaking and convergence may be an issue, particularly when coupling/decoupling charged compounds. For HSAF, one needs only to simulate one dimer out of the 24-mer because the presumed binding site is located at a monomer interface. The details of implementing such a calculation are out of the scope of this review, but the interested reader is encouraged to review other literature such as Gilson and Zhou (2007).

4. SUMMARY

We described a state-of-the-art method for deriving MM parameters for small anesthetic molecules by comparison to QM energies as a gold standard, as well as certain experimental quantities. The parameters are compatible with the CHARMM force fields for proteins and lipids, allowing for simulations of drug–receptor interactions in complex environments, as well as binding affinity predictions. Ketamine was presented as an example molecule.

Highlights.

• Anesthetic molecules are often studied using computational methods.

• A method for rigorously choosing molecular mechanics parameters is given.

• This can enhance the accuracy of computational studies of anesthetics.