Meaning of Intracranial Pressure-to-Blood Pressure Fisher-Transformed Pearson Correlation–Derived Optimal Cerebral Perfusion Pressure: Testing Empiric Utility in a Mechanistic Model

Supplemental Digital Content is available in the text.

Abstract

Objectives:

Time-averaged intracranial pressure-to-blood pressure Fisher-transformed Pearson correlation (PR_x) is used to assess cerebral autoregulation and derive optimal cerebral perfusion pressure. Empirically, impaired cerebral autoregulation is considered present when PR_x is positive; greater difference between time series median cerebral perfusion pressure and optimal cerebral perfusion pressure (Δ_CPP) is associated with worse outcomes. Our aims are to better understand: 1) the potential strategies for targeting optimal cerebral perfusion pressure; 2) the relationship between cerebral autoregulation and PR_x; and 3) the determinants of greater Δ_CPP.

Design:

Mechanistic simulation using a lumped compartmental model of blood pressure, intracranial pressure, cerebral autoregulation, cerebral blood volume, Paco₂, and cerebral blood flow.

Setting:

University critical care integrative modeling and precision physiology research group.

Subjects:

None, in silico studies.

Interventions:

Simulations in blood pressure, intracranial pressure, Paco₂, and impairment of cerebral autoregulation, with examination of “output” cerebral perfusion pressure versus PR_x-plots, optimal cerebral perfusion pressure, and Δ_CPP.

Measurements and Main Results:

In regard to targeting optimal cerebral perfusion pressure, a shift in mean blood pressure or mean intracranial pressure with no change in mean blood pressure, with intact cerebral autoregulation, impacts optimal cerebral perfusion pressure. Second, a positive PR_x occurs even with intact cerebral autoregulation. In relation to Δ_CPP, for a given input blood pressure profile, with constant intracranial pressure, altering the degree of impairment in cerebral autoregulation or the level of Paco₂ maintains differences to within ±5 mm Hg. Change in intracranial pressure due to either an intermittently prolonged pattern of raised intracranial pressure or terminal escalation shows Δ_CPP greater than 10 mm Hg and less than –10 mm Hg, respectively.

Conclusions:

These mechanistic simulations provide insight into the empiric basis of optimal cerebral perfusion pressure and the significance of PR_x and Δ_CPP. PR_x and optimal cerebral perfusion pressure deviations do not directly reflect changes in cerebral autoregulation but are, in general, related to the presence of complex states involving well-described clinical progressions with raised intracranial pressure.

A key concern in the management of patients with severe traumatic brain injury (TBI) is whether cerebral autoregulation (CA) is intact and able to minimize alterations in cerebral blood flow (CBF) due to changes in cerebral perfusion (1–3). Because there are a number of processes underlying CA and CBF control, we have two main clinical challenges to consider: variance in the upper and lower limits of CA, and not knowing patient-specific optimal levels in intrinsic physiologic factors such as Paco₂, blood pressure (BP), and intracranial pressure (ICP) (4–6).

These are two general approaches studying indirectly whole brain circulation pathophysiology (6). First, an empirical approach using observational and epidemiologic evidence to establish statistical relationships and correlations between inputs and outputs. This approach is best exemplified by studies in severe TBI using ICP to BP Fisher-transformed Pearson correlation (“PR_x”) (i.e., 5–7 min of time-averaged ICP and BP data to calculate mean Fisher-transformed Pearson correlation) to derive, by statistical analyses, the cerebral perfusion pressure (CPP, the difference between mean BP and mean ICP) optimal for an individual (i.e., optimal CPP [CPP_Opt]). Briefly, by inference, because positive PR_x is considered representative of disturbed CA and negative PR_x is reflective of intact CA (7), the CPP_Opt is defined as the CPP at which PR_x is at its minimum (7–10). In severe TBI, the difference between contemporaneous time series median CPP (CPP_Med) and CPP_Opt (i.e., difference between time series CPP_Med and CPP_Opt [Δ_CPP]) 0–5 mm Hg is associated with favorable outcome, whereas Δ_CPP –10 to –15 mm Hg occurs only in those with unfavorable outcome (8). Such empiric associations can lead to new hypotheses and, possibly, pragmatic trials. However, these observations cannot provide better understanding of pathophysiology or even the determinants of CPP_Opt. Second, we have a mechanistic approach to indirect assessment of global cerebrovascular behavior using electrical analog models of CA control pathways, feedback loops, and arterial network structure (2, 3, 7, 11–20). Here, in silico evidence is rationalized according to the fluid dynamics or electronics of inputs and outputs. In 1988, Ursino (11, 12) proposed the first “lumped compartmental model” of cerebral circulation physiology that included CA. Since then, the modeling mechanistic approach has been used to better understand patient data from, for example, transcranial Doppler studies of middle cerebral artery flow velocity (6, 21, 22). To date, such models have not been used to provide mechanistic insight into the questions of “What does PR_x-derived CPP_Opt mean?” and “What is the effect of manipulating BP, ICP and Paco₂?”

In this report, we use the lumped compartmental model of brain circulation physiology and CA, with its system operating CPP, to assess PR_x and calculated CPP_Opt. Our aims are to simulate the physiology in severe TBI and better understand: 1) the potential strategies for targeting CPP_Opt; 2) the relationship between CA and PR_x; and 3) the determinants of Δ_CPP.

MATERIALS AND METHODS

This experimental in silico study did not require Local Ethics Committee approval.

Lumped Compartmental Model of CA

We have implemented the model by Ursino et al (2), Ursino and Giannessi (3), Ursino (11, 12), and Ursino and Lodi (13, 14) to first test potential strategies for targeting CPP_Opt. Figure 1 shows the electrical analog of our model with its four compartments that account for interactions among BP, ICP, CA, cerebral blood volume, Paco₂, and CBF. Supplemental Digital Content 1 (http://links.lww.com/CCM/D992) provides more information about the model and the transient 6-hour change in BP profile (with 50 Hz sampling rate) used in the simulations (11, 14, 23). At baseline, the model operates with BP, CPP, CBF, and ICP at 100 mm Hg, 90.5 mm Hg, 12.5 mL/s (750 mL/min), and 10 mm Hg, respectively.

Figure 1.

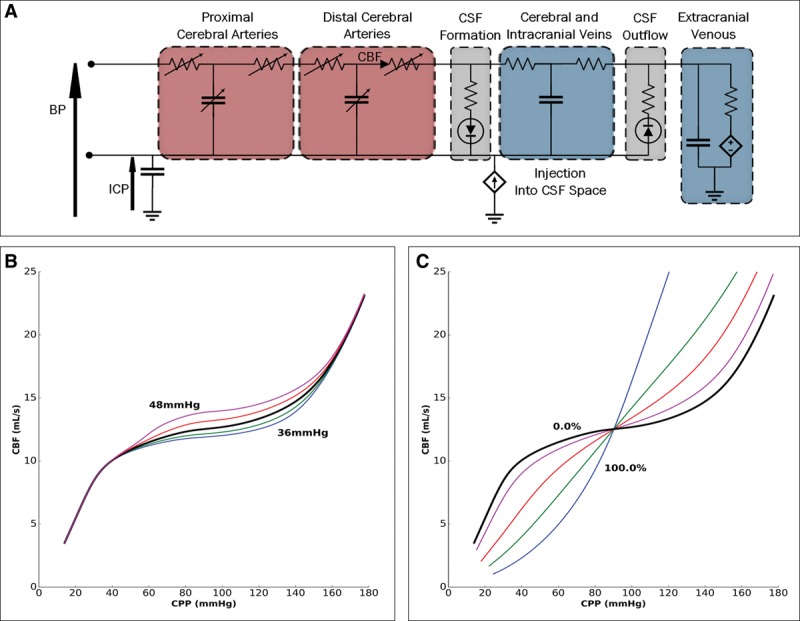
The electrical circuit equivalent of the lumped compartment model and some baseline physiologic operating characteristics. A, The model includes different segments: proximal and distal cerebral arteries, cerebral and intracranial veins, extracranial venous, and cerebrospinal fluid (CSF) formation and outflow. B, The dependence of cerebral blood flow (CBF) on cerebral perfusion pressure (CPP) under steady-state conditions at various Paco₂ values (36, 38, 40, 42, and 44 mm Hg). Increasing Paco₂ increases CBF at any given CPP. C, The dependence of CBF on CPP when cerebral autoregulation (CA) gain varies. CPP variation leads to more alteration in CBF as CA impairment increases (0%, 25%, 50%, 75%, and 100%). BP = blood pressure, ICP = intracranial pressure.

PR_x and Estimation of CPP_Opt

We have simulated changes in BP, Paco₂, CA state, and ICP (by fluid injection into the cerebrospinal fluid [CSF] space). CPP is calculated from BP and ICP signals. CPP_Med is the CPP_Med for the whole simulation.

To compute PR_x, we average BP and ICP over 10 seconds, and then use 40 consecutive time-averaged samples. Individual correlations are collated throughout the simulation. Mean CPP during each time series correlation calculation is then associated with the individual PR_x. Then, the range in these mean CPP values is divided into 5 mm Hg width “bins,” and the mean PR_x corresponding to each bin is plotted—hereafter called the “PR_x-plot.” We use these data in another exploratory plot to calculate the minimum of the curve that defines CPP_Opt (4, 7, 8, 24). The Δ_CPP is also evaluated as a difference category (Δ_Category) according to previously used ranges (9).

RESULTS

Figure 1 shows the steady-state characteristics of the electrical analog model under conditions of Paco₂ variation and CA gain. There is the expected dependence of CBF on CPP: for any given value in CPP, an increase in Paco₂ causes the expected increase in CBF, whereas a decrease in Paco₂ leads to the expected decrease in CBF (Fig. 1B). Figure 1C shows that when CA is impaired, there is more significant alteration in CBF with variation in CPP.

Potential Influencers of CPP_Opt

Change in BP. We tested different BP profiles using fully intact CA and constant ICP and Paco₂, 10 and 40 mm Hg, respectively. An example of the full graphical process for each “input” BP to “output” PR_x-plot is shown in Figure S1 (Supplemental Digital Content 2, http://links.lww.com/CCM/E35). Figure S2 (Supplemental Digital Content 2, http://links.lww.com/CCM/E35) shows that degree and pattern of change in BP impact the PR_x-plot and derivation of CPP_Opt.

Figure 2 shows the effect of shifting by a fixed amount one of the BP profiles from Figure S2E (Supplemental Digital Content 2, http://links.lww.com/CCM/E35—see bold black line originating at 80 mm Hg), thereby maintaining the same BP profile but with different median BP (BP_Med) during the whole simulation (Table S1, Supplemental Digital Content 3, http://links.lww.com/CCM/E36). A shift in BP_Med (Fig. 2A) has an impact on the position of the minimum in the PR_x-plots (Fig. 2B) and CPP_Opt (Table S1, Supplemental Digital Content 3, http://links.lww.com/CCM/E36). A downward shift in BP profile by 10 mm Hg, from the line originating at 80 mm Hg (Fig. 2A, black line) to the line originating at 70 mm Hg, leads to a similar 10 mm Hg downward shift in CPP_Med (from 71 to 61 mm Hg) and similar downward shift in CPP_Opt (from 68 to 56 mm Hg) (Table S1, Supplemental Digital Content 3, http://links.lww.com/CCM/E36). On inspecting these data with the same BP profile, BP_Med or CPP_Med (if ICP is at a constant level) determines the position of CPP_Opt.

Figure 2.

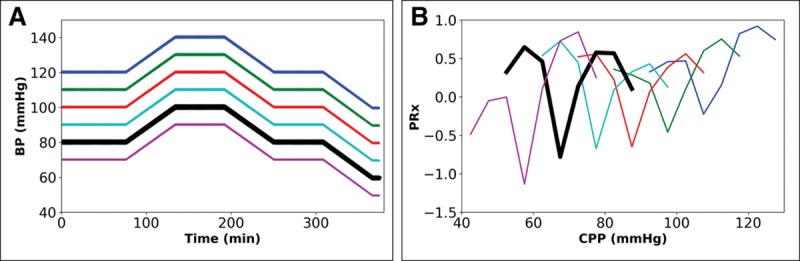
Impact of shifting the 6-hr mean blood pressure (BP) profile on intracranial pressure-to-BP Fisher-transformed Pearson correlation (PR_x) when cerebral autoregulation is intact. Paired graphs with input BP profiles (A) and output cerebral perfusion pressure (CPP) PR_x-plots before final curve fitting (for details and text, see Fig. S2, Supplemental Digital Content 2, http://links.lww.com/CCM/E35). A, BP profile shifted either up or down by fixed amount, giving six inputs differing in mean BP. B, Output PR_x-plots for profiles in A, showing that difference in mean BP, but fixed pattern, results in shift in the minima in the plots (for results of final mathematical transformation to calculate optimal CPP [see text], see Table S1, Supplemental Digital Content 3, http://links.lww.com/CCM/E36).

Change in Paco₂. The impact of change in Paco₂ on CPP_Opt is minimal (Fig. S3, Supplemental Digital Content 2, http://links.lww.com/CCM/E35; and Table S1, Supplemental Digital Content 3, http://links.lww.com/CCM/E36). Alterations in Paco₂ (32–48 mm Hg) lead to small changes in ICP and little impact on the position of the minimum in the PR_x-plots. The increase in CPP_Opt with increase in Paco₂ from 32 to 48 mm Hg was 5 mm Hg (87–92 mm Hg).

Change in ICP. The effects of changes in ICP profile—when CA is intact and 40 mm Hg Paco₂—on the PR_x-plot show increasing shift with constantly increased ICP. When using the BP profile from Figure 2A (see red line originating at 100 mm Hg) with six constant levels in ICP, the output PR_x-plots are shown (Fig. 3). For comparison, Figure S4 (Supplemental Digital Content 2, http://links.lww.com/CCM/E35), using the BP profile in Fig. S2C (Supplemental Digital Content 2, http://links.lww.com/CCM/E35), illustrates the output PR_x-plots with the same constant shift in ICP). Figure 3 and Table S1 (Supplemental Digital Content 3, http://links.lww.com/CCM/E36) show that a constant shift of 10 mm Hg (from 20 to 30 mm Hg) results in a downward shift in CPP_Med by 9 mm Hg (from 81 to 70 mm Hg). CPP_Opt also decreases by 9 mm Hg (from 79 to 70 mm Hg). Therefore, similar to the findings in Figure 2, A and B, the position of CPP_Opt is determined by constant rise in ICP level or constant change in CPP with a constant BP profile.

Figure 3.

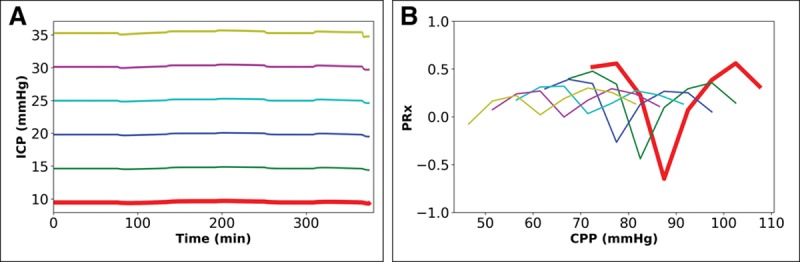
Impact of fixed change in mean intracranial pressure (ICP) profile over 6 hr when cerebral autoregulation is intact and Paco₂ is 40 mm Hg. Paired graphs with input ICP profiles (A) and output cerebral perfusion pressure (CPP) ICP-to-blood pressure (BP) Fisher-transformed Pearson’s correlation (PR_x) plots before final curve fitting (the BP profile is the same in all simulations). A, The effect of injection of fluid into the cerebrospinal fluid space at six different rates (0.0–0.05 mL/s) to raise mean ICP to six constant levels (10, 15, 20, 25, 30, and 35 mm Hg). B, Output PR_x-plots for profiles in (A) showing shift similar to that seen with fixed alteration in BP (Fig. 2B for comparison; for results of final mathematical transformation to calculate optimal CPP, see Table S1, Supplemental Digital Content 3, http://links.lww.com/CCM/E36).

Figures 4 and 5 use the same BP profile to Figure S2C (see also Fig. S4, Supplemental Digital Content 2, http://links.lww.com/CCM/E35). (Table S1 [Supplemental Digital Content 3, http://links.lww.com/CCM/E36] shows for comparison the findings when using the ICP profiles in Fig. 3A with the BP profile from Fig. S2C [Supplemental Digital Content 2, http://links.lww.com/CCM/E35].) Figure 4 shows the effect of a series of peaks in ICP. (Of note, Fig. S5E [Supplemental Digital Content 2, http://links.lww.com/CCM/E35] shows that during such wave-like changes, PR_x goes from a negative value to a positive value, and back to a negative value in the course of each wave in ICP.) An upward shift in peak ICP by 10 mm Hg (20–30 mm Hg) results in minimal downward shift in CPP_Med by approximately 2 mm Hg (from 86 to 84 mm Hg), but CPP_Opt shows an upward shift by approximately 10 mm Hg (from 63 to 73 mm Hg).

Figure 4.

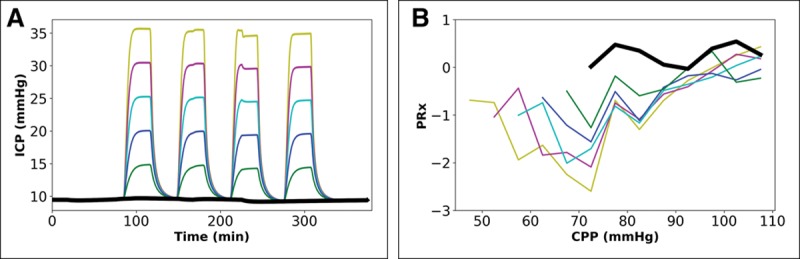
Impact of serial peaks in intracranial pressure (ICP) over 6 hr, when cerebral autoregulation is intact and Paco₂ is 40 mm Hg. Paired graphs with input ICP profiles (A) and output cerebral perfusion pressure (CPP) ICP-to-blood pressure (BP) Fisher-transformed Pearson correlation (PR_x) plots before final curve fitting (the BP profile is the same in all simulations). A, Four serial peaks in ICP with five different peak levels (color-coding similar to Fig. 3, see text for details). B, Output PR_x-plots for profiles in A, (for results of final mathematical transformation to calculate optimal CPP, see Table S1, Supplemental Digital Content 3, http://links.lww.com/CCM/E36).

Figure 5.

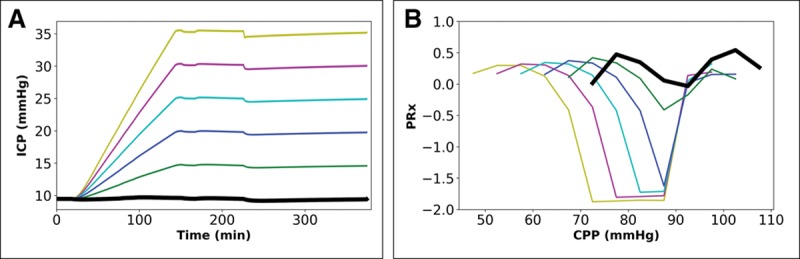
Impact of escalation in intracranial pressure (ICP) profile over 6 hr to a terminal plateau when cerebral autoregulation is intact and Paco₂ is 40 mm Hg. Paired graphs with input ICP profiles (A) and output cerebral perfusion pressure (CPP) ICP-to-blood pressure (BP) Fisher-transformed Pearson correlation (PR_x) plots before final curve fitting (the BP profile is the same in all simulations). A, Five patterns of escalation in ICP (color-coding similar to Fig. 3, see text for details). B, Output PR_x-plots for profiles in A, showing shift in curves (for results of final mathematical transformation to calculate optimal CPP, see Table S1, Supplemental Digital Content 3, http://links.lww.com/CCM/E36).

Figure 5 shows the effect of an escalation in ICP profile, with the same BP profile used in Figure 4. In this instance, an upward shift in the final peak in ICP by 10 mm Hg (20–30 mm Hg at peak) results in downward shift in CPP_Med by 10 mm Hg (from 78 to 68 mm Hg), but CPP_Opt exhibits a smaller downward shift (≈4 mm Hg, from 85 to 81 mm Hg) (Table S1, Supplemental Digital Content 3, http://links.lww.com/CCM/E36).

CA and PR_x

At baseline state (40 mm Hg Paco₂ and 10 mm Hg ICP with consistent BP profile), change in CA gain—an indicator of impairment of feedback systems—has minimal consequence on the position of the minimum in the PR_x-plots (Table S1, Supplemental Digital Content 3, http://links.lww.com/CCM/E36). The increase in CPP_Opt with increasingly impaired CA from 0% to 50% was small (≈2 mm Hg, from 89 to 91 mm Hg). However, mean PR_x at CPP_Opt changes –0.14 to 0.25, to 0.80 with increase in CA impairment from 0% to 25%, to 50%, respectively.

On inspection of Table S1 (Supplemental Digital Content 3, http://links.lww.com/CCM/E36), it is also evident that in simulations with fully intact CA, it is still possible to obtain a positive mean PR_x at so-called CPP_Opt; that is, a positive coefficient is not necessarily an indicator of impaired CA. (Fig. S6 [Supplemental Digital Content 2, http://links.lww.com/CCM/E35] summarizes the findings of a full analysis with 756 separate simulations, which comes to the same conclusion as Table S1, Supplemental Digital Content 3, http://links.lww.com/CCM/E36.)

The Determinants of Δ_CPP

A fixed change in BP (Fig. 2A) or a constant rise in ICP (Fig. 3A), using the same BP profile, resulted in Δ_CPP values in the Δ_Category 0–5 mm Hg (Table S1, Supplemental Digital Content 3, http://links.lww.com/CCM/E36). We could only simulate a state with Δ_Category 5–10 mm Hg when selecting a lower BP profile (with constant ICP 10 mm Hg), and CPP_Med approximately 61 mm Hg. We could simulate Δ_CPP –19.9 mm Hg if we used a different BP profile (Fig. S2C, Supplemental Digital Content 2, http://links.lww.com/CCM/E35) and constantly raised ICP of 25 mm Hg.

In the simulations with serial peaks in ICP (20–35 mm Hg; Fig. 4), the Δ_Category was consistently greater than 10 mm Hg (Table S1, Supplemental Digital Content 3, http://links.lww.com/CCM/E36). Last, an escalating rise in ICP (Fig. 5) with peak 15–25 mm Hg resulted in Δ_Category –10 to –5 mm Hg. An escalating ICP peak 30–35 mm Hg resulted in Δ_Category less than –10 mm Hg (Table S1, Supplemental Digital Content 3, http://links.lww.com/CCM/E36).

DISCUSSION

PR_x-derived CPP_Opt, with calculation of Δ_CPP and Δ_Category, are statistical constructs and have proven value in patient risk stratification and in epidemiologic association with poor outcome (4, 7–9, 23–26). However, CPP is not physiologically controlled in homeostasis; there is no sensor, error signal, set point, or optimum within the operating range between the upper and lower limits of CA. Hence, CPP_Opt-guided management may be a testable pragmatic therapeutic approach, but, intrinsically, empiricism has limitations to understanding mechanistic functions (27). How could a mechanistic model of cerebrovascular pathophysiology improve on an empirical approach that is already able to predict outcome during real-time monitoring of BP and ICP in severe TBI? In this report, we describe three insights. First, in regard to targeting CPP_Opt, a shift in BP_Mean or mean ICP, with intact CA, impacts CPP_Opt. Second, a positive PR_x at CPP_Opt, which should signify impaired CA, in the lumped model also occurs with intact CA. Last, in relation to Δ_CPP, the compartmental model confirms that greater deviation from zero is associated with more severe 6-hour profiles in ICP.

We should first note potential limitations in our simulations. Our model simplifies a complex system. We could add more feedback systems, but have settled on the balance between complexity and the ability to model a system, which is an approach now commonly used in so-called “personalized, model-based critical care medicine” (28). Other limitations of the model are that CBF is derived without accounting for changes in cerebral metabolism, the effects of medications or CSF diversion on cerebrovascular dynamics, and the consequence of surgical interventions (e.g., craniotomy, hematoma evacuation). Neither does the model account for brain heterogeneity in CA and microvascular nonnutritive phenomena such as shunt flow (29). That said, there are four advantages of our in silico testing: 1) “ground truth” CA is known and model parameters can be set to desired values; 2) changes in BP and ICP can be controlled and examined; 3) confounding factors can be controlled or eliminated; and 4) measurement errors can be removed as noise level can be controlled.

Potential Strategies for Targeting CPP_Opt

Our first finding about strategies in targeting CPP_Opt when CA is intact found that shift in either BP or ICP has an impact on CPP_Opt. CPP_Opt is also sensitive to the low-frequency characteristics of the BP and ICP profiles. Because CPP is a derived variable and mathematically coupled to both BP and ICP, we show in a separate mathematical analysis that CPP_Opt can change just by changing the input BP or ICP profiles, which confirms the findings in our simulations (Supplemental Digital Content 4, http://links.lww.com/CCM/E37). The equations also show that even when PR_x does not change substantially, there can be significant change in CPP_Opt. These features may explain why PR_x-derived CPP_Opt has applications in pediatric severe TBI even though children have lower BP (10, 30). Returning to adult severe TBI, a recent analysis of CPP_Opt in 104 patients managed in two European centers found heterogeneity in CPP_Opt between the centers, which was attributed to different management protocols, especially different CPP targets, and different demographic factors like age-related BP_Mean (31). Our report provides in silico and mathematical underpinnings for these expected observations and an explanation as to how these factors should be considered in practice.

CA and PR_x

In theory, a positive PR_x should be associated with impaired CA, whereas negative values should reflect intact CA. In our simulations, we found that even when CA is fully intact, it is possible to obtain a positive mean PR_x at the value of CPP_Opt, which is at odds with the pressure reactivity concept. In the mathematical analysis (Supplemental Digital Content 4, http://links.lww.com/CCM/E37), the equations confirm that impairment of CA will have an impact on PR_x, but no major difference in Δ_CPP, which in our simulations remained within ±5 mm Hg (see below). That said, under controlled conditions, in which impairment in CA is known to be present, more positive PR_x does reflect more severe impairment. However, when using only ICP, BP, and CPP data, we cannot always know whether CA is impaired or not. Hence, taken in isolation, monitoring PR_x is not providing added information about CA.

Δ_Category and Outcome

Several clinical studies have used the PRx-based estimate of CPP_Opt (4, 7–10, 24–26) with some adult patient cohorts demonstrating an association between outcome after severe TBI and Δ_Category (9, 25). In a case series of 299 adults with severe TBI, Aries et al (8) found the following: when their summary of Δ_Category for the whole period of ICP monitoring (using a moving window of 4 hr over and average of 4 d of data) was less than –10 mm Hg, all patients died; when their summary Δ_Category was greater than 10 mm Hg, approximately 30% survived with favorable outcome, approximately 60% survived with severe disability, and the remainder died. Our simulations add to the face validity of these associations and also provide further insight. They show that during constant decrease in BP or nonextreme constant increase in ICP, shift in CPP_Opt is similar to shift in CPP_Med, and so the Δ_CPP remains within ±5 mm Hg. The mathematical handling (Supplemental Digital Content 4, http://links.lww.com/CCM/E37) also indicates that even when CA impairment has an impact on PR_x, there may not be a major change in Δ_CPP, which in our simulations also remained within ±5 mm Hg. In order to generate a Δ_Category more typical of those associated with poor outcomes in the clinical literature (8, 25), our simulations needed to incorporate a major abnormality in ICP 6-hour profile. A constant ICP at 25 mm Hg or escalation in ICP without remission to greater than 30 mm Hg gave Δ_Category less than –10 mm Hg. A series of peaks in ICP up to 20–35 mm Hg resulted in Δ_Category greater than 10 mm Hg.

CONCLUSIONS

Taken together, our simulations provide mechanistic insight into the interpretation of PR_x, CPP_Opt, and Δ_Category. These empirically derived variables do provide a numerical summary of complex states involving well-described clinical progression and deterioration with raised ICP (32). This feature has epidemiologic importance, and we also wonder whether these composite indices may serve to provide a threshold for shift in treatment paradigm when managing cases with severe TBI—such as moving from medical to surgical interventions. Last, as illustrated by this report, the value of empirical and model-based mechanistic approaches in critical care medicine should be considered as complementary and potentially synergistic (27).

Supplementary Material

ccm-46-e1160-s001.docx ^{(36KB, docx)}

ccm-46-e1160-s002.docx ^{(13.9MB, docx)}

ccm-46-e1160-s003.docx ^{(158.6KB, docx)}

ccm-46-e1160-s004.docx ^{(90.8KB, docx)}