Improving malignancy prediction through feature selection informed by nodule size ranges in NLST

Abstract

Computed tomography (CT) is widely used during diagnosis and treatment of Non-Small Cell Lung Cancer (NSCLC). Current computer-aided diagnosis (CAD) models, designed for the classification of malignant and benign nodules, use image features, selected by feature selectors, for making a decision. In this paper, we investigate automated selection of different image features informed by different nodule size ranges to increase the overall accuracy of the classification. The NLST dataset is one of the largest available datasets on CT screening for NSCLC. We used 261 cases as a training dataset and 237 cases as a test dataset. The nodule size, which may indicate biological variability, can vary substantially. For example, in the training set, there are nodules with a diameter of a couple millimeters up to a couple dozen millimeters. The premise is that benign and malignant nodules have different radiomic quantitative descriptors related to size. After splitting training and testing datasets into three subsets based on the longest nodule diameter (LD) parameter accuracy was improved from 74.68% to 81.01% and the AUC improved from 0.69 to 0.79. We show that if AUC is the main factor in choosing parameters then accuracy improved from 72.57% to 77.5% and AUC improved from 0.78 to 0.82. Additionally, we show the impact of an oversampling technique for the minority cancer class. In some particular cases from 0.82 to 0.87.

I. Introduction

In this paper we show that with the division of a training dataset into subsets based on nodule size we can classify lung nodules as benign or malignant more accurately due to having different models and representative features the nodule size subsets [1], [2], [3], [4], [5]. As a result, even with a reduced number of training cases (that imbalance the class sizes in the subsets as well) training on a subset improves accuracy and area under the Receiver Operating Characteristic curve (AUC) to predict nodules as benign and malignant. “AUC shows the probability that a randomly chosen diseased subject is (correctly) rated or ranked with greater suspicion than a randomly chosen non-diseased subject [6]. Page 1.”

Jin et al. [7] shows in his work that AUC is a more discriminating feature accuracy. Thus, we compared our results with previous work for both metrics: accuracy and AUC.

We show that a good choice of classifier [8] significantly decreases variation in performance (both accuracy and AUC).

One of the most important parameters of a nodule in malignancy prediction is its size. As representative of nodule size, we use LD (longest diameter was chosen as a nodule evaluation parameter due to its common usage by radiologists). In order to estimate it’s importance one can look at the result of Naive Bayes training on Cohort 1 and testing on Cohort 2 which will be discussed in the proceeding, when only the LD of the nodule is presented. Based only on LD we can correctly classify 70.88% of nodules a benign or malignant.

II. Dataset

In this study, we used a subset of cases from the NLST dataset divided into two cohorts based on clinical information.

The NLST contains CT images at multiple time points (approximately one year gap between screenings:1999–,T0, 2000–T1, 2001–T2). For both cohorts, we used CT image volumes from T0 for feature extraction. Based on the NLST protocol, all lung cancer cases in this analysis had a baseline positive screen (T0) that was not lung cancer and then were diagnosed with lung cancer at either the first follow-up screen (N = 104) or the second follow-up screen (N = 92). The 92 lung cancer cases that were diagnosed in the second follow-up screen also had a positive screen that was not lung cancer in the first follow-up screen.

Cohort 1 consists of 261 cases with 85 cancer cases and 176 non-cancer cases. Cohort 2 consists of 237 cases with 85 cancer cases and 152 non-cancer cases. Cohort 1 was used as the training set and Cohort 2 as the testing set.

III. Data preparation and classifiers

Segmentation and feature extraction were done by Definiens [10] software. Originally there were 219 features (a complete list of features can be found in the paper by Balagurunathan et al. [11]) which describe the size, shape, location and texture information of a nodule. From the original subset we extracted feature subsets which were considered the most informative during test/re-test filtering on the RIDER dataset [12]. Additionally, we used features from the same filter, but based on Cohort 1 over time information (C1 stable).

The list of feature subsets:

• 219 features

• Rider stable features (23 features)

• Cohort 1 stable features (37 features)

Even though, we used a test/re-test filter initial selection, we looked for a model which is able to classify data with a small number of features. For that purpose, we used feature selectors ReliefF (RfF) [18], [19], [20] and Correlation-based Feature Selector (CFS) [21]. In each case, we selected the top 5 or 10 ranked features.

One of the benefits we gain from splitting datasets is the independent usage of classifiers. For each subset we applied the classifiers:

• Decision tree – J48 [14];

• Rule Based Classifier – JRIP [15];

• Naive Bayes [17];

• Support Vector Machine [16];

• Random Forests [13].

In the case of SVM we utilized a radial basis function as a kernel and also a linear kernel. C and Gamma were found on the training set using Grid Search.

All the experiments where done in Weka version 3.6.13 [21].

IV. Splitting training and testing subsets

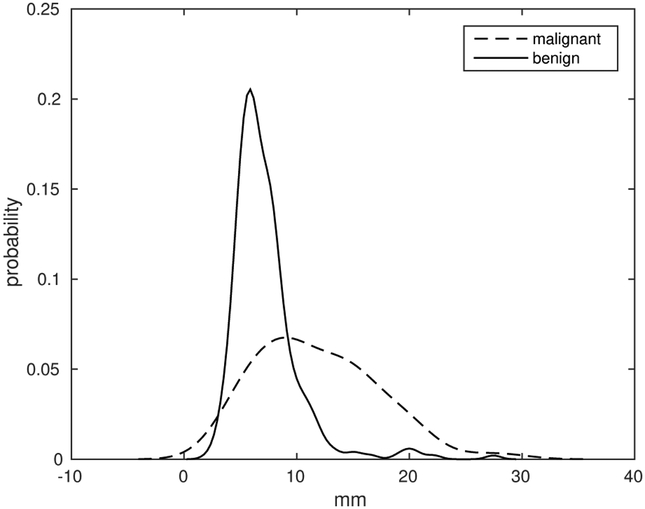
In Cohort 1, the nodules’ longest diameters vary from 2.24 mm to 28.64 mm. In order to select thresholds for division we used the histogram of diameters. For normalization, only for display, we computed probability of values inside each class. Figure 1 is the normalized histogram of the LD feature in Cohort 1.

Fig. 1:

LD parameter histogram for all patients in Cohort 1 for cancer and non-cancer cases.

We divided the datasets into three subsets according to nodule sizes – small, medium and large. As we see from Figure 1 malignant and benign nodules have two different distributions of LD.

For the experiments we used two thresholds: t₁ and t₂. We used formulas 1 and 2 for their computation, where μ_c and μ_nc define mean values for nodule’s longest diameter in Cohort 1 for malignant and benign cases respectively.

$$t_1=\frac{{\mu }_c+{\mu }_{nc}}{2}-1$$ (1)

$$t_2=t_1\cdot 2$$ (2)

We used the average of the means of these two distributions as the first threshold. We decreased it by one, in order to extract medium nodules because the average value can be considered as medium and for simplicity we rounded down t₁. t₂, which is used to define medium, and large nodules is t₁ doubled. For Cohort 1 we got t₁ =8 mm and t₂ = 16 mm.

Thus, nodules with LD less than 8 millimetres, which represent the left part of a histogram according to its average, are considered small. Nodules with LD greater or equal to 8 millimetres and less than 16 millimetres, which represent the right part of histogram according to its average, are considered medium size nodules. Finally, nodules with LD greater than or equal to 16 millimetres are considered large.

Table I shows the number of cases in each subset and each cohort with respect to their classes.

TABLE I:

Number of cases in subset.

Cohort	subset	Cancer	Non-cancer	total
C1	small	21	112	133
	medium	47	57	104
	large	17	7	24
C2	small	42	85	127
	medium	24	59	83
	large	19	8	27

V. Impact of splitting on accuracy

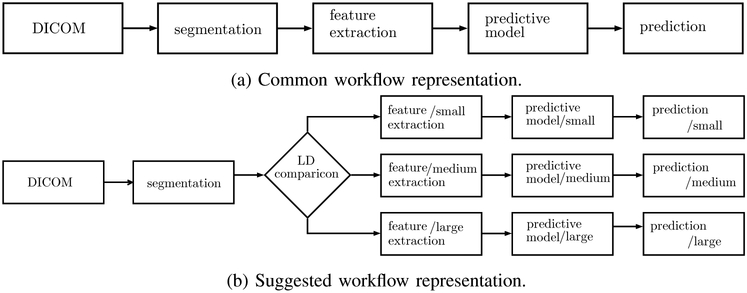
Splitting datasets leads to a change in workflow. Previously, we used the workflow shown in Figure 2a [9] where all available training data was used to select representative features and later to train a classifier. During testing we use all data to evaluate performance. In the new model, Figure 2b, after extracting features we add one more step. We check the longest diameter and define to which subgroup the nodule belongs. Then we do feature selection and training independently for each group.

Fig. 2:

schematic representation of workflow in previous works and a workflow for a splitting datasets.

We have predictions for three groups. We used results which were obtained from training on all 261 cases and testing on all 237 cases.

For training we used the settings shown in Table II and all the data from Cohort 1. For testing we used one subset of Cohort 2 one at a time. Thus, we obtained the performance for each subset individually. The first row shows results when an SVM with radial basis kernel function was trained on all cases of Cohort 1 and tested on nodules from Cohort 2 with LD less then 8 millimetres (subset of “small” nodules). Similarly, the second and the third rows show results when the classifier was tested on “medium” and “large” subsets of Cohort 2 respectively. Finally, the last row shows the result of testing on Cohort 2 without splitting subsets.

TABLE II:

Results of training on Cohort 1 and testing on Cohort 2 without splitting.

Test set	Feature subset	Feature selector	Classifier	Accuracy(%)	AUC
C2 small	Rider	RfF 10	SVM-rbf	73.22	0.61
C2 medium	Rider	RfF 10	SVM-rbf	74.69	0.69
C2 large	Rider	RfF 10	SVM-rbf	81.48	0.69
C2 w/o splitting	Rider	RfF 10	SVM-rbf	74.68	0.69

Table III shows confusion matrices for both cases: when we used all 261 cases of Cohort 1 for training and when we used subsets of Cohort 1 for training.

TABLE III:

Comparison of confusion matrices in case where use all data from Cohort 1 for training versus its subsets were used for training.

		Training on all 261 cases		Training on subsets
		CC	NC	CC	NC
Small	CC	11	31	21	21
	NC	3	82	3	82
Medium	CC	13	11	14	10
	NC	10	49	6	53
Large	CC	19	0	19	0
	NC	5	3	5	3
Overall	CC	43	42	54	31
	NC	18	134	14	138

After dividing Cohort 1 into subsets for training, we tested the corresponding subset from Cohort 2. Results are shown in Table IV. The first three rows show results for testing when classifiers were trained on a particular subset of Cohort 1 and tested on a corresponding subset of Cohort 2. The last row shows overall accuracy computed from summation of confusion matrices for each subset and overall AUC, which were computed from the merged probabilities over all three subsets.

TABLE IV:

Results of training on Cohort 1 and testing on Cohort 2 after splitting.

Test set	Feature subset	Feature selector	Classifier	Accuracy(%)	AUC
C2 small	Rider	RfF 5	Naive Bayes	81.1	0.78
C2 medium	Rider	RfF 10	SVM-rbf	79.52	0.75
C2 large	C1 st.	RfF 5	Random forests	81.48	0.67
Overall	–	–	–	81.01	0.79

When splitting the training dataset, we get results each subset individually. Overall accuracy was computed from the summation of confusion matrices for all three subsets and overall AUC is the average across the three subsets.

As we can see from Table IV overall accuracy is increased from 74.68% to 81.01%. Also, we can see the “small” subset benefits the most from splitting datasets. Even though the “small” subset is the one which is the most imbalanced (21 cases versus 112 cases), splitting mostly improves accuracy for the minority class.

For the “small” and “medium” subsets we can also see improvements in AUC.

VI. Impact of splitting on AUC

In the previous section, the main goal of training and testing was to evaluate accuracy. If AUC is the main factor in choosing parameters then we obtain different feature selectors and classifiers.

The best AUC and model settings for the case when we use all the data from Cohort 1 in training is shown in Table V. In the case of splitting Cohort 1 into subsets based on the LD parameter of a nodule AUC results are in Table VI.

TABLE V:

Best AUC for training on Cohort 1 without splitting.

Test set	Feature subset	Feature selector	Classifier	Accuracy(%)	AUC
C2 small	Rider	RfF 10	Random forests	70.07	0.77
C2 medium	Rider	RfF 10	Random forests	75.9	0.81
C2 large	Rider	RfF 10	Random forests	74.07	0.74
C2 w/o splitting	Rider	RfF 10	Random forests	72.57	0.78

TABLE VI:

Best AUC for training on Cohort 1 after splitting.

Test set	Feature subset	Feature selector	Classifier	Accuracy(%)	AUC
C2 small	C1 st.	RfF 10	Naive Bayes	80.31	0.8
C2 medium	Rider	CFS 5	Naive Bayes	75.9	0.81
C2 large	C1 st.	CFS 10	Naive Bayes	77.77	0.85
Overall	–	–	–	77.5	0.81

As before, for comparison results from the case where all the data is used and the case where classifiers are trained and tested on subsets of Cohort 1 and 2 respectively, we used the settings from the previous work [23] and for testing used subsets of Cohort 2.

VII. Improving AUC with with over-sampling technique

As we can see from the results, splitting Cohort 1 improves overall accuracy. Nevertheless, one of the disadvantages of splitting is that subsets became imbalanced, except the “medium” subset. In the “large” subset the minority class is 29.16% of cases. In ‘small‘ subset the minority class is 15.79% of the subset.

Due to the significant difference in number of cases between minority and majority classes we applied the SMOTE technique [22] to generate artificial instances for the minority class and thus balance subsets. For each subset the number of cases generated by SMOTE was equal to the difference between the cardinality of the majority and minority classes. Thus, we balanced subsets and then repeated testing.

Table VII shows results of testing after applying SMOTE. As we can see, for the “medium” subset AUC is improved slightly due to the small number of generated instances. The “large” subset is the one which benefits the most.

TABLE VII:

Results of training on Cohort 1 and testing on Cohort 2 with SMOTE.

Test set	Feature subset	Feature selector	Classifier	Accuracy(%)	AUC
C2 small	C1 st.	CFS 10	Naive Bayes	74.02	0.78
C2 medium	219 features	CFS 10	Naive Bayes	80.72	0.83
C2 large	C1 st.	CFS 5	Naive Bayes	81.48	0.87
Overall	–	–	–	77.21	0.82

For the “small” subset, SMOTE slightly decreased AUC. The reason is likely the number of generated instances – 91 artificial. Also, for the “large” subset we used only 3 neighbours for generating a new instance due to the small amount of cases in the minority class (by default the number of neighbours is equal to 5, but there were 7 cases).

VIII. Feature analysis

We selected classifiers and feature selectors based on their accuracy. As we can see from Table IV for all subsets we used the same feature selector – ReliefF. For the “small” and “large” subsets we used the 5 top ranked features, but for “medium” we used 10. Nevertheless, the feature selectors are the same, the datasets to which ReliefF was applied are different.

In order to analyze features we applied the ReliefF (the feature selector which showed the highest accuracy) to each subset and compared how many features are unique for across all of the data subsets. The list of features extracted from each subset is shown in Table VIII with features shown in the order they are ranked by ReliefF.

TABLE VIII:

List of features selected from particular subset of Cohort 1 during training.

Small	Medium	Large
Attached To Pleural Wall	Circularity	MIN Dist To Border
Mean [HU]	Roundness	Mean [HU]
Relative Border To Lung	Longest Diameter	Relative Volume AirSpaces
Relative Border To Pleural Wall	Short Axis times Longest Diameter	AirSpaces Volume
Short Axis times Longest Diameter	SD Dist To Border	Longest Diameter
-	Asymmetry	-
-	StdDev [HU]	-
-	MAX Dist To Border	-
-	Short Axis	-
-	Relative Border To Lung	-

For comparison, we computed how many features intersect among different subsets. Also, we extracted features from the cases where all data from Cohort 1 is used for training and compared these features with those that extracted from each particular subset. Results are shown in Table IX. As we can see, the number of intersecting features among subsets is small.

TABLE IX:

Intersection matrix of selected features among subsets and whole Cohort 1.

	Small	Medium	Large	All 261 cases
Small	5	2	1	2
Medium	2	10	1	8
Large	1	1	5	3
All 261 cases	2	8	3	10

The interesting fact is that features used for the “medium” subset are 80% the same with the features used during training on all data from Cohort 1.

IX. Features vs Classifiers

As we saw from the previous section, features for each subset are mostly unique and as we can see from Table IV the classifiers, which use these features, are also unique.

For evaluating the influence of classifiers and selected features we computed the standard deviation of testing results for each subset with respect to a feature selector and with respect to the classifiers. We used both accuracy and AUC as measurements of classifiers. Tables X and XI show the results.

TABLE X:

Standard deviation of accuracy.

	Small	Medium	Large	Average
std dev for feature selectors	3.44	3.09	5.75	4.1
std dev for classifiers	5.4	5.26	7.64	6.1

TABLE XI:

Standard deviation of AUC.

	small	Medium	Large	Average
std dev for feature selectors	0.046	0.029	0.069	0.043
std dev for classifiers	0.104	0.066	0.109	0.093

As we can see, the standard deviation of the classifiers was higher both for accuracy and for AUC. It seems that classifiers play a more important role in reaching a higher accuracy and AUC value.

X. Conclusion

In this work, we show that different subsets for training have different representative features and by applying different classifiers we can improve overall accuracy and AUC. Nodules with higher values of LD can be classified using less data due to different representative features in each subgroup. After splitting training and testing datasets into three subsets based on the longest diameter (LD) parameter, accuracy was improved from 74.68% to 81.01% and the AUC improved from 0.69 to 0.79. We show that if AUC is the main factor for choosing parameters then accuracy improved from 72.57% to 77.5% and AUC improved from 0.78 to 0.82. Additionally, we show the impact of an oversampling technique. In some particular cases AUC increased from 0.82 to 0.87. Average AUC across all three subsets slightly improved, we should take into account that division of data into subsets allows us to apply different techniques to them. Thus, we can apply SMOTE only to the “large” subset and then AUC for one increases from 0.67 to 0.87.

As mentioned before, we analyze one of the possible ways to subdivide datasets. We plan to analyze how the subset generation process influences prediction outcomes. In addition, different factors can be used as a basis for splitting.