Collective gradient sensing and chemotaxis: modeling and recent developments

Abstract

Cells measure a vast variety of signals, from their environment’s stiffness to chemical concentrations and gradients; physical principles strongly limit how accurately they can do this. However, when many cells work together, they can cooperate to exceed the accuracy of any single cell. In this Topical Review, I will discuss the experimental evidence showing that cells collectively sense gradients of many signal types, and the models and physical principles involved. I also propose new routes by which experiments and theory can expand our understanding of these problems.

I. INTRODUCTION

To perform the intricate functions of tissues and organs, cells often cooperate to make decisions, which can cause clusters of cells to have completely different behaviors from single cells. Cell cooperation has broad biological relevance to both healthy and diseased states. During embryogenesis and immune response, collections of cells work together in order to sense signals indicating the location for a morphological feature or a danger [1–3]. Collective cell migration may also be relevant to metastasis, where small clusters of tumor cells may be significantly more dangerous than single-cell metastases, indicating significant cooperativity [4–6].

Collective gradient sensing is the process where cells work together to sense and follow a gradient of a signal, which might be chemical, mechanical, or electrical; our most common example will be collective chemotaxis, when the gradient involved is a soluble chemical. Collective gradient sensing in biological systems [7] like the embryonic neural crest migration [2] and white blood cell swarms or clusters [3, 8] has a great potential for interplay between biology and physics. Collective chemotaxis links important biological questions like “how do white blood cells work together to locate a wound” to areas where physics has useful tools and insight, such as collective cell migration (active matter) [9–11], and statistical limits of sensing and information processing [12, 13].

In this Topical Review I will highlight the role of physics in understanding chemotaxis and collective motion (Section II), discuss the current experimental measurements of how cells cooperate to sense a gradient (Section III), characterize quantitative and qualitative models of collective gradient sensing (Sections IV–VI), and then consider potential future directions for the field (Section VII).

II. CHEMOTAXIS AND COLLECTIVE CELL MIGRATION: THE ROLE OF PHYSICS

A. Basic physical principles limit many cell measurements

Physics can play a limiting role in a cell’s ability to perceive its environment. A classic example is the Berg-Purcell bound: if a cell wants to measure the concentration of a chemical species, its ability is limited by both the rate at which new molecules can diffuse to the cell and the rate at which molecules can bind and unbind from the cell’s surface [14–16]. Similar physics can apply to cells sensing gradients in chemical concentration, i.e. performing chemotaxis [17–20]. In both concentration sensing and gradient estimation, single cells often perform near their physical limits [16, 21, 22]. This suggests that sensing processes are highly optimized, and looking for basic physical principles that limit detection can be fruitful [23] – understanding what would be optimal for cells or cell clusters may guide our thinking and create useful predictions.

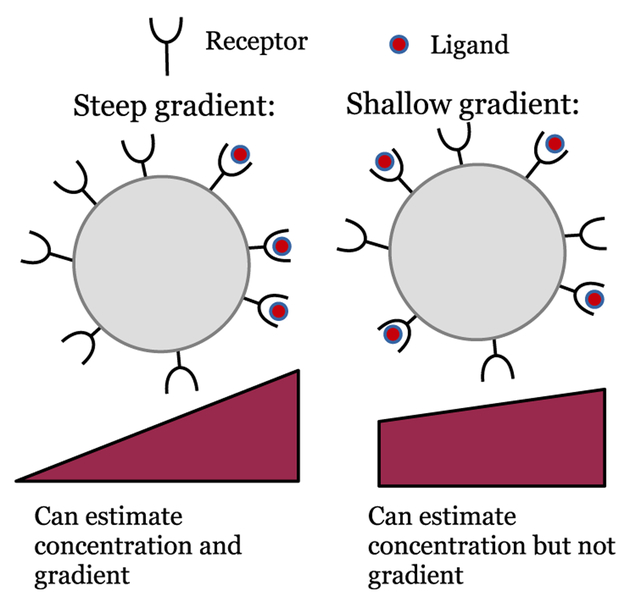
A simple illustrative example of this result is determining the accuracy with which a single cell can sense a chemical gradient via ligand-receptor binding (Fig. 1), as derived by Hu et al. [17, 18]. A cell placed in a shallow exponential chemoattractant gradient with percentage change p across the cell, can measure the gradient’s direction by using a single snapshot of the occupation of the cell’s receptors with uncertainty

$${\sigma }_{\varphi }^2=\frac{1}{p^2}\frac{8{\left(c_0+K_D\right)}^2}{n_r{K}_D{c}_0}$$ (1)

where c₀ is the mean concentration across the cell, n_r the number of receptors on the cell surface, and K_D the dissociation constant of the receptor-chemoattractant interaction, i.e. in ligand concentration c the probability a receptor is occupied is c/(c + K_D). If a cell could make n_meas independent measurements, it would reduce the variance in Eq. 1 by a factor of n_meas. One strategy would then be to average measurements of receptor binding over a time T; the uncertainty ${\sigma }_{\varphi }^2$ will be reduced by a factor proportional to T/τ, where τ is a correlation time of the receptor-ligand interaction (assuming T > τ). Correlation times for receptors depend on both the kinetics of ligand-receptor binding, and the stochastic diffusion of ligands through the space around the receptor. Computing τ is not trivial in general, and can have many subtleties; I suggest the discussion in [15, 16, 18, 24]. In practice, in eukaryotic chemotaxis, often receptor on and off rates are small compared to the rate of ligand diffusion to the receptor, leading to dynamics that is receptor-dominated [25]. In this limit, $\tau \approx \frac{1}{k_{+}c+k_{-}}$ for simple ligand-receptor kinetics, where ligand binding occurs at the rate ck₊ and detachment occurs at rate k₋, i.e. K_D = k₋/k₊. Though varying from system to system, this receptor timescale can be on the order of seconds for single eukaryotic cells like Dictyostelium when ligand concentrations are near the receptor K_D.

FIG. 1.

Sketch of statistical limits on single-cell chemotaxis. Single cell gradient sensing is limited by ligand-receptor binding kinetics. As gradients become increasingly shallow, the difference in bound ligand between back and front becomes increasingly small compared to counting fluctuations, leading to inaccurate chemotaxis (right). However, even if chemotaxis is inaccurate, concentration sensing may remain quite precise.

The example of Eq. 1 and its extensions discussed above are prototypical: to understand the limits of sensing, it is necessary to characterize the origins of stochasticity (e.g. the stochastic kinetics of binding) and find the dynamics of this noise.

B. Collective cell motility as active matter

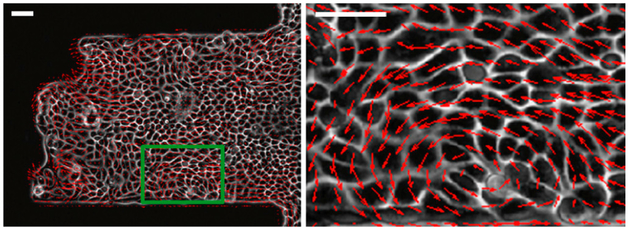
Physics also influences the dynamics and behavior of cell motility, especially when cells work together. Cells actively generate force, pushing off their environment in order to create motion. This ability to autonomously generate directed motion by using biochemically-stored energy distinguishes tissues from materials in thermal equilibrium, placing them in the general category of “active matter” which also includes animal herds and flocks as well as collections of synthetic actively-driven objects [11]. Interesting phenomena arising from this directed cell motility include fingering instabilities [26], persistent rotational motion [27–30], mechanical waves[31], and vortices and large-scale alignment of cell motion within cell sheets [32]; an example of a vortex is shown in Fig. 2. The phenomenology and modeling of collective cell migration has been recently reviewed by several papers [9, 10, 33].

FIG. 2.

Example of collective flow and vortex in a monolayer of MDCK cells on a micropatterned adhesive stripe [32]. Scale bar is 50 microns; right panel shows enlargement of green box.

III. COMBINING CHEMOTAXIS AND COLLECTIVE MIGRATION: EXPERIMENTAL EVIDENCE THAT CELLS CAN COOPERATE TO SENSE GRADIENTS

Single cells can often sense chemical gradients and chemotax effectively [12]. Nevertheless, some single cells fail to chemotax [2, 21, 34], especially if the gradient is so shallow that the mean difference in number of molecules bound on the cell front and back is small compared to counting fluctuations (Fig. 1). Even when single cells cannot sense gradients, how ever, clusters of interacting cells can still follow a gradient. This gradient sensing can be called “emergent,” to highlight that it arises from the interactions of many cells.

Emergent gradient sensing is seen in response to many signals, including soluble chemical gradients (chemotaxis) [2, 8, 35], gradients of ligand density bound to a substrate (haptotaxis) [36], gradients of the cell’s environmental stiffness (durotaxis) [37] and electrical potential gradients (galvanotaxis) [38, 39]. These experiments span many cell types, suggesting the broad relevance of cooperative gradient sensing. I show examples of interesting experiments showing collective gradient sensing to three different signals in Fig. 3. I’ll focus primarily on eukaryotic gradient sensing – but there is also evidence of emergent chemotaxis in swarms of myxobacteria [40] and emergent phototaxis in swarms of fish [41].

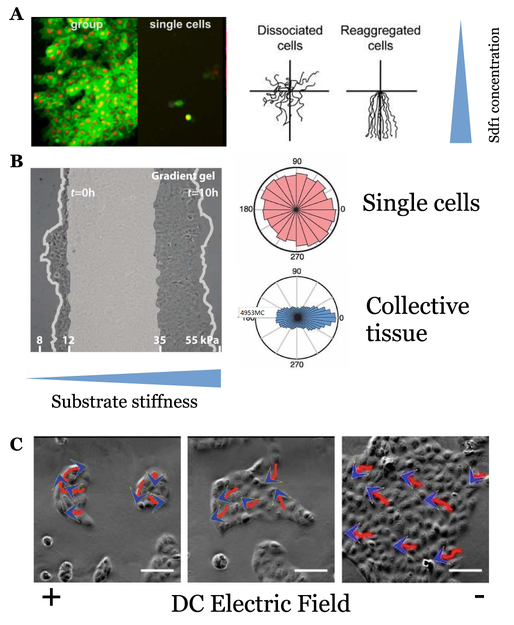
FIG. 3. Experiments showing collective gradient sensing.

A: Neural crest cells show chemotaxis to Sdf1 in groups, but not relevantly when disaggre-gated; adapted from [2] as permitted by Creative Commons license. Left: fluorescence microscopy image. Right: trajectories of single cells and clumps. B: MDCK monolayers respond to shallow gradients of substrate stiffness, but isolated cells do not; adapted from [37] with permission from AAAS. Left: microscopy of MDCK sheet, with initial location of sheet shaded. Right: angular distributions of cell trajectories relative to gradient direction C: MDCK cells are more directional and follow electric fields better in groups; lines with arrowheads show migration path and direction. Adapted from [38].

A. In vitro experiments

One significant early in vitro experiment showing evidence of emergent collective gradient sensing was the measurement of Xenopus mesoderm by Winklbauer et al. [36, 42], who studied explanted tissues as an model of gastrulation. In Xenopus, mesoderm migrates across the blastocoel roof toward the embyro’s animal pole. Transferring the blastocoel roof to a substrate to create a “conditioned” substrate, Winklbauer et al. found that these conditioned substrates were sufficient to have mesoderm explants migrate along the animal pole direction on the conditioned substrate: substrate guidance cues can orient mesoderm. However, isolated mesoderm cells were unpolarized and did not show directed movement, instead engaging in random-walk behavior, while small clusters of 10–20 cells persistently moved toward the animal pole. This critical early experiment points at the role of of cell-cell interactions in gradient measurements made by developing tissues. These conditioned substrates, though, did not allow for systematic control of the type or concentration of ligands, making identifying even the origin of directionality difficult to interpret.

An important step forward was taken by Theveneau et al.[2]; I show data from this experiment in Fig. 3A. In these in vitro experiments, neural crest cells were explanted from Xenopus embryos, and exposed to a gradient of the chemoattractant Sdf1 (also known as CXCL12). This gradient was generated by using a Sdf1-soaked bead, which could then be manipulated, allowing clear demonstration that the neural crest cells chemotax to Sdf1. Theveneau et al. established several features of the collective chemotaxis. First, N-cadherin-dependent cell contacts are required; if cells are dissociated, or if N-cadherin is inhibited, collective chemotaxis fails, suggesting N-cadherin contact-dependent processes like contact inhibition of locomotion (CIL) [30, 43–46] are critical (Fig. 3A, right). Secondly, Theveneau et al. measured Rac activation as a measure of cell polarity, and found that cells at the cell boundary are polarized within the cluster with high levels of Rac pointing to the outside edge, rather than toward the chemoattractant; interior cells were relatively unpolarized. Theveneau et al. also found that small and large clusters had similar chemotactic indices. Later experiments in the same system also identified co-attraction via the complement fragment C3a as necessary for guidance [47]. These experiments, though groundbreaking, provide some difficulties in quantitative modeling, as the chemoattractant profile is difficult to precisely characterize.

Malet-Engra et al. performed a quantitative study on collective chemotaxis in clusters of lymphocytes from the chronic lymphocytic leukemia-derived cell line JVM3 to a gradient of CCL19 [8]. In their experiments, single cells and clusters of widely varying sizes coexist; clusters may assemble from aggregation of cells. By exposing cells and clusters to a linear gradient of CCL19 of controllable strength, they found that single cells could develop widely varying responses to chemoattractant, including chemoattraction, chemorepulsion, and no response, while clusters robustly chemotaxed up gradients of CCL19; similar results were found in other cell lines. These experiments have two key advantages over earlier ex-plant experiments: first, using a controlled environment allows the gradient to be set precisely, and secondly, the use of cell lines may reduce the degree of hetereogeneity between cells compared to that of [2, 36]. This allowed Malet-Engra et al. to make quantitative measurements of cluster velocity and directedness as a function of cluster size, chemoattractant gradient, etc. These results and the modeling performed by Malet-Engra et al. are discussed in detail in Section V A. In addition to straightforward translation in response to gradients, Malet-Engra et al. noted the presence of events where clusters rotate or develop disordered motion; transitions between these states were recently modeled as arising from competition between cells attempting to polarize away from the cluster and aligning with their neighbors [48].

B. In vivo measurements

Many aspects of collective gradient sensing in neural crest have been confirmed to function similarly within Xenopus and the in vitro experiments discussed above [47, 49, 50]. However, measurements of chick cranial neural crest in vivo by McLennan et al. also show that cells at the front of the invading neural crest express different genes than trailing cells [51]. This leader-follower expression difference is not reproduced in culture unless cells are exposed to the chemoattractant VEGF, and even then, the genes activated in leader and follower differ between in vitro and in vivo experiments, suggesting the importance of the local environment [52]. The results of McLennan et al. emphasize potential differences between in vitro and in vivo mechanisms and reminds us of the importance of understanding multiple populations of cells, such as the distinctions between leaders and followers McLennan et al. highlight and model [51, 52]. Other researchers have also studied the leader-follower distinction in collective migration [26, 53, 54].

Quantitative measurements of cluster or group velocity along the lines of Malet-Engra et al. [8] are also possible in vivo. An interesting recent example in this direction is the work of Cai et al. [55], which focuses on the border cell cluster in the Drosophila egg chamber. The border cell cluster is a clump of six to eight cells that migrates from one side of the egg chamber, invading between nurse cells, before reaching the oocyte; multiple chemotactic guidance factors have been identified [56]. Border cell migration is necessary for the formation of fertile eggs. This cluster migration requires communication between the cells via a mechanism using adherens junction components [57]. Cai et al. track cluster velocities as a function of cluster size and distance along the migration path; I discuss these further in Section V.

IV. MODELS TO CONSIDER: WHAT IS CONSISTENT WITH EXPERIMENT?

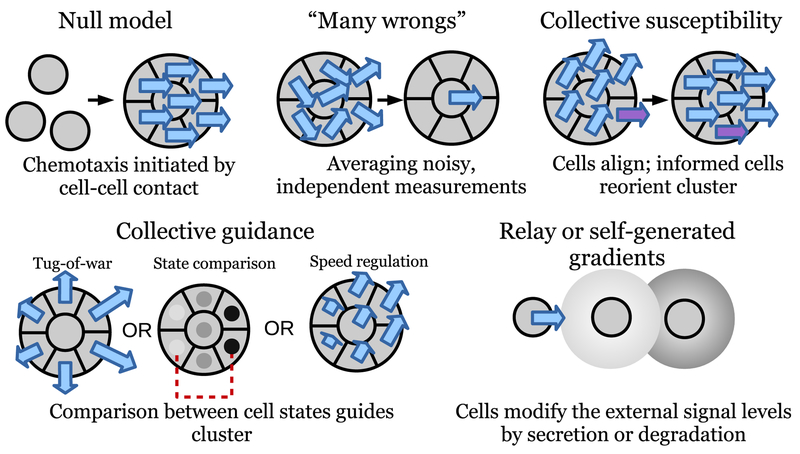
I will propose five broad classes of models that can explain why clusters of cells can have significantly different chemo-tactic responses than single cells; these are illustrated in Fig. 4. I will also discuss specific implementations of these ideas below, including more extensive detail in Section V for “collective guidance” models.

FIG. 4. Illustration of potential mechanisms for presence of collective gradient sensing.

See text for detailed explication of each class.

These classes are:

• The null model: chemotaxis is regulated by cell-cell contact. In the most extreme case, the null model could be that cells only switch on gradient sensing when in contact with neighbors. This is mostly uninteresting from a theory standpoint, but must be considered.

• “Many wrongs make a right”: if each cell makes a noisy but independent estimate of the gradient, the cluster, aggregating these estimates by mechanically linking the cells, will have a more accurate estimate than any individual cell.

• Collective susceptibility: a few informed cells sense the gradient, while the majority only follow.

• Collective guidance: each individual cell makes a measurement of signal concentration, and the cluster makes a comparison between the resulting single-cell measurements to estimate the gradient. This comparison can be made via many different mechanisms, including a tug-of-war where cells sensing a larger signal pull more strongly.

• Chemotactic relay and self-generated gradients: cells may secrete additional signals or degrade signaling molecules, allowing them to communicate to sense gradients even when not in contact

I emphasize that this cannot be a comprehensive list, nor are the possibilities mutually exclusive: any given biological system may combine more than one. Still, this set of models are useful starting points to consider, as each one could be a potential sufficient explanation for why cell clusters have significantly more accurate chemotaxis than single cells.

A. The unsatisfying null model: chemotaxis regulated by cell-cell contact.

Cell-cell adhesion is not only a mechanical linkage between cells, but can lead to signaling events [58, 59]; the presence of different cadherins will alter a cell’s biochemical repolarization on cell-cell contact [60]. This suggests one, perhaps somewhat unsatisfying, explanation for why there is a qualitative difference between single- and many- cell chemotaxis: cell-cell contact is a needed ingredient for chemotaxis to operate, or cell-cell interaction significantly alters the response of single cells. In many experiments, I view this this null model as unlikely, with data weighing against it – but is also perniciously difficult to rule out.

When is this a likely possibility, and when can it be ruled out? The critical question may be whether cells cannot sense the gradient, or whether they can sense it, but have a response that does not involve motility or chemotaxis. In [35], the authors reduce the chemoattractant gradient’s steepness to a level where single cells are insensitive to it, suggesting that this gradient is below the threshold for directed motion [21, 34] – the gradient is too shallow to be sensed by a single cell. By contrast, [8] find that under conditions where single lymphocytes are chemorepelled from a CCL19 gradient, clusters move up the gradient. Single lymphocytes are clearly competent to sense this gradient strength: could the differing cluster behavior be the result of merely reversing their chemo-tactic propensity after contact? This is, however, not an immediately likely explanation for this data, as [8] observe cell protrusions to be directed out from the cluster, rather than following the gradient.

However, even if single cells are below basic physical and information-theoretical limits for gradient sensing, this does not completely rule out increased accuracy in collective chemotaxis arising without requiring a qualitative change in behavior. In eukaryotic gradient sensing, the accuracy with which a single cell can sense a gradient depends on both the number of receptors expressed on the cell’s surface, and the time over which the cell integrates the measured signal (see Eq. 1 and the discussion following it) [17, 18, 61]. Longer integration times or larger receptor numbers allow cells to sense shallower gradients – so if cell-cell contact leads to increased receptor expression (or expression of receptors with a different equilibrium constant) or longer maintenance of cell memory, improved chemotaxis would result naturally. This would only be ruled out with quantitative comparisons of receptor expression [62] between single cells and clusters or comparisons of time averaging between single cells and clusters (i.e., determining the length of memory as in [63]). In many experimental systems, these measurements have not yet been performed, suggesting that the null hypothesis, while disfavored, may remain a stubborn possibility there.

Why should cells change receptor expression or measurement times when cell-cell contact is present? One potential explanation is that single cells and cell clusters perform different functions, leading to different optimal behaviors. For instance, if single cells must respond quickly to a changing gradient (i.e. while finding their way to a larger cluster), a shorter memory could be advantageous. Similarly, the presence of other cells may act as prior information: if cell clusters are more likely to need to sense shallow gradients, or gradients at a different mean concentration level, different responses will be optimal.

B. Many wrongs make a right

If each cell makes a noisy but independent estimate of the gradient, the combination of these estimates – the cluster estimate – will have a reduced noise. This will occur without any particular interactions within cells other than keeping the cluster tightly connected. In the context of collective cell migration, a specific minimal model including only this feature is discussed briefly in [64], and more extensively under the name “individual-based chemotaxis” in [65]; however, this is a well-known phenomenon in animal migration more generally, under the name of the “many wrongs principle” [66].

“Many wrongs” is itself almost a null model: it assumes that the primary effect of cell interactions is cohesiveness, and the only communication is averaging many estimates. However, it serves as a critical comparison point. For instance, “many wrongs” chemotaxis can always become more accurate with increasing numbers of cells; mechanisms with saturating chemotactic accuracy, as found experimentally by [35], and theoretically by [24, 67], are guaranteed to be suboptimal at large cluster size if chemotactic accuracy is the only goal.

C. Collective susceptibility

A generic feature of many active matter systems is polar alignment: objects in proximity with one another tend to develop aligned velocities. (Though I note nematic alignment is also a possibility [68, 69].) If cells within a cluster become aligned and travel in a consistent direction even in the absence of a signal, as appears to be the case for neural crest clusters [2, 50], then individual cells that measure the gradient can lead to the entire cluster following the gradient.

The basic idea of cell clusters being reoriented by specific “informed” cells can take on different variations. For instance, Coburn et al. [70] showed that when cell align with neighbors through a contact inhibition of locomotion mediated by cell-cell collisions, even small numbers of cells (< 5%) biased to move up a gradient were sufficient to eventually, after many collisions, reorient an entire population. Other simulation studies focused on animal flocks and herds have also shown that alignment effects can allow a group to follow a leader with useful information, and allow decisions or compromises between multiple leaders [71–73].

Unlike animals, it seems less likely that there are explicitly informed and uninformed cells – there must be a rationale why some cells are leaders and some are followers. McLennan et al. model neural crest migration with leaders that sense the gradient and followers [51], finding that migration can be more efficient with fewer leaders. Fewer informed cells can be beneficial in the example McLennan et al. study, as cells are sensing a gradient that extends over a relatively small range – only a few cell lengths – so cells far away from the front are ill-informed, and are better served by following their neighbors. A second study by this group models switching between leaders and followers [52].

An interesting related question is the dynamics of cluster reorientation: the simulations of [70] show that reorientation by rare cells may be very slow compared to the time it takes a cell to move its length. Clusters without a leader may still become spontaneously polarized in a random direction if there is alignment between cells [74]; clusters must be able to quickly reorient from their old polarization to respond to new information. As clusters become larger, they may become more persistent (see the results of, e.g. [75], though there are some interesting wrinkles!) – and possibly more difficult to align. While reorientation dynamics have been extensively explored for natural flocks [76–78], they are not as fully studied in collective cell motility. One nice example of combining reorientation dynamics and gradient sensing dynamics in collective cell migration is that of Lalli et al. [39], who find that though clusters of cells more accurately follow the electric field than single cells, the speed of cluster alignment to a change in electric field is slower than that for single cells. More recent work from the same group suggests both collective- and single-cell gradient sensing is dependent on E-cadherin [79].

D. Collective guidance

I define “collective guidance” in a broad way, following[80], as the idea that each cell reads out the local concentration of the signal as a local cell state, and the cluster then makes a decision based on comparing these states. In this sense, collective guidance is a gradient measurement on the cluster scale, rather than on the single-cell scale. This is a contrast from the previous three mechanisms, which all are, at their heart, measurements at the single-cell level. There is a natural advantage to measuring on this scale, if possible: the difference in concentration between the front and back of the cluster is much more than the difference between the front and back of a single cell. (A nice study of this comparison has recently been published [65]).

While the central idea that cells measure concentration, not gradients, is very broad, there are widely varying ways in which cell clusters could implement this measurement. One simple and straightforward approach is for each cell to polarize out from its neighbors, and pull proportional to the concentration it measures [8, 64]. As a result of a tug-of-war, the cluster will move toward higher concentration. This idea is supported by experiments showing that cells at the outer edge of lymphocyte and neural crest clusters are polarized away from the cluster, rather than polarized up the gradient [2, 8]; velocities of lymphocyte clusters also scale with cluster size in ways consistent with quantitative models based on this idea [8, 64], which I will describe more in Section V. However, simple tug-of-war models have certain features which appear unfavorable: if forces are simply proportional to the detected signal, clusters will respond weakly to small signal concentrations, but tear themselves apart trying to respond to large signals. In other words, simple tug-of-war models lack the ability to adapt to differing signal levels. Adaptation is a common feature of single-cell gradient sensing, and is often described with a LEGI (local excitation, global inhibition) framework. Integrating LEGI into tug-of-war models of cluster migration allows clusters to adapt and sense gradients more robustly [67, 81].

While tug-of-war models are suggested by the details of the lymphocyte and neural crest cluster systems, other mechanisms for collective guidance are possible; any method to compare states between cells at the cluster front and cluster back can gain the benefits of collective guidance. One cell state property potentially regulated by concentration is speed. Could clusters be guided merely by cell speed changes? A recent experiment on schooling golden shiners may provide a clue [41]: Berdahl et al. found that groups can negotiate light fields merely by having individuals adjust their speed depending on the local light level. This effect, combined with the tendency toward alignment, directs the groups to their preferred level. Interestingly, a similar mechanism was proposed in 1964 for phototaxis in the Dictyostelium slug, where single cells do not respond to one-sided illumination, while the slug stage does [82] – though the effect of light on cell speed was not clearly established. Phototaxis and thermotaxis in the Dictyostelium slug may also provide an additional mechanism for computation via a collective-guidance mechanism. Marée et al. proposed a model making use of the waves of cyclic AMP which are created by cells that, when excited, secrete cyclic AMP [83, 84]; if temperature or light regulates the excitability of cells within the slug, this excitability can reorient the wave – and the slug migration.

E. Relay and/or self-generated gradients

The earlier mechanisms discussed primarily describe clusters of relatively strongly bound cells (though this is not necessary for some variants of tug-of-war [67] or collective susceptibility [70]). However, cooperative sensing of gradients can also occur when cells are significantly separated, as in the in vivo case of neutrophil recruitment to a wound [3, 85]. Here, the primary signal of fMLP is supplemented by secretion of LTB₄; if this secretion is regulated by fMLP, a secondary gradient is formed, allowing for guidance at longer distances, as recently modeled [86]. Similarly, cells may degrade an external chemoattractant, shaping a gradient [87–90]; this may also potentially amplify pre-existing gradients, or bring concentration levels to the point where gradients may be more accurately sensed. A recent calculation by Segota and Frank for single cells suggests that degradation of chemoattractant by secreted enzymes can improve chemotactic signal-to-noise ratios when the chemoattractant concentration is significantly above the receptor K_D [91]; similar mechanisms could be at work in collective chemotaxis.

V. CLUSTER VELOCITY MEASUREMENTS IN COLLECTIVE GUIDANCE: BENEFITS AND PITFALLS

Clusters, like single cells, can be tracked, and their motion characterized. Natural parameters to characterize are the cluster’s mean velocity in the direction of the gradient, and measurements of its directedness toward the motion. Directedness can be characterized by various types of chemotactic indices, e.g. measuring the average of the velocity in the gradient direction normalized by the cell speed, or the total displacement of the cluster in the gradient direction divided by the total length of the path.

Systematic measurements of cluster velocity in the gradient direction have been performed by Ref. [8] and Ref. [55] for the in vitro lymphocyte cluster system and the in vivo border cell cluster migration, measuring how cluster velocity varies with changing cluster sizes; other quantitative velocity measurements include the galvanotaxis measurements of [38]. I show examples of this data and the systems involved in Fig. 5. A significant amount of modeling effort has been devoted to understanding how cluster directionality, velocity, and related properties scale with cluster size [8, 55, 64, 67, 81, 92]. These calculations have primarily been made with the central assumption of collective guidance, as defined generally in Section IV – the models are motivated by the assumption that cells respond to the signal concentration, not its gradient. In this section, I will review these models in some detail.

FIG. 5. Quantitative measurements of cluster velocity.

A: cluster velocity measurements in the lymphocyte system; figure adapted from [8] with permission of Elsevier. Top is frames from experimental movie, bottom velocity of clusters as a function of area. Data is presented for three gradient strengths (0–25, 0–100, and 0–500 ng/ml). Green line indicates minimal tug-of-war model. B: cluster velocity measurement in the border cell cluster in the Drosophila egg chamber, adapted from [55]. Top is illustration of the border cell geometry, bottom velocity as a function of cluster size; note cluster diameter is plotted here, in comparison to cluster area in A. Circles are small clusters derived from E-cadherin knockdown, squares are wild-type, and diamonds are a variety of mutants that create extralarge clusters. Solid line: fit to full theory including confinement. Dashed black line: that theory shown without the effect of confinement. Dashed red line: fit to data excluding wild-type clusters.

A. Scaling arguments for tug-of-war chemotaxis: cluster size, organization, and cell number

Minimal models and simple scaling arguments can be very informative about how cluster velocities depend on cluster size. A prototypical example of this sort of argument is given in [8], who propose a tug-of-war model to describe lymphocyte cluster chemotaxis. In this model, they assume that a cluster is driven by force exerted normally around its perimeter (as in the “tug-of-war” illustrated in Fig. 4). This force is set by the chemoattractant through a minimal model of receptor-chemoattractant binding to be $f(r)=f_0\frac{c(r)}{c(r)+K}\widehat{n}$, with K a characteristic concentration and where n is the outward normal of the cluster. If the cluster is exposed to a shallow linear gradient, c(r) = c₀(1 + r · g), c/(c + K) can be expanded about r = 0, $\frac{c}{c+K}\approx \frac{c_0}{c_0+K}+r\cdot g\frac{c_{0}K}{{\left(c_0+K\right)}^2}+\cdots$. The total force F^tot on a circular cluster of radius R can be computed by integrating around the cluster edge:

$$F^{\text{tot}}=R{\int }_0^{2\pi }d\theta f(r)\approx f_0\pi R^2\frac{c_{0}K}{{\left(c_0+K\right)}^2}g$$ (2)

The result that F^tot ~ R² can be understood because the difference in concentration between front and back is proportional to cluster radius: this effect is integrated around the perimeter, which adds another factor of R, leading to F^tot ~ R². Extensions can also be worked out for clusters beyond the shallow-gradient limit [8], but the key scaling laws are more obvious in the shallow-gradient case.

In an overdamped system, this force must be balanced by friction between the substrate and cluster, which can be hypothesized to take on a form −λV, where V is the cluster velocity; then F^tot −λV = 0. (The critical hypothesis here is that the force is linear in cluster velocity, as if its origin is fluid friction between cluster and substrate; detailed models of protein-ligand binding at the cell-substrate interface can yield this model, but can also create nonlinear “stip-slick” forces [93–98].) Ref. [8] suggest several forms for how λ depends on cluster sizes, depending on the origin of this frictional force. If only edge cells are engaged with the substrate, λ ~ R would be natural; if all cells are active, λ ~ R² would be the most natural assumption. As a result, depending on this behavior, different scaling laws occur:

$$V=\frac{1}{\lambda }{F}^{\text{tot}}~\frac{c_{0}K}{{\left(c_0+K\right)}^2}g\times \frac{R^2}{\lambda (R)}$$ (3)

Malet-Engra et al. observe that, above a critical cluster size of around 20 cells, the cluster velocity appears to be roughly independent of cluster size (see data in Fig. 5A), suggesting that their lymphocyte clusters are well described by λ(R) ~ R². However, below that critical size, they did not observe cluster chemotaxis, pointing at potential limitations of the model [8]. Malet-Engra et al. also studied the variance of the velocity and the “Forward Migration Index” (a measure of chemotactic accuracy) as a function of cluster size, using this data to suggest that fluctuations in cell velocities are correlated at small cluster sizes; they found that cluster accuracy increased as cluster size increased.

The next extension of the tug-of-war theory beyond the initial minimal model of Malet-Engra et al. [8] was presented by Camley et al. [64]. In this paper, my coauthors and I studied a simple model of cells as self-propelled particles, motivated by the experimental results of [2] on neural crest cells. In our model of neural crest cells, there were two primary interactions between cells: 1) physical adhesion, mediated by cadherins, and 2) contact inhibition of locomotion (CIL), when cells in contact repolarize away from one another, leading to the cluster attempting to tear itself apart. This model is:

$${\partial }_t{r}^i=p^i+\sum _{j\ne i}{F}^{ij}$$ (4)

$${\partial }_t{p}^i=\underset{\text{Ornstein-Uhlenbeck terms}}{\underbrace{-\frac{1}{\tau }{p}^i+\sigma {\mathbf{\xi }}^i(t)}}+\underset{\text{CIL}}{\underbrace{{\beta }^i\sum _{j~i}{\widehat{r}}^{ij}}}$$ (5)

where each cell i is given a position rⁱ and a polarity pⁱ. The cell polarity is the direction and speed a cell would “like” to travel with: an isolated cell with polarity pⁱ has velocity pⁱ. The cell’s motion is overdamped: physical forces such as cell-cell adhesion and volume exclusion change the cell’s velocity. Thus, the velocity of cell i is pⁱ plus the net force other cells exert on it, Σ_j≠i F^ij (Eq. 4), where F^ij is the force exerted on cell i by cell j.

In [64], we modeled cell polarity with an Ornstein-Uhlenbeck process [99, 100] (the first two terms on the right of Eq. 5): pⁱ relaxes to zero with timescale τ, but is driven away from zero by the noise ξ(t), whose amplitude is set by the root-mean-square speed of the cell. This corresponds with a cell that is orientationally persistent over a time of τ. ξⁱ(t) are Gaussian Langevin noises with $\langle {\xi }_{\mu }^i(t){\xi }_{\nu }^j\left(t^{\prime }\right)\rangle =2{\delta }_{\mu \nu }{\delta }^{ij}\delta \left(t-t^{\prime }\right)$, where μ, v run over the dimensions x, y. The biochemical interaction between cells via CIL alters a cell’s polarity pⁱ; this is the last term in Eq. 5, which biases cell i away from its neighbors j ~ i.

To implement the tug-of-war, we assumed that the CIL susceptibility of each cell βⁱ is proportional to signal, ${\beta }^i={\beta }_0+\overline{\beta }c(r)$. This increased susceptibility to CIL leads cells at larger concentration to be more strongly polarized away from their neighbors. Our assumption here modeled the experimental result of [2] that the chemoattractant Sdf1 stabilized protrusions induced by CIL.

For fixed cell cluster geometry and shallow gradients c(r) ≈ c₀ (1 + r · g), the mean cluster velocity arising from Eqs. 4–5 can be found as [64]:

$${\langle V\rangle }_c\approx \overline{\beta }\tau c_0\mathcal{M}\cdot g$$ (6)

〈⋯〉_c is an average over the fluctuating pⁱ but with fixed cell configuration rⁱ. The matrix $\mathcal{M}$ only depends on the cells’ configuration,

$${\mathcal{M}}_{\mu \nu }=\frac{1}{N}\sum _i{q}_{\mu }^i{r}_{\nu }^i$$ (7)

where N is the number of cells and $q^i={\sum }_{j~i}{\widehat{r}}^{ij}$ is a vector that points out from the cluster; this vector is not necessarily of unit magnitude, but will obey some intuition of the idea of a normal vector for a small collection of cells.

The “mobility matrix” $\mathcal{M}$ can be easily computed for any specified cluster geometry; several analytical examples are given in [64]. In particular, for cells packed in a hexagonal cluster of Q layers, ${\mathcal{M}}_{\mu \nu }=f(Q){\delta }_{\mu \nu }$, with $f(Q)\text{=}\frac{9Q^2+3Q}{2+6Q+6Q^2}$. As the number of layers Q becomes larger, $\mathcal{M}$ saturates – thus Eq. 6 also predicts that cluster velocities should be constant at large cluster sizes, as in the experiments and theory of [8]. However, unlike the theory of [8], Eq. 6 predicts that as cluster size becomes smaller, the mean cluster velocity significantly decreases (Fig. 6, top). In particular, for a single cell, there is no chemotaxis. This is not surprising, as our assumption was that the chemoattractant only influenced the interactions between cells (CIL); we did not model single-cell chemotaxis or chemorepulsion, which could be added as an additional effect.

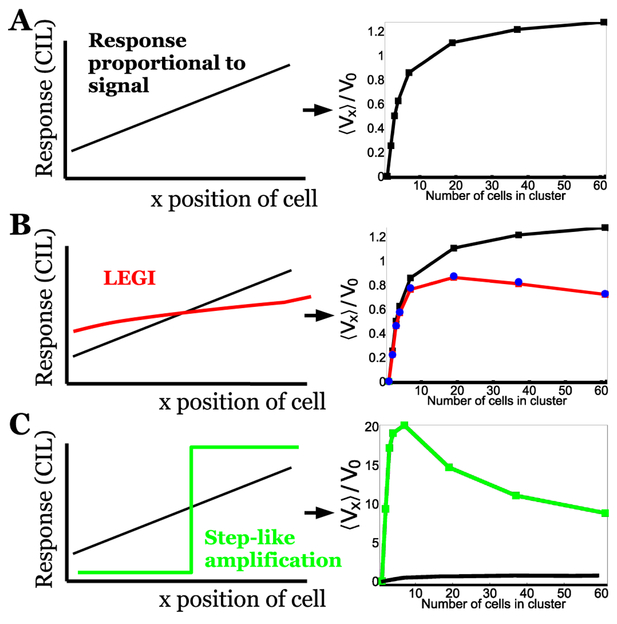
FIG. 6. Signal processing qualitatively alters cluster velocity in response to a gradient.

A: Minimal tug-of-war model of [64] where signal directly regulates CIL susceptibility βⁱ, creating a linear response across the cluster, predicts cluster velocity increases, then slowly saturates, as motivated by scaling arguments discussed in Section V A. (From [64], copyright American Physical Society.) B: LEGI tug-of-war model [67] where signal is processed by LEGI mechanism to create the CIL susceptibility response leads to a response that is nonlinear across the cluster, and becomes shallower at large cluster sizes; as a result, at large cluster sizes, cluster velocity decreases slightly. Black curve shows result of minimal tug-of-war. C: Amplified tug-of-war model [67] where response is switchlike over the cluster; as the response no longer scales with cluster size, at large cluster sizes, cluster velocity drops significantly. Note differing scale for velocity; amplification significantly increases cluster velocity relative to the natural scale V₀. V₀ is defined slightly differently between A and B, C; all panels assume a rigid cluster of hexagonally-packed cells. For further details, see [67].

The basic qualitative features of these results persist even beyond the limit of rigid clusters treated analytically in Eq. 6. In Ref. [64], we simulated fluid clusters by appropriate choice of cell-cell forces F^ij, and found similar scaling with cluster size, though also found that clusters could fragment as they moved up the gradient. The model of Ref. [64] provides a way to take the principles of tug-of-war collective guidance, as suggested by (among others) Rørth [80], and given a quantitative model by Malet-Engra et al. [8], and transform them into a mechanical model for cell migration. We also used a similar model of CIL to explain traction force measurements in an expanding monolayer [101].

B. Cluster velocities critically depend on signal processing

In the approach of both Malet-Engra et al. [8] and Camley et al. [64], as discussed above, the outward polarization of each cell is directly controlled by the local concentration of signal, and does not take into account the concentration measured at other cells. As a result, for sufficiently small concentrations, clusters will not move – and for sufficiently large concentrations, clusters will either tear themselves apart [64] or drop to zero velocity as the response saturates [8]. In other words, the forces in these models do not have the property of adaptation, where different levels of signal can lead to similar forces. By contrast, adaptation is well-known to be present in eukaryotic single-cell gradient sensing; see, e.g. [102] and references within. The presence of chemotaxis in an adapting system is often modeled with local excitation, global inhibition (LEGI) models [103]. Other signal-processing events occur in single cell chemotaxis, and may have relevant analogs within collective chemotaxis. For instance, in single Dictyostelium amoebae and other cells, known elements of the chemotaxis pathway like PI(3,4,5)P₃ are not merely proportional to the local signal, but are strongly amplified, developing almost switchlike responses, turned on in the front while absent in the cell back [104].

To what extent are signals processed within cell clusters performing collective chemotaxis, and how does this affect the cluster velocity? There is not strong direct evidence of collective adaptation to my knowledge, though I note that the LEGI model provided a good explanation for the ability of mam-mary epithelial organoids to detect shallow gradients [24, 35]. Amplification of signals, though, is clear in some in vivo systems: both cell protrusion and Rac activity are highly polarized in the border cell cluster, with only the lead cells protruding [57].

In [67], my coauthors and I studied the consequences of different signal processing mechanisms in an extension of the model presented in Eqs. 4–5. These results are summarized in Fig. 6. In Fig. 6A, the cluster velocity as a function of cluster size N is shown for a minimal model where the CIL susceptibility βⁱ is regulated directly by chemoattractant concentration, as in [64]. Results from an extension to a LEGI scheme are shown in Fig. 6B. In this collective LEGI scheme, the signal creates an activator, which promotes CIL susceptibility βⁱ but remains localized to one cell, and an inhibitor, which diffuses throughout the cluster, reducing βⁱ. In effect, the inhibitor tracks the mean signal concentration across the cluster, while the activator tracks the local signal level, so the response βⁱ is large when the signal is larger than the cluster average. If the diffusion of the inhibitor is infinitely fast, the response βⁱ will be directly proportional to the signal, and the LEGI model will be almost equivalent to the minimal model of [64], summarized in Fig. 6A. However, when diffusion is slow compared to the rate at which the inhibitor degrades (i.e. k_−I/k_D ≪ 1/N, where N is the number of cells in the cluster [67]), communication across the cluster is not perfectly effective. In this circumstance, when clusters become larger, the response no longer tracks the signal (Fig. 6B, left). As a result, as cluster size increases, velocity first increases, then decreases (Fig. 6B, right); the location of this peak depends on the kinetics of diffusion and inhibitor degradation.

Signal amplification also provides a striking change in cluster velocities (Fig. 6C). Here, we assumed that clusters implement a switchlike response – turning on CIL susceptibility βⁱ in the cluster front, while suppressing it entirely in the back. Consider the scaling arguments of Section V A. In minimal tug-of-war models, cluster velocity saturates with increasing cluster size because the response at the edge scales like cluster radius R (R ~ N^1/2 for a hexagonally-packed cluster). The amplified response has two immediate effects. First, amplification significantly increases cluster velocity as cells no longer compete via tug-of-war (compare green and black curves in Fig. 6C, right). Secondly, the difference in the CIL response between front and back is now constant with cluster size, rather than scaling as R. As a result, at large cluster sizes the cluster velocity decreases with 1/R (or N^{− 1/2}).

The examples shown in Fig. 6BC show that signal processing can have strong effects on cluster velocity; related effects are seen on other cluster statistics like chemotactic index [67]. Different types of amplification mechanism are also possible (e.g. where response is proportional to the square of the signal [103]), and will lead to different results. Our findings in [67] suggest that cluster velocity cannot be interpreted directly unless details of the collective signal processing are known. This is a strong restriction on our understanding of velocity curves like those in Fig. 5. In Section VII, I will discuss some potential routes to gain additional understanding of these signal processing networks at the quantitative level necessary.

C. Effect of dimensionality and mechanical environment

Recently, Cai et al. measured the velocity of border cell cluster migration as a function of cluster size, finding that cluster speed drastically increases, then decreases abruptly once cluster size hits a critical size [55] (I show parts of this data in Fig. 5B). Larger and smaller clusters were generated by either inducing wild-type clusters to break apart by knocking down E-cadherin or by exploiting mutations creating larger cluster sizes.

There are two key differences between the in vivo environment of the border cell cluster and the earlier experiments on neural crest cell clusters and lymphocyte clusters. First, the clusters are roughly spherical, rather than existing as thin layers on a substrate. Secondly, the clusters are highly confined, surrounded by the mechanical environment of the nurse cells within the Drosophila egg chamber. Cai et al. find these points are sufficient to explain their data. Generalizing the discussion of Section V A from two to three dimensions, they find that traction forces for a spherical cluster will scale like R³ – from the linear response to concentration gradient ~ R, integrated over the surface area of the sphere (~ R²). The drag force, if it arises from the independent friction of cells in contact with the nurse cells, will scale like λ(R) ~ R². Cai et al. also propose that drag forces could have a different origin: hydrodynamic dissipation, as the cluster moves through the “fluid” of the tissue. If this is true, then there will be a drag force that scales like the cluster radius R – the usual Stokes drag λ = 6πη_effR, where η_eff is the effective viscosity of the nurse cells. Therefore, Cai et al. predict that cluster velocity should increase as R or R² via the three-dimensional version of Eq. 3, depending on which drag is dominant; the observed faster-than-linear increase (Fig. 5B) suggests hydrodynamic drag is dominant. These assumptions explain the initial increase in cluster velocity with cluster size, but are inconsistent with the sudden drop at a critical size. To explain this, Cai et al. argue that clusters traveling within the narrow environment of the border cell cluster should experience an increased hydrodynamic drag arising from the flow of the nurse cells around them; this is analogous to attempting to push a plug down a cylindrical tube of fluid when the plug nearly fills the tube, leading to a friction factor λ that diverges as the cluster reaches a critical radius [55]. This diverging friction arises if it is assumed that there is no slip between the tissue layer surrounding the egg chamber and the flow of the nurse cells.

There are several caveats to this analysis: first, as Cai et al. note, creating large and small clusters requires biochemical intervention, which may also affect cluster velocity. Secondly, the limits of modeling the complex tissue of the nurse cells surrounding the border cell cluster as a homogeneous Newtonian fluid are not clear; investigation with models resolving nurse cell mechanics like [105] may be necessary. Thirdly, I emphasized in Section V B that signal processing and amplification can also create differences in cluster speed as a function of cluster size, and I note that there is relevant amplification of the border cell cluster response [57]. Minimal tug-of-war models may have to be extended to address this amplification.

D. Robust signatures of collective guidance

Signal processing, dimensionality, geometry, and gradient strength can all affect the velocity of a chemotaxing cluster, even with the central assumption that the cluster chemotaxes by collective guidance. These features are dependent on the detailed model chosen [8, 55, 64, 67]. In [64], we proposed a signature of collective guidance that is relatively robust to these details, and depends only on the central collective guidance assumption: that cells measure signal concentration, not gradient. If this is the case, elongated clusters will have highly anisotropic velocity in response to gradients – a property embedded in Eq. 6 and Eq. 7, as the mobility matrix $\mathcal{M}$ will transform under rotation of the cluster.

A simple example of this orientation-dependence is a pair of cells just touching along (cos θ, sin θ) (I take the cell diameter to be the unit of length, so the cells are separated by unit distance). If θ = 0, the pairs are along the axis, and observe different signals; however, if θ = π/2, both cells observe exactly the same signal concentration, and therefore cannot chemotax. More explicitly, by Eq. 7, ${\mathcal{M}}_{xx}=\frac{1}{2}{\cos }^2\theta$, ${\mathcal{M}}_{xy}={\mathcal{M}}_{yx}=\frac{1}{2}\cos \theta \sin \theta$, ${\mathcal{M}}_{yy}=\frac{1}{2}{\sin }^2\theta$. Choosing the signal gradient in the x direction, ${\langle V_x\rangle }_c=\frac{V_0}{2}{\cos }^2\theta$ and ${\langle V_y\rangle }_c=\frac{V_0}{2}\cos \theta \sin \theta$, where $V_0=\overline{\beta }\tau c_{0}g$. This strong anisotropy is plotted in Fig. 7, which is adapted from [64].

FIG. 7. Adherent pairs of cells undergo highly anisotropic chemotaxis.

This figure is taken, with permission, from [64], copyright the American Physical Society. The average chemotactic velocity of a strongly adherent cell pair 〈V_x〉_c depends on the angle θ between the cell-cell axis and the chemotactic gradient. Lines are theory (Eq. 6) and points from numerical evaluation of Eqs. 4–5. $V_0\equiv \overline{\beta }\tau c_{0}g$ sets the scale of the velocity; c₀g = 0.025. The cluster velocity 〈V_μ〉_c is computed by tracking the instantaneous angle, then averaging over all velocities within the appropriate angle bin. Error bars are one standard deviation of the mean, calculated using bootstrap methods. Over n = 13, 000 trajectories of 6τ (120 minutes) are simulated.

The presence of an anisotropy as in Fig. 7 is robust: it depends only on the basic assumption of collective guidance, that cells sense concentration. However, the magnitude of the anisotropy depends on, e.g., the mechanical interactions between the cells and the speed of their reorientation [64], and could potentially depend on signal processing mechanisms as well. How plausible is it to detect this anisotropy? For our simulations of cell pairs, we needed large numbers of pairs (> 13, 000) to achieve reasonable statistical accuracy for the angular dependence. However, this is in part due to the low levels of rotational diffusion of pairs observed in [64], and could also be mitigated by choosing fewer angular bins. The strength of the anisotropy could also be increased by increasing cluster length, e.g. by creating long chains of cells. An ideal test would be to establish long chains of cells at different angles, then remove the confinement; this experiment could be performed with dynamic micropatterns [106]. An experiment of this type could convincingly establish whether collective guidance is relevant for a particular cell type and signal, as well as providing an assay to determine what biological features are relevant in communication.

VI. FUNDAMENTAL BOUNDS: WHAT IS THE BEST ESTIMATE A CLUSTER CAN MAKE?

In the previous sections, I primarily reviewed mechanistic models that describe how a cluster interprets and processes a signal gradient, and how the individual cells regulate their motion in response to this information. However, there is also a more fundamental question: given the information that the cells can possibly obtain, what is the best estimate of the gradient strength and orientation that they can make? This question has been extensively studied for single cells sensing gradients and concentrations, where stochastic ligand-receptor binding and other factors limit accuracy [14–22, 61, 107]; I presented one of these results above, in Eq. 1.

Should we think of collective gradient sensing as just single-cell gradient sensing, but at different length and time scales? This would correspond to the idea that large clusters can be thought of as a “scaled up” version of cells [108]. Some of the ideas and controversies I discussed for gradient sensing in a cluster indeed have their counterparts in the history of the study of single cell chemotaxis. For instance, though it has become widely believed that there is a long-range inhibitory effect in single-cell migration, as in a LEGI model, at least one early model of single-cell chemotaxis used a tug-of-war-like mechanism [109]. However, there is a critical and unavoidable difference between single-cell and collective gradient sensing. This is that even genetically identical cells can have significantly different motility and mechanical properties, and responses to signals [110–114]. Collective gradient sensing must deal with this “cell-to-cell variability” (CCV).

These cell-to-cell variations (CCV) can occur simply because the number of regulatory proteins is small, and so unavoidable fluctuations in their numbers create intrinsic variations [110, 111]; variability may also be actively regulated [112]. CCV can persist over several division times – up to 48 hours in human cells [111]. CCV in motility properties may be particularly important in studying three-dimensional motility and motility in vivo [115, 116]. For instance, presence of a subset of cells with a large motile response to PDGF predicts patient outcomes in glioblastoma [116].

A. Cell-to-cell variability may limit cluster chemotaxis accuracy

Wouter-Jan Rappel and I created a model of chemotaxis with cell-to-cell variability in each cell’s response to chemoattractant concentration c(r) [92]. We treated CCV in signal response by assuming that, instead of accurately measuring c_i, cell i in a cluster instead observes the “measured signal” M given by

$$M_i=\left[c_i+\delta c_i{\eta }_i\right]/\overline{c}+{\sigma }_{\Delta }{\Delta }_i$$ (8)

where δc is the strength of noise from stochastic ligand-receptor binding and σ_Δ sets the scale of CCV; $\overline{c}$ is the mean concentration across the cluster, and η and Δ are Gaussian random variables.

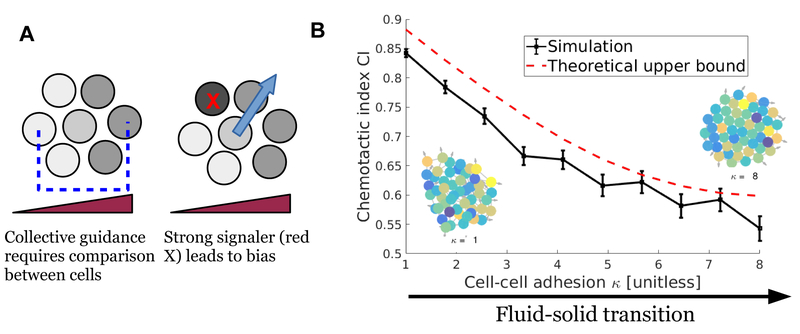
We found that cell-to-cell variability significantly limits the accuracy of gradient sensing by clusters. This is simple to understand intuitively. In order to gain accuracy from making a measurement across the entire cluster, the cluster must make a comparison between different cells (Fig. 8A). In the presence of significant variability, clusters will become biased toward “loud” large-Δ cells and away from “quiet” small-Δ ones (Fig. 8A). This idea can be made more quantitative using the Cramér-Rao bound, showing that the any unbiased estimator $\widehat{\mathbf{\text{g}}}$ of the gradient g must have at least the variance

$$\begin{array}{ll}{\sigma }_{g,0}^2\hfill & \equiv \langle {|\widehat{g}-g|}^2\rangle \hfill \\ \hfill & \approx \frac{2}{\chi }\left(\underset{\text{CCV error}}{\underbrace{{\sigma }_{\Delta }^2}}+\underset{\text{Ligand-receptor error}}{\underbrace{\begin{array}{ll}\frac{1}{n_r}\hfill & \frac{{\left(\overline{c}+K_D\right)}^2}{\overline{c}{K}_D}\hfill \end{array}}}\right)\hfill \end{array}$$ (9)

Here, $\chi =\frac{1}{2}{\sum }_i{|\mathit{\delta }{r}^i|}^2$ is a shape parameter, and δrⁱ =rⁱ − r_cm is cell position relative to cluster center of mass. The second term on the right-hand-side of Eq. 9, which arises from stochastic ligand-receptor binding, is analogous to Eq. 1 for single cells (though Eq. 1 shows the error on the angle alone, not the gradient g). If σ_Δ= 0, Eq. 9 would predict that clusters have highly similar bounds to scaled-up single cells. However, if the cell-to-cell variability in signal response is at the level of 10% (σ_Δ > 0.1), as is likely the case experimentally, the ligand-receptor binding is swamped by noise from CCV. This argues that many of the factors controlling optimal single-cell chemotactic sensing, e.g. the ligand-receptor dissociation constant, number of receptors, and the receptor dynamics time, are not as critical for collective gradient sensing. Instead, the degree of CCV and the correlation time of the CCV may be more important.

FIG. 8.

A. Collective guidance requires, through some mechanism, a comparison between cell states to create an estimate of gradient direction (blue arrow). These estimates are biased if each cell’s response to the concentration measurement is highly variable. I show schematically how this estimate is biased toward a cell that has an anomalously strong response (cell with red X). B. When cell-to-cell variability is large, the cluster fluidity can control the cluster accuracy (chemotactic index); here the fluidity is regulated by cell-cell adhesion, taking the cluster from fluid to solid. Also shown are corresponding fluid and solid clusters, with colors indicating degree of signaling strength. This panel is adapted from [92], and simulation details can be found there.

B. If cell-to-cell variation is large, cluster mechanics may matter a great deal

Our initial results with this model show that mechanical properties of the cluster play a large role in improving accuracy in the presence of this CCV [92] (Fig. 8B), with clusters becoming significantly more accurate (larger chemotactic index) as their fluidity is increased. This simulation result is an example of a larger principle: cluster mechanics and rheology can limit signal accuracy. Why? In single cells, as I discussed below Eq. 1, averaging a measurement over time can reduce error by combining effectively independent samples. However, the cell-to-cell variability may be highly persistent (potentially over several cell division times [111]) – thus the error due to CCV in Eq. 9 is highly persistent. Time-averaging is only successful here if a cluster averages over times long compared to cluster re-arrangement. As a consequence, cluster chemotactic accuracy is a function of cluster fluidity (Fig. 8B). We used this principle to derive an explicit bound on the accuracy of cluster chemotaxis as a function of cluster fluidity [92]:

$${\sigma }_{g,T}^2=\frac{{\sigma }_{g,0}^2}{1+T/{\tau }_r}$$ (10)

where σ_g,T is the uncertainty in gradient measurement, σ_g,0 the uncertainty without time-averaging (Eq. 9), T the length of time over which clusters measure, and τ_r a correlation time of cluster rearrangement. τ_r is defined from the correlation function C_rr(t) ≡ 〈δr(t) · δr(0)〉/〈|δr²|〉, δr is the displacement of a cell from the cluster center of mass. Theory and simulations suggest that often, C_rr(t) ~ exp(−t/τ_r) [92], giving a single natural timescale; however for non-exponential relaxation, there are straightforward generalizations of Eq. 10. The bound of Eq. 10 can be translated into a bound on chemotactic index, which is also shown in Fig. 8B.

It is not currently clear whether cell clusters that collectively chemotax exploit time-averaging over a long enough time to benefit from the error reduction in Eq. 10. To gain this benefit, clusters must maintain a memory over times long compared with re-arrangement; this will often be at least tens of minutes. However, re-arrangement is common in collectively chemotaxing clusters, including border cell cluster rotation and re-arrangement [117–119] and lymphocyte cluster tumbling [8, 48].

If time-averaging is long enough so that fluidity controls chemotactic accuracy, as we hypothesized in [92], changes in cell and tissue behavior that would normally decrease accuracy and up-gradient speed of cluster migration can actually improve them: there will be tradeoffs between increased reliability in following the estimated gradient $\widehat{\mathbf{\text{g}}}$ and in decreasing the error in $\widehat{\mathbf{\text{g}}}$ by creating cluster rearrangement. We studied two examples of these tradeoffs extensively in [92], showing that cluster rotation can be optimal for sufficiently long averaging times, and that added single-cell stochastic motility can also increase cluster accuracy. This last case shows an extreme example of this tradeoff, where added noise can improve measurement accuracy!

Our result in Eq. 10 shows how cluster re-arrangement can improve chemotaxis. I should mention two interesting tangentially related papers. First is Iyengar and Rao [120], who predict that rearrangement at the receptor level can help observe a time-varying signal; the ideal time-dependent configuration switches between active clustering, stationary lattices, and passive diffusion. Secondly, Uriu and Morelli [121, 122] propose that synchronization between cells can be improved by tissue rearrangement, using a self-propelled particle model with cells also having phase oscillators that couple between neighbors. These suggest interesting places of potential contact to gradient sensing at the collective level.

The model of [92] that leads to Eq. 10 and its generalizations requires one key biological hypothesis: the presence of a long-term cluster-scale memory with a timescale T. What could the origin of this memory be, and how can its presence be experimentally tested? Since in [92], it was assumed that the memory is maintained at the cluster scale, it would be natural to first posit that the memory is exterior to the cluster. This could be due to information stored in extracellular matrix structure (e.g. deformation) or a trail with a long lifespan, such as those known to occur in single-cell motion [123]. In addition, supracellular actin structures such as actin cables can influence cell protrusion and leader cell formation [53]. The orientation of the cluster could then be encoded in the density of actin cable. These hypotheses suggest general routes to test these ideas: if the memory is disrupted, accuracy should decrease (via Eq. 10); in addition, I would expect the cluster’s motion to be less persistent. The putative memories could be disrupted via the use of a strong hydrodynamic cross-flow in microfluidics (to remove any potential secreted memory) or by active cutting of the actin cable via photoablation [53]. I also note that, in contrast to the assumption of a global memory, it is possible to keep the memory at the individual cell level by cells estimating their own bias level Δⁱ and compensating for it; in this case, disrupting these factors would not lead to changes in memory. Understanding this mechanism will require additional modeling.

VII. ROUTES FORWARD: WHAT COMES NEXT?

A. Establishing signal processing mechanisms

In Section V B above, I argued that how the cluster collectively processes a signal can alter many aspects of its response, including cluster velocity, etc. With this in mind, more quantitative understanding of how clusters take signal measurements and create motility and protrusion would be valuable, e.g. quantitative comparison between applied signal gradients and downstream activity, as performed earlier for single cells [104, 124] or determining how clusters respond when elements of the signaling network are perturbed [125, 126]. These perturbations may highlight the mechanism of communication. For instance, in the mammary organoids of [35], inhibition of gap junctions prevents collective gradient sensing; gap junction function is also critical for neural crest collective motility [127, 128]. These suggest that communication through gap junctions is a strong candidate for cell-cell communication. However, the interpretation of these experiments may be complicated by the recent discovery that Connexin43, a primary component of the gap junction, also controls N-cadherin transcription, altering adhesion and contact inhibition of locomotion [129]. Mechanical communication between cells has also been suggested as relevant in the border cell cluster, as cell-cell adhesion is critical in the directionality of the cluster, even when it is not necessary for cluster cohesion [57]. Determining the specific inhibitor or inhibitors in a LEGI-like model is also nontrivial, and not settled in the single cell context [130].

Recent work by the author and collaborators has started to address the more general question of how to determine signal processing networks from experimental data on collective cell migration, determining which signal processing motifs are compatible with earlier experimental results, including measurements of photoactivation of Rac in border cell clusters [131]. This sort of analysis may be matched with screening approaches to characterize the influence of multiple factors [132]. Dealing with the complexity of the true signaling network with approaches like this may be valuable in establishing putative inhibitory factors; our models allow us to make predictions for how impaired cell-cell communication affects chemotaxis, and determine how generic these predictions are when the rest of the network structure is varied.

B. Collective sensing beyond chemotaxis: more than gradients, more than chemosensing

I have primarily focused on experiments and theory studying the response of cell clusters to chemical gradients. However, as highlighted in Section III, the accuracy of gradient sensing improves for clusters of cells sensing gradients of vast numbers of signal types. A future challenge will be understanding the extent to which earlier modeling can be extended to, e.g. galvanotaxis or durotaxis. One-dimensional models of collective durotaxis have recently been developed [37, 133], but dependence on cluster size and shape remains an open question. Perhaps more interesting is the question of sensing signals beyond simple gradients. Collective concentration sensing has also been studied experimentally and theoretically [134–137]. Recent experiments have also shown that a traveling wave of ERK activation, created optogenetically, can create guided motility in an epithelial monolayer [138]. Understanding how clusters can optimally respond to dynamic inputs of this sort, or suddenly changing signals (as studied for single cells [139]), is another natural route forward.

C. Systematic measurement of cell-to-cell variation

I argued above and in [92] that cell-to-cell variability may be a limiting factor in collective chemotaxis, especially if collective guidance is assumed. A natural prediction from these results is that, when viable collective gradient sensing occurs, cell-to-cell variability must be either reduced by regulation or somehow compensated for, e.g. by time-averaging. Quantita tive measurements of cell-to-cell variation of elements of the chemotaxis network are possible; an in vivo example showing relatively weak CCV is the quantitative measurement of Sdf1 signaling in the zebrafish lateral line primordium [87]. Protein and mRNA concentrations can also be measured quantitatively [140, 141]. As quantitative measurements of the relevant experimental systems improve, models must develop increasing biochemical fidelity in order to understand the effect of variability at different points in the network; the proposal of Eq. 8 is a valuable minimal model, but sacrifices the ability to straightforwardly measure the CCV parameter σ_Δ.

In addition, while Eq. 8 models variation in how cells respond to a chemoattractant signal, there may also be significant CCV in motility properties, e.g. cell speed and persistence [115]. Understanding to what extent these properties will alter the ability of cell clusters to follow gradients, and whether this effect will dominate those potential biases identified in [92], is a natural next step. The critical nature of understanding CCV in motility and signaling also highlights the need for new computational tools to extract these parameters from experimental observations [142].