Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2019 Nov 1.
Published in final edited form as: Schizophr Res. 2018 Jun 12;201:217–223. doi: 10.1016/j.schres.2018.06.007

Reduced higher-dimensional resting state fMRI dynamism in clinical high-risk individuals for schizophrenia identified by meta-state analysis

Eva Mennigen a,1, Robyn L Miller a, Barnaly Rashid a, Susanna L Fryer c,d, Rachel L Loewy c, Barbara K Stuart c, Daniel H Mathalon c,d,*, Vince D Calhoun a,b,*
PMCID: PMC6252113  NIHMSID: NIHMS975244  PMID: 29907493

Abstract

New techniques to investigate functional network connectivity in resting state functional magnetic resonance imaging data have recently emerged. One novel approach, called meta-state analysis, goes beyond the mere cross-correlation of time courses of distinct brain areas and explores temporal dynamism in more detail, allowing for connectivity states to overlap in time and capturing global dynamic behavior. Previous studies have shown that patients with chronic schizophrenia exhibit reduced neural dynamism compared to healthy controls, but it is not known whether these alterations extend to earlier phases of the illness. In this study, we analyzed individuals at clinical high-risk (CHR, n= 53) for developing psychosis, patients in an early stage of schizophrenia (ESZ, n= 58), and healthy controls (HC, n= 70). ESZ individuals exhibit reduced neural dynamism across all domains compared to HC. CHR individuals also show reduced neural dynamism but only in 2 out of 4 domains investigated. Overall, meta-state analysis adds information about dynamic fluidity of functional connectivity.

Keywords: psychosis risk, resting-state fMRI, functional connectivity, group independent component analysis, meta-state analysis

1. Introduction

Functional network connectivity (FNC) has gained much interest in recent years as a measure of functional brain integrity that often appears disrupted in neurological and psychiatric disorders (Calhoun et al., 2014; Fornito et al., 2015). The analysis of FNC has potential to further our understanding of the neural mechanisms underlying disabling psychiatric and neurological disorders. Most often, FNC is analyzed using resting state functional magnetic resonance imaging (rs-fMRI) data. After initial acquisition and pre-processing of the data, there are multiple options to further analyze functional connectivity (van den Heuvel & Hulshoff Pol, 2010), including group independent component analysis (GICA; Calhoun et al., 2001; Erhardt et al., 2011), graph theoretical approaches (Bullmore & Sporns, 2009), and dynamic causal modelling (Friston et al., 2014).

In the current paper, we focus on independent component analysis (ICA) and one of its diverse applications. ICA is a purely data-driven approach that does not make assumptions about the shape of the time courses of the blood oxygenation level dependent (BOLD) signal. GICA estimates maximally independent spatial components with common time courses that can be characterized as intrinsic connectivity networks (ICN) and further grouped into functional domains. Recently, there has been considerable development of various aspects of GICA. The first established GICA measure was static FNC (Jafri et al., 2008) that involves calculation of whole brain connectivity, i.e., correlation of time courses, across the entire resting state scan. Subsequent work focused on the development of a dynamic FNC approach, as it has been shown that functional connectivity is highly dynamic throughout the duration of a typical resting state scan (Chang & Glover, 2010; Hutchison et al., 2013).

In dynamic FNC, time courses are parceled into temporal windows, each with a size of multiple repetition times (TR) allowing for a finer temporal resolution than static FNC. Across the windowed FNC matrices, recurring connectivity patterns have been identified and summarized as discrete states based on cluster centroids, i.e., matrices most distinctively representing each state. It has been shown that these states occur independently of the population studied, including healthy and clinical populations (Abrol et al., 2017). Even though dynamic FNC analysis can uncover abnormalities in patient samples relative to healthy controls that are obscured in static FNC analyses (Damaraju et al., 2014; Rashid et al., 2014), it still appears to be an oversimplified measure of complex brain dynamics.

In order to further investigate brain dynamics, Miller et al. (Miller et al., 2016) introduced an approach to analyze meta-states: instead of ‘forcing’ windowed FNC matrices into one specific state membership, this approach builds distance vectors to the cluster centroids for each windowed FNC matrix. More specifically, windowed FNCs are modeled as “weighted sums of maximally independent connectivity patterns (CP)” (Miller et al., 2016). Discretized CP distance vectors are called meta-states. A meta-state analysis enables the estimation of different measures of neural dynamism, for example, the total distance traveled in the n-dimensional state space (n reflecting the number of distinct CPs), number of distinct meta-states, span of meta-states, and number of meta-state changes. Thereby it is a new approach to depict neural dynamics beyond the analysis of static and dynamic FNC. With finer temporal resolution than typically examined in FNC, this technique allows to assess how dynamic and ‘agile’ functional connectivity is across the duration of the resting state scan, including how many distinct meta-states individuals exhibit and how often they switch among states.

Schizophrenia is one of the most extensively studied psychiatric illnesses. It is viewed as a neurodevelopmental disorder characterized by structural and functional dysconnectivity (Calhoun, 2009; Fornito et al., 2012). Dysconnectivity, the abnormal functional and structural ‘communication’ between brain areas, can lead to erroneous integration of perception, which might explain symptoms such as hallucinations and delusions. Furthermore, it has recently been shown that dynamic changes of functional connectivity are essential for cognitive processing (Shine et al., 2016; Vatansever et al., 2015). Given that schizophrenia is often accompanied by cognitive decline, the thorough investigation of brain dynamics in schizophrenia seems important in order to better understand underlying neural mechanism.

With regard to neural dynamism in meta-state analysis in patients with schizophrenia, Miller et al (Miller et al., 2016) showed that compared to healthy controls, patients exhibit reduced dynamism: they switch less often between meta-states, occupy fewer meta-states in general, and explore a restricted range in the meta-state space compared to healthy controls. These findings provide novel extensions of the evidence for global dysconnectivity in schizophrenia, which to date has been assessed predominantly with static FNC techniques.

Most patients with first episode schizophrenia retrospectively describe a prodromal state, typically lasting a few years, preceding the onset of their full-blown psychotic symptoms. Prospectively, individuals who exhibit symptoms resembling the psychosis prodrome are said to be at clinical high-risk for psychosis (CHR), meeting criteria for a psychosis-risk syndrome characterized by attenuated psychotic symptoms, brief intermittent psychotic episodes, and/or genetic risk and recent functional decline, as well as associated impairments in social and cognitive functions (Fusar-Poli et al., 2013; McGlashan et al., 2010). In order to understand the pathogenesis of underlying brain dysfunction in schizophrenia, it is essential to investigate the CHR state. As has been shown in previous work, the CHR state is already characterized by functional dysconnectivity in static as well as dynamic FNC analyses (Du et al., 2017a; Du et al., 2017b; Mennigen et al., “The chronnectomics of schizophrenia risk: dynamic functional network connectivity in clinical high-risk, early illness schizophrenia, and healthy control individuals” at Society for Neuroscience, 2016, San Diego, CA)2. Findings from Du and colleagues indicated that the level of dysconnectivity observed in CHR individuals fell intermediately between patients with early-illness schizophrenia and healthy controls (Du et al., 2017a).

In the current study, we analyzed the same sample of CHR, early illness schizophrenia (ESZ), and healthy control (HC) individuals as presented in Du et al. and Mennigen et al. in order to investigate temporal dynamism in both a CHR sample as well as in an early stage of schizophrenia using the meta-state approach introduced by Miller et al. (Miller et al., 2016) but focusing on k-means clustering. Based on our previous studies using these data, as well as a general theoretical framework that posits less severe brain dysfunction in CHR individuals relative to ESZ patients, either due to progressive decline of brain function or the presence of more severe dysfunction in only the subgroup of CHR individuals destined to transition to full psychosis, we hypothesized that CHR individuals would exhibit alterations in neural dynamism that are intermediate, falling in between ESZ and HC individuals.

2. Material and methods

2.1. Participants

CHR individuals (n=53) were recruited from University of California, San Francisco (UCSF) Early Psychosis Clinical Research Program, local clinics, and school counseling centers. The CHR for psychosis syndrome was diagnosed based on the Criteria of Prodromal Syndromes (COPS; T. J. Miller et al., 2002) as assessed using the Structured Interview for Prodromal Syndromes (SIPS; McGlashan et al., 2001). Individuals met criteria for one or more of three non-mutually exclusive prodromal syndromes: Attenuated Psychotic Symptoms (92.5%), Brief Intermittent Psychotic Symptoms (1.9%), and Genetic Risk and Deterioration (7.5%) (T. J. Miller et al., 2003).

ESZ patients (n=58) were recruited from the Early Psychosis Clinical Research Program at USCF and from local community clinics. ESZ patients met DSM-IV criteria for schizophrenia (n=63.8%), schizoaffective (n=27.6%) or schizophreniform (n=6.9%) disorder based on the Structured Clinical Interview for DSM-IV (SCID; First et al., 2002) administered by a trained interviewer. The mean illness duration for ESZ patients was 2.09 years (standard deviation, SD, 1.37).

Symptom severity was assessed by trained clinical raters using the Scale of Prodromal Symptoms (SOPS; T. J. Miller et al., 2003) for CHR individuals and the Positive and Negative Syndrome Scale (PANSS; Kay et al., 1987) for ESZ patients.

HC individuals (n=70) were recruited from the community and did not meet criteria for any axis I diagnosis based on the SCID. For participants < 16 years of age, the Schedule for Affective Disorders and Schizophrenia for School-Age Children (Kiddie-SADS), Present and Lifetime Version (Kaufman et al., 1997) was used in order to assess for Axis I diagnoses in younger teenagers.

General exclusion criteria included DSM-IV substance dependence in the past year (except nicotine), a history of head injury with loss of consciousness, neurological disorders, or a first-degree relative with a psychotic illness (for HC individuals only).

Written informed consent was obtained from participants, or from their parents/legal guardians in the case of minors (who also provided written assent), under protocols approved by the institutional review board at UCSF. Demographic data are presented in Table 1. The final sample comprised 70 HC, 53 CHR, and 58 ESZ individuals and groups did not differ significantly with regard to age and gender. 12 CHR (22.6%) and 53 ESZ (91.4%) individuals were medicated with antipsychotics (supplementary table 1) at the time of fMRI scanning.

Table 1.

Demographic data;

HC (n=70) CHR individuals (n=53) ESZ patients (n=58) p value
Mean SD Mean SD Mean SD
Age (Years) 21.9 5.6 20.4 4.5 21.8 3.8 .189^
PANSS Positive Symptoms -- -- -- -- 13.7+ 4.8 n/a
PANSS Negative Symptoms -- -- -- -- 17.4+ 6.6 n/a
SOPS Positive Symptoms -- -- 9.14* 4.6 -- -- n/a
SOPS Negative Symptoms -- -- 12.2* 5.8 -- -- n/a
Maximum of absolute translation
motion displacement (mm) 		0.8 0.6 1.1 1.4 1.2 1.3 0.11^
Maximum of absolute rotation
motion displacement (degrees) 		0.8 1.0 1.0 0.9 0.9 0.8 0.48^
n % n % n %
Male 41 59% 32 62% 38 65% .714∞
Open in a new tab

SD = standard deviation; HC = healthy control individuals, CHR = clinical high-risk individuals, ESZ = early illness schizophrenia patients; PANSS = Positive And Negative Symptom Scale, SOPS = Scale Of Prodromal Symptoms;

+

indicates n=56 ESZ individuals with valid clinical data,

*

indicates n= 36 CHR individuals with valid clinical data (within 2 weeks after fMRI scanning);

group differences tested with ^analysis of variance or ∞Chi-squared test

2.2. Data acquisition

Resting state fMRI data were collected at the UCSF Neuroimaging Center using a 3T Siemens Trio (Erlangen, Germany) scanner.

2.2.1. Resting state fMRI pre-processing

Participants were instructed to keep their eyes closed while scanning and to stay awake. Resting state scans were acquired using a high-speed whole brain echo planar imaging sequence (32 axial slices, thickness 3.5mm, FOV 24cm, TR 2s, echo time 29ms, flip angle 75°). Pre-processing was computed with SPM 8 (http://www.fil.ion.ucl.ac.uk/spm) and the Data Processing Assistant for Resting State fMRI (DPARSF) toolbox (Yan & Zang, 2010). The first 10 images were discarded due to equilibration effects, leaving 170 images for further analysis. Further pre-processing included slice time correction, realignment to the first volume, spatial normalization to a standard MNI template, reslicing to a voxel size of 3×3×3mm, and smoothing with a 6mm Gaussian kernel. Individuals included did not exceed 4mm/4 degrees movement across volumes.

2.3. Functional network connectivity analysis

The meta-state analysis is based on windowed FNC matrices. Therefore, we describe all FNC processing steps in detail below.

2.3.1. Group Independent Component Analysis (GICA)

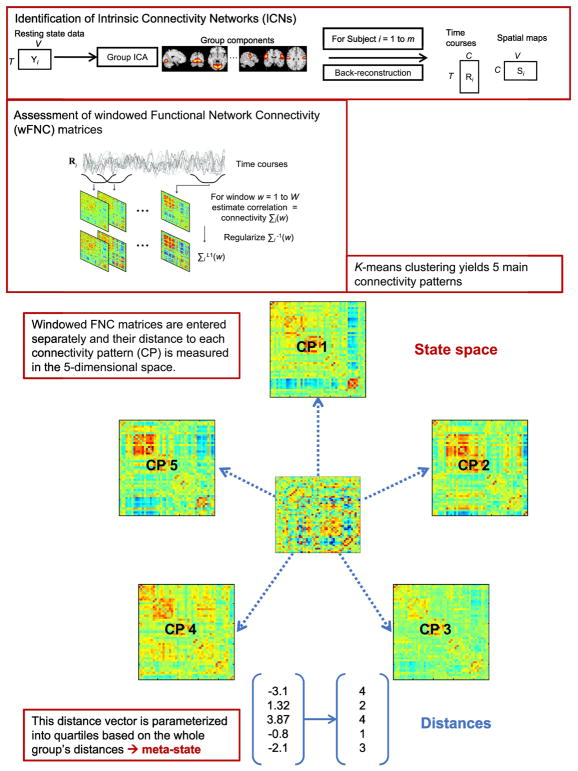
Figure 1 depicts analysis steps for GICA and for the k-means meta-state approach. Spatial GICA (Calhoun & Adali, 2012; Calhoun et al., 2001) decomposes the whole brain rs-fMRI data into linear mixtures of spatially independent components. GICA was performed using the Group ICA fMRI toolbox (GIFT) (http://mialab.mrn.org/software/gift/index.html) with two data reduction steps using principal component analysis: 1) a subject-specific reduction of time points from 170 time points to 120 temporal principle components comprising weighted sums of time points, and 2) a group-wise reduction of the concatenated subject-reduced data to 100 aggregate components each consisting of a spatial map and a corresponding time course using the expectation-maximization algorithm (Roweis, 1998). Pre-processing in GIFT included z-scoring of time courses in order to normalize variance. ICA was repeated 20 times in ICASSO (Himberg & Hyvärinen, 2003) using the infomax (Bell & Sejnowski, 1995) algorithm in order to ensure stability of estimation. We used spatial-temporal back reconstruction (Erhardt et al., 2011) to estimate subject-specific time courses and spatial maps for each independent component. The resulting 100 independent components were manually reviewed in order to identify meaningful ICNs based on the Automated Anatomic Labeling atlas (Tzourio-Mazoyer et al., 2002). ICNs should show peak locations in gray matter with minimal overlap with white matter, ventricles, blood vessels, and non-brain structures. Further, spectral power of the time courses of meaningful ICNs should obey the power law, showing exponentially higher power at the lowest frequencies and lowest power at the highest frequencies. Inspection of the 100 independent components yielded 47 meaningful ICNs which were assigned to 8 functional domains based on prior scientific literature (http://neurosynth.org/): subcortical (SC), salience (SAL), auditory (AUD), sensorimotor (SM), visual (VIS), cognitive control (CC), default mode network (DMN), and cerebellum (CB). Supplementary figure 1 shows all functional domains and supplementary table 2 contains ICNs assigned to each domain.

Figure 1.

Figure 1

Open in a new tab

General approach for group independent component analysis (GICA) and meta-state analysis using k-means clustering

2.3.2. Post-processing of time courses

Post-processing of time courses included linear, quadratic, and cubic detrending and regression of motion parameters (in x-, y-, and z-direction as well as pitch, roll, and yaw) as well as their derivatives and squares, in a single multiple regression framework (Power et al., 2014). Time courses were also despiked. Spikes were defined as time points with a root mean square of the frame-wise displacement >0.5mm. These were identified based on the 3Ddespike algorithm as implemented in Analysis of Functional NeuroImages (AFNI; Cox, 1996) and interpolated using a 3rd order spline fit to ‘clean’ neighboring data. Temporal filtering was applied with a bandpass 5th order Butterworth filter (passband 0.01 – 0.15 Hz). FNC was computed after post-processing and interpolation of time points identified as spikes.

2.3.3. Windowed functional network connectivity matrices

As in earlier studies (Allen et al., 2012; Damaraju et al., 2014; Rashid et al., 2014), we applied a sliding temporal window approach to rs-fMRI data in order to capture fluctuations of functional connectivity. A rectangular window (width 22 TRs = 44s) was convolved with a Gaussian of sigma 3 TRs in order to obtain tapering along the edges of the window and slid in steps of 1 TR across concatenated time courses. For each window, a separate FNC matrix consisting of cross-correlations of ICNs (size ICN x ICN) was calculated.

2.3.4 Connectivity patterns (CP) and meta-states

Unlike Miller et al. (Miller et al., 2016), we solely applied a k-means clustering algorithm to windowed FNC (wFNC) matrices (representing a connectivity pattern in an individual at a certain point in time) in order to make results between the dynamic FNC approach and the meta-states approach more comparable. Estimated wFNC matrices were clustered based on the k-means algorithm implemented in Matlab (7.12.0 (R2011a), The MathWorks Inc., Natick, MA) with squared Euclidean distance as similarity measure (150 iterations, 5 replicates). The optimal number of cluster centroids was estimated to be 5 based on the elbow criterion (supplementary figure 2). Supplementary figure 3 shows the k-means clustering process in more detail.

The resulting cluster centroids were used as main connectivity patterns (CPs) in order to generate distance vectors for each wFNC matrix. The distance was measured as squared Euclidean distance of each wFNC matrix to the five cluster centroids in the 5-dimensional meta-state space resulting in a vector consisting of 5 distances, see Figure 1. This distance vector is then parameterized by replacing each concrete distance value with the quartile this distance falls in based on the group’s distance. These parameterized vectors are called meta-states.

The following measures of dynamism can be calculated from the discretized distance vectors:

  • The number of changes of meta-states, i.e., how often does an individual switch between distinct meta-states;

  • The number of distinct meta-states, i.e., how many unique distance vectors are present in an individual;

  • The span of meta-states, i.e., the actual range of the 5-dimensional meta-state space that one individual covers during the entire scan;

  • The total distance traveled through the meta-state space.

Using analysis of variance (ANOVA), we tested for differences between groups separately for each measure of neural dynamism (significance level p<0.05). Significant results were followed up using the inbuilt Matlab (7.12.0 (R2011a), The MathWorks Inc., Natick, MA) function multcompare that uses Tukey’s HSD tests in order to determine which groups differed. Tukey’s HSD test was designed to control for type 1 errors and corrects for multiple comparisons by itself (Sato, 1996).

2.3.4.1. Summary

In the current study, a meta-state represents a whole brain connectivity pattern in time consisting of overlapping manifestations of 5 main connectivity patterns. Thus, the term meta-state refers to a high-level summary of overlapping connectivity states. Meta-states are then used to calculate metrics reflecting dynamic properties of whole-brain connectivity, i.e., number of meta-states changes, number of meta-states, span of meta-states, and total distance travelled in the 5-dimensional meta-state space.

2.3.5. Association between neural dynamism and symptom severity

In order to investigate possible associations between neural dynamism and symptom severity, we computed bivariate Pearson’s correlations for CHR and ESZ groups and each dynamic measure. Positive and negative symptom scores based on SOPS for CHR individuals and PANSS for ESZ individuals were correlated with measures of neural dynamism. Results were considered significant when reaching a Bonferroni adjusted α-level of 0.0031 (0.05/16, i.e. nominal type I error/number of tests). Clinical data were available for 36 CHR and 56 ESZ individuals for this analysis.

2.3.6 Influence of antipsychotic medication on neural dynamism in CHR individuals

In order to test medication effects, we compared measures of dynamism in unmedicated (N= 41, 77.4%) vs. medicated (N= 12, 22.6%) CHR individuals. Due to the unbalanced sample size, we computed non-parametric Wilcoxon rank sum tests. Since there were not enough ESZ patients without antipsychotic medication (n= 5, 8.6%) we could not apply the same approach to the ESZ sample.

3. Results

3.1. Analysis of variance for group differences in measures of neural dynamism

For an overview of means and standard deviations of measures of neural dynamism see Table 2: HC individuals show highest values of neural dynamism, whereas CHR individuals fall intermediately between HC individuals and ESZ patients. We found significant differences between groups for the number of meta-state changes (F= 6.26, p= 0.0024), number of meta-states (F= 4.66, p= 0.0107), metastate span (F= 5.72, p= 0.0039), and total distance travelled in the meta-state space (F= 6.72, p= 0.0015). Tukey HSD tests showed that ESZ patients, relative to HC individuals, had significantly lower temporal dynamism as reflected by reductions in the number of meta-state changes (p= 0.0043), number of metastates (p= 0.0066), meta-state span (p= 0.0021), and the total distance travelled (p= 0.0021). CHR individuals, relative to HC individuals, had significantly lower dynamism for the number of meta-state changes (p= 0.0138) and the total distance travelled in the meta-state space (p= 0.0156) compared to HC individuals. CHR and ESZ groups did not significantly differ on any of the four dynamic measures.

Table 2.

A. Means and standard deviation (SD) of four measures of dynamism, B. ANOVA results;

Analysis of variance – number of meta-state changes

Analysis of variance – number of unique meta-states

Analysis of variance – meta-state span

Analysis of variance – total distance travelled in 5-dimensional meta-state space

A.
Meta-state changes (mean, SD) Number of meta-states (mean, SD) Meta-state span (mean, SD) Total distance (mean, SD)
HC (n=70) 34.47 (7.54) 25.51 (8.56) 8.86 (2.33) 39.51 (10.07)
CHR (n=53) 30.85 (7.11) 23.32 (7.97) 8.32 (2.1) 34.92 (8.86)
ESZ (n=58) 30.48 (6.46) 21.24 (6.95) 7.6 (1.74) 34.05 (8.03)
B.
Analysis of variance – number of meta-state changes
Source SS df MS F p
Group 628.1 2 314.05 6.26 0.0024
Error 8.9327e+03 178 50.18
Total 9.5608e+03 180
Post hoc comparison (only significant comparisons)

  • HC vs CHR: p= 0.0138

  • HC vs ESZ: p= 0.0043

Analysis of variance – number of unique meta-states
Source SS df MS F p
Group 581.6 2 290.8 4.66 0.0107
Error 1.1110e+04 178 62.41
Total 1.1691e+04 180
Post hoc comparison (only significant comparisons)

  • HC vs ESZ: p= 0.0066

Analysis of variance – meta-state span
Source SS df MS F p
Group 49.89 2 24.95 5.72 0.0039
Error 775.9979 178 4.36
Total 825.8895 180
Post hoc comparison (only significant comparisons)

  • HC vs ESZ: p= 0.0021

Analysis of variance – total distance travelled in 5-dimensional meta-state space
Source SS df MS F p
Group 1.1141e+03 2 557.03 6.72 0.0015
Error 1.4762e+04 178 82.93
Total 1.5876e+04 180
Open in a new tab

HC = healthy control individuals, CHR = clinical high-risk individuals, ESZ = early illness schizophrenia patients; SS= sum of squares, df= degrees of freedom, MS= mean squares, F= F-statistic, p= p-value

3.2. Correlation of clinical symptom scores

Neither the CHR group nor the ESZ group exhibited significant correlations between symptom severity (SOPS/PANSS positive and negative symptom scores) and measures of dynamism.

3.3. Wilcoxon rank sum test for differences between medicated and unmedicated clinical high-risk individuals in measures of neural dynamism

Statistical tests for each measure of neural dynamism did not yield significant differences between medicated and unmedicated CHR individuals (number of meta-state changes: p= 0.3434, z-statistic= 0.95; number of meta-states: p= 0.2133, z-statistic= 1.24; meta-state span: p= 0.787, z-statistic= −0.27; total distance travelled: p= 0.4374, z-statistic= 0.78).

4. Discussion

Even though the analysis of meta-states is a new approach that has not yet been widely applied, it offers an opportunity to further our understanding of temporal dynamism of functional connectivity in severe neurological and psychiatric illnesses. Previous attempts to capture brain dynamics in rs-fMRI data, even data-driven approaches, somewhat oversimplify the underlying temporal structure of the data by focusing on spatial patterns of dysconnectivity. The meta-state approach (Miller et al., 2016) carefully preserves as much information as possible about underlying dynamics in time courses, while also providing intuitive summary measures, thereby allowing a more detailed analysis of underlying neural behavior.

We applied the k-means meta-state approach to a sample of clinical high-risk individuals for developing psychosis, patients in an early stage of schizophrenia, and healthy controls, and found that neural dynamism is not only reduced in early schizophrenia but also prior to psychosis onset in individuals exhibiting the psychosis risk syndrome.

4.1. Neural dynamism – Number of meta-states, meta-state changes, state span, and distance travelled

In both studies using this approach so far (Miller et al., 2016 and the current study) HC individuals exhibited highest numbers in all measures of dynamism reflecting greater dynamism. Again, indicating that HC individuals show more variable connectivity patterns and greater agility with regard to changes of connectivity patterns compared to patients with chronic schizophrenia (Miller et al., 2016), ESZ patients, and CHR individuals (as shown by the current study).

ESZ individuals show significantly reduced neural dynamism in all measures investigated compared to healthy controls: they exhibit a lower number of distinct meta-states, switch less often between these, and traverse less of the five-dimensional state space. These results are consistent with and extend previous findings by Miller et al. (Miller et al., 2016). Whereas Miller et al. examined meta-state dynamism in chronic schizophrenia, we find similar alterations present at an earlier stage of the disorder (mean illness duration 2.09 years). In CHR individuals, on the other hand, 2 out of 4 metrics were significantly reduced compared to healthy controls. This suggests that alterations in CHR individuals are not as pronounced as in ESZ patients both compared to HC individuals albeit differences between CHR and ESZ groups were non-significant. This furthers our understanding of deficits in neural dynamics in schizophrenia by highlighting the fact that it is not a late emerging deficit associated with illness chronicity and further, that it is presumably not a deficit that emerges de novo following the onset of schizophrenia since reduced dynamism is captured in CHR individuals as well. Moreover, the presence of these deficits in neural dynamism in CHR individuals renders unlikely the possibility that the deficits are secondary consequences of antipsychotic medication since there were no significant differences between medicated and unmedicated CHR individuals. Fewer significant differences between CHR and HC individuals might be explainable by the following:

  • a)

    The CHR group is very heterogeneous with regard to transition rates because only about one third of CHR individuals will actually develop a psychotic disorder (Bechdolf et al., 2012). This heterogeneity may ‘water down’ the true effect of the psychosis prodrome on neural dynamism, which might in fact be even more similar to abnormalities observed in early-illness schizophrenia if the analyses were limited to those at-risk individuals who subsequently transition to psychosis;

or

  • b)

    Abnormalities in neural dynamism progressively worsen as individuals transition from the psychosis risk syndrome to full-blown psychosis.

Unfortunately, the clinical follow-up data and number of transitions to psychosis in our CHR sample were insufficient to permit analyses aimed at evaluating these alternative explanations.

4.2. Conclusion

In this study, we applied a new connectivity analysis to samples of CHR individuals, ESZ patients, and HC individuals. Deficits in measures of neural dynamism were evident in early illness schizophrenia, consistent with prior work showing such deficits in chronic schizophrenia. Moreover, some deficits were present in the psychosis risk syndrome despite the fact that full psychosis had yet to emerge. The attenuated nature of the neural dynamism deficits in CHR individuals could arise from the presence of modest deficits in most individuals, consistent with neural dynamism deficits progressively worsening from the psychosis risk syndrome to full blown schizophrenia. Alternatively, these attenuated deficits could result from an admixture of normal or mild deficits in most individuals and more severe deficits in the minority of individuals destined to convert to full psychosis. Distinguishing between these alternatives requires clinical follow-up data on psychosis conversion status, data that are not available in the current sample. Nonetheless, the presence of these deficits in the psychosis risk syndrome, supports the conclusion that neural dynamism deficits precede the onset of psychosis.

The meta-state analysis adds information on fluctuations of FNC which extends our knowledge of brain dynamics. To further show that patients with schizophrenia (chronic and early-illness) and CHR individuals exhibit alterations in temporal brain dynamics complements findings of spatial dysconnectivity found in previous studies. Beyond this, it is known from task-based fMRI studies (Shine et al., 2016; Vatansever et al., 2015) that the dynamic reconfiguration of functional connectivity plays an important role in cognitive processing. This suggests that the diminished fluidity of brain connectivity as observed with the meta-state approach during resting state fMRI in patients with chronic schizophrenia (Miller et al., 2016), early-illness schizophrenia and clinical high-risk individuals (current study) might be connected to cognitive performance and decline thereof in schizophrenia and the prodromal state. Future studies are needed to test this hypothesis specifically.

4.3. Limitations

A main limitation of the current study is the novel method of meta-state analysis. Regarding the interpretation of results, it is important to recall that instead of making assertions about spatial patterns of dysconnectivity, meta-state analysis explores temporal dynamics and rather asks how fluidly whole brain connectivity patterns change. Whether this impaired fluidity is also associated with poorer task performance in schizophrenia should be explored in future research; an approach which would also test the validity of meta-state analysis in more detail.

Even though, no significant differences between medicated and unmedicated CHR individuals were observed, future studies should consider a more in-depth analysis of medication effects in CHR and ESZ populations. Again, the analysis of longitudinal data including conversion status of CHR individuals seems most urgent.

Supplementary Material

supplement

Acknowledgments

We thank all study participants for taking time to participate in the study.

Footnotes

Contributors

Authors DHM and SLF designed the study and wrote the protocol. Authors RLL and BKS managed psychometric data assessment. Authors EM and RLM undertook the statistical analysis, and author EM wrote the first draft of the manuscript. All authors contributed to and have approved the final manuscript.

Conflict of interest

All authors declare that there are no conflicts of interest.

Author disclosure

This work was supported by National Institutes of Health grants 5P20RR021938/P20GM103472 (to VDC), R01EB020407 (to VDC), and U01MH076989 (to DHM), National Science Foundation grant 1539067 (to VDC). EM was funded by the Max Kade Foundation, New York City, New York, USA.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Bibliography

  1. Abrol A, Damaraju E, Miller RL, Stephen JM, Claus ED, Mayer AR, Calhoun VD. Replicability of time-varying connectivity patterns in large resting state fMRI samples. NeuroImage. 2017 doi: 10.1016/j.neuroimage.2017.09.020. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Allen EA, Damaraju E, Plis SM, Erhardt EB, Eichele T, Calhoun VD. Tracking Whole-Brain Connectivity Dynamics in the Resting State. Cerebr Cortex. 2012;24(3):663–676. doi: 10.1093/cercor/bhs352. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bechdolf A, Wagner M, Ruhrmann S, Harrigan S, Putzfeld V, Pukrop R, … Klosterkotter J. Preventing progression to first-episode psychosis in early initial prodromal states. Br J Psychiatr. 2012;200(1):22–29. doi: 10.1192/bjp.bp.109.066357. [DOI] [PubMed] [Google Scholar]
  4. Bell AJ, Sejnowski TJ. An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 1995;7(6):1129–1159. doi: 10.1162/neco.1995.7.6.1129. [DOI] [PubMed] [Google Scholar]
  5. Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci. 2009;10(3):186–198. doi: 10.1038/nrn2575. [DOI] [PubMed] [Google Scholar]
  6. Calhoun VD. Functional brain networks in schizophrenia: a review. Front Hum Neurosci. 2009;3 doi: 10.3389/neuro.09.017.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Calhoun VD, Adali T. Multisubject Independent Component Analysis of fMRI: A Decade of Intrinsic Networks, Default Mode, and Neurodiagnostic Discovery. IEEE Reviews in Biomedical Engineering. 2012;5:60–73. doi: 10.1109/RBME.2012.2211076. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Calhoun VD, Adali T, Pearlson Gd, Pekar JJ. A method for making group inferences from functional MRI data using independent component analysis. Hum Brain Mapp. 2001;14(3):140–151. doi: 10.1002/hbm.1048. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Calhoun VD, Miller RL, Pearlson G, Adalı T. The Chronnectome: Time-Varying Connectivity Networks as the Next Frontier in fMRI Data Discovery. Neuron. 2014;84(2):262–274. doi: 10.1016/j.neuron.2014.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Chang C, Glover GH. Time–frequency dynamics of resting-state brain connectivity measured with fMRI. NeuroImage. 2010;50(1):81–98. doi: 10.1016/j.neuroimage.2009.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Cox RW. AFNI: Software for Analysis and Visualization of Functional Magnetic Resonance Neuroimages. Comput Biomed Res. 1996;29(3):162–173. doi: 10.1006/cbmr.1996.0014. [DOI] [PubMed] [Google Scholar]
  12. Damaraju E, Allen EA, Belger A, Ford JM, McEwen S, Mathalon DH, Mueller BA, Pearlson GD, Potkin SG, Preda A, Turner JA, Vaidya JG, van Erp TG, Calhoun VD. Dynamic functional connectivity analysis reveals transient states of dysconnectivity in schizophrenia. NeuroImage: Clinical. 2014;5:298–308. doi: 10.1016/j.nicl.2014.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Du Y, Fryer SL, Fu Z, Lin D, Sui J, Chen J, Damaraju E, Mennigen E, Stuart B, Mathalon DH, Calhoun VD. Dynamic functional connectivity impairments in early schizophrenia and clinical high-risk for psychosis. NeuroImage. 2017a doi: 10.1016/j.neuroimage.2017.10.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Du Y, Fryer SL, Lin D, Sui J, Yu Q, Chen J, Stuart B, Calhoun VD, Mathalon DH. Identifying functional network changing patterns in individuals at clinical high-risk for psychosis and patients with early illness schizophrenia: A group ICA study. NeuroImage: Clinical. 2017b doi: 10.1016/j.nicl.2017.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Erhardt EB, Rachakonda S, Bedrick EJ, Allen EA, Adali T, Calhoun VD. Comparison of multi-subject ICA methods for analysis of fMRI data. Hum Brain Mapp. 2011;32(12):2075–2095. doi: 10.1002/hbm.21170. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. First MB, Spitzer RL, Gibbon M, Williams JBW. Structured Clinical Interview for DSM-IV-TR Axis I Disorders, Research Version, Patient Edition. New York: Biometrics Research, New York State Psychiatric Institute; 2002. [Google Scholar]
  17. Fornito A, Zalesky A, Breakspear M. The connectomics of brain disorders. Nat Rev Neurosci. 2015;16(3):159–172. doi: 10.1038/nrn3901. [DOI] [PubMed] [Google Scholar]
  18. Fornito A, Zalesky A, Pantelis C, Bullmore ET. Schizophrenia, neuroimaging and connectomics. NeuroImage. 2012;62(4):2296–2314. doi: 10.1016/j.neuroimage.2011.12.090. [DOI] [PubMed] [Google Scholar]
  19. Friston KJ, Kahan J, Biswal B, Razi A. A DCM for resting state fMRI. NeuroImage. 2014;94:396. doi: 10.1016/j.neuroimage.2013.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Fusar-Poli P, Borgwardt S, Bechdolf A, Addington J, Riecher-Rössler A, Schultze-Lutter F, … Yung A. The Psychosis High-Risk State: A Comprehensive State-of-the-Art Review. JAMA Psychiatry. 2013;70(1):107. doi: 10.1001/jamapsychiatry.2013.269. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Himberg J, Hyvärinen A. Icasso: software for investigating the reliability of ICA estimates by clustering and visualization. Neural Networks for Signal Processing, 2003. NNSP’03. 2003 IEEE 13th Workshop on; IEEE; 2003. pp. 259–268. [Google Scholar]
  22. Hutchison RM, Womelsdorf T, Gati JS, Everling S, Menon RS. Resting-state networks show dynamic functional connectivity in awake humans and anesthetized macaques. Hum Brain Mapp. 2013;34(9):2154–2177. doi: 10.1002/hbm.22058. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Jafri MJ, Pearlson GD, Stevens M, Calhoun VD. A method for functional network connectivity among spatially independent resting-state components in schizophrenia. NeuroImage. 2008;39(4):1666–1681. doi: 10.1016/j.neuroimage.2007.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kaufman J, Birmaher B, Brent D, Rao U, Flynn C, Moreci P, … Ryan N. Schedule for Affective Disorders and Schizophrenia for School-Age Children-Present and Lifetime Version (K-SADS-PL): Initial Reliability and Validity Data. J Am Acad Child Adolesc Psychiatr. 1997;36(7):980–988. doi: 10.1097/00004583-199707000-00021. [DOI] [PubMed] [Google Scholar]
  25. Kay SR, Flszbein A, Opfer LA. The positive and negative syndrome scale (PANSS) for schizophrenia. Schizophr Bull. 1987;13(2):261. doi: 10.1093/schbul/13.2.261. [DOI] [PubMed] [Google Scholar]
  26. McGlashan TH, Miller TJ, Woods SW, Hoffman RE, Davidson L. Instrument for the Assessment of Prodromal Symptoms and States. In: Miller T, Mednick SA, McGlashan TH, Libiger J, Johannessen JO, editors. Early Intervention in Psychotic Disorders. Springer; Netherlands: 2001. pp. 135–149. [Google Scholar]
  27. McGlashan T, Walsh B, Woods S. The Psychosis-Risk Syndrome: Handbook for Diagnosis and Follow-Up. Oxford University Press; USA: 2010. [Google Scholar]
  28. Miller RL, Yaesoubi M, Turner JA, Mathalon DH, Preda A, Pearlson G, … Calhoun VD. Higher Dimensional Meta-State Analysis Reveals Reduced Resting fMRI Connectivity Dynamism in Schizophrenia Patients. PLOS ONE. 2016;11(3):e0149849. doi: 10.1371/journal.pone.0149849. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Miller TJ, McGlashan TH, Rosen JL, Cadenhead K, Ventura J, McFarlane W, … Woods SW. Prodromal assessment with the structured interview for prodromal syndromes and the scale of prodromal symptoms: predictive validity, interrater reliability, and training to reliability. Schizophr Bull. 2003;29(4):703. doi: 10.1093/oxfordjournals.schbul.a007040. [DOI] [PubMed] [Google Scholar]
  30. Miller TJ, McGlashan TH, Rosen JL, Somjee L, Markovich PJ, Stein K, Woods SW. Prospective Diagnosis of the Initial Prodrome for Schizophrenia Based on the Structured Interview for Prodromal Syndromes: Preliminary Evidence of Interrater Reliability and Predictive Validity. JAMA Psychiatry. 2002;159(5):863–865. doi: 10.1176/appi.ajp.159.5.863. [DOI] [PubMed] [Google Scholar]
  31. Power JD, Mitra A, Laumann TO, Snyder AZ, Schlaggar BL, Petersen SE. Methods to detect, characterize, and remove motion artifact in resting state fMRI. NeuroImage. 2014;84:320–341. doi: 10.1016/j.neuroimage.2013.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Rashid B, Damaraju E, Pearlson GD, Calhoun VD. Dynamic connectivity states estimated from resting fMRI Identify differences among Schizophrenia, bipolar disorder, and healthy control subjects. Front Hum Neurosci. 2014;8 doi: 10.3389/fnhum.2014.00897. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Roweis S. EM algorithms for PCA and SPCA. Advances in neural information processing systems. 1998:626–632. [Google Scholar]
  34. Sato T. Type I and Type II Error in Multiple Comparisons. J Psychol. 1996;130:293–302. [Google Scholar]
  35. Shine JM, Bissett PG, Bell PT, Koyejo O, Balsters JH, Gorgolewski KJ, Moodie CA, Poldrack RA. The Dynamics of Functional Brain Networks: Integrated Network States during Cognitive Task Performance. Neuron. 2016;92:544–554. doi: 10.1016/j.neuron.2016.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, … Joliot M. Automated Anatomical Labeling of Activations in SPM Using a Macroscopic Anatomical Parcellation of the MNI MRI Single-Subject Brain. NeuroImage. 2002;15(1):273–289. doi: 10.1006/nimg.2001.0978. [DOI] [PubMed] [Google Scholar]
  37. van den Heuvel MP, Hulshoff Pol HE. Exploring the brain network: A review on resting-state fMRI functional connectivity. Eur Neuropsychopharmacol. 2010;20(8):519–534. doi: 10.1016/j.euroneuro.2010.03.008. [DOI] [PubMed] [Google Scholar]
  38. Vatansever D, Menon DK, Manktelow AE, Sahakian BJ, Stamatakis EA. Default Mode Dynamics for Global Functional Integration. J Neurosci. 2015;35:15254–15262. doi: 10.1523/JNEUROSCI.2135-15.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Yan C-G, Zang Y. DPARSF: A MATLAB Toolbox for “Pipeline” Data Analysis of Resting-State fMRI. Front Syst Neurosci. 2010;4 doi: 10.3389/fnsys.2010.00013. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

supplement
NIHMS975244-supplement.doc (2.9MB, doc)

RESOURCES