Modeling a rotator cuff tear: Individualized shoulder muscle forces influence glenohumeral joint contact force predictions

Abstract

Background:

Rotator cuff tears in older individuals may result in decreased muscle forces and changes to force distribution across the glenohumeral joint. Reduced muscle forces may impact functional task performance, altering glenohumeral joint contact forces, potentially contributing to instability or joint damage risk. Our objective was to evaluate the influence of rotator cuff muscle force distribution on glenohumeral joint contact force during functional pull and axilla wash tasks using individualized computational models.

Methods:

Fourteen older individuals (age 63.4yrs (SD 1.8)) were studied; 7 with rotator cuff tear, 7 matched controls. Muscle volume measurements were used to scale a nominal upper limb model’s muscle forces to develop individualized models and perform dynamic simulations of movement tracking participant-derived kinematics. Peak resultant glenohumeral joint contact force, and direction and magnitude of force components were compared between groups using ANCOVA.

Findings:

Results show individualized muscle force distributions for rotator cuff tear participants had reduced peak resultant joint contact force for pull and axilla wash (P≤0.0456), with smaller compressive components of peak resultant force for pull (P=0.0248). Peak forces for pull were within the glenoid. For axilla wash, peak joint contact was directed near/outside the glenoid rim for three participants; predictions required individualized muscle forces since nominal muscle forces did not affect joint force location.

Interpretation:

Older adults with rotator cuff tear had smaller peak resultant and compressive forces, possibly indicating increased instability or secondary joint damage risk. Outcomes suggest predicted joint contact force following rotator cuff tear is sensitive to including individualized muscle forces.

1.0. Introduction

Rotator cuff tears (RCT) are a prevalent musculoskeletal injury in older individuals.¹ Rotator cuff muscles provide shoulder stability by situating the humeral head in the glenoid fossa² through combined action of concave-compression and anterior-posterior (transverse) and superior-inferior force couples.^3,4 Glenohumeral joint contact force (JCF) is a quantitative measure of joint stability, with reduced compression and forces directed outside the glenoid rim indicative of instability.^5–7 The JCF will be dynamically driven by both limb kinematics during a task and the forces generated by muscles. Kinematics of task performance are known to be altered following RCT in older adults.⁸ While the proportion of individual muscle volumes at the shoulder is preserved across healthy adult age groups,^9–11 RCT can alter the volume of injured muscles,¹² dramatically changing the muscle force distribution across the joint. However, the extent to which muscle volume, and thus force-generating capacity, is altered may vary across individuals. If RCT causes a force imbalance at the glenohumeral joint, it may result in loss of dynamic joint control,¹³ induce dyskinesis, or precipitate abnormal joint loading scenarios that lead to deleterious wear of articular cartilage on the glenoid and humeral head.¹⁴ Understanding the specific effects of altered muscle force and altered kinematics after RCT on the associated glenohumeral JCF can provide insight into secondary consequences of RCT injury.

Since JCFs cannot be measured in vivo without invasive procedures (e.g. instrumented joint replacement), computational modeling is a useful approach to explore biomechanical consequences of injured muscle-tendon units and altered movement, and elucidate factors contributing to risk for subsequent glenohumeral joint damage. Several detailed upper limb models are currently available,^15–19 but these models represent a single specimen or average force-generating capabilities of young adults. Inclusion of age-and injury-related muscle changes are essential for more accurate predictions of the force profile of older individuals. In previous studies, models incorporating subject-derived strength characteristics have shown improved predictive qualities^8,20 for individual patients or specific populations. Specifically, the individual pattern of injury across individuals and the combined influence of aging may alter rotator cuff muscle force distribution, and thus predicted JCF, at the glenohumeral joint.

Our objective was to evaluate the effect of individualized muscle force and kinematics following rotator cuff injury on glenohumeral JCF predictions. To do this, we developed individualized computational models by scaling model muscle force-generating characteristics to correspond with subject-derived measurements of rotator cuff muscle volume. Dynamic simulations of movement were performed with individualized computational models and subject-derived kinematics of two upper limb tasks to examine the influence of muscle force distribution across the glenohumeral joint on predicted glenohumeral JCF. We hypothesized that altered muscle forces for RCT patients would result in a JCF profile that included reduced compressive forces and JCF directed closer to the glenoid fossa boundary.

2.0. Methods

The Wake Forest Health Sciences Institutional Review Board approved this study; all participants provided written informed consent. Fourteen older individuals (age 63.4yrs (SD 1.8)) participated (Table 1), including 7 participants (4M/3F) with a supraspinatus tendon tear (RCT group) and 7 age-, (within 2 years) sex-matched controls. Rotator cuff tear participants who presented to our institution’s orthopaedic clinic with symptoms of shoulder pain and were diagnosed with at least a high grade partial-thickness (>50% tendon thickness) degenerative, MRI-confirmed supraspinatus tendon tear were recruited; 5 participants had full-thickness tear, 2 had partial-thickness supraspinatus tear (Table 1). Asymptomatic control participants were recruited from the community, did not have history of shoulder pain or injury, and were further screened using a modified Jobe’s test for asymptomatic RCT (sensitivity: 81%; specificity: 89%).²¹ The Jobe’s test was performed with the participant’s arms elevated 90° in the scapular plane with neutral arm rotation while a small, downward force (~2kg) was manually applied. Exclusionary criteria included a test eliciting pain or weakness. In accordance with prior studies of participants with RCT,^8,12 the injured arm was studied for RCT participants, and the dominant arm was investigated for asymptomatic controls (Table 1).

Table 1:

Participant characteristics and peak muscle forces for model muscle actuators, calculated from individual muscle volume measures.

									Peak muscle forces (N) of model muscle actuators
Participant	Age (years)	Height (cm)	Height percentilea	Body mass (kg)	Body mass percentilea	Dominant arm	Injured arm	Supraspinatus tear characterization	DELT1	DELT2	DELT3	SUPSP	INFSP	SUBSC	TMIN	TMAJ
RF01	65	149.9	2	53.5	15	Right	Left	Full	600.0	491.8	70.8	-	326.8	310.5	87.2	35.5
RF02	63	160	35	73.5	90	Right	Right	Full	585.9	480.2	69.2	-	404.8	508.9	89.3	61.9
RF03	65	162.6	50	65.8	70	Right	Left	Partial	425.6	348.8	50.3	-	259.2	326.1	95.2	39.7
RM01	61	167.6	10	83.9	70	Right	Left	Full	817.3	669.9	96.5	-	840.1	736.3	238.0	123.5
RM02	64	177.8	65	108	99+	Left	Left	Full	1412.4	1157.7	166.8	-	1037.4	875.5	228.8	116.0
RM03	64	182.9	85	88.5	80	Right	Left	Full	1029.1	843.6	121.5	-	964.9	833.3	222.4	112.5
RM04	62	177.8	65	95.3	90	Left	Left	Partial	1084.0	888.5	128.0	-	1060.1	1003.1	251.1	87.0
CF01	67	172.7	95	70.8	85	Right	-	-	616.7	505.5	72.8	331.6	652.3	617.2	204.8	66.2
CF02	65	162.6	50	65.8	70	Right	-	-	474.0	388.5	56.0	222.3	454.2	488.9	80.1	80.4
CF03	64	160	35	60.3	45	Right	-	-	543.2	445.2	64.1	279.0	522.1	561.1	151.1	70.6
CM01	61	177.8	65	99.8	97	Right	-	-	1254.6	1028.3	148.1	333.9	897.7	938.5	264.1	90.5
CM02	64	182.9	85	86.2	75	Right	-	-	972.6	797.2	114.9	456.7	984.6	905.8	172.1	94.3
CM03	62	172.7	35	73.5	35	Right	-	-	1034.5	847.9	122.2	486.5	1034.5	922.9	234.1	107.7
CM04	61	175.3	50	70.3	25	Right	-	-	880.7	721.9	104.0	478.1	870.3	822.9	148.0	93.5
RCT mean (SD)	63.4(1.5)	168.4(11.8)	44.6(30.5)	81.2(18.4)	69.2(28.0)
Control mean (SD)	63.4(2.2)	172.0(8.1)	59.3(23.5)	75.2(13.4)	61.7(27.0)

^aHeight and body mass percentiles were calculated according to Gordon et al.²⁶

R: rotator cuff tear subject

C: control subject

F: female subject

M: male subject

DELT1: anterior compartment of deltoid

DELT2: middle compartment of deltoid

DELT3: posterior compartment of deltoid

SUPSP: supraspinatus

INFSP: infraspinatus

SUBSC: subscapularis

TMIN: teres minor

TMAJ: teres major

2.1. Functional task kinematics

Participants completed 2 functional tasks based on everyday activities while seated (chair height=0.53m). Loaded functional pull and axilla wash (Fig. 1A) were chosen for assessment because they represented both planar and multiplane tasks, and statistically significant differences in self-selected kinematics were identified between RCT and control groups for these tasks in prior work.⁸ Using previously described methods,²² seven Hawk motion capture cameras (Motion Analysis Corporation, Santa Rosa, CA, USA) were used to track positions of twelve 1cm-diameter retroreflective markers placed on anatomical locations on the upper limb and torso²² as participants performed each task. Participants were instructed on task start and finish positions, but could freely choose their joint postures and speed of movement. Three trials of each task were recorded, with 60sec of rest between trials and 2min rest between tasks. Participants were instructed to stop and notify study staff if they felt any pain or discomfort during performance of any task. The second trial of each task for each participant was used for analysis. Marker data were post-processed using Cortex software (Cortex, Motion Analysis Corporation, Santa Rosa, CA, USA) and smoothed with the program’s internal 6Hz Butterworth filter. Joint kinematics were calculated using a nominal upper limb model¹⁷ in OpenSim (v.3.1)²³ using methods described below.

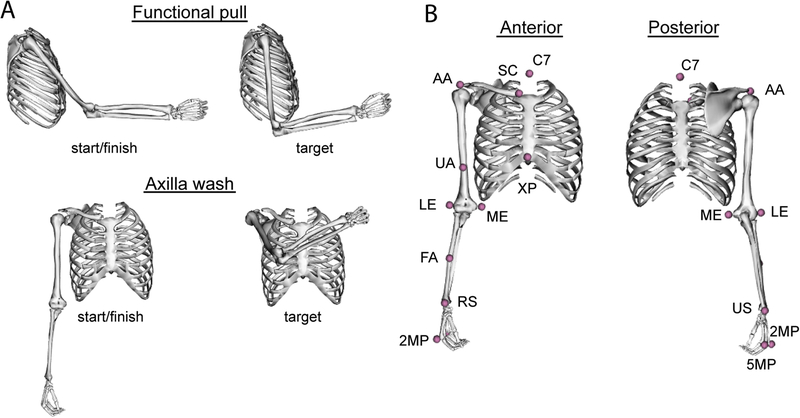
Fig. 1:

(A) Functional tasks performed by participants, including a functional pull (top) and axilla wash (bottom). Start/finish (left) and target (right) positions for each task are shown. For the functional pull, participants were seated at a table (height = 0.775m) and pulled against 2.72kg (6lb) resistance from a pulley system. The functional pull task started with the arm forward flexed a distance of 80% of the subject’s forearm length (length was marked on the table) and handle from a weight machine, pull the handle until the arm is in neutral flexion (target), then finish by returning to the start position. For the axilla wash, which is an unloaded task, the participant remained seated but the table was removed. The task started with the elbow extended and arm in neutral, resting quietly at the side. Participants then reached across the torso to touch the lateral aspect of the contralateral shoulder (target), then finished the task by returning to the starting position, with the arm resting quietly at the side in neutral posture. (B) Anatomical locations of retro-reflective markers used with motion capture (pink spheres). Twelve markers were placed at locations including: C7: 7^th cervical vertebra; SC: ventral aspect of the sternoclavicular joint; XP: xiphoid process; AA: lateral aspect of acromial angle of scapula; UA: upper arm, mid-length; LE: lateral epicondyle of humerus; ME: medial epicondyle of humerus; FA: forearm, mid-length; RS: styloid process of radius; US: styloid process of ulna; 5MP: 5^th metacarpophalangeal joint; 2MP: 2^nd metacarpophalangeal joint. An additional marker (not shown) was affixed to the top of the handle used for the functional pull task.

2.2. Model development

To calculate joint kinematics for functional pull and axilla wash tasks, the nominal dynamic upper limb model¹⁷ was scaled to each subject’s anthropometry using OpenSim’s scaling tool and marker positions recorded from motion capture with a static trial. Joint kinematics for each functional task were calculated using inverse kinematics and the scaled model. Briefly, inverse kinematics calculates joint angles of each model degree of freedom using a least squared algorithm to minimize distance between marker locations recorded using motion capture and positions of virtual markers (cf. Fig. 1B, pink spheres) in the model.²³ Joint angle trajectories were filtered off-line with a zero-phase digital filter with a custom Matlab program (The Mathworks, Natick, MA, USA).

To calculate glenohumeral JCF with subject-derived joint kinematics, individualized computational models used for dynamic simulations of movement were developed using the nominal dynamic upper limb model as a foundation. This model includes joint descriptions of Saul et al.¹⁷ and maintains kinematic descriptions originally described by Holzbaur et al.¹⁵ Individualized models in this work maintained the bony geometry and kinematic descriptions from the nominal model, including representing scapulo-humeral articulation as a ball-and-socket joint, scapulo-humeral rhythm according to regression equations reported by de Groot and Brand,²⁴ and axis descriptions of thoracohumeral motion (elevation plane, elevation, axial rotation) according to International Society of Biomechanics recommendations .²⁵ Range of motion of shoulder generalized coordinates and associated muscle paths were augmented to permit the full range of observed thoracohumeral motion for recorded tasks and maintain proper interaction of muscle actuators with their associated wrapping surfaces. Elevation plane range of motion was expanded to allow −95° to 130° of rotation and humeral axial rotation range of motion was expanded to permit −90° to 120° of rotation. Muscle paths and behavior within previously described joint limits were unaltered.^15,17

2.3. Subject-derived muscle force calculations

Individualized models representing each participant were developed by scaling forces of muscle actuators representing muscle-tendon units in the model. Peak muscle forces of the nominal model’s 50 muscle actuators were scaled to represent the moment-generating capacity of individual participants, as derived from individual muscle volume calculations. This approach was selected because using muscle volume permits estimation of individual muscle forces, compared to isometric joint moment-generating capacity measurements that only measure collective strength of a muscle group. Shoulder musculature, including individual rotator cuff muscles (supraspinatus, infraspinatus, subscapularis, teres minor), and teres major and deltoid muscle volumes, were measured for each subject from magnetic resonance (MR) images¹² using imaging, manual segmentation, and analysis methods previously described.¹¹ Briefly, the perimeter of each muscle was traced in each MR image and three-dimensional surfaces created from the boundaries were used to calculate muscle volume. Volumes for remaining muscles crossing the shoulder, elbow, and forearm were obtained from mean male and female values previously reported for healthy older adults.¹¹ Peak muscle force, $F_0^m$, was calculated for each muscle using Equation 1 (Table 1); σ is muscle specific tension (50.8N/cm²); V_m is muscle volume; $l_0^m$ is muscle optimal fiber length.

$$F_0^m=\sigma \times \frac{V_m}{l_0^m}$$ (1)

Values for σ and $l_0^m$ were maintained as defined in the nominal model, based on previously measured values from anatomical and functional upper limb studies.¹⁷ Segment inertial properties were scaled to correspond to masses of a 50^th percentile male and female²⁶ for male and female models, respectively, using OpenSim’s scaling tool. To represent the tear in RCT participants, the supraspinatus muscle actuator was removed from models of RCT participants, reflecting that the tendon was torn and could not directly transmit force.

2.4. Computational simulations

Dynamic simulations of movement were conducted using OpenSim’s computed muscle control (CMC)²⁷ tool. Briefly, CMC calculates predicted muscle activations necessary to track experimentally-measured joint kinematics. Simulations were performed using each individualized model and corresponding subject-derived functional task kinematics. For simulations of functional pull, a 26.69N external force in the anterior horizontal direction was added to correspond with the weight machine’s resistance; no external forces were applied for unweighted axilla wash simulations. Reserve torque actuators were permitted to supply up to 5Nm of joint torque when required to track kinematics. Predicted muscle activations from CMC were used to calculate glenohumeral JCF using OpenSim’s joint analysis tool. Force coordinates represent anterior-posterior (x-axis), superior-inferior (y-axis), and medial-lateral (z-axis) directions. Forces were transformed into the anatomical reference frame aligned with the scapular plane²⁸ for analysis by applying 30° anterior rotation about the y-axis (superior-inferior axis). The resultant JCF vector, which has an origin in the geometric center of the humeral head, was calculated and the peak resultant force identified. Direction and magnitude of peak resultant force and its vector components were calculated. Peak resultant JCF vectors were projected onto the glenoid fossa. A generic description based on the model’s scapular geometry of the glenoid rim was used; the glenoid fossa was estimated as an ellipse, defined by maximum anterior-posterior (28.4mm) and superior-inferior (36.6mm) dimensions of the nominal model’s glenoid fossa. To enable assessment of the effect of individualized muscle forces derived from measured muscle volume on predicted JCF, an additional simulation using muscle force-generating properties of the nominal model (with supraspinatus removed for RCT participants) and the participant’s kinematics was performed.

Data normality was assessed with the Shapiro-Wilk test. Root mean square (RMS) error was calculated to assess differences between experimentally-measured joint kinematics and CMC-calculated kinematics. Group differences in magnitude and direction of peak JCF were evaluated with analyses of covariance (ANCOVA), with adjustments for age and sex as continuous and categorical variables, respectively. To evaluate the normalized magnitude of calculated JCF values, peak load was divided by each subject’s body weight (BW). Normalized peak JCF by BW was also compared between groups using ANCOVA. The ratio between superior-inferior and medial-lateral components of peak JCF was calculated and compared between nominal and individualized models. Statistical analyses were performed using SAS software (v.9.3, SAS Institute, Inc., Cary, NC, USA); P≤0.05 was considered significant.

3.0. Results

3.1. Computational simulations

Mean RMS error between input kinematics and CMC results for the three shoulder degrees of freedom was 0.98° for functional pull and 1.75° for axilla wash (Table 3). One RCT model (RF03) was excluded from axilla wash analyses due to poor tracking of input kinematics (Supplemental Fig. 1); for this subject, mean RMS error for shoulder degrees of freedom was 9.1°.

Table 3:

Root mean square error (RMSE) calculations between subject-derived kinematics and computed muscle control (CMC)-calculated kinematics for shoulder degrees of freedom (DOFs). *indicates participant that was excluded from analysis due to poor tracking of the CMC algorithm (cf. Supplemental Fig.1).

	Functional pull			Axilla wash
	Elevation angle (°)	Shoulder elevation (°)	Shoulder rotation (°)	Elevation angle (°)	Shoulder elevation (°)	Shoulder rotation (°)
RF01	0.09	0.10	1.41	0.88	0.20	1.53
RF02	3.60	0.93	1.81	1.63	0.26	0.59
RF03	1.64	0.61	1.06	20.00*	5.31*	2.90*
RM01	0.14	0.09	1.19	0.11	0.15	1.17
RM02	0.11	0.09	1.17	2.08	0.23	1.98
RM03	0.08	0.08	1.19	0.29	0.19	1.10
RM04	0.09	0.14	1.29	2.52	0.46	1.12
CF01	12.15	1.41	0.86	8.40	0.84	0.95
CF02	0.19	0.08	1.23	4.35	0.96	2.65
CF03	1.31	0.34	1.00	8.34	1.95	2.11
CM01	0.06	0.05	0.91	0.20	0.13	1.13
CM02	0.06	0.05	1.01	0.30	0.26	2.06
CM03	0.25	0.16	1.26	0.49	0.23	1.14
CM04	0.11	0.12	1.59	11.39	2.07	1.78
Mean	1.42	0.30	1.21	3.15	0.61	1.49
Mean of all shoulder DOFs		0.98			1.75

DOFs: degrees of freedom

3.2. Functional pull

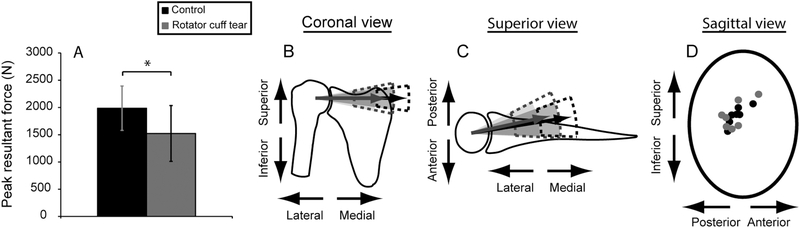
When using individualized muscle forces to predict JCF for functional pull, the RCT group had significantly reduced peak resultant force compared to controls (P=0.0244) (Fig. 2A; Tables 2, 4); specifically the compressive (medial-lateral) component of peak resultant force was reduced (P=0.0248) (Fig. 2B,C; Table 4). There were no differences in force vector orientation between groups (P≥0.3127; Table 4). Peak resultant JCF was oriented within the glenoid rim for all participants (Fig. 2D); glenoid dimensions and projected distance from the humeral head center to articular surface were measured from the model’s bony representations of scapula and humerus. The RCT group had smaller mean normalized peak resultant JCF compared to the control group (1.91 (SD 0.44) times BW vs. 2.72 (SD 0.52) times BW, respectively, P=0.0141; Table 4).

Fig. 2:

Joint contact force comparisons for the functional pull for rotator cuff tear (gray) and control (black) participants. (A) Mean (SD) peak resultant joint contact force was significantly smaller for the rotator cuff tear group (P=0.0244). The compressive (medial-lateral) component of the peak joint contact force was significantly reduced for the rotator cuff tear group (P=0.0248), which can be seen in the (B) coronal and (C) superior views of the joint. Shaded cones represent 1 SD of the mean position of the resultant vector; dashed lines represent 1 SD of the mean magnitude of the resultant force vector. (D) Anterior-posterior and superior-inferior components of the peak joint contact force are overlayed on an oval representing the glenoid fossa.

Table 2:

Peak resultant joint contact force (JCF) and the constituent compressive (medial-lateral), anterior-posterior, and superior-inferior components for each participant for functional pull and axilla wash tasks.

Functional pull
Participant	Compressive component (N)	Anterior(+)/posterior(−) component (N)	Superior(+)/inferior(−) component (N)	Peak resultant JCF (N)
RF01	913.4	−292.3	124.5	967.1
RF02	1291.2	−331.2	127.7	1339.1
RF03	935.2	216.4	413.3	1045.1
RM01	1574.7	−112.9	−31.9	1579.1
RM02	1223.9	−85.0	439.2	1303.1
RM03	2134.5	−533.8	−80.0	2201.7
RM04	2187.3	−360.4	−154.6	2222.2
CF01	1990.5	−455.7	−210.9	2052.8
CF02	1385.2	209.3	418.7	1462.1
CF03	1419.0	−136.2	206.1	1440.3
CM01	1912.4	−136.3	471.7	1974.4
CM02	2239.2	−115.3	322.0	2265.2
CM03	2484.3	−501.9	87.8	2536.0
CM04	2125.0	−363.3	286.7	2174.8
RCT mean (SD)	1465.7 (525.2)	−214.2 (243.5)	119.8 (233.2)	1522.5 (511.9)
Control mean (SD)	1936.5 (408.8)	−214.2 (246.5)	226.0 (231.2)	1986.5 (406.8)

Axilla wash
Participant	Compressive component (N)	Anterior(+)/posterior(−) component (N)	Superior(+)/inferior(−) component (N)	Peak resultant JCF (N)
RF01	793.6	−49.0	886.8	1191.1
RF02	1297.4	−247.1	327.9	1360.9
RM01	1099.9	−374.5	−778.4	1398.6
RM02	1817.3	141.6	948.3	2054.7
RM03	1457.8	−336.3	410.8	1551.5
RM04	2208.6	−231.6	340.7	2246.7
CF01	1704.4	130.7	670.7	1836.3
CF02	1466.4	−73.5	422.7	1527.8
CF03	1647.1	−286.2	305.2	1699.4
CM01	1740.7	267.9	1119.7	2087.0
CM02	1496.4	−353.4	−937.3	1800.7
CM03	2229.8	156.4	1145.4	2511.7
CM04	2339.7	305.5	585.2	2431.0
RCT mean (SD)	1445.8 (507.3)	−182.8 (194.9)	356.0 (620.2)	1633.9 (420.8)
Control mean (SD)	1803.5 (345.3)	21.0 (263.2)	473.1 (700.2)	1984.9 (372.7)
Nominal model (RF01)	2297.9	−410.2	793.3	2465.3
Nominal model (RF02)	3215.5	−468.2	831.0	3354.0
Nominal model (RM01)	1922.0	175.1	843.1	2106.1
Nominal model (RM02)	2706.9	153.2	−111.4	2713.5
Nominal model (RM03)	1996.9	−17.9	594.0	2083.4
Nominal model (RM04)	1027.8	288.0	554.6	2565.1
Nominal model (CF01)	2983.1	424.8	1093.2	3205.4
Nominal model (CF02)	3785.0	−186.3	1414.2	4044.9
Nominal model (CF03)	3398.8	−584.7	959.3	3579.6
Nominal model (CM01)	2095.2	378.1	1057.4	2377.2
Nominal model (CM02)	2383.0	−685.4	−348.8	2504.0
Nominal model (CM03)	2492.6	403.4	1549.1	2962.4
Nominal model (CM04)	2983.0	56.1	1434.7	3310.5
Nominal RCT mean (SD)	2194.5 (747.0)	−46.7 (320.0)	584.1 (362.4)	2547.9 (468.0)
Nominal Control mean (SD)	2874.4 (594.7)	−27.7 (470.9)	1022.7 (644.4)	3140.6 (586.4)

Table 4:

P-values for statistical analyses comparing joint contact force magnitude and vector directions between rotator cuff tear and control groups, with adjustments for age and sex.

	Joint contact force magnitude					Joint contact force vector direction
	Resultant	Anterior-posterior component	Superior-inferior component	Medial-lateral component	Body weight normalized	Anterior-posterior	Superior-inferior	Medial-lateral
Functional pull	0.0244*	0.9999	0.4475	0.0248*	0.0141*	0.7137	0.9606	0.3127
Axilla wash	0.0456*	0.1734	0.8074	0.0967	0.0277*	0.1566	0.8967	0.6125

^*indicates statistical significance (p ≤ 0.05).

3.3. Axilla wash

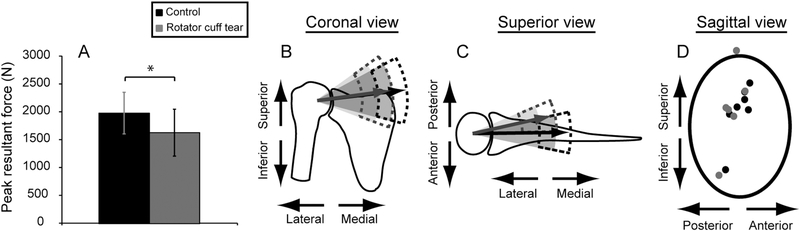
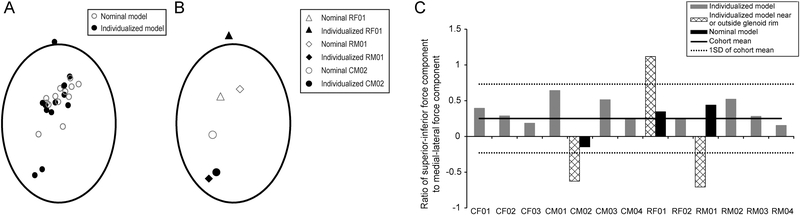
Simulations with individualized models indicated that RCT reduced peak JCF and that muscle force distribution was an important factor in determining JCF for axilla wash. The RCT group had smaller peak resultant JCF (P=0.0456; Table 4) compared to controls (Fig. 3A; Tables 2, 4), although significant differences were not detected in magnitude of individual components (P≥0.0967) nor for orientation (P≥0.1566) of peak resultant JCF (Fig. 3B,C; Table 4). Peak resultant JCF was located near the glenoid rim for three participants, one of whom had peak resultant JCF located outside the nominal glenoid boundary (Fig. 3D). Repeated simulations with the nominal model including nominal muscle forces (supraspinatus removed for RCT models) using kinematics of each participant no longer identified peak resultant force near the glenoid rim (Fig. 4A). Assessment of specific differences were performed for participants (RF01, RM01, CM02) with forces near or outside the glenoid rim (Fig. 4B), including examination of the ratio of superior-inferior to medial-lateral components of peak JCF vector (Fig. 4C). Simulations performed with individualized models indicated that these three participants had ratios exceeding 1SD of cohort values. This finding suggests that the altered distribution of muscle forces for individualized models compared to the nominal model affects JCF prediction. On average, magnitudes of resultant JCF and JCF components were 1.3 and 1.6 times higher, respectively, for simulations using the nominal model compared to simulations with individualized models (Table 2), highlighting the importance of including individualized muscle forces in predictive computational simulations. Normalized by BW, RCT participants had smaller mean peak resultant JCF than controls (2.00 (SD 0.28) times BW vs. 2.73 (SD 0.60) times BW, respectively, P=0.0277; Table 4).

Fig. 3:

Joint contact force comparisons for the axilla wash for rotator cuff tear (gray) and control (black) participants. (A) Mean (SD) peak resultant joint contact force was significantly smaller for the rotator cuff tear group (P=0.0456). (B) Coronal and (C) superior views of the joint do not exhibit significant differences between the magnitude or direction of the planar components of the resultant force vector for the two groups. Shaded cones represent 1 SD of the mean position of the resultant vector; dashed lines represent 1 SD of the mean magnitude of the resultant force vector. (D) Anterior-posterior and superior-inferior components of the peak joint contact force are overlayed on an oval representing the glenoid fossa, where the superior component of the peak resultant force for one subject with a rotator cuff tear extended beyond the boundary of the glenoid fossa.

Fig. 4:

(A) Comparison of peak resultant joint contact force location within the glenoid rim for computational models with individualized muscle forces (solid markers) and computational models using the muscle forces from the nominal model (hollow markers). (B) Simulations with the nominal model using subject-specific kinematics have peak joint contact forces located closer to the center of the glenoid rim. (C) The ratio of the superior-inferior and medial-lateral components of the peak joint contact force was calculated for simulation results with individualized models (gray bars). Mean (solid line), SD (dashed line) of cohort ratio values are shown. CM02, RF01, and RM01 had peak joint contact forces located near or outside the glenoid rim (panel A) and also had ratio values exceeding 1SD of the cohort values (hashed bars, panel B), with results from analyses with generic models (black bars, panel B) within 1SD of cohort values.

4.0. Discussion

This study evaluated the influence of muscle force distribution following RCT on glenohumeral JCF using individualized models and dynamic simulations. Simulations using individualized models predicted that the RCT group would have reduced compressive JCF components. Three participants had peak JCF forces located near the glenoid boundary for axilla wash but not functional pull. Simulations employing individualized muscle force-generating properties derived from measured muscle volume, when compared to muscle forces from a nominal model, demonstrate that distribution of muscle force at the shoulder affects force couples across the joint, influencing magnitude and location of glenohumeral JCF during functional movements. Study outcomes show that including an individual’s muscle force-generating profile in a computational model enables prediction of individualized JCF characteristics,^20,29 including changes in JCF magnitude and location with respect to the glenoid rim, which would not be ascertained using a nominal model.

Our individualized dynamic simulations predicted JCF characteristics consistent with prior experimental and computational studies. Simulation results revealed that RCT and asymptomatic control groups had peak resultant force magnitudes which were 1.9 and 2.7 times BW, respectively, for pull, and 2.0 and 2.7 times BW, respectively, for axilla wash. These findings are consistent with Anglin et al.,³⁵ who calculated peak joint force magnitudes of 1.3–2.4 times BW for several upper limb tasks in healthy older individuals. In vivo studies with instrumented shoulder implants^36,37 also reported shoulder loads exceeding BW (up to 1.32 times BW) during basic upper limb tasks. The overall reduced load seen for the RCT group is primarily driven by a reduced compressive component of resultant JCF, likely a consequence of reduced muscle volume crossing the shoulder and lack of supraspinatus force contribution (supraspinatus removed for RCT participants’ models).¹² Although RCT group participants sought treatment for shoulder pain symptoms, the results presented here have minimized the influence of pain, as only pain-free joint kinematics for axilla wash and functional pull were evaluated. Therefore, it is more likely that our results represent muscular contributions and associated joint loading scenarios, rather than a pain artifact. The current results also corroborate previous studies on cadavers, whereby isolated supraspinatus tear does not alter the transverse force couple components, which includes the subscapularis muscle anteriorly and the infraspinatus and teres minor muscles posteriorly.³² Specifically, our simulation results did not identify peak JCF vectors near or outside the glenoid rim in the anterior-posterior direction, which would indicate transverse force couple alterations, but rather the superior-inferior direction, which is in accordance with the supraspinatus force contribution. Functional pull results are also consistent with a computational study of static posture (79° elevation plane, 46° elevation, 31° external rotation, 90° elbow flexion),⁷ in which isolated supraspinatus removal did not result in altered JCF or induce instability.

Muscle force changes associated with RCT collectively influence kinematic performance of functional tasks, distribution of muscle force across the glenohumeral joint, and JCF during task performance. Prior work⁸ with this cohort demonstrated that these RCT participants have altered their movement kinematics to successfully complete a task, even if these compensations alter joint loads in a way that could lead to secondary development of further joint damage.¹⁴ However, altered kinematics alone may not represent the largest contributor to joint degeneration often observed in RCT patients. We performed repeated simulations for axilla wash using subject-derived kinematics and the nominal model, which predicted JCF locations near the center of the glenoid surface. These results suggest that self-selected kinematics during functional tasks are not the only factor contributing to alterations in JCF characteristics, and that muscle force is an important factor.

Distribution of muscle forces across the glenohumeral joint influences joint loading characteristics, which may lead to development of joint damage in the RCT population. Previous work¹¹ demonstrates that both upper limb strength and muscle volume are reduced by 30% in healthy older adults compared to a healthy young cohort,^9,30 with strength reductions of 45% at the shoulder. A RCT has been shown to further compound shoulder muscle strength deficits.¹² RCTs are associated with muscular atrophy and weakness, which affect joint stability by reducing compression at the glenohumeral joint.^3,4,31–34 Results of the current study are in accordance with this premise, as dynamic simulations revealed that RCT participants had lower peak resultant and compressive components of JCF than controls. The diminished compressive force identified for the RCT group could lead to superior humeral head migration and less anterior-posterior stability.^3,4 Previous work with both a computational model and cadaveric specimens demonstrated that joint posture and individual muscle forces can influence joint stability,³¹ although these authors focused on the influence of infraspinatus and pectoralis major muscles in their perturbation assessment. Further, repeated simulations using the nominal model demonstrate that changes to muscle force distribution across the glenohumeral joint can affect JCF characteristics during functional upper limb tasks (cf. Fig. 4, Table 2), and may contribute to altered loading that could lead to reduced stability or increased risk for secondary problems, like humeral head translation or subacromial impingement.⁴ The authors caution against direct extrapolation of simulation results for diagnosing specific pathologies in individual patients, due to isolated changes of muscle forces in the models and estimation of the glenoid boundary as an ellipse rather than its intrinsic “pear shape” dimensions in vivo. Nevertheless, our results demonstrate that important relationships among changes in JCF from changes to muscle force across the glenohumeral joint can be ascertained.

There are some aspects of our models that could be improved in future studies. The current model represents the glenohumeral joint as a ball-and-socket joint, permitting rotation but not translation. Future work should directly evaluate humeral head translation^38–42 and its effect on joint loading during functional upper limb movements. Generalized descriptions of translation for inclusion in a model are currently unavailable, although they are the target of ongoing research.^38,41 Due to the clinical population studied, joint stability cannot be assumed; thus, mathematical constraints to enforce glenohumeral joint stability were not implemented. The current model does include stiffness constraints at end ranges of rotational motion representing contributions from ligamentous tissues that contribute to joint stability. Model peak muscle forces were scaled from subject-derived muscle volume measures, although only shoulder muscle forces were individualized. To isolate effects of muscle force variation on predicted JCF, a nominal model representing 50^th percentile male/female was used. Future models could include descriptions of participant limb mass and mass distribution. Models were scaled using muscle volume because pain was elicited during some strength assessments for some participants with RCT (see¹² for strength data), potentially limiting their ability to maximally activate the muscle. While pain is a primary concern for RCT patients, we have indirectly accounted for pain in this study by using pain-free subject-derived kinematics to drive dynamic simulations, thereby preventing painful postures in modeling simulations.

There are limitations that should be considered when evaluating study results. This study included a small sample of participants with full- and partial-thickness tears on dominant and non-dominant sides. Tear characteristics may have affected self-selected kinematics and recorded muscle volume measures. However, despite the sample size and participant characteristics, differences between groups were observed. Ongoing work should include a larger, homogenous sample to more fully characterize the influence of functional movement and muscle force on glenohumeral joint force predictions. One subject was excluded from axilla wash analyses due to poor tracking of recorded kinematics by the CMC algorithm. This subject’s kinematics included high velocity in elevation plane with relatively smaller angles in shoulder rotation and shoulder elevation. This resulted in a combination of joint angles with aligned or nearly aligned joint rotation axes (i.e. gimbal lock⁴³), which was challenging for the CMC algorithm to track (cf. Supplemental Fig. 1). Nevertheless, high accuracy in CMC’s kinematics tracking was observed in all other simulations (0.98° for functional pull; 1.75° for axilla wash), consistent with reported peak RMS error of 1.5° from studies of running in OpenSim.⁴⁴ In this work, we modeled a full-thickness supraspinatus tear by completely removing this muscle actuator from the model because it is unknown how muscle force production changes with increased tendon tear size. While some patients were diagnosed with a high grade partial-thickness tear, supraspinatus was removed from all RCT models for consistency. Thus, these results represent a simplified and possible worst-case scenario through complete removal of supraspinatus. Additionally, these results do not imply whether joint dislocation will occur, as other joint structures (e.g. glenoid labrum, glenoid fossa geometry) influence the dislocating effect of resultant JCFs. Despite this limitation, predictive information regarding the influence and characterization of muscle force distribution on magnitude and location of glenohumeral JCF can be achieved. Conversely, some patients had tears extending into the infraspinatus or subscapularis tendons, although none were full-width. Since demarcation of supraspinatus-infraspinatus tendon intersection is not immediately clear due to tendon fiber overlap,⁴⁵ infraspinatus and subscapularis were left intact in all models because it is likely that forces could still be transmitted to the humerus. Even following a tear, the interconnected nature of rotator cuff tendons may permit epimuscular force transmission,⁴⁶ enabling muscle force conduction via surrounding connective tissue.⁴⁷ Including epimuscular forces in models may improve their performance when representing individual patients. Similarly, measuring muscle activity with electromyography can inform individual muscles’ roles in ADL performance. While electromyography was not measured in this study, future studies should include these measurements. Finally, this work evaluated a group of asymptomatic controls as a reference group. While controls were screened using manual assessments, imaging confirmation was not available here. Asymptomatic RCTs are common in the older adult population^1,48 and future studies should include ultrasound or MR imaging to confirm absence of an asymptomatic tear.

5.0. Conclusions

We conclude that individual muscle force distribution across the glenohumeral joint can influence JCF predictions. Specifically, these RCT participants demonstrated reduced peak resultant JCF and compressive components at the glenohumeral joint. Subject-derived muscle force-generating properties may be an important addition to computational models that can inform whether JCF predictions are located within the glenoid or to assess risk of instability or subsequent injury following a RCT. The reduced glenohumeral JCF identified here may suggest an increased risk for developing subsequent joint injury due to lower glenohumeral joint stability during functional upper limb movement.

Highlights.

• Rotator cuff tears result in reduced compression and peak joint contact force

• Rotator cuff muscle distribution affects glenohumeral joint contact force

• Joint contact forces after rotator cuff tear may increase secondary injury risk

• Individualized computational models enable more relevant joint force predictions