Habitat choice meets thermal specialization: Competition with specialists may drive suboptimal habitat preferences in generalists

Significance

In contrast to the classically expected coupling between ecological specialization and low dispersal propensity, theory predicts that dispersal with habitat choice (i.e., individuals that choose habitats maximizing their performance) should evolve in specialists, while generalists should disperse more randomly. Here, we show in ciliate microcosms that thermal specialists indeed prefer optimal habitats, whereas surprisingly, generalists also perform habitat choice but with a preference for suboptimal habitats. To tackle the question of why generalists should prefer suboptimal habitats, we developed a metapopulation model and showed that competition between generalists and specialists may favor a preference for niche margins in generalists under environmental variability. Our results point out the importance of dispersal strategies for ecological and evolutionary dynamics.

Abstract

Limited dispersal is classically considered as a prerequisite for ecological specialization to evolve, such that generalists are expected to show greater dispersal propensity compared with specialists. However, when individuals choose habitats that maximize their performance instead of dispersing randomly, theory predicts dispersal with habitat choice to evolve in specialists, while generalists should disperse more randomly. We tested whether habitat choice is associated with thermal niche specialization using microcosms of the ciliate Tetrahymena thermophila, a species that performs active dispersal. We found that thermal specialists preferred optimal habitats as predicted by theory, a link that should make specialists more likely to track suitable conditions under environmental changes than expected under the random dispersal assumption. Surprisingly, generalists also performed habitat choice but with a preference for suboptimal habitats. Since this result challenges current theory, we developed a metapopulation model to understand under which circumstances such a preference for suboptimal habitats should evolve. We showed that competition between generalists and specialists may favor a preference for niche margins in generalists under environmental variability. Our results demonstrate that the behavioral dimension of dispersal—here, habitat choice—fundamentally alters our predictions of how dispersal evolve with niche specialization, making dispersal behaviors crucial for ecological forecasting facing environmental changes.

Dispersal and ecological specialization are widely accepted as important drivers of population and species responses to environmental changes (1–9). Ecological specialization favors local adaptation and thus, diversification (10–12), and it can play an important role in species tolerance to environmental changes (6, 13, 14). Limited dispersal propensity is also classically considered as a prerequisite for ecological specialization to evolve (2, 6, 12, 15–17). Generalists are thus expected to show greater dispersal propensity compared with specialists (2, 6, 12, 15–17). This coupling between specialization and low dispersal can arise, because dispersal may hinder local adaptation and thus, the evolution of specialization (18–20) or because generalists are more likely to find suitable habitats after dispersal than specialists and should thus evolve higher dispersal propensity (12, 15–17). Accordingly, recent studies found that generalists show greater dispersal propensity compared with specialists across animals (21, 22). In the context of current global changes, the more generalist organisms are thus generally predicted to show a higher ability to shift their range distributions owing to a greater dispersal propensity coupled with a tolerance of a broader range of environments (2, 4, 6, 14, 21, 23, 24).

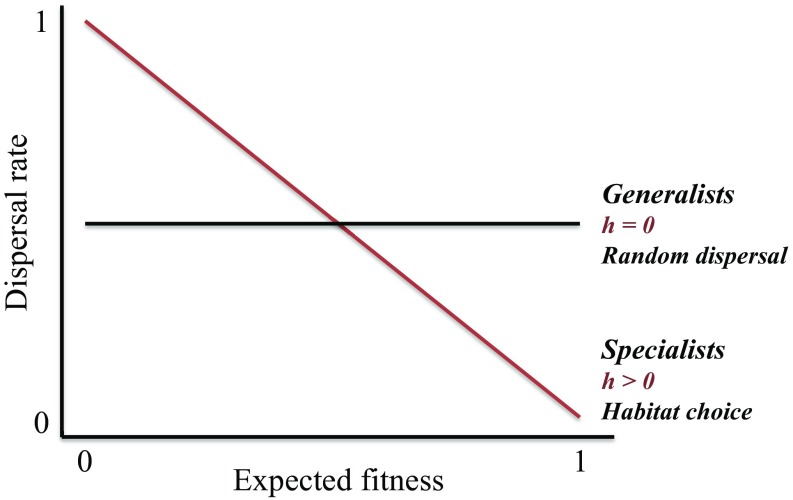
However, current theories predicting a coupling between ecological specialization and low dispersal propensity assume dispersal to be random, an assumption that contrasts with the accumulating evidence for nonrandom dispersal (7, 9, 25, 26). Instead of dispersing randomly, individuals may indeed modify their dispersal decisions depending on the environmental context to selectively stay in or disperse toward habitats that maximize their performance (27–30). This process, named habitat choice, is predicted to break the coupling of specialization and limited dispersal predicted by classical theory: specialists should not evolve low dispersal propensity as expected but rather, should modify their dispersal decisions depending on the environmental context to preferentially live in habitats that they are specialized for (Fig. 1) (27–29, 31). Indeed, habitat choice should allow individuals to live preferentially in optimal habitats and thus, reduce movements toward suboptimal ones (e.g., the margin of the niche) (30–33). Habitat choice should, therefore, favor niche conservatism by decreasing exposure to selection of new mutations potentially favoring fitness at the margin of the species’ niche (27, 31, 32, 34, 35). Such context-dependent dispersal in specialists should improve their ability to track suitable environmental conditions facing environmental changes (2, 6, 12, 14–17). However, we still lack empirical investigation of this predicted link between habitat choice and ecological specialization, with specialists adjusting dispersal decisions to the environmental context, while generalists perform random dispersal.

Fig. 1.

Predictions for the relationship between dispersal decisions and expected fitness illustrated for dispersal at emigration (i.e., decision to stay or leave the local habitat depending on local expected fitness). Specialists should modify their dispersal decisions depending on the environmental context to preferentially live in habitats that they are specialized for (i.e., habitat choice h > 0), while generalists should disperse randomly (h = 0).

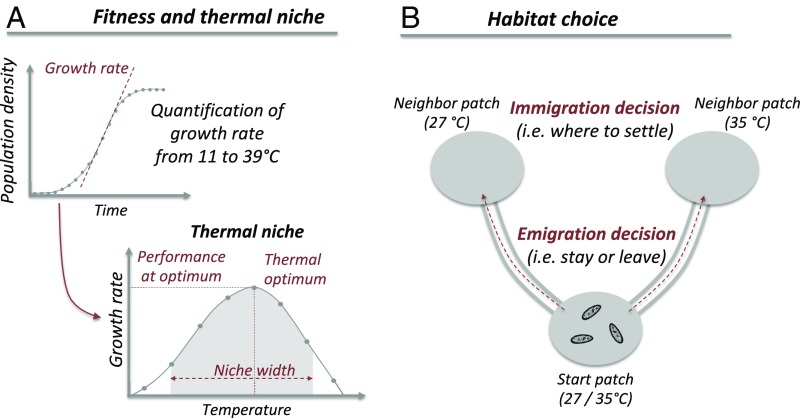
Here, we tested this predicted relationship between specialization and habitat choice using microcosms, an approach that has proven powerful for experimentally addressing key questions in ecology and evolution (36, 37). We used Tetrahymena thermophila, a ciliate naturally living in freshwater ponds under spatiotemporal thermal variability. A recent study showed that this species can adjust dispersal decisions depending on temperature (i.e., temperature-dependent habitat choice) and demonstrated that dispersal with habitat choice can favor rather than hinder local adaptation (30). Given the importance of temperature-related dispersal and thermal niche specialization in the context of current climate change (3, 6, 38), we crucially need to quantify variability in habitat choice and how it covaries with niche specialization. To do so, we quantified thermal specialization (i.e., niche width) and temperature-dependent habitat choice separately for each of 12 clonally reproducing genotypes of T. thermophila (Fig. 2). We used dispersal systems in which patches differed in their temperature (Methods) to quantify habitat choice as the ability to adjust dispersal depending on expected fitness (i.e., growth rate): that is, the fitness that a genotype would reach if choosing a given temperature. Since dispersal decisions can occur at different steps of the dispersal process (25, 29, 39), we quantified habitat choice at both emigration (whether to leave the local temperature) and immigration (where to settle).

Fig. 2.

Experimental design to (A) measure thermal niche of genotypes and their expected fitness in the tested temperatures and (B) quantify temperature-dependent habitat choice at emigration and immigration. (A) The fitness of each genotype along a thermal gradient (11 °C to 39 °C) was quantified to reconstruct its thermal niche (SI Appendix, Fig. S1). From these thermal niches, we quantified the expected fitness $\overline{f}$ at each focal environmental condition (e.g., 35 °C expected fitness: growth rate at 35 °C relative to performance at optimum) (Methods). (B) Genotypes were initially inoculated in the central patch of three-patch systems (start patch and temperature set at either 27 °C or 35 °C) connected to one 27 °C patch and one 35 °C patch. Genotypes were thus allowed to choose their habitat at emigration (stay or leave the start patch) and immigration (where to settle). T. thermophila silhouette was obtained from Phylopic.org.

Based on current theory, we predicted that habitat choice ability should increase with niche specialization, while more generalist genotypes should disperse more randomly (Fig. 1). Surprisingly, we found that, although the more specialist genotypes showed the expected habitat choice behavior, generalists also performed habitat choice and preferred suboptimal habitats, although better ones were available. This finding challenges current theory that considers generalism as an alternative to habitat choice and brings up the question of why generalists would prefer suboptimal habitats. We thus constructed a metapopulation model to test the hypothesis that, under spatiotemporal variability of temperature, competitive interactions between specialists and generalists might favor the evolution of a preference for suboptimal habitats in generalists.

Results

We measured habitat choice at emigration and immigration for each genotype. Habitat choice can range from −1 to 1: h = 0 for random dispersal, h > 0 for a preference for optimal habitats, and h < 0 for a preference for suboptimal habitats (Fig. 1 and SI Appendix). We found evidence for among-genotype variability in temperature-dependent habitat choice in T. thermophila. Of the 12 genotypes tested, 11 showed significant habitat choice at emigration, and 8 showed significant habitat choice at immigration (SI Appendix, Table S2). We found that habitat choice h of the different genotypes ranged from −0.46 to 0.60 at emigration and from −0.93 to 0.95 at immigration.

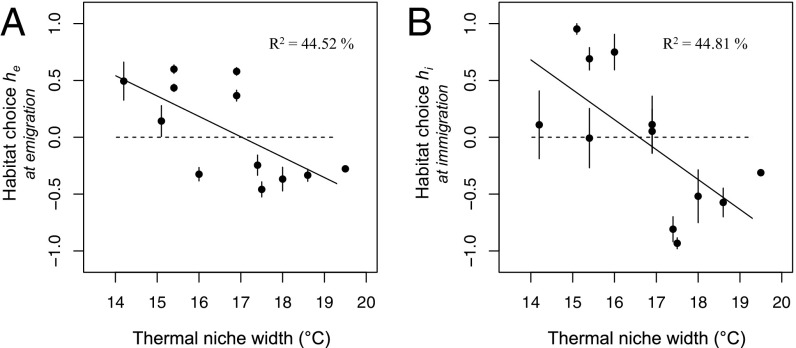
We quantified the relationship between habitat choice and niche specialization and found that habitat choice correlated negatively with niche width (emigration: estimate ± SE = −0.179 ± 0.063; t₁₁ = −2.83; P = 0.018; R² = 44.52%; immigration: −0.263 ± 0.092; t₁₁ = −2.85; P = 0.017; R² = 44.81%; 95% confidence interval with bootstrap at emigration: [−0.210; −0.099]; 95% confidence interval with bootstrap at immigration: [−0.289; −0.164]) (Methods). As predicted by theory, genotypes with the highest thermal specialization showed positive habitat choice values (Fig. 3), meaning that they preferentially stayed in or joined habitats maximizing their expected fitness. Specialists did not, on average, disperse more or less than generalists (regression of average dispersal propensity Dp_e on niche width: −0.006 ± 0.021; t₁₁ = −0.27; P = 0.79) (SI Appendix) but instead, modified their dispersal decisions depending on temperature (Fig. 1).

Fig. 3.

Habitat choice correlates with niche specialization at emigration (A) and immigration (B). Each dot represents the estimation of habitat choice h for a given genotype (mean ± SE). Thermal niche width was computed as the temperature range containing 80% of the thermal niche expressed in degrees Celsius. R² values of the regression of habitat choice over niche width are shown.

In contrast, the more generalist genotypes showed negative habitat choice (Fig. 3), meaning that they preferred to stay in or join the temperature in which their expected fitness was the lowest. Note that these suboptimal conditions still represent viable habitats for genotypes and that the quality of patches that genotypes had access to in our experiment was independent of their level of thermal specialization (Methods). Since we found that the more generalist genotypes tend to also have a cooler thermal optimum (Pearson correlation coefficient: −0.66; t₁₁ = −2.78; P = 0.02; no significant correlation with performance at optimum: −0.38; t₁₁ = −1.32; P = 0.22), we applied variance-partitioning analyses to determine if thermal specialization or thermal optimum drove variance in habitat choice. We found that thermal specialization is the main contributor to the variance in habitat choice at emigration and that 11.5% of variance at immigration is explained by thermal specialization itself, while 33.3% is commonly explained by thermal specialization and thermal optimum (SI Appendix, Table S3).

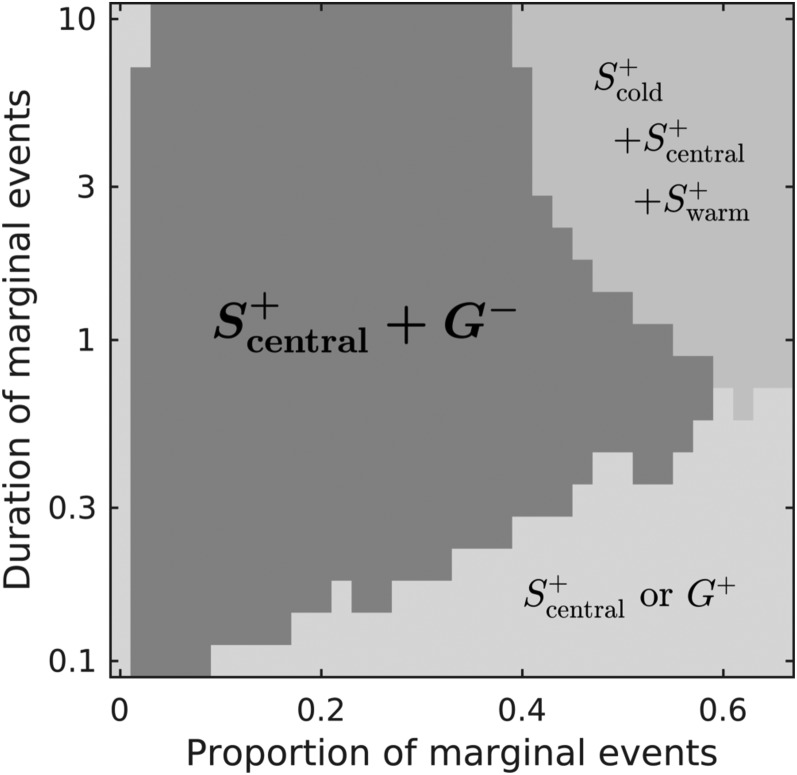
Since we found that generalists performed habitat choice and preferred suboptimal habitats in our experiment instead of dispersing randomly as theoretically predicted, we constructed a simple metapopulation model to explore the conditions under which such a strategy could be favored. Specifically, we hypothesized that competitive interactions between generalists and specialists might favor a preference for fundamentally suboptimal habitats in generalists. Providing that the metapopulation faces spatiotemporal variability of thermal conditions, we found that generalists with a preference for suboptimal habitats can coexist with specialists of the central temperature that prefer their optimal temperature. Specifically, this coexistence occurs when the proportion of marginal temperatures (i.e., p_m, the proportion of time during which the temperature is marginal) is below 50% (except for very low durations of marginal temperatures; i.e., very small t_m) (Fig. 4). When the proportion of marginal temperatures increases, either a single generalist or three specialists (for cold, central, and warm conditions) are favored (for low and high duration of marginal temperatures conditions t_m, respectively), and in all cases, they show positive habitat choice (i.e., preference for optimal habitat). When the proportion of marginal temperatures is too low, a specialist for the central temperature excludes all other strategies (Fig. 4).

Fig. 4.

Habitat choice strategies and coexistence of specialists and generalists depend on the proportion and duration of marginal conditions (p_m and t_m, respectively) (SI Appendix, Fig. S2 has an illustration of the spatiotemporal variability implemented). The duration of marginal conditions t_m is expressed relative to generation time (e.g., marginal conditions last for one generation when t_m = 1). S and G refer to specialists and generalists, respectively. S_central, S_cold, and S_warm refer to specialist of the central patch, cold margin, and warm margin, respectively; + and − denote positive and negative habitat choice, respectively. The dark gray area illustrates the parameter space where a generalist with negative habitat choice (h = −1; G⁻) can coexist with a specialist with positive habitat choice (h = 1; S_central⁺) (relative abundance and degree of specialization are in SI Appendix, Fig. S4). In the lower right region, only one strategy with positive habitat choice is favored, with specialization level that decreases when the proportion of marginal events increases (i.e., S_central⁺ toward G⁺ when p_m increase). This means that, although always showing a preference for the central temperature, there is a smooth transition in this region from a specialist toward a generalist. Increasing p_m values above 0.7 expands the two regions on the right of the graph: either a single generalist (for low duration of marginal events t_m) or specialists with positive habitat choice are favored (for higher t_m).

Discussion

Classical theory predicts low dispersal propensity to evolve together with ecological specialism (2, 12, 15–17). However, several studies have predicted that specialists should not evolve limited dispersal propensity but instead, evolve efficient prospecting skills, allowing individuals to preferentially find and live in specific habitats that they are specialized for (27, 31, 33–35). Using a microcosm approach, we showed that habitat choice correlates with thermal niche specialization. Genotypes with the greatest thermal specialization performed habitat choice, preferring to stay in or join optimal habitats. This result provides empirical demonstration that ecological specialists perform habitat choice, a link that should make specialists more likely to track suitable conditions under environmental changes than expected under the random dispersal assumption (2, 6, 12, 14–17).

On the other side of the thermal specialization gradient, we found that the more generalist genotypes also performed habitat choice but with a preference for suboptimal habitats. This habitat choice strategy is in opposition to current theory that typically considers generalism as an alternative to habitat choice (40–43). Furthermore, choosing suboptimal habitats when better ones are available seems unlikely to evolve: all individuals should prefer better habitats, especially if dispersal incurs costs or in the absence of competition with specialists.

Our results thus bring up the question of why generalists should evolve a preference for suboptimal habitats. Habitat choice has been previously suggested to favor specialist–generalist coexistence in source–sink systems (44), but whether generalists actively preferring suboptimal habitats can be favored is still unexplored. A key point in our experiment is that the quality of habitats was quantified relative to each genotype’s fundamental niche (i.e., without competition among genotypes and everything other than temperature kept constant). Although generalists are by definition able to deal with a larger range of environmental conditions, specialists usually achieve greater efficiency at their ecological optimum and hence, should exclude generalists from their optimal habitats (45). Competitive interactions should thus lead to major differences between the fundamental and realized niche of generalists as illustrated by numerous theoretical and experimental studies that provide evidence for competitive exclusion of generalists by specialists (12, 35, 45, 46). A generalist competing with a specialist sharing a similar niche optimum should thus achieve higher realized fitness in fundamentally suboptimal habitats (45, 47, 48), which may favor a preference for niche margins in generalists.

The results of our model support this hypothesis: generalists with a preference for suboptimal habitats can be favored and coexist with specialists. Importantly, our model revealed that environmental variability is crucial for generalists with a preference for suboptimal habitats to be favored. While specialists of niche margins can persist only when the proportion of marginal conditions is high (Fig. 4), a reduced proportion of marginal temperature events, as often found in natural systems (49, 50), favors generalists with a preference for suboptimal habitats coexisting with specialists with a preference for optimal habitats (Fig. 4). A preference for suboptimal habitats in generalists should favor the spatial segregation of specialists and generalists and thus, the likelihood of specialist–generalist coexistence in metapopulations and metacommunities, pointing out the importance of dispersal strategies in community assemblage and dynamics (29, 44, 51, 52).

Genotypes were isolated in our experiments, yet the more generalist genotypes still preferred suboptimal habitats, despite the absence of competition with more specialized genotypes. This suggests that generalists might choose habitats depending on temperature, preferring suboptimal temperatures where they are unlikely to compete with specialists (53, 54), instead of directly relying on the presence of specialist competitors to plastically adjust their habitat choice. Obtaining information about temperature in a potential habitat might indeed be easier or more reliable than quantifying the degree of specialism of competitors. More generally, identifying the mechanisms and drivers of dispersal decisions is an important step forward (55). In this study, we showed that dispersal decisions vary depending on local and neighboring temperature, an information use process that might involve, for instance, prospecting or social information (56–59). Note that habitat choice here rarely approaches −1 or 1 (SI Appendix, Table S2). Such imperfect decisions are expected, since information available about local and neighboring environmental conditions is usually limited and because performing informed dispersal decision usually involves costs (29, 39, 41, 60). Furthermore, dispersal decisions might involve different cues about the environment or the fitness that an organism can reach. Here, we found that the expected rate of reproduction (i.e., growth rate) and the expected size of the resulting populations (maximal density) are two correlated components of fitness that may underlie habitat choice decisions. Finally, additional effort should be devoted to the study of the occurrence of generalist habitat choice and the identification of the environmental conditions where such a strategy can be favored. Indeed, the consequences of habitat choice strategies for populations and community dynamics under environmental changes are expected to differ depending on whether generalists disperse randomly, show fixed habitat preferences, or adjust their habitat choice to the presence and abundance of specialists (29, 61).

Our understanding and ability to forecast population and community responses to environmental changes are among the main current challenges in ecology and evolutionary research. Critical to tackle these challenges is a deep understanding of the variability in life history strategies as pointed out by numerous recent studies (1, 4–6, 38, 62–64). In particular, dispersal strategies and other associated life history traits, like niche specialization, can profoundly affect ecological and evolutionary dynamics, such as community assembly, species range shifts, and adaptation in the face of environmental changes (3, 6, 7, 29, 30, 38). Our experimental results using a microcosm system challenge the idea that specialists usually evolve reduced dispersal compared with generalists, pointing out the importance of the behavioral rules underlying dispersal movement for biodiversity response to current environmental changes (3, 7, 30).

Methods

Culture Conditions and Genotypes.

T. thermophila is a 30- to 50-μm unicellular eukaryote, a ciliated protozoa naturally living in freshwater ponds and streams in North America and used as a model organism in cell and molecular biology (65). Here, we used 12 isolated clonal genotypes originally sampled by F. P. Doerder in different locations in North America (SI Appendix, Table S1) (66). In contrast to a previous study where genotypes were mixed to test whether habitat choice favors local adaptation compared with random dispersal (30), here genotypes were kept isolated to quantify among genotype variability in habitat choice, niche specialization, and how they covary. Cells were maintained in axenic-rich liquid growth media (0.6% Difco proteose peptone, 0.06% yeast extract) at 23 °C. All manipulations were performed in sterile conditions under a laminar flow hood.

Thermal Niche.

To reconstruct the thermal niche of each genotype, we quantified population growth rate along a thermal gradient (from 11 °C to 39 °C) as our proxy of fitness. To do so, small numbers of cells (∼100) from a single genotype were transferred to 96-well plates (250-μL wells) filled with growth media, with five replicates per genotype. These cultures were maintained at 11 °C, 19 °C, 23 °C, 27 °C, 31 °C, 35 °C, and 39 °C, and population growth was quantified through absorbance measurements at 550 nm twice a day until the populations reached their carrying capacity (from about 10 d at 39 °C to 3 wk at 11 °C) using a microplate reader (Synergy H1; BioTek). Absorbance, as classically used in cell culture research, is significantly and linearly correlated with cell density within the range of densities observed under our laboratory conditions (30, 67). After smoothing growth curves using a general additive model [gam; using the gam R-package (68)] to avoid any bias due to slight technical variability in absorbance measures, we computed the growth rate as the maximum slope of population growth for each genotype at each temperature using the gcfit function (grofit R-package) with spline fit (30).

We inferred the thermal niche of each genotype from the relationship observed between growth rate and temperature fitted by a gam (Fig. 2A), a nonparametric statistical model commonly used in ecological niche modeling that does not require any assumption regarding the shape of the curve (69); gam was fitted using local cubic splines with four degrees of freedom for smoothness [a value considered flexible enough to model response curves in biology without over fitting (69)] and a Gaussian error distribution. We then computed three niche parameters for each genotype from these curves (Fig. 2A): (i) niche width (i.e., a proxy for thermal specialization) was computed as the temperature range containing 80% of the thermal niche [i.e., 80% of the area under the curve (70); 70 and 90% temperature ranges led to similar results: niche width computed with 80% temperature range compared to 70%: Pearson correlation = 0.989; compared to 90%: correlation = 0.992]; (ii) thermal optimum, the temperature at maximal growth rate; and (iii) performance at optimum, the growth rate at thermal optimum (SI Appendix, Fig. S1 has an illustration of genotypes’ thermal niches).

Dispersal and Habitat Choice.

To quantify habitat choice for each genotype, we used dispersal systems consisting of three linearly connected patches (Fig. 2B) (5-mL standard Eppendorf tubes) connected by corridors (4-mm-internal diameter silicon tube; 5 cm long) and filled with growth media (30, 71). Patches are, therefore, separated by ∼2,500 times the size of T. thermophila cells, and we previously demonstrated that dispersal among patches in these microcosms influences local adaptation by generating gene flow among patches and affecting population differentiation (30). Isolated genotypes were separately inoculated in the central patch of the three-patch systems at standard density (start patch temperature set at either 27 °C or 35 °C; five replicates for each start patch temperature; ∼40,000 cells), connected to one 27 °C patch and one 35 °C patch, defined to maximize fitness differences between the tested temperatures. To quantify dispersal decisions without introducing variability due to density-dependent dispersal, dispersal systems were inoculated with a standardized population size of ∼40,000 cells. Since the fitness associated with the two environmental conditions differs among genotypes, we quantified for each genotype the expected fitness $\overline{f}\left(T\right)$ in these two conditions as the growth rate relative to the performance at optimum as identified in the thermal niche quantification (see above): $\overline{f}\left(T\right)=f\left(T\right)/f_{Topt}$ (Fig. 2A).

The expected fitness of genotypes in the better of the two temperatures varies between 0.42 and 0.93 (mean ± SE = 0.73 ± 0.04), and in the suboptimal temperature, it varies between 0.21 and 0.56 (0.45 ± 0.03). Importantly, the quality of patches that genotypes had access to in our experiment was independent from their thermal specialization: the expected fitness in these two environmental conditions did not significantly correlate with thermal niche width (relationship between thermal niche width and expected fitness in a genotype’s most optimal patch: estimate ± SE = 0.042 ± 0.026; t = 1.591; P = 0.143; in suboptimal temperature: 0.013 ± 0.021; t = 0.613; P = 0.554).

Temperature in patches was manipulated using dry bath systems (H2O3 Dry Bath Incubator; Coyote Bioscience) placed in incubators. Genotypes were allowed to disperse and thus, to choose their habitat at emigration (stay or leave the start patch) and immigration (where to settle) (Fig. 2B) (29). Following previous experiments (58, 59), we chose to let cells disperse for 6 h. This species shows a latency time before growth initiation [at 27 °C: mean ± SE = 17.34 ± 1.80 h; at 35 °C: 9.97 ± 2.49 h (66)], meaning that population growth is negligible during the 6 h of dispersal assay and thus, does not affect estimates of dispersal rates as previously shown (58).

To compute the emigration rate (proportion of cells that dispersed from the central patch) and the immigration rate (proportion of the dispersers that joined each neighboring patch; see below), we used a standardized procedure to quantify cell densities in patches: from each culture, we measured five samples (10 μL each) pipetted into counting slides (Kima precision cell) and took digital pictures under dark-field microscopy (30, 56, 58, 71–74). Cell density in cultures was measured based on an automatic analysis of pictures using IMAGEJ software (version 1.47; NIH; https://imagej.nih.gov/ij) (73).

To quantify habitat choice at emigration and immigration for each genotype, we then quantified the relationship between dispersal decisions (emigration and immigration rates) and the expected fitness in each habitat (two values of growth rate per genotype corresponding to the two temperatures tested: 27 °C and 35 °C; see above). This means that habitat choice describes how dispersal rate varies depending on the fitness that a genotype would reach if choosing a given temperature (Fig. 1). To do so, we fitted a simple model in which dispersal rates depend on expected fitness $\overline{f}$ and habitat choice (h_e at emigration, h_i at immigration) (SI Appendix). This method allows for quantifying standardized habitat choice parameters between −1 and 1 and yields results that are highly correlated with simple regression estimates (SI Appendix). We expected no relationship between dispersal and expected fitness under random dispersal (h = 0) (Fig. 1), a positive relationship for habitat choice with a preference to either stay in or join optimal habitats (h > 0), and a negative relationship when habitat choice consists of preferentially staying or joining suboptimal habitats (h < 0) (Fig. 1) (29). Finally, the proxy of fitness used here (i.e., growth rate) is significantly correlated to another important characteristic of population growth, which is maximal density (i.e., carrying capacity; at 27 °C: 0.85; t₁₀ = 5.13; P < 0.001; at 35 °C: 0.98; t₁₀ = 15.98; P < 0.001). Growth rate and maximal density are two components of fitness that both might underlie dispersal decisions, and we found that estimates of habitat choice based on maximal density as a measure of expected fitness are significantly correlated to those based on growth rate (at emigration h_e: 0.79; t₁₀ = 4.02; P = 0.002; at immigration h_i: 0.57; t₁₀ = 2.17; P = 0.054).

Statistical Analyses.

We tested for a link between habitat choice and thermal niche width using linear models (lm, stats R-package), with habitat choice ability h as the dependent variable and thermal niche width as the explanatory variable. Model residuals followed a normal distribution in all cases. To account for the variance in the estimation of thermal niche parameters (i.e., niche width, thermal optimum, and performance at optimum), we computed bootstrap confidence intervals of the slope of the relationship between habitat choice and niche width by bootstrapping 1,000 times the growth rate values along the thermal gradient and quantifying habitat choice h and thermal niche width for each bootstrap sampling. Finally, analyses with linear models were followed by variance partitioning analyses (regr function, yhat R-package) (75, 76) to account for the correlation between thermal specialization and thermal optimum (Results).

Model

We constructed a simple metapopulation model to explore the conditions under which generalists with a preference for fundamentally suboptimal habitats can be favored. Individuals differing in their degree of specialization, thermal optimum, and habitat choice (hereafter called “strategies”) compete in metapopulations consisting in three fully connected patches.

Environmental Variability.

Because we expected environmental variability to determine the strategies that are favored, we modeled metapopulation dynamics with each patch subjected to local temperature conditions that can change between patches and over time (i.e., spatiotemporal variability). We assumed that temperature T can take three values: a cold T₁, a central T₂, and a warm temperature T₃. Temperature in each patch switches between the three values T₁, T₂, and T₃ sequentially (i.e., T₁, T₂, T₃, T₂, T₁, etc.). Each temperature variability profile is characterized by two parameters: the proportion of time p_m during which the temperature is marginal (i.e., T₁ or T₃), and the duration t_m of these periods of marginal conditions (49, 50). Spatiotemporal variability profiles with different proportion and duration of periods of marginal conditions are illustrated in SI Appendix, Fig. S2.

Population Dynamics.

The dynamics of abundance N_ik of strategy i in patch k are given by the differential equation:

$$\frac{d{N}_{ik}}{dt}=r_{ik}{N}_{ik}\left(1-\frac{{{\displaystyle \sum }}_j{N}_{jk}}{K_{ik}}\right)+{\displaystyle \sum _{l\ne k}}{d}_{ilk}{N}_{il}-{\displaystyle \sum _{l\ne k}}{d}_{ikl}{N}_{ik}.$$

The first term on the right-hand side corresponds to local population growth in patch k, with r_ik indicating the intrinsic growth rate of strategy i in patch k, K_ik indicating the carrying capacity, and N_ik and N_jk indicating the local population sizes of strategies i and j, respectively. The second term corresponds to immigration from patches l, and the third term corresponds to emigration to patches l, with d_ilk indicating the dispersal rate of strategy i from patch l to patch k and N_il indicating the neighboring patch population size of strategy i.

As in the analysis of the experimental data, we used the maximal slope of the growth curve as our proxy of fitness. For the logistic growth of the model, this implies that fitness f_ik of strategy i in patch k should be proportional to the product of r_ik and K_ik. Because intrinsic growth rate r and carrying capacity K are significantly correlated in the experimental system (Pearson correlation coefficient for growth at 27 °C: 0.85; t₁₀ = 5.13; P < 0.001; growth at 35 °C: 0.98; t₁₀ = 15.98; P < 0.001), we assumed a similar dependence of r_ik and K_ik on f_ik (i.e., $r_{ik}=r_0\sqrt{f_{ik}}$ and $K_{ik}=K_0\sqrt{f_{ik}}$).

Denoting the fitness of strategy i at temperature T by f_i(T), the fitness of strategy i in patch k is equal to f_ik = f_i(T_k), where T_k is the temperature of patch k. This means that the fitness f_ik (i.e., growth rate) of a strategy i changes through time according to changes in local temperature. To mirror the analyses performed on experimental data, we defined the expected fitness, taking values between zero and one, as the fitness of strategy i in patch k relative to fitness at thermal optimum ${\overline{f}}_{ik}=f_{ik}/f_{\left(Topt\right)}$.

Habitat Choice.

To model habitat choice, we let dispersal rate d_ikl depend on the expected fitness of strategy i:

$$d_{ikl}=d_0\left(1+h_i\left({\overline{f}}_{il}-{\overline{f}}_{ik}\right)\right),$$

with h_i indicating the habitat choice parameter of strategy i and d₀ indicating a reference dispersal rate. We used expected fitness [fitness relative to fitness at thermal optimum f_(Topt)] in the dispersal rate d_ikl to not artificially limit the habitat choice potential of generalists, for which the absolute fitness difference f_il − f_ik is typically small. Habitat choice parameter h_i is between −1 and 1 (h = 0 for random dispersal, in which case d_ikl = d₀; h > 0 for preference for optimal habitats; h < 0 for a preference for suboptimal habitats). Note that we modeled habitat choice as a one-step process, with the decision to leave a patch and join another depending on the expected fitness difference between the local and neighboring patches. This assumption is coherent with the consistency of habitat preferences found between emigration and immigration (SI Appendix, Table S2).

Niche Specialization.

Each strategy i has a thermal niche, which is characterized by a thermal optimum (3i.e., the temperature at which fitness is maximal; here, T₁, T₂, or T₃) and a degree of specialization s_i determining the fitness difference between the optimal habitat and the other temperatures (SI Appendix, Fig. S3). Specialization s_i is a number between zero (perfect generalist) and one (perfect specialist). The relationship between fitness and temperature furthermore satisfies a specialist–generalist tradeoff${\displaystyle {\sum }_T{f}_i{\left(T\right)}^{\frac{1}{\alpha }}=1}$. Temperature T runs over the three temperatures (cold, central, warm), and α is the tradeoff strength (40, 77) (here, α = 0.7). Competing strategies, therefore, differ in their degree of specialization s_i and thermal optimum as illustrated in SI Appendix, Fig. S3.

To specify the model, we fixed the overall model parameters (that is, r₀, K₀, d₀, and α) and for each strategy I, its degree of specialization s_i and its habitat choice parameter h_i (SI Appendix). We set r₀ equal to one, so that all times are expressed in units of reference generation times, and K₀ equal to one, so that all population sizes are expressed in units of reference carrying capacities. Reference dispersal rate d₀ was fixed to one; the specialist–generalist tradeoff strength α was 0.7. We verified that qualitatively similar results were obtained for other values of parameters d₀ and α (SI Appendix, Fig. S5).

The model dynamics were simulated starting from randomly generated initial conditions until reaching a stationary regime. We repeated this simulation procedure for a range of environmental variability parameters p_m and t_m (within [0; 0.7] and [0.1; 10], respectively).