Acoustic phonon lifetimes limit thermal transport in methylammonium lead iodide

Significance

Hybrid organic–inorganic perovskites are a promising class of materials for efficient and low-cost solar cells. Unlike conventional inorganic semiconductors such as silicon and gallium arsenide, hybrid perovskites feature significant dynamic disorder in their crystal structure. This dynamic disorder can be broadly classified into lattice vibrations (phonons) and molecular rotations. Phonons interact with charge carriers through electron–phonon coupling, which has substantial impacts on the operation of solar cells. Our study shows that acoustic phonons, the type responsible for transmitting heat in conventional semiconductors, have extraordinarily short lifetimes in the archetypal hybrid perovskite methylammonium lead iodide. These short lifetimes have direct implications on the cooling and transport of electrons and reflect a key difference between hybrid perovskites and conventional photovoltaic semiconductors.

Abstract

Hybrid organic–inorganic perovskites (HOIPs) have become an important class of semiconductors for solar cells and other optoelectronic applications. Electron–phonon coupling plays a critical role in all optoelectronic devices, and although the lattice dynamics and phonon frequencies of HOIPs have been well studied, little attention has been given to phonon lifetimes. We report high-precision momentum-resolved measurements of acoustic phonon lifetimes in the hybrid perovskite methylammonium lead iodide (MAPI), using inelastic neutron spectroscopy to provide high-energy resolution and fully deuterated single crystals to reduce incoherent scattering from hydrogen. Our measurements reveal extremely short lifetimes on the order of picoseconds, corresponding to nanometer mean free paths and demonstrating that acoustic phonons are unable to dissipate heat efficiently. Lattice-dynamics calculations using ab initio third-order perturbation theory indicate that the short lifetimes stem from strong three-phonon interactions and a high density of low-energy optical phonon modes related to the degrees of freedom of the organic cation. Such short lifetimes have significant implications for electron–phonon coupling in MAPI and other HOIPs, with direct impacts on optoelectronic devices both in the cooling of hot carriers and in the transport and recombination of band edge carriers. These findings illustrate a fundamental difference between HOIPs and conventional photovoltaic semiconductors and demonstrate the importance of understanding lattice dynamics in the effort to develop metal halide perovskite optoelectronic devices.

One of the distinguishing properties of hybrid organic–inorganic perovskites (HOIPs) compared with conventional semiconductors is the presence of considerable dynamical disorder in the lattice (1–3). In methylammonium lead iodide (MAPbI₃, herein MAPI; MA = methylammonium = CH₃NH₃⁺), the organic cation undergoes rapid reorientations about its average lattice position (4, 5). Complicating the dynamical picture, these cation motions couple strongly to the inorganic lead-halide inorganic framework, as observed in both theory (6) and experiments (7). The lattice dynamics are relevant to both the cooling and transport of photoexcited charge carriers because these phenomena are influenced by the coupling between electronic excitations and lattice vibrations (i.e., electron–phonon interactions) (8, 9).

The lattice dynamics in MAPI have attracted significant research attention. Most studies have focused on the dynamics of the MA cation and the related tetragonal-to-cubic perovskite phase transition at 327 K (10), with recent work suggesting the existence of local dynamic tetragonal domains above the phase transition temperature (11–14). The measured phonon dispersions in MAPI agree well with first-principles lattice dynamics calculations (13–16). Phonon lifetimes are critically important as well, as they provide insight into both electron–phonon and phonon–phonon scattering (17). Recent preliminary reports suggest that the phonon lifetimes in MAPI are significantly shorter than those in conventional semiconductors. Theoretical studies employing molecular dynamics (MD) (18) and phonon many-body perturbation theory (19) predict short lifetimes in MAPI due to anharmonic phonon–phonon scattering. Recent experimental studies support these findings, with reports of acoustic phonon lifetimes of 1–20 ps from inelastic X-ray scattering (14) and 3–5 ps from inelastic neutron scattering (20). However, there remains a need for high-precision momentum-resolved measurements to probe phonon lifetimes throughout the Brillouin zone. The paucity of such measurements limits current understanding of charge carrier cooling and transport, both of which are fundamental aspects of the optoelectronic properties of HOIPs.

Phonon lifetimes are directly related to the lattice thermal conductivity and ultralow thermal conductivity in the range of 0.2–0.5 W⋅K⁻¹⋅m⁻¹ has been measured for MAPI in both single crystals and polycrystalline samples (21, 22), with low values also computed from MD simulations (18, 23, 24) and third-order perturbation theory (19). The thermal conductivity of MAPI is 100–500 times smaller than that of conventional semiconductors such as GaAs (37 W⋅K⁻¹⋅m⁻¹) and Si (124 W⋅K⁻¹⋅m⁻¹) (25) and resembles that of amorphous polymers (26). While low thermal conductivity makes HOIPs exciting candidates for thermoelectric applications (23), inefficient thermal transport also has important consequences for the operation of optoelectronic devices. If phonons are slow to dissipate heat, this can create nonequilibrium phonon populations and affect carrier relaxation and scattering processes. If the relaxation dynamics are controlled, these mechanisms could potentially enable hot carrier solar cells capable of exceeding the Shockley–Queisser limit (27–29).

A detailed understanding of phonon–phonon interactions and thermal conductivity in MAPI is limited by the lack of precise measurements of the phonon lifetimes and, more generally, of the lattice dynamics. We have measured the acoustic phonon dispersions and lifetimes in MAPI along two branches, in two Brillouin zones, and in the orthorhombic, tetragonal, and cubic phases of MAPI using high-resolution neutron spectroscopy (30). The use of large, fully deuterated single crystals of (CD₃ND₃)PbI₃ (d⁶-MAPI) facilitated our study by reducing the strong incoherent scattering from hydrogen atoms. Our data reveal extremely short acoustic phonon lifetimes of 20 ps close to the Brillouin zone center and <1 ps near the zone boundary. First-principles modeling of the lattice dynamics with third-order perturbation theory indicates that three-phonon scattering processes are responsible for these short lifetimes and shows that these interactions are facilitated by strong phonon–phonon interactions and a high density of low-energy optical phonon modes. Furthermore, we fit our measured phonon dispersion relations to extract the momentum-resolved acoustic phonon group velocity and determine the acoustic phonon mean free paths (MFPs), which range from 0.5 to 7 nm, in some cases smaller than a single unit cell (1). These short lifetimes confirm the inability of acoustic phonons to dissipate heat efficiently in MAPI. Finally, our measurements of the quasielastic scattering (QES) in deuterated d⁶-MAPI shows reorientational cation dynamics with 1-ps lifetimes in the cubic and tetragonal phases, which are similar to those observed in protonated samples (4, 5). This suggests that the lattice dynamics we observe are consistent with those of nondeuterated MAPI.

Results and Discussion

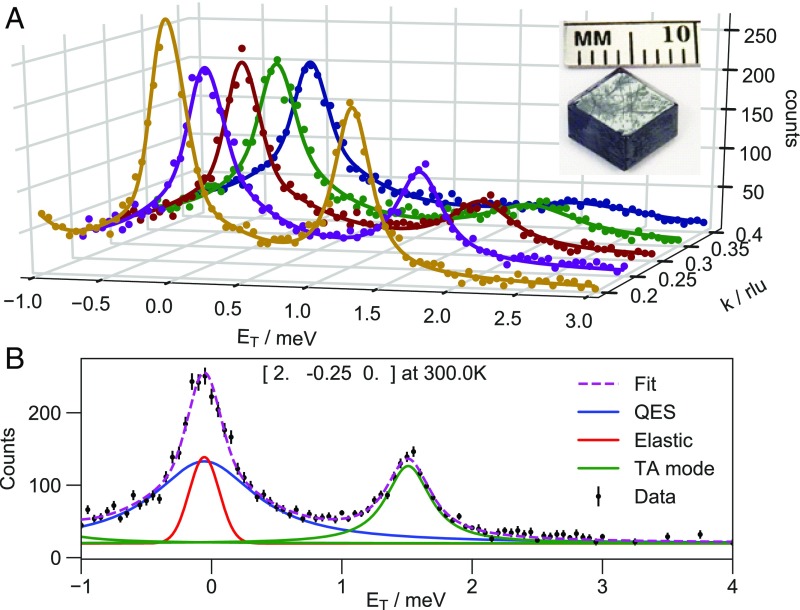
In our experimental geometry, we vary the energy transfer E_T while keeping the momentum transfer Q constant (i.e., we measure constant-Q scans). Each constant-Q scan captures the interaction between incident neutrons and the crystal lattice as a function of energy transfer. Positive (negative) E_T describes neutrons losing energy to (gaining energy from) the lattice. Each constant-Q scan exhibits a central peak at E_T = 0 containing both an elastic and QES component. In addition, if a phonon mode with energy E_ph has a sufficient structure factor S(Q, E_ph), the constant-Q scan will exhibit peaks centered on positive and negative E_ph corresponding to phonon creation and annihilation, respectively. Fig. 1A illustrates how constant-Q scans at different momentum transfer enable us to map phonon modes through the Brillouin zone.

Fig. 1.

Constant-Q scans and fits. (A) Constant-Q scans and their fits measured along the [2, −k, 0] direction. As k increases, the TA phonon energy increases and the linewidth broadens. The curves are colored yellow (k = 0.2), purple (0.25), red (0.3), green (0.35), and blue (0.4). (Inset) Fully deuterated d⁶-MAPI single crystal weighing 420 mg. (B) Constant-Q scan at [2, −0.25, 0] (purple curve in A) with fit and components shown. Reprinted with permission from ref. 30, which is licensed under CC BY-NC 3.0.

Fitting the constant-Q scans to an appropriate model enables us to extract the phonon energies and linewidths as a function of reduced wavevector k, where k represents the distance from Q to the Brillouin zone center measured in reciprocal lattice units (31). For the central peak, the elastic incoherent component corresponds to static diffuse scattering and is well described by a Gaussian lineshape with a fixed width determined by the instrumental resolution. The QES component corresponds to nonpropagating (or incoherent) lattice dynamics and is fit to a Lorentzian profile. The phonon peaks are well-described by Voigt profiles, where the Lorentzian and Gaussian components correspond to the intrinsic phonon linewidth and instrument resolution, respectively. The amplitudes of the phonon creation and annihilation peaks are related by detailed balance (31). Fig. 1B illustrates the fit for a representative constant-Q scan. Details of the fitting procedure are provided in Methods and SI Appendix.

Whitfield et al. (12) have reported that partial and full deuteration do not affect the crystal structure of MAPI or the phase transition temperatures. We measured the elastic neutron scattering from our deuterated crystal and observed the orthorhombic–tetragonal transition at 163 ± 2 K and the tetragonal–cubic transition at 327.5 ± 1 K (SI Appendix, Fig. S1), values identical to those in protonated MAPI (1). This suggests similar dynamic behavior of deuterated and protonated MAPI, which is further supported by our measurements of the QES (discussed below).

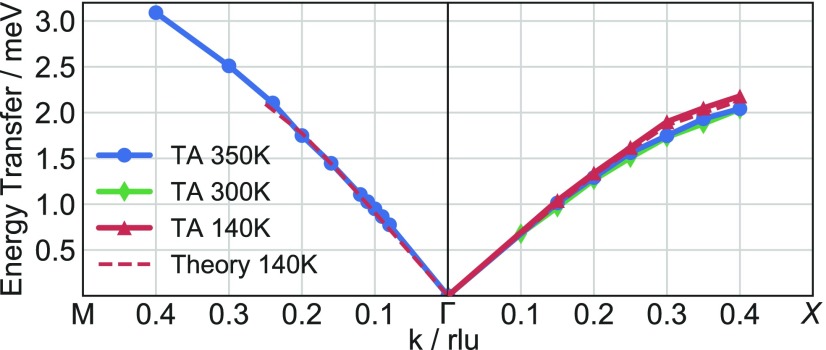
The transverse acoustic (TA) phonon dispersion along [110] ($\text{Γ}-M$) in the cubic phase (350 K) and the TA dispersion along [100] ($\text{Γ}-X$) in the cubic, tetragonal (300 K), and orthorhombic (140 K) phases are shown in Fig. 2. The momentum transfer Q in all three phases is referenced relative to the pseudocubic unit cell for simplicity (SI Appendix). Both phonon branches soften slightly (i.e., shift to lower energy) on heating from the orthorhombic to the tetragonal phase, but they show little difference between the tetragonal and cubic phases. Constant-Q scans measured in the orthorhombic phase show splitting of the TA phonon, likely due to crystal twinning (SI Appendix, Supplementary Text and Fig. S2). In Fig. 2, we plot the lower energy of these TA peaks, so this plot represents a lower bound on the TA mode energies in the orthorhombic phase and a lower bound to the softening that occurs at the phase transition. Our observation of equivalent phonon dispersions in the tetragonal and cubic phases is consistent with studies that report the microscopic equivalence of these phases around the phase transition temperature (11–14). For example, Beecher et al. (14) propose that MAPI is made up of small dynamic tetragonal domains at 350 K, even though the average structure is cubic. Our measurements qualitatively support this picture.

Fig. 2.

TA phonon dispersions along $M-\text{Γ}-X$. Blue circles, green diamonds, and red triangles correspond to the cubic (350 K), tetragonal (300 K), and orthorhombic (140 K) phases, respectively. The dashed lines show the dispersion simulated from ab initio lattice-dynamics calculations. Reprinted with permission from ref. 30, which is licensed under CC BY-NC 3.0.

We have also measured the longitudinal acoustic (LA) phonon dispersion along [100] ($\text{Γ}-X$). However, the spectrometer vertical resolution is sufficiently relaxed that we observe contamination from the TA mode that complicates the fitting (32). We include the LA phonon in the dispersions plotted in SI Appendix, Fig. S3, and other measurements of the LA phonon are shown in subsequent plots of SI Appendix.

We compare our measurements to the phonon dispersion of the orthorhombic structure calculated using ab initio lattice dynamics based on density functional theory (Methods) (19). The calculated TA dispersions along $\mathrm{\Gamma }-X$ and $\mathrm{\Gamma }-M$ are in excellent quantitative agreement with the experimental measurements, and the calculations also give a good reproduction of the LA dispersion measured along $\mathrm{\Gamma }-X$ (SI Appendix, Fig. S3). While identical calculations have been performed on the cubic phase (15, 19), these may not be as representative of the actual structure: First, soft phonons have been experimentally identified in the cubic phase (13, 14), which lead to imaginary harmonic modes in the calculations (6), and, second, the harmonic phonon calculations are based on a static structure that does not account for the cation reorientational dynamics in the cubic and tetragonal phases (4, 5). In contrast, the orthorhombic structure has no imaginary modes (19) and a well-defined cation orientation (10), so we expect calculations for this phase to give a good reproduction of the structural dynamics. Furthermore, as described above, the high-temperature cubic phase exhibits local domains of lower symmetry, so the orthorhombic structure may be a better theoretical model to describe lattice dynamics on this basis. The complete calculated phonon dispersions are plotted in SI Appendix, Fig. S4.

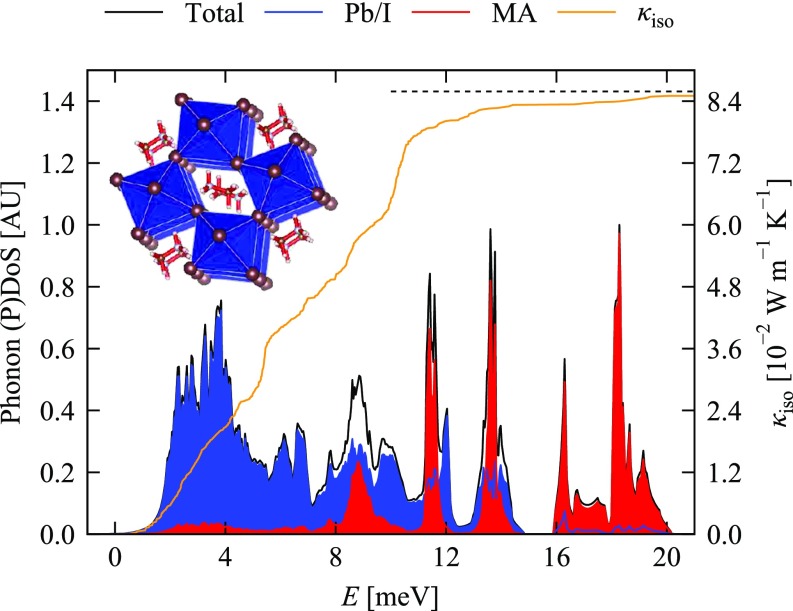
Our neutron scattering measurements can also provide insight into the contribution of specific phonon modes to the thermal conductivity via the phonon lifetimes. From a theoretical standpoint, the thermal conductivity is the product of heat capacity, phonon group velocity, and phonon MFP, summed over phonon branches and averaged over wavevectors (33). Using our harmonic lattice dynamics calculations and calculated phonon lifetimes (Methods), we calculate the room-temperature lattice thermal conductivity of MAPI to be 0.086 W⋅m⁻¹⋅K⁻¹, in rough agreement with experiments and MD simulations. In Fig. 3, we plot the phonon density of states (DoS) overlaid with the cumulative lattice thermal conductivity to show the contributions from modes in different energy ranges. The cumulative lattice thermal conductivity (i.e., the thermal conductivity corresponding to phonon modes with energy ≤E) demonstrates that acoustic phonon modes in MAPI (E < 3 meV; SI Appendix, Fig. S4) contribute relatively little to the thermal conductivity, with the majority of heat transport occurring via low-energy optical modes (E < 10 meV). This is distinct from conventional semiconductors such as GaAs and CdTe, in which acoustic phonons are responsible for conducting the majority of the heat (19).

Fig. 3.

Phonon DoS of MAPI for phonon energies from 0 to 20 meV (black) with projections onto the Pb–I cage (blue) and MA cation (red). The cumulative lattice thermal conductivity ${\kappa }_{iso}$ at 300 K is overlaid in orange. The dashed black line shows the total thermal conductivity summed over all modes, including the “pure” molecular modes at higher energies. (Inset) Schematic of orthorhombic-phase MAPI crystal structure with Pb–I octahedral cage in blue and MA cation in red. Reprinted with permission from ref. 30, which is licensed under CC BY-NC 3.0.

Our results do not agree with the conclusion of Li et al. (20), who measured short optical phonon lifetimes (<1 ps) and concluded that optical modes in MAPI are not responsible for significant heat transport. However, Li et al. (20) specifically probed optical modes corresponding to the MA cation with energies above 10 meV, and our simulation confirms that these modes contribute little to the thermal conductivity. Instead, Fig. 3 demonstrates that the lower-energy optical modes related to the Pb–I cage are responsible for the majority of heat transport in MAPI. Fig. 3 also reveals substantial coupling between phonon modes corresponding to the inorganic cage (Pb–I octahedra) and the organic molecule, as evidenced by the overlap between the partial DoS projected onto the cage and MA cation atoms between 8–14 meV. This overlap suggests a large cross-section for energy-conserving phonon–phonon scattering events, which we discuss below.

As shown in Fig. 3, our calculations suggest that acoustic phonons in MAPI transport heat inefficiently. To verify this, we experimentally investigated the contribution of the measured TA phonon modes to the lattice thermal conductivity by considering the phonon group velocity and MFP, whose product is related to the thermal conductivity as described above. The slope of the dispersion curves in Fig. 2, $d\omega /dq$, gives the group velocity, which is the speed at which a phonon mode can propagate energy through the lattice. To calculate the momentum-resolved acoustic phonon group velocity from our measurements, we fit a second-order polynomial to the measured dispersion relation and then evaluated the derivative as a function of k. At k = 0, these fits reveal zone center group velocities (speed of sound) ranging from $\sim$2,400 m/s for the LA mode to 1,200 m/s for the TA mode along $\text{Γ}-X$. This agrees with prior neutron scattering measurements that report 2,800 and 1,200 m/s, respectively (20). These group velocities are somewhat slow: In comparison, Si has a speed of sound ranging from 4,500 to 9,000 m/s (34).

The phonon MFP is the product of the momentum-resolved phonon group velocity and phonon lifetime; the latter describes the average lifetime of a phonon mode before scattering. Phonon lifetimes are related to the phonon energy linewidth via the Heisenberg uncertainty relation, as phonon-defect scattering, phonon-electron scattering, and the anharmonic processes responsible for phonon–phonon scattering all serve to broaden the phonon peaks measured in constant-Q scans (35). After accounting for instrumental broadening, the intrinsic phonon half width at half maximum (HWHM) gives the reciprocal of the phonon lifetime (36, 37). Measuring phonon lifetimes is challenging due to the strict requirements on instrumental energy resolution. While Raman scattering techniques can achieve resolution in the microelectronvolt range, and are thus capable of resolving lifetimes as long as nanoseconds, these measurements only probe zone-center optical modes (16). Inelastic X-ray scattering techniques can probe phonon modes throughout the Brillouin zone, but they are limited to energy resolutions of 1–2 meV (38), which are insufficient to resolve picosecond lifetimes.

Our high-resolution neutron scattering measurements provide an order-of-magnitude-better energy resolution, of the order 0.1 meV HWHM, that enables us to measure intrinsic linewidths corresponding to lifetimes shorter than $\sim$20 ps. This technique has been previously employed in superconducting materials to probe phonon lifetimes above the superconducting phase transition (39, 40). In addition, we calculated phonon lifetimes for the orthorhombic perovskite structure using third-order perturbation theory (33). Our analysis only considers third-order (three-phonon) scattering processes, so the calculated lifetimes should overestimate the real lifetimes, which include phonon–phonon scattering to all orders as well as phonon–defect and phonon–electron scattering.

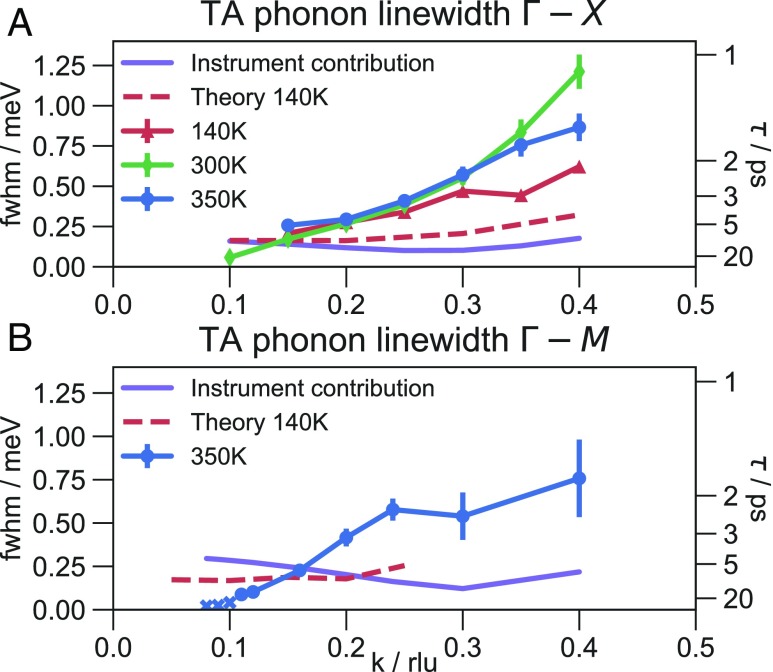
Fig. 4 shows our measurements of the intrinsic TA phonon linewidth along $\mathrm{\Gamma }-X$ and $\mathrm{\Gamma }-M$, together with the instrumental contribution to the phonon peak broadening (Methods) and our calculations of the TA phonon lifetimes. Our measurements show that the TA phonon broadens dramatically toward the zone boundary, as predicted for anharmonic acoustic phonon decay (41). Throughout the Brillouin zone, the TA phonon lifetimes are extremely short, from 1 to 20 ps along both directions, and equivalently short for the LA phonon along $\mathrm{\Gamma }-X$ (SI Appendix, Fig. S5). Although first-principles calculations tend to overestimate lifetimes as described above, our calculations show impressive agreement with the measurements: The calculated lifetimes are within a factor of 2 of the measured lifetimes for the $\mathrm{\Gamma }-X$ direction and within a factor of 5 for the $\mathrm{\Gamma }-M$ direction. This lends confidence to our theoretical analysis of the thermal transport.

Fig. 4.

Intrinsic TA phonon linewidths and lifetimes. Error bars represent the SE in the fitted values; errors in the orthorhombic phase are larger due to crystal twinning. Cross markers denote fitted values below the resolution limit. Dashed lines show the calculated linewidths of the orthorhombic phase. Purple lines show the instrumental contribution to the linewidths. (A) TA phonon along $\text{Γ}-X$ in the orthorhombic (140 K), tetragonal (300 K), and cubic (350 K) phases. (B) TA phonon along $\text{Γ}-M$ in the cubic phase (350 K). Reprinted with permission from ref. 30, which is licensed under CC BY-NC 3.0.

In most of our measurements, the intrinsic linewidths are larger than the instrumental contribution. The exception is the TA phonon along $\text{Γ}-M$, where lifetimes near the zone center are in the tens of picoseconds, with corresponding linewidths below the resolution limit of our instrument. Error bars represent the SE from the least-squares fitting algorithm; however, they do not take into account the energy resolution of each data point and thus will slightly underestimate the SE. As noted, crystal twinning results in overlapping TA phonon peaks in the orthorhombic phase scans, which complicates the fitting (SI Appendix, Fig. S2). We report the fitted linewidths of the lower-energy peak and do not include error bars, with the understanding that SEs may be significantly higher for the orthorhombic lifetimes.

Overall, the TA phonon lifetimes we measure in MAPI are markedly shorter than those in conventional semiconductors. In Si and GaAs, long-lived phonons have correspondingly narrow intrinsic linewidths that are hard to measure given typical resolution limits. However, prior calculations of the acoustic phonon lifetimes in Si and GaAs report acoustic phonon lifetimes of 1 μs near the zone center and 50–100 ps near the zone boundary (42, 43). In comparison, the lifetimes we measure in MAPI are 50–100 times shorter. Additionally, we calculated phonon lifetimes in GaAs and CdTe employing the same methodology we used for MAPI, and we find phonon lifetimes in MAPI to be ∼100–500 times shorter than in these conventional semiconductors (SI Appendix, Fig. S6).

To investigate the microscopic origin of the short acoustic phonon lifetimes in MAPI, we carried out first-principles calculations of the three-phonon scattering processes using the methodology developed in ref. 33. (SI Appendix, Supplementary Methods). For a given phonon mode, the line broadening can be written as the product of two terms: (i) the two-phonon DoS, which describes the density of energy- and momentum-conserving scattering pathways available for collision (two phonons in, one phonon out) and decay (one phonon in, two phonons out) processes and (ii) an averaged three-phonon interaction strength, which describes the extent of physical coupling to other modes. SI Appendix, Fig. S6 compares the calculated phonon lifetimes, two-phonon DoS, and three-phonon interaction strength as a function of phonon energy for MAPI, GaAs, and CdTe. We find that both the two-phonon DoS and the three-phonon interaction strengths are one to two orders of magnitude higher for acoustic phonons in MAPI than in the other two semiconductors.

The increased density of three-phonon scattering pathways in MAPI is related to the organic cation: The MA cation introduces three translational and three rotational degrees of freedom, which couple to the Pb–I cage and introduce low-energy optical phonon branches in the dispersion, increasing the number of available scattering channels. In contrast, the binary semiconductors CdTe and GaAs have fewer optic branches and more tightly distributed DoS, resulting in fewer scattering pathways. The origin of the high three-phonon interaction strengths is harder to determine conclusively, but two explanations are likely. First, the soft nature of the inorganic cage leads to large atomic displacements, beyond the harmonic regime where the restoring force is quadratic. Second, deformations of the Pb–I cage cause perturbations to the electronic structure, which can couple into the other phonon modes.

To further analyze the line broadening of the acoustic modes, we computed a 2D histogram of the contributions from pairs of phonon modes to the observed line broadening (short lifetimes) of the acoustic and low-energy optical modes in MAPI (E < 3 meV; SI Appendix, Fig. S7). This analysis clearly identifies “hotspots” corresponding to collisions involving bands of modes where motion of the Pb–I cage is coupled to the organic cation, together with substantial broadening from low-energy Pb–I cage modes which we expect to behave anharmonically. This further supports our conclusion that the short phonon lifetimes in MAPI arise from a combination of a high density of scattering pathways related to the MA cation and strong three-phonon interaction strengths due to low-frequency anharmonic motions of the soft Pb–I framework.

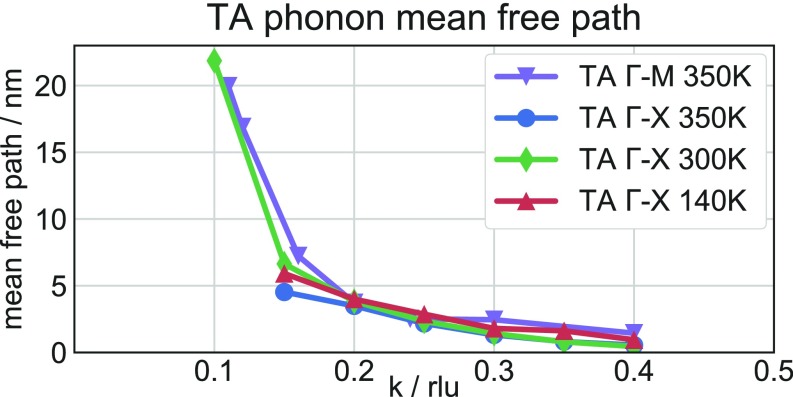
Now that we understand the origin of the short lifetimes, we investigate the phonon MFPs by taking the product of the measured phonon group velocity and lifetime. Fig. 5 shows our measurement of ultrashort phonon MFPs from $\sim$20 nm near the zone center to <1 nm near the zone boundary. In particular, the MFPs near the zone boundary are shorter than a single unit cell. We find similarly short MFPs for the LA mode (SI Appendix, Fig. S8). These short MFPs clearly demonstrate the inability of acoustic phonon modes to dissipate heat efficiently in MAPI and reflect the low contribution of these modes to the thermal conductivity evident in the calculations.

Fig. 5.

TA phonon MFPs in MAPI along $\mathrm{\Gamma }-X$ and $\mathrm{\Gamma }-M$. Reprinted with permission from ref. 30, which is licensed under CC BY-NC 3.0.

On the microscopic scale, the short phonon lifetimes and inefficient thermal transport will have a direct impact on hot carrier cooling (decay of higher-energy carriers to the band edges) and band edge carrier transport. A “hot phonon bottleneck,” that is, the observation that hot carrier cooling rates decrease dramatically at high carrier concentrations, has been reported in MAPI (27–29). In hot carrier cooling, energy from hot carriers is transferred to optical modes with appropriate energies, and these optical phonons subsequently transfer the energy into acoustic modes through scattering events. In conventional semiconductors, these acoustic modes rapidly transfer the energy to the far field (44). However, short acoustic phonon lifetimes may affect hot carrier cooling: Inefficient acoustic phonon propagation will result in local heating, creating a nonequilibrium population of optical phonons that can effectively reheat carriers, leading to long hot carrier lifetimes (29, 45). Our measurements and calculations support this hypothesis by demonstrating the extreme inefficiency of acoustic phonon heat transport in the MAPI lattice.

The transport of band edge charge carriers also depends on lattice vibrations. A longstanding and important question in the field of HOIPs is how nonradiative recombination rates can be so low in solution-processed HOIPs that likely have a high concentration of defects (2, 46). We posit that short acoustic phonon MFPs in MAPI will limit trap-assisted Shockley–Read–Hall (SRH) recombination rates via local heating and carrier detrapping. The microscopic description of SRH recombination requires the dissipation of an amount of energy equal to roughly half the band gap ($\sim$0.8 eV) twice, once during carrier trapping and again during ground-state relaxation. As in hot carrier cooling, low-energy acoustic phonons are unlikely to be directly scattered by charge carriers. Rather, carrier trapping results in a population of vibrational states localized at the defect center (47), which subsequently decay into acoustic phonons (44). In conventional semiconductors, acoustic modes can efficiently dissipate the thermal energy to the far field. However, in MAPI, these acoustic modes will scatter within picoseconds, leading to persistant local lattice heating within a few nanometers of the trap and facilitating thermal detrapping. Measured nonradiative recombination rates in MAPI suggest lifetimes of hundreds of nanoseconds (46), and thus we speculate that picosecond acoustic phonon lifetimes may play a role in reducing nonradiative recombination rates via carrier detrapping.

Finally, we fit the broad central peak in each constant-Q scan to characterize the momentum-resolved QES. QES is sensitive to motions on picosecond-to-nanosecond timescales and has been used to probe the cation reorientation in protonated MAPI (4, 5). In the present work, the measured QES intensity is roughly constant throughout the Brillouin zone and dramatically increases in intensity on heating from the orthorhombic phase into the tetragonal phase (SI Appendix, Fig. S9). These observations are the same as in protonated MAPI (4, 5), indicating that the QES may arise from the incoherent scattering associated with MA cation reorientations, although we cannot rule out other origins. By fitting the QES linewidth, we measure timescales of $\sim$1 ps in the tetragonal and cubic phases, which matches the timescale for MA cation reorientation measured in protonated MAPI.

Conclusion

Our measurements show that the acoustic phonon lifetimes in the prototypical hybrid perovskite MAPI are 50–500 times shorter than in conventional semiconductors. We have used high-energy resolution neutron scattering to measure the TA phonon dispersions as well as the critically important phonon lifetimes, which range from 1 to 20 ps throughout the Brillouin zone. Anharmonic lattice dynamics calculations reveal that the short lifetimes result from a high-density of low-energy optical modes, arising from the degrees of freedom of the organic cation, together with strong phonon–phonon interactions. In addition to the impact on the thermal conductivity, these short lifetimes likely affect hot carrier cooling and may also play a role in reducing the nonradiative recombination of band edge carriers. Further research into electron–phonon coupling is key to understanding the fundamental limits on optoelectronic properties such as carrier mobilities. As research continues in the field of HOIPs, careful consideration of the lattice dynamics may enable the rational design of new materials in this family for applications in solar cells and other devices.

Methods

Preparation of Deuterated (MA-d₆)PbI₃ Single Crystals.

Deuterated (CD₃ND₃)I ((MA-d₆)I) was prepared as described in SI Appendix. Single crystals of (MA-d₆)PbI₃ were grown using an adaptation of the method reported by Saidaminov et al. (48), from a 1:1 molar ratio of (MA-d₆)I and PbI₂ (details in SI Appendix). We obtained two black rhombic dodecahedral crystals: a 420-mg crystal with dimensions of ca. 8 × 7 × 3 mm and a 698-mg crystal with dimensions of ca. 9 × 9 × 4 mm.

Elastic Neutron Scattering and Inelastic Neutron Spectroscopy.

Elastic scattering data were measured on the thermal neutron triple-axis spectrometer (BT4) at the NIST Center for Neutron Research (NCNR). Inelastic neutron spectroscopy was performed on the cold neutron triple-axis spectrometer (SPINS) at NCNR. The incoherent elastic instrumental energy resolution was measured using a vanadium standard and the Gaussian width of the phonon Voigt function was calculated considering the slope of the phonon dispersion. Our use of a Voigt function to describe the phonon scattering data represents a 1D convolution of the Gaussian instrumental energy resolution function with the Lorentzian (damped harmonic oscillator) phonon cross-section. The Gaussian widths are documented in SI Appendix, Table S1. Additional details and a description of the fitting procedure are provided in SI Appendix.

First-Principles Calculations of Phonon Dispersion and Linewidths.

Density functional theory calculations were carried out on the orthorhombic phase of MAPI using the VASP code (49) using a computational setup similar to that in our previous studies (15, 19). The starting point for our calculations was the optimized 48-atom unit cell from the study in ref. 15. The second-order interatomic force constants (IFCs) calculated in a 2 $\times$ 2 $\times$ 2 expansion of the unit cell (384 atoms), which is commensurate with all of the symmetry points in the Pnma Brillouin zone, were taken from our previous work (19). The third-order IFCs were obtained using the Phono3py code (33) for a single unit cell (i.e., 48 atoms), requiring 10,814 independent calculations, with a displacement step of 2 $\times$ 10⁻² Å. The harmonic phonon dispersion and atom-projected DoS were obtained by Fourier interpolation, the latter on a uniform $\text{Γ}$-centered q-point grid with 36 $\times$ 36 $\times$ 36 subdivisions. The phonon lifetimes were sampled on a $\text{Γ}$-centered 6 $\times$ 6 $\times$ 6 grid using Gaussian smearing with a width of 0.1 THz to integrate the Brillouin zone. Further details are provided in SI Appendix.