Self-cleavage of the glmS ribozyme core is controlled by a fragile folding element

Significance

Riboswitches are structured mRNA elements that regulate gene expression in response to metabolite ligands. The bacterial glmS riboswitch regulates a protein with a key role in cell wall biosynthesis. This riboswitch follows an unusual mechanism, acting as a ligand-activated self-cleaving ribozyme. Understanding how this RNA folds may aid development of antibiotics targeting it. We used optical tweezers to investigate this ribozyme riboswitch at the single-molecule level. We found that folding and function are intertwined in this system, with a dynamically unstable folding transition controlling catalysis. Furthermore, binding of the ligand fails to stabilize the weakly favored folded state. Hence, the glmS ribozyme does not follow the conventional model for riboswitch switching, in which ligand binding stabilizes a particular switch conformation.

Abstract

Riboswitches modulate gene expression in response to small-molecule ligands. Switching is generally thought to occur via the stabilization of a specific RNA structure conferred by binding the cognate ligand. However, it is unclear whether any such stabilization occurs for riboswitches whose ligands also play functional roles, such as the glmS ribozyme riboswitch, which undergoes self-cleavage using its regulatory ligand, glucosamine 6-phosphate, as a catalytic cofactor. To address this question, it is necessary to determine both the conformational ensemble and its ligand dependence. We used optical tweezers to measure folding dynamics and cleavage rates for the core glmS ribozyme over a range of forces and ligand conditions. We found that the folding of a specific structural element, the P2.2 duplex, controls active-site formation and catalysis. However, the folded state is only weakly stable, regardless of cofactor concentration, supplying a clear exception to the ligand-based stabilization model of riboswitch function.

Riboswitches are ligand-responsive, cis-regulatory mRNA elements found in all three domains of life (1, 2). Riboswitches generally function via either a kinetic or a thermodynamic competition between alternatively folded RNA structures: an aptamer, which recognizes and binds to the cognate ligand, and an expression platform, which affects downstream gene expression in one of several ways, for example by modulating transcription or translation (1). In the conventional model of riboswitch function, the binding energy of the ligand is converted into additional RNA folding stability, which favors the aptamer-bound configuration, holding the riboswitch in the “on” state (3, 4). However, not all riboswitches form alternatively folded structures. A counterexample is provided by the bacterial glmS riboswitch, which has been found to fold into nearly the same structure regardless of whether ligand is bound or not (5, 6). The glmS riboswitch regulates the expression of glucosamine-6-phosphate synthase (GlmS), an enzyme that catalyzes synthesis of the essential bacterial cell wall precursor, glucosamine 6-phosphate (GlcN6P) (7). Understandably, this riboswitch has become a target for antibiotic development (8, 9). Unique among the known riboswitches, the glmS riboswitch functions as a self-cleaving ribozyme activated by its ligand, GlcN6P, which also serves as a catalytic cofactor for the cleavage reaction (10, 11). Cleavage generates a 5′-hydroxyl end that targets the glmS mRNA for subsequent degradation by RNase J1 (12), thereby down-regulating GlmS protein expression. The nearly identical structures of the ribozyme with and without cofactor bound presumably reflect equivalent low-energy states. However, prior work has not addressed the stability of the fully folded state or how ligand binding might affect the dynamic ensemble of conformational states formed by this riboswitch.

The full glmS ribozyme carries a core domain, comprising a double pseudoknot that forms the active site (5, 6), which is sufficient for GlcN6P-dependent self-cleavage activity (10, 13) (Fig. 1A). The isolated core domain folds from just 66 nucleotides (14)—and potentially fewer, due to the P1 hairpin being of variable length (11)—making it an attractive model system for biophysical study. We investigated this core domain using optical force spectroscopy, a powerful tool for studying the folding and activity of individual, structured RNAs (3, 15–18). Here, we report the free energy landscape traversed by the core glmS ribozyme during folding—from a fully unfolded ssRNA to a functional ribozyme—and its relationship to catalytic activity. Measurement of the folding and biochemical behaviors of single molecules in real time, under various ligand conditions, revealed a close interplay of structural dynamics, cofactor binding, and catalysis.

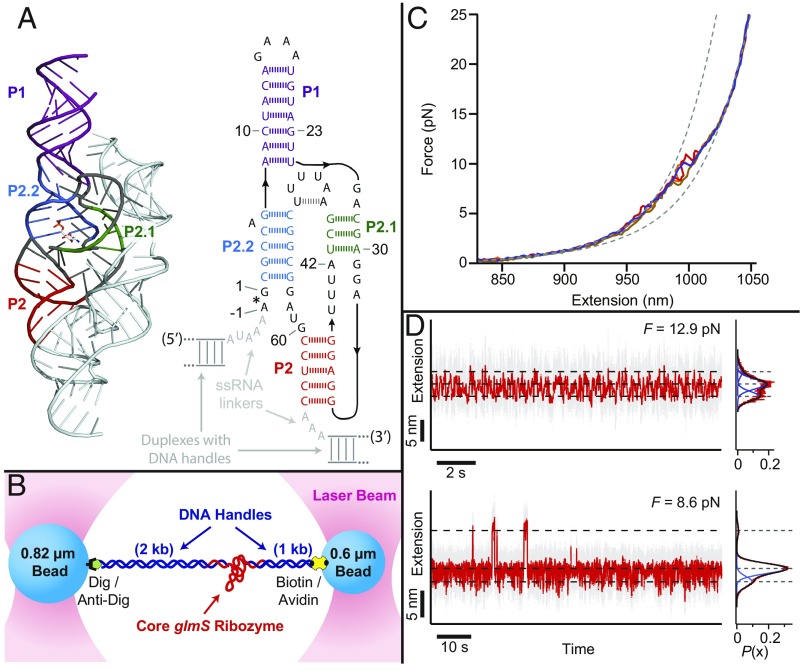
Fig. 1.

Optical tweezers measurements of core glmS ribozyme folding using the dumbbell assay. (A, Left) Thermoanaerobacter tengcongensis glmS ribozyme crystal structure, Protein Data Bank (PDB) ID code 2Z75, showing the duplex elements P1, P2, P2.1, and P2.2 (core domain, dark colors; noncore domain, pale cyan). (A, Right) Secondary structure of the 66-nt core construct used in this study (same color scheme). (B) Cartoon of the optical trapping dumbbell assay geometry (not to scale), showing the two traps and beads attached to handles hybridized on either side of a core ribozyme molecule. (C) Representative records of FECs for core glmS ribozyme (solid colors), showing WLC model fits (dashed gray lines) (Materials and Methods) to the completely folded (low-force) and fully unfolded (high-force) states. (D) Representative records at constant force (gray, raw data; red, median-smoothed), with the corresponding extension histograms show to the right, fit to sums of Gaussians (red, histogram data; blue, individual Gaussians; black, sum of Gaussians).

Our studies were conducted on a consensus core ribozyme construct (14) (Fig. 1A). Molecules of in vitro-transcribed core glmS ribozyme were attached by their 5′ and 3′ ends to polystyrene microspheres via DNA handles, facilitating measurement of the molecular extension under external forces produced by a dual-beam optical tweezers, using the so-called dumbbell assay (Materials and Methods and Fig. 1B). The unfolding of ribozyme constructs was investigated by performing a series of force-ramp experiments, in which molecular extension was monitored with nanometer-level precision as the distance between the two optical traps was increased linearly with time. Worm-like chain (WLC) model fits to the fully folded and fully unfolded states in the resulting force-extension curves (FECs) (Fig. 1C) returned the change in contour length due to complete unfolding, ∆L_c = 34.5 ± 1.1 nm (Materials and Methods). This distance is consistent with release of all 66 nucleotides from a fully folded state with an initial molecular width of 4.4 ± 1.1 nm (Materials and Methods), which is similar to the 3.3-nm width of the core domain based on crystal structures (5, 6).

Higher-resolution details of the folding dynamics were investigated by subjecting individual ribozymes to constant forces while measuring their molecular extensions over time (Materials and Methods). Performing such near-equilibrium measurements across a range of fixed loads, we observed several distinct, thermally induced “hopping” transitions between folding states in characteristic force regimes (Fig. 1D). The associated extension changes, ∆x, were determined for the transitions of each single-molecule record by fitting a sum of Gaussians to the overall extension histogram (Fig. 1D). Likewise, the probabilities of folding for each transition, P_folded, were determined from the folded-state occupancies and fit to a Boltzmann function to determine the corresponding F_1/2 value, that is, the force where P_folded = 0.5 (e.g., Fig. 2A) (Materials and Methods). As in prior work (15, 19), transitions were assigned to the folding/unfolding of individual structural intermediates based on several strategies, including comparisons of the measured ∆x values with WLC-model predictions based on the associated structural elements, and measurements of the effects of adding “blocking” DNA oligos, chosen to be complimentary to selected regions of the ribozyme sequence (Materials and Methods and SI Appendix, Fig. S1 and Table S1). We determined that, as the force is reduced, renaturation from the unfolded ssRNA proceeds as follows: First, the P1 hairpin folds (via a frayed intermediate; F_1/2 ≈ 14.2 pN, 12.6 pN), followed by the P2–P2.1 pseudoknot (F_1/2 ≈ 10.0 pN), and, finally, the P2.2 duplex, F_1/2 ≈ 5.7 pN (Fig. 1D and SI Appendix, Table S1).

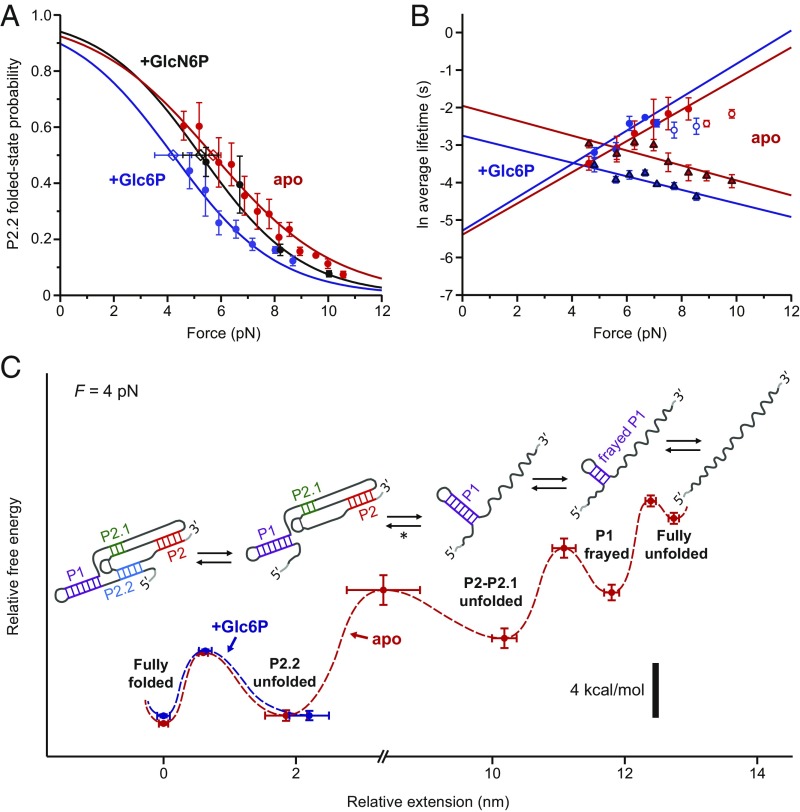
Fig. 2.

P2.2 folding is not stabilized in the presence of cofactor. (A) Force dependence of P_folded(P2.2), with Boltzmann sigmoidal fits (Materials and Methods), for various ligand conditions. Open diamonds: F_1/2 values from fits, with error bars indicating SE. (B) Force dependence of P2.2 ln(τ_folded), triangles, and ln(τ_unfolded), circles, with linear fits (Materials and Methods). White-filled circles: higher-force ln(τ_unfolded) data which deviated from linearity, not used for fitting. Apo and +G6P P_folded fits in A are to region with linear ln(τ_unfolded) vs. force. (A and B) Data points: averages from ≥3 traces (>100 folding/unfolding events per trace); error bars: SEM. (C) Reconstructed free energy landscape for folding of the core glmS ribozyme, displayed for 4-pN applied load (red dashed line, apo state; blue dashed line, +Glc6P). Potential wells correspond to experimentally observed folding states (labeled); barrier heights were derived from the load dependencies of the transition rates between these states (mean ± SE). Cartoons depict the RNA secondary structures for these states deduced from the data. Note the break in scale. [*: ∆x for this broad transition was ∼3.5 nm less than expected for complete P2–P2.1 folding plus P1 reorientation at F_1/2 = 10.0 pN, possibly attributable to a separate P1 reorientation step that was obscured by noise or drift (Materials and Methods).]

P2.2, the last ribozyme element to fold, is the key to forming both the active site and the cofactor-binding site, with the cleavage dinucleotide appearing directly 5′ to the first strand of this duplex (Fig. 1A). It was therefore of interest to determine how P2.2 folding was affected by the presence of the ribozyme cofactor. In particular, does ligand-binding energy lead to additional stabilization of the folded state, as embodied in the standard model (3, 4)? To address this question, we compared the thermodynamics of P2.2 folding in the apo (ligand-free) ribozyme to that in the presence of 10 mM Glc6P, a noncleaving cofactor analog that has been found to bind to the ribozyme in an essentially identical fashion to GlcN6P (5, 6, 20, 21). No additional Glc6P-induced stabilization of P2.2 formation was observed, with F_1/2(apo) = 5.7 ± 0.3 pN and F_1/2(Glc6P) = 4.2 ± 0.7 pN (Fig. 2A). If anything, the data indicate a minor destabilization induced by cofactor binding, but the observed effect is within 2σ. We confirmed that the absence of any ligand-induced stabilization was not specific to the cofactor analog we used by comparing the thermodynamics of P2.2 folding in the presence and absence of saturating levels of the natural ligand, GlcN6P (10 mM), based on records obtained prior to self-cleavage events; these returned a similar value of F_1/2(GlcN6P) = 5.2 ± 0.7 pN (Fig. 2A). We also determined the average P2.2 folded and unfolded state lifetimes as functions of force (Materials and Methods) and found that the cofactor did not stabilize P2.2 kinetically either, with no increase in the folded-state lifetime observed when Glc6P was present. On the contrary, if anything, the presence of the analog Glc6P induced a ∼2σ decrease in τ_folded(0), the folded-state lifetime extrapolated to zero load (Fig. 2B and SI Appendix, Table S1).

Thus, the glmS ribozyme stands in contrast to other riboswitches that have been studied (3, 4), in that binding the cognate ligand neither kinetically nor thermodynamically stabilizes the bound state. Instead, ligand binding activates the fully formed riboswitch by functioning as a catalytic cofactor to enable self-cleavage. This conclusion seems reasonable from a biophysical perspective: Whereas the folding stability of nucleic acid duplexes is primarily a result of base-stacking interactions (22), GlcN6P/Glc6P binds to the ribozyme between A(-1) and G1, which do not stack with one another, nor with the bases in P2.2, in either apo or ligand-bound structures (5, 6, 20, 21). Regardless of cofactor interactions, P2.2 is only mildly stable at room temperature: Its zero-force folding energy, averaged over all ligand conditions, was ∆G_fold(0) ≈ −0.9 kcal/mol (∼1.5 k_BT at 25 °C) (SI Appendix, Table S1).

Measurements of the force dependence of the quantities P_folded, τ_folded, and τ_unfolded for all transitions yielded the thermodynamic and kinetic parameters for each folding substructure (SI Appendix, Table S1). Based on these parameters, we were able to reconstruct the free energy landscape of folding for the core glmS ribozyme (Materials and Methods and Fig. 2C), normalized to F = 4 pN. Distinct from prior work, which studied aspects of Mg²⁺-induced folding of the ribozyme (23, 24), the landscape determined here reveals secondary and tertiary refolding behavior for the core ribozyme when fully equilibrated with Mg²⁺.

We sought to understand the relationship between ribozyme folding and catalytic activity. Toward that end, the ribozyme self-cleavage rate was measured over a range of external forces by determining the “survival time,” operationally defined as the time to tether rupture for an optically trapped ribozyme following the introduction of GlcN6P (Materials and Methods and Fig. 3A). We found that the self-cleavage rate depended both upon the level of the external force and the presence of GlcN6P, showing that optically trapped ribozymes retained functionality (Fig. 3B). As the force was increased, the GlcN6P-stimulated cleavage rate, k_obs(clvg), decayed from 1.2 to 1.5 min⁻¹ to below 0.1 min⁻¹, the buffer/Glc6P background level, following a sigmoidal (Boltzmann) trend with a half-maximal force of F_max/2 = 4.9 ± 1.2 pN (Materials and Methods, Fig. 3B, and SI Appendix, Table S3). Having already determined the folding energy landscape of the ribozyme, we were therefore able to compare the load dependence of the self-cleavage rate with that of the folding probability for each of the folding intermediates, and thereby determine which aspects of ribozyme folding control catalysis. The decay of P_folded for the P2.2 structural element (but no other substructure) closely mirrored the observed decay in catalytic rate, k_obs(clvg), in the presence of either GlcN6P or Glc6P (Fig. 3B and SI Appendix, Table S1).

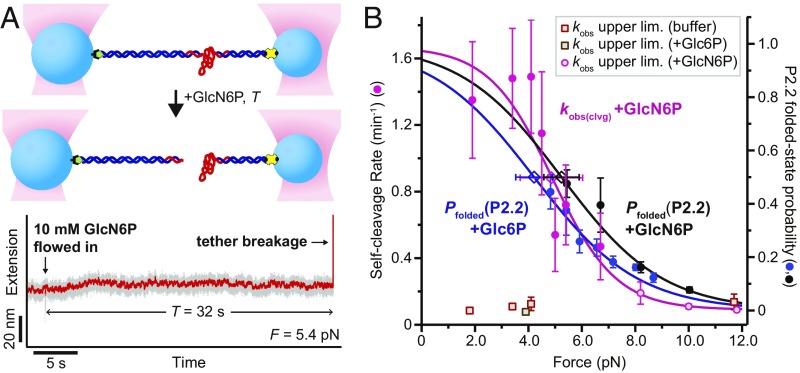
Fig. 3.

Folding and self-cleavage of the core glmS ribozyme. (A, Top) Schematic of the single-molecule self-cleavage assay. Trapping geometry as in Fig. 1B. (A, Bottom) Example self-cleavage experiment trace (gray, raw data; red, median-smoothed). (B) Self-cleavage rate k_obs(clvg), left axis, overlaid with P_folded(P2.2), right axis, with sigmoidal fits (Materials and Methods). P_folded data shown are same as in Fig. 2A. Cleavage rate data points: averages from ≥4 independent measurements; error bars: SEM. Open diamonds: folding F_1/2 and rate F_max/2 from fits (error bars, SE).

The close correspondence of the force dependencies for P2.2 folding and self-cleavage rate is consistent with a simple, two-state model: When P2.2 is folded, the ribozyme is competent to perform self-cleavage; otherwise, it is not. External loads applied to the ends of the RNA reduce the cleavage rate purely by reducing the probability that P2.2 is folded. Although P2.2 folding is favored under unloaded conditions, it is only mildly so, and the average folded-state lifetime is only ∼0.1 s, which is some 360-fold shorter than the average time to cleavage (SI Appendix, Tables S1 and S4). Thus, we conclude that complete ribozyme folding is a transient phenomenon and that the vast majority of P2.2 closure events in the presence of saturating GlcN6P levels do not result in catalysis. This finding is consistent with a dynamic structure–function relationship, based on a fixed sequence of stochastic events: P2.2 must remain in its short-lived folded state long enough for the cofactor to bind. Next, the cofactor-bound folded state—which is found to have equivalent stability—must persist long enough for the system to undergo self-cleavage. The P2.2 duplex was previously proposed to be essential for catalysis based on structural inferences, mutational results, and trans-cleaving ribozyme design (21). Here we have measured P2.2 folding directly and confirmed its requirement for catalysis, further defining the underlying structure–function relationship. Our results may be contrasted with findings recently reported for the twister ribozyme from Oryza sativa. In that case, transient folding from a dominant unfolded state was found to be sufficient to achieve maximal catalytic activity, and most folding events led directly to self-cleavage (25). In light of the stark differences, it would appear that a range of qualitatively different relationships between folding and catalysis are available to ribozymes. For the case of the glmS ribozyme, catalysis is controlled by a combination of cofactor binding and a thermally labile, transient folding interaction. Given this finding, we predict that drugs which serve to stabilize P2.2 folding would tend to promote self-cleavage, reducing GlmS levels, and thereby function as antibiotics.

Materials and Methods

RNA Sequences and Preparation.

The consensus glmS ribozyme core construct sequence was based on the “construct 1” sequence previously characterized by Soukup (14). Our RNA construct consisted of the construct 1 glmS ribozyme core sequence [66 nt, A(-1) to C65, as published] flanked by 5′ (AUAAA, also matching the Soukup construct) and 3′ (AAA) linker sequences (Fig. 1A), which were in turn flanked by 5′ and 3′ sequences designed to hybridize to each of the two DNA handles, forming DNA:RNA duplexes of 31 and 37 bp, respectively (Fig. 1 A and B). RNA sequences were generated by in vitro transcription, as described (19). Briefly, the transcription template was prepared by PCR amplification from a pALB3 vector with a glmS core insert at the unique BstEII restriction site. The glmS core insert was prepared by annealing sense and antisense DNA oligonucleotides synthesized by IDT. Transcription was performed using the MEGAScript T7 kit (Ambion), and the RNA products were purified by PCA extraction followed by isopropanol precipitation. RNAs were resuspended and stored in Hepes buffer (pH 7.5) and further purified by passage through NucAway spin columns (Thermo Fisher Scientific) before storage.

Assembly of “Dumbbell” Complexes for Optical Tweezers Assay.

Measurements of individual RNA molecules were performed using a dumbbell assay based on dual-beam optical tweezers (Fig. 1B). Each dumbbell consisted of one RNA construct annealed to two dsDNA handles, which were in turn attached to the two polystyrene microspheres (beads), each held in one of the two optical traps. The DNA handles each had ssDNA overhangs on one end (for hybridization to the RNA construct) and a biotin or digoxygenin chemical modification on the opposite end (for binding to the corresponding bead, coated with either anti-digoxygenin antibody or avidin). The handles (2,018 bp with 37-nt 5′ overhang and 1,044 bp with 31-nt 3′ overhang) were the same as in refs. 19 and 26. Handles were prepared and annealed to the RNA construct as described (19), except that annealing reactions were run at 1:1:1 molar ratios (20 nM each handle, 20 nM RNA). The RNA:handles annealing mixture was diluted to 1 nM in PHC buffer [50 mM Hepes, pH 8, 150 mM KCl, 4 mM Mg(OAc)₂, 100 µM EDTA, and 1 mM DTT]. To produce dumbbells, annealing mixture was incubated together with 0.6 µm avidin-coated beads and 0.82-µm anti-digoxygenin–coated beads for 1 h at room temperature (final concentrations ranged from ∼0.5 to ∼1.0 nM RNA:handles, ∼50 pM each bead). After incubation, the dumbbell preparation was diluted 1:10 into assay buffer [50 mM Hepes, pH 8, 150 mM KCl, 4 mM Mg(OAc)₂, 100 µM EDTA, 1 mM DTT, 0.03 U/µL glucose oxidase (Sigma), and 1% wt/vol β-d-glucose]. Dumbbell preparations in assay buffer were micropipetted into microscope flowcells to perform trapping experiments. Any additional solution components needed for particular experiments, for example Glc6P, were added (in assay buffer) by micropipette either before or after mounting the flowcell on the microscope, depending upon the experiment. Dumbbells were captured in the optical trapping assay geometry (Fig. 1B) by using the trapping beams to lift the stuck beads from the flowcell surface and suspend them optically in the bulk medium.

Optical Tweezers.

The dual-beam optical trapping instrument used to perform the measurements reported in this work has been described in detail and summarized (15, 16, 26, 27). Briefly, one trap (which held the larger, 0.82-μm-diameter bead) was set to be several times stronger than the other and was steered using acousto-optical deflectors under computer control, while the position of the smaller, 0.6-μm-diameter bead, held by the weaker trap, was measured using a duolateral position-sensitive diode. All measurements were performed with the weak trap stiffness set to 0.25–0.31 pN/nm. Data were sampled at either 2 kHz or 5 kHz (generally, 2 kHz for force-ramp experiments and 5 kHz for force-clamp experiments) and filtered to the appropriate Nyquist frequency using a low-pass Bessel filter. All data collection was performed using custom software written in LabView (National Instruments). Measurements were performed at a sample temperature of 25 °C in a room controlled to within ±0.2 °C.

Force-Ramp Experiments.

Unfolding force-ramp experiments were performed by moving the strong trap away from the weak trap programmatically at constant speed, using an acousto-optic deflector, in a direction parallel to the dumbbell axis, at a fixed step size and rate (e.g., 2.4 nm at 10 Hz in Fig. 1C), up until a preset maximum force was reached, typically ∼25–30 pN. Plots of the molecular end-to-end extension vs. applied force were generated from measurements of the position of the 0.6-μm-diameter bead. These FECs were analyzed on a record-by-record basis, similar to refs. 15 and 19, to determine the overall contour length change for ribozyme core unfolding. In brief, the low-force region of each FEC, prior to any unfolding transitions (indicated by “rips” in the FEC, with corresponding drops in force as extension increases), was taken to correspond to the fully folded state. The low-force region of each FEC was fit to a single WLC model for the ∼3 kb of handle dsDNA. The high-force region of each FEC, observed following all unfolding steps (all rips), was taken to represent the fully unfolded state, and fit with a double WLC model, with one term for the dsDNA handles (using the parameters determined from the fully folded state fit) and another for the ssRNA released during ribozyme unfolding. The modified Marko–Siggia interpolation formula (28) was used to describe each WLC, with ssRNA mechanical parameters set to the same values used previously (15, 16, 19): 1.0 nm persistence length and 1,600 pN/nm elastic modulus, with an elastic modulus for dsDNA of 1,200 pN/nm. FEC analysis was performed using custom fitting routines in LabView (National Instruments) and Igor Pro (Wavemetrics). Unfolding FECs were generated for each dumbbell studied, before further measurements. Dumbbells whose fully folded region fits yielded persistence lengths below 20 nm were rejected from further study or analysis, because such a low persistence length indicates the presence of more than one DNA tether connecting the beads. The change in contour length of the system arising from the release of ssRNA in the unfolded state, ∆L_c, is related to the amount of ssRNA released in complete unfolding of the ribozyme construct through ∆L_c = (n∙L_c^nt) − w, where n is the number of nucleotides ssRNA released, L_c^nt is the ssRNA contour length per nucleotide, set to 0.59 nm/nt (15, 16, 19), and w is the initial molecular width (along the dumbbell axis) of the RNA construct in its fully folded state, which contributes to the extension of the folded state but not that of the unfolded state. Our FEC measurements yielded ∆L_c = 34.5 ± 1.1 nm (average from n = 19 molecules, ≥3 records per molecule). For a 66-nt construct, n∙L_c^nt = 38.9 nm. Based on these values, our results are consistent with full glmS core unfolding from an initial width w = 4.4 ± 1.1 nm. This width is closely comparable to w = 3.3 nm, the value that we estimated for the distance between the 5′ and 3′ termini of the core ribozyme, based on crystal structures of the full-length glmS ribozyme (5, 6). This analysis follows closely the approach taken by Ritchie et al. (29) to account for the physical width of RNA pseudoknots in a previous optical trapping study. FECs acquired for each RNA molecule were also evaluated to determine the magnitude of any force offset (defined as the average difference of the FEC baseline from F = 0), and the forces in any subsequent constant-force folding or self-cleavage experiments were corrected for such offsets.

Constant-Force (Force-Clamped) Folding Experiments.

Details of folding intermediates were studied by near-equilibrium experiments conducted at a constant applied force, maintained using computer feedback (16, 30). Our force clamp was run with a refresh period of 4 ms and yielded an SD of ±0.3 pN for the preset average force. Elms et al. (31) have noted that feedback-based, constant-force experiments can distort the estimated rate constants and distances to the folding transition state, primarily due to missed transitions, which become more prevalent for shorter average state lifetimes. They conclude that the sum of distances to the transition state, ∑|∆x^‡|, should be compared with the measured extension change for the transition, ∆x, to determine the extent of this distortion, with similar values indicating that the number of missed transitions is negligible. Based on this criterion, our measurements of folding rates and transition-state distances are not substantially distorted: We find that ∑|∆x^‡| is within error of ∆x for the fast P1 hairpin fraying and P2.2 duplex folding transitions, and within 2σ for the fast P1 frayed↔unfolded transition as well as the slow P2–P2.1 folding transition (SI Appendix, Table S1).

The majority of constant-force experiments were performed at a data collection rate of 5 kHz (low-pass-filtered to the Nyquist rate, 2.5 kHz). Once a single-molecule dumbbell was identified by force-ramp experiments, folding dynamics for the ribozyme core molecule were recorded by setting the force clamp to different, fixed force values and collecting extension data for each condition. Constant-force behavior was explored for forces ranging from ∼1 to ∼25 pN, with collection intervals of ∼15 to ∼400 s, depending on the transition rates.

Analysis of constant-force data was performed using custom scripts written in Igor Pro (Wavemetrics). Baseline drift was removed by subtracting a smoothed baseline from the data (generated from the unfiltered data using the Loess smoothing function in Igor Pro). The baseline function was calculated using standard robust Loess smoothing (i.e., locally weighted regression to a quadratic form, using a Gaussian weighting function) over a 2.5- to 12.5-s window size, typically 2.5 s for 5 kHz data (32). For traces with more than transient occupancy of states on both sides of the large P2–P2.1 transition, the baselines for portions of traces in the extension ranges above and below the P2–P2.1 transition extension change were treated separately. In all cases, the baseline generated was visually compared with the raw data to ensure that it faithfully reflected apparent baseline drift. The drift-corrected data were median-smoothed over a 20- to 50-ms window for visual inspection.

Constant-force folding behavior was analyzed using methods similar to those reported (15, 19, 33). For each record at a given force, histograms of the median-smoothed extension (2- to 5-ms smoothing window) were generated. These extension histograms were fit to sums of multiple Gaussian peaks using the built-in multipeak fitting routine in Igor Pro. Each component peak was taken to represent a single folding state of the ribozyme, with the peak position supplying the average extension of the associated state and the distances between adjacent peaks supplying ∆x, the extension change for the corresponding folding transition. The relative areas of the component peaks supply the relative probabilities of the molecule being found in the corresponding states under the given force condition. Each transition (corresponding to a pair of peaks, with characteristic ∆x and force range over which it is observable) was treated as a two-state system. The reported value for ∆x was the average ∆x from records with folding probability, P_folded, as close as possible to 0.5, for all transitions except the lowest-force transition, P2.2. For unfolding P2.2, ∆x was determined from an average of all records, because optical trapping records suffer from higher thermal noise at the lowest forces, and transitions could not be clearly observed below a threshold of ∼4.5–5.0 pN. The probability that each transition was in its folded state as a function of force was fit to a two-state Boltzmann probability function to determine F_1/2, the force at which the intermediate state has a 50% chance of being folded (34), with P_folded(F) = 1 − (1 + exp[−(F − F_1/2)∆x/(k_BT)])⁻¹. Each transition supplied characteristic values of ∆x and F_1/2 that allowed for its unique identification.

The unloaded free energies of folding for each transition, ∆G_fold(0), were estimated from measurements using ∆G_fold(0) = F_1/2 ∙ ∆x − ∆G_stretch, where ∆G_stretch is the free energy of stretching the additional ssRNA released by unfolding at F_1/2, determined by integrating a WLC function for this amount of ssRNA (33, 35).

Records were median-smoothed over a 20- to 50-ms window for kinetic analysis. The kinetics for each transition were analyzed as a two-state system, using a threshold-based approach, as described in refs. 15, 19, and 33. Briefly, for each trace, extension thresholds for the folding/unfolding of each state were established at the halfway point between the associated peak positions, as described above. The dead time-corrected (36) average folded and unfolded state lifetimes were determined for each transition based on these thresholds, either by isolation of individual transitions along with MLE fitting of the distribution of folding state lifetimes to a single exponential function [using MEMLET (36)] or by dividing the total time spent in each folding state by the number of transitions out of it. These two approaches gave equivalent results when applied to isolated, two-state folding trajectories.

Average lifetimes, τ, were determined for each state over a range of forces. Linear fits to ln(τ) vs. F allowed determination of (i) an additional estimate of F_1/2, (ii) the transition rate at this force, k_1/2 = 1/τ_1/2, obtained from the intersection of fits to ln(τ_folded) and ln(τ_unfolded), and (iii) the distances to the transition state, ∆x^‡_folding and ∆x^‡_unfolding, based on the corresponding slopes (33, 34). This analysis also returned the folded/unfolded state lifetimes, and therefore the rates of unfolding/folding, as functions of force. The parameters for each transition scored are tabulated in SI Appendix, Table S1. Fitting was performed using Igor Pro. Transition rates under load, k(F), were converted to the corresponding energy barriers, ∆G^‡(F), using the prefactor k₀ = 10⁵ s⁻¹, established in prior work (15, 19, 33). Rates extrapolated to zero force supplied an additional estimate of the unloaded stability, since ∆G_fold(0) = ∆G^‡_folding(0) + ∆G^‡_unfolding(0) − ∆G_stretch (34).

As noted in the caption to Fig. 2, fits to ln(τ_unfolded) vs. F for the P2.2 transition deviated from linearity at high forces (F ≥ ∼8–9 pN), and points in this high-force regime were omitted from fits (Fig. 2 A and B). The nonlinearity might reflect another process related to the adjacent P2–P2.1 folding transition, which has a ∼5% chance of being unfolded at ∼8 pN (SI Appendix, Table S1).

State Assignments.

To aid in state assignment, the ∆x for each transition was compared with the predicted value, ∆x_pred, from a model of the transition: ∆x_pred = Δx_WLC(n) + ∆w, where Δx_WLC(n) is the expected extension of n nt ssRNA released during unfolding at F_1/2, based on the WLC model (with the same parameters as in force-ramp experiments, above); ∆w accounts for any change in width of the folded portion of the ribozyme associated with the unfolding transition. For example, for unfolding of the P1 hairpin, ∆w was set to −2.2 nm, corresponding to the width of a dsRNA helix (A-form) in its folded state, as in refs. 15, 16, and 19. Conversely, ∆w was set to 0 for the fraying of P1, where the helix width contributes equally to both unfolded and folded states. For the remaining transitions, ∆w = 0 was set for P2.2, and ∆w = (5.4–2.2) = 3.2 nm for P2–P2.1, corresponding to a 5.4-nm interresidue width of the folded state (i.e., the distance between the termini of residues A8 and C65 in the core ribozyme), based on crystal structures (5, 6), minus the 2.2-nm width of the P1 hairpin, which is assumed to align with the pulling axis during the unfolding of P2–P2.1. Values for ∆x and ∆x_pred for each transition are found in SI Appendix, Table S1. As noted in Fig. 2C, the solitary discrepancy between measured and expected values was for the intermediate-force transition. We modeled this transition as P2–P2.1 pseudoknot folding/unfolding followed by P1 reorientation, but the measured extension (8.7 ± 0.5 nm) fell short of the 12.3 nm predicted at F_1/2 = 10.0 pN (SI Appendix, Table S1). We speculate that the rapid, “hopping” transition observed may obscure a portion of the initial unfolding, which is hidden by baseline drift and/or thermal noise, that is, rapid fluctuations that average into an apparently gradual extension change. In particular, it is possible that we may be missing a separate P1 hairpin reorientation step, expected to account for an additional ∼2–3 nm, preceding unfolding of the pseudoknot.

As in previous work (15), state assignments based on the extension values and opening forces were supplemented by a series of confirmatory experiments performed using antisense oligonucleotides (“blocking oligos”), selected to hybridize with target elements of the ribozyme. When the binding of a blocking oligo is sufficiently tight, it will suppress refolding of the targeted substructure(s), and the corresponding transition(s) disappear from (or diminish in) force-clamped records of near-equilibrium folding. Results from blocking oligo experiments supported the state assignments, as follows. An oligo targeting the first strand of P2.2 strongly suppressed the transition assigned to P2.2 folding. A tightly binding oligo targeting the adjacent first strands of the P2.2 and P1 elements completely suppressed the transitions assigned to P2.2 folding and P1 folding. An oligo targeting the P2–P2.1 pseudoknot completely suppressed the transition assigned to P2–P2.1 folding (as well as P2.2 folding), but not the transition assigned to P1 hairpin folding, as expected. These results are summarized in SI Appendix, Fig. S1.

See SI Appendix for further discussion of state assignments, including comparison of our measurements to mfold predictions (37).

Single-Molecule Self-Cleavage Experiments.

To perform single-molecule measurements of self-cleavage activity, candidate dumbbells were first optically captured, and the tethers tested by force ramps to confirm that they carried single molecules, as described above. Then, each dumbbell was placed under constant load using the force clamp, and an assay buffer containing GlcN6P (or a negative control) was introduced into the flowcell, using methods described previously (16). The instrumental signature for the introduction of fresh assay buffer, signaled by an artifactual, brief spike in the voltage of the position signal, marked the starting time for each measurement. The survival time was taken to be the difference in time between the starting signal and tether rupture, indicated by the position signal rapidly slewing toward its highest possible value (set by the maximum trap separation), as the feedback circuit attempts to maintain tether tension in the absence of any mechanical linkage between the two beads.

For each force and ligand condition, the average survival time, τ, was determined from multiple records and used to determine the rate, k_obs(clvg) = 1/τ. For a subset of measurements (namely, those performed under high-force conditions with GlcN6P, and negative controls with Glc6P or buffer only) only a minimal bound on τ was determined, because tethers remained unbroken over long observation times. In such cases, we report only an upper limit for k_obs(clvg). The ribozyme was quite stable in negative-control conditions, with little spontaneous tether breakage. In a few cases, lower limits for the self-cleavage rate were collected from multiple molecules after a single flow of assay buffer (or Glc6P). The self-cleavage rate with GlcN6P was plotted as a function of force and fit to the Boltzmann expression k_obs(clvg)(F) = k_min + (k_max − k_min)[1 − (1 + exp[−(F − F_max/2)∆x/(k_BT)])⁻¹], where k_min and k_max are the low- and high-rate asymptotes, F_max/2 is the force of half-maximal self-cleavage rate, and ∆x is a sensitivity (steepness) parameter with dimensions of extension. Fitting was performed using Igor Pro.

At low forces (≤4.1 pN), we measured a self-cleavage rate of ∼1.5 min⁻¹ in the presence of GlcN6P, compared with <0.1 min⁻¹ (upper limit) in buffer or with Glc6P. From the fit to the cleavage rate vs. force, the extrapolated cleavage rate at F = 0 is 1.7 ± 0.9 min⁻¹. The value we obtained for the GlcN6P cleavage rate is higher than ∼0.2 min⁻¹, the value previously reported by Soukup (14) for this construct. We do not believe that the difference is attributable to the assay buffers [our use of Hepes vs. Tris, or 150 mM KCl, 4 mM Mg(OAc)₂ vs. 0 mM KCl, 20 mM MgCl₂ (14)]. Soukup’s slower rate was likely dominated by a rate-limiting folding step (associated with the introduction of Mg²⁺ to induce ribozyme folding) which may be ∼20-fold slower than the cleavage reaction itself, based on measurements for a trans-cleaving version of the glmS ribozyme (23, 24).

Folding Energy Landscape Reconstruction.

The free energy landscapes for folding of the apo and +Glc6P glmS ribozyme core were reconstructed as previously described (15, 19). Briefly, the locations and heights of energy barriers between states, as well as relative depths of energy wells corresponding to the states, were determined from our constant-force folding kinetics data (SI Appendix, Table S1). The extension difference between the fully folded and the fully unfolded states was derived from the total unfolding contour length and the folded state width based on analysis of FECs, as discussed above. Extension changes and energies were computed for a common force of 4 pN, using WLC model calculations and linear extrapolations of the k(F) values, respectively. As previously, when ∑|∆x^‡| from kinetic analysis did not precisely equal ∆x from relative extension peak positions (due to experimental uncertainties), the values of ∆x^‡ for folding and unfolding were scaled such that ∑|∆x^‡| = ∆x (15).

Reported Uncertainties.

Unless otherwise indicated, uncertainties reported for experimentally determined parameters in this work are statistical SEMs, or SEs of SEM-weighted fit parameters.