Criticality in tumor evolution and clinical outcome

Significance

How mutation and selection co-determine the course of cancer evolution remains an open, fundamental question. We construct a mutation-selection phase diagram, using tumor mutation load (ML) and selection strength (dN/dS) as key variables, and assess their association with clinical outcome. The results reveal a biphasic evolutionary regime whereby beyond a critical ML, tumor fitness decreases with the number of mutations, although the proteome evolves near neutrality—that is, without strong selection. Deviations from neutrality at extreme ML show how positive selection (at low ML) and purifying selection (at high ML) may act to maintain tumor fitness. These results corroborate the existence of a critical state in cancer evolution predicted by theory and have fundamental and likely clinical implications.

Abstract

How mutation and selection determine the fitness landscape of tumors and hence clinical outcome is an open fundamental question in cancer biology, crucial for the assessment of therapeutic strategies and resistance to treatment. Here we explore the mutation-selection phase diagram of 6,721 tumors representing 23 cancer types by quantifying the overall somatic point mutation load (ML) and selection (dN/dS) in the entire proteome of each tumor. We show that ML strongly correlates with patient survival, revealing two opposing regimes around a critical point. In low-ML cancers, a high number of mutations indicates poor prognosis, whereas high-ML cancers show the opposite trend, presumably due to mutational meltdown. Although the majority of cancers evolve near neutrality, deviations are observed at extreme MLs. Melanoma, with the highest ML, evolves under purifying selection, whereas in low-ML cancers, signatures of positive selection are observed, demonstrating how selection affects tumor fitness. Moreover, different cancers occupy specific positions on the ML–dN/dS plane, revealing a diversity of evolutionary trajectories. These results support and expand the theory of tumor evolution and its nonlinear effects on survival.

The paradigm of tumor clonal evolution by acquisition of multiple mutations has been firmly established since the landmark work of Knudson (1), Cairns (2), and Nowell (3). Similarly to microbial populations (4–6), tumors evolve under constant selective pressure, imposed by the microenvironment as well as by therapy, such that surviving tumor cell lineages harbor mutations that confer selective advantage and resistance to treatment. This has been demonstrated both in space, showing intratumor branched evolution across different anatomical sites (7), and in time, showing the existence of a population bottleneck following treatment and rapid emergence of resistant phenotypes (8). Under this paradigm, the evolutionary trajectories of cancers can be viewed as different realizations of the same evolutionary process, shaped by the specific microenvironment, the genomic makeup of each tissue and individual, and the unique history of mutations in each clone (3, 9).

Notwithstanding the importance of epigenetics, tumor evolution is marked by a wide range of genomic aberrations and instabilities. These genomic changes occur at every length scale and accumulate in a highly nonlinear manner, as exemplified by local elevated mutation rates (kataegis) (10), complex short insertions and deletions (11), hypermutation and microsatellite instability (12), punctuated equilibrium and chromosomal rearrangements (chromoplexy) (13), and biased distribution of mutations across different genomic regions (14). Eventually, these somatic aberrations provide for the ability of cancers to proliferate, invade, and metastasize (15) by affecting a plethora of cellular functions (16).

Although recent advances in cancer genomics have greatly improved our understanding of how somatic genomic aberrations are linked to tumor progression and patient survival (17–20), the fundamental question of how mutation and selection jointly determine the clinical outcome remains open (21–23). The population-genetic theory of tumor evolution predicts that there exists a critical mutation-selection state that corresponds to a transition between evolutionary regimes (24−25). Below the critical state, mutations that increase tumor fitness, known as cancer drivers (26–28), are the main factors of tumor evolution, whereas above the critical state, accumulation of (moderately) deleterious passenger mutations outcompetes the drivers, eventually leading to tumor regression through mutational meltdown (25), a process known in population genetics as Muller’s ratchet (29). However, the rarity of spontaneous tumor regression, coupled with strong evidence of increased cancer risk at high mutational loads (MLs) in hypermutator genotypes (30), contests the existence and relevance of such criticality in clinical outcome.

Furthermore, recent studies indicate that the bulk of cancers (31) and most genes (32−33) in tumors evolve neutrally. Conversely, somatic evolution of some normal tissues appears similar to that detected in certain cancers (34), in particular showing comparable signatures of positive selection (35). Together, these findings prompt the fundamental question of how different mutation-selection regimes of tumor evolution determine cancer fitness and ultimately patient survival. Here, we address this question by exploring the dependence of tumor fitness and clinical outcome on ML and selection and demonstrate the existence of criticality in tumor evolution.

Results

Population Genetics Approach for Assessing Tumor Evolution and Fitness.

To study the interrelationship between mutation, selection, and clinical outcome on a large scale, we quantified the evolutionary state of 6,721 tumors that represent 23 different cancer types from The Cancer Genome Atlas (TCGA) database (Methods and SI Appendix, Fig. S1). All tumors in this dataset are primary, except for melanoma tumors.

The time of tumor initiation and the nonlinearity in the accumulation of mutations during its evolution to a primary state are unknown. Further, although the number of cancer-stem cells that confer tumorigenic renewal potential is believed to be small, their actual prevalence and impact on the fitness of tumors remains incompletely understood (36−37). Thus, from the available data that typically present a single snapshot in time of primary tumor states, the effective population size (Ne) cannot be reliably determined. Therefore, we define the evolutionary status of each tumor by the overall ML—that is, the sum of nonsilent (N) local somatic genomic alterations including point mutations, small deletions, and insertions—and by the strength of selection (dN/dS)—that is, the ratio of nonsynonymous to synonymous nucleotide substitution rates, acting on the entire protein-coding exome (hereafter, proteome) (Methods and SI Appendix, Figs. S2 and S3).

Respectively, dN/dS and ML can at least conceptually serve as proxies for the effective Ne and the mutation rate (µ), the key variables that are conventionally used in population genetics (21), which determine the evolutionary fates of all organisms (38). This is the case because dN/dS and Ne are inversely related (39) so that high Ne implies dominance of purifying selection, a common evolutionary regime in prokaryotes and unicellular eukaryotes, whereas low Ne implies the dominance of neutral evolution by genetic drift, a typical scenario in at least some groups of multicellular eukaryotes (40−41). The case of ML, an important clinical measure, is somewhat more complicated. It represents the integration of all N somatic point mutations across the proteome over an unknown but defined time interval. Because some mutations could have accumulated before tumor initiation (42), this interval can be defined as the time from the birth of the cell that eventually transformed into a neoplastic cell to the primary tumor state. Thus, ML represents the product of µ and an effective evolutionary time; nonetheless, it can be translated into µ under simplifying assumptions, as we discuss below.

Assuming that the survival of patients is inversely proportional to the fitness of tumors, we explored how ML and dN/dS correlate with survival. We used both the semiparametrized Cox regression analysis and the empirical Kaplan–Meier (KM) log-rank test as two complementary approaches to increase the significance of the analysis (Methods). These tests were applied to both clinical overall survival (OS) and disease-free survival (DFS) times.

Criticality in Clinical Outcome as Function of ML.

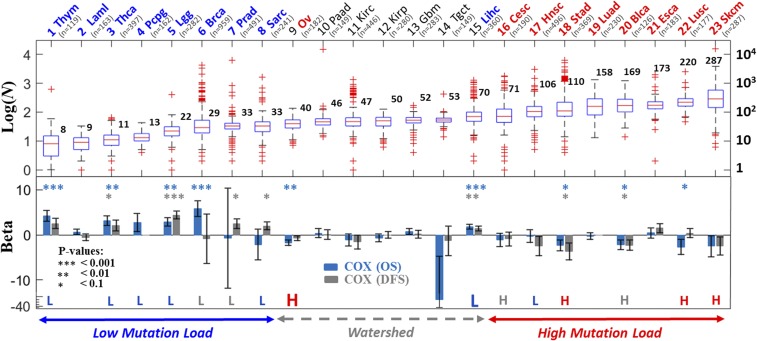
First, we explored how ML correlates with clinical outcome. To estimate ML, we considered all N somatic mutations in each patient, including missense (82.3%), in- and out-of-frame insertions and deletions (8.6%), nonsense (5.8%) and splice-site/region (3.2%) variants (SI Appendix, Fig. S1). The distribution of ML across the 23 cancer types is in full accord with the well-known ordering of cancers (27−28), in which thymoma and acute myeloid leukemia (AML) have the lowest ML, whereas lung and melanoma exhibit the highest ML (Fig. 1, Top).

Fig. 1.

ML criticality in clinical outcome across cancer types. Log distributions of the number of N mutations per proteome/sample in each cancer type (Top) and the corresponding results of Cox regression analysis (Bottom) are shown. Statistical significance is indicated for three thresholds: *P < 0.1, **P < 0.01, and ***P < 0.001. The KM results (SI Appendix, Fig. S4) are superimposed; the cases where a low (L, blue) or high (H, red) number of mutations was associated with better survival (P ≤ 0.1) are highlighted. Gray letters (L or H) indicate an observed but not significant (P > 0.1) correlation. Complementing Cox regression models stratified by cancer types are summarized in Table 1. Cancers are ordered by the median ML (N). Oncotree codes: (1) Thym, thymoma; (2) Laml, AML; (3) Thca, thyroid carcinoma; (4) Pcpg, pheochromocytoma and paraganglioma; (5) Lgg, brain lower grade glioma; (6) Brca, breast invasive carcinoma; (7) Prad, prostate adenocarcinoma; (8) Sarc, sarcoma; (9) Ov, ovarian serous cystadenocarcinoma; (10) Paad, pancreatic adenocarcinoma; (11) Kirc, kidney renal clear cell carcinoma; (12) Kirp, kidney renal papillary cell carcinoma; (13) Gbm, glioblastoma; (14) Tgct, testicular germ cell cancer; (15) Lihc, liver hepatocellular carcinoma; (16) Cesc, cervical squamous cell carcinoma and endocervical adenocarcinoma; (17) Hnsc, head and neck squamous cell carcinoma; (18) Stad, stomach adenocarcinoma; (19) Luad, lung adenocarcinoma; (20) Blca, bladder urothelial carcinoma; (21) Esca, esophageal carcinoma; (22) Lusc, lung squamous cell carcinoma; (23) Skcm, skin cutaneous melanoma.

We performed a univariate Cox analysis for each cancer type separately. To ensure that the hazard ratios (HRs) associated with the different ML variables are comparable across cancer types, the values of ML within each cancer type were normalized to 0–1 (Methods). The Cox analysis of both OS and DFS of each cancer type reveals two opposing trends of clinical outcome (Fig. 1, Bottom). Among the low-ML cancers (first 8; median ML < 40), those that have accumulated higher numbers of N mutations, on average, have poorer prognoses than those with lower numbers of N mutations (β > 0, where β is the coefficient of the Cox analysis such that HR = e^β; see Methods for details). However, the relationship between ML and survival reverses in high-ML cancers (last 8; median ML > 70), where a higher number of N mutations corresponds to a better prognosis (β < 0). Cancers with medium ML (#9 to #15) do not show a significant association with survival (β ∼ 0) except for ovarian (#9, median ML = 40) and liver (#15, median ML = 70) at the two sides of the mutation “watershed,” where the pattern of ML distributions flattens (ML medians ∼50). The complementary KM analysis, where we compared the prognosis for patients with low- and high-ML values within each cancer, is concordant with the univariate Cox analysis (Fig. 1 and SI Appendix, Fig. S4). Notably, ovarian cancer behaves as a typical high-ML cancer type, whereas liver cancer behaves as a low-ML cancer type, indicating that the mutation watershed represents a critical point in the ML-survival dependency. Viewing the flat mutation watershed as a point in ML, it is conceivable that cancers in its vicinity can swap positions, such that liver exhibits characteristics of a low-ML cancer type, whereas ovarian cancer exhibits characteristics of a high-ML cancer type.

Fig. 1 depicts a striking overall correlation between the behavior of β and ML across cancer types (SI Appendix, Fig. S5). Nonetheless, because the Cox and KM analyses of some individual cancers are not statistically significant, presumably due to the small number of patients, we further tested the existence of opposite regimes, by increasing the statistical power of the analysis. To this end, we compared between two groups of cancers below and above the watershed: the low- (L) ML cancers (#1–8) with the high- (H) ML cancers (#16–23). To account for differences between cancer types, we performed Cox regression analyses, in which the data were stratified by the cancer types in each group (Methods). The results of this analysis substantiate the significance and existence of opposing regimes in low- (β < 0) versus high- (β > 0) ML cancers (Table 1). This biphasic effect is highly robust, as exemplified by its rapid convergence as more cancers are considered for analysis in each group and by its insensitivity to the exclusion of any particular cancer type in the analysis of either group (SI Appendix, Fig. S6). The complementary KM analysis, which does not stratify the data, is more sensitive. It displays a weak biphasic effect for the L and H groups; nonetheless, the effect becomes significant for cancers further away from the watershed, aggregating data across cancers that exhibit association with survival (β ≠ 0) in their respective tests (SI Appendix, Fig. S7). Last, in breast cancer, the cancer type with the largest number of patients, we verified that β is robust with respect to stratifying ML by subtypes (i.e., Ductal/Lobular, and estrogen receptor, progesterone receptor, and human epidermal growth factor receptor 2 statuses) (SI Appendix, Fig. S8).

Table 1.

Stratified Cox regression analysis of ML, overall CNA, DNA burden, and dN/dS in different cancer groups

	OS		DFS
Variables (Set)	Βeta (SE)	P value	Βeta (SE)	P value
ML, all	−1.63 (1.16)	0.1621	−1.14 (1.00)	0.2575
ML, L	3.48 (1.46)	0.017	2.81 (0.89)	0.0015
ML, H	−4.79 (1.73)	0.0057	−4.18 (1.73)	0.0155
CNA, all	0.9 (0.19)	2e-6	1 (0.2)	7.3e-7
CNA, L	1.98 (0.31)	2e-9	1.35 (0.32)	1.8e-5
CNA, H	0.27 (0.22)	0.22	0.21 (0.25)	0.39
Burden, all	0.48 (0.1)	2.5e-6	0.37 (0.11)	6.8e-4
Burden, L	1.17 (0.22)	1.9e-7	0.86 (0.21)	2.9e-5
Burden, H	0.14 (0.15)	0.35	−0.07(0.17)	0.71
dN/dS, all	−0.5 (0.4)	0.21	−0.12 (0.39)	0.76
dN/dS, L	−0.62 (0.55)	0.26	−0.54 (0.53)	0.31
dN/dS, H	0.48 (0.58)	0.41	1.08 (0.68)	0.11

For each tested variable, the estimated scaling coefficient β (i.e., HR = e^β), its SE,and the corresponding P value of the stratified Cox regression model are shown for OS and DFS. Statistically significant trends are indicated by bold type. Cancer groups (L, H) correspond to the low-ML (#1–8) and high-ML (#16–23) cancer types (Fig. 1). In each test/group, variables are normalized to 0–1 and are stratified by the cancer type (Methods).

Robustness and Validation of Criticality in Clinical Outcome.

To test how robust the distinction between the opposite cancer evolution regimes with respect to ML is, we estimated ML using different sets of genes, including known cancer genes and random sets (Methods). The emergence of opposite evolutionary regimes around the watershed was highly robust to the choice of the set of genes compared (SI Appendix, Fig. S9). This robustness stems from the high correlation between ML values estimated for different sets of genes, which results in similar associations of the ML of each set of genes with patients’ survival. Thus, the existence of criticality does not seem to depend on a particular set of mutations or genes but is rather a consequence of the overall accumulation of diverse mutations in the proteome.

Given that the overall ML represents summation over different types of mutational events, it appears likely that other somatic aberrations could provide a comparable signal predictive of survival. Thus, we tested how copy-number alterations (CNAs) predict survival. We used two standard estimators (linear and gistic) to evaluate the overall CNAs as well as the overall level of deletions and amplifications in each proteome (Methods). We found that CNA and ML are moderately correlated (Spearman ρ = 0.44) (SI Appendix, Fig. S10). However, Cox analysis applied to each cancer type showed that, although at low ML, high CNA corresponds to poor prognosis (β > 0), it does not predict the transition in clinical outcome around the mutation watershed (SI Appendix, Fig. S10). Thus, the transition at high ML, most likely, is caused primarily by point mutations and other small-scale mutational events. These observations were confirmed with a stratified Cox analysis comparing low- with high-ML cancers (Table 1). Further, we tested the association of the commonly used variable, DNA burden, defined by the fraction of genes affected by CNAs, finding that it displays similar behavior to the overall CNAs (Table 1). The contrast between the substantial effect of CNAs in low-ML cancers and the lack of such effect in high-ML cancers (Table 1 and SI Appendix, Fig. S10) suggests nonlinearity, whereby the positive effect of increased CNAs on tumor fitness is diminished as ML increases, consistent with previous findings indicating the association of intermediate copy-number DNA burden values with worse prognosis (20).

Testing for the effects of possible confounding factors, including age, stage, and grade, by building stratified multivariate Cox regression models (Methods), established that ML is the only factor responsible for the transition in clinical outcome (SI Appendix, Table S1). Advanced age and stage, and to a lesser extent, grade, were significantly associated with poorer clinical outcome (β > 0), both in low- and high-ML cancers. However, the transition between the low-ML cancers (β > 0) and high-ML cancers (β < 0) was observed only for ML (SI Appendix, Table S1), in agreement with the results shown in Table 1.

Lastly, we validated the existence of the transition in clinical outcome by analyzing an independent recent cohort of ∼10,000 patients (43) (Methods and SI Appendix, Fig. S11). Although in this dataset only ∼400 genes were sequenced, which limits the attainable statistical significance, compared with the TCGA pan-cancer dataset, we observed that for low-ML cancers, the prognostic factor β was always positive, whereas in most of the high-ML cancer types, β was negative (SI Appendix, Fig. S11). Thus, the results of this analysis on an extended dataset largely recapitulate the transition in clinical outcome as a function of ML.

Dominance of Neutral Evolution in the Pan-Cancer Dataset.

We next estimated the dN/dS acting on the entire tumor proteome in each patient (Methods). Because of the highly variable rates of mutations across a tumor genome and the small overall number of mutations, a conventional direct estimation of selection at the gene level in a patient is impossible, unless integration of mutations across patients is permitted (SI Appendix, Fig. S2). Therefore, to explore the potential link between the selection at the patient level (rather than the gene level) and the survival of the respective patient, we estimated the selection that affects the entire proteome in each patient (Methods and SI Appendix, Fig. S2). Specifically, we calculated the ratio between the number of nonsynonymous mutations per nonsynonymous site (pN) and the number of synonymous mutations per synonymous site (pS) across all genes, considering the proteome (or a large group of genes) as a single sequence. The ratio pN/pS was used as a proxy for selection (dN/dS). In cancer, pN/pS is a valid approximation of dN/dS, assuming that a site is not mutated more than once during tumor evolution, such that correction for multiple mutations that effectively transforms pN/pS into dN/dS is unnecessary (Methods). Estimation at the proteome level is not sensitive to statistical biases that are usually encountered at the gene level (Methods and SI Appendix, Fig. S3) due to the increased statistical power of integrating mutations over thousands of genes.

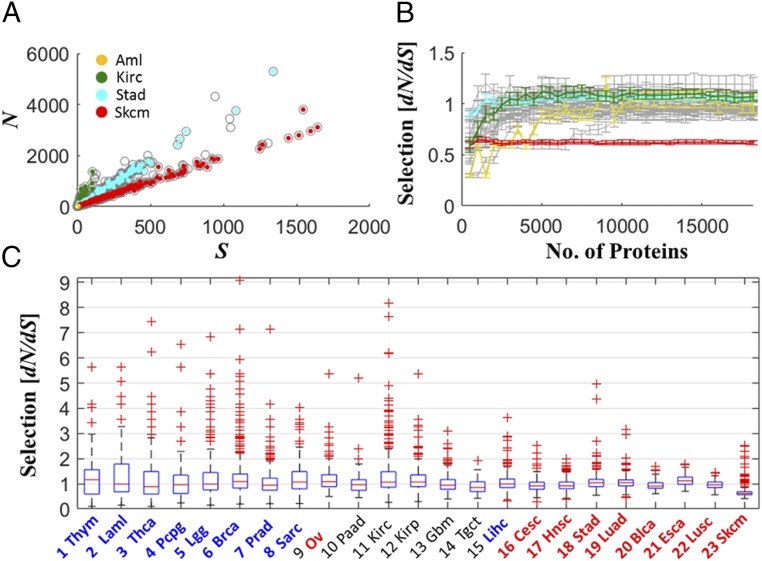
Estimation of the number of mutations in the entire proteome of each patient shows that, in accord with many previous observations on evolving organisms (44), the numbers of N and silent (S) mutations are highly correlated and display a linear relationship, albeit with different ratios across cancer types, suggesting some diversity of evolutionary regimes (Fig. 2A). To ensure that our estimate yielded a stable measure of selection, characteristic of the diversity among cancer types, we examined the dependency of dN/dS on the number of genes used for the estimation. The median dN/dS value in each cancer type reached a plateau rapidly as more genes were included, and the variance across patients in each cancer type was low (Fig. 2B). Thus, the median dN/dS across an entire proteome appears to be an adequate measure for a pan-cancer comparative analysis. The distributions of dN/dS indicate a (near) neutral evolutionary regime, where for most cancer types, dN/dS values were distributed around 1 across patients (Fig. 2 B and C). This observation was robust to using only missense point substitutions, instead of all N mutations, for the dN/dS estimation (SI Appendix, Fig. S12). Near-neutral evolution was observed also when evaluation of dN/dS was based on mutations in diploid regions or based on mutations in regions affected by CNAs, whereby dN/dS in the latter was slightly lower (SI Appendix, Fig. S13).

Fig. 2.

Proteomic selection (dN/dS) across cancer types. (A) The relationship between the numbers of N and S mutations per tumor proteome, where representative cancer types that span the different ML regimes are color-coded. (B) Stability of the proteomic measure of selection for comparative analysis between cancer types. The median of protein-level selection (dN/dS) across patients is shown as a function of the number of proteins considered for the evaluation of dN/dS, in each cancer type (gray). Selected cancer types are highlighted as in A. Genes are ordered alphabetically. The tendency to low dN/dS at the transient is due to low statistical power (SI Appendix, Fig. S3). (C) Distributions of dN/dS in the tumor proteome across patients, for different cancer types.

This result is consistent with those of three recent studies, each using a different approach to estimate selection in tumors (and genes), but all coming to similar conclusions on the prevalence of neutral evolution in the pan-cancer data: (i) an integrative approach which fits the distribution of subclonal mutations in each patient to a 1/f power law model, by accurate calling of the allele frequencies (f) (31); (ii) an integrative approach that infers the selection acting on genes, by a applying a Bayesian framework to the overall distribution of mutations (32); and (iii) inference of the exact substitutions rates in different mutational contexts, using a model with 192 parameters (33). Although some differences exist among the methods and conclusions of these studies (Methods), all of them show that the majority of tumors (and genes) evolve close to neutrality. The convergence of all these studies on the predominant neutral regime of tumor evolution additionally indicates that, at least at the entire proteome level, measures of selection capturing neutral evolution are insensitive to the exact characteristics of mutations (e.g., clonal vs. subclonal) or the distinct (nonlinear) dynamics by which different mutations accumulate in the proteome (e.g., variable substitution rate and allele frequency).

Deviations from Neutrality in Low- and High-ML Cancers.

Notwithstanding the prevalence of neutral evolution (dN/dS ∼ 1), Fig. 2 also reveals deviations from neutrality at extreme MLs. In thymoma, the cancer type with the lowest ML, the median of dN/dS is greater than 1, and more generally, heavier tails of dN/dS > 1 are observed in low-ML but not in high-ML cancers, indicative of positive selection at low ML. In contrast, in melanoma, the cancer type with the highest ML, dN/dS was distributed completely below 1 (except for a few patients), which is indicative of purifying selection acting on the tumor proteome. These observations were robust to using only missense point substitutions (SI Appendix, Fig. S12).

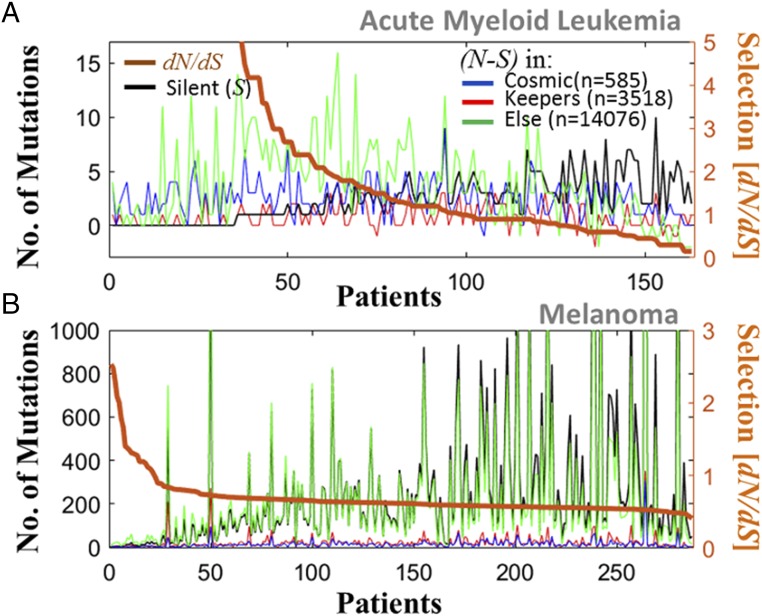
To elucidate how these deviations from neutrality emerge across the proteome and to assess their significance, we examined in detail the distribution of mutations, across different groups of genes, in AML (Fig. 3A) and melanoma (Fig. 3B), which represent the cancer types with extreme ML values. AML was selected as an example of a low-ML cancer to analyze the heavy tails that are indicative of positive selection because, on average, AML appears to evolve neutrally. The analysis of AML patients (n = 163) shows that 64 patients had dN/dS ≥ 1 and 63 had dN/dS < 1 (Fig. 3A), leading to the observed median of dN/dS = 1. The remaining 36 patients harbored many N mutations but not a single S mutation (i.e., dN/dS = Inf, which is discarded from analysis); hence, the heavy tail in AML patients (cf. Fig. 2C) is underestimated. The signature of positive selection (dN/dS > 1), manifested by heavy tails of the dN/dS distributions, was detected in AML patients that harbored numerous mutations (despite AML being classified as a low-ML cancer) and, therefore, could not be an artifact caused by the small number of mutations in low-ML cancers. The dN/dS < 1 values in AML patients were a consequence of the large number of S mutations (and not of increased statistical power). In contrast, in the case of melanoma, dN/dS values were below unity in the vast majority of samples and sharply dropped with the increasing number of mutations in the proteome, in a clear sign of purifying selection correlated with the ML (Fig. 3B). More generally, the relationship between dN/dS and ML is diverse across the pan-cancer data. In most cancers, these variables are not (or very weakly) correlated, but a positive correlation exists in some low-ML cancers (hence, high dN/dS is not due to low statistics), and only in melanoma (and, to a smaller extent, in bladder) are dN/dS and ML negatively correlated (SI Appendix, Fig. S14). Nevertheless, all cancers, on average, evolve near neutrality, except for melanoma (cf. Fig. 2C).

Fig. 3.

Distribution of mutations in different groups of genes, in cancer with extreme ML values. (A) AML patients (n = 163). The number of N minus the number of S mutations (left y axis) indicates the excess of N mutations in each group of genes separately (color). The number of S mutations in the entire proteome is superimposed (black). Patients are ordered by the dN/dS acting on the proteome (right y axis). (B) Melanoma patients (n = 287). In AML, for more than half of the patients, dN/dS > 1, and cancer genes harbor a substantial fraction of the N mutations. In melanoma, dN/dS is below unity in the vast majority of patients, and dN/dS sharply drops with the number of mutations in the proteome, which, coupled with β < 0, indicates mutation meltdown (Muller’s ratchet).

To assess the evolutionary pressures that affect different classes of genes in tumors, we compared the dN/dS distributions for known cancer genes (26) (n = 585) and house-keeping genes (45) (n = 3,518) (Methods). The results of this analysis could not be as significant as those for all genes, due to the relatively small number of genes in each set (especially the cancer genes). Despite this limitation, dN/dS in the cancer genes across all cancer types was significantly higher than in randomly selected genes, which was not the case for the house-keeping genes (SI Appendix, Fig. S15). Thus, cancer genes appear to be subject to stronger than average positive selection. Nonetheless, the accumulation of many N mutations outside of the set of known cancer genes indicates that positive selection can affect diverse genes in a tumor, with the implication that many cancer-related genes remain to be discovered. In contrast, in melanoma, purifying selection (dN/dS < 1) was found to act on large portions of the proteome (SI Appendix, Fig. S15). This signature of purifying selection is manifested by a sharp increase in ML, with the number of S mutations growing faster than that of N mutations across the proteome (Fig. 3B). Coupled with the observation of better prognosis (β < 0) in these melanoma patients (cf. Fig. 1), this expansion of mutations across the proteome appears to be a sign of a looming mutational meltdown. Proteomic measures of selection can provide information on the evolutionary regimes of different groups of genes but not of individual genes (Methods). Nevertheless, our results are concordant with previous findings (32) showing that in AML more genes are subject to positive than to purifying selection, whereas in melanoma, the opposite is the case. Furthermore, in melanoma, the number of genes under purifying selection was found to be greater than in any other cancer type.

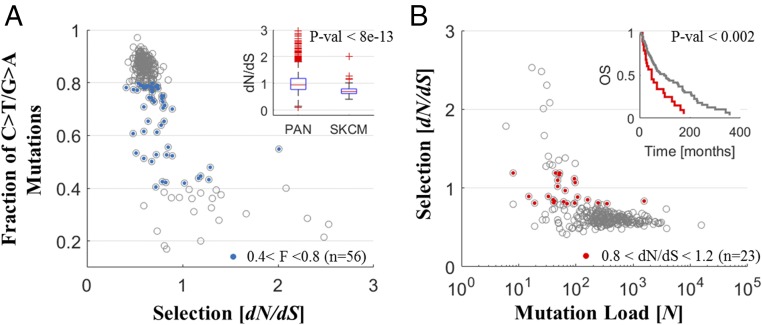
Nonetheless, melanoma is characterized by a long evolutionary trajectory that requires further investigation. While other high-ML cancers (e.g., bladder, lung) also exhibit better prognosis (β < 0), they evolve near neutrality (dN/dS ∼ 1), and only melanoma evolves under purifying selection (dN/dS < 1), which intensifies with the increasing ML. Indeed, it is largely driven by exposure to UV radiation, which causes mostly C > T/G > A mutations (46) in specific contexts (e.g., CC > TT) (47). At the gene level, this can lead to an overestimation of negative selection (33). Hence, we explored how the mutational context affects dN/dS of tumor proteomes using accordingly designed tests. We used the 12-context formalism to classify the mutations (i.e., A/T/C/G > X), given that previous studies have demonstrated comparable performances of parameter-low and parameter-rich models (48). The distributions of the 12 contexts were diverse across cancer types, with melanoma patients exhibiting the largest fraction (>80%) of C > T/G > A mutations (SI Appendix, Fig. S16). The dN/dS values and the fraction of C > T/G > A mutations negatively correlated in some cancers, but this correlation was substantially higher and more significant for melanoma than it was for other cancers (Fig. 4A and SI Appendix, Fig. S17).

Fig. 4.

Analysis of melanoma patients. (A) The fraction of UV-associated mutations (C > T/G > A) are plotted against dN/dS, depicting a strong correlation, more than in any other cancer type (SI Appendix, Fig. S17). Patients with 0.4 < Fraction < 0.8 (n = 56, blue) have lower dN/dS (<1) in melanoma than in any other cancer type; each displays dN/dS values distributed around unity (SI Appendix, Fig. S18) (Inset). Extreme test, of removal of C > T/G > A mutations from evaluation of dN/dS, also indicates negative selection in melanoma (SI Appendix, Fig. S19). (B) The selection (dN/dS) vs. the ML. Patients with 0.8 < dN/dS < 1.2 (n = 23, red) have worse clinical outcome (Inset).

We performed two tests to assess the relative impact of the C > T/G > A mutations on the dN/dS in melanoma and other cancers. First, we compared between the selection in patients with a medium range of C > T/G > A mutations (fraction 40–80%). For these patients, dN/dS values were distributed around unity in all cancers, expect in melanoma, where dN/dS was below unity (Fig. 4 A, Inset and SI Appendix, Fig. S18). Second, a straightforward estimation of dN/dS weighted by contexts (dN/dS = ∑wi × dNi/dSi/∑wi; wi the weight of context i in the proteome) is not feasible, because of data sparsity (i.e., dNi/dSi = 0 or ∞ for some contexts, rendering the weighted dN/dS biased). Hence, we performed an extreme test. We increasingly removed C > T/G > A mutations from analysis and reestimated dN/dS in patients. Also in this test, melanoma patients had significantly lower dN/dS values compared with any other cancer type, even at the extreme case of complete removal of these mutations (hence eliminating any surrounding contexts) (SI Appendix, Fig. S19). Together these results suggest that negative selection affects the majority of melanoma patients, although UV-associated mutations may contribute to an overestimation of its extent. All of the melanoma samples analyzed here are annotated as metastatic, which might explain the difference between melanoma and all other cancer types (in particular other high-ML cancers, with β < 0 and dN/dS ∼ 1), with the metastatic state characterized by an excess level of mutations, far beyond the critical point, exposing a long evolutionary trajectory and the action of purifying selection (Discussion).

Clinical Outcome Weakly Depends on Selection.

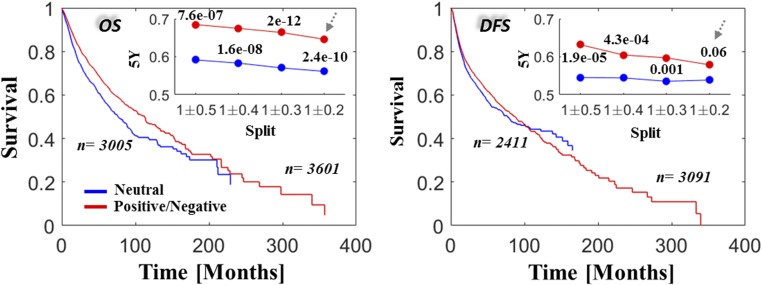
To determine whether any of the selection regimes in tumors affect survival, we tested the potential link between dN/dS and prognosis, under the assumption that the scatter of the dN/dS values within tumor types represents biological variation rather than noise alone. First, we performed KM analysis in each cancer type, comparing positive vs. purifying selection (SI Appendix, Fig. S20). All of these tests failed to detect a significant predictive signal of differential survival. A complementary Cox regression, comparing between the pan-cancer data and the two groups of cancers types with low and high ML, stratifying the data by cancer types in each test, verified the lack of association of purifying or positive selection with clinical outcome (Table 1). Nonetheless, KM analysis shows that, in certain cancer types (Gbm, Cesc, and Lusc, but significantly Skcm), intermediate values of selection around neutrality (dN/dS ∼ 1) were associated with poorer prognosis than either positive or purifying selection (Fig. 4B and SI Appendix, Fig. S21). Indeed, neutral evolution was associated with poorer prognosis when the comparison was performed across all cancer types, although this connection was less significant for DFS (Fig. 5).

Fig. 5.

Selection versus survival in the pan-cancer data. KM OS (Left) and DFS (Right) rates are compared across all studies for cases of neutral evolution (intermediate values around dN/dS = 1, blue) and cases of positive and negative selection (red). Insets depict the 5-y survival rates and the corresponding P values of log-rank tests for each cutoff. The survival curves in the larger panels correspond to the case of dN/dS = 1 ± 0.2 as indicated by the arrows in the Insets. Complementary Cox regression analysis, stratifying by cancer types, is provided in Table 1.

Discussion

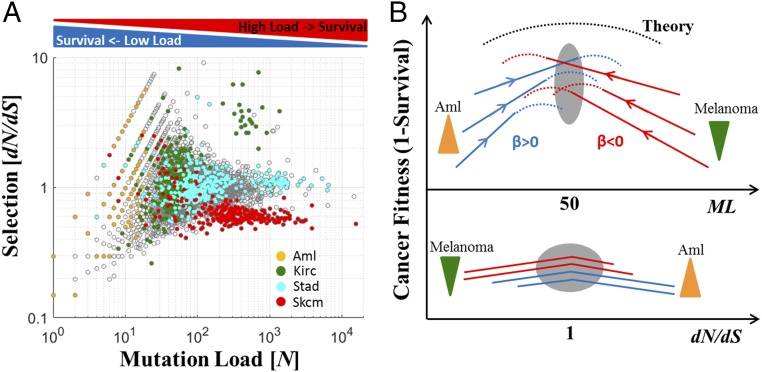
The results of the present analysis can be best interpreted by projecting ML and dN/dS onto an empirical mutation-selection phase diagram that emphasizes the existence of distinct evolutionary regimes (Fig. 6A). This diagram shows how ML and dN/dS jointly determine cancer fitness, which is assumed to be inversely related to the patient survival (Fig. 6B). In low-ML cancer types, tumor fitness increases with the number of mutations (β > 0). In this regime, some tumors appear not to have acquired a sufficient number of driver mutations, and therefore, positive selection (dN/dS > 1) promotes driver mutations to increase or maintain the tumor fitness (e.g., AML). In contrast, at high ML, cancer fitness decreases with the number of mutations (β < 0), due to the accumulation of deleterious passenger mutations. Although for the vast majority of tumors, the mean value of dN/dS is close to unity, which corresponds to near-neutrality, in extremely high ML, the expansion of mutations can lower the fitness of tumors such that purifying selection becomes notably stronger (dN/dS < 1). As we observed for melanoma, this purifying selection eliminates deleterious mutations, thus avoiding tumor collapse by mutational meltdown (Muller’s ratchet). Importantly, the findings for melanoma, a special case of a tumor type with a long evolutionary trajectory, likely due to transitions to metastatic states, are consistent with this view, whereby dN/dS is below unity in samples with large ML but turns toward unity in patients with lower ML, with tumors that evolve near neutrality, on average, being associated with a worse prognosis (Fig. 4B). This deviation from neutrality in melanoma is consistent with recent independent studies that estimate selection at the sample level (31) and at the gene level (32). The phase diagram (Fig. 6B) hence predicts that purifying selection can be observed in high-ML cancers, during the transition to a metastatic state if such a transition is accompanied by an excess level of mutations that pushes tumors further toward the Muller’s ratchet zone. Conversely, in low-ML cancers, this transition could be accompanied by an increase in dN/dS because these tumors evolve below criticality.

Fig. 6.

Empirical mutation-selection phase diagram of tumor evolution. (A) Mutation-selection empirical diagram for all analyzed cancers (gray) and selected cancer types (color-coded) that show distinct evolutionary regimes depending on the ML. (B) A schematic conceptual depiction of the emerging fitness landscape of tumors as a function of the ML (Top) and selection (Bottom). Dashed curves are theoretical, and solid curves are observed. Down-triangles (green) indicate purifying selection and up-triangles (orange) positive selection. The gray ovals show the critical area.

In contrast to the clear dependency on ML, tumor fitness is only weakly correlated with dN/dS, such that the majority of cancers evolve near neutrality (Fig. 2), consistent with previous findings (31–33). This lack of detectable proteomic-level selection signatures is likely due to the fact that tumor fitness mostly depends on a small number of drivers, whereas the bulk of the fixed mutations are neutral or slightly deleterious passengers (33). Indeed, more detailed analysis demonstrated significant differences in selection between groups of genes, in particular positive selection in cancer genes, with an overall neutral effect on the entire proteome (Fig. 3 and SI Appendix, Fig. S15). Thus, in summary, under neutrality, a sufficient number of drivers can accumulate, whereas the overall deleterious effect of passengers is balanced, explaining the association (albeit weak) of neutrality with poor prognosis (Fig. 5). Taken together, our results corroborate the theory of tumor evolution that predicts the existence of a critical mutation-selection state (25). Nonetheless, the existence of tumors with high ML, some of these with poor prognosis, suggests that other somatic aberrations could increase or maintain tumor fitness, to compensate for the deleterious effect of the passengers. This seems to be the case for microsatellite instability. In many hypermutation tumors, microsatellite instability is associated with better prognosis, thus apparently reducing tumor fitness (12), and high-ML tumors across different cancer types, on average, have low microsatellite instability (49). Thus, a compensatory relationship appears to exist between point mutations and microsatellite instability with respect to the tumor fitness. Further, both high ML (50) and high microsatellite instability (51) evoke immune response, due to the generation of neo-antigens, such that, in addition to intracellular mechanisms, negative selection could be exercised by the immune system (52).

In addition to these general trends, examination of the empirical dN/dS–ML plane reveals a diversity of tumor evolution regimes. For example, in kidney renal clear cell carcinoma, we identified a cluster of patients with high ML and dN/dS > 1, suggesting that the specific microenvironment and other factors, such as competition between subclones (21, 53), could be important for understanding the precise relationship between ML, dN/dS, and survival. Hence, coupled with the overall weak association of selection with survival, selection appears to maintain cancer fitness in diverse microenvironmental conditions, genomic contexts, and phases of evolution, leading to a diversity of roughly equally successful evolutionary strategies (with respect to dN/dS) of extant cancers, while the neutral evolutionary regime dominates overall. Further analysis, specifically of cancers within the watershed, is needed to assess the nature of the critical point and determine whether it is a stable point.

Our analyses indicate that the overall ML is a key determinant of patient survival. The ML counts all N mutations, wherever they occur in the tumor genome (including portions involved in structural variation, such as gene duplication) and whenever they emerge during the lifetime of tumor cells. Given that the survival dependency on ML captures the transition in the clinical outcome, the effects of various mutations appear to be context-dependent, so that, in a given genomic state, mutations can lead to either an increase or a decrease in the tumor fitness. Accordingly, all mutations should be included to assess the patient’s prognosis. Thus, the total ML becomes a key variable for clinical assessment, which is not sensitive to cellularity, ploidy, clonality, and other specific features of tumors. The high correlations between the ML values for different classes of genes (SI Appendix, Fig. S9) as well as between those for different mutation classes (Fig. 2A and SI Appendix, Fig. S12), with all these values being tissue-specific (27−28), suggest that ML is a stable measure that reflects the effective (tissue-specific) evolutionary age of a tumor (weighted by the respective variable µs). This is consistent with recent observations showing that the tissue-specific cell division rate is a key determinant of cancer risk and the ML in diverse tissues, whereby about two-thirds of the mutations accumulate at random due to replication errors (54−55). Our findings are also consistent with the observation that both genetic and epigenetic characteristics of the original normal cell are key determinants of the mutational spectrum of the respective cancer cell (56). Due to this tissue specificity, the attainable values of ML of a given cancer type are constrained, being determined by the tissue properties (e.g., number of stem cell and cell division rate) and, presumably, by the microenvironment, such that each cancer spans only a portion of the phase plane, often a small one (Fig. 6B).

The criticality observed around the mutation watershed corresponds to the transition in the clinical outcome at ML of ∼50 N mutations per tumor proteome. Under certain simplifying assumptions, this value can be linked to previous results. Data-driven theoretical studies suggest that, for ∼60 passengers (P = N + S − D; P, total number of passenger mutations; D, number of drivers among the N mutations), there are ∼10 drivers (24). Thus, for the critical point as identified here, N ∼ 50, S ∼ 20, and D ∼ 10. To accumulate 10 drivers, it takes ∼5–50 y with a cell division rate of ∼4 d (i.e., the number of cell generations G = 450–4,500) (24). Thus, we can estimate that the range of µs (per locus per cell division) associated with N ∼ 50 is µ ∼ 5 × 10⁻⁹ – 5 × 10⁻¹⁰ (µ = N/Ns/G; Ns, the total number of N sites in the proteome). This range of µs closely matches the lower range of rates where a nonmonotonic accumulation of passengers vs. drivers starts to be detectable, leading to the effect of Muller’s ratchet predicted by theory (25). Further, if D ∼ 10 and each clone in a tumor harbors a small number of drivers (∼2–3), then the critical number of clones for tumor progression is ∼3–4, in agreement with recent findings (20).

Theoretically, in the plane of the µ and selection coefficient of passenger mutations (s_p), the critical state is reached at very small s_p (25). In the framework of our model, this state would correspond to the effectively neutral evolution at the proteome level, with a small number of positively and negatively selected mutations. The sum of selection coefficients of the few drivers (s_d) and numerous passengers (where |s_p|<<|s_d|) should approach zero around criticality. However, given that many if not most passengers could accumulate through hitchhiking, which would affect the inference of the selection coefficients, and also because clonal interference could play an important role in tumor evolution, the complete theoretical interpretation of the empirical results presented here awaits further investigation.

Concluding Remarks

To summarize, in addition to known genomic markers (18, 20), our results reveal major, global features of cancer genome evolution that affect tumor fitness and, accordingly, clinical outcome. In accord with theoretical predictions, we show that the dependency of tumor fitness on the ML is nonmonotonic, with a critical region where the evolutionary regime changes, empirically corroborating the theory of tumor evolution, as a tug of war between driver and passenger mutations (25). In contrast, the dependency of tumor fitness on proteome-level selection is weak. We conclude that tumor fitness and clinical outcome strongly depend on the total ML and that most tumors evolve under a predominantly neutral regime, with relatively small contributions of both purifying and positive selection that become stronger only at extreme ML values. These conclusions are compatible with the well-accepted view that tumors evolve and progress via random accumulation of a few driver mutations.

By analyzing proteomes of a broad range of cancers, we identify tumors that evolve in different regimes that are characterized by opposite effects of ML. Knowledge of the evolutionary status of a given tumor could have implications for therapy that would aim to either increase or decrease the ML, depending on the position of the given tumor on the dependency curve. This might be particularly important for immunotherapy, where ML plays a critical role (57). Our results further imply that targeted therapy can be effective in low ML, where few drivers determine the course of tumor evolution, whereas at high ML, alternative strategies, such as immunotherapy, are likely to be more effective, consistent with the well-known success of immunotherapy in melanoma (58−59). The present analysis could also serve as a framework for future research to study how the transition from the primary to the metastatic state and how therapy could change the status of tumors in the ML–dN/dS–β hyperplane.

Materials and Methods

Datasets.

The complete raw data from all TCGA studies (n = 23) that included at least 100 patients each were downloaded from cBioPortal (60) (www.cbioportal.org/). All tumors in this dataset are primary, except for melanoma, which is metastatic. For analysis, we considered all “three-way complete” samples (i.e., containing somatic point mutations, CNAs, and gene expressions data, relative to matched-normal samples; n = 6,721) and all human protein-coding genes for which we identified both SwissProt and NCBI-Entrez unique accessions (n = 18,179). This data matrix (samples by genes) as well as patients’ clinical data were also downloaded from Firehorse (https://gdac.broadinstitute.org/) for comparison, verifying that there is little discrepancy between the two databases and that each mutation had at least 10 reads of the tumor variant (standard quality control) and are fully nonredundant (i.e., a variant in a given sample and gene are not counted more than once). Data from cBioPortal were downloaded also via Matlab application program interface (API), which routinely updates annotations of mutations, and were used to remove germ-line mutations from analysis. Clinical survival data included OS for 98.3% of the patients (n = 6,609) and DFS for 82% of the patients (n = 5,508). Distribution of patients’ race and age, tumor stage and grade as well as the distribution of variants across different mutational classes are provided in SI Appendix, Fig. S1.

Known cancer genes were downloaded from COSMIC database (26) (https://cancer.sanger.ac.uk/census). House-keeping genes were extracted from a recent survey (45). For validation (SI Appendix, Fig. S11), a recent cohort of ∼10,000 patients with advanced cancer (MSK-impact-2017), where 43% of the samples originate from metastatic sites and 414 cancer genes were sequenced (43), was downloaded via cBioPortal. Data for all samples and genes, including all of the information needed for full reproducibility of the results in this study, are provided in Dataset S1.

CNAs.

To estimate gene CNA, we extracted and analyzed both the “linear” and “gistic” measures. Linear measures provide continuous variables that represent the extent of amplification and deletions of each gene. The gistic measure implements additional computation inferencing the zygotic gain/loss using integers (−2 to 2). For evaluation of the overall level of CNA (Table 1 and SI Appendix, Table S1), we used summation over the linear measure, verifying that it correlated with the summation over the gistic values (SI Appendix, Fig. S10). The copy-number DNA burden was also calculated, using the gistic measure, as the fraction of altered genes (gain or loss) in the proteome (Table 1).

Selection in Tumor Proteomes.

Protein-level selection (dN/dS) at the molecular level is measured by comparing two sequences and computing the ratio between the nonsynonymous substitution rate (dN) and the synonymous substitution rate (dS) (61). Generally, this is done in two steps: (i) calculating the number of N sites (nN) and the number of S sites (nS) over the length of the compared sequences and calculating the number N mutations per N sites (pN = N/nN) and the number of S mutations per S sites (pS = S/nS), and (ii) applying methods, such as Jukes and Cantor (62) or Goldman and Yang (63), that transform the counts pN and pS into the respective rates dN and dS, by considering the possibility that, over time, a single locus mutates several times before fixation, in a context-dependent manner. Over long evolutionary distances, this second step is crucial. During cancer evolution, however, the likelihood for a particular locus to mutate more than once is low (9) and a considerable number of mutations might not be fixed, such that estimates of selections should be based on the integration of mutation counts rather than rates (64). Hence, we chose to approximate dN/dS by the ratio pN/pS.

Selection can be assigned and computed at different length scales (e.g., locus, domain, gene). In practice, the pan-cancer mutation data are highly sparse such that a gene in a patient rarely harbors both N and S mutations (SI Appendix, Fig. S2). Thus, a direct estimation of dN/dS at the gene level in a patient is not feasible, and integration of mutations, either over patients providing estimates of selection in individual genes or over genes providing estimates of selection in individual patients, is necessary. Estimation of selection in genes suffers from strong statistical biases, due to the relatively low number of patients (∼100–500 per cancer type) (SI Appendix, Fig. S3). Measures of selection at the gene level that correct for these biases have been recently developed, using both a Bayesian framework (32) and a context-dependent inference of substitution rates (33). Here, our goal was to investigate the link between the patient survival and the selection acting on the respective tumor proteome, so data from different patients should not be integrated. Therefore, we compute selection at the patient level, integrating mutations over genes (g) within a patient’s tumor proteome and treating them as a single concatenated sequence, such that there are sufficient numbers of N and S mutations for statistical inference of dN/dS:

$$\frac{dN}{dS}\approx \frac{pN}{pS}=\frac{{{\displaystyle \sum }}_g{N}_g/{{\displaystyle \sum }}_{g}n{N}_g}{{{\displaystyle \sum }}_g{S}_g/{{\displaystyle \sum }}_{g}n{S}_g}.$$ [1]

The dN/dS values were estimated using Eq. 1, for each patient, considering the mutations in the entire proteome (Fig. 2), or groups of genes, such as known cancer genes or house-keeping genes (SI Appendix, Fig. S15). Practically, to calculate the dN/dS ratios, the canonical amino acid sequences of all human proteins and their respective DNA coding sequences were extracted primarily from Ensembl (65) and from GeneBank for completeness. For each nucleotide sequence, translation into the exact respective canonical protein sequence in SwissProt was verified. The numbers of nN and nS in each protein were calculated, considering all alternative nucleotides in each position. Importantly, the estimation of selection at the proteome level does not suffer from low statistical power effects (SI Appendix, Fig. S3), because of the integration across many observations (i.e., 18,179 genes), as evident from Fig. 2. Selection in genomes cannot be directly compared with selection in genes. Nonetheless, the full accord of the selection in entire proteomes (Fig. 2) with the dominance of neutral evolution in the pan-cancer data, reported by recent studies, using different methodologies to estimate selection both at the sample level (31) and at the gene level (32, 33), independently validates the choice of Eq. 1 as adequate for large-scale comparative analyses of patients and cancer types.

Survival Analysis.

To test the association of variables with survival, we used both KM log-rank test (66, 67) and Cox proportional hazard regression analysis (68), and applied these approaches to both OS and DFS clinical data. KM is a nonparameterized empirical test that compares the survival curves using long-rank test for censored data. In this analysis, groups of patients are defined and compared by splitting the tested variable. This approach allows flexibility in defining and testing different ranges of the tested parameter, albeit at the risk of losing robustness. Hence, to assess the stability of this test, we used several cutoffs as indicated for each analysis. Cox regression is a semiparameterized approach that fits the survival clinical data to a hazard function [h(t) = −d[logS(t)]/dt, where S(t) is the survival probability at time t] and tests the effect of variables (X) under the “proportional hazard” assumption [h(X,t) = h_o(t)e^Xβ; h_o the baseline hazard]—namely, that the tested hazard functions are log-linearly scaled by a constant factor beta (β), which determines the HR (i.e., HR = e^β). This assumption, however, does not always hold for real data. Hence, the KM and Cox analyses are complementary.

Using Cox analysis, we normalized each tested variable (e.g., ML, dN/dS, CNA) in each test to 0–1, such that the results of different tests can be easily compared (see also ref. 20). Hence, in Fig. 1, ML is normalized in each cancer type to 0–1, and a univariate Cox analysis is performed in each cancer type separately. Similarly, when several cancer types were grouped (e.g., low or high ML in Table 1), the aggregated distribution of the MLs across patients in each group was normalized to 0–1, and the variables were stratified by the cancer types to build stratified regression models for each group separately.

Using Cox analysis, we also built stratified multivariate regression models, testing the effects of possible confounding factors such as age, stage, and grade (SI Appendix, Table S1). The categorical clinical data, stages I–IV and grades I–IV, were tested each using dummy indicator variables, relative to the reference category stage/grade I, respectively. Subcategories were grouped (e.g., stages IA–IC were assigned stage I). Any stage or grade outside the range I–IV (e.g., stage/grade “X”) were not included in this analysis and were not given any value (i.e., Nan). Variables were stratified by cancer types. The constants of each Cox proportional hazard regression model (β, its error, and the P value) are provided in each figure and in Table 1 for each test.

Analysis and Code Availability.

All of the analyses were performed in Matlab R2016b, using only built-in functions, under license to University of Maryland (UMD), Institute of Advanced Computer Studies (UMIACS), Center of Bioinformatics and Computational Biology (CBCB). Matlab files, including the datasets and analysis scripts, which fully reproduce the results as they appear in the manuscript, are available upon request from the authors (contact E.P.).