Solid State Polyselenides and Polytellurides: A Large Variety of Se–Se and Te–Te Interactions

Abstract

A large variety of different interactions between the chalcogen atoms, Q, occur in the solid state structures of polyselenides and polytellurides, including both molecular and infinite units. The simplest motifs are classical Q₂^2– dumbbells and nonlinear Q_n^2– chains (n = 3, 4, 5, ..), e.g. found in alkali metal polychalcogenides. In addition, nonclassical so-called hypervalent motifs exist in the form of linear Q₃^4– units or within larger units such as Q₄^4– and Q₅^4–. Infinitely extended Q units include zigzag, cis/trans and linear chains, as well as planar and slightly puckered layers. Several of those are susceptible to Peierls distortions, leading to the formation of both commensurate and incommensurate superstructures and anomalies in transport properties, including metal-nonmetal transitions.

1. Introduction

Solid state materials based on chalcogenides, i.e., sulfides, selenides and tellurides, play a large role in today’s society. Examples include semiconductor devices, e.g. in solid state electronics [1], fast-ion conductors [2,3], rechargeable batteries [4], data storage including phase-change materials [5,6,7], chalcogenide glasses [8], and the thermoelectric energy conversion [9,10,11,12]. Polychalcogenides, like the potential thermoelectric material HfTe₅, are materials that comprise homonuclear bonds between negatively charged chalcogen atoms, e.g. a Se–Se bond within Se₂^2– pairs of Rb₂Se₂ [13]. These bonds occur in chalcogen-rich materials, where the chalcogen atom cannot be reduced to attain the closed-shell formation as in Q^2–. For example, Se carries a charge of –1 in Rb₂Se₂, like O in SrO₂, and therefore forms one Se–Se bond. As such, Rb₂Se₂ is a typical Zintl phase. Zintl phases AX_x consist of an electropositive element A (here: Rb) and a more electronegative element X of the later (post transition) main groups (here: Se). Assuming a complete charge transfer of all of A’s valence-electrons to X, the cation A^z+ possesses a full octet, and the (formal) anion X^z/x- attains the octet by forming homonuclear X–X bonds in addition to the reduction by A. In most cases, these bonds are classical single bonds (two-center two-electron, 2c-2e), i.e. exactly one bond is formed for each electron missing to complete the octet of X [14,15,16].

The rich structural chemistry in particular of the polyselenides and polytellurides is the scope of this review, going beyond the common 2c-2e bonds: hypervalent interactions as found in XeF₂ [17] or SF₆ [18] are often observed in various fragments of these materials [19]. In addition, weaker fractional bonds or cohesive interactions of different lengths, as in elemental tellurium, render the Se/Te substructures intriguingly complex [20,21], which in turn may be beneficial for the thermoelectric energy conversion [22]. Four reviews about polychalcogenides from the years 1995 to 2000 underline the importance of this field [20,23,24,25].

2. Results and Discussion

2.1. Molecular units in polyselenides and polytellurides

2.1.1. Oligomeric Q_n^2– motifs

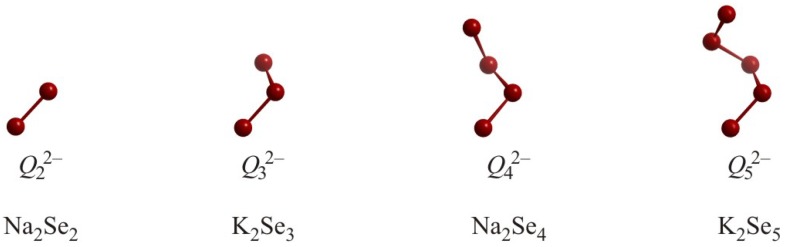
The simplest polychalcogenide motif is the dumbbell unit Q₂^2–, occurring for example in Na₂Se₂ [26], Rb₂Se₂ and Rb₂Te₂ with Se–Se and Te–Te distances of 2.38 Å, 2.47 Å and 2.78 Å, respectively (Figure 1). These dumbbells are also found in organic compounds with similar bond lengths, e.g. in [N(CH₃)₄]₂Te₂ (d_Te–Te = 2.74 Å) [27] and [Na(CH₃OH)₃]₂Te₂ [28]. Assigning charges is straightforward in these examples, e.g. (Na⁺)₂Se₂^2–, with Se₂^2– being isoelectronic to Br₂ and I₂, with 14 valence-electrons for the dumbbells, which are therefore held together by one 2c-2e bond. While generally these distances compare well with the sum of the single bond radii, r_Se = 1.17 Å and r_Te = 1.37 Å [29], the influence of the cations is evident, for the Se–Se bond in Rb₂Se₂ is approximately 0.1 Å longer than in Na₂Se₂.

Figure 1.

From left to right: Oligomeric Q_n^2– motifs in Na₂Se₂, K₂Se₃, Na₂Se₄, and K₂Se₅.

The dumbbells can formally be extended to oligomeric chain-like units Q_n^2– (with n = 3, 4, 5, 6, 12, 13) by adding neutral Q atoms to the chain, wherein the terminal Q atoms remain negatively charged. Each neutral Q atom participates in two 2c-2e bonds, comparable to the elemental structures of selenium and tellurium. Se₃^2– groups (with one central neutral Se atom) occur for example in, K₂Se₃ [30], Sr₂SnSe₅ [31] and Ba₂SnSe₅ [32], with bond lengths of approximately 2.4 Å, and Te₃^2– groups in K₂Te₃ with d_Te–Te = 2.80 Å [33] and in Ba₇Au₂Te₁₄ with d_Te–Te = 2.89 Å [34]. It is evident that the lengths of regular single (2c-2e) bonds may vary substantially, noting that these bonds are significantly elongated compared to 2× r_Se = 2.34 Å and 2× r_Te = 2.74 Å, respectively.

The Q₃^2– anions are bent, ideally exhibiting C_2v symmetry, with typical Q–Q–Q bond angles of 105° - 110°, in accordance with the VSEPR concept, which suggests tetrahedral arrangement of the two bonds and two free electron pairs around the central Q atom. The packing of the three-dimensional structure may cause a severe distortion of the angle as well, e.g. down to 92° in Ba₇Au₂Te₁₄.

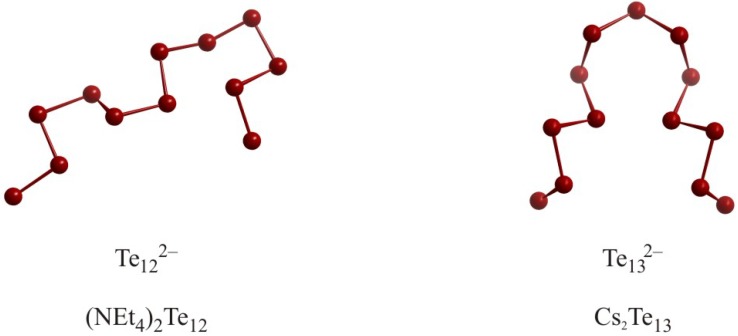
Anions with larger n, such as Se₄^2– in Na₂Se₄ (d_Se–Se = 2.35 Å and 2.36 Å) [35], Te₄^2– in (Ph₄P)₂Te₄∙2CH₃OH (d_Te–Te = 2.72 Å and 2.76 Å) [36], Se₅^2– in K₂Se₅ (2.34 Å ≤ d_Se–Se ≤ 2.37 Å) [37], and Se₆^2– in [Me₃N(CH₂)₁₃CH₃]Se₆ (2.27 Å ≤ d_Se–Se ≤ 2.35 Å) [38] are best described as oligomeric zigzag or helical chain fragments. Larger chain-like polychalcogenide anions, though extremely rare, do exist, like Te₁₂^2– in [N(C₂H₅)₄]₂Te₁₂ [39] and Te₁₃^2– in Cs₂Te₁₃ [40] (Figure 2), and they are often - as in these two examples - interconnected via longer interchain interactions (here: 3.14 Å and 3.18 Å). These interactions are much shorter than twice the van der Waals radius and will be discussed later in this review.

Figure 2.

Oligomeric Te_n^2– motifs in (NEt₄)₂Te₁₂ (left) and Cs₂Te₁₃ (right).

2.1.2. Oligomeric Q_n^4– motifs

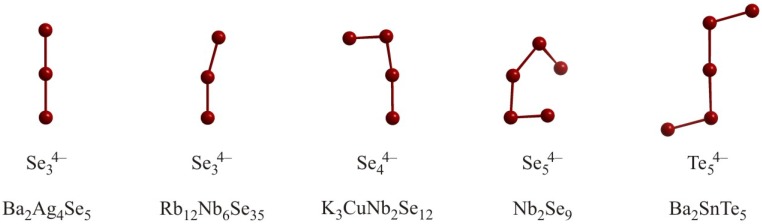
Since the Q_n^4– fragments comprise two more valence-electrons than their Q_n^2– counterparts, they cannot contain the same 2c-2e bonds. n = 2 is a hypothetical case only, as it would correspond to two isolated closed-shell Q^2– anions. n = 3 is realized in Se₃^4– units of Ba₂Ag₄Se₅ [41], and Rb₁₂Nb₆Se₃₅ [42]. In the former, Se₃^4– exhibits the highest symmetry possible, namely linearity and equidistant interactions, thus point group D_∞h, while Rb₁₂Nb₆Se₃₅ is comprised of two differently distorted, almost linear Se₃^4– units of C_2v and C₁ symmetry, respectively. In these two compounds, the Se–Se–Se bond angle of Se₃^4– varies between 180° and 164°, and the Se–Se bond lengths between 2.59 Å and 2.77 Å (Figure 3).

Figure 3.

From left to right: Se₃^4– (D_∞h), Se₃^4– (C_2v), Se₄^4–, cis-Se₅^4– and trans-Te₅^4–.

Ba₂Ag₄Se₅ contains two isolated Se^2– anions and one Se₃^4– per formula unit, according to the ionic formulation (Ba²⁺)₂(Ag⁺)₄Se₃^4–(Se^2–)₂. Electronic structure calculations and electrical conductivity measurements confirmed the semiconducting, hence electron precise character of this compound [41]. Rb₁₂Nb₆Se₃₅ is a special case, containing both Se₃^2– and Se₃^4– units, according to the formula (Rb⁺)₁₂(Nb⁵⁺)₆(Se₃^2–)₂(Se₂^2–)₇(Se₃^4–)₃(Se^2–)₆. Since diffuse reflectance measurements supported the semiconducting and thus closed-shell character of Rb₁₂Nb₆Se₃₅ [42], this treatment of Rb₁₂Nb₆Se₃₅ within the Zintl concept is justified.

With 22 valence-electrons, Se₃^4– is isoelectronic with hypervalent linear XeF₂ and I₃^–. Several examples are known that contain the linear I₃^– motif, including CsI₃ [43] and [Ph₄As]I₃ [44]. Ideally the two I–I distances are equivalent, with a bond angle of 180° as in [Ph₄As]I₃ (d_I–I = 2.90 Å), but deviations from the centrosymmetric arrangement are often found with smaller cations, like in CsI₃ with I–I bonds of 2.84 Å and 3.04 Å and a bond angle of 178°. The linear arrangement is well understood based on Rundle’s model [45], which treats the s orbitals as well as the p orbitals of π symmetry as lone pairs. Then the frontier orbital set consists of one filled σ bonding, one filled nonbonding, and one empty σ antibonding molecular orbital, formed by the p_z orbitals when z corresponds to the molecular axis. The nonbonding orbital contains a nodal plane at the center of the triatomic unit, resulting in a three-center-four-electron (3c-4e) bond. The validity of Rundle’s model waswas - in principle - confirmed for Se₃^4– via Gaussian calculations using the B3LYP functional [41].

Since the 3c-4e bonds are electron deficient, containing only one bonding molecular orbital for two bonds (which is why they are often called "half" bonds), they are longer than the regular 2c-2e bonds. Correspondingly, the I–I single bond in I₂ of 2.76 Å is much shorter than the above-mentioned I–I bonds (2.84 Å and 3.04 Å), and Se–Se single bonds (2.34 Å) are shorter than the Se–Se bonds of Se₃^4– (2× 2.77 Å in Ba₂Ag₄Se₅ and 2.59 Å - 2.65 Å in Rb₁₂Nb₆Se₃₅). In Rb₁₂Nb₆Se₃₅, the bond angles of approximately 164° deviate substantially from linearity, which is likely caused by the packing effect. Despite the distortion, the Se₃^4– unit of Rb₁₂Nb₆Se₃₅ can easily be distinguished from the Se₃^2– unit occurring in the same structure, which shows bond distances of 2.39 Å and a bond angle of 94°.

While no isolated, linear hypervalent Te₃^4– anion has been reported so far, the isoelectronic linear units P₃^7–, As₃^7–, Sb₃^7–, and Bi₃^7– all occur in the numerous representatives of the Ca₁₄AlSb₁₁ type [46], including Ca_14-xEu_xMnSb₁₁, which exhibits colossal magnetoresistance [47], and the high temperature thermoelectric Yb₁₄MnSb₁₁ [48].

The only Q₄^4– representative known to date is Se₄^4– in K₃CuNb₂Se₁₂ [49], which is basically an almost linear Se₃^4– unit (bond angle: 166°) with an additional Se atom attached via a single bond to one end. Therefore, its ideal valence-electron number is 28, namely 22 for the Se₃^4– fragment plus six for the additional Se atom. Within this model, we interpret the two bonds of the linear part as 3c-4e bonds and the exo bond as 2c-2e. This is in accord with the 2.73 Å and 2.54 Å distances for the (pseudo) collinear bonds, and the short 2.39 Å bond to the fourth Se atom with a bond angle of 93°. K₃CuNb₂Se₁₂ is another example for a complex selenide with three topologically different Se units, namely tetrameric Se₄^4–, Se₂^2– pairs, and isolated Se^2–, according to (K⁺)₃Cu⁺(Nb⁵⁺)₂Se₄^4–(Se₂^2–)₃(Se^2–)₂.

Representatives for Q_n^4– with n = 5 exist both among selenides and tellurides. In all cases, the Q₅^4– units contain a central (almost) linear hypervalent unit, with the two remaining Q atoms attached via a single bond to both ends of the linear part, like the fourth atom in Se₄^4–. By analogy, we conclude an ideal valence-electron number of 34, namely 22 for the Q₃^4– fragment plus 2× six for the two additional Q atoms, hence Q₅^4–: 5× 6 valence-electrons (from the neutral Q atoms) plus four for the negative charges equals 34.

The two terminal Q atoms may be in cis or trans conformation. The cis variant is realized in the heavily distorted Se₅^4– of Nb₂Se₉, wherein the hypervalent bonds of 2.64 Å and 2.66 Å exhibit a bond angle of only 143°, and the terminal single bonds of 2.36 Å/2.37 Å are both connected with a 83° bond angle. Considering the presence of a 2.90 Å Nb–Nb bond, Nb is most likely in the 4+ state, and noting the presence of two Se₂^2– pairs per formula unit, (Nb⁴⁺)₂Se₅^4–(Se₂^2–)₂ is also a closed-shell material [50].

The trans conformation is only known within the tellurides, occurring in NaTe ((Na⁺)₆Te₅^4–Te^2–) [51] and Ba₂SnTe₅ ((Ba²⁺)₆(Sn⁴⁺)₃Te₅^4–(Te^2–)₁₀) [52]. An isoelectronic cationic variant is I₅⁺ in I₅AsF₆ [53], while analogous pnictides have not been reported yet.

The largest representative of the series Q_n^4– currently known is Te₇^4–, coordinated to an Ag⁺ or Hg²⁺ cation via the central Te and the two terminal Te atoms [54,55]. The Te₇^4– anion can formally be constructed from adding two neutral Te atoms to a cis-Te₅^4–. In case of the Ag compound, the central Te₃ unit contains hypervalent bonds of 2.87 Å and 3.23 Å with a bond angle of 174°, and the additional Te atoms form regular 2c-2e bonds of 2.71 Å to 2.76 Å.

Two interpenetrating Te₃^4– units forming an almost square planar Te₅^6– unit with a central four-bonded Te atom are found in K₂SnTe₅ with distances of 3.02 Å and 3.06 Å [56]. These units can polymerize [57], the products of which will be discussed later in this manuscript. Adding two more Te atoms via single bonds, for example, results in bicyclic Te₇^2– [58].

2.2. Infinite motifs in polyselenides and polytellurides

2.2.1. One-dimensional motifs: chains

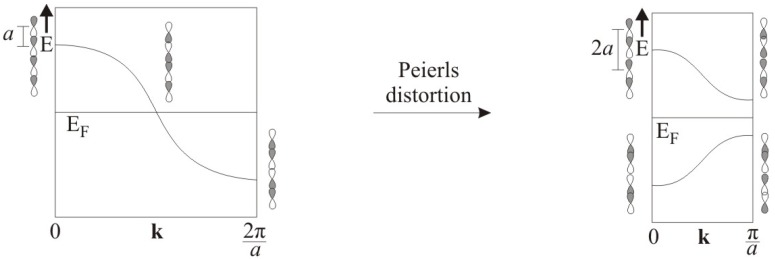
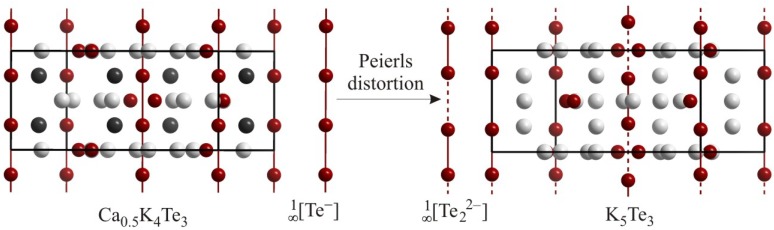
The above-mentioned fragments Q_n^2– and Q_n^4– can form higher dimensional arrays such as infinite chains, ribbons or layers. At least two bonds are required per Q atom in infinite chains, but the Q atoms may only participate in two 2c-2e bonds, when their oxidation state is 0. Such neutral chains exist in the elements selenium and tellurium. On the other hand, Te is especially well known for its ability to form electron deficient multicenter bonds, thereby producing linear ${}_{\infty }{}^1[$ Te^–] chains. These chains occur in CuTe [59], UTe₂ [60] and Ca_0.66K₄Te₃ [61] with typical intrachain distances between 3.0 Å and 3.1 Å. These interactions are delocalized 2c-1e (“half”) bonds, wherein one p orbital is half-filled, indicating a one-dimensional metal.

Such linear equidistant chains may undergo a Peierls distortion, i.e. exhibit alternating short and long distances, occurring with a metal-insulator transition (Figure 5) [62]. There are also examples of distorted linear chains of Te atoms with a formal charge of –1 such as in Cs₅Te₃ [63] or K₅Te₃ [64]. In these compounds, the Te atom chain features two different Te–Te distances, one of around 2.8 Å and the other larger than 3.5 Å. Thus, a description as ${}_{\infty }{}^1[$ Te₂^2–] is more appropriate for these compounds, wherein van der Waals forces connect the pairs to linear chains.

Figure 5.

Peierls distortion of a linear ${}_{\infty }{}^1[$ Te^–] chain.

^–] chain.

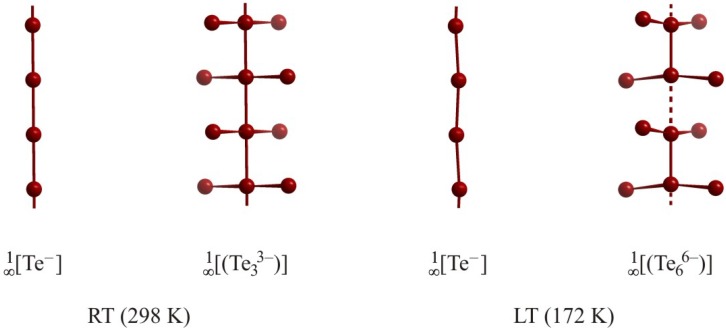
The dimorph TlTe is a nice example of a material exhibiting different Te atom chains [65]. The room temperature (RT) modification of TlTe represents an equidistant ${}_{\infty }{}^1[$ Te^–] chain with Te–Te distances of 3.08 Å. A parallel running, second linear equidistant Te atom chain within the same structure is more complex, as two additional Te atoms are connected to each chain atom via hypervalent bonds of 3.01 Å, yielding a ${}_{\infty }{}^1[$ Te₃^3–] chain (Figure 6). Thus, the RT modification may be written as (Tl⁺)₄Te₃^3–Te^–. In the low temperature (LT, 172 K) modification, both chains are distorted. Every second ${}_{\infty }{}^1[$ Te₃^3–] chain is not equidistant with alternation distances of 2.86 Å and 3.30 Å, while the other ${}_{\infty }{}^1[$ Te₃^3–] remain undistorted. Moreover, the linear equidistant ${}_{\infty }{}^1[$ Te^–] chain of the RT form is slightly bent in the LT form. Overall, the LT phase may be viewed as (Tl⁺)₁₆Te₆^6–(Te₃^3–)₂(Te^–)₄.

Figure 6.

Various Te atom chains of TlTe.

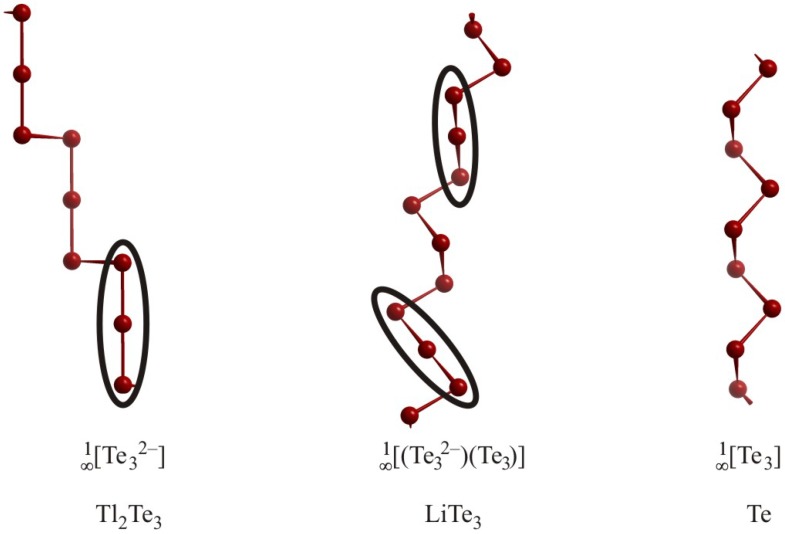
By reducing the number of valence electrons from 7 per atom in such a one-dimensional unit, the conditions become more and more complicated. The Te atoms in Tl₂Te₃, for example, have a valence electron concentration (VEC(Te)) of 6⅔, forming an infinite Te chain that can be described as polymerized linear Te₃^4– fragments (Figure 7). The bonds between the Te₃^4– units decrease the negative charges, leading to the description ${}_{\infty }{}^1[$ Te₃^2–] [66]. Two different distances were found in this chain due to different bonding situations. The short distance of 2.83 Å, a typical length for a 2c-2e Te–Te bond, is found between the Te atoms of charge –½, the second distance (3.02 Å) occurs between Te^1– and Te^½–, indicative of a 3c-4e bond.

Figure 7.

Infinite Te atom chains with different VEC(Te) in Tl₂Te₃ (left), LiTe₃ (center) and Te (right).

In LiTe₃ [67], the VEC(Te) within the chain is lowered to 6⅓. Consequently, this chain exhibits parts known from the Te atom chains in Tl₂Te₃ as well as from elemental Te [68], and can therefore be viewed as ${}_{\infty }{}^1[$ (Te₃)(Te₃^2–)]. The distances within this chain are 2.85 Å for the 2c-2e bonds in the neutral Te₃ part of the chain, 3.02 Å for the 3c-4e bond in the Te₃^2– unit and 2.91 Å for the bond connecting these fragments.

2.2.2. One-dimensional motifs: Ribbons

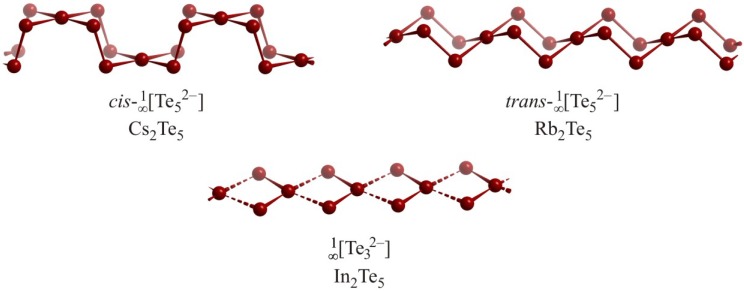
Only very few polychalcogenides exist that contain one-dimensionally extended Q atom substructures with more than two Q–Q bonds per Q atom. The dialkali pentatellurides show two different forms of intercondensation of above-mentioned Te₅^6– squares to yield ${}_{\infty }{}^1[$ Te₅^2–] ribbons with VEC(Te) = 6.4, namely the cis conformation in Cs₂Te₅ [69] and the trans conformation in Rb₂Te₅ [70] (Figure 8).

Figure 8.

Infinite Te ribbons with different modifications in Cs₂Te₅ (top left), Rb₂Te₅ (top right) and In₂Te₅ (bottom center).

The distances in these ribbons range from 2.78 Å in Rb₂Te₅ and 2.77 Å in Cs₂Te₅ for the 2c-2e bond between the Te₅ units to 3.04 Å in Rb₂Te₅ and 3.05 Å in Cs₂Te₅ for the 3c-4e bond within the Te₅ units. In₂Te₅ [71] possesses a similar unit with a higher VEC(Te) of 6⅔, which causes a distortion, namely an alternation of short and long Te–Te distances of 2.83 Å (solid lines) and 3.36 Å (dashed lines). Therefore it is best described as a one-dimensional arrangement of Te₃^2– fragments.

2.2.3. Two-dimensional motifs: Layers

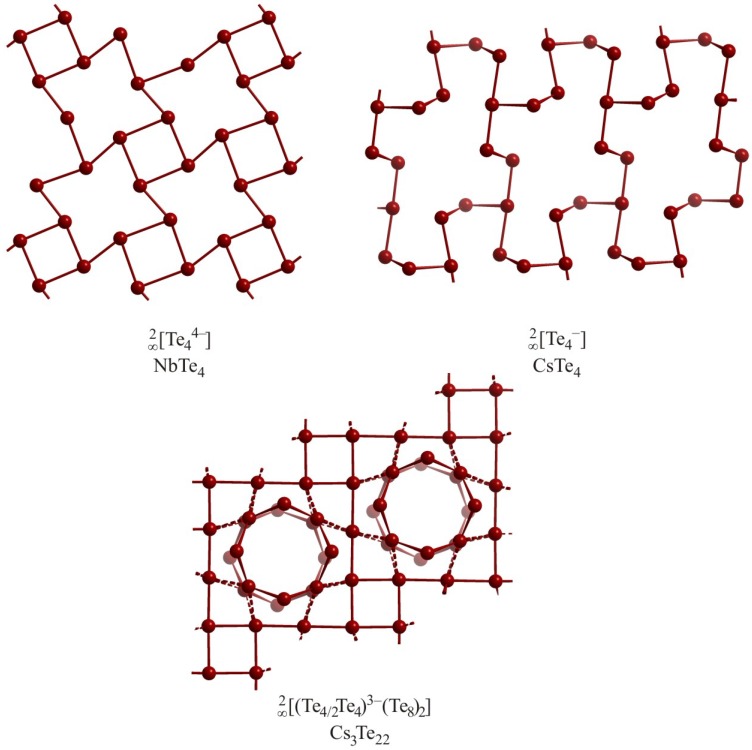
Compounds with hypervalently bonded Te atoms that are arranged in planar or puckered layers are often dominated by T-shaped fragments. These building blocks are then either directly connected to each other or bridged via other Te atoms. An overview of (schematic) T nets was published in the year 2004 [72]. One of the simplest examples of a T network containing Te atoms can be found in the planar layers of NbTe₄ [73]. Each Te atom in this layer is surrounded by three other Te atoms in form of a heavily distorted T. Four-membered rings, exhibiting Te–Te distances of 3.30 Å, are connected to surrounding four-membered rings via shorter bonds of 2.88 Å (Figure 9). This hole-style arrangement in NbTe₄ is subject to a distortion, driven by a charge density wave along the Nb atom chains perpendicular to the layer of interest. Considering the large difference of 0.4 Å between these distances, one could view this layer as loosely connected Te₂^2– units. This is in contrast to the Sb atom layer of Hf₅Sb₉ [74], wherein all bonds are between 2.99 Å and 3.03 Å, i.e. all bonds of that T net are electron deficient multicenter bonds [75].

Figure 9.

Different T nets in NbTe₄ (top left), CsTe₄ (top right) and Cs₃Te₂₂ (bottom center).

CsTe₄ [76] also features T-shaped Te atom units forming a layer, which is comprised of a polymerized Te₄^4– anion. This anion loses, due to this polymerization, three charges and builds a puckered layer that could be described as ${}_{\infty }{}^2[$ Te₄^–]. The distances in the original T-shaped fragment in this layer are 2.92 Å and 3.14 Å for the collinear bonds, and 2.84 Å for the perpendicular bond. The connection between two (similar or different) fragments is slightly shorter (2.76 Å). The majority of the Te atoms are twofold coordinated and provide bonding angles between 96° and 103°. Therefore, the bonds within the Te₄^4– fragments could be considered as asymmetric 3c-4e bonds and the remaining bonds as 2c-2e bonds.

Cs₃Te₂₂ provides an example of an electron-poor layer of Te atoms [77]. Cs₃Te₂₂ contains also neutral eight-membered Te rings, and can be described as (Cs⁺)₃(Te₈)₂(Te₄Te_4/2)^3–. Its planar ${}_{\infty }{}^2[$ Te₄Te_4/2^3–] layer consists of two- and threefold connected Te atoms, with the former being linearly coordinated and the latter T-shaped. The linearly bonded atoms interconnect the Te₄ squares comprising the T connected Te atoms. All Te–Te distances are between 3.00 Å and 3.07 Å. Band structure calculations indicate that this layer would be semiconducting with a charge of –4, but its actual charge of –3 renders it metallic [78].

2.2.4. Two-dimensional motifs: Chains connected to layers

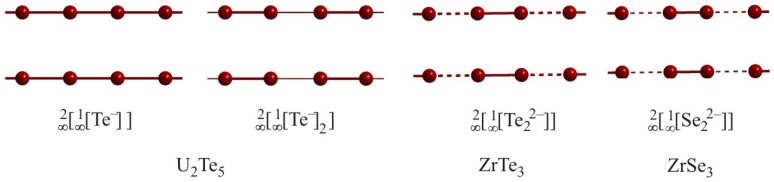
The previously discussed lower dimensional fragments can be connected to two-dimensional layers in several ways. The binary chalcogenides UTe₂ [79], U₂Te₅ [80], α-UTe₃ [81] and ZrQ₃ [82,83] all contain linear chains aligned to form planar layers (Figure 10).

Figure 10.

Planar layers of linear chains in U₂Te₅ (left), ZrTe₃ (center) and ZrSe₃ (right).

The structure of U₂Te₅ contains two different kinds of planar Te atom layers, i.e. ${}_{\infty }{}^2[{}_{\infty }{}^1[$ Te^–]] and ${}_{\infty }{}^2[{}_{\infty }{}^1[$ Te^–)₂]]. The ${}_{\infty }{}^2[{}_{\infty }{}^1[$ Te^– $]]$ layer is sandwiched between two puckered [UTe] double layers, while two ${}_{\infty }{}^2[{}_{\infty }{}^1[$ Te^–)₂]] layers are separated by a van der Waals gap and sandwiched between puckered double slabs. Both layers are comprised of linear chains with interchain distances of 4.18 Å. Within the ${}_{\infty }{}^2[{}_{\infty }{}^1[$ Te^–]] layer, almost equidistant intrachain bond lengths of 3.03 Å and 3.05 Å occur, while the ${}_{\infty }{}^2[{}_{\infty }{}^1[$ Te^–)₂]] layer exhibits Te₂^2– pairs (2.90 Å) interconnected by longer interactions of 3.18 Å to a linear chain.

A very similar almost equidistant chain is found in UTe₂ as well (3.05 Å and 3.08 Å), while the distortion in α-UTe₃ is more severe with alternating distances of 2.75 Å and 3.35 Å. Similarly, the isostructural ZrTe₃ contains Te chains with alternating intrachain distances of 2.79 Å and 3.11 Å and interchain distances of 3.93 Å. The most severe distortion is present in the analogous ZrSe₃ with intrachain distances of 2.34 Å and 3.06 Å and an interchain distance of 3.77 Å.

Furthermore, many more complex variants, mostly tellurides, are known in this class, including UTe₅ [84], incommensurately modulated ALn₃Te₈ (A = K, Rb, Cs; Ln = La - Nd) [85], and LnSeTe₂ (Ln = La - Nd, Sm) [86], which exhibit corrugated chains interconnected to planar or slightly puckered layers. A detailed discussion of all these materials would go beyond the scope of this review; square nets and their distortions were featured in a review published in 2002 [21].

2.2.5. Two-dimensional motifs: oligomeric units connected to layers

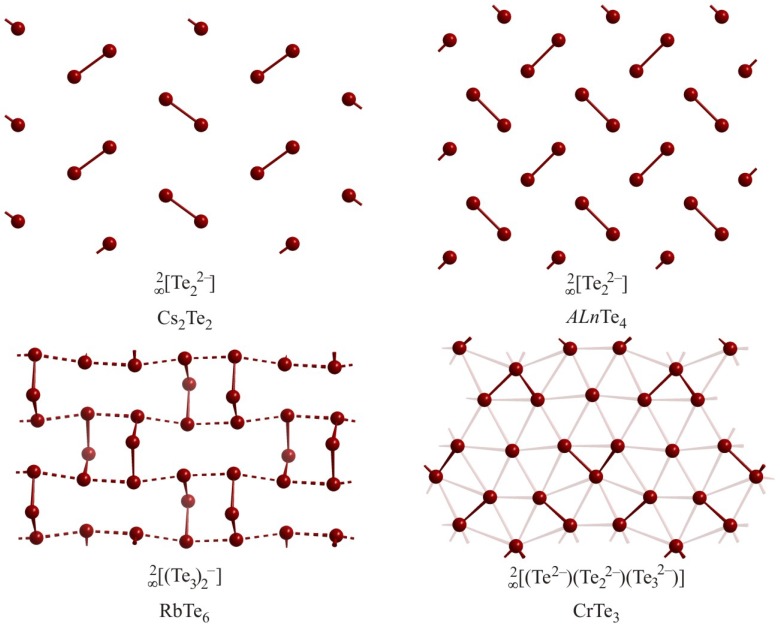
An enormous variety of compounds contain fragments arranged to form layers, e.g. the Q₂^2– and Q₂^3– units. The structure of Cs₂Te₂ [87] features Te₂^2– dumbbells with a Te–Te distance of 2.78 Å, arranged in a herringbone-like pattern (Figure 11), and stacked between layers of cesium atoms. The distances between these dumbbells of 4.71 Å and 5.01 Å are too long for bonding interactions. Another planar layer formation only consisting of Te₂^2– dumbbells (d_Te–Te = 2.78 Å) occurs in the crystal structure of ALnTe₄ [88,89] with an interpair distance of 3.50 Å, which is shorter than a van der Waals contact.

Figure 11.

Layers of oligomeric Te atom fragments in Cs₂Te₂ (top left), ALnTe₄ (top right), RbTe₆ (bottom left), and CrTe₃ (bottom right).

The structure of RbTe₆ [90] features a ${}_{\infty }{}^2[$ Te₆^– $]$ layer that is puckered because of its bent Te₃ units, where the central Te atom takes a position either beneath or above the layer plane. Within these bent Te₃ units, the Te–Te distances are 2.78 Å and 2.79 Å, respectively, with a bond angle of 102°, while the distances between these units are 3.20 Å and 3.21 Å. The charge of the ${}_{\infty }{}^2[$ Te₆^– $]$ layer cannot be readily understood; ignoring the 3.2 Å distances would indicate a charge of –2 for each Te₃ unit, while treating them as hypervalent half bonds would ideally result in neutral Te₃ units.

The structure of CrTe₃ contains Te atoms in three different oxidation states in a nearly planar layer [91]. The ${}_{\infty }{}^2[$ Te₃^3–] layer of this compound contains Te^2– ions and Te₂^2– and Te₃^2– units, with typical Te–Te distances of 2.82 Å. The assignment of charges is straightforward and yields a balanced formula for Cr in its +3 state: (Cr³⁺)₂Te₃^2–Te₂^2–Te^2–.

2.2.6. Three-dimensional motifs

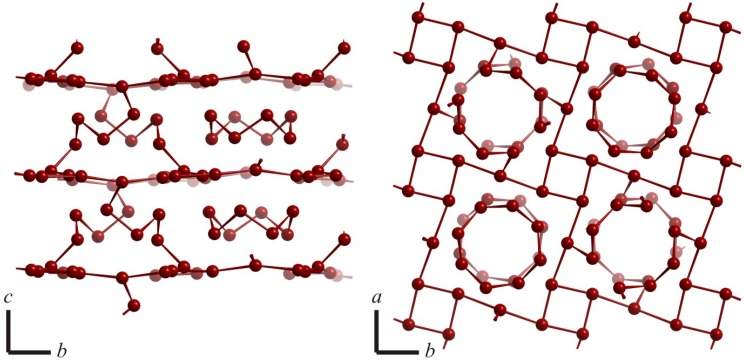
The only known compound that is comprised of a three-dimensional, covalently bonded network of Te atoms is Cs₄Te₂₈ [40]. The Te atom network is similar to the one in Cs₃Te₂₂, but in this case, half of the Te₈ rings are broken into Te₄ units that connect to one of the former linearly bonded atoms (Figure 12), which then assumes an oxidation state of zero.

Figure 12.

Three-dimensional network of Te atoms in Cs₄Te₂₈.

This covalently bonded three-dimensional network could be considered as (Cs⁺)₄Te₈[(Te₄)_4/2(Te₄Te_4/2)₂^4–], wherein the neutral Te₈ ring is comprised of typical 2c-2e bonds (2.79 Å - 2.83 Å) like elemental sulfur. The Te–Te bonds of the connecting (also neutral) Te₄ fragments are comparable (2.77 Å and 2.79 Å), as are the connections of these Te₄ units of 2.80 Å with the layer of Te atoms. As a result of the connection with the Te₄ units, all Te atoms of the layer are connected in a T-like shape exhibiting hypervalent bonds >2.9 Å, in contrast to the twofold linearly connected Te atoms in the structure Cs₃Te₂₂.

3. Conclusions

An overview of the variety of Se–Se and Te–Te interactions occurring in the solid state of both inorganic and organic polychalcogenides was presented. In contrast to polysulfides, the Se and Te atoms are capable of forming electron deficient multicenter (hypervalent) bonds. This adds significantly to the connectivity possibilities, e.g. the formation of T-shaped Te motifs or linear Se/Te fragments, which in turn increases the complexity of these polychalcogenides, a desired feature for, e.g., thermoelectric materials.

The tendency of Te towards higher coordination numbers is reflected in the higher abundance of complex Te atom layers, compared to Se. However, within the oligomeric units, the selenides and tellurides are quite comparable, so that more polyselenides with related two-dimensional motifs are likely to be uncovered in the near future as well.

Figure 4.

Infinite Te^1– chains in Ca_0.5K₄Te₃ (left) and K₅Te₃ (right).