Patient-Specific Pose Estimation in Clinical Environments

Abstract

Reliable posture labels in hospital environments can augment research studies on neural correlates to natural behaviors and clinical applications that monitor patient activity. However, many existing pose estimation frameworks are not calibrated for these unpredictable settings. In this paper, we propose a semi-automated approach for improving upper-body pose estimation in noisy clinical environments, whereby we adapt and build around an existing joint tracking framework to improve its robustness to environmental uncertainties. The proposed framework uses subject-specific convolutional neural network models trained on a subset of a patient’s RGB video recording chosen to maximize the feature variance of each joint. Furthermore, by compensating for scene lighting changes and by refining the predicted joint trajectories through a Kalman filter with fitted noise parameters, the extended system yields more consistent and accurate posture annotations when compared with the two state-of-the-art generalized pose tracking algorithms for three hospital patients recorded in two research clinics.

We propose a semi-automated approach for improving upper-body pose estimation in noisy clinical environments, whereby we adapt and build around an existing joint tracking framework to improve its robustness to environmental uncertainties. The proposed framework uses subject-specific convolutional neural network models trained on a subset of a patient's RGB video recording chosen to maximize the feature variance of each joint. Furthermore, by compensating for scene lighting changes and by refining the predicted joint trajectories through a Kalman filter with fitted noise parameters, the extended system yields more consistent and accurate posture annotations when compared to two state-of-the-art generalized pose tracking algorithms for three hospital patients recorded in two research clinics.

I. Introduction

Accurate patient joint tracking and posture estimates provide quantitative data that can be experimentally and clinically informative. Upper-body annotations for long-term continuous video of patients in the epilepsy monitoring unit (EMU), for example, can be used to further explore the relationship between neural activity and unconstrained human movement when combined with a neural recording system [1], [2]. Analysis of neural correlates to behavioral labels extracted from long duration naturalistic datasets collected in the hospital could then provide a pathway for more robust brain-computer interfaces (BCI’s). These include assistive robotic arms [3]–[5] and neural prostheses [6], [7] for those with limb loss or total paralysis. Alternatively, posture annotations can be used to objectively score patient motor capabilities to enhance current subjective assessments. For instance, the Unified Parkinson’s disease rating scale (UPDRS) [8] is the current standard for evaluating the severity of motor impairment associated with Parkinson’s disease, but it involves a qualitative evaluation by interview and clinical observation. The outcome of this process is limited to the clinician’s interpretation during examination and can be inconsistent between evaluators. Combining such assessments with additional insight from objective motion analysis could help improve the efficacy of treatment protocols. Other motor scoring assessments (e.g., BOT-2 [9], FMA [10], MAS [11]) would benefit similarly.

Several studies in automated motor scoring incorporate wearable devices (such as inertial measurement units [12], [13], accelerometers [14]–[16], and internet-connected personalized healthcare systems (PHS) [17]) that collect kinematic data of subject appendages, but may risk complications from prolonged wear of physical sensors [18]. These systems can be complemented with less invasive video-based tracking methods that supplant physical sensors when they are temporarily removed for relief. Additionally, for patients who are unable to wear such sensors due to injuries at the wrists or at other attachment areas, video-based joint tracking can create a nonintrusive means to monitor their safety and well-beings.

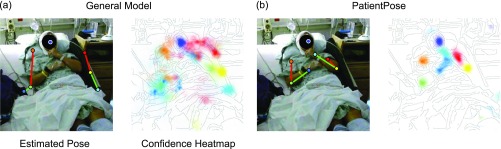
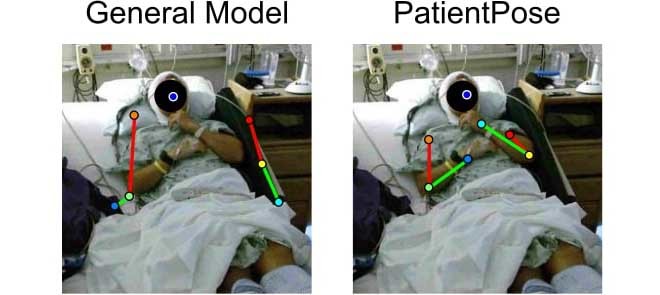
To this end, we introduce PatientPose, an adaptation of Caffe-Heatmap [19] for semi-automated pose estimation in clinical environments. Our additions to the existing pose estimation framework include three key elements that enable more accurate and consistent patient posture tracking than before: 1) a preprocessing step to accommodate for the frequent scene lighting changes found in hospital rooms; 2) a training technique that targets separate convolutional neural network (CNN) models specifically to each patient to capture the high variance of postures a subject can realize during their hospital stay; and 3) a Kalman filter with tuned noise parameters which refines the predicted joint trajectories. We show that for three subjects recorded in two research clinics, the extended system provides an increase in tracking performance when compared to two state-of-the-art generalized frameworks (Fig. 1).

FIGURE 1.

Comparison of pose estimation models. Upper-body posture annotations and their corresponding probability heatmaps using (a) a prepackaged model and (b) our patient-specific model. Both models were developed using the Caffe-Heatmap architecture. Our proposed framework accounts for variability in clinical environments to improve pose estimates and can be more confident and accurate than generalized methods. Subject 1 is depicted in these images.

Related Work

The importance and potential impact of human pose estimation is supported by the substantial history of research in this field. Recent work in computer vision [19]–[27] suggests using deep CNN’s to automatically estimate joint locations in long-term recording sessions. Toshev and Szegedy [25] were the first to use CNN’s for human pose estimation and regressed joint coordinates directly from a cascade of deep CNN regressors. More recently, Pfister et al. [19] instead regressed confidence heatmaps for the joint positions of each input frame and improved estimates by aligning and pooling heatmaps with neighboring frames. This framework was then extended by Charles et al. [26] who recursively processed the estimates for further improvements. Cao et al. [27] used a two-branch multi-stage CNN architecture to encode the location and orientation of body parts into a set of 2D vector fields and achieved real-time multi-person pose estimation.

While general pose estimation frameworks are effective when subjects are located in uncluttered settings, they can be unreliable when applied to noisy environments such as epilepsy monitoring and intensive care units. Such locations present several visual challenges that these generic frameworks do not account for, including variance in lighting conditions throughout a recording session, non-subject (e.g., clinician, nurse, visitor) interferences, and environmental occlusions (e.g., bed blankets, head wrapping, hospital gown). As a result, joint confidence heatmaps generated from hospital video using all-inclusive pose estimators may either be weak and distributed across the whole image, or confidently confused with another object in the room (Fig. 1a).

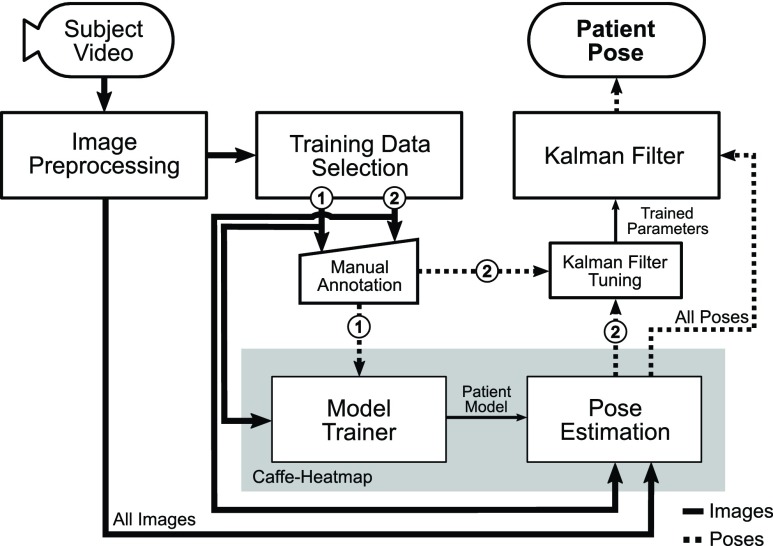
Previous works on improving pose estimation performance in complex clinical environments take advantage of a wide range of available sensors [28]–[33]. Achilles et al. [28] used a single depth camera to regress joint coordinates specifically for body tracking under blanket occlusion, and Liu et al. [29] relied on a novel infrared image acquisition technique using a bird’s-eye view in order to monitor patient sleeping postures. Belagiannis et al. [30] combined information from multiple RGB cameras to track surgeons and medical staff in operating rooms, and Kadkhodamohammadi et al. [31] improved upon pose estimation in operating rooms by using depth sensors in tandem with multiple RGB cameras. Chaaraoui et al. [32] also used a multi-camera setup but for vision-based monitoring and action recognition by learning subject activity patterns from estimated silhouettes. However, none have attempted to extract high-quality joint estimates to track freely-behaving patients in hospitals across hours of data using a single RGB camera. Capturing RGB video is trivial with the current state of consumer technology, and to our knowledge this work is the first to create a pose estimation framework that specifically targets subjects in clinical environments using only one angle of recorded RGB video. Additionally, the proposed extensions to Pfister et al.’s Caffe-Heatmap [19] do not modify the original framework’s central CNN architecture and could potentially be adopted to improve other general pose estimators (Fig. 2), and our framework is capable of a real-time implementation after a patient’s initial training procedure.

FIGURE 2.

Pipeline of proposed framework. The proposed framework extends Caffe-Heatmap to improve pose estimation of patient video recorded in clinical environments. Prior to estimation, a new patient-specific CNN model is trained using a subset of preprocessed video frames that maximizes feature variance (①). This model is then used to estimate the joint positions of the same patient from additional video, which are then refined using a Kalman filter with noise parameters trained using another subset of preprocessed frames (②). This work used 2,000 frames for ① and 500 frames for ②.

II. Methods and Procedures

A. Subject Recording and Dataset Description

In this study, we conducted our experiments using a novel dataset. Three patients with intractable epilepsy were enrolled according to protocols approved by the Institutional Review Board (IRB) at the New York University (NYU) Langone Comprehensive Epilepsy Center and the Rady Children’s Hospital (RCH), San Diego, Pediatric Epilepsy Center. Video was recorded using a Microsoft Kinect v2 during each patient’s stay, targeting 1–2 days post-implant of electrodes when the subjects were expected to be most active. Video was recorded using multiple modalities (i.e., RGB, depth, infrared), but only the RGB images were considered for this study. Specific details regarding the duration of each subject’s recording session and the number of frames used for framework training/evaluation are provided in Table 1. Note that the Kinect v2 RGB camera samples at either 15 or 30 frames-per-second (fps) depending on room luminance and horizontally flips all images when saving to disk. Our data acquisition system was fit onto a custom-built mount that stood five feet tall and was placed about 20 degrees to the left of Subjects 1 and 3 (S1 and S3) and 45 degrees to the left of Subject 2 (S2).

TABLE 1. Dataset Summary.

Subject	Study ID	Hours	Number of Frames
			Total	Training	Testing
S1	NY531	1.8	94,470	2,500	3,000
S2	RCH1	5.8	625,127	2,500	1,000
S3	RCH3	22.2	2,399,469	2,500	1,000

B. Image Preprocessing

1). Cropping

To maintain memory efficiency during GPU training, recorded RGB frames were cropped and resized from 19201080 to 256256 pixels in width and height. The location of cropping was centered around the patient and manually selected once per patient dataset.

2). Scene Lighting Normalization

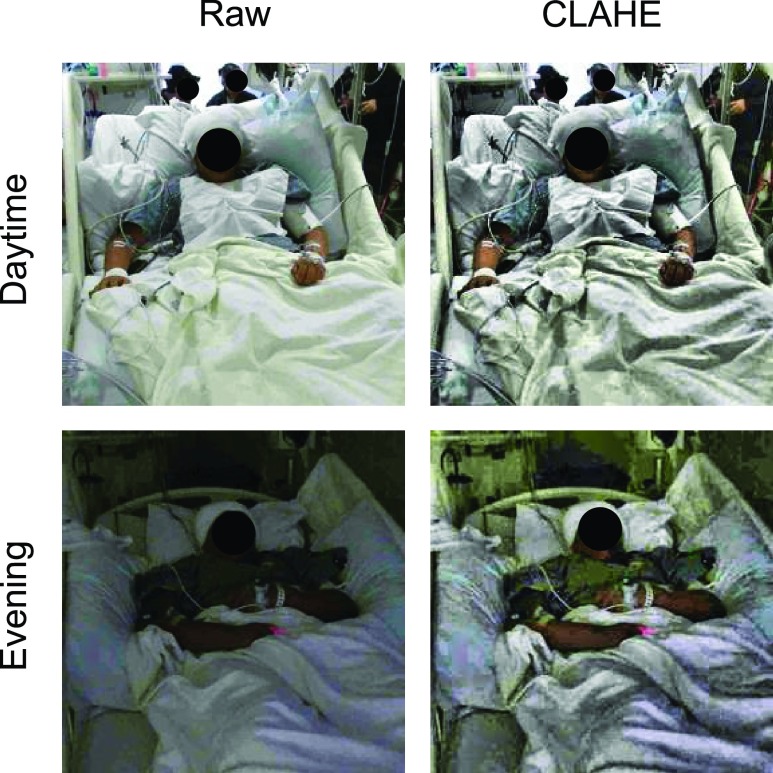
To account for the fluctuations in lighting conditions often found in hospital rooms, image brightness was normalized by first transforming each frame to the Hue-Saturation-Value (HSV) color space and then applying contrast-limited adaptive histogram equalization (CLAHE) [34] onto the value layer with an 88 tile size. Regions with similar surroundings (e.g., bed sheets) were susceptible to noise amplification when normalized using global or regular adaptive equalization [35], and CLAHE limited the amount those regions could increase in contrast (Fig. 3).

FIGURE 3.

Scene lighting normalization. Raw patient images (left) during daytime (top) and evening (bottom) were significantly different in lighting conditions for the same clinic. However, after applying contrast-limited histogram equalization (CLAHE, right), the frames across a dataset became more consistent in brightness. Subject 3 is depicted in these images.

C. Convolutional Neural Network Models

1). Motivation

Convolutional neural networks can be used to build models that predict subsequent data by learning and extracting patterns from a training set; this machine learning technique is used in a wide range of applications aside from pose estimation, such as human action recognition [36], predicting blood glucose levels [37], natural language processing [38], and more [39]–[42]. However, the performance of a trained model is heavily reliant on the quality of its training data. In human pose estimation, prepackaged CNN models trained using movie or video frames work well against other generic pose estimation datasets (e.g., British Broadcasting Corporation (BBC) Pose [43], Common Objects in Context (COCO) [44], Frames Labeled in Cinema (FLIC) [45], Max Planck Institute for Informatics (MPII) Human Pose [46]), but can be less reliable when applied to videos of hospital patients due to various challenges unique to the clinical setting. Therefore, we trained a separate CNN model for each of our subjects using an extracted subset of frames held out from the test set (Fig. 2). These high-quality training sets were designed to capture the wide range of postures the corresponding patient may naturally take on throughout a recording session.

2). Extracting High-Quality Training Data

To maximize posture diversity and therefore feature variance in a patient’s training data, frames were selected from both movement and non-movement periods. This was accomplished by first applying the Gunnar-Farnebäck dense optical flow algorithm [47] onto the raw RGB video of the same patient to calculate the average magnitude of scene movement between adjacent frames. A threshold on this average flow empirically set to 0.15 pixels per frame then partitioned patient RGB video into periods of movement and idleness. Afterwards, a subset of frames was uniformly sampled from the segmented video such that frames drawn from movement and rest periods were distributed 70%/30%. Using this strategy, 2,000 frames for model training were selected across the entire span of each patient’s dataset which captured different postures the patient may take on during their stay. Frames with significant patient occlusions were manually excluded.

3). Patient-Specific Model Training

Ground truth 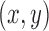coordinates of the seven joints (i.e., head, left/right hands, elbows, and shoulders) were manually marked for each training set using a custom labeling script. A CNN model was then trained for each patient using the Caffe-Heatmap model training architecture [19] on an NVIDIA GeForce GTX 1080 Ti GPU with the annotated images. One million iterations of batch size 14 were used with a learning rate of 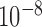and momentum of 0.95, and each iteration took approximately 0.75 seconds for a total of nine days of training per model; these hyperparameter values were chosen to match those of the original Caffe-Heatmap. The resulting models learned features specific to each patient through the high-quality training set. Using the same hardware and configurations, training a generic model on the FLIC dataset with about 4,500 frames would span around twelve days.

D. Inference via Patient-Specific Model

To enable easy adoption of our augmentations onto other pose estimators, we did not directly modify the Caffe-Heatmap framework. We therefore treated it as a black box, with the inputs as the patient-specific Caffe [48] model and 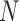number of frames, and an output of seven 256256 confidence heatmaps for each frame. Each joint location was then taken to be at the 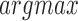of its corresponding heatmap, resulting in a 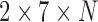structure of 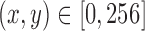joint coordinates. For each frame, inference spanned ~0.03 seconds when using the same NVIDIA GeForce GTX 1080 Ti (compared to ~10 seconds per frame on an Intel Xeon CPU E5-2630), enabling the potential for a real-time implementation. Specific details of the Caffe-Heatmap architecture can be found in [19].

E. Kalman Filter

1). Motivation

Joint locations estimated by a patient-specific CNN model were generally reasonable, but occasionally contained jitter or large jumps when a patient moved quickly or was occluded. Therefore, a standard Kalman filter [49] was used as a post-processing step to leverage the temporal information found between frames in order to refine any noisy measurements. The Kalman filter consists of two primary components (a state transition function and a measurement function) that model the underlying physics of a system to predict its state over time, making it an appropriate choice for denoising estimated joint trajectories. In addition, we chose to use a Kalman filter (as opposed to a non-causal Kalman smoother [50]) to preserve our framework’s potential to be implemented in real-time due to the filter’s causality.

2). General Equations

The Kalman filter is a recursive two-step process which iteratively predicts a system’s next state using past information and a predefined model, then updates its predictions using external sensor measurements. These two functions are defined by the linear state transition and measurement matrices 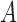and 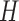. In addition, the estimated state 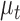at each 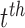iteration is accompanied with a covariance 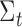that measures the accuracy of the estimate at that time step. In the Kalman filter’s prediction step, we have:

where the hat indicates that these values are purely estimates by the filter without considering any outside measurements yet. The 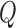term above is the covariance of the process noise that captures the error between the transition model and the true dynamics of the system, and it is assumed to be Gaussian distributed in this work. In the update step, we have:

where 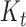is the Kalman gain that adjusts the next predicted state 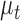and covariance 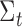depending on the accuracy of the model. In this step, external sensor measurements 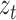provide the filter with additional information on the system’s next possible state, and the 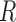term captures the noise in these measurements (also assumed to be Gaussian). Complete derivations of these equations can be found in [51]–[53].

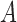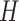In this work, we used a constant velocity model [54] to define the state transition and measurement matricies and in these equations, and we assumed independent movement between the seven joints. Therefore, we ran a separate Kalman filter on each joint, in which the 4D state estimates 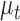contained a joint’s 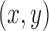pixel position and velocity at time 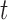. Additionally, we used the 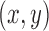coordinates provided by a patient’s CNN model as the external 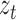measurements to update the filter’s predictions on the system’s state. These Kalman filter equations recursively computed a next-best-guess on a joint’s position using the predefined constant velocity model and the pose estimates by the CNN model.

3). Learning the Noise Parameters

The 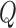and 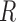process and measurement noise covariances are critical components to the Kalman filter that model unforeseen perturbations on the system. In the context of this work, the 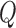term captures how erroneous the constant velocity model is to the real dynamics of a patient and the 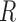term captures the variability in the CNN’s pose estimates to the true positions. However, these matrices are frequently difficult to estimate and are often constructed using prior knowledge of the problem, tediously tuned by hand, or assumed to be independent between variables for convenience. Abbeel et al. [55] demonstrated that 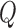and 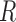can be learned by maximizing the joint likelihood between the states and the measurements of a training dataset. More specifically, for 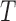number of training datapoints, the optimal parameters 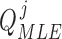and 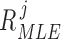for each 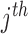patient joint can be formulated as:

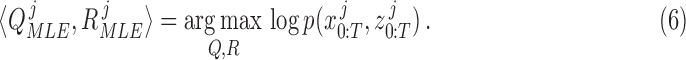Here, the joint probability distribution between the sequence of ground truth states 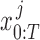and CNN pose estimate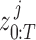s is:

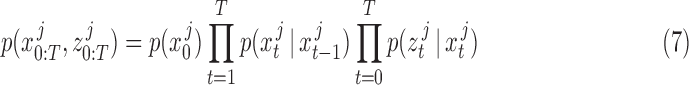with some prior 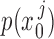, where the Gaussian motion and observation models are:

Substituting (7), (8), and (9) into (6) and then computing the closed form solutions results in the equations:

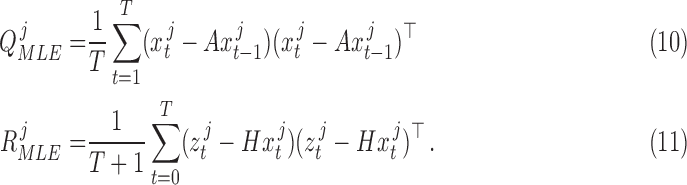4). Patient-Specific Noise Parameter Training

Equations (10) and (11) require ground truth states 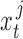and CNN pose estimates 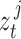from a set of training data for each patient joint. In addition, because (10) depends on states at times 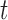and 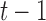, the training joints must be continuous over time. Therefore, in an attempt to capture the process variability across the entire span of a patient dataset, we constructed a “semi-continuous” training subset using the following steps. First, we segmented a patient’s video into periods of movement and idleness using the same optical flow method as described in Section II-C.1. Afterwards, we extracted the first 10 frames of a movement period for 50 periods chosen uniformly across the span of the patient’s video. This resulted in a set of 500 “semi-continuous” frames (50 discontinuous movement periods of 10 continuous frames each) for each patient which we used to train patient-specific noise parameters. Occluded segments, movements less than 10 frames in length, and frames used for evaluation were excluded during period selection. After extraction, these 500 frames were manually annotated for ground truth joint positions. To obtain the ground truth states 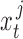, joints were assumed to have zero initial velocity at the start of each movement period, and the remaining velocity values were calculated as the difference in pixel position between adjacent frames within the same period. The frames of each segment were then sent through Caffe-Heatmap’s pose estimator along with the corresponding patient-specific model to obtain .

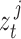To calculate a patient’s set of measurement noise covariances 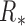, we directly implemented (11) for each joint such that 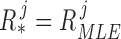using all 500 training datapoints. Equation (11) only depends on values at time 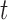, and therefore its training set need not be continuous. However, because (10) depends on values at times 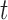and 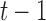, we first calculated a separate 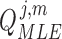for each 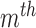movement period of length 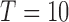frames in the semi-continuous set using (10). The resulting 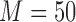matrices per joint were the covariances that maximized the data likelihood in their corresponding movement sequence. A joint’s process noise parameter 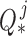was then taken to be the average of these covariances, such that:

These calculated parameters 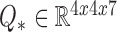and 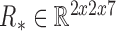for each patient modeled any unforeseen perturbations on the system throughout a patient’s dataset at runtime of the filter.

III. Results

In this section, we first provide an analysis of each component to convince the reader that our additions to the original framework are reasonable for improving pose estimation in clinical environments. Then, to validate our methods as a whole, we present pose estimation accuracy comparisons between our framework and two state-of-the-art generalized frameworks using selected test sets of patient data for three subjects recorded in various clinical monitoring units. A representative demo video of patient pose estimation can be viewed at https://youtu.be/c3DZ5ojPa9k.¹

A. Analysis of Components

1). Scene Lighting Normalization

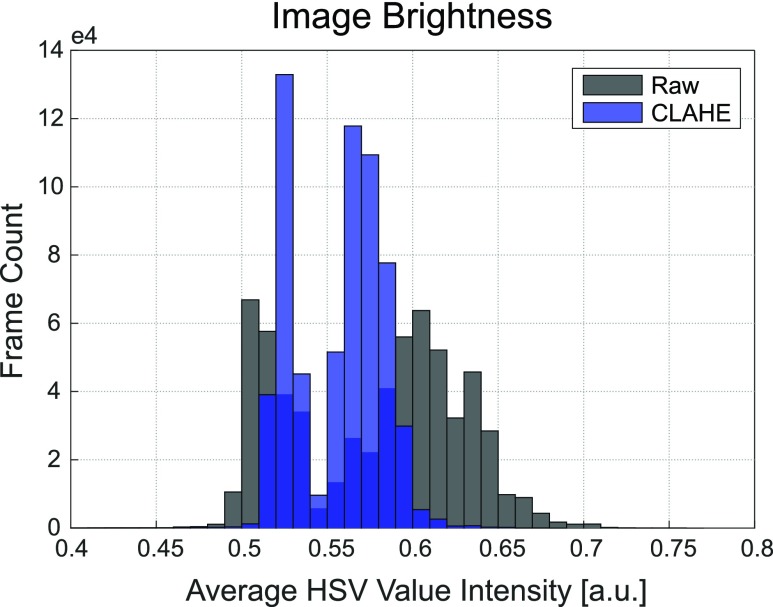
After normalizing image brightness by applying CLAHE onto the value layer of each HSV frame, we observed a significant reduction in scene lighting variance throughout each patient dataset. This reduction is depicted by the histograms of the mean V-channel magnitude for each frame in the S2 dataset using 0.005 bin widths before and after lighting normalization (Fig. 4). The value-layer in the HSV color space corresponds to image brightness, and therefore the lower histogram variance after normalization indicates a higher similarity in lighting conditions within the patient dataset than before. This translates into joint features that are more likely to be consistent in visibility.

FIGURE 4.

Mean frame brightness before and after CLAHE normalization. Overlaid distributions of the average image brightness before (gray) and after (blue) CLAHE confirm that the lighting conditions across images are more similar after equalization. Average brightness of a frame was measured by taking the mean of a frame’s value-layer intensity. Each histogram used the entire Subject 2 dataset (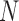 = 625,127 frames).

2). High-Quality Training

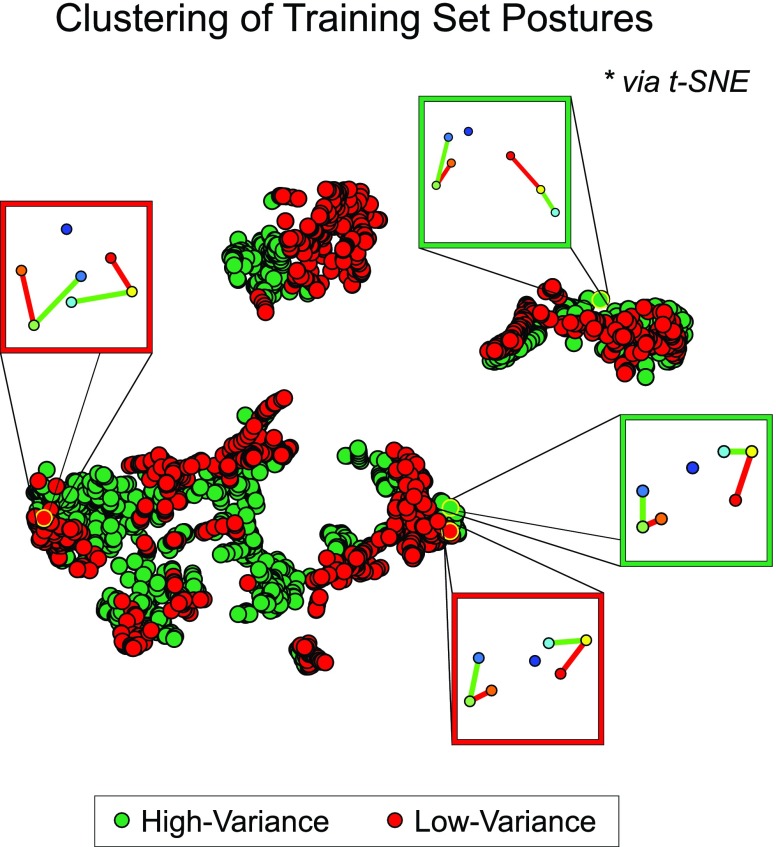
To establish that our high-quality training strategy can capture a large variety of postures within a patient dataset, we compared against another manually annotated subset defined as the first 15 minutes of frames for the same patient (~13.5k frames at 15 fps). Patients were observed to engage in different postures depending on the time of day (e.g., upright vs. rest), and we therefore inferred that frames extracted using our “high-variance” (HV) training strategy would contain greater posture diversity than frames within this “low-variance” (LV) set. To investigate this, we first defined each posture as a 14-dimensional vector containing the 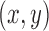pixel coordinates for each of the seven joints. These vectors were then projected down to 2-dimensional space using t-distributed stochastic neighbor embedding (t-SNE) [56] for a graphical intuition of the posture coverage between the two strategies. Only unique datapoints were considered in this analysis, and we observed that the HV set initially contained twice as many unique postures than the LV set. Therefore, prior to t-SNE dimensionality reduction, we uniformly sampled the HV set to ensure an equal number of datapoints that would have otherwise biased the t-SNE manifold towards the more represented HV postures. In addition, the two sets were concatenated prior to projection to ensure compatibility in the output space. In this analysis, the exact t-SNE algorithm was implemented with a standard Euclidean distance metric for 1,000 iterations at a perplexity of 50 and a learning rate of 500, and the two subsets were derived from S1.

The results after projecting the 14D postures onto a 2D space (Fig. 5) represent a low-dimensional clustering of different patient postures extracted from the two training strategies. Each color-coded datapoint represents a unique set of seven joint coordinates, and points within the same cluster resemble similar postures. Despite downsampling the HV set to match the size of the LV set for an unbiased projection, the HV set still visually occupies a larger area in the projected space. This suggests that our high-quality training strategy can capture a diverse collection of patient postures. In addition, the spread of the HV datapoints encompasses nearly all of the LV points, indicating that there may be little to no trade-off between posture diversity and coverage quality when extracting training frames from the entire span of video. Therefore, our high-quality training strategy constructs a more informative training set when compared to frames extracted from a limited window of time and can provide the CNN architecture with more representations of each joint to train on.

FIGURE 5.

Visualization of posture varieties covered by training strategies. Manually annotated postures from two training strategies were projected onto a 2D space using t-SNE to provide a graphical intuition of the various poses included in each set. “High-variance” training frames were selected from periods of movement and rest across the entire span of the patient dataset, whereas “low-variance” training frames were the first 15 minutes of recording. Note that the “high-variance” set initially contained twice as many unique postures than “low-variance” but was uniformly downsampled to prevent bias in the projection. Points within the same cluster resemble similar postures.

3). Kalman Filter With Trained Noise Parameters

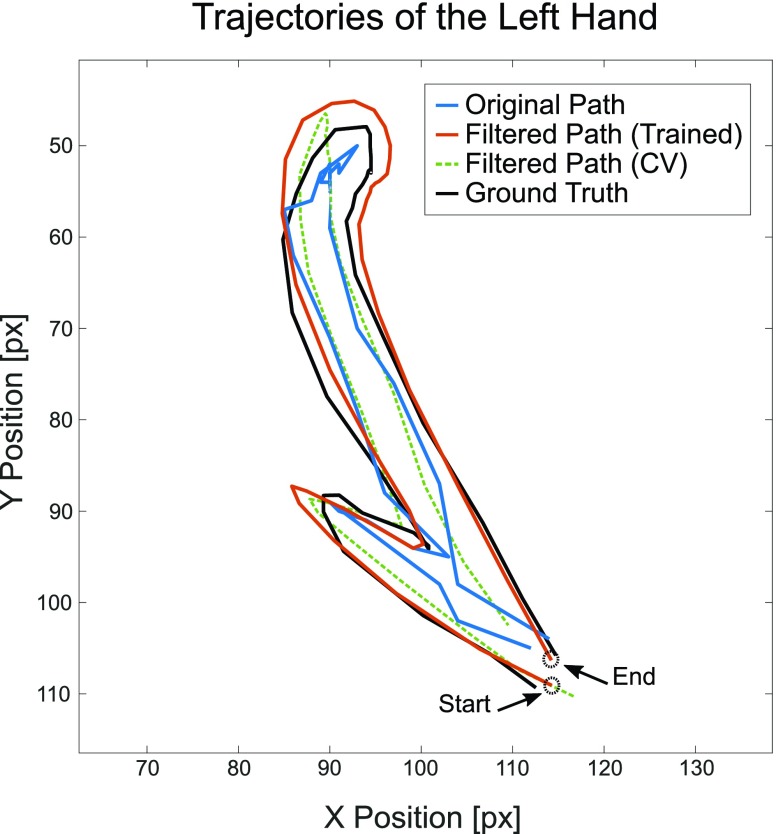
Immediate joint coordinates estimated by Caffe-Heatmap using a patient-specific CNN model are still subject to inconsistencies during periods of quick movements or patient occlusions. However, a Kalman filter with trained noise parameters refines these predictions and reduces the jitter and noise within estimated paths. Prior to optimizing S1’s left hand in the testing data, the original trajectory demonstrated reasonable tracking with an average error of 10.42 ± 5.85 pixels from the ground truth. In contrast, a denoised trajectory using patient-specific parameters followed the true path more closely at an average error of 8.23±5.19 pixels and exhibited less jitter at sharp turns. This is illustrated in Fig. 6 which shows a segment of S1’s left hand trajectory using the different 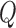and 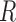noise parameters. For reference, using stock constant velocity parameters resulted in an average error of 9.94 ± 6.34 pixels within the same test set. These observations were consistent throughout all joints and subjects.

FIGURE 6.

Comparison of trajectories. Estimated 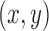coordinates of S1’s left hand during an example segment of movement before (blue) and after (orange) using a Kalman filter with fitted noise parameters, as compared to the ground truth (black). A filtered path using constant velocity (CV) noise parameters (green) is also provided for reference. Across all testing data for Subject 1’s left hand, the trained Kalman filter produced a lower average prediction error of 8.23 ±5.19 pixels from the ground truth, compared to the original path’s error of 10.42 ±5.85 pixels.

B. Pose Estimation Results

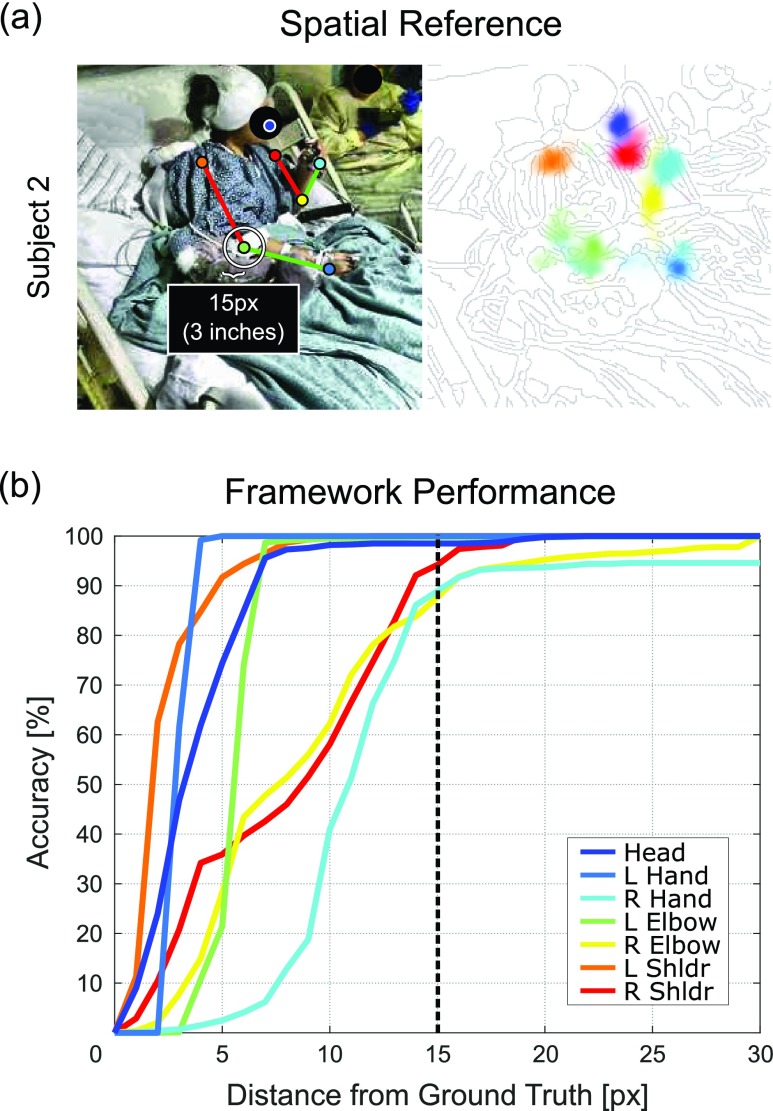
Performance was measured using the Euclidean distance of estimated joint coordinates against an additional set of manually annotated frames held out from the training set for each patient. These frames were chosen for their variety in postures, fluctuations in lighting conditions, and occasional nurse appearances. For each patient test set, we compared our framework’s pose estimation performance against two state-of-the-art generic frameworks by evaluating joint estimates from each method at distances between 0 and 30 pixels (px) from the ground truth. These methods included Caffe-Heatmap by Pfister et al. [19] trained on FLIC and OpenPose by Cao et al. [27] trained on COCO.² Fig. 7a provides a spatial reference of 15 pixels (approximately 3 inches) and Fig. 7b shows the joint accuracies at varying tolerances for Subject 2’s test set. For a progression of pose estimation performance after each proposed contribution, refer to Fig. 9.

FIGURE 7.

Spatial reference and S2 performance. (a) Example skeleton and heatmap with a 15-pixel (3-inch) radius for spatial reference, and (b) Subject 2 accuracy curves between 0 and 30 pixel tolerances from the ground truth.

FIGURE 9.

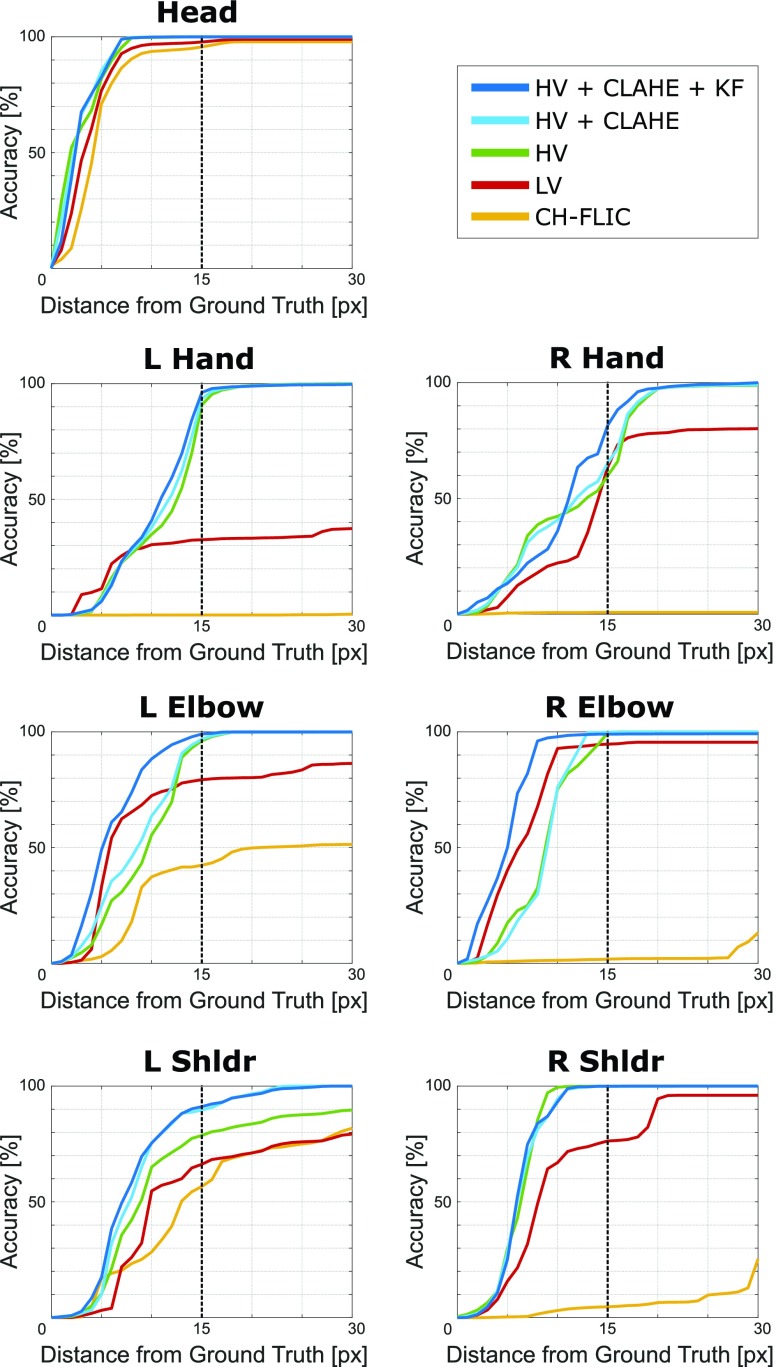
Step-wise performance. A progression of pose estimation performance after each contribution for all joints is shown above, comparing combinations of high-variance training (HV), lighting normalization (CLAHE), and Kalman filtering (KF) to low-variance training (LV) and Caffe-Heatmap with FLIC (CH-FLIC). The results for Subject 1’s test set are shown here.

At a tolerance of 15 pixels, our framework was more accurate than Caffe-Heatmap by 42.4 ± 8.3% and OpenPose by 11.4 ± 3.9% on average across our three patient test sets (Table 2). Patient hands and elbows were typically the most challenging joints to estimate for every method, but we saw more consistent tracking in these categories using our framework. Fig. 8 shows a complete performance comparison against the two generalized methods for all three subjects. With Subjects 1 and 2, we observed a considerable improvement on tracking performance for all seven joints, and our framework labeled at least 80% of frames for any joint within 15 pixels from the ground truth. In addition, our framework provided ~50% more hand annotations at this tolerance when compared to OpenPose for these two subjects.

TABLE 2. Pose Estimation Accuracy Rates @ 15px [%].

Subject 1
Method	Head	Hands	Elbows	Shoulders	Average
CH-FLIC	95.6	0.4	22.1	30.7	49.8 ±41.0
OpenPose	99.4	37.3	93.4	88.4	83.7 ±28.6
Ours	99.9	87.8	99.1	95.6	96.5 ±5.6
Subject 2
Method	Head	Hands	Elbows	Shoulders	Average
CH-FLIC	78.4	2.0	16.6	48.8	49.2 ±34.1
OpenPose	99.4	49.4	69.2	92.9	82.3 ±23.1
Ours	98.5	94.5	93.7	97.1	96.8 ±2.2
Subject 3
Method	Head	Hands	Elbows	Shoulders	Average
CH-FLIC	82.0	38.9	23.9	12.0	49.7 ±30.9
OpenPose	97.9	48.0	52.5	79.5	75.6 ±23.5
Ours	99.4	60.1	73.0	80.2	82.5 ±16.4

FIGURE 8.

Pose estimation comparison. Performance of our proposed method as compared to OpenPose and Caffe-Heatmap with FLIC (CH-FLIC) for each subject is shown above. The left column provides the accuracies of each joint at various tolerances from the ground truth using our framework, and the middle compares the error rates at 15 pixels. The right column compares the accuracies of each category of joints averaged between the left and right body parts.

In contrast to the test sets for Subjects 1 and 2, Subject 3’s chosen test set contained more frequent hand occlusions in which Subject 3 often placed their left and right hands behind their head during rest. This decreased the overall tracking consistency across all methods for these two joints. However, our framework still on average provided 22.0 ± 9.5% and 9.8 ± 6.8% more hand labels than Caffe-Heatmap and OpenPose, respectively. For Subject 3’s elbows, the second most challenging category, we saw an overall increase in performance by 38.2 ± 17.7% against Caffe-Heatmap and 11.3 ± 5.7% against OpenPose when using our framework. This suggests that our framework can be more consistent within reasonable spatial tolerances for particularly noisy segments of video compared to general methods.

IV. Conclusion

In this paper, we presented several extensions onto an existing pose estimation framework to improve posture tracking in clinical environments. By extracting images from periods of movement and idleness across the entire span of a patient’s dataset, we can construct a subset of training frames that captures a diverse collection of postures for a patient-specific CNN model. Furthermore, by accounting for the frequent lighting changes often found in these environments and by refining the predicted trajectories through a Kalman filter with trained noise parameters, our framework can provide more reliable annotations on a patient’s pose in these settings when compared to generic pose estimation frameworks.

Our framework relies solely on low-resolution RGB images to be implemented and therefore can be used by anyone with a means of recording RGB video. In addition, our augmentations can be potentially adopted to improve other pose estimators, and our framework is capable of running in real-time after training as a consequence of the Kalman filter’s causality. We have open-sourced our standalone PatientPose toolbox,³ and we encourage others to use our framework for their own experimental or clinical studies or to apply and build upon our methods. However, we suggest that the trade-off between PatientPose and generalized frameworks should be considered before use. In particular, although we have demonstrated the potential to substantially improve posture estimation quality with our add-ons, we note that our framework’s upfront cost of labeling and training a separate CNN model for each patient is greater. Frameworks that are built independent from subjects and environments are often prepackaged with general models that can be applied to patient data right away without any additional work, and therefore may be the preferred choice for those seeking an immediate solution. However, for others who require a more custom approach which can result in a higher consistency and accuracy of pose annotations in these environments, we encourage them to look into PatientPose as a means to extend beyond current general methods.

This trade-off directly motivates future work that could explore the use of insights from generalized frameworks in order to reduce the upfront efforts per patient, or to develop a framework for “hospital-specific” models that generalize across patients within the same hospital using techniques such as transfer learning. Specifically, a reduction in training time can be achieved by using more powerful hardware and software solutions as this area of research and development continues to mature, and a “hospital-specific” framework which meets halfway between general and specific methods could mitigate concerns of model overfitting in more varied clinical environments. Work in this field will continue to expand with the increasing desire for automated behavioral labels, since these labels can be informative for both research studies and clinical applications. Analysis of neural correlates to natural behaviors extracted from pose estimates, for example, could enable more robust brain-machine prostheses that would benefit those with motor disabilities. In addition, patient tracking can provide a way to automate patient safety monitoring and could improve current motor scoring assessments, overall patient management, and the effectiveness of treatment protocols. Such studies and applications all seek to improve the quality of our health care.

Funding Statement

This work was supported in part by the Hellman Fellowship, the UCSD ECE Department Medical Devices & Systems Initiative, the UCSD Centers for Human Brain Activity Mapping (CHBAM) and Brain Activity Mapping (CBAM), the UCSD Frontiers of Innovation Scholars Program, and the Qualcomm Institute Calit2 Strategic Research Opportunities (CSRO) Program.