Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Jun 4;9(11):2815–2823. doi: 10.1021/acschemneuro.8b00223

Gibbs Free-Energy Gradient along the Path of Glucose Transport through Human Glucose Transporter 3

Huiyun Liang †, Allen K Bourdon ‡, Liao Y Chen †,*, Clyde F Phelix §, George Perry ∥
PMCID: PMC6256350  PMID: 29865792

Abstract

graphic file with name cn-2018-002233_0008.jpg

Fourteen glucose transporters (GLUTs) play essential roles in human physiology by facilitating glucose diffusion across the cell membrane. Due to its central role in the energy metabolism of the central nervous system, GLUT3 has been thoroughly investigated. However, the Gibbs free-energy gradient (what drives the facilitated diffusion of glucose) has not been mapped out along the transport path. Some fundamental questions remain. Here we present a molecular dynamics study of GLUT3 embedded in a lipid bilayer to quantify the free-energy profile along the entire transport path of attracting a β-d-glucose from the interstitium to the inside of GLUT3 and, from there, releasing it to the cytoplasm by Arrhenius thermal activation. From the free-energy profile, we elucidate the unique Michaelis–Menten characteristics of GLUT3, low KM and high VMAX, specifically suitable for neurons’ high and constant demand of energy from their low-glucose environments. We compute GLUT3’s binding free energy for β-d-glucose to be −4.6 kcal/mol in agreement with the experimental value of −4.4 kcal/mol (KM = 1.4 mM). We also compute the hydration energy of β-d-glucose, −18.0 kcal/mol vs the experimental data, −17.8 kcal/mol. In this, we establish a dynamics-based connection from GLUT3’s crystal structure to its cellular thermodynamics with quantitative accuracy. We predict equal Arrhenius barriers for glucose uptake and efflux through GLUT3 to be tested in future experiments.

Keywords: Glucose transporter, facilitated diffusion, binding affinity, free energy, molecular dynamics

Introduction

Glucose is the most important monosaccharide of the human body. Because of its hydrophilic property, glucose easily circulates in the bloodstream but it needs to be transported across the cell membrane by the glucose transporters (GLUTs), membrane proteins in the family of sugar transporters1 that belongs to the major facilitator superfamily (MFS).2 Upon its uptake into a cell, glucose is either readily consumed (in, e.g., neurons) or converted for storage (in, e.g., hepatocytes). In many physiological processes, the facilitated transmembrane diffusion of glucose is the rate limiting factor for its utilization.3,4 Therefore, it is fundamentally relevant to know the atomistic structures and the thermodynamic details of GLUTs5 in addition to their functional characteristics. Currently, there are 14 GLUTs identified with different substrate specificities and distinct tissue distributions.1,6−12 For the central nervous system (CNS), for example, GLUT1 is the main transporter of glucose from the blood into the interstitium7 while GLUT3 is responsible for the neuron’s glucose uptake from there.8,13,14 In addition to the clear importance of GLUTs in human physiology, dysregulations or mutations of GLUTs have been correlated to diseases such as diabetes, hyper- and hypoglycemia, heart disease,1 and Alzheimer’s disease.15 Furthermore, overexpressions of GLUTs have been identified in various cancer types for the increased glucose uptake necessitated by the uncontrolled cellular proliferation of cancer cells.16−18

In this paper, we focus on GLUT3 that has been investigated very extensively (reviewed in, e.g., refs (5), (6), and (8)) due to its importance in the energy metabolism of the CNS. In the CNS, GLUT3 is polarly deployed on the dendrites and axons where the synaptic activities are high.19 Its high affinity with glucose (KM ∼ 1.4 mM8 in comparison with GLUT1’s KM ∼ 6.5 mM20) is critical for the neurons’ uptake of glucose from the interstitial fluid where the glucose level is low.21−28 GLUT3 is also expressed in lymphocytes, monocytes, macrophages, and platelets where it is stored in the intracellular vesicles and, when needed for an increase in glucose demand, it can be translocated and fused to the plasma membrane upon cellular activation.6,29 In the structural studies of GLUTs that are resolved to atomistic resolutions only recently, multiple crystal structures of GLUT3 have been determined,30 all in the outward-open/occluded (exofacial) conformations but none inward-open/occluded (endofacial). Interestingly, multiple crystal structures of GLUT1 are currently available in the endofacial conformations31,32 but none exofacial. On the theoretical–computational front in the recent literature, extensive molecular dynamics (MD) simulations have been performed on how GLUT130,33,34 transforms from the exofacial conformation to the endofacial conformation to carry a glucose from the extracellular fluid to the cytoplasm. Similar MD studies have been carried out on how E. coli xylose (XYP) transporter (XylE) transforms from the exofacial conformation to the endofacial conformation to carry an XYP from the extracellular space to the intracellular side along with changes in the protonation states of relevant residues.30,35 Very recently, the free-energy profile along the XYP binding path has been mapped out36 in accurate agreement with the experimentally measured affinity.

However, an essential part of the β-d-glucose (BGLC)-GLUT3 thermodynamics remains to be elucidated in the current literature. Some fundamental questions still need to be addressed. For example, what characteristics are in the Gibbs free-energy profile along the BGLC-GLUT3 binding-and-releasing path? How is the Michaelis–Menten constant KM (that is direction-dependent) related to the dissociation constant KD (that is direction-independent)? What is the dynamics-based connection from the crystal structure of GLUT3 to its unique thermodynamic characteristics in low KM and high VMAX to satisfy the neurons’ high demand of energy? In this paper, we answer these questions with a quantitative study of the binding affinity (1/KD), the transport path of BGLC from the extracellular fluid through GLUT3 to the intracellular space, and the Michaelis–Menten characteristics of BGLC transport through GLUT3 based on MD simulations of an all-atom model system built from the crystal structure (illustrated in Figure 1). We compute the potential of mean force (PMF) along the entire transport path of the facilitated diffusion, which represents the chemical potential of BGLC, namely, the change in the system’s Gibbs free energy as a function of BGLC’s displacement along the diffusion path. As a further validation of our study, we also compute the hydration energy of BGLC as a problem of binding BGLC from vacuum to inside a bulk of water. The accuracy of our study is shown in the close agreement between our computed values and the experimental data in GLUT3-BGLC affinity, BGLC hydration energy, and so forth. The Michaelis–Menten characteristics drawn from our free-energy profile demonstrate how GLUT3 is specifically suitable for neurons’ glucose uptake at maximum velocity from the extracellular interstitium where the glucose concentration is low.

Figure 1.

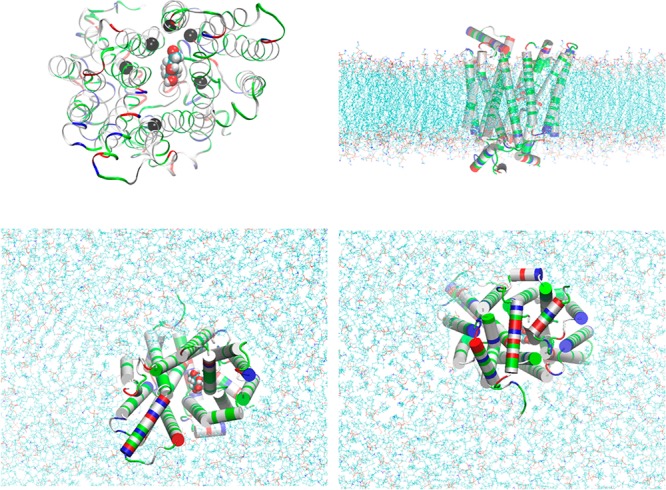
Figure 1

Open in a new tab

GLUT3-BGLC complex embedded in a lipid bilayer. Top left panel, the protein-sugar complex viewed from the extracellular side. Protein is in ribbons colored by residue types (hydrophobic, white; hydrophilic, green; positively charged, blue; negatively charged, red). Glucose is in large spheres colored by atom names (C, cyan; O, red; H, white). Six α-carbons on six transmembrane helices in the vicinity of BGLC are marked as black spheres (Ser21CA on TM1, Ser71CA on TM2, Val163CA on TM5, Val280CA on TM7, Gly312CA on TM8, and Glu378CA on TM10), which are chosen as six centers for the helices to pivot. Their z-coordinates (six degrees of freedom in total) are fixed during simulations after long equilibration but their x- and y-degrees of freedom are free in all simulations. Bottom left, top right, and bottom right panels, respectively, the extracellular, the side, and the intracellular views of the protein–sugar complex embedded in a lipid bilayer. The coordinates were from the last frame of 200 ns MD to fully equilibrate the system. Waters, ions, and some lipids are not shown for clear views of the protein (in cartoons colored by residue types). The lipids are shown in lines colored by atom names (in addition to the afore-listed, P, purple; N, blue). All molecular graphics were rendered with VMD[28].

Results and Discussion

In this section, we first present the problem of glucose hydration, which has fundamental relevance to many biological processes and serves to verify the accuracy of the CHARMM36 force field parameters used in this study of the sugar–protein complex and the algorithm of our approach. We then give the detailed, quantitative results on the glucose transport through GLUT3 and elucidate the dynamics-based connection from the atomistic coordinates of the crystal structure to the thermodynamic characteristics fit for satisfying neurons’ high demand of energy from their low-glucose environments.

Hydration of BGLC

In Figure 2, we plot the PMF along the path of hydrating a glucose molecule from vacuum to inside a bulk of water by steering two centers (the C2 and C5 atoms of BGLC shown in Figure 2 insets as large blue spheres). In the Supporting Information (SI), Movie S1 illustrates such a path of hydrating BGLC. The fluctuations of the two steering centers in vacuum and in water are shown in the bottom panel of Figure 2. From the combination of the PMF difference, ΔPMF = −17.9 kcal/mol, and the two partitions of BGLC in water and in vacuum, we obtain the hydration energy of BGLC, ΔGhydr = −18.0 kcal/mol. From the vapor pressure (0.813 μPa) and the solubility (909 g/L) of β-d-glucose,37 one can find the experimental value of BGLC hydration energy, −17.8 kcal/mol, which is in close agreement with our computation. This confirms the accuracy of the parameters and the algorithm employed in this work.

Figure 2.

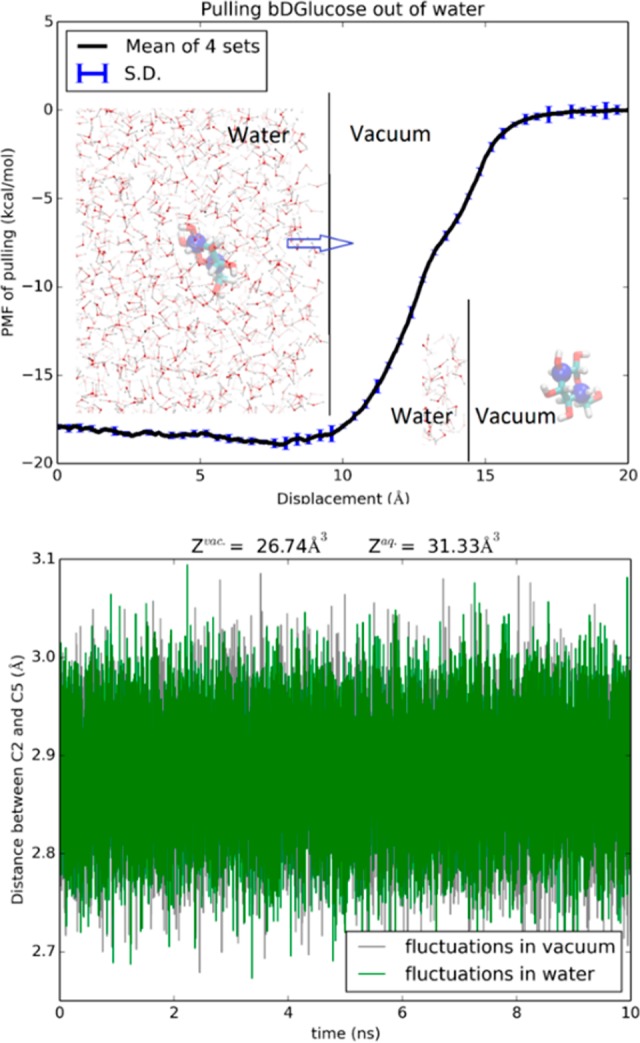
Figure 2

Open in a new tab

Hydration of BGLC. Shown in the top panel is the 6D PMF along a dehydration path of pulling BGLC out of water by its C2 and C5 atoms. Insets: BGLC is shown as licorices colored by atoms (H, white; C, cyan; O, red) with C2 and C5 shown as blue spheres. Some waters are shown as ball-and-sticks colored by atom names. Shown in the bottom panel are the fluctuations of the C2 and C5 atoms in water and in vacuum from which the molecule’s partitions in water and in vacuum were computed, respectively.

Comparing the partial partitions of BGLC in water and in vacuum, the slightly larger fluctuations in water than in vacuum gives a contribution of −0.1 kcal/mol to the total free energy of hydration (−17.8 kcal/mol). When fully hydrated, BGLC can form around 12 hydrogen bonds with waters in its hydration shell. The competition among hydrogen-bonding waters slightly increases the sugar’s fluctuations, leading a slightly greater partial partition in water than in vacuum.

The steepest part of the hydration PMF curve is when the sugar is outside and near the water-vacuum interface (z = 10 Å, Figure 2). In that range, the van der Waals attractions between the sugar and the waters are the strongest and multiple hydrogen bonds are involved between them as well. When the sugar is deeper inside the water box, it breaks more hydrogen bonds between waters while forming more hydrogen bonds with waters. All these together give rise to the nonmonotonic behavior of the PMF from z = 10 Å to z = 0, indicating possibility of higher sugar concentration near the surface than deep inside the bulk of water.

Path of Facilitated BGLC Diffusion

This path is illustrated in Figure 3 and in Movies S2–S4. The first part of the transport path is the binding path of BGLC from the extracellular space to the inside of GLUT3. It was sampled as the inverse of the “most probable” path of unbinding BGLC from the binding site (z = 4 Å) inside GLUT3 by steering BGLC away from the binding site toward the extracellular fluid at a speed of 0.1 Å/ns along the z-axis while the x- and y-degrees of freedom were free to fluctuate. The second part of the transport path is the path of releasing BGLC from GLUT3 to the cytoplasm which was sampled by steering BGLC away from the binding site toward the intracellular space at a speed of 0.1 Å/ns along the negative z-axis while the x- and y-degrees of freedom were free to fluctuate. Since the steering speed is sufficiently slow, the x- and y-degrees of freedom can relax to equilibrium at every step of advancing the z-coordinate by 1.0 × 10–7 Å. The PMF curve along the entire diffusion path is plotted in Figure 4 which represents 1 or 2 ns force sampling in each window of 0.1 Å in the z-coordinate along the transport path. The agreement between our computed affinity and the experimental data indeed validates our approach (detailed in the next subsection).

Figure 3.

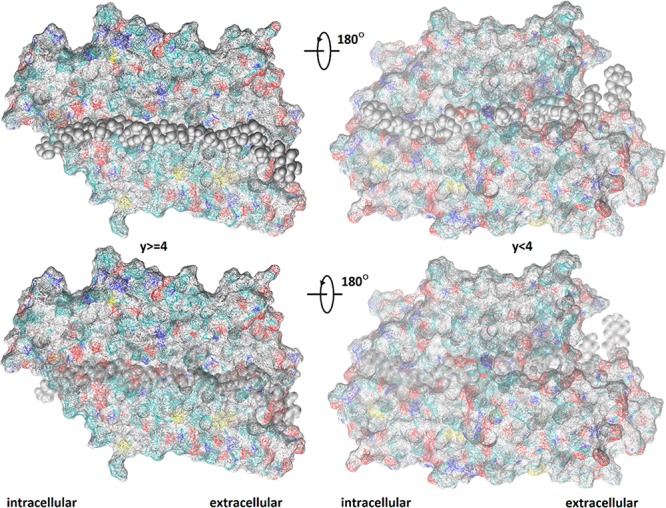
Figure 3

Open in a new tab

Path of facilitated diffusion of BGLC through GLUT3. Shown in the two left panels are all the GLUT3 atoms whose y-coordinates y ≥ 4 Å. Shown in the two right panels are the GLUT3 atoms whose y-coordinates y < 4 Å. The protein is shown in wire-frame surface colored by atom names (H, white; C, cyan; O, red; N, blue; S, yellow) so that the cyan-whitish locations are hydrophobic and the reddish/blueish locations are hydrophilic. BGLC is shown as gray spheres in multiple positions along the transport path. The bottom panels are identical to the corresponding top panels except that the BGLC spheres are transparent so that all GLUT3 atoms are visible.

Figure 4.

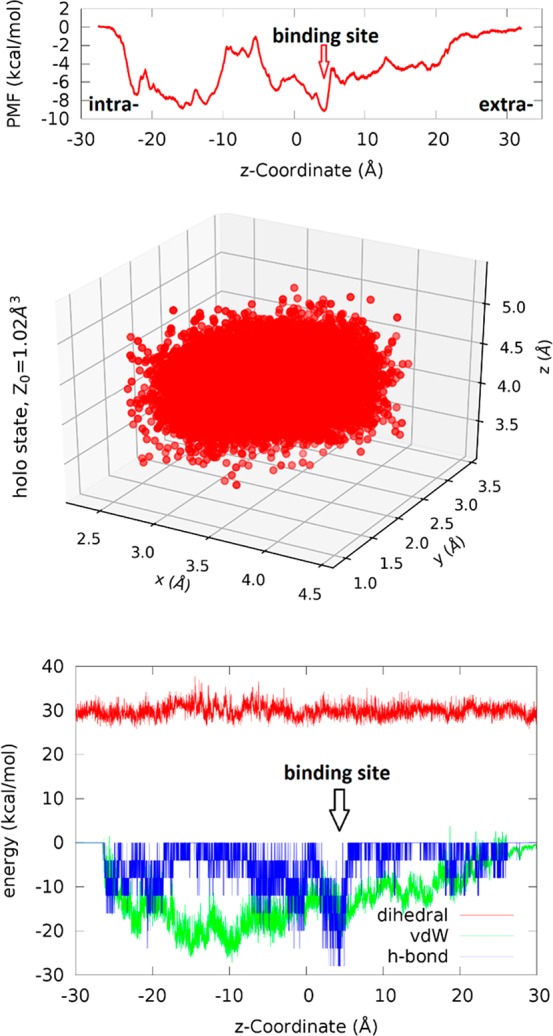
Figure 4

Open in a new tab

Transporting BGLC through GLUT3. Top panel, PMF along the glucose transport path (most probable path). Center panel, fluctuation of BGLC in the bound state (around z = 4 Å). Bottom panel, the van der Waals and hydrogen-bond interactions between BGLC and GLUT3 as well as the dihedral energy of BGLC along its transport path.

Along the binding path, the PMF falls almost monotonically from zero (unbound state on the extracellular side) down to −9.0 kcal/mol in the bound state (inside GLUT3, marked as binding site in Figure 4). This first part of the glucose transport is fast like free diffusion. Along the releasing path, the PMF rises (from −9.0 kcal/mol at the binding site) nonmonotonically back to the zero level in unbound state on the intracellular side but, no dips are below −9.0 kcal/mol and no bumps above zero. This second part, which limits the rate of glucose uptake (the turnover number), gives the highest possible turnover number for a given value of the Michaelis–Menten constant KM approximately twice the dissociation constant KD, in contrast to the hypothetical cases (A) and (C) illustrated in Figure 5. It should be noted that glucose is charge-neutral and, therefore, its PMF (i.e., the change of the system’s Gibbs free energy) along the glucose transport path goes from zero in the extracellular bulk to zero in the intracellular bulk. In other words, the free-energy cost of dissociating BGLC from its binding site inside GLUT3 (or another protein) to the extracellular fluid is equal to the cost of dissociating it to the intracellular bulk. This equality is a necessary and strong validation any theoretical–computational research such as this work must pass.

Figure 5.

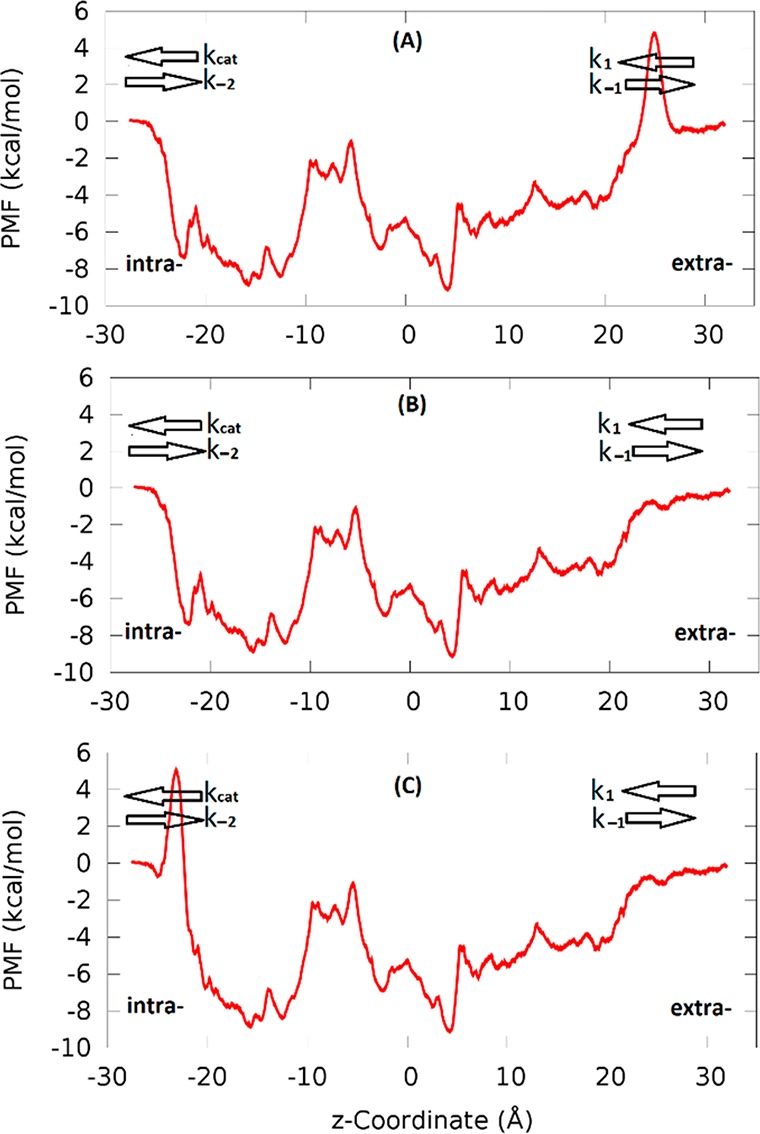
Figure 5

Open in a new tab

Hypothetical free-energy profiles (A) and (C) in comparison with profile (B) for the glucose transport through GLUT3. The uptake direction is along the negative z-axis. The binding site is around z = 4 Å. The extra- and intracellular sides are so marked. The rate constants from the extracellular side to the binding site and its reverse are noted as k1 and k–1, respectively. The rate constants from the binding site to the intracellular side and its reverse are noted as kcat and k–2, respectively. BGLC-GLUT3 and these two hypothetical cases have identical KD’s but very different KM’s because an extra 5 kcal/mol barrier is on the extracellular side (in case (A)) or the intracellular side (in case (C)).

Standard Binding Free Energy of BGLC-GLUT3

To compute the standard binding free energy, we sampled the fluctuations of BGLC in the bound state inside GLUT3 (around z = 4 Å) (shown in Figure 4, central panel) for the bound-state partition. From the PMF difference, ΔPMF = −9.0 kcal/mol, the partial partition in the bound state (Z0 = 1.02 Å3), and the partial partition in the unbound state (Z∞ = 1), we computed the Gibbs free energy of binding, using eq 4, ΔGbind = −4.6 kcal/mol. From the experimental data of the dissociation constant, KD = 0.7 mM (KM = 1.4 mM),8 we obtain the free energy of binding to be ΔGbindexp = kBT ln(KD/c0) = −4.4 kcal/mol. The difference between the experimental data and our computed binding free energy is less than kBT, indicating that chemical accuracy can be achieved in all-atom simulations when the statistical mechanics is adequately implemented. The current force field parameters (in this study, CHARMM 36) are sufficiently optimized for quantifying protein–sugar interactions with chemical accuracy.

In the bottom panel of Figure 4, we show how BGLC interacts with GLUT3 along the transport path. The small fluctuations in BGLC dihedral energy and the all-negative van der Waals (vdW) interaction between BGLC and GLUT3 show that there are no steric clashes between them when the center of mass of BGLC is steered/pulled from the extracellular fluid to the binding site and to the intracellular space at the pulling speed of 0.1 Å/ns. The extracellular side of GLUT3 has sufficient room to accommodate a glucose along with multiple waters (shown in Movie S5) dragged along with BGLC. The intracellular side of GLUT3 does not have sufficient room or hydrophilicity to allow as many waters following BGLC (Movie S5) but it does have sufficient flexibility for BGLC traversing through without steric clashes, which are also illustrated in Figures 6 and 7. In Figures 6 and 7, we chose nine representative frames along the glucose diffusion path from the extracellular to the intracellular side. In frame 1, the BGLC center-of-mass z-coordinate z = 27.7 Å, GLUT3 side chains that come to within 5 Å from BGLC are THR 60, HIS 425. Frame 2: z = 22.6, GLU 35, LYS 39, THR 60, TRP 63, TYR 290, PRO 421, HIS 425. Frame 3: z = 16.3, ASN 32, ILE 285, ASN 286, ALA 287, PHE 289, TYR 290, THR 293, PHE 420. Frame 4: z = 10.3, PHE 24, THR 28, ASN 32, VAL 67, PHE 70, SER 71, ILE 285, ASN 286, PHE 289, TYR 290, ASN 413, GLY 417. Frame 5: z = 4.1, PHE 24, THR 28, GLN 159, ILE 162, VAL 163, ILE 166, GLN 280, GLN 281, ILE 285, ASN 286, PHE 289, ASN 315, PHE 377, GLU 378, GLY 382, PRO 383, TRP 386, ASN 409, ASN 413. Frame 6: z = −1.8, PHE 24, THR 28, PRO 139, GLY 155, ASN 158, GLN 159, ILE 162, ILE 166, GLN 280, PHE 377, PRO 381, GLY 382, PRO 383, ILE 384, PRO 385, TRP 386, PHE 387, ILE 388, ASN 409. Frame 7: z = −7.3, THR 135, PRO 139, ILE 142, GLY 143, ARG 151, GLY 152, ALA 153, GLY 155, THR 156, ASN 158, GLN 159, VAL 326, PRO 383, ILE 384, PRO 385, TRP 386, PHE 387, ILE 388, MET 402. Frame 8: z = −13.0, PRO 139, MET 140, ILE 142, GLY 143, GLU 144, SER 146, ARG 151, GLY 152, GLY 155, ARG 331, PHE 387, ALA 390, GLU 391, PHE 393, ARG 398, MET 402, PHE 458. Frame 9: z = −19.2, GLY 143, SER 146, THR 148, ARG 151, ARG 210, GLU 241, GLU 245, TRP 386, ALA 390, GLU 391, ARG 398, MET 402, PHE 458.

Figure 6.

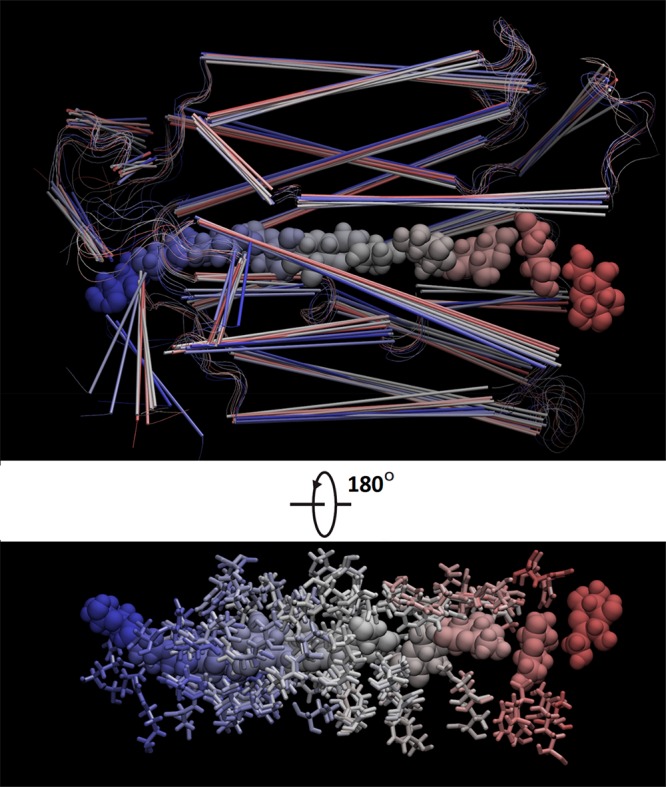
Figure 6

Open in a new tab

GLUT3 and BGLC shown in nine representative frames along the glucose diffusion path. BGLC is shown as large spheres, protein as cartoons, and the protein side chains within 5 Å of BGLC as licorices, all colored by frame numbers.

Figure 7.

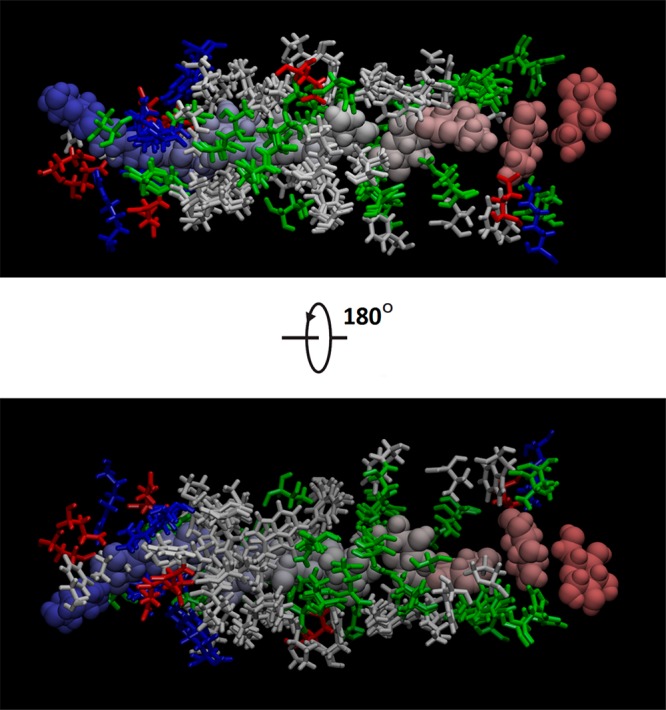
Figure 7

Open in a new tab

BGLC (spheres colored by frame numbers) and nearby GLUT3 side chains (licorices colored by residue types: white, hydrophobic; green, hydrophilic; red, negatively charged; blue, positively charged). The choice of frames and residue selections are identical to those in Figure 6.

Interestingly, there is a deep dip at z = 4 Å in both the vdW and the hydrogen-bonding interactions between BGLC and GLUT3. (Here the assumption of −4 kcal/mol per hydrogen bond is only for the illustration purpose. Using another number, e.g., −2 kcal/mol, would lead to the same conclusion because the PMF was computed from direct force samplings without a presumed value for hydrogen bonds.) Therefore, we observe that the BGLC-GLUT3 binding is due to the vdW attractions and the hydrogen bonds between BGLC and the GLUT3 residues30 forming the binding site. Going from the binding site to the intracellular side, waters hydrogen-bonded to BGLC are forced by GLUT3 to break away from BGLC, which contributes partly to the barrier in PMF on the intracellular side of the binding site (z = −10 to −5 Å). The other contributors to this barrier are the lower hydrophilicity of GLUT3 (fewer hydrogen bonds between GLUT3 and BGLC) and the less negative vdW indicating closer contacts between BGLC and GLUT3 on the repulsive side of the vdW wells (Figure 4, bottom panel). All these dynamic, atomistic interactions, based on the crystal structure,30 parametrized by CHARMM 36 force field parameters,38,39 can give an accurate account of the thermodynamic characteristics of BGLC transport through GLUT3 when the statistical mechanics is implemented correctly with sufficient sampling in theoretical–computational investigations such as this current work.

Additionally, we also conducted two independent studies of GLUT3 transport of α-d-glucose and β-d-glucose, which involve large-scale conformational changes illustrated in Figure S1. The PMF curves for the two anomers, shown in Figures S2 and S3, are similar to one another. They both confirm the Michaelis–Menten characteristics of low KM and high VMAX of GLUT3, in support of the main study.

Michaelis–Menten Characteristics

The Michaelis–Menten characteristics of glucose transport facilitated by GLUT3 can be better understood when contrasting it with the simple cases of hypothetical free-energy profiles shown in Figure 5. All three cases have identical binding affinity and thus identical KD because they have identical PMF at the bound state −9 kcal/mol at z = 4 Å and identical fluctuation characteristics indicated by the local curvatures of the PMF curve around z = 4 Å. However, the three cases have very different Michaelis–Menten characteristics for the uptake transport (facilitated diffusion from the extra- to the intracellular side, along the negative z-axis). In case (A), we have KM(A) ≫ 2KD. In case (B), KM = 2KD. In case (C), KM(C) = KD.

In terms of the on and off rates illustrated in Figure 5, the dissociation constant (inverse affinity),

graphic file with name cn-2018-002233_m001.jpg 1

Here, k1 is the rate constant for a substrate to bind onto the protein from extracellular side and k–1 is the rate constant for the substrate to revert back to the extracellular side. kcat is the rate of catalysis, namely, the rate constant for the product (which is identical to the substrate in this study of transport rather than the general case of reaction) to come off the protein into the intracellular side. k–2 is the rate constant for the product to bind back to the protein from the intracellular side. Within the context of our transport study, the substrate concentration on the intracellular side is zero. Therefore, we have the following Michaelis–Menten equation for the transport velocity

graphic file with name cn-2018-002233_m002.jpg 2

for the total protein concentration [E0] and the substrate concentration on the extracellular side [S]. The Michaelis constant

graphic file with name cn-2018-002233_m003.jpg 3

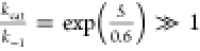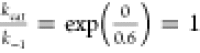Considering the numeric factors, kBT ∼ 0.6 kcal/mol, the well depth 9 = kcal/mol, and the barriers in cases (A) and (C) = 5 kcal/mol. We have these results: (A) Inline graphic; (B) Inline graphic; and (C) Inline graphic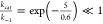. The transport of a substrate molecule from the extra- to the intracellular side involves the Arrhenius thermal activation over (A) an extra barrier on the extracellular side, (B) no extra barrier, and (C) an extra barrier on the intracellular side. These three cases have very different Michaelis constants even though they have identical affinity for the substrate.

The maximum velocity VMAX = kcat [E0], the saturated rate of transport when the substrate concentration is far greater than the Michaelis constant, [S] ≫ KM. Even though case (A) and case (B) have equal maximum rate which is greater than the maximum rate of case (C), VMAX(A) = VMAX ≫ VMAX(C), it takes a much higher substrate concentration in case (A) than in case (B) to attain the maximum rate because KM ≫ KM(B).

In light of the differing transport characteristics of the two hypothetical profiles, we note that case (B) has the highest maximum rate possible for a given protein–substrate affinity (dissociation constant KD) and the maximum rate is attainable at relatively low substrate concentrations KM ∼ 2KD. Therefore, the free-energy profile of glucose transport through GLUT3 in case (B) is an optimal scenario for a near-maximum uptake of substrate from an environment where the substrate concentration is low.

Limitations

At this point, it is appropriate to discuss the applicability and limitations of this theoretical–computational work.

First, GLUT3 facilitates diffusion of glucose down the concentration gradient. It is not an active transporter but a passive facilitator. It is a uniporter which may or may not act in ways identical to many other members of MFS, especially symporters/antiporters that rely on the proton/ion gradients to drive the transport of a substrate across the cell membrane. Therefore, applicability of this study is not expected for MFS in general even if it is applicable to other passive uniporters.

Second, the aim of this work is limited. It is not to validate or invalidate the long-held hypothesis that the large-scale conformational change of GLUT3 is required for glucose transport but, instead, to elucidate the free-energy profile of GLUT3 that agrees with the existing experimental facts on this one uniporter. Our free-energy profile of glucose transport through GLUT3 is validated by the experimental evidence of GLUT3’s high VMAX and low KM (high affinity) in the Michaelis–Menten characteristics. Interestingly, our simulations without invoking large-scale conformational changes produced results in full agreement with the experimental facts. Furthermore, our simulations of GLUT3 invoking large-scale conformational changes produced similar free-energy profiles that are also in full agreement with the experimental facts, which are detailed in Figures S1–S3. In the latter set of simulations, the transmembrane helices were steered so that GLUT3 transforms from the exofacial conformation (Figure S1, left column) to the endofacial conformation (Figure S1, right column) while glucose was held in place at the binding site. The free-energy profiles in the endofacial conformation (red curves in Figures S2 and S3) differ from the curve obtained without invoking the conformational change (Figure 4). The barrier between z = −10 Å and z = 2 Å disappears because glucose does not have to squeeze through the protein side chains as allowed by their thermal fluctuations (Figures 6 and 7). However, these two PMF curves in the endofacial conformation do not differ significantly from the one shown in Figure 4 in that they all produce similar the Michaelis–Menten characteristics of high VMAX and low KM in glucose transport.

Third, from the extensive experimental studies of GLUTs, the crystal structures of GLUT3 have only been found in the exofacial conformation. (Interestingly, GLUT1 has only been crystallized in the endofacial conformation.) The exofacial-to-endofacial conformational changes of GLUTs have only been in the MD simulations where the transmembrane helices were biased (forced) to rotate. Unforced rotations of transmembrane helices have not observed in unbiased MD simulations or in experiments. However, the Michaelis–Menten characteristics for glucose transport through GLUT3 are unambiguous: high VMAX and low KM. And there is no doubt that GLUT3 is not an active transporter but a uniporter facilitator, which dictates that the correct free-energy profile levels off to the same level on the intra- and the extra-cellular sides away from the membrane. Our study produced free-energy profiles satisfying all these requirements with/without the hypothesized exofacial-endofacial conformational changes. The free-energy profile does level off to the same level on both sides away from the protein. And it does not have an extra barrier above the bulk level on either the extracellular or the intracellular side. Otherwise, we would not have both high VMAX and low KM. Even though this work is in full agreement with existent experimental facts, it is incapable of validating or invalidating the alternating-access theory of the current literature of GLUTs. More experiments are needed to answer the question whether glucose transport through GLUTs requires large-scale conformational changes of a uniporter protein.

Conclusions

Based on the quantitative agreements between the computed hydration energy and the experimental data and between the computed GLUT3 affinity for glucose and the experimental values of the Michaelis constant, it is fair to state that our all-atom MD study is accurate for glucose transport across the cell membrane facilitated by GLUT3. The free-energy profile along the glucose transport path shows that GLUT3 is ideal for glucose uptake from the extracellular fluid of low glucose concentration with the highest possible maximum velocity. The protein structure of GLUT3 presents no major barriers for glucose to overcome either on the extracellular side or on the intracellular side. The bottleneck of the facilitated diffusion is largely the Arrhenius thermal activation over a 9 kcal/mol climb from the biding site to the intracellular side. This free-energy profile corroborates the functional experiments in that GLUT3 has high affinity for glucose and that GLUT3 has high maximum velocity of glucose transport. In this, we now have a dynamics-based connection from the atomistic coordinates of the crystal structure to the thermodynamic characteristics in the transporter protein’s functional roles in human physiology.

Methods

All-Atom Model Systems

For the glucose hydration problem, a BGLC is placed inside a 60 Å × 60 Å × 60 Å cubic box of water. The sugar is centered at the origin of the Cartesian coordinates which is 10 Å beneath the top side of the water box (the plane of z = 10 Å in parallel to the xy-plane). Reflective boundary conditions are implemented for water molecules (but not for BGLC) on the planes of z = 10 Å and z = −50 Å, which keep the water molecules inside the system box when BGLC moves out of the water box into the vacuum above the plane of z = 10 Å. This all-atom model system consists of 20 502 atoms. Periodic boundary conditions are enforced on the x- and y-dimensions.

For the glucose transport problem, we take the coordinates of the GLUT3 and BGLC from the high-resolution crystal structure of Deng et al.30 (PDB code: 4ZW9), translate and rotate the BGLC-GLUT3 complex so that its center is located at the origin of the Cartesian coordinates and its orientation is such that the protein opens toward the z-axis for computational convenience, embed the complex in a patch of Phosphatidylethanolamine (POPE) lipid bilayer, solvate the sugar-protein–membrane complex with a cubic box of water whose dimensions are 100 Å × 100 Å × 120 Å, and then add sodium and chloride ions to neutralize the net charges of the protein and to salinate the system to the physiological concentration of 150 mM NaCl. The all-atom model system so constructed is illustrated in Figure 1. It consists of 107 970 atoms.

Simulation Parameters

In all the MD runs, CHARMM36 force field parameters38,39 were used for all the intra- and intermolecular interactions. The Langevin stochastic dynamics was implemented with NAMD40 to simulate the systems at the constant temperature of 298 K and the constant pressure of 1 bar using the Langevin pistons. The damping constant was 5.0/ps. The time step was 1.0 fs. The bonded interactions were updated every time-step while the long-range forces every two time-steps. The covalent bonds of hydrogens were not fixed. The van der Waals interactions were smoothly switched off at 10 Å (starting at 9.0 Å). Explicit solvent (water) was represented with the TIP3P model. Full electrostatics was implemented via particle mesh Ewald at the level of 128 × 128 × 128 for the BGLC transport problem.

We followed the standard protocol of the literature41−43 to embed a membrane protein in a lipid bilayer, to melt lipid tails, and to equilibrate the system. In particular, we conducted 0.25 ns MD run (after initial energy minimization) to melt the lipid tails during which the protein and the lipid heads were fixed. Then we ran 6.0 ns equilibration with protein constrained only. During these two equilibration runs, the water molecules (if they fall inside the membrane near the lipid tails) were pushed constantly into the aqueous spaces on the two sides of the membrane. Then we conducted 25 ns MD run with the α-carbons on the transmembrane helices constrained to fully equilibrate the system. After all these, we conducted 200 ns MD run without any constraints. All the afore-stated MD runs were under constant temperature and constant pressure.

Steered MD Runs for PMF

We followed the multisectional protocol detailed in ref (44). Briefly, we divided the entire range of the membrane region from z = −28 Å to z = 32 Å into 60 evenly divided sections. We steered (pulled) the center-of-mass z-coordinate of BGLC for 10 ns at a speed of 0.1 Å/ns across each of the 60 sections. Pulling BGLC from the binding site (z = 4 Å) to the extracellular side (z ≥ 32 Å) with its x- and y-degrees of freedom being free (unconstrained), the path so sampled is nearly reversible and thus taken as the dissociation path because the protein remains in the exofacial open conformation during the entire process. (Reversibility was tested and confirmed over five sections from z = 4 Å to z = 9 Å. From z = 9 Å to the extracellular side, there is no hindrance in the way of BGLC being dissociated that may give rise to an irreversible contribution to the pulling path.) The total force on the BGLC center-of-mass by all other degrees of freedom of the entire system was recorded for computing the work needed to dissociate BGLC along the dissociation path, which will be shown as the PMF curve on the extracellular side.

From the binding site (z = 4 Å) to the intracellular side (z ≤ −28 Å), the center-of-mass z-degree of freedom of BGLC was steered for 10 ns over one section for a z-displacement of −1.0 Å to sample a forward path over that section. At the end of each section, the z-coordinate of the BGLC center-of-mass was fixed (or, technically, pulled at a speed of 0.0 Å/ns) while the system was equilibrated for 12 ns. From the end of the 12 ns equilibration, the z-coordinate of BGLC center-of-mass was pulled for 10 ns for a z-displacement of +1.0 Å to sample a reverse path. The total force on the z-degree of freedom of BGLC center-of-mass was recorded along the forward and the reverse pulling paths for computing the PMF along the dissociation path from the binding site to the intracellular side. The PMF was approximated as the simple average between the forward and the reverse paths. This part of the PMF computation is more difficult than the extracellular side because BGLC has to move through the protein side chains as they thermally fluctuate.

Absolute Binding Free Energy from PMF in 3nD

Following the standard literature (e.g. ref (45)), one can relate the standard (absolute) free energy of binding to the PMF difference in 3n dimensions (3nD) and the two partial partitions as follows:

graphic file with name cn-2018-002233_m007.jpg 4

Here c0 is the standard concentration of 1 M, kB is the Boltzmann constant, T is the absolute temperature, Z0 is the partial partition of the sugar in the bound state which can be computed by sampling the fluctuations in 3n degrees of freedom of the sugar and invoking the Gaussian approximation for the fluctuations in the bound state,46,47 and Z∞ is the partial partition of the sugar in the unbound state for the 3(n – 1) degrees of freedom of the sugar when three degrees of freedom are fixed so that the sugar rotates and fluctuates in the aqueous bulk far away from the protein. In this study, we choose n = 1 and use the center-of-mass coordinates of glucose to represent its position. The partial partition of the unbound state Z∞ = 1. The PMF is 3D, and Z0 contains the 3D fluctuations of glucose in the bound state. We fix the z-coordinate of six Cα atoms of GLUT3 near BGLC, each on a transmembrane helix, Ser21CA on TM1, Ser71CA on TM2, Val163CA on TM5, Val280CA on TM7, Gly312CA on TM8, and Glu378CA on TM10 (Figure 1). The x- and y-coordinates of these six Cα atoms are freely subject to the stochastic dynamics of the system without any constraints. Therefore, the six transmembrane helices can freely move in the lateral dimensions (in parallel to the cell membrane) and they can pivot around their centers.

It should be emphasized that eq 4 can be applied from either the extracellular or the intracellular side to produce a unique value for the Gibbs free energy of binding. It definitely indicates inaccuracy of a theoretical–computational study if the two sides give differing values for this equilibrium function of the state.

Hydration Energy from PMF in 3nD

The problem of hydrating glucose is simply a problem of binding a glucose molecule to a large bulk of water. The bound state is when glucose is completely inside the water bulk and the unbound state is when it is in the vacuum far away from the water-vacuum interface. eq 4 can be easily adapted into the following form for the hydration energy:

graphic file with name cn-2018-002233_m008.jpg 5

Here Zaq and Zvac are the partial partition of glucose in the hydrated and in the dehydrated states, respectively. In this study, we use n = 2 for the hydration problem for computing efficiency. The C2 and C5 atoms are chosen as the two centers to represent glucose’s position and orientation. The PMF is in 6D and the partial partition of glucose is 3D involving rotation of one center around the other center (two degrees of freedom) and the vibration between the two centers (one degree of freedom).48

Acknowledgments

The authors thank Roberto Rodriguez for helpful discussions. The authors acknowledge the computing resources provided by the Texas Advanced Computing Center at University of Texas at Austin.

Glossary

Abbreviations

GLC

d-glucose, glucopyranose

CNS

central nervous system

GLUT

human glucose transporter

MD

molecular dynamics

MFS

major facilitator superfamily

nD

n dimensions, n-dimensional

PMF

potential of mean force, chemical potential

XylE

E. coli xylose permease

XYP

xylose, xylopyranose

Supporting Information Available

Five movies that are discussed but not included in the main context. . The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acschemneuro.8b00223.

  • Hydration of BGLC (AVI)

  • Facilitated diffusion of BGLC through GLUT3 viewed from the extracellular side (AVI)

  • Facilitated diffusion of BGLC through GLUT3 viewed from the intracellular side (AVI)

  • Facilitated diffusion of BGLC through GLUT3 viewed from the membrane (AVI)

  • Waters following BGLC along its transport path through GLUT3 (AVI)

  • Two additional studies of d-glucose transport through GLUT3: one on α-d-glucose and one on β-d-glucose (PDF)

Author Contributions

H.L. and A.K.B. contributed equally. G.P. initiated the research. L.Y.C. conducted the simulations and drafted the manuscript. All authors contributed to analyses and manuscript edits.

The authors acknowledge support from the NIH (Grant GM121275), San Antonio Life Sciences Institute (SALSI) Brain Health-Clusters in Research Excellence, Semmes Foundation.

The authors declare no competing financial interest.

Supplementary Material

cn8b00223_si_001.avi (23.2MB, avi)
cn8b00223_si_002.avi (36.7MB, avi)
cn8b00223_si_003.avi (35.7MB, avi)
cn8b00223_si_004.avi (20MB, avi)
cn8b00223_si_005.avi (8.9MB, avi)
cn8b00223_si_006.pdf (978KB, pdf)

References

  1. Augustin R. (2010) The protein family of glucose transport facilitators: It’s not only about glucose after all. IUBMB Life 62, 315–333. 10.1002/iub.315. [DOI] [PubMed] [Google Scholar]
  2. Reddy V. S.; Shlykov M. A.; Castillo R.; Sun E. I.; Saier M. H. (2012) The major facilitator superfamily (MFS) revisited. FEBS J. 279, 2022–2035. 10.1111/j.1742-4658.2012.08588.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Furler S. M.; Jenkins A. B.; Storlien L. H.; Kraegen E. W. (1991) In vivo location of the rate-limiting step of hexose uptake in muscle and brain tissue of rats. American Journal of Physiology - Endocrinology And Metabolism 261, E337. 10.1152/ajpendo.1991.261.3.E337. [DOI] [PubMed] [Google Scholar]
  4. Ziel F. H.; Venkatesan N.; Davidson M. B. (1988) Glucose Transport Is Rate Limiting for Skeletal Muscle Glucose Metabolism in Normal and STZ-Induced Diabetic Rats. Diabetes 37, 885. 10.2337/diab.37.7.885. [DOI] [PubMed] [Google Scholar]
  5. Yan N. (2017) A Glimpse of Membrane Transport through Structures—Advances in the Structural Biology of the GLUT Glucose Transporters. J. Mol. Biol. 429, 2710–2725. 10.1016/j.jmb.2017.07.009. [DOI] [PubMed] [Google Scholar]
  6. Thorens B.; Mueckler M. (2010) Glucose transporters in the 21st Century. American Journal of Physiology - Endocrinology And Metabolism 298, E141. 10.1152/ajpendo.00712.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Harik S. I.; Hall A. K.; Richey P.; Andersson L.; Lundahl P.; Perry G. (1993) Ontogeny of the erythroid/HepG2-type glucose transporter (GLUT-1) in the rat nervous system. Dev. Brain Res. 72, 41–49. 10.1016/0165-3806(93)90157-6. [DOI] [PubMed] [Google Scholar]
  8. Simpson I. A.; Dwyer D.; Malide D.; Moley K. H.; Travis A.; Vannucci S. J. (2008) The facilitative glucose transporter GLUT3:20 years of distinction. American Journal of Physiology - Endocrinology And Metabolism 295, E242. 10.1152/ajpendo.90388.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Cushman S. W.; Wardzala L. J. (1980) Potential mechanism of insulin action on glucose transport in the isolated rat adipose cell. Apparent translocation of intracellular transport systems to the plasma membrane. J. Biol. Chem. 255, 4758–4762. [PubMed] [Google Scholar]
  10. Suzuki K.; Kono T. (1980) Evidence that insulin causes translocation of glucose transport activity to the plasma membrane from an intracellular storage site. Proc. Natl. Acad. Sci. U. S. A. 77, 2542–2545. 10.1073/pnas.77.5.2542. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Thorens B. (1992) Molecular and Cellular Physiology of GLUT-2, a High-KmFacilitated Diffusion Glucose Transporter. In International Review of Cytology (Friedlander M., and Mueckler M., Eds.), pp 209–238, Academic Press. [DOI] [PubMed] [Google Scholar]
  12. Uldry M.; Thorens B. (2004) The SLC2 family of facilitated hexose and polyol transporters. Pfluegers Arch. 447, 480–489. 10.1007/s00424-003-1085-0. [DOI] [PubMed] [Google Scholar]
  13. Kalaria R. N.; Gravina S. A.; Schmidley J. W.; Perry G.; Harik S. I. (1988) The glucose transporter of the human brain and blood-brain barrier. Ann. Neurol. 24, 757–764. 10.1002/ana.410240610. [DOI] [PubMed] [Google Scholar]
  14. Maher F.; Simpson I. A. (1994) The GLUT3 glucose transporter is the predominant isoform in primary cultured neurons: assessment by biosynthetic and photoaffinity labelling. Biochem. J. 301, 379–384. 10.1042/bj3010379. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. An Y.; Varma V. R.; Varma S.; Casanova R.; Dammer E.; Pletnikova O.; Chia C. W.; Egan J. M.; Ferrucci L.; Troncoso J.; Levey A. I.; Lah J.; Seyfried N. T.; Legido-Quigley C.; O’Brien R.; Thambisetty M. (2018) Evidence for brain glucose dysregulation in Alzheimer’s disease. Alzheimer’s Dementia 14, 318–329. 10.1016/j.jalz.2017.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Adekola K.; Rosen S. T.; Shanmugam M. (2012) Glucose transporters in cancer metabolism. Curr. Opin. Oncol. 24, 650. 10.1097/CCO.0b013e328356da72. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. McCracken A. N.; Edinger A. L. (2013) Nutrient transporters: the Achilles heel of anabolism. Trends Endocrinol. Metab. 24, 200–208. 10.1016/j.tem.2013.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Younes M.; Brown R. W.; Stephenson M.; Gondo M.; Cagle P. T. (1997) Overexpression of Glut1 and Glut3 in stage I nonsmall cell lung carcinoma is associated with poor survival. Cancer 80, 1046–1051. . [DOI] [PubMed] [Google Scholar]
  19. Mantych G. J.; James D. E.; Chung H. D.; Devaskar S. U. (1992) Cellular localization and characterization of Glut 3 glucose transporter isoform in human brain. Endocrinology 131, 1270–1278. 10.1210/endo.131.3.1505464. [DOI] [PubMed] [Google Scholar]
  20. Manolescu A. R.; Witkowska K.; Kinnaird A.; Cessford T.; Cheeseman C. (2007) Facilitated Hexose Transporters: New Perspectives on Form and Function. Physiology 22, 234. 10.1152/physiol.00011.2007. [DOI] [PubMed] [Google Scholar]
  21. Gruetter R.; Novotny E. J.; Boulware S. D.; Rothman D. L.; Mason G. F.; Shulman G. I.; Shulman R. G.; Tamborlane W. V. (1992) Direct measurement of brain glucose concentrations in humans by 13C NMR spectroscopy. Proc. Natl. Acad. Sci. U. S. A. 89, 1109–1112. 10.1073/pnas.89.3.1109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Squire L. R., Bloom F. E., Spitzer N. C., Gage F., and Albright T. (2009) Encyclopedia of Neuroscience: Vol. One, Elsevier Science. [Google Scholar]
  23. Gruetter R.; Novotny E. J.; Boulware S. D.; Rothman D. L.; Mason G. F.; Shulman G. I.; Shulman R. G.; Tamborlane W. V. (1992) Direct measurement of brain glucose concentrations in humans by 13C NMR spectroscopy. Proc. Natl. Acad. Sci. U. S. A. 89, 1109–1112. 10.1073/pnas.89.3.1109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Seaquist E. R.; Damberg G. S.; Tkac I.; Gruetter R. (2001) The Effect of Insulin on In Vivo Cerebral Glucose Concentrations and Rates of Glucose Transport/Metabolism in Humans. Diabetes 50, 2203. 10.2337/diabetes.50.10.2203. [DOI] [PubMed] [Google Scholar]
  25. Nielsen J. K.; Djurhuus C. B.; Gravholt C. H.; Carus A. C.; Granild-Jensen J.; Ørskov H.; Christiansen J. S. (2005) Continuous Glucose Monitoring in Interstitial Subcutaneous Adipose Tissue and Skeletal Muscle Reflects Excursions in Cerebral Cortex. Diabetes 54, 1635. 10.2337/diabetes.54.6.1635. [DOI] [PubMed] [Google Scholar]
  26. Bittner C. X.; Loaiza A.; Ruminot I.; Larenas V.; Sotelo-Hitschfeld T.; Gutiérrez R.; Córdova A.; Valdebenito R.; Frommer W. B.; Barros L. F. (2010) High Resolution Measurement of the Glycolytic Rate. Front. Neuroenerg. 2, 26. 10.3389/fnene.2010.00026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Meierhans R.; Béchir M.; Ludwig S.; Sommerfeld J.; Brandi G.; Haberthür C.; Stocker R.; Stover J. F. (2010) Brain metabolism is significantly impaired at blood glucose below 6 mM and brain glucose below 1 mM in patients with severe traumatic brain injury. Critical Care 14, R13. 10.1186/cc8869. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Hwang J. J.; Jiang L.; Hamza M.; Sanchez Rangel E.; Dai F.; Belfort-DeAguiar R.; Parikh L.; Koo B. B.; Rothman D. L.; Mason G.; Sherwin R. S. (2017) Blunted rise in brain glucose levels during hyperglycemia in adults with obesity and T2DM. JCI Insight 2, e95913. 10.1172/jci.insight.95913. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Fidler T. P.; Campbell R. A.; Funari T.; Dunne N.; Balderas Angeles E.; Middleton E. A.; Chaudhuri D.; Weyrich A. S.; Abel E. D. (2017) Deletion of GLUT1 and GLUT3 Reveals Multiple Roles for Glucose Metabolism in Platelet and Megakaryocyte Function. Cell Rep. 20, 881–894. 10.1016/j.celrep.2017.06.083. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Deng D.; Sun P.; Yan C.; Ke M.; Jiang X.; Xiong L.; Ren W.; Hirata K.; Yamamoto M.; Fan S.; Yan N. (2015) Molecular basis of ligand recognition and transport by glucose transporters. Nature 526, 391–396. 10.1038/nature14655. [DOI] [PubMed] [Google Scholar]
  31. Kapoor K.; Finer-Moore J. S.; Pedersen B. P.; Caboni L.; Waight A.; Hillig R. C.; Bringmann P.; Heisler I.; Müller T.; Siebeneicher H.; Stroud R. M. (2016) Mechanism of inhibition of human glucose transporter GLUT1 is conserved between cytochalasin B and phenylalanine amides. Proc. Natl. Acad. Sci. U. S. A. 113, 4711–4716. 10.1073/pnas.1603735113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Deng D.; Xu C.; Sun P.; Wu J.; Yan C.; Hu M.; Yan N. (2014) Crystal structure of the human glucose transporter GLUT1. Nature 510, 121–125. 10.1038/nature13306. [DOI] [PubMed] [Google Scholar]
  33. Fu X.; Zhang G.; Liu R.; Wei J.; Zhang-Negrerie D.; Jian X.; Gao Q. (2016) Mechanistic Study of Human Glucose Transport Mediated by GLUT1. J. Chem. Inf. Model. 56, 517–526. 10.1021/acs.jcim.5b00597. [DOI] [PubMed] [Google Scholar]
  34. Park M.-S. (2015) Molecular Dynamics Simulations of the Human Glucose Transporter GLUT1. PLoS One 10, e0125361. 10.1371/journal.pone.0125361. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Wisedchaisri G.; Park M.-S.; Iadanza M. G.; Zheng H.; Gonen T. (2014) Proton-coupled sugar transport in the prototypical major facilitator superfamily protein XylE. Nat. Commun. 5, 4521. 10.1038/ncomms5521. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Wambo T. O.; Chen L. Y.; Phelix C.; Perry G. (2017) Affinity and path of binding xylopyranose unto E. coli xylose permease. Biochem. Biophys. Res. Commun. 494, 202–206. 10.1016/j.bbrc.2017.10.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Oja V.; Suuberg E. M. (1999) Vapor Pressures and Enthalpies of Sublimation of d-Glucose, d-Xylose, Cellobiose, and Levoglucosan. J. Chem. Eng. Data 44, 26–29. 10.1021/je980119b. [DOI] [Google Scholar]
  38. Best R. B.; Zhu X.; Shim J.; Lopes P. E. M.; Mittal J.; Feig M.; MacKerell A. D. (2012) Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone ϕ, ψ and Side-Chain χ1 and χ2 Dihedral Angles. J. Chem. Theory Comput. 8, 3257–3273. 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Vanommeslaeghe K.; MacKerell A. D. Jr (2015) CHARMM additive and polarizable force fields for biophysics and computer-aided drug design. Biochim. Biophys. Acta, Gen. Subj. 1850, 861–871. 10.1016/j.bbagen.2014.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Phillips J. C.; Braun R.; Wang W.; Gumbart J.; Tajkhorshid E.; Villa E.; Chipot C.; Skeel R. D.; Kalé L.; Schulten K. (2005) Scalable molecular dynamics with NAMD. J. Comput. Chem. 26, 1781–1802. 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. de Groot B. L.; Grubmüller H. (2001) Water Permeation Across Biological Membranes: Mechanism and Dynamics of Aquaporin-1 and GlpF. Science 294, 2353–2357. 10.1126/science.1062459. [DOI] [PubMed] [Google Scholar]
  42. Jensen M. Ø.; Park S.; Tajkhorshid E.; Schulten K. (2002) Energetics of glycerol conduction through aquaglyceroporin GlpF. Proc. Natl. Acad. Sci. U. S. A. 99, 6731–6736. 10.1073/pnas.102649299. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Ke M.; Yuan Y.; Jiang X.; Yan N.; Gong H. (2017) Molecular determinants for the thermodynamic and functional divergence of uniporter GLUT1 and proton symporter XylE. PLoS Comput. Biol. 13, e1005603. 10.1371/journal.pcbi.1005603. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Chen L. Y. (2011) Exploring the free-energy landscapes of biological systems with steered molecular dynamics. Phys. Chem. Chem. Phys. 13, 6176–6183. 10.1039/c0cp02799e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Woo H.-J.; Roux B. (2005) Calculation of absolute protein–ligand binding free energy from computer simulations. Proc. Natl. Acad. Sci. U. S. A. 102, 6825–6830. 10.1073/pnas.0409005102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Chen L. Y. (2015) Hybrid Steered Molecular Dynamics Approach to Computing Absolute Binding Free Energy of Ligand–Protein Complexes: A Brute Force Approach That Is Fast and Accurate. J. Chem. Theory Comput. 11, 1928–1938. 10.1021/ct501162f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Rodriguez R. A.; Yu L.; Chen L. Y. (2015) Computing Protein–Protein Association Affinity with Hybrid Steered Molecular Dynamics. J. Chem. Theory Comput. 11, 4427–4438. 10.1021/acs.jctc.5b00340. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Wambo T. O.; Chen L. Y.; McHardy S. F.; Tsin A. T. (2016) Molecular dynamics study of human carbonic anhydrase II in complex with Zn2+ and acetazolamide on the basis of all-atom force field simulations. Biophys. Chem. 214, 54–60. 10.1016/j.bpc.2016.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

cn8b00223_si_001.avi (23.2MB, avi)
cn8b00223_si_002.avi (36.7MB, avi)
cn8b00223_si_003.avi (35.7MB, avi)
cn8b00223_si_004.avi (20MB, avi)
cn8b00223_si_005.avi (8.9MB, avi)
cn8b00223_si_006.pdf (978KB, pdf)

Articles from ACS Chemical Neuroscience are provided here courtesy of American Chemical Society

RESOURCES