Conversion Coefficients for Proton Beams using Standing and Sitting Male Hybrid Computational Phantom Calculated in Idealized Irradiation Geometries

Abstract

The aim of this study was the calculation of conversion coefficients for absorbed doses per fluence (D_T/Φ) using the sitting and standing male hybrid phantom (UFH/NCI) exposure to monoenergetic protons with energy ranging from 2 MeV to 10 GeV. Sex-averaged effective dose per fluence (E/Φ) using the results of D_T/Φ for the male and female hybrid phantom in standing and sitting postures were also calculated. Results of E/Φ of UFH/NCI standing phantom were also compared with tabulated effective dose conversion coefficients provided in ICRP publication 116. To develop an exposure scenario implementing the male UFH/NCI phantom in sitting and standing postures was used the radiation transport code MCNPX. Whole-body irradiations were performed using the recommended irradiation geometries by ICRP publication 116 antero-posterior (AP), postero-anterior (PA), right and left lateral, rotational (ROT) and isotropic (ISO). In most organs, the conversion coefficients D_T/Φ were similar for both postures. However, relative differences were significant for organs located in the lower abdominal region, such as prostate, testes and urinary bladder, especially in the AP geometry. Results of effective dose conversion coefficients were 18% higher in the standing posture of the UFH/NCI phantom, especially below 100 MeV in AP and PA. In lateral geometry, the conversion coefficients values below 20 MeV were 16% higher in the sitting posture. In ROT geometry, the differences were below 10%, for almost all energies. In ISO geometry, the differences in E/Φ were negligible. The results of E/Φ of UFH/NCI phantom were in general below the results of the conversion coefficients provided in ICRP publication 116.

INTRODUCTION

The Monte Carlo technique coupled with computational phantoms is a powerful tool that allows the estimation of organ dose conversion coefficients. Conversion coefficients relate protection with physical quantities; for example, effective dose per fluence or absorbed dose per air kerma⁽¹⁾. These coefficients are useful to estimate doses from occupational exposures since protection quantities ‘equivalent dose’ and ‘effective dose’ are not measurable⁽¹⁾. Several authors have calculated fluence-to-dose conversion coefficients for protons using stylized (mathematical and voxel) phantoms in the standing posture^(2–5). There are few studies in the literature that attempt to calculate doses in computational phantom in the sitting posture, but even in these studies only photon, electron or positron doses were calculated^(6–11). In a previous paper, organ dose conversion coefficients for protons were calculated using the sitting and standing female hybrid phantom and the influence of the posture in absorbed dose was discussed⁽¹²⁾. It turns out that changing the posture of the computational phantom may contribute to differences in absorbed dose in organs and tissues and, depending on the irradiation scenario, phantoms with variable stature in standing or sitting configurations can be used to contribute to reducing the uncertainties^{(6, 12)}. To better represent these posture differences, this study presents adult male hybrid anthropomorphic phantoms, in both standing and sitting positions, for calculation of organ and effective dose conversion coefficients. Hybrid anthropomorphic phantom are representation of the human body developed using tomographic images like voxel phantoms but adjusted using a 3D modeling software to better represent organ, tissues and external contours of a real person. First the phantom is polygonized then internal organs are modeled to match reference organ volume and smooth contours via polygon mesh and NURBS (nonuniform rational B-spline) surface and afterward the phantom is voxelized^(12–14).

Protons contribute to doses delivered to passenger and aircraft crew members, especially at aircraft cruising altitudes, because the Earth is continually bombarded by galactic cosmic radiation (GCR) that is formed almost 98% by nuclei in which 88% of these nuclei are protons⁽¹⁵⁾. GCR can have energies up to 10¹¹ GeV, but the most frequent energy distribution is at a few hundred MeV to 1 GeV per nucleon⁽¹⁶⁾. When the GCR and the plasma of protons and electrons coming from the sun interact with the earth atmosphere, nuclear reactions occur producing secondary radiation, which together with primary incident particles lead to radiation exposure that decreases in intensity with decreasing altitude^(15–18). In atmospheric region, the geometrical condition that closely represents the aircrew exposure to cosmic radiation field is usually assumed to be the isotropic (ISO) geometry^{(19, 20)}. Other idealized irradiation geometries such as antero-posterior (AP), postero-anterior (PA), right and left lateral (RLAT and LLAT) and rotational (ROT) may be taken as approximations to actual conditions of exposure. AP, PA and lateral geometries are considered to approximate a scenario in which single sources are at large distance from the body surface. ROT geometry approximates, for example, a scenario that a person is irradiated from a widely dispersed planar source⁽¹⁾.

The aims of this study were calculate absorbed dose conversion coefficients for protons using the standing and sitting adult male hybrid phantom and effective dose conversion coefficients using male and female hybrid phantom (UFH/NCI)^{(14, 21)} for exposure to monoenergetic protons in AP, PA, RLAT, LLAT, ROT and ISO geometries. The conversion factors from different postures were compared to each other. Sex-averaged effective dose conversion coefficients⁽²²⁾ were obtained from the results of the absorbed dose conversion coefficients for the male phantom calculated in this study and the results for the female hybrid phantom presented in a previous paper⁽¹²⁾. Results of effective dose conversion coefficients of UFH/NCI standing phantom were also compared with tabulated effective dose conversion coefficients provided in ICRP publication 116⁽¹⁾ concerning external irradiation beam of protons using the reference phantom of the ICRP publication 110⁽²³⁾.

MATERIALS AND METHODS

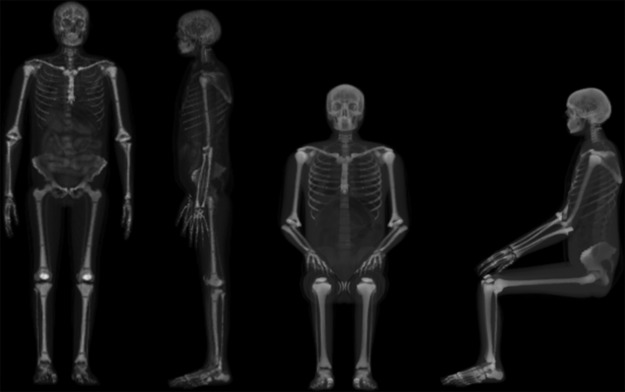
MCNPX code (version 2.7.0)⁽²⁴⁾ was used to simulate irradiation geometries and calculate fluence-to-dose conversion coefficients for the UFH/NCI adult male hybrid phantom in sitting and standing posture (Figure 1). A source of monoenergetic protons was used to expose the phantom placed in vacuum from 2 MeV to 10 GeV in six irradiation geometries (AP, PA, RLAT, LLAT, ROT and ISO) as described in ICRP publication 116⁽¹⁾. The source plane respectively for the standing and sitting phantom has 58.2 ×  175.8 cm² and 54 × 135.3 cm², in AP and PA geometries, 31.2 × 175.8 cm² and 79.2 × 135.3 cm², in lateral geometries. In the ROT geometry, the phantoms are within a cylindrical source of 178.8 cm height and 33.35 cm radius, for the standing posture, and 135.3 cm height and 48.41 cm radius, for the sitting posture. In the ISO geometry the source is a sphere of 94.84 cm radius, for the standing phantom, and 83.74 cm radius, for the sitting phantom. Secondary particles (neutrons, photons, protons etc) generated when protons interact with matter were also transported by the Monte Carlo code. No transport of electron delta rays from direct protons interactions are done by MCNPX code, instead the electron energy is locally absorbed. The transport energy cutoff for protons and secondary particles were set to 10 GeV in the upper energy limit and the default values of low energy cutoff presented in the MCNPX code, except neutrons that was set to 1.10⁻⁹ MeV. The total histories were 10⁸ for each simulation resulting in a calculation time between 3 and 50 hours, respectively for 2 MeV and 10 GeV of source energy. One billion histories (10⁹) were simulated from 10 to 30 MeV in AP, PA and lateral geometries and from 10 to 50 MeV in ROT and ISO geometries. More details about the sitting hybrid phantom can be found in our previous paper and in Han et al.^{(12, 25)}. Details of the UFH/NCI adult male phantom can be found in Lee et al.⁽²¹⁾. Red bone marrow (RBM) and endosteum are defined in sophisticated spongiosa and medullary cavity structures in the UFH/NCI male phantom. Therefore, the absorbed dose in RBM and endosteum was determined by averaging the absorbed dose in each spongiosa and medullary cavity, which contain RBM and endosteum tissue, multiplied with the mass ratios of RBM and endosteum contained in each region, as recommended in ICRP publication 116⁽¹⁾. Energy deposited by all particles transported in the simulations was normalized by incident proton fluence to derive organ dose conversion coefficients (pGy cm²). Organ dose conversion coefficients (D_T/Φ) of the standing and sitting UFH/NCI adult male phantoms were compared to each other. Effective dose conversion coefficients (E/Φ) were calculated using the sex-average equivalent doses obtained from the average of equivalent dose of male and female phantoms, as recommended in ICRP publication 103⁽²²⁾. E/Φ was obtained for the sitting and standing phantom posture and results were compared to each other and with the results presented in ICRP publication 116 using the ICRP reference phantoms⁽²³⁾.

Figure 1.

3D renderings of the UFH/NCI adult male hybrid phantoms in the standing (left) and sitting (right) postures.

RESULTS AND DISCUSSION

Calculated fluence-to-absorbed dose conversion coefficients in units of pGy cm² are provided in electronic format in Tables A1–A6 for the 27 organs of the standing and sitting UFH/NCI male phantom. As presented in these tables, statistical uncertainties for most organs irradiated in AP, PA, RLAT, LLAT, ROT and ISO geometry were <10% considering 10⁸ particle histories in each simulation. Statistical uncertainties were ~10% for smallest and/or deeper organs (such as adrenals, gall bladder and prostate) since fewer numbers of particles interact in these organs in low energy proton range (<50 MeV). In order to obtain uncertainties below 10% in these deeper and smaller organs it was simulated 10⁹ particle histories. Statistical uncertainties were very low in skin, RBM, bone surface and muscle for almost all proton energies studied since the region between these tissue and protons is large.

Relative differences between fluence-to-dose conversion coefficients in standing and sitting posture for all irradiation geometries are also presented in Tables A1–A6. It was observed differences <10% for some organs and tissues.

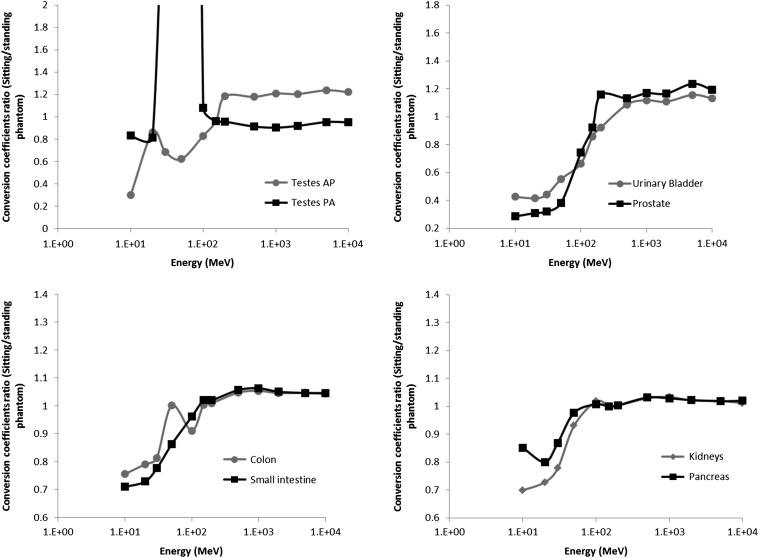
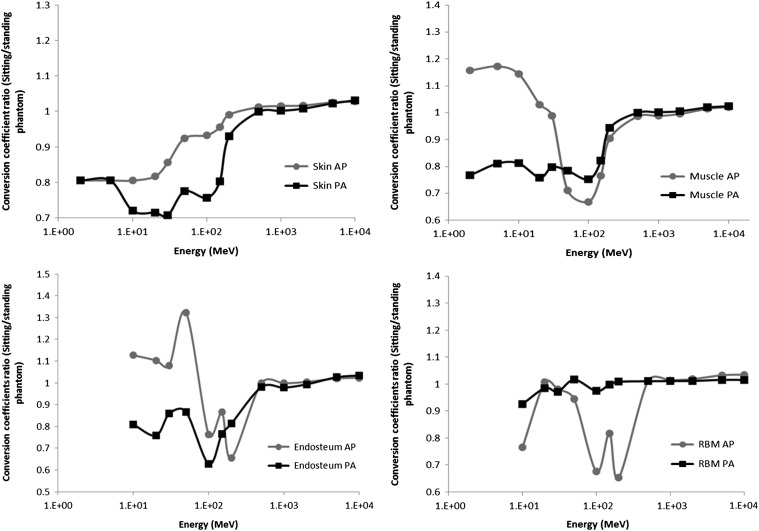
In AP geometry the highest differences occurred for organ and tissues located in the pelvic and lower abdominal region, such as testes, urinary bladder, prostate, colon and small intestine. In energy below 150 MeV, conversion coefficients in the standing posture were higher than in the sitting posture and from 150 MeV it was observed the opposite (Figure 2). This occurred because the upper legs of the phantom in the sitting posture contribute to reduce proton energy in low energy range, while in high energy range the upper legs contribute to increase the forward scattering that deliver more dose in organs in the bottom of the trunk region. Similar results were observed in organ located at the abdominal region (adrenals, kidneys, pancreas, spleen and gall bladder) in which the arms and hands are located in front of the phantom in the sitting posture, while in the standing posture these structures are positioned to the trunk side (Figure 1). In AP and PA geometry, differences observed in skin, muscle and endosteum were due to the region of interaction between incident protons and these tissues, which is much higher in the standing posture as can be seen in Figure 3. In this study skin dose coefficient refers to dose averaged over the whole skin of the phantom. However below 50 MeV, conversion coefficients in muscle and endosteum were higher in the sitting posture than in the standing posture in AP geometry (Figure 3). In this case, arms and hands are rotated 90° between standing and sitting postures (Figure 1), so muscle and bones of all fingers are irradiated unshielded in the sitting posture, while in the standing posture the fingers shield each other. Conversion coefficients in RBM were higher in the standing posture between 100 and 200 MeV mainly because the upper legs position. The interaction between proton beam and the RBM inside the femur contribute more to the dose in the standing than in the sitting posture. In PA geometry, differences in RBM were <5% in all energy studied (Figure 3) mainly because the bone sites that contain higher amount of RBM are at the back of the phantom⁽¹²⁾. Conversion coefficients in testes were much higher in the sitting than in the standing posture in PA geometry, differently to the result of AP geometry. In this case, proton energy was decreased by the structures around the testes in the standing phantom resulting in a lower organ dose in this posture. In prostate, small intestine and urinary bladder, conversion coefficients were higher in the standing posture, but the differences are smaller compared to the same organs in AP irradiation.

Figure 2.

Fluence-to-absorbed dose coefficients (D_T/Φ) ratio between sitting and standing postures for testes, urinary bladder, prostate, colon, small intestine, pancreas and kidneys in AP geometry and testes in PA geometry.

Figure 3.

Fluence-to-absorbed dose coefficients (D_T/Φ) ratio for skin, muscle, endosteum and RBM in AP and PA geometry.

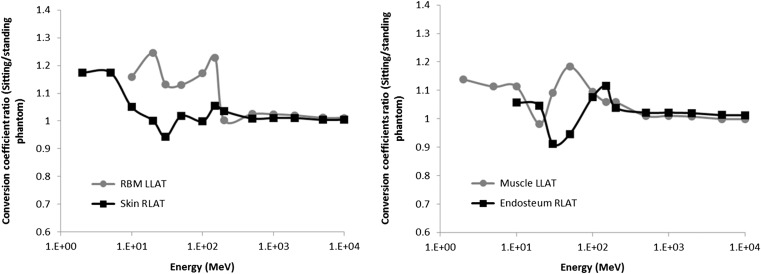
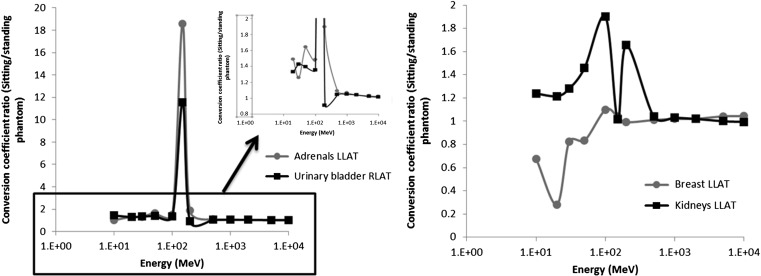
In right and left lateral irradiation geometry were observed similar results. For example, in skin, muscle, endosteum and RBM the conversion coefficients were slightly higher in the sitting posture (Figure 4). Skin and muscle presented in arms and hands contribute to increase the absorbed dose in these tissues, because these structures are positioned in a way that the region of interaction with proton beam is higher in the sitting posture than in the standing posture. Organs and tissues located in chest and abdominal region like adrenals, colon, gall bladder, stomach, urinary bladder, prostate, kidneys, liver, pancreas, small intestine, spleen and lungs presented conversion coefficients in the sitting posture greater than in standing posture (Figure 5). In this case arms and hands structures contribute to reduce the energies of protons that irradiate the phantom laterally. In contrast, conversion coefficients in breast (Figure 5) and thymus were higher in the standing posture due to the structures of upper arms (Figure 1).

Figure 4.

Fluence-to-absorbed dose coefficients (D_T/Φ) ratio for skin, endosteum, RBM and muscle in lateral geometries.

Figure 5.

Fluence-to-absorbed dose coefficients (D_T/Φ) ratio for urinary bladder in RLAT geometry and for adrenals, breast and kidneys in LLAT geometry.

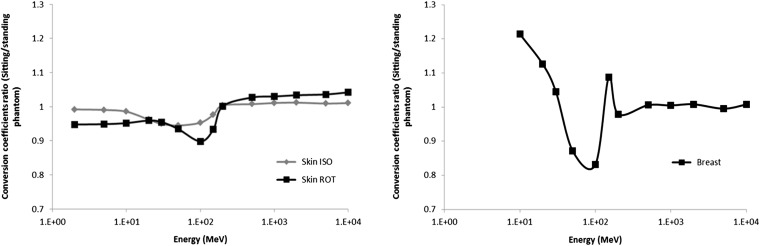
In ROT and ISO geometry, fluence-to-skin dose coefficients were very similar in both postures, in which <10% of relative differences were observed (Figure 6). Other organs presented different conversion coefficients for standing and sitting phantom due to the difference in position of arms, hands and upper legs which contribute to reduce the protons energy or enhance the region of interaction between protons and tissues. For example, conversion coefficient in breast was higher in the standing posture in 50 MeV and 100 MeV in ISO geometry (Figure 6) because the thighs of the sitting phantom contribute to reduce the protons energy in upward irradiation while in other direction there is no difference in breast irradiation.

Figure 6.

Fluence-to-absorbed dose coefficients (D_T/Φ) ratio for skin and breast in ISO geometry and for skin in ROT geometry.

Effective dose coefficients were also calculated for both posture from sex-averaged organ dose coefficients of UFH/NCI male (given in this study) and female phantom⁽¹²⁾. These coefficients are presented in Table 1 for all irradiation geometry (AP, PA, RLAT, LLAT, ROT and ISO) as well as relative differences between effective dose coefficients of sitting and standing phantom. In AP and PA geometry were observed differences >5% in E/Φ between standing and sitting phantom from 2 to 100 MeV. Below 30 MeV, conversion coefficients in standing phantom were around 18% higher than in the sitting phantom. Absorbed dose conversion coefficient in skin contributes to the effective dose coefficients estimation much more than other organ and tissues in energies below 100 MeV, and as discussed above and in a previous paper⁽¹²⁾ the skin dose conversion coefficients were higher in the standing phantom than in the sitting phantom. Although breast-dose conversion coefficients between 30 and 100 MeV in AP geometry contribute more to effective dose estimation than skin-dose conversion coefficients, differences between standing and sitting conversion coefficients in breast were minimal. Above 100 MeV, relative differences in conversion coefficients between standing and sitting phantom were <5% in AP geometry and negligible in PA geometry. Results of E/Φ in RLAT and LLAT geometry were very similar. Until 20 MeV of energy, conversion coefficients in sitting phantom were higher than in standing phantom due to the same reason presented previously for the AP and PA geometry, but in lateral geometries skin dose was much higher in the sitting than in the standing phantom as discussed earlier. However, breast-dose conversion coefficients were higher in standing than in sitting male phantom in 30 MeV and 50 MeV; therefore, effective dose coefficients were also higher in the standing phantom in these energies. In 100 MeV and 150 MeV, conversion coefficients in the sitting posture were around 20% higher than in the standing posture due to the contribution of testes and abdominal organs conversion coefficients to effective dose. In ISO geometry, effective dose coefficients were very similar in sitting and standing posture. Exceptions were in energies between 20 and 100 MeV, in which conversion coefficients were higher in standing posture than in sitting posture, but even then differences were <10% (Table 1). In ROT geometry, until 100 MeV, conversion coefficients were higher in standing posture than in sitting posture, and above 100 MeV it was observed the opposite. However, except in 30 MeV and 50 MeV, all differences were around or <5%. This result is due the minimal differences observed in skin-dose coefficients below 30 MeV. Above 30 MeV of energy, differences in testes, urinary bladder, prostate and muscle are significant.

Table 1.

Sex-averaged effective dose conversion coefficients (pSv.cm²) under AP, PA, RLAT, LLAT, ROT and ISO irradiation geometry on UFH/NCI standing and sitting phantom from monoenergetic protons.

Proton energy (MeV)	Sitting phantom		Standing phantom		Relative difference (RD) (%)
	E/Φ (pSv.cm²)	Relative error (%)	E/Φ (pSv.cm²)	Relative error (%)
AP
2	5.63	0.01	6.83	0.01	−18
5	14.05	0.01	17.06	0.01	−18
10	28.04	0.01	34.04	0.01	−18
20	110	0.2	120	0.2	−8
30	523	0.1	550	0.2	−5
50	973	0.09	1035	0.1	−6
100	2056	0.04	2198	0.04	−7
150	2291	0.04	2354	0.04	−3
200	1789	0.04	1841	0.04	−3
500	1165	0.05	1133	0.05	3
1000	1103	0.06	1071	0.07	3
2000	1100	0.08	1072	0.09	3
5000	1248	0.09	1212	0.1	3
10 000	1478	0.1	1439	0.1	3
PA
2	5.64	0.01	6.84	0.01	−18
5	14.07	0.01	17.08	0.01	−18
10	28.07	0.01	34.07	0.01	−18
20	36.09	0.01	44.23	0.01	−18
30	32.53	0.02	39.49	0.02	−18
50	75.47	0.05	81.43	0.04	−7
100	1074	0.04	1103	0.05	−3
150	2565	0.04	2588	0.05	−1
200	1928	0.04	1940	0.04	−1
500	1179	0.05	1189	0.05	−1
1000	1117	0.06	1128	0.07	−1
2000	1117	0.07	1124	0.09	−1
5000	1252	0.08	1257	0.1	−0.4
10 000	1496	0.09	1501	0.1	−0.4
RLAT
2	4.51	0.02	3.88	0.01	16
5	11.26	0.02	9.67	0.01	16
10	22.46	0.02	19.30	0.01	16
20	32.11	0.05	29.77	0.07	8
30	62.0	0.3	64.2	0.2	−3
50	275	0.2	295	0.2	−7
100	801	0.1	856	0.07	−6
150	1592	0.08	1396	0.04	14
200	2013	0.07	2004	0.05	0.5
500	1154	0.07	1140	0.05	1
1000	1099	0.08	1084	0.06	1
2000	1103	0.1	1089	0.07	1
5000	1265	0.1	1253	0.08	1
10 000	1514	0.1	1499	0.09	1
LLAT
2	4.51	0.02	3.88	0.01	16
5	11.26	0.02	9.67	0.01	16
10	22.47	0.02	19.30	0.01	16
20	32.51	0.06	31.06	0.09	5
30	65.0	0.3	73.2	0.2	−11
50	277	0.3	292	0.2	−5
100	966	0.09	800	0.07	21
150	1828	0.07	1427	0.04	28
200	2017	0.06	2072	0.05	−3
500	1154	0.07	1142	0.05	1
1000	1097	0.08	1085	0.06	1
2000	1100	0.1	1090	0.07	1
5000	1258	0.1	1254	0.08	0.3
10 000	1503	0.1	1501	0.09	0.1
ROT
2	6.07	0.03	6.30	0.02	−4
5	15.03	0.04	15.60	0.03	−4
10	29.30	0.06	30.29	0.06	−3
20	57.8	0.3	60.2	0.3	−4
30	176	0.5	192	0.4	−8
50	419	0.3	482	0.3	−13
100	1270	0.1	1357	0.1	−6
150	2223	0.1	2139	0.1	4
200	2096	0.1	1988	0.09	5
500	1251	0.1	1184	0.1	6
1000	1186	0.1	1122	0.1	6
2000	1189	0.2	1122	0.2	6
5000	1343	0.2	1274	0.2	5
10 000	1606	0.2	1517	0.2	6
ISO
2	4.85	0.02	4.83	0.02	0.5
5	11.97	0.03	11.93	0.03	0.3
10	23.10	0.04	23.14	0.05	−0.2
20	44.05	0.2	45.8	0.2	−4
30	138	0.3	147	0.3	−6
50	387	0.2	410	0.3	−6
100	959	0.09	1023	0.1	−6
150	1696	0.08	1705	0.08	−0.5
200	1810	0.07	1823	0.08	−0.7
500	1157	0.07	1152	0.08	0.4
1000	1099	0.09	1093	0.1	0.5
2000	1104	0.1	1097	0.1	1
5000	1268	0.1	1263	0.1	0.5
10 000	1518	0.1	1505	0.2	1

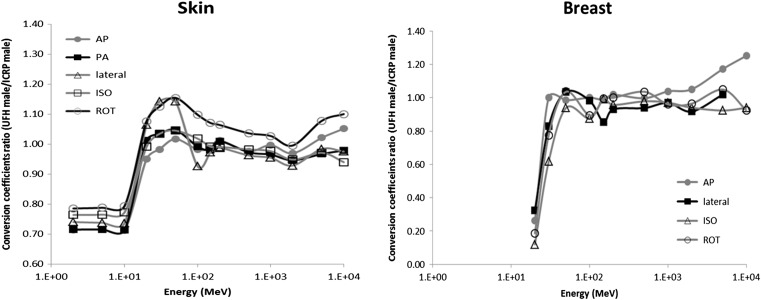
Table 2 presents the comparison between results of sex-averaged effective dose coefficients of the UFH/NCI in standing posture and the effective dose coefficients of the reference phantom obtained in ICRP publication 116⁽¹⁾. It was observed large differences in E/Φ between ICRP reference phantom and UFH/NCI phantom, especially in energies below 100 MeV in all geometries studied. As discussed in Alves et al.⁽¹²⁾, the mayor contributor to differences in organ dose coefficients and consequently in effective dose coefficients between UFH/NCI and the ICRP reference phantom is the voxel size in which the male and female UFH/NCI phantoms have 3 × 3 × 3 mm³ and the male and female ICRP reference phantom have respectively 2.137 × 2.137 × 8 mm³ and 1.775 × 1.775 × 4.84 mm³. This contribute to differences in skin dose conversion coefficients between ICRP and UFH/NCI phantom, in which below 20 MeV were higher in ICRP phantom than in UFH/NCI phantom, as can be seen in Figure 7. Since effective dose between 2 and 10 MeV is due only to skin dose contribution, then differences in skin dose coefficients explain the differences observed in E/Φ. Although UFH/NCI phantom have no significant differences in organ masses compared to mass reference values in ICRP publication 89^{(21, 26)}, structural differences such as organ position and tissue layer also contribute to differences in conversion coefficients on UFH/NCI and ICRP reference phantom. For example, dose coefficients in breast were lower in UFH/NCI phantom in AP, ROT, ISO and lateral geometries below 30 MeV (Figure 7) because there is a layer of adipose tissue around the breasts which reduces the dose. Besides, some parts of the breast in ICRP phantom are exposed direct to the protons because there are lacking some voxels that represent the skin around the breast. These two features explain the differences below 50 MeV between ICRP and UFH/NCI effective dose coefficients. Despite differences, it is interesting that the magnitude of effective dose coefficients on both UFH/NCI and ICRP reference phantom are almost the same in all geometry simulated, especially at energies above 100 MeV where the dose is less dependent of structural variations.

Table 2.

Sex-averaged effective dose conversion coefficients (pSv.cm²) under AP, PA, RLAT, LLAT, ROT and ISO irradiation geometry obtained from ICRP 116 and calculated on UFH/NCI phantom from monoenergetic protons.

	ICRP reference phantom	UFH/NCI phantom
Proton energy (MeV)	E/Φ (pSv.cm²)	E/Φ (pSv.cm²)	Relative error (%)	Relative difference (RD) (%)
AP
2	10.90	6.83	0.01	37
5	27.30	17.06	0.01	38
10	54.90	34.04	0.01	38
20	428	200	0.2	72
30	750	550	0.2	27
50	1180.00	1035	0.1	12
100	2510.00	2198	0.04	12
150	2380.00	2354	0.04	1
200	1770.00	1841	0.04	−4
500	1150.00	1133	0.05	1
1000	1090.00	1071	0.07	2
2000	1120.00	1072	0.09	4
5000	1230.00	1212	0.1	2
10 000	1410.00	1439	0.1	−2
PA
2	10.90	6.84	0.01	37
5	27.30	17.08	0.01	37
10	54.60	34.07	0.01	38
20	43.60	44.23	0.01	−2
30	36.10	39.49	0.02	−9
50	71.50	81.43	0.04	−14
100	1190.00	1103	0.05	7
150	2820.00	2588	0.05	8
200	1930.00	1940	0.04	−1
500	1240.00	1189	0.05	4
1000	1230.00	1128	0.07	8
2000	1280.00	1124	0.09	12
5000	1450.00	1257	0.1	13
10 000	1740.00	1501	0.1	14
RLAT
2	5.62	3.88	0.01	31
5	14.00	9.67	0.01	31
10	28.10	19.3	0.01	31
20	78.80	29.77	0.07	62
30	172	64.2	0.2	63
50	372	295	0.2	21
100	818	856	0.07	−5
150	1460.00	1396	0.04	4
200	2180.00	2004	0.05	8
500	1210.00	1140	0.05	6
1000	1200.00	1084	0.06	10
2000	1250.00	1089	0.07	13
5000	1410.00	1253	0.08	11
10 000	1670.00	1499	0.09	10
LLAT
2	5.61	3.88	0.01	31
5	14.00	9.67	0.01	31
10	28.10	19.3	0.01	31
20	82.80	31.06	0.09	63
30	180	73.2	0.2	59
50	379	292	0.2	23
100	994	800	0.07	20
150	1640.00	1427	0.04	13
200	2150.00	2072	0.05	4
500	1210.00	1142	0.05	6
1000	1180.00	1085	0.06	8
2000	1250.00	1090	0.07	13
5000	1390.00	1254	0.08	10
10 000	1630.00	1501	0.09	8
ROT
2	8.98	6.3	0.02	30
5	22.10	15.6	0.03	29
10	50.10	30.29	0.06	40
20	165	60.2	0.3	64
30	296	192	0.4	35
50	532	4812	0.3	9
100	1440.00	1357	0.1	6
150	2160.00	2139	0.1	1
200	1960.00	1988	0.09	−2
500	1220.00	1184	0.1	3
1000	1190.00	1122	0.1	6
2000	1230.00	1122	0.2	9
5000	1350.00	1274	0.2	6
10 000	1560.00	1516.76	0.21	3
ISO
2	7.02	4.83	0.02	31
5	17.30	11.93	0.03	31
10	45.80	23.14	0.05	50
20	136	45.8	0.2	66
30	249	147	0.3	41
50	451	410	0.3	9
100	1130.00	1023	0.1	10
150	1790.00	1705	0.08	5
200	1840.00	1823	0.08	1
500	1180.00	1152	0.08	2
1000	1150.00	1093	0.1	5
2000	1220.00	1097	0.1	10
5000	1430.00	1263	0.1	12
10 000	1780.00	1505	0.2	16

Figure 7.

Fluence-to-absorbed dose coefficients (D_T/Φ) ratio for skin and breast between UFH/NCI and ICRP male phantom.

CONCLUSIONS

Organ dose coefficients for external proton beams in six idealized irradiation geometries (AP, PA, RLAT, LLAT, ROT and ISO) were calculated using the UFH/NCI adult male phantom in standing and sitting postures. As discussed in a previous paper for a female phantom⁽¹²⁾, changing the posture of the phantom leads to differences in energy deposition in organs and tissues due to the dependence of the conversion coefficients values with the morphology and the irradiation geometry. A set of sex-averaged effective dose conversion coefficient were calculated and provided. The result was compared with conversion coefficients provided in ICRP publication 116 and it was observed that in general the UFH/NCI conversion coefficients values were below the reference values. Below 100 MeV the differences were much higher due to the differences in skin and breast dose coefficients. Conversion coefficients are very sensitive to differences in voxel size and organ position. Results for effective dose coefficients in standing and sitting postures of the phantom were also compared. Effective dose coefficients were around 18% higher in the standing posture especially below 100 MeV in AP and PA geometry. For lateral geometries and below 20 MeV, values in the sitting phantom were around 16% higher. In ISO and ROT geometries the differences were, for almost all energies, below 5% and 10% respectively.

Supplementary Material

Supplementary material can be found at RADIATION PROTECTION DOSIMETRY online.